Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Aug 4;4:5941. doi: 10.1038/srep05941

Light-induced vibration in the hearing organ

Tianying Ren 1,a, Wenxuan He 1, Yizeng Li 2, Karl Grosh 2,3, Anders Fridberger 4,5
PMCID: PMC4120310  PMID: 25087606

Abstract

The exceptional sensitivity of mammalian hearing organs is attributed to an active process, where force produced by sensory cells boost sound-induced vibrations, making soft sounds audible. This process is thought to be local, with each section of the hearing organ capable of amplifying sound-evoked movement, and nearly instantaneous, since amplification can work for sounds at frequencies up to 100 kHz in some species. To test these fundamental precepts, we developed a method for focally stimulating the living hearing organ with light. Light pulses caused intense and highly damped mechanical responses followed by traveling waves that developed with considerable delay. The delayed response was identical to movements evoked by click-like sounds. This shows that the active process is neither local nor instantaneous, but requires mechanical waves traveling from the cochlear base toward its apex. A physiologically-based mathematical model shows that such waves engage the active process, enhancing hearing sensitivity.

Speech, music, and other sounds can be perceived after the excitation of auditory sensory hair cells. These cells are stimulated by sound-evoked waves that travel along the basilar membrane1. Depending on the frequencies of the sound that impinges on the eardrum, these waves peak at different locations along the length of the cochlea2. The cochlea can therefore be regarded as a mechanical frequency analyzer that decomposes the acoustical stimulus into its component frequencies. As a result, humans can perceive very small frequency changes, while retaining a sensitivity limited only by the thermal noise of the hair cell transduction3,4.

The mechanical and biophysical mechanisms that underlie the remarkable frequency resolving capacity and sensitivity of the auditory system remain incompletely described5. As sound-induced vibration propagates along the basilar membrane, it forms a peak at a location that depends on the health of the cochlea as well as the frequency and amplitude of the stimulus. The classical model idealization of the cochlea is as a series of damped resonators, whose resonant frequencies vary along the cochlear partition and are coupled mainly through the inner ear fluids1,6. More sophisticated mathematical models7,8,9,10 include the fundamental hypothesis that frequency analysis and sensitivity is enhanced by mechanical forces generated by the outer hair cells5,11,12,13,14,15,16,17,18,19. These forces are assumed to modulate the sound-evoked motion of each individual segment of the cochlear partition. Because outer hair cells can generate forces at sound frequencies up to 100 kHz20,21, this local active process is commonly thought to be operational within microseconds. In this work, we investigated the time course of the active process in the cochlea through a set of experiments and a mathematical model that includes active processes.

To determine the delay of the cochlear amplifier, one must devise a way to locally stimulate the basilar membrane when the active process is functional. To this date, the only means of exciting the sensitive cochlea for mechanical measurements were to use sound22,23,24,25,26 or electrical currents27,28,29; in either case, a focal force directly applied on the active cochlear partition is impossible. Our method (Figure 1) relies on forces that develop as photons interact with matter. Absorption of photons causes rapid local heating30,31,32, which is followed by cooling when the light goes off. This leads to a transient pressure change33 and a local force that acts on the basilar membrane. We show that such a local stimulus does not immediately trigger effective force production by the outer hair cells. Such force production only occurs when waves travel slowly from the base of the cochlea toward the apex. The modeling analysis suggests that the amplified response results from a tightly coordinated multi-cellular process that operates with a delay caused by the travel time of mechanical waves on the basilar membrane.

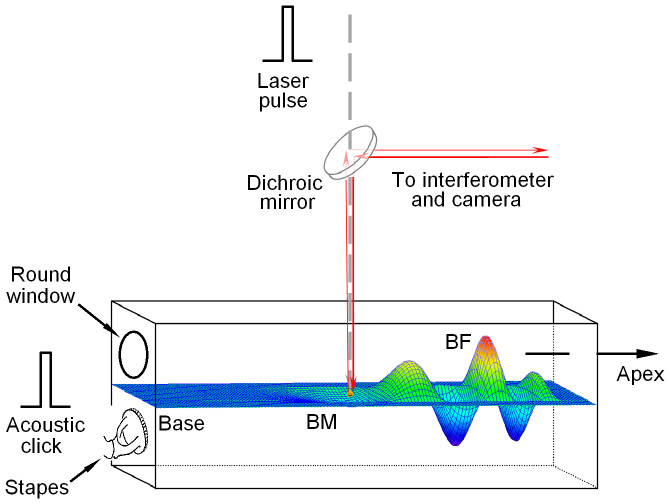
Figure 1. Diagram of the experimental setup.

Figure 1

Open in a new tab

Infrared laser pulses were focused on the basilar membrane (BM) or on a bead on the BM in the basal turn of the cochlea. Acoustical clicks were delivered to the external ear canal, which vibrated the stapes and resulted in the BM vibration. The BM vibration was measured by focusing the object beam from a laser interferometer on the reflective bead. Magnitude and phase of the vibration were determined by detecting Doppler frequency shift of the light reflected from the bead. BF: best frequency.

Results

To determine the cochlear partition's response to a local force stimulus, Mongolian gerbils were anesthetized and surgically prepared for recording the basilar membrane vibration2,34,35. Recordings were performed with a scanning heterodyne laser interferometer from the basal turn of the cochlea that responds optimally to sounds at frequencies ~13–16 kHz. In each animal, we first verified that compressive nonlinearity and sound-evoked responses to low-level tones were present, as expected in a sensitive cochlea36. Then, 30-μs infrared laser pulses were aimed on a gold-coated glass bead, which was placed on the basilar membrane. Upon laser excitation, the upper surface of the bead moved toward the laser beam and then returned to its equilibrium position as the light turned off (Figure 2a). This polarity of motion is consistent with thermal expansion of the excited bead and tissues. Following this initial spike of movement were physiologically vulnerable, gradually increasing wavelets that peaked after about 0.5 ms and then decayed. The frequency content of these wavelets increased rapidly over time (Figure 2a, lower panel). All eight sensitive preparations in this report showed initial peaks and delayed wavelet responses when laser pulses and measurement point were collocated.

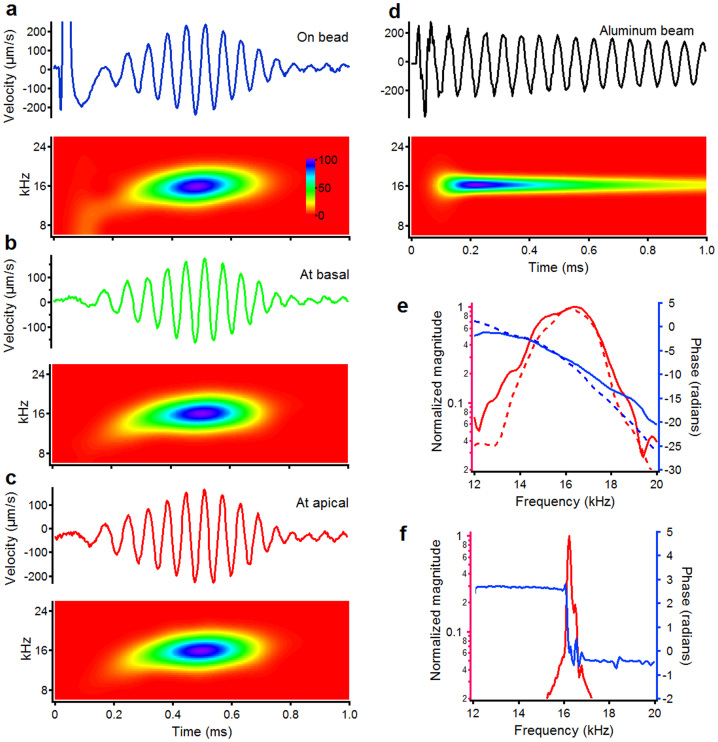
Figure 2. Laser pulse-induced basilar membrane vibrations and response from a simple resonator.

Figure 2

Open in a new tab

(a) Time waveform of the BM response to laser pulses (15 μJ/pulse) focused on a glass bead shows a periodic oscillation with a gradual onset and offset. The spectrogram shows that the instantaneous frequency of the ringing response increases with time. (b, c) BM responses to laser pulses focused on a basal (b) or apical (c) location ~50 μm from the bead are similar to those in panel a. (d), In contrast to panels a–c, the vibration from an aluminum beam shows instantaneous long-lasting periodic oscillation at a resonant frequency. (e) Magnitude and phase spectra of laser pulse-induced BM ringing response (red and blue solid lines) are similar to those of 30-dB SPL swept tone-induced responses (red and blue dashed lines). (f) Magnitude and phase spectra of the resonant response (red and blue line) show a sharp peak and ~3.14-radians phase shift at the resonant frequency. Data presented in panels a–c were collected from one cochlea.

Then, the laser pulse was focused 50 μm closer to the base of the cochlear partition, while maintaining the response measurement spot at the original location. Under this condition, the initial spike of motion was nearly extinguished (Figure 2b). Apart from the change in the initial movement, the wavelets had nearly identical delay and temporal content (compare Figure 2a and b). Spectrograms were also unchanged and displayed the same upward frequency glide (Figure 2b, lower panel). Finally, the excitation location was moved 50 μm closer to the apex of the cochlea (Figure 2c). Again, apart from the initial movement, this did not alter the vibrations at the measurement site, which continued to show a delayed response with an upward frequency glide indistinguishable from those measured at the two other excitation sites. Cross-correlation analysis revealed no measureable time lag among the three responses in the same animal. Hence, with the exception of the initial spike, a 100-μm change of the excitation location did not alter the delayed response. According to the group velocity of the traveling wave at the best frequency near the measured location (~3 m/s), ~33-μs delay is expected if a backward traveling wave was responsible for the reverse transmission. In contrast to the basilar membrane responses, a simple and lightly damped resonant system, an aluminum beam, displayed its maximum vibration amplitude immediately after the light pulse and frequency glides were absent (Figure 2d).

The magnitude spectrum of the laser pulse-induced responses of the basilar membrane revealed a peak centered at ~16 kHz (Figure 2e; red solid line, left scale), and a rapid phase decrease with frequency (blue solid line, right scale). The shapes of the magnitude and phase spectra were similar to those of sound-evoked motions at a stimulus level of 30 dB SPL (dashed lines). In both cases, the responses were typical for a forward traveling wave37. In contrast, the magnitude and phase spectra of the aluminum beam vibration were very different (Figure 2f) in which the sharpness of tuning was higher and the phase underwent an abrupt shift only near the resonance frequency.

When the power of the laser pulse was attenuated, the magnitude of the local stimulus decreased and a change in the mechanical response occurred (Figure 3a). At the pulse power of 15 μJ/pulse, a rapid initial movement was followed by oscillations that peaked at ~0.4 ms. As the power of the laser pulse decreased, the responses of the basilar membrane were essentially amplitude-scaled replicas of one another. These data are consistent with the known near-linear behavior of the basilar membrane vibration at low sound pressure levels34. As in Figure 2b and c, when laser pulses were focused on the basilar membrane 50 μm away from the measurement location on either side, the early motion spike was abolished but there was no substantial change in waveforms of the delayed response (Figure 3b and c).

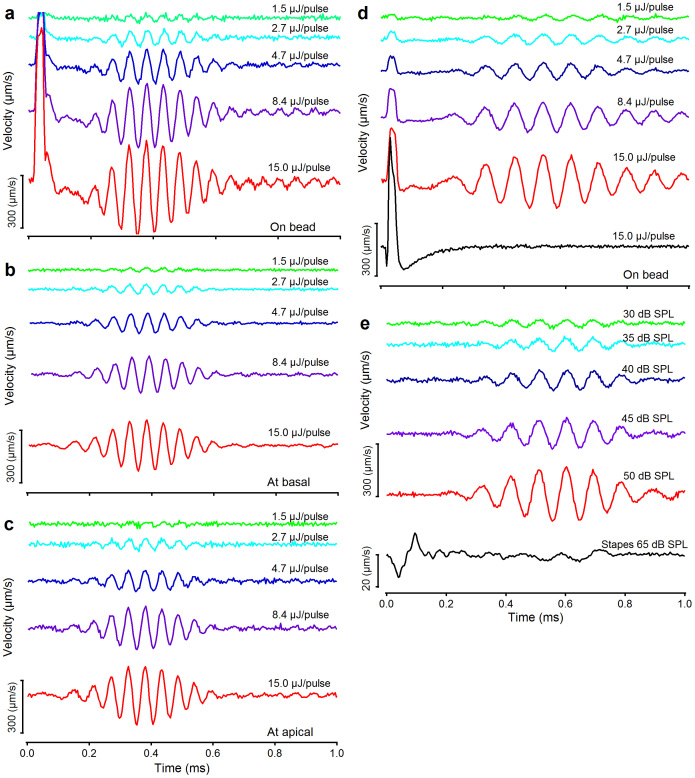
Figure 3. Laser pulse- and acoustic click-induced basilar membrane vibrations.

Figure 3

Open in a new tab

(a–c) Laser pulse-induced BM vibrations at optical power from 1.5 to 15 μJ/pulse by 5 dB per step. Data in panels a–c were collected when laser pulses were focused on the bead (a) or on a location ~50 μm basal (b) or apical (c) to the bead. Data in panels a–c are from one cochlea and those in panels d and e from another. Those animals are different from that for data in Figure 2. The light-induced ringing responses disappeared in the insensitive cochlea (black line in panel d). (e) Click-induced BM responses at different sound levels are similar to the laser pulse-induced ringing responses.

We also compared laser pulse-induced responses to those induced by acoustical clicks delivered by a speaker connected to the animal's ear canal. Laser pulses induced delayed wavelet response (Figure 3d) is similar in shape to those induced by an acoustical impulse (Figure 3e). By aligning the onset of stapes motion (lowermost record in Figure 3e) with the beginning of the laser pulse (Figure 3d) we found that the delay of the light-evoked response (0.451 ± 0.036 ms, n = 8) was similar to that of the acoustically induced response (0.45–0.47 ms in Figure 3e). This indicates the rapid transfer of energy from the spot of laser excitation toward the base of the cochlea, causing a physiologically vulnerable wave that travels forward, from the base of the cochlea toward its apex35,38.

The response was very different in the insensitive cochlea. In this case, the initial spike of motion remained but the delayed response was absent (black solid line in Figure 3d). Within 200 μs of the start of the pulse, there was a close correspondence between responses recorded in the sensitive ear and those recorded postmortem (black line in Figure 3d). This data confirm that the physiologically vulnerable force-generating mechanism of the outer hair cells11 was not involved in the immediate response of the basilar membrane to laser pulses. The death of the animal abolished all the later components of the response, demonstrating that force production of outer hair cells is important for the slowly developed wavelet observed in the sensitive cochleae.

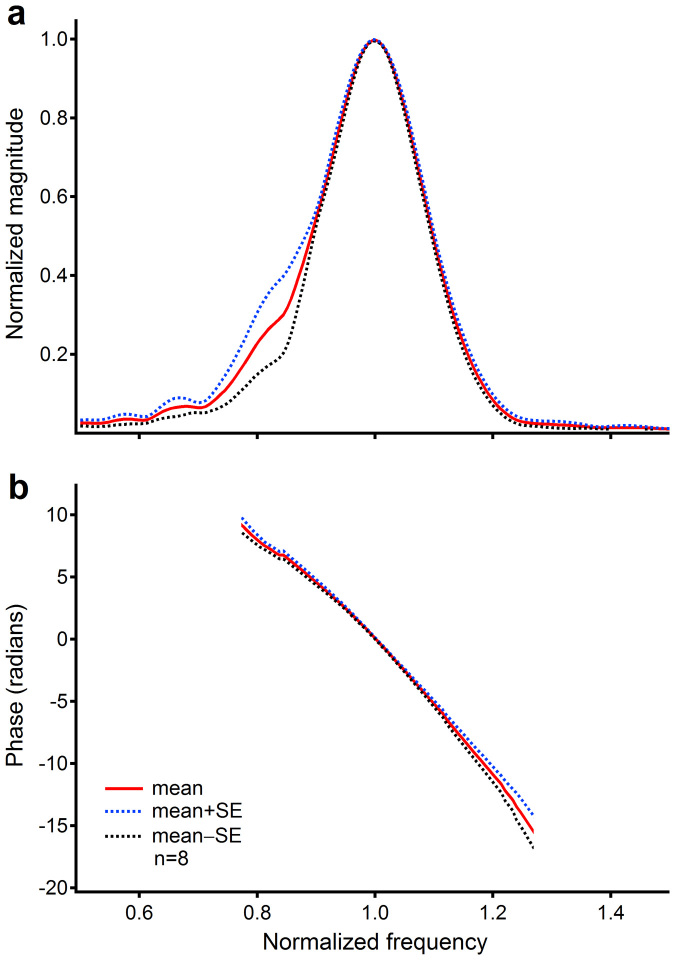
The waveforms between 0.1 and 1.0 ms in Figures 2a–c, 3a–c, and 3d from three different gerbils indicate that laser pulse-induced delayed basilar membrane response is similar across animals. To further show this similarity, the magnitude and phase spectra of the delayed responses induced by 15.0-μJ laser pulses measured from eight gerbils are presented in Figure 4. In order to compare data across animals and to obtain means and standard errors, the frequency and magnitude were normalized to the peak frequency and the peak magnitude respectively. The phase curves were shifted vertically to zero at frequency 1.0. The mean magnitude curve in panel a shows a sharply tuned peak centered at normalized frequency 1.0. The mean phase curve in panel b indicates that phase decreased with frequency. Small magnitude and phase standard errors in panels a and b demonstrate high repeatability of the measurement. Thus, grouped data in Figure 4 confirm that similar laser pulse-induced delayed responses exist in all sensitive cochleae.

Figure 4. Magnitude and phase spectra of laser pulse-induced delayed responses.

Figure 4

Open in a new tab

(a) The mean magnitude curve (the solid red line) shows a sharply tuned peak centered at normalized frequency 1.0. (b) The mean phase curve (the red solid line) indicates that phase decreased with frequency. Data were collected at 15-μJ pulse power from 8 animals. The frequency and magnitude were normalized to the peak frequency and the peak magnitude respectively. The phase curves were shifted vertically to zero at frequency 1.0. SE: standard error.

Discussion

To test the hypothesis that a local stimulus can induce an instant active response of the cochlear partition, a precisely defined local stimulus is needed. Such a stimulus cannot rely on direct mechanical contact, which would instantly disrupt sensory cell function. Electrical stimulation suffers from the large space constant of the cochlear ducts, which causes the stimulus to reach many hair cells simultaneously26. Similar problems are evident in the case of acoustical stimuli. Our method used intense but brief pulses of infrared light that generated a pressure pulse, but did not disrupt the sensitivity of the cochlea. Upon absorption by tissue at the focal point, the laser pulse heated the tissues and caused a pressure impulse31,39. This local stimulus is indicated by the initial spike response when the laser pulse was focused on the measured location (Figures 2a, 3a, and 3d). The absence of the initial spike when the excitation and measurements sites were separated (Figures 2b, 2c, 3b, and 3c) indicates that the mechanical stimulus was a local one. A distributed initial vibration would have caused an early peak even after separation of the measurement and excitation locations.

One may wonder whether the laser pulse-induced basilar membrane responses resulted from neural activation. It has been demonstrated that optical stimulation with an infrared (1,844–1,869 nm) laser elicits compound action potentials similar to responses to electrical stimulation40,41. Because the laser power used in the current study (1.5–15 μJ/pulse with peak power 50–500 mW and average power 0.0015–0.015 mW) is much smaller and the laser wavelength is shorter than those used in reported experiments, optically-induced neural activation likely was not significantly involved in the present experiment.

Mathematical models were developed to understand the laser pulse-induced basilar membrane vibration. In many cochlear models, such as one-dimensional models6, only non-symmetric fluid modes, which results in the cochlear slow or traveling wave, are admitted. We used this common approximation in conjunction with a point force applied to the basilar membrane to simulate the excitation due to the laser light. Our model was a modified version of a previous model42 with the parameters from Table 1. Under impulse excitation, the model predicted an immediate transient response followed by a wavelet that arrived with twice the delay observed experimentally. There was no combination of parameters that allowed the model to predict a delay similar to those in Figure 2a–c and Figure 3a–d. Hence a more sophisticated model is needed.

Table 1. Parameters for the cochlear model (x is in meters). BM: basilar membrane. OHC: outer hair cells. TM: tectorial membrane. HB: hair bundle. RL: reticular lamina.

Parameters Values
β (40°C) 385 × 10−6/K
cp (40°C) 4.178 J/gK
α 0.3
Duct height 0.5 mm
BM length 11 mm
OHC length 25 μm (base) to 65 μm (apex)
TM radial length [Ref. 45] 87 μm (base) to 180 μm (apex)
Effective TM cross-sectional mass 1.08 × 10−6e84.1x kg/m
Electromechanical coupling coefficient −0.122 (base) to −0.152 (apex) N/m/mV
Oval window stiffness 1.8 × 108 N/m3
Round window stiffness 1.8 × 107 N/m3
TM bending stiffness 1.233 × 104e−672.7x N/m2
TM shear stiffness 1.233 × 104e−672.7x N/m2
HB stiffness 1.879 × 104e−706.4x N/m2
RL stiffness 4.008 × 103e−706.4x N/m2
OHC stiffness 4.008 × 103e−706.4x N/m2
TM longitudinal shear modulus 5 kPa
TM longitudinal shear damping 0.075 Pa s
Mechanoelectrical transducer sensitivity 3.6016 × (LHB0/LHB)e−252.3x S/rad/m
Open in a new tab

In order to include all the relevant physical effects, we relaxed the restriction that only non-symmetric waves were allowed in the model by admitting the symmetric solutions as well. These symmetric modes typically represent fast compressional waves in the fluid. The excitation to this three-dimensional cochlear model42 consisted of two point heat sources, above and below the basilar membrane, with slightly different amplitudes (see the cochlear model in Methods). The amplitude of the excitation was estimated from the laser light heat absorption30. The early response of the model resembled the experimental results in several ways. The initial brief response was dominated by a large transient at the location of the heating sources (Figure 5a). Just as in the experiments, this large initial response was not seen when the heat sources were 50 μm away from the observation position (Figure 5b and c). Secondly, in this mathematical model including the cochlear active process, the delayed wavelet response was seen, just as in experimental data. Simulation results from acoustical stimulation (Figure 5d) show that the group delay of laser pulse-induced response (Figure 5a–c) was the same as the acoustical click-induced response, which is consistent with the experimental data in Figure 3d and e. Both experimental and modeling results indicate that energy is propagated rapidly from the location of the heating source to the base of the cochlea, subsequently generating a forward traveling wave. We also performed simulations when outer hair cell force production was turned off. In this case, the initial highly damped transient remained while the delayed wavelet response was eliminated, just as in the post-mortem data as shown in Figure 3d. The model predicts that the delayed response is mediated by outer hair cell motility.

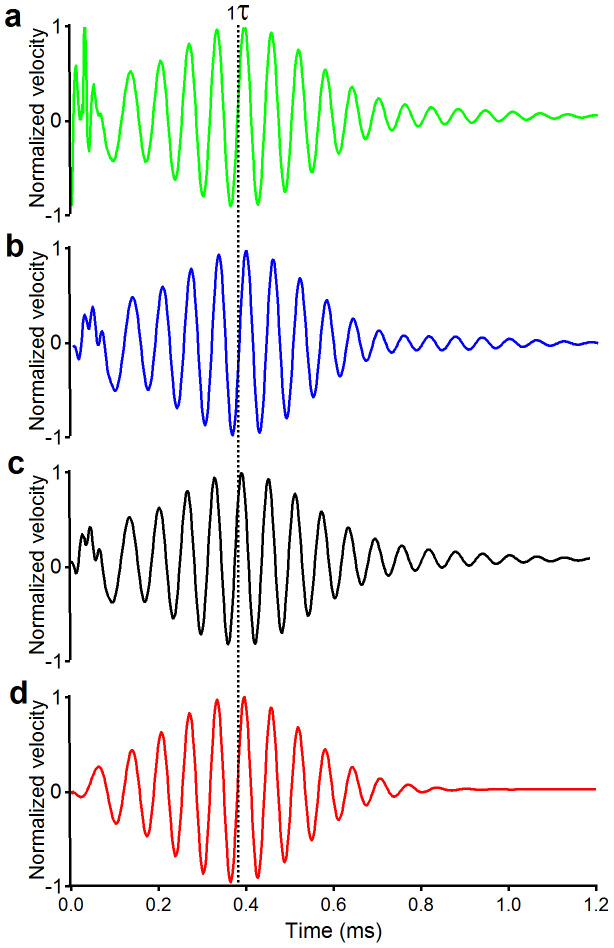
Figure 5. A three dimensional model of the cochlea predicts the correct delays.

Figure 5

Open in a new tab

(a–c) The result from a cochlear model, which allows fast transmission of energy in the cochlear fluid. Due to negligible delay resulted from the fast wave, the ringing response reaches its peak at a time equal to the cochlear traveling wave delay from the stapes to the best-frequency location (τ). Laser pulse was focused on the bead (a), at a location ~50 μm basal (b) or apical (c) to the bead. (d) Predicted acoustical impulse-induced response. Except for the lack of the initial peak, the response reaches the maximum at time 1τ and is very similar to the laser-induced response.

Both the experiment and the model present a surprising result: the large initial response generated from the laser pulses does not result in an immediately amplified response. Hence, the effective engagement of the active mechanism that enhances the response of the cochlea to low-level sounds cannot be initiated instantly by a local point force applied on the basilar membrane. For either light or acoustical stimulation, the generation of an enhanced response (Figure 3d and e) requires the presence of a traveling wave. This wave coordinates the electromechanical response of the outer hair cells along the length of the basilar membrane to enhance hearing sensitivity. In retrospect, this is an appropriate design for processing external sounds that travel from the base of the cochlea toward the apex.

Methods

Generation and delivery of laser pulses

An infrared laser diode (SDL-6380-A, JDS Uniphase Corporation, San Jose, CA) was used to generate laser pulses at wavelength of 930 nm. A 30-μs positive electrical pulse was used to control the laser power, which was limited to 0.5 W in front of the objective lens. There was no detectable sound generated at any laser pulse levels (from 1.5 to 15 μJ/pulse) through optoacoustic mechanism43 in the air, likely due to relatively short wavelength and low laser power. A dichroic mirror was used to introduce the infrared laser beam into the optical path of the laser interferometer and to focus laser pulses on the basilar membrane through a 20× objective lens (NA, 0.42) (gray dashed line in Figure 1). The position of the laser focal spot was changed by moving the collimating lens with an x-y translation stage, while the focal spot of the object beam of the laser interferometer (solid red lines in Figure 1) was unchanged.

Measurement of the basilar membrane vibration

Twenty-eight healthy young Mongolian gerbils (40–80 g) with normal hearing were used in this study. Animal preparation and surgical procedures were as previously described2,35. The animal use protocol was approved by the Oregon Health & Science University Institutional Animal Care and Use Committee. Laser pulse- and acoustic click-induced basilar membrane vibrations were measured using a scanning heterodyne laser interferometer34,37. The voltage output from the laser interferometer controller was proportional to the vibration velocity of a gold-coated bead, which can reliably track the basilar membrane vibration44. The stapes vibration was also measured using the same interferometer34,37.

Data reported in the Result section are from 8 among 28 gerbils. Twenty animals were excluded from this report due to either high-frequency hearing loss or poor transparency of the inner ear fluids caused by invasive surgery and bleeding. The results presented in Figures 2, 3a–c, and 3d and e are from 3 different gerbils and those in Figure 4 are from all 8 animals showing sensitive responses.

Since the each segment of the cochlear partition has been thought to function as a resonator, the laser pulse-induced response from a simple resonator was also measured. The resonator was made of a ~0.1-mm thick ~1-mm wide aluminum beam. The aluminum beam was held using custom-made forceps attached to a 3-dimensional positioning system. The resonant frequency was varied by changing the length from the holding point to the tip of the strip, where the laser pulse was focused.

Signal generation and data acquisition

A 30-μs rectangular pulse was used to control the laser-diode current and to drive a speaker. The laser pulse or acoustic click was presented at the rate of 10 times per second. The signal from the interferometer controller was averaged 10–200 times depending on the signal-to-noise ratio. Frequency spectra and spectrograms of the averaged signal were obtained through the Wigner transform using Igor Pro software (Wavemetrics, Inc. Lake Oswego, OR). The delay of click-evoked vibration was the time interval between the onset of motion at the stapes and the basilar membrane. Similarly, the delay of laser pulse-induced basilar membrane vibration was calculated as the time difference between the onset of the laser pulse and the basilar membrane vibration. The peak time of the basilar membrane vibration was determined by the maximum of the signal envelope obtained through the Hilbert transform using Igor Pro software.

The cochlear model

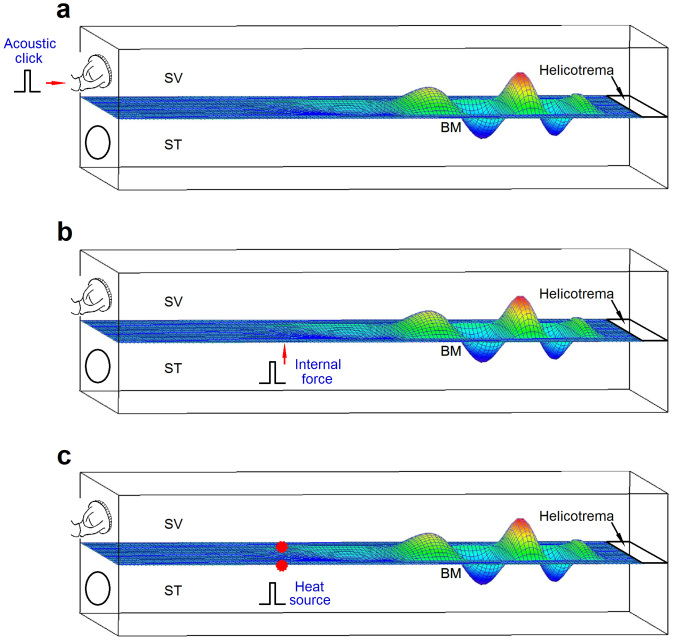
The mathematical model was developed from a previous physiologically based linear model that couples the mechanical, electric, and acoustic fields of the cochlea10,42,45. The acoustic click was modeled as an impulse force on the stapes or the oval window (Figure 6a). The internal force was modeled as an impulse force on the basilar membrane42 at a single location (Figure 6b). Laser light absorption was modeled as a heating source according to the linear acoustics equations30. Under such localized laser heating (Figure 6c), the governing equation for the intracochlear fluid pressure, p, is

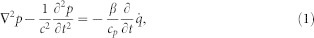graphic file with name srep05941-m1.jpg

where c is the speed of sound in the cochlear fluid. β and cp are, respectively, the coefficient of thermal expansion and the specific heat capacity at constant pressure of the fluid. Inline graphic is the heat absorbed by the fluid per unit time and per unit volume. We approximate the heating from the laser pulses as a boxcar function which can be written as

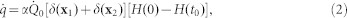graphic file with name srep05941-m2.jpg

where 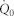Inline graphic is the power of the laser (0.5 W), α is the estimated fraction of power absorbed by the fluid, x1 and x2 are the positions vector of the laser focal heating (located just above and below the BM) at a distance of 0.245 mm, 0.25 mm, and 0.255 mm away from the base (depending on the focal point of the laser), t0 is the duration of the laser pulse (30 μs), and H(t) is the Heaviside function in time. The Dirac delta functions δ(X1) and δ(X2) have the dimension of inverse volume. Hence, Equation (1) can be rewritten as

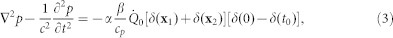graphic file with name srep05941-m3.jpg

where δ(t) has the dimension of inverse time. Time harmonic solutions of the form exp(−iωt) are sought. Equation (3) can be written in the frequency domain as

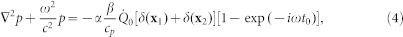graphic file with name srep05941-m4.jpg

which is the governing equation for the intracochlear fluid pressure with the existence of a localized heat source, P is the Fourier transform or frequency domain representation of the pressure. The right-hand side of Equation (4) is the forcing term corresponding to the heat source shown in Figure 5c. To represent the asymmetric heat absorption below and above the basilar membrane, an absorption ratio of 0.53:0.47 is used. For an α value of 0.3, then 30% of the power is absorbed as heat.

Figure 6. Schematics of the cochlear model and three stimulation methods.

Figure 6

Open in a new tab

SV: scala vestibuli. ST: scala tympani. BM: basilar membrane (a) Acoustic impulse stimulation through the oval window. (b) An internal impulse force simulating the force generated by the laser pulses focused on the bead. (c) Internal heat sources above and below the BM when laser pulses were focused on a basal or apical location.

A model for gerbils was developed and used for the simulation. The parameters for gerbils were derived from those for guinea pigs10,42 based on the length of the basilar membrane. The scaled or adjusted parameters from the guinea pig model are listed in Table 1. Impulse responses were obtained through Fourier Transformation of the data in the frequency domain to the time domain.

Author Contributions

T.R., W.H. and A.F. designed the study; T.R. and W.H. performed the experiments; Y.L. and K.G. developed the theoretical model. T.R., W.H., Y.L., K.G. and A.F. analyzed the data, and wrote the paper.

Acknowledgments

This work was supported by NIH grants DC-004554 (T.R. and W.H.), DC-004084 (K.G. and Y.L.), the Swedish Research Council (K2011-63X-14061-11-39 to A.F.), the Research Council for Health, Working Life and Welfare (2006–1526, A.F.), Hörselskadades Riksförbund (A.F.) and the Tysta skolan foundation (A.F).

References

  1. von Békésy G. Travelling waves as frequency analysers in the cochlea. Nature 225, 1207–1209 (1970). [DOI] [PubMed] [Google Scholar]
  2. Ren T. Longitudinal pattern of basilar membrane vibration in the sensitive cochlea. Proc. Natl. Acad. Sci. USA. 99, 17101–17106 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hudspeth A. J. & Corey D. P. Sensitivity, polarity, and conductance change in the response of vertebrate hair cells to controlled mechanical stimuli. Proc. Natl. Acad. Sci. USA. 74, 2407–2411 (1977). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen F. et al. A differentially amplified motion in the ear for near-threshold sound detection. Nat. Neurosci. 14, 770–774 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ashmore J. et al. The remarkable cochlear amplifier. Hear. Res. 266, 1–17 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Zwislocki J. J. & Kletsky E. J. Tectorial membrane: a possible effect on frequency analysis in the cochlea. Science 204, 639–641 (1979). [DOI] [PubMed] [Google Scholar]
  7. Mammano F. & Nobili R. Biophysics of the cochlea: linear approximation. J. Acoust. Soc. Am. 93, 3320–3332 (1993). [DOI] [PubMed] [Google Scholar]
  8. Chadwick R. S., Dimitriadis E. K. & Iwasa K. H. Active control of waves in a cochlear model with subpartitions. Proc. Natl. Acad. Sci. USA. 93, 2564–2569 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Neely S. T. & Kim D. O. An active cochlear model showing sharp tuning and high sensitivity. Hear. Res. 9, 123–130 (1983). [DOI] [PubMed] [Google Scholar]
  10. Meaud J. & Grosh K. The effect of tectorial membrane and basilar membrane longitudinal coupling in cochlear mechanics. J. Acoust. Soc. Am. 127, 1411–1421 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Brownell W. E., Bader C. R., Bertrand D. & de Ribaupierre Y. Evoked mechanical responses of isolated cochlear outer hair cells. Science 227, 194–196 (1985). [DOI] [PubMed] [Google Scholar]
  12. Dallos P. The active cochlea. J. Neurosci. 12, 4575–4585 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Santos-Sacchi J. Asymmetry in voltage-dependent movements of isolated outer hair cells from the organ of Corti. J. Neurosci. 9, 2954–2962 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. He D. Z. & Dallos P. Somatic stiffness of cochlear outer hair cells is voltage-dependent. Proc. Natl. Acad. Sci. USA. 96, 8223–8228 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Liberman M. C. et al. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature 419, 300–304 (2002). [DOI] [PubMed] [Google Scholar]
  16. Fettiplace R. & Hackney C. M. The sensory and motor roles of auditory hair cells. Nat. Rev. Neurosci. 7, 19–29 (2006). [DOI] [PubMed] [Google Scholar]
  17. Ricci A. Active hair bundle movements and the cochlear amplifier. J. Am. Acad. Audiol. 14, 325–338 (2003). [PubMed] [Google Scholar]
  18. Hudspeth A. J. Making an effort to listen: mechanical amplification in the ear. Neuron 59, 530–545 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sotomayor M., Weihofen W. A., Gaudet R. & Corey D. P. Structure of a force-conveying cadherin bond essential for inner-ear mechanotransduction. Nature 492, 128–132 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Nowotny M. & Gummer A. W. Nanomechanics of the subtectorial space caused by electromechanics of cochlear outer hair cells. Proc. Natl. Acad. Sci. USA. 103, 2120–2125 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ashmore J. Cochlear outer hair cell motility. Physiological Reviews 88, 173–210 (2008). [DOI] [PubMed] [Google Scholar]
  22. Rhode W. S. Observations of the vibration of the basilar membrane in squirrel monkeys using the Mossbauer technique. J. Acoust. Soc. Am. 49, 1218–1231 (1971). [DOI] [PubMed] [Google Scholar]
  23. Ruggero M. A. & Rich N. C. Application of a commercially-manufactured Doppler-shift laser velocimeter to the measurement of basilar-membrane vibration. Hear. Res. 51, 215–230 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Russell I. J. et al. Sharpened cochlear tuning in a mouse with a genetically modified tectorial membrane. Nat. Neurosci. 10, 215–223 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Cooper N. P. & Rhode W. S. Basilar membrane tonotopicity in the hook region of the cat cochlea. Hear. Res. 63, 191–196 (1992). [DOI] [PubMed] [Google Scholar]
  26. Fridberger A. et al. Organ of corti potentials and the motion of the basilar membrane. J. Neurosci. 24, 10057–10063 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hubbard A. E. & Mountain D. C. Alternating current delivered into the scala media alters sound pressure at the eardrum. Science 222, 510–512 (1982). [DOI] [PubMed] [Google Scholar]
  28. Yates G. K. & Kirk D. L. Cochlear electrically evoked emissions modulated by mechanical transduction channels. J. Neurosci. 18, 1996–2003 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ren T. & Nuttall A. L. Extracochlear electrically evoked otoacoustic emissions: a model for in vivo assessment of outer hair cell electromotility. Hear. Res. 92, 178–183 (1995). [DOI] [PubMed] [Google Scholar]
  30. Temkin S. Elements of Acoustics. (Acoustical Society of America, 2001). [Google Scholar]
  31. Wang L. V. & Hu S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science 335, 1458–1462 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Fridberger A. & Ren T. Local mechanical stimulation of the hearing organ by laser irradiation. Neuroreport 17, 33–37 (2006). [DOI] [PubMed] [Google Scholar]
  33. Zhang K. Y. et al. Optoacoustic induced vibrations within the inner ear. Optics express 17, 23037–23043 (2009). [DOI] [PubMed] [Google Scholar]
  34. Ren T., He W. & Gillespie P. G. Measurement of cochlear power gain in the sensitive gerbil ear. Nat. Commun. 2, 216 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ren T. Reverse propagation of sound in the gerbil cochlea. Nat. Neurosci. 7, 333–334 (2004). [DOI] [PubMed] [Google Scholar]
  36. Ren T., He W. & Porsov E. Localization of the cochlear amplifier in living sensitive ears. PLoS One 6, e20149 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. He W., Fridberger A., Porsov E., Grosh K. & Ren T. Reverse wave propagation in the cochlea. Proc. Natl. Acad. Sci. USA. 105, 2729–2733 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. He W. & Ren T. Basilar membrane vibration is not involved in the reverse propagation of otoacoustic emissions. Sci. Rep. 3, 1874 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rosencwaig A. Photoacoustic spectroscopy of biological materials. Science 181, 657–658 (1973). [DOI] [PubMed] [Google Scholar]
  40. Richter C. P. et al. Optical stimulation of auditory neurons: effects of acute and chronic deafening. Hear. Res. 242, 42–51 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shapiro M. G., Homma K., Villarreal S., Richter C. P. & Bezanilla F. Infrared light excites cells by changing their electrical capacitance. Nat. Commun. 3, 736 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Li Y. & Grosh K. Direction of wave propagation in the cochlea for internally excited basilar membrane. J. Acoust. Soc. Am. 131, 4710–4721 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Teudt I. U., Maier H., Richter C. P. & Kral A. Acoustic events and “optophonic” cochlear responses induced by pulsed near-infrared laser. IEEE Trans. Biomed. Eng. 58, 1648–1655 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Cooper N. P. Vibration of beads placed on the basilar membrane in the basal turn of the cochlea. J. Acoust. Soc. Am. 106, L59–64 (1999). [DOI] [PubMed] [Google Scholar]
  45. Ramamoorthy S., Deo N. V. & Grosh K. A mechano-electro-acoustical model for the cochlea: response to acoustic stimuli. J. Acoust. Soc. Am. 121, 2758–2773 (2007). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES