Benchmark Study of the SCC-DFTB Approach for a Biomolecular Proton Channel

Abstract

The self-consistent charge density functional tight binding (SCC-DFTB) method has been increasingly applied to study proton transport (PT) in biological environments. However, recent studies revealing some significant limitations of SCC-DFTB for proton and hydroxide solvation and transport in bulk aqueous systems call into question its accuracy for simulating PT in biological systems. The current work benchmarks the SCC-DFTB/MM method against more accurate DFT/MM by simulating PT in a synthetic leucine-serine channel (LS2), which emulates the structure and function of biomolecular proton channels. It is observed that SCC-DFTB/MM produces over-coordinated and less structured pore water, an over-coordinated excess proton, weak hydrogen bonds around the excess proton charge defect and qualitatively different PT dynamics. Similar issues are demonstrated for PT in a carbon nanotube, indicating that the inaccuracies found for SCC-DFTB are not due to the point charge based QM/MM electrostatic coupling scheme, but rather to the approximations of the semiempirical method itself. The results presented in this work highlight the limitations of the present form of the SCC-DFTB/MM approach for simulating PT processes in biological protein or channel-like environments, while providing benchmark results that may lead to an improvement of the underlying method.

Introduction

Calculations using ab initio quantum mechanical (QM) methods can in principle be quite accurate for describing various kinds of systems at the atomic level. QM methods are also well suited for describing chemical reactions in which bond breaking and formation occur. However, the cost of the QM calculations limits not only the system size but also the sampling that is required to calculate statistically meaningful quantities for condensed phase systems, such as free energies of binding or a potential of mean force (PMF) for solute or ion transport. Therefore, it is sometimes necessary to develop approximations to ab initio QM methods that offer a balance between accuracy and computational efficiency. The self-consistent charge density functional tight binding (SCC-DFTB) method¹ is a fast semi-empirical QM algorithm that has become popular in recent years for simulating chemical processes in biomolecular systems due to the high degree of interest in studying such systems.² The SCC-DFTB method is derived from density functional theory (DFT) by approximation and parameterization of multi-center electron integrals.¹ The computational speed gained by these approximations can be 2-3 orders of magnitude compared to more accurate and “first principles” standard DFT.³ While the SCCDFTB approach is understandably popular, the method has been shown to have substantial limitations for predicting structural, energetic and dynamic properties of proton transport (PT)⁴ and hydroxide transport in bulk water.⁵ Despite recent SCC-DFTB developments,^{3,6, 7} these issues remain unresolved. The SCC-DFTB method was also, e.g., recently shown to poorly describe noncovalent interactions involving sulfur atoms.⁸ Given the increased use of quantum mechanics/molecular mechanics (QM/MM) with SCC-DFTB as the QM method (SCC-DFTB/MM) to study proton hydration and transport in biomolecular systems,^9-11 there is a need to benchmark its present level of accuracy and potential limitations in such environments.

The current work establishes a systematic benchmark of SCC-DFTB/MM method against arguably more accurate QM/MM methods that employ both generalized gradient approximation (GGA) level and hybrid-GGA level DFT theories for the QM calculation. The comparison is made in the context of condensed phase molecular dynamics (MD) simulations of PT in channel systems. All the methods under investigation have a comparable amount of sampling time, which has seldom been done to date. The synthetic leucine-serine channel (LS2, Figure 1)¹² is chosen as the simulation system. Although it is synthetic, LS2 possesses key features that are representative of proton channels in nature, such as high proton selectivity, a nonuniform pore radius along the channel axis, a hydrophilic pore due to pore-lining serine residues, and a macrodipole formed by parallel α helices.^12-15 In addition, it is small enough to enable sufficient sampling for the convergence of statistical quantities extracted from MD simulations, which is both essential for condensed phase analysis and computationally demanding for the higher level QM/MM approaches.

Figure 1.

LS2 channel system filled with a protonated water wire. The two red circles denote the regions where the excess proton CEC is restrained in the QM/MM simulations. The protein backbones and side chains are depicted as the ribbons and sticks, respectively. On the left is the scale of the channel along the z direction.

It has been argued⁶ that the conclusions drawn from previous SCC-DFTB benchmark studies of PT in bulk water⁴ may not be relevant to PT in the biological systems for two reasons: first, the charge delocalization of the excess protonic defect may be smaller in biological systems; and second, the pKa values of biological titratable groups may dominate PT energetics. However, in this work it is observed that the present ‘state-of-the-art’ SCC-DFTB method fails to reproduce important aspects of the more accurate DFT results in a channel environment. Furthermore, by also running simulations in a hydrophobic channel (a nanotube) it is shown that the inaccuracies of SCC-DFTB/MM are more related to the approximations of the semiempirical QM method itself, rather than to the approximations introduced by a simple point charge based QM/MM electrostatic coupling scheme.¹⁶ These combined results provide an important benchmark of the current SCC-DFTB/MM method that can help researchers to gauge the reliability of this approach for studying PT in realistic biomolecular systems. These results can also help underpin possible improvement of the method if in fact such an improvement is possible without resorting to an excessive degree of empiricism that would undermine the purpose of a QM approach in the first place.

Methodology

2.1 SCC-DFTB method

The SCC-DFTB method is derived by Taylor series expansion of the DFT Kohn-Sham energy in terms of the charge density fluctuations, and the Hamiltonian matrix elements are evaluated using a minimal basis set of pseudoatomic orbitals with a two-center approximation. The total energy for the full 3rd order SCC-DFTB method is expressed as:³

$$E_{total}^{SCC-DFTB}=\sum _{i\mu v}{c}_{\mu }^i{c}_{\mu }^i{H}_{\mu v}^0+E_{rep}+\frac{1}{2}\sum _{\alpha \beta }{\gamma }_{\alpha \beta }\Delta q_{\alpha }\Delta q_{\beta }+\frac{1}{3}\sum _{\alpha \beta }{\Gamma }_{\alpha \beta }\Delta q_{\alpha }^2\Delta q_{\beta }$$ Eq 1

where $H_{\mu v}^0$ are the Hamiltonian matrix elements and $c_{\mu }^i$ and $c_{\mu }^i$ are the wave function expansion coefficients, E_rep accounts for short-range repulsive term, and Δq_α and Δq_β are the charge fluctuation terms associated with atoms α and β, respectively. The γ_αβ function is determined by

$${\gamma }_{\alpha \beta }=\frac{1}{R_{\alpha \beta }}-S_{\alpha \beta }\times f_{\alpha \beta },f_{\alpha \beta }=\{\begin{array}{cc}\exp \left[-{\left(\frac{U_{\alpha }+U_{\beta }}{2}\right)}^{\zeta }{R}_{\alpha \beta }^2\right],\hfill & \text{if}(\alpha \text{or}\beta =\mathrm{H})\hfill \\ \text{or}\hfill & \hfill \\ 1,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ Eq 2

otherwise where S_αβ is an exponentially decaying short-range function. The damping function f_αβ is introduced to help describe hydrogen-bonding interactions, where U_α and U_β are the atomic Hubbard parameters related to the chemical hardness of atoms α and β, respectively. The parameter ζ is determined by fitting to hydrogen bonding energies for select clusters from higher-level QM calculations.¹⁷ The last term in eq 1 is a third order correction that was initially introduced with only the on-site third order term,¹⁷ but was recently implemented with the complete third-order term.³ The Γ_αβ describes derivatives of the γ function with respect to atomic charges. The introduction of this 3rd order correction is suggested to improve the description of charged systems.^{3, 17}

In ref ⁷ a new parameter set named 3OB was designed such that both the electronic and repulsive potential parameters (appearing in the first and second terms in eq 1, respectively) are optimized for full 3rd order SCC-DFTB calculations. In gas phase calculations this parameter set was shown to outperform the old MIO parameter set due to an improved geometry of nonbonded interactions and reduction of overbinding errors.⁷ In the present work, we benchmark the newest, full 3rd order SCC-DFTB method using the 3OB parameter set. The SCC-DFTB related parameters are taken from ref ⁷.

2.2 LS2 QM/MM simulation

The LS2 system (shown in Figure 1) was constructed using the same protocol as described in detail in ref ¹⁵. A reduced system was composed of the LS2 channel with pore waters inside and a 10 Å–thick layer of equilibrated water molecules on either side of the channel, but with the lipid bilayer surrounding LS2 removed. Two layers of virtual atoms were added at the position of lipid head groups to prevent water molecules from entering the membrane region (see Figure 1). The virtual atoms had zero charge, Lennard-Jones (LJ) parameters of σ = 1.781797Å and ε = 0.11 kcal/mol, and were hexagonally close-packed with spacing of 1.95 Å. The parameters of the virtual atoms were chosen to minimize their effect on the pore water, while preventing water molecules from leaking into the lipid bilayer region. To maintain the integrity of the LS2 channel structure, harmonic position restraints with force constants of 1000 kJ/mol/Ų were applied to the C_α atoms. These restraints were previously shown to maintain the channel geometry and pore water diffusion constants of the realistic composite system.¹⁵ The protein was described by the CHARMM22 force field^{18, 19} and the classical water molecules by the TIP3P²⁰ model modified for the CHARMM force field.

To equilibrate the system, initial velocities were assigned consistent with a temperature of 300 K that was then maintained with a Nosé-Hoover thermostat using a relaxation time constant of 0.1 ps for 10ns of constant NVT simulation. The integration time step was 1 fs. The cutoff radius for LJ interactions was 12 Å employing a switching function starting at 10 Å. The cutoff radius for real space electrostatic interactions was 12 Å and the long-range electrostatics were treated by Particle-Particle Particle-Mesh (PPPM) method ²¹ with an accuracy threshold of 10⁻⁴.

To set up a protonated water wire inside the LS2 channel, an excess proton was placed near one of the channel waters, forming a classical hydronium cation parameterized consistently with the MS-EVB3 model.²² A chloride counter ion was added to the bulk water region to maintain charge neutrality. A harmonic potential with a 4 kcal/mol/Ų force constant was applied to the hydronium oxygen atom to restrain its z coordinate around z = −6.5 Å, coinciding with a minimum in the previously calculated free energy profile for PT through the channel.¹³ The protonated system was equilibrated for 1ns at 300 K using the same settings as described above. All equilibration simulations were performed with the LAMMPS package (http://lammps.sandia.gov).²³

The last snapshot of the MS-EVB3 equilibration was used as the initial structure for the QM/MM simulation. For the unprotonated LS2 system, the QM region included all of the channel water molecules (22-25 water molecules). For the protonated system, the QM region included all channel water molecules plus the excess proton. For the DFT/MM setup, the QM box size was 12 Å × 12 Å × 32 Å, with the z direction aligned with the channel axis. A quadratic confining wall potential was used to restrain the QM atoms within the QM box, with a wall skin thickness of 1 Å × 1 Å × 2.5 Å. The QM box size was chosen such that the quadratic wall potential did not affect the QM atoms for the majority of the simulation. The QM region was treated with several different density functionals under the Gaussian plane wave (GPW) scheme.²⁴ Two generalized gradient approximation (GGA) level exchange-correlation functionals were employed: the BLYP functional^{25, 26} with a empirical dispersion corrections²⁷ and the HCTH/120 functional²⁸ (hereafter denoted as BLYP-D and HCTH, respectively). In addition, the hybrid GGA level DFT method B3LYP²⁹ with a dispersion correction²⁷ (B3LYP-D) was employed to improve accuracy. For BLYP-D and HCTH, the Goedecker-Teter-Hutter (GTH) pseudopotentials³⁰ were used and the Kohn-Sham orbitals were expanded in the Gaussian TZV2P basis set. The electron density was expanded by auxiliary plane wave basis set up to 300 Ry. For B3LYP-D, GTH pseudopotentials for BLYP were used, and the wavefunction was expanded in the Gaussian DZVP basis set with an energy cutoff of 300 Ry for the plane wave basis set. The Gaussian Expansion of the Electrostatic Potential (GEEP) scheme was used to treat the QM/MM electrostatic coupling with periodic boundary conditions (PBCs),^{31, 32} and the spurious QM/QM periodic image interactions were decoupled as described in ref ³³. The QM/MM van der Waals (vdW) interactions were described by the CHARMM22 force field Lennard-Jones (LJ) parameters. The motion of nuclei was integrated using a time step of 0.5 fs, and the wavefunction was optimized to the Born-Oppenheimer surface by an orbital transformation method³⁴ with a convergence criterion of 10⁻⁶. All DFT/MM simulations were run using the CP2K package.³⁵

For the SCC-DFTB/MM setup, the QM atoms were chosen in the same way as DFT/MM and planar restraining potentials were used to prevent the boundary QM atoms from diffusing out of the channel. Again, the QM atoms within the boundary defined by the planes were not affected. The point charge based Ewald summation was used to treat QM/MM electrostatic coupling under PBCs.¹⁶ Just as for the DFT/MM simulations, the SCC-DFTB/MM vdW interactions were described by the CHARMM22 force field LJ parameters. The time step was set as 0.5fs, and the SCC-DFTB convergence criterion of 10⁻⁸ was used. The SCC-DFTB/MM simulations were carried out using the CHARMM simulation package.³⁶

In previous studies the PT free energy profile through the LS2 channel features several local minima separated by energy barriers that are several times that of the thermal energy, thus impeding the free translocation of the excess proton.¹³ In order to make a statistically meaningful comparison between SCC-DFTB and DFT methods for the PT properties within a limited simulation time (~100 ps), we chose to enhance the sampling of the excess proton in two regions inside the LS2 channel (one wider and one narrower region). In particular, the z position was restrained with a harmonic potential around z = − 6.5 Å (Figure 2), which corresponds to a wide region in the channel where the complete first solvation shell of the excess proton can be accommodated and a minimum in the PT free energy profile was previously reported (Figure 2 in ref ¹³), and z = − 3.5 Å, corresponding to a narrow channel region and a barrier in the PT free energy profile.

Figure 2.

Snapshots of protonated water wire in LS2 with excess proton CEC restrained at z = -6.5 Å from (A) BLYP-D simulation (B) SCC-DFTB simulation. The serine residues are colored in blue, the most hydronium-like oxygen O* and the water oxygens within 3 Å of O* are colored in green, and the rest of the water oxygens are colored in red. One of the hydrogens closest to the O* is shown by H* and the next closest oxygen in the special pair, O_1x, is also shown in panel A. Notice the oversolvation of SCC-DFTB O* and the bifurcated hydrogen bond indicated by the red lines in panel B.

The charge defect associated with the excess proton was tracked via the center of excess charge (CEC) defined in this work as:³⁷

$$\overrightarrow{\xi }={\Sigma }_{i=1}^{N_H}{\overrightarrow{r}}^{H_i}-{\Sigma }_{j=1}^{N_O}{w}^{O_j}{\overrightarrow{r}}^{O_j}-{\Sigma }_{i=1}^{N_H}{\Sigma }_{j=1}^{N_O}{f}_{sw}\left(d_{O_j{H}_i}\right)({\overrightarrow{r}}^{H_i}-{\overrightarrow{r}}^{O_j}),$$ Eq 3

where the “O” and “H” denotes oxygen atoms and hydrogen atoms in the QM region, the weighting factor w^O_j's are set to 2, d_OjHi is the distance between atom O_j and atom H_i, and f_sw (d_OjHi) = 1/(1 + exp [(d_OjHi - r_sw)/d_sw]) is the switching function describing the coordination of H_i to O_j. with the parameters chosen as d_sw = 0.03 Å, d_sw = 0.13 Å.³⁷ This excess proton CEC definition has been shown to adequately locate the excess proton charge defect in previous QM/MM simulations of biological PT channels.^11,37 This quantity will be referred to often in the following discussion so the readers should take note of this acronym and its definition.

Following 200 steps of steepest descent geometry minimization, the systems were heated up and the temperature then maintained at 300 K using a Nosé-Hoover thermostat with a relaxation time constant of 0.1 ps for all of the methods. For the all of the methods, both restrained and unrestrained simulations of the protonated LS2 channel were run, with the latter starting from the last snapshot of the corresponding method's restrained simulation. All the QM/MM simulations were equilibrated for at least 30 ps and run for another 70-100 ps in the constant NVT ensemble.

2.3 Carbon nanotube QM/MM simulation

A (8,8) single-wall carbon nanotube (CNT) of length 29.47 Å was first solvated in a large box of equilibrated TIP3P water. The LJ parameters for carbon atoms were σ = 3.40 Å and ε = 0.086kcal/mol, corresponding to the sp² carbon atoms in the AMBER force field³⁸ All the carbon atoms were fixed. The cutoffs for LJ and real space electrostatic interactions were 10 Å, employing switching function starting at 8 Å for the LJ interactions. To equilibrate the system, initial velocities were assigned to 300 K followed by 20 ps of constant NVT and then 2ns of constant NPT equilibration. On average 38 water molecules resided in the CNT during the NPT equilibration. One snapshot was taken from the last 10% of the equilibration run, in which 38 water molecules were inside the CNT, and water molecules outside the CNT were removed. Then the simulation box was set up with PBC of 20 Å × 20 Å × 29.47 Å, and the longest dimension of simulation box was aligned with tube axis to create an infinitely long CNT. The system was equilibrated at 300 K using Nosé-Hoover thermostat for 1ns. One excess proton was then added near one water molecule, and the equilibration was continued for 1ns using the same classical hydronium model as used in the LS2 equilibration. All the equilibration simulations were again carried out with LAMMPS.

The last snapshot of equilibration was used to construct the QM/MM simulation. The QM atoms were chosen to be all the water molecules and the excess proton. Following 40 ps of constant NVT simulation at 300 K using a Nosé-Hoover thermostat, the production constant NVE runs were continued for at least 80 ps. The DFT/MM simulations were run with the BLYP-D and HCTH functionals. The QM/MM settings were the same as those used in the LS2 channel, except that the energy cutoff for plane wave basis set was increased to 360 Ry and the convergence criterion was decreased to 10⁻⁷ to better conserve total energy. For the SCCDFTB/MM simulations, the convergence criterion was 10⁻⁸. For all QM/MM simulations, the motion of nuclei was integrated using a time step of 0.5 fs.

Results

3.1 Water structure and dynamics in the LS2 channel

The water molecules filling the LS2 channel make hydrogen bonds with one another and with pore lining serine side chains, resulting in a continuous hydrogen-bonded water wire across the entire channel.^15,39 It is beneficial to first investigate the properties of pure water in the LS2 channel. The BLYP functional with dispersion corrections (BLYP-D) and HCTH/120 functional are chosen as the benchmark QM methods because both methods were shown to reduce the excessive structuring and sluggish dynamics of bulk water predicted by the BLYP functional.^40-44 These functionals were in turn benchmarked by simulations using the arguably more accurate B3LYP functional with dispersion corrections (B3LYP-D). To save computational cost, B3LYPD was combined with GTH pseudopotentials for BLYP and the DZVP basis set. We note that B3LYP should generally be used with a large basis set augmented by diffuse functions in order to guarantee a highly accurate hydrogen bond description.⁴⁵ Although this was not computationally feasible, the B3LYP-D employed in our QM/MM simulations still provide more accurate forces and energies than GGA level DFT methods. (See Supporting Information)

In the following, the water oxygen, water hydrogen and serine oxygen atoms will be denoted as O_w, H_w and O_s, respectively. To probe the structural properties of the water within the channel, radial distribution functions (RDFs) were calculated and normalized to bulk water density. From the O_w-O_w RDF (Figure 3 (A)), it is apparent that SCC-DFTB predicts a more pronounced first peak. The coordination number, obtained by integrating over the first peak, is larger for SCCDFTB due to a more compact and dense first solvation shell. In addition, the second peak in the O_w-O_w RDF and the density depletion region between second and third peaks in the O_w-H_w RDF (Figure 3 (B)) are less pronounced for SCC-DFTB than for the DFT methods, which corresponds to a second solvation shell water encroaching on the first solvation shell. This suggests that the water wire predicted by SCC-DFTB is less ordered inside the LS2 channel. In line with this observation, SCC-DFTB predicts less distinct peaks and valleys in the pore water density profile along the z axis (Figure 4) compared to both DFT methods, indicating that the water molecules deep in the pore region (−10 Å to 10 Å) are more mobile.

Figure 3.

RDFs of (A) O_w-O_w and(B) O_w-H_w in the LS2 channel filled with water and no excess proton. The coordination numbers, indicated in the legend, are larger for the SCC-DFTB method due to less structured 2^nd shell waters encroaching on the 1^st solvation shell.

Figure 4.

Distribution of the pore water oxygen atoms along the z axis of the unprotonated LS2 channel. The decreased peaks and valleys for the SCC-DFTB results indicate more mobile water within the channel.

The decreased structure in the LS2 channel water could be caused by weaker water-water hydrogen bonds in SCC-DFTB compared to those in the DFT methods. To quantitatively investigate the hydrogen bond properties, we define the water-water hydrogen bond as when the O_w---O_w separation is less than 3.5Å (corresponding to the location of the first minimum in the O_w-O_w RDF) and the H_w-O_w---O_w angle is less than 30°.^{46, 47} The number of water-water hydrogen bonds each water molecule makes is averaged over the entire 90 ps production trajectory and listed in Table 1. It is observed that the channel water described by SCC-DFTB forms fewer hydrogen bonds than those described by the DFT methods, which are in close agreement with each other. To compare the longevity of the hydrogen bonds, we calculated the continuous hydrogen bond time correlation function C_c(t) = 〈h(0) · H(t)〉/〈h〉, where h(t) is unity when a tagged pair of atoms are hydrogen bonded at time t, and zero otherwise. H(t) is defined as unity when the tagged pair of atoms is continuously hydrogen bonded from time 0 to time t, and zero otherwise. A semi-log plot of C_c(t) is shown in Figure 5 (A). The continuous hydrogen bond time correlation functions are then fit to the sum of 3 exponential functions, and the average relaxation time is estimated by the amplitude-averaged relaxation time,^48,49 as summarized in Table 2. It is observed that SCC-DFTB produces a shorter hydrogen bond relaxation time compared to the DFT methods, again confirming shorter (and likely weaker) water-water hydrogen bond interactions.

Table 1.

Averaged number of hydrogen bonds per water molecule in the LS2 channel as a function of QM/MM methodology.

Methods	water-water hydrogen bond	serine-water hydrogen bond
BLYP-D	1.64 ± 0.03	1.14 ± 0.01
HCTH	1.66 ± 0.02	1.17 ± 0.02
B3LYP-D	1.60± 0.02	1.17 ± 0.02
SCC-DFTB	1.51 ± 0.01	1.06 ± 0.02

Figure 5.

Semi-log plot of continuous hydrogen bond time correlation function for the (A) water-water and (B) water-serine hydrogen bonds. The faster decay of time-correlation functions reflects weaker hydrogen bonds described by SCC-DFTB compared to the DFT methods.

Table 2.

Average water-water, water-serine hydrogen bond relaxation time, and orientational correlation time in the LS2 channel as a function of QM/MM methodology.

Method	water-water hydrogen bond relaxation time (ps)	water-serine hydrogen bond relaxation time (ps)	water orientational correlation time (ps)
BLYP-D	1.26	0.86	24
HCTH	1.20	1.03	28
B3LYP-D	1.38	0.93	23
SCC-DFTB	0.21	0.42	7

The interaction between water and the serine side chains also plays an important role in shaping the structure and slowing down the dynamics of water inside the LS2 channel.³⁹ The O_w-O_s RDF (Figure 6) reveals that SCC-DFTB fails to reproduce the DFT density depletion region after the first peak and the presence of a second peak. Similar to the situation with water-water interactions, the less ordered structure revealed in the SCC-DFTB RDF reflects weaker interactions between water and serine side chains. With the water-serine hydrogen bond defined using the same distance and angle cutoff as the water-water hydrogen bond (described above), we calculated the average number of water-serine hydrogen bonds each water makes (listed in Table 1) and the continuous hydrogen bond correlation function together with the hydrogen bond relaxation time (Figure 5 (B) and Table 2). The fewer number of water-serine hydrogen bonds with each water molecule and the faster relaxation of those hydrogen bonds for SCC-DFTB suggest that the weaker water-serine interaction results from fewer and weaker hydrogen bonds.

Figure 6.

RDF of O_w-O_s in the LS2 channel filled with water and no excess proton. The less structured RDF produced by SCC-DFTB indicates weaker water-serine interactions due to weaker and fewer hydrogen bonds.

The consequence of weaker water-water and water-serine interactions is a less structured water wire inside the LS2 channel with accelerated orientational dynamics in the SCC-DFTB simulations. To probe the orientational dynamics, the second rank orientation time-correlation function C₂(t) = 〈P₂(u(0) · u(t))〉/〈P₂(u(0) · u(0))〉 was calculated, where u is the unit vector in the direction of one of the O-H bonds in water and P₂ is second order Legendre polynomial. The last 30% of C₂(t) is fit to a single exponential function to get the rotational relaxation times, which are summarized in Table 2. It is found that the SCC-DFTB method predicts water reorientation much faster than the two DFT methods, again indicating more dynamic and disordered water in the LS2 channel.

Overall, SCC-DFTB predicts an overcoordinated and more disordered water structure featuring faster dynamics of water molecules compared to the DFT methods. These differences in the structural and dynamical properties of unprotonated water are in turn linked to differences in the structure and dynamics of PT, as will be discussed below.

3.2 Proton solvation and transport in a wider region of the LS2 channel

In the following the hydronium oxygen, the 3 closest hydrogen atoms to that oxygen, and the next closest oxygen atom will be denoted as O*, H* and O_1x, respectively (see Figure 2 (A)). The O_1x is the so-called “special pair” oxygen that is forming an especially short strong hydrogen bond with the hydronium at that instant in time. Proton transfer often, but not always, occurs along this special pair coordinate.⁵⁰ From the RDFs of O*-O_w and O_1x-O (O here denotes O* and O_w) (Figure 7 (A) and (B)), it is apparent that SCC-DFTB predicts an overcoordinated hydronium oxygen, with a coordination number of 3.56 compared to those predicted by the DFT methods (all ~3). Also, the solvation shell around the O* is less structured in the SCC-DFTB simulations than the DFT counterparts. Where the DFT methods predict a distinct density depletion after the first peak of the O*-O_w RDF (at separation distance of 2.8 Å corresponding to the boundary of the first solvation shell), SCC-DFTB predicts a density decay region that extends beyond 3.4 Å. The overcoordination of O* and lack of distinct density depletion beyond the first solvation shell suggests that second solvation shell water molecules penetrate into the first, making the solvation structure less ordered compared to DFT simulations. In fact, it is observed that in DFT simulations the hydronium is consistently coordinated by 3 first solvation shell water molecules, forming a stable H₉O ⁺₄ Eigen complex, which is further stabilized by hydrogen bond interactions with nearby serine side chains and second solvation shell water molecules (Figure 2 (A)). In contrast, the SCC-DFTB method predicts an overcoordinated hydronium due to a second solvation shell water molecule frequently entering the 3 Å range of O*, leading to a bifurcated hydrogen bond (one hydrogen coordinated to two water oxygens) and disrupting the Eigen complex solvation structure (Figure 2 (B)). As will be discussed below, the SCC-DFTB hydronium is also directly coordinated to serine side chains much of the time, further increasing its overcoordination. In addition, the SCC-DFTB first solvation shell waters are also overcoordinated as indicated by the large coordination number shown in the RDF's of O_1x-O (Figure 7 (B)), which is in line with this method's tendency to overcoordinate water as discussed in section 3.1.

Figure 7.

RDFs of (A) O*-O_w and (B) O_1x-O, where O includes both O* and O_w, in protonated LS2. RDFs of (C) O*-O_w and (D) O_1x-O, where O includes both O* and O_w, in protonated water filled CNT. Coordination numbers are indicated in the legend. SCC-DFTB predicts an overcoordinated excess proton and less structured solvation complex compared to the DFT methods.

The overcoordinated excess proton structure described by SCC-DFTB leads to an abnormal hydrogen bond network around the excess proton. To illustrate this, the RDF of H*-O_w, where H* is any of the three hydrogens bound to O*, is plotted for LS2 (Figure 8 (A)). The absence of density depletion in the region 2-2.5 Å in the SCC-DFTB results reflects the encroaching second solvation shell water and bifurcated hydrogen bond donated by the hydronium. This observation is perhaps even more clear in Figure 9 (A), which shows the distribution of 1^st and 2^nd closest water oxygens to each H*. Clearly, there is an overlap region between the two distributions for SCC-DFTB simulations, which is absent in the DFT results. The overlap is a consequence of the SCC-DFTB method not localizing the first solvation shell water molecules, making it more likely to form a bifurcated hydrogen bond with two waters in its first solvation shell (see Figure 2 (B)).

Figure 8.

(A) RDF of H*-O_w in the protonated LS2, (B) RDF of H*-O_w in water filled protonated CNT. The absence of density depletion in the distance region 2-2.5 Å in the SCC-DFTB results reflects the encroaching 2^nd solvation shell water and bifurcated hydrogen bond donated by the hydronium.

Figure 9.

Distribution of H*-O_w distances in protonated (A) LS2 channel and (B) CNT. The first and second peaks correspond to the closest and second closest O_w to H*. The overlap of the two peaks in the SCC-DFTB simulation suggests that hydrogen bonding around the excess proton is too weak to localize the position of its first solvation shell water molecules, making it more likely to form a bifurcated hydrogen bond with two waters in its first solvation shell.

Although SCC-DFTB results in an increased probability of forming a bifurcated hydrogen bond, the water penetrating the first solvation shell is not hydrogen bonded to the O*-H* at all for a significant amount of time. Figure 10 (A) shows the distribution of the distance between O* and the nearest water oxygen atoms that are not hydrogen bonded to it. In the SCC-DFTB simulations, for both the LS2 and CNT channels, an unphysical configuration is frequently observed where a water molecule within the range of first solvation shell (2.8 Å of O*) is not hydrogen bonded to it. More surprisingly, the O_w not hydrogen bonded to or forming a bifurcated hydrogen bond with O* can even belong to the closest water molecule for a significant portion of the simulation time. It has been shown that in a bulk aqueous system during the long intervals between PT events (aka non-PT intervals), the closest oxygen to O* (O_1x) switches between the 3 surrounding water oxygens in the Eigen complex, resulting in a “special pair dance” mechanism.⁵⁰ The existence of a penetrating water molecule that is closest to O* but not hydrogen bonded to it will alter PT dynamics and limit SCC-DFTB's ability to correctly capture the special pair dance dynamics in the LS2 channel. To probe this, we calculated the average number of distinct O_w atoms that have been O_1x during non-PT intervals. As shown in Figure 11 the DFT simulations show a mechanism in which O_1x rotates among the 3 hydrogen bond accepting waters around O*.⁵⁰ Correspondingly, the number of different water oxygens that have once been O_1x levels off at 3 in 0.4 ps. However, the SCC-DFTB method predicts more than 3 O_1x water molecules exhibiting this behavior. Moreover, the curve shows no sign of leveling off near 0.5 ps. In the SCC-DFTB simulations, the O_w chosen as special partner, O_1x, sometimes belongs to a water molecule accepting a hydrogen bond from O*, while at other times it belongs to the penetrating water molecule not hydrogen bonded to or forming one of the bifurcated hydrogen bonds with O*. These situations interchange frequently resulting in a qualitatively different dynamical picture than that predicted by DFT.

Figure 10.

Distribution of O*-O distance, where O is the closest atom not hydrogen bonded to O* in the (A) protonated LS2 channel and (B) CNT. The noticeable peak before 2.8 Å produced by SCC-DFTB indicates that on average some first solvation shell water molecules are not hydrogen bonded to the hydronium, which perturbs the “special pair dance” dynamics in the resting state of PT (see main text).

Figure 11.

Average number of different O_1x partners to O* as a function of time during non-transfer intervals for the (A) LS2 channel and (B) CNT. The SCC-DFTB curve fails to level off and indicates that it does not reproduce the “special pair dance” behavior seen from the DFT results.

To further illustrate the weak hydrogen bond around O* in SCC-DFTB from a dynamical point of view, we applied the same analysis of average hydrogen bond relaxation times as was shown for the unprotonated water in LS2. Table 3 compares the relaxation times of hydrogen bonds within 4 Å of the excess proton CEC (defined in section 2.2) for different methods in both the LS2 and CNT systems. Not only is the SCC-DFTB hydrogen bond relaxation time much shorter than those predicted by the DFT methods, but the differences between SCC-DFTB and the DFT methods are much larger than those found for the unprotonated situation. This suggests that the effect of charge defect delocalization in enhancing hydrogen bond strength around the excess proton CEC is relatively weaker for SCC-DFTB than for the DFT methods. Thus, improving the description of hydrogen bond around the hydrated excess proton needs to be addressed in future SCC-DFTB developments.

Table 3.

Average hydrogen bond relaxation time for hydrogen bond around 4 Å of excess proton CEC in the LS2 channel and CNT as a function of QM/MM methodology.

Method	LS2 hydrogen bond relaxation time (ps)	CNT hydrogen bond relaxation time (ps)
BLYP-D	17.3	13.7
HCTH	19.8	10.0
B3LYP-D	11.2	NA
SCC-DFTB	1.8	1.4

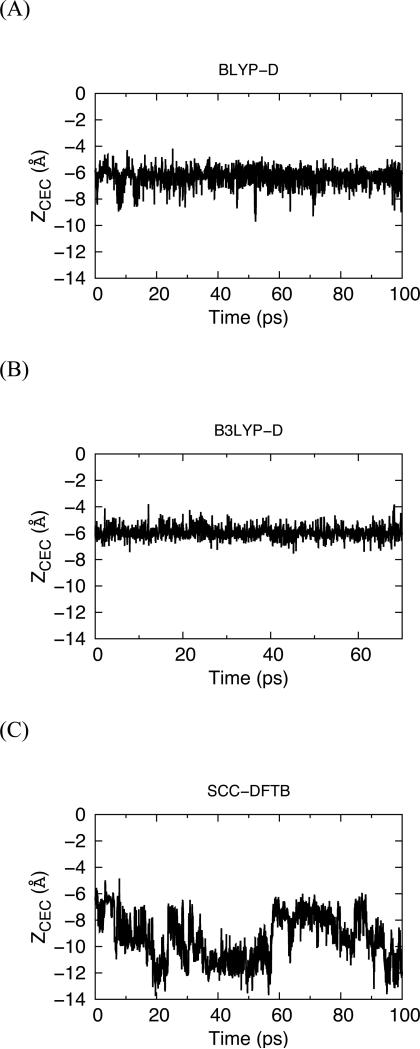
Overall, compared to the arguably more accurate DFT approaches, the SCC-DFTB method predicts the incorrect solvation structure of water and the excess proton, weak water-water and water-serine hydrogen bond interactions, a bifurcated hydrogen bond donated by the hydronium-like oxygen O*, and an unphysical special pair dynamics pattern related to the weak hydrogen bonds around the excess proton CEC. These all lead to qualitatively different PT dynamics in the LS2 and CNT channels. The PT dynamics can also be described by the time evolution of the excess proton CEC z coordinate after the quadratic restraints on it are released, as shown in Figure 12. For the DFT methods, the excess charge is stabilized in the form of an Eigen complex, which is further stabilized by the surrounding water and serine residues. During more than 70 ps of simulation the excess proton CEC z coordinate fluctuates around z = −6 Å, which is close to the reference point where the restraint was added. This suggests that the chosen region in the LS2 channel corresponds to a distinct free energy minimum in the free energy profile described by the DFT methods, in agreement with the previous MS-EVB result.¹³ In sharp contrast, the excess proton CEC z coordinate in the SCC-DFTB simulations deviates as far as 6 Å from the previous reference point, which indicates that the excess proton is not stabilized in an Eigen complex. It hops around the overcoordinated, less ordered and loosely bound solvation shell in an unpredictable manner, and gradually hops away from the region where it was originally restrained. This can be attributed to the combined effect of weaker water-water and water-serine interactions, the overcoordinated hydronium O*, the weak and sometimes bifurcated hydrogen bond around the excess proton CEC, as well as the unphysical O_1x switching events.

Figure 12.

Z coordinate of the excess proton CEC as a function of time for unconstrained simulations using the (A) BLYP-D, (B) B3LYP-D, and (C) SCC-DFTB methods. The SCCDFTB simulations show deviations as far as 6 Å from the previous reference point of the restraint, which indicates that the excess proton is not stabilized in an Eigen complex.

The tendency for SCC-DFTB to yield irregular excess proton solvation and transport remains even when the excess proton CEC motion is more trapped in the constrained simulations. In the constrained simulation SCC-DFTB predicts an O*-O_s RDF featuring a spurious first peak within 3 Å (Figure 13 (A)). This is caused by O* being directly hydrogen bonded to serine side chain hydroxyl groups for significant amounts of the simulation, something that is not observed in the DFT simulations. It is important to note that this close interaction between serine side chain oxygen atoms and the hydronium further exacerbates the overcoordination issue already caused by excessive water molecules around the SCC-DFTB hydronium in the LS2 channel. To illustrate this, the RDF of O*-O, where O denotes both O_w and O_s, is plotted in Figure 13 (B). Comparing the coordination numbers in Figure 7 (A) and Figure 13 (B) (3.6 versus 3.9) demonstrates that the overcoordination around the excess proton is more pronounced when the serine oxygen atoms are included. Figure 13 (B) shows that SCC-DFTB predicts an O* coordinated by four oxygen atoms, in contrast to three as predicted by the DFT methods. This observation is revealing because it shows that the SCC-DFTB hydronium O* favors an oxygen coordination number of 4. When its water coordination number is less than 4 in a confined environment (as shown in Figure 7 (A)), the serine side chain oxygen atoms tend to further coordinate O* to saturate its solvation shell if allowed by local geometry.

Figure 13.

(A) RDF of O*-O_s between the excess proton complex and serines in the protonated LS2 channel. The first peak predicted by SCC-DFTB method reveals that the hydronium is directly hydrogen bonded to serine side chain hydroxyl groups for significant amounts of the simulation. (B) The RDF of O*-O, where O includes both O_w and O_s. Compared with Figure 9(A), the coordination numbers indicate that the serine side chains exacerbates the overcoordination issue of O* in SCC-DFTB simulations.

3.3 Proton solvation and transport in a narrower region of the LS2 channel

Clearly, narrow channel regions also play an important role in PT processes, as previously demonstrated for the LS2 channel.^{13, 15} It is, therefore, both important and instructive to also study the proton solvation structure and transport mechanism in a narrower region (z = - 3.5 Å) close to the top of a barrier in a previously reported LS2 PMF.¹³ As shown in Figure 14 (A) and (B), the DFT methods predict a H₇O ₃⁺ solvation structure of the excess proton, i.e., the hydronium solvated by two nearby water molecules and one serine hydroxyl group. In contrast, the SCC-DFTB method predicts an overcoordinated excess proton, just as it did in the wider region of the LS2 channel, with an additional water and serine hydroxyl in the first solvation shell. Also similar to the wider region, the absence of density depletion (around 2.0-2.5 Å in Figure 14 (C)) in the SCC-DFTB results reflects a bifurcated hydrogen bond being donated by the hydronium. Therefore, the SCC-DFTB method displays similar defects in a more confined local environment. More results for the narrower region of the protonated LS2 channel can be found in the Supporting Information.

Figure 14.

RDFs of O*-O_w (A), O*-O where O includes both O_w and O_s, (B), and H*-O_w, (C) in a narrower region of protonated LS2 channel. The coordination numbers in panels A and B indicate that SCC-DFTB's overcoordination of O* remains in the narrow region of the channel. The absence of density depletion in panel C (around 2-2.5 Å) in the SCC-DFTB results reflects the encroaching 2^nd solvation shell water and bifurcated hydrogen bond donated by the hydronium ion are very similar to the case of the wider region (compare to Figure 8 (A)).

3.4 Proton solvation and transport in (8,8) single-wall carbon nanotube

The QM/MM electrostatic coupling scheme employed in the current work follows that of ref ¹⁶. The electrostatic interaction between SCC-DFTB atoms and MM atoms are calculated based on point charges. The point charges on QM atoms are the Mulliken charges Δq_α defined in the SCC-DFTB energy expression (Eq 1). In the recent work of Hou et al.⁵¹ a new QM/MM coupling scheme was implemented for SCC-DFTB/MM, which takes into account the finite size of QM and MM charge distributions by using a Klopman-Ohno functional form for the QM/MM electrostatic coupling. The new SCC-DFTB/MM coupling scheme improves the short range QM/MM interactions when the QM atoms are highly charged. In the LS2 channel some of the QM atoms (the excess proton and solvating water molecules) are positively charged and are close to the serine side chains described by MM. In order to test whether the inaccuracies of the SCC-DFTB/MM LS2 simulations described above are a result of the original point charge based electrostatic coupling scheme,¹⁶ a hydrophobic proton channel system was created from a (8,8) single-wall carbon nanotube (CNT) filled with water molecules and one excess proton. In this system the QM and MM atoms only interact via the same LJ potential for all the methods under comparison (see section 2.3). The effective pore radius of the CNT (~ 4 Å) is comparable to the wide region of the LS2 channel, accommodating one complete solvation shell around the hydronium O* (i.e., the H₉O₄⁺ Eigen complex). Similar properties were calculated for the CNT as were for the LS2 channel, and are plotted in Figure 7 (C), (D), and Figures 8-11 (B). These results reveal that the SCC-DFTB inaccuracies discussed above for LS2 remain in the CNT, including the overcoordinated excess proton, weak hydrogen bond around the excess proton CEC, and PT dynamics at odds with the DFT results. Therefore, the inaccurate description of PT in the LS2 channel by SCC-DFTB/MM should not be attributed to using an approximate electrostatic coupling scheme, but rather to inherent limitations of SCC-DFTB method itself.

Conclusions

This benchmark study has shown that the SCC-DFTB method provides qualitatively different behavior for the solvation and transport of an excess proton in the LS2 channel. These differences, when compared to more exact DFT methods which the SCC-DFTB approach is meant to approximate, include a less ordered water structure, an over-coordinated excess proton, weak hydrogen bonding around the excess proton CEC, and altered PT dynamics. These differences are also seen for the hydrated excess proton in a carbon nanotube involving only van der Waals interactions between QM and MM atoms, verifying that the SCC-DFTB inaccuracies relative to DFT in the LS2 channel result from the semiempirical QM method itself, rather than the QM/MM electrostatic coupling scheme. In addition, SCC-DFTB is shown to predict higher local water density in channel environments, similar to that which has been shown in a previous study to cause clearly unphysical large pockets of vacuum in SCC-DFTB simulations of bulk aqueous systems.^4,5 The less accurate descriptions of water and the hydrated excess proton results in qualitatively and quantitatively different structural and dynamical properties for PT in confined channel environments, calling into question the ability of the current SCC-DFTB method to accurately simulate excess proton transport in realistic biomolecular systems. At the same time, the presented results provide an important set of benchmarks by which the method can potentially be improved in the future to bring it more in line with more accurate, but more computationally costly, DFT-based QM/MM methods.