Abstract
The Non-Coding RNA (ncRNA) elements in the 3′ Untranslated Regions (3′-UTRs) are known to participate in the genes’ post-transcriptional regulations. Inferring co-expression patterns of the genes through clustering these 3′-UTR ncRNA elements will provide invaluable insights for studying their biological functions. In this paper, we propose an improved RNA structural clustering pipeline. Benchmark of the new pipeline on Rfam data demonstrates over 10% performance improvements compared to the traditional hierarchical clustering pipeline. By applying the new clustering pipeline to 3′-UTRs of Drosophila melanogaster’s genome, we have successfully identified 184 ncRNA clusters with 91.3% accuracy. One of these clusters corresponds to genes that are preferentially expressed in male Drosophila. Another cluster contains genes that are responsible for the functions of septate junction in epithelial cells. These discoveries encourage more studies on novel post-transcriptional regulation mechanisms.
Keywords: bioinformatics, non-coding RNA, RNA secondary structure, clustering, 3′ untranslated region, post-transcriptional regulation, Drosophila genome
1 Background
Post-transcriptional control is the regulation at the protein level through the existing mRNAs by modifying their stability, translation efficiency and subcellular locations. Many of the regulations are found to be triggered by RNA–protein or RNA-RNA interaction, which usually occurs in the 3′ Untranslated Regions (3′-UTRs) of the mRNA (Besse and Ephrussi, 2008; Martin and Ephrussi, 2009; Mazumder et al., 2003). In eukaryotes, the sequence or structural elements in the 3′-UTR of some genes under regulation serve as ‘zip-code’, determining the fate of their corresponding mRNAs through interaction with transportation or entrapment proteins or signalling molecules (Jansen, 2001). For instance, the NOS translational control element, cis-regulates the expression of Nanos protein through binding with the Smaug protein, which in turn determines the proper morphogenesis of the Drosophila embryo (Crucs et al., 2000). The sequence and structure features of the translational control elements, which determine the fate of the corresponding mRNA through specific recognition of partner RNAs or proteins, are thus critical in understanding the expression pattern and functionalities of the corresponding genes. For example, the conserved histone 3′-UTR stem loop (Dominski and Marzluff, 1999) suggests that the histone genes are co-regulated and co-expressed, which implies their potential collaborations in nucleosome packing. In this work, we are particularly interested in identifying common non-coding RNA (ncRNA) elements from the 3′-UTRs and using such information to infer the corresponding genes’ co-regulation or co-expression patterns.
Recently, Rabani et al. (2008) identified a number of 3′-UTR ncRNA elements from Drosophila melanogaster genome using improved Stochastic Context-Free Grammar (SCFG; Eddy and Durbin, 1994). They detected several structured ncRNA elements from experimentally verified co-localised genes (Lecuyer et al., 2007). Because experimental determination of the gene expression patterns (both temporal and spatial) can be expensive, we propose to computationally infer the genes’ potential co-regulation pattern through structural clustering before conducting real experiments. Currently, there exist many computational tools for de novo identification of ncRNA elements from multiple alignments, such as RNAz (Washietl et al., 2005), Evofold (Pedersen et al., 2006), MSARI (Coventry et al., 2004), QRNA (Rivas and Eddy, 2001) and ddbRNA (di Bernardo et al., 2003). We will first use these ncRNA identification tools to reveal the candidate structured regions in the 3′-UTRs, and then use pairwise structural alignment tools such as LocARNA (Will et al., 2007), which implements the alignment of pairing-probability matrices (Hofacker et al., 2004; McCaskill, 1990), to compute the structural similarities between the candidate ncRNA elements. Finally, we will cluster the candidate ncRNA elements from 3′-UTRs based on their sequence and structural similarity, and predict the co-expression patterns of the genes whose 3′-UTR RNA elements are clustered.
However, the clustering performance, despite the fact that high-quality pairwise alignments can be generated by many state-of-the-art alignment tools (i.e. LocARNA achieves over 80% sum-of-pair score even for RNA sequences with <40% identity), remains relatively low (the F-measure for clustering pipeline based on LocARNA is only 64.8%). We conjecture that the performance bottleneck may exist in the clustering algorithm itself, rather than in the structural alignment quality. Specifically, we notice that the local structural alignment scores, which appear to be length-dependent, are fed into the hierarchical clustering algorithm without normalisation. The consequence is that hierarchical clustering may merge longer ncRNA candidates with higher priority, rather than those with higher structural similarity. Such problems also exist in many of the existing clustering pipelines (see e.g. Kaczkowski et al., 2009; Ritchie et al., 2007; Torarinsson et al., 2007; Tseng et al., 2009). To normalise the structural alignment scores, we simulate the RNA structure alignment score distribution through a number of randomly generated alignment scores. We then compute statistically meaningful p-values for the structural similarity scores. We also take advantage of the normalised measures, and devise a more efficient and robust CLique-finding CLustering (CLCL) algorithm, to replace the traditional hierarchical clustering. In addition, CLCL is also capable of outputting disjoint clusters without further human interaction, which is a highly desirable feature when analysing a large data set.
We have conducted benchmark experiments against the LocARNA clustering pipeline on Rfam (Griffiths-Jones et al., 2003) to demonstrate the performance gains made by our proposed clustering method improvement. We chose the same data set (see Section 2) and structural alignment tool (LocARNA) for the comparison. We have seen that by incorporating the clique clustering method, we are able to increase the F-measure, a comprehensive measurement for recall and precision, from 64.8% to 74.9%. A more detailed analysis suggests that the score normalisation is responsible for ~70% of the performance gain, and the application of CLCL is responsible for ~30% of the performance gain. Note that in order to reach the LocARNA clustering performance, the correct Rfam classification is required to parse the hierarchical tree and determine the optimal cutting level with the specified recall rate. Such information is not usually available, and the optimal cutting level for the benchmark data set is not necessarily optimal for the data set of interest. On the other hand, our results can be achieved completely automatically and require no additional information. As a result, we have provided a novel clustering pipeline which is more efficient, automatic and accurate.
We then have applied our clique clustering method to the 3′-UTR of D. melanogaster genes and have found 184 3′-UTR ncRNA families, among which 91.3% are predicted to contain a structural element by RNAz. It implies that most clusters identified in this study contain RNA elements with conserved sequences and structures, which further implies that they can possibly be co-regulated. The histone stem-loops are rediscovered among these clusters with high accuracy, in addition to many other gene clusters whose cooperations under certain physiological processes are suggested by existing studies. In addition, we also present two other gene clusters, where one cluster contains genes that are highly expressed in male Drosophila and the other contains genes that are essential for septate junction function in Drosophila.
2 Methods
2.1 Generating random RNA structural alignment scores
We propose that the valid random ncRNA structures should have the following two properties: (1) low free energy such that they can be considered to be stable under natural conditions and (2) the same length to rule out the length bias. Therefore, given the ncRNA sequence of interest, we generate the random RNA sequences that preserve the original dinucleotide frequency and length using the Altschul–Erickson algorithm (Altschul and Erickson, 1985). Then, we use RNAfold (Hofacker et al., 1994) to compute the base-pairing probabilities of the random ncRNA sequences. Finally, we aligned pairing probability matrices of the random sequences with the probability matrix of the sequence of interest using LocARNA. We consider the resulting alignment scores as the background score distribution associated with the sequence of interest.
2.2 Optimal parameters fitting
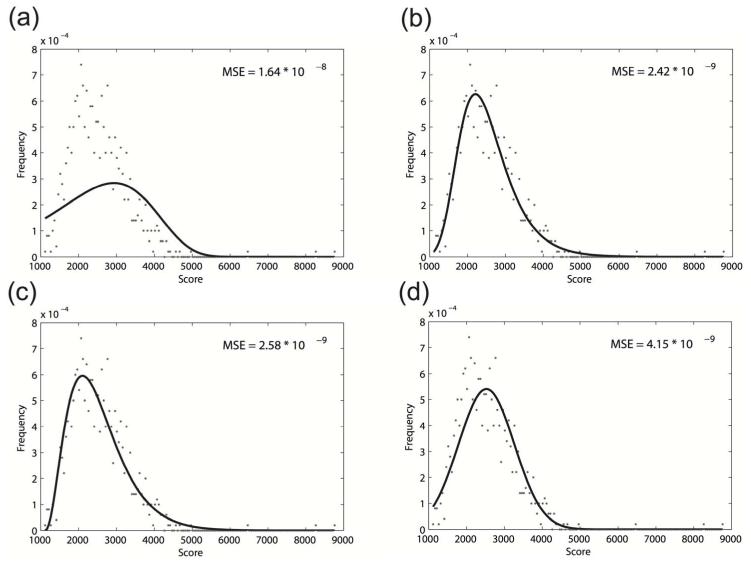
We intend to find a distribution that can be used to model the simulated background alignment scores. Note that the local sequence alignment scores have been shown to follow the extreme value distribution (Karlin and Altschul, 1990), while the behaviour of local structural alignment score has not yet been studied. To investigate the local structural alignment score distribution, we tested two forms of extreme value distributions. The first one is the widely used two-parameter Gumbel’s distribution and the second one is the three-parameter general extreme value distribution (using MATLAB built-in functions evfit and gevfit). We also fit the observed alignment score frequency with Gamma distribution and normal distribution (using MATLAB built-in functions gamfit and normfit), as they have also been previously used to model sequence alignment scores (Pang et al., 2005). The fitting results of these four distributions with background alignment scores associated with the Rfam 5S rRNA consensus structure are shown in Figure 1.
Figure 1.
The fitting of 500 5S rRNA similarity scores using different distributions. (a) Gumbel’s distribution; (b) general extreme value distribution; (c) Gamma distribution; (d) normal distribution. The Mean Square Error (MSE) is used to measure the goodness of fit. The general extreme value distribution can optimally model the local structural alignment scores
The goodness of fit is calculated using the Mean Square Error (MSE) between the sampled alignment score frequencies and the theoretical frequencies under certain distribution assumptions. The experiment results suggest that Gumbel’s distribution may not be a model for the local sequence alignment score distribution. Therefore, the more sophisticated three-parameter general extreme value distribution is used for all successive analysis.
2.3 Extracting ncRNA clusters
After curve fitting, we can estimate the statistical significance of the pairwise alignment scores through the computation of their p-values. We denote the alignment score distribution associated with the ncRNA element i as . Given the two-dimensional matrix S, where Si,j is the pairwise structural alignment score between ncRNA elements i and j, we denote as the p-value of the alignment score Si,j when assuming as background. Let Pc be an empirical p-value cut-off, we can convert S into a Boolean matrix I, where Ii,j indicates whether the ncRNA elements i and j are significantly structurally similar to each other:
Using this conversion, we are able to remove most of the insignificant edges between candidate structures and speed up the successive clustering analysis. The traditional hierarchical clustering generates a hierarchical tree and requires human intervention to output disjoint clusters. Since the number of candidate RNA elements in genome-wide analysis can be large, it is desirable to devise an algorithm that can automatically output disjoint clusters without human intervention. We formulate the cluster extraction problem into a clique-finding problem. Inspired by Bron–Kerbosch’s algorithm (Bron and Kerbosch, 1973) and Cluster Affinity Search Technique (CAST) algorithm (Ben-Dor et al., 1999), we devised a heuristic algorithm named CLCL to solve this problem. The pseudo-code for each stage of the CLCL algorithm, which finds the potential maximum clique in a given graph, is outlined in Figure 2.
Figure 2.
The pseudo-code for a single stage of the CLCL algorithm. At each stage, the heuristic algorithm tries to identify the clique with the largest size from the given unit-weighted, undirected graph. Notation: (vi, vj) denotes an edge connecting the vertices vi and vj; adj(vi) denotes the set of vertices that are adjacent to vertex v
The major idea of the algorithm is the following. We keep a set (the set in Figure 2) which stores vertices that form a clique (i.e. each vertex in the set is connected to all other vertices in the set). As the algorithm proceeds, we add a new vertex to at each phase. The new vertex has to connect to all vertices in . To ensure this property, we associate each vertex with its clique connectivity (cc(v) in Figure 2), which depicts the number of edges between v and the vertices in . If v connects to all vertices in , it will be a valid candidate for expanding . Since we try to identify a clique that is as large as possible, we will select the candidate vertex that has the largest degree, which implies higher potential of connecting to other vertices that have not yet been added. The algorithm will terminate when no candidate vertex is found.
To analyse the time efficiency of this algorithm, denote the number of vertices in the graph as |V |, the edges in the graph as |E| and the size of the maximum clique as z. We claim that the algorithm outlined in Figure 2 can be finished in O(z|E|) time. To see the time complexity, we can divide the algorithm into phases, with each phase corresponding to an execution of the ‘while’ loop. Each phase contains two ‘for’ loops, and both ‘for’ loops are indexed by existing edges in the graph. Therefore, the running time for each phase is bounded by O(|E|). Since each phase includes exactly one vertex into the clique, the total number of phases is clearly O(z). As a result, the time complexity of the algorithm shown in Figure 2 is O(z|E|).
After analysing the time complexity for extracting one clique from a given graph, we can extend the analysis to the algorithm’s application in extracting all cliques from a given graph. As soon as a clique has been identified, the corresponding vertices will be removed from the original graph, and the same algorithm will be applied to the remaining graph to identify the next clique. Let the size of the ith clique be zi and the time required for extracting the ith clique Ti; the total time T that is required for extracting all cliques can be written as
Since most of the biological graphs are scale-free (Barabasi and Albert, 1999), we can expect that O(|E|) = O(|V|), and CLCL will be finished in quadratic time. The CLCL algorithm thus outperforms the traditional hierarchical clustering algorithm with respect to both the running time and the capability of automatically generating disjoint clusters.
The algorithm will output disjoint cliques in the graph. However, the complete connection restriction of clique definition may be too stringent, such that in some cases it separates an RNA family into many subfamilies. To compensate for this drawback, we merged the output cliques which have high connectivity. Similar to clustering coefficient, the connectivity kU, V, between cliques U and V can be written as
where vUi is ith vertex in clique U and |U | is the size of the clique U. IsConnect is a Boolean function defined as the following:
kU, V is empirically set to 0.4 for all experiments.
2.4 Rfam data set
We generated two data sets to investigate the performance of the clique clustering method. The first data set is exactly the same as the one used in the LocARNA clustering benchmark. It contains 3901 individual RNA structures from 499 families in the Rfam (Griffiths-Jones et al., 2003) seed alignment (with sequences longer than 400 bp and having >80% sequence identities filtered out). This data set is referred to as ‘Rfam’ data set in the following sections. The second data set contains 263 individual RNA structures from seven families in Rfam seed alignment whose average sequence identities are <50%. These families include 6S, RNase_MRP, RNaseP_nuc, SECIS, T-box, tmRNA and yybp-ykoy. We compiled this data set to confirm that the clique clustering pipeline will also work well on ncRNA families with low sequence identity. This data set is referred to as ‘Rfam_LowID’ data set in the following sections.
2.5 D. melanogaster 3′-UTR candidate ncRNA elements
The D. melanogaster genome and multiple alignments were downloaded from UCSC genome browser (version dm3). The gene annotation was taken from FlyBase (D. melanogaster version 5.12; Drysdale, 2008). The multiple alignments of the 3′-UTR of each gene were cut and fed into standard RNAz (Washietl et al., 2005) analysis pipeline (using 120 bp window size and 40 bp step size). Sequences with RNAz RNA class probability value greater than 0.5 were taken as potential candidate regions. In total, 3657 candidate regions were collected. Their base-pairing probability matrices were computed using RNAfold (Hofacker et al., 1994).
3 Results
3.1 Benchmarking using Rfam database
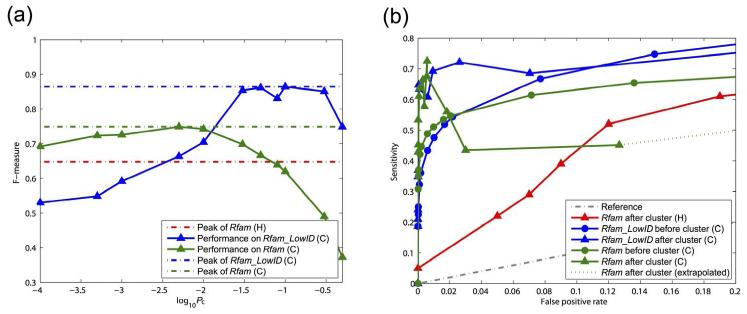
Here we compare the clustering performance of our clique clustering method, to the traditional hierarchical clustering method (as used in the LocARNA pipeline). The F-measure, which is the harmonic mean of recall and precision, is compared between the two clustering experiments. Figure 3(a) shows the F-measure for LocARNA hierarchical clustering on Rfam data set (red) and the clique clustering on Rfam (green). It is observed that the clique clustering pipeline outperforms the hierarchical clustering by over 10% of F-measure (74.9% compared to 64.8%). The peak performance of the clique clustering method is observed around p-value cut-off 0.01. This p-value cut-off is then used in the real-world application of this clustering pipeline in analysing Drosophila 3′-UTR. The benchmark results confirm our conjecture that improving the clustering performance itself is as important as developing accurate pairwise structural alignment methods.
Figure 3.
F-measure and ROC curves for clique (C) and hierarchical (H) clustering pipeline at different p-value cut-offs. Red series: hierarchical clustering with Rfam data set by Will et al. (2007). Green series: clique clustering pipeline with Rfam data set. Blue series: clique clustering pipeline with Rfam_LowID data set. (a) F-measure of the clustering performance on different data sets. The peak performances of the three series are 64.8%, 74.9% and 86.4%, respectively (denoted by broken lines). Note that the cut-off used by Will et al. (2007) is recall rate, for which the corresponding p-value cut-off is difficult to estimate. Therefore, only the peak performance is presented. (b) ROC curves of clique and hierarchical clustering pipelines for different data sets. The term ‘before cluster’ refers to the performance of clustering before clique extraction (only score normalisation has been applied). The term ‘after cluster’ refers to the performance of clustering after clique extraction (both score normalisation and clique extraction have been applied). When the best overall performance is achieved (with corresponding FPR 8 × 10−3), the score normalisation contributes to the ~70% of the performance gain, while the clique extraction contributes the other ~30%
Surprisingly, the performance of the clique clustering pipeline on the Rfam_LowID data set is even better than that on the Rfam data set. Figure 3(a) shows the F-measure of clique clustering on Rfam_LowID (blue) data set, which has achieved 86.4% for its peak performance. Table 1 shows the more detailed family-wise performance of the clique clustering. The results indicate that our clique clustering method is capable of handling low-identity ncRNA families with high accuracy. We have carefully examined the clustering results and conclude that the high performance of the Rfam_LowID (blue) data set is due to the exclusion of ncRNAs families that are highly similar to each other. For example, the microRNAs and snoRNAs are divided into tens of subfamilies in Rfam, which greatly reduces the clustering performance if those belonging to different subfamilies are clustered together.
Table 1.
Detailed clustering results on Rfam _LowID data set
| Rfam ID | Family | Ave. identity | Ave. length | Count | # Clusters | Sensitivity | Specificity |
|---|---|---|---|---|---|---|---|
| RF00013 | 6S | 45% | 180.10 | 5 | 1 | 100% | 71.4% |
| RF00030 | RNase_MRP | 42% | 321.70 | 18 | 1 | 72.2% | 100% |
| RF00009 | RNaseP_nuc | 45% | 312.40 | 38 | 2 | 84.2% | 100% |
| RF00031 | SECIS_1 | 45% | 64.50 | 44 | 2 | 95.5% | 100% |
| RF00230 | T-box | 49% | 225.70 | 40 | 1 | 99.8% | 97.5% |
| RF00023 | tmRNA | 48% | 356.60 | 61 | 2 | 90.2% | 100% |
| RF00080 | yybp-ykoy | 49% | 121.80 | 57 | 1 | 91.2% | 94.5% |
Notes:
Ave. identity: average sequence identity of the ncRNA family.
Count: total number of individual ncRNAs in the family that have been included in the benchmark experiment.
Ave. length: average sequence length of the ncRNA family.
Clusters: number of major clusters for the ncRNA family.
Sensitivity: number of clustered ncRNAs over total size of the family.
Specificity: number of ncRNAs of the same family over total size of the cluster.
The improvement of our clustering pipeline is made by normalising the structure alignment scores and incorporating the clique-finding algorithm in clustering. It is important to understand the contribution of each step to the improvement of overall performance, as the answer may provide insights into this problem and lead to more desirable applications of the pipeline. To separate the contributions of these two steps, we use the Receiver Operating Characteristic (ROC) curves, which are generated by plotting true positive rate versus false positive rate, to represent the clustering performances (1) after structure alignment score normalisation and (2) after score normalisation and CLCL. We named the first performance as ‘before cluster’ and the second performance as ‘after cluster’. To draw the ROC curve, we define true positive for ‘before cluster’ as the number of edges that connects two vertices whose corresponding ncRNAs are clustered in the same RNA family (as defined by Rfam) in the original graph, and that for ‘after cluster’ as the number of ncRNA pairs that are clustered (by us) in the same group and in the same RNA family (as defined by Rfam). The false positive, true negative and false negative are defined correspondingly.
We show the ROC curves in Figure 3(b). In Figure 3(b), we can observe that when the best overall performance is achieved (where the FPR is 8 × 10−3), the score normalisation contributes ~70% of the performance gain (subtracting the value of the red line with triangular labels from the value of the green line with round labels), while the clique extraction contributes the other ~30% of the performance gain (subtracting the value of the green line with round labels from the value of the green line with triangular labels). We can also observe that the performances for ‘after cluster’ are higher than ‘before cluster’ at the low false positive rate range for both Rfam and Rfam_LowID data sets. This is because with stringent p-value cut-off, the merging step of the CLCL algorithm can correct some false negatives. On the other hand, with a loose p-value cut-off, the merging step will produce more false positives than the false negatives which it may reduce. As a result, it is more desirable to apply relatively strict p-value cut-off to the clustering pipeline.
3.2 Finding ncRNA elements in D. melanogaster 3′-UTR
After benchmarking the clique clustering pipeline on the Rfam data sets, we applied it to the real ncRNA candidates generated from D. melanogaster 3′-UTR (with p-value cut-off 0.01). We identified 524 significant clusters that contain at least three structural elements at the beginning. To further assure the clusters’ quality, we first removed the overlapping sequences, which are included by the candidate screening strategy used by RNAz discovery pipeline. We also ensured that the local region aligned within each cluster is consistent. To extract the consistently aligned local regions, we reperformed the pairwise alignments on the clustered ncRNA candidates. We represented each candidate by its longest local region that was commonly (aligned to all other candidates in the cluster) and structurally (annotated as structured region) aligned. If such a region is too short (<60% of the longest local common structural region within the cluster) or does not exist, we removed the corresponding candidate from the cluster. This process was carried out iteratively until a high-quality consensus local structural region was identified or the number of potential candidates dropped below three. Finally, we collected 184 ncRNA clusters with high confidence.
We sorted the 184 clusters based on their average in-cluster p-values. For each cluster, we used mLocARNA to generate the corresponding multiple alignments on their commonly aligned local regions without structural constraint. We also used RNAz to evaluate the quality of the multiple alignments. Since the multiple alignments were generated using a structural alignment approach, we chose a dinucleotide background model and a structural RNA alignment quality decision model of the RNAz for evaluation (Gruber et al., 2010). We identified 168 (91.3% of all identified clusters) clusters that have RNAz RNA class probability value >0.95, indicating potential true structural elements in these clusters. We have compiled all information regarding these clusters including consensus structures of the clusters and GO term analysis. In addition, we have also provided the differentiated expression information of each cluster of genes in terms of different tissues, based on the experimental results and T-test performed by FlyAtlas (Chintapalli et al., 2007). Such information can be found at our supplementary website http://genome.ucf.edu/fly3UTRcluster.
3.3 Histone stem-loop clusters
The two clusters that are ranked top among all 184 clusters correspond to the histone 3′-UTR stem-loop structures (Dominski and Marzluff, 1999). The histone genes are divided into five major subfamilies: His1, His2A, His2B, His3 and His4. There are 23, 20, 23, 23 and 22 genes annotated as the five subfamilies by FlyBase. Only 13 His1 genes’ and 18 His2A genes’ 3′-UTR were included in the candidate regions after RNAz screening (possibly due to the flanking sequence contamination). The first cluster (C1) contains ten out of 13 annotated His1 genes and one other gene, while the second cluster (C2) contains 18 out of 18 annotated His2A genes and three other genes. The three missed His1 genes are clustered together in cluster C7.
While the known histone 3′-UTR structural elements have been rediscovered with high accuracy, the annotation of the remaining clusters is more challenging as they contain many unannotated genes. However, we were still able to identify several interesting clusters with significant functional enrichments, as we will present in the following.
3.4 Cluster of genes that are preferentially expressed in Drosophila testis
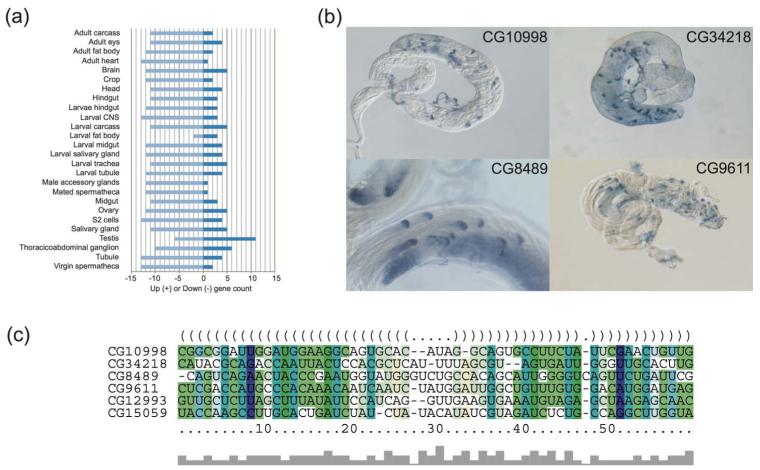
Gene cluster C19 is a striking example of a cluster of 20 transcripts with functionally related genes (see Table 2). Many of the genes in this cluster show either a male-biased and/or testes-enriched expression pattern (see Figure 4a), and/or localised expression in post-meiotic spermatids. Of the genes for which data are available, 65% (11/17) show male-biased expression (fold enrichment: min 5-fold, max 6762-fold, median 734-fold), 69% (9/13) show expression enriched in testes compared to ovaries (fold enrichment: min threefold, max 772-fold, median 175-fold) and 80% (4/5) show a highly specific expression pattern in spermatids (see Table 2). The spermatid expression is very specific with transcription occurring in post-meiotic spermatids and subcellular localisation of the mRNA (described as either ‘cup’ or ‘comet’) to the distal region of spermatids (Barreau et al., 2008). This expression pattern is also highly unusual and was only observed in 24 testes-expressed genes (among 529 genes that have been investigated). Given the fact that our cluster contains only five genes which have been investigated, and four of them exhibit the ‘cup’ or ‘comet’ localisation pattern (see Figure 4b), hypergeometric test indicates that the probability to observe this result by chance is less than 1.6 × 10−5. The enrichment of genes with male-biased expression pattern in this cluster and their highly specific localisation patterns suggest the potential post-transcriptional regulation induced by their common 3′-UTR ncRNA elements.
Table 2.
Expression profile of the gene cluster C19. The shaded cells in the table indicate the genes that are highly expressed in male Drosophila
|
Expression profile
|
|||||||
|---|---|---|---|---|---|---|---|
| FlyBase ID | CG ID | Symbol | modENCODE 1 | FlyAtlas 2 | FlyTED 3 | ||
|
| |||||||
|
Adult males
5 days |
Adult females
5 days |
Testis | Ovary | Spermatogenesis | |||
| FBgn0004403 | CG1524 | RpS14a | 32115 | 53897 | 705 | 2785 | n.d. |
| FBgn0010316 | CG1772 | dap | 309 | 1813 | 45 | 1117 | n.d. |
| FBgn0028487 | CG9611 | f-cup | 5786 | 755 | 1419 | 148 | Cup |
| FBgn0029809 | CG15767 | CG15767 | 734 | 0 | 134* | 1 | n.d. |
| FBgn0031142 | CG10998 | r-cup | 2008 | 14 | n.d. | n.d. | Cup |
| FBgn0031546 | CG8851 | CG8851 | 4241 | 2 | n.d. | n.d. | n.d. |
| FBgn0032176 | CG13127 | CG13127 | 360 | 0 | 175* | 1 | n.d. |
| FBgn0033848 | CG13330 | CG13330 | n.d. | n.d. | 895* | 3 | n.d. |
| FBgn0034374 | CG15086 | CG15086 | 5501 | 0 | 1237* | 2 | n.d. |
| FBgn0036687 | CG6652 | CG6652 | 9250 | 6 | 1544* | 2 | Spermatocytes |
| FBgn0038170 | CG14367 | CG14367 | 1889 | 364 | 29 | 11 | n.d. |
| FBgn0038225 | CG8489 | soti | 6762 | 0 | 143* | 2 | Comet |
| FBgn0038499 | CG31256 | Brf | 470 | 932 | 9 | 94 | n.d. |
| FBgn0038683 | CG11779 | CG11779 | 4905 | 2739 | n.d. | n.d. | n.d. |
| FBgn0062517 | CG16984 | CG16984 | 6630 | 230 | 1393* | 3 | n.d. |
| FBgn0086358 | CG7417 | Tab2 | 1554 | 3470 | 87 | 382 | n.d. |
| FBgn0250827 | CG34218 | whip | 5358 | 1 | n.d. | n.d. | Comet |
| FBgn0261799 | CG32159 | dsx-c73A | n.d. | n.d. | n.d. | n.d. | n.d. |
| FBgn0262515 | CG8029 | VhaAC45 | n.d. | n.d. | n.d. | n.d. | n.d. |
| FBgn0262740 | CG11727 | CG 11727 | n.d. | n.d. | n.d. | n.d. | n.d. |
Notes:
modENCODE RNA-Seq data were downloaded from Flybase (average RNA-Seq RPKM reported in FlyBase Annotation Release 5.26).
FlyAtlas microarray expression data were downloaded from FlyBase (Annotation Release 5.26).
RNA tissue in situ hybridisation data obtained from Fly-TED.
Genes with strong expression are confined to the testis and low expression in the fat body.
Figure 4.
The expression profile of genes clustered in C19 and the consensus structure and multiple alignments of their conserved 3′-UTR RNA elements. (a) FlyAtlas expression levels of the genes clustered in C19 in different tissues. (This figure is generated by searching FlyMine with all genes that are clustered in C19.) A majority (11) of these genes are highly expressed in fly testis, while no similar pattern can be observed for the other tissues. (b) The ‘cup’ or ‘comet’ localisation patterns of four genes identified by 3′-UTR RNA clustering in fly testes. These four images were created in the laboratory of Dr. Helen White-Cooper, are copyright © Helen White-Cooper and were first published in FlyTED, the Drosophila Testis gene Expression Database (http://flyted.zoo.ox.ac.uk/), from which these copies were obtained. (c) The consensus secondary structure and multiple alignments of the 3′-UTR RNA elements of the four genes that are shown in (b) and two high-score hits that have been identified by searching the secondary structure profile against 3′-UTR of Drosophila melanogaster genome using cmsearch
To further confirm the correlation between the 3′-UTR ncRNA element and the genes’ expression patterns, we conducted a search for genes with similar 3′-UTR elements. We used cmsearch (Nawrocki et al., 2009) to search the 3′-UTR ncRNA element profile against the entire 3′-UTR of the D. Melanogaster genome. We identified two candidate genes: CG12993 and CG15059. The first ncRNA element lies 105 bp downstream of the translational ending site of CG12993. The gene CG12993 is called presidents-cup, which also shows the ‘cup’ expression pattern in spermatids (Barreau et al., 2008). The expression of the gene is highly male-biased as well, with 1549 expression level for adult male of five days and two for adult female of five days. Furthermore, this gene is annotated to be highly expressed in testis by FlyBase. The second ncRNA element strides over the translational ending site of CG15059. The gene CG15059 is also highly male-biased expressed, showing expression level of 1497 for adult male of five days and 0 for adult female of five days. These evidences further support the correlation between the 3′-UTR ncRNA element and these genes’ expressions and functionalities. The multiple structural alignment of the 3′-UTR structured elements of these genes and the consensus secondary structure are shown in Figure 4(c).
3.5 Clusters of genes that are essential for the functions of septate junction
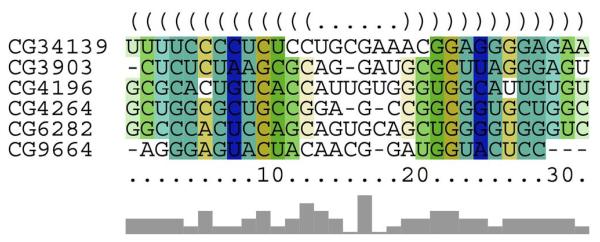
Gene cluster C37 contains six genes that share a common 3′-UTR element shown in Figure 5. These genes may play important roles for maintaining the proper function of septate junction in Drosophila, which is responsible for the formation of paracellular diffusion barrier. The first gene CG34139 is suggested to code for a transmembrane protein neuroligin by FlyBase report, based on its sequence homology to human neuroligin gene. Neuroligin acts as ligands for neurexin, which is also a transmembrane protein that is known to glue together neurons at the synapse. Alternations of these two genes will cause a cognitive disease in human (Sudhof, 2008). The second gene CG3903 (also known as Gli) codes for gliotactin protein, which is critical in forming blood-nerve barrier (Auld et al., 1995). This protein is almost exclusively expressed in neuroglia cells which maintain the proper external environment and provide support and protection for the neurons in the brain. The third gene CG9664 is annotated with the biological function of lipid metabolic process and lipid transport (Sambandan et al., 2008). The gene has also been suggested by OrthoDB (Waterhouse et al., 2011) to code for a membrane protein that has ATP binding potential and ATPase activity. These genes (i.e. neurexin, gliotactin and ATPase) are responsible for maintaining the extracellular environment through the formation of paracellular diffusion barrier and are essential for septate junction function in Drosophila (Genova and Fehon, 2003). The fourth protein CG4264 (Heat shock 70-kDa protein cognate 4 or Hsc70-4) has also been found to express in neuroglia cells (Schmucker et al., 1997). This gene is responsible for the protection of synapse under high temperature (Karunanithi et al., 2002), and it is possible that the protein is also responsible for the protection of paracellular diffusion barrier in other tissues. The functions of other two genes, CG4196 and CG6282, are not annotated, but they are inferred as membrane- and lipid metabolic-process-related proteins by FlyAtlas curators, which are possibly also responsible for maintaining the paracellular diffusion barrier.
Figure 5.
The consensus secondary structure and multiple alignments of the 3′-UTR RNA elements of all six genes that have been clustered in C37
We investigated the expression profiles of the genes in C37 from FlyAtlas (Chintapalli et al., 2007), and outline their expressions in head, eye, crop, male accessory gland and spermetheca (both virgin and mated) in Table 3. The gene CG34139 has extremely low expressions in all tissues, whose exact expression level may be difficult to measure by microarray technique. Therefore, we exclude this gene from our studies. We found that 80% (four of five) of the genes in this cluster show enriched expression in head. On the other hand, only 40% (two of five) of them show increased expressions in brain. This indicates that the genes in this cluster may participate in the maintenance of paracellular diffusion barrier in the head rather than the central nervous system, for example in the eye where all genes (five of five) show significant enrichment. Besides its important functions in the nervous system, paracellular diffusion barrier is also known to be required for proper nutrition absorption or secretion (Fasano, 2000; Firth, 2002). Indeed, these genes also show enriched expression in crop, male accessory gland and spermetheca (both virgin and mated) where secretion appear to be important for maintaining the proper physiological environment (see Table 3). Investigating the commonalities of the physiological environments in these tissues may help elucidate these gene’s specific functions and interactions.
Table 3.
Expression profile of the gene cluster C37. The shaded cells in the table indicate the genes that are significantly (based on FlyAtlas T-test) enriched in the specific tissues. FlyAtlas microarray expression data was downloaded from FlyBase (Annotation Release 5.26)
| mRNA signal level (fold enrichment to whole fly) | ||||||||
|---|---|---|---|---|---|---|---|---|
|
|
||||||||
| FlyBase ID | CG ID | Symbol | Head | Eye | Crop | Male acc.1 | Virgin sp.2 | Mated sp.3 |
| FBgn0083975 | CG34139 | CG34139 | 4 (2.4) | 2 (1.5) | 2 (1.3) | 3 (2.3) | 1 (0.7) | 1 (0.7) |
| FBgn0001987 | CG3903 | Gli | 234 (2.6) | 378 (4.2) | 311 (3.4) | 157 (1.7) | 219 (2.4) | 343 (3.8) |
| FBgn0260659 | CG4196 | CG4196 | 481 (1.3) | 749 (2.1) | 398 (1.1) | 694 (1.9) | 412 (1.1) | 416 (1.2) |
| FBgn0001219 | CG4264 | Hsc70-4 | 3873 (1.0) | 6556 (1.7) | 6037 (1.5) | 4610 (1.2) | 4690 (1.2) | 4930 (1.3) |
| FBgn0035914 | CG6282 | CG6282 | 278 (8.5) | 611 (18.6) | 31 (0.9) | 72 (2.2) | 6 (0.2) | 7 (0.2) |
| FBgn0031515 | CG9664 | CG9664 | 74 (2.8) | 55 (2.1) | 78 (2.9) | 9 (0.4) | 115 (4.3) | 73 (2.7) |
Notes:
Male accessory gland.
Virgin spermetheca.
Mated spermetheca.
Source: Chintapalli et al. (2007)
4 Conclusions
In this work, we are particularly interested in finding 3′-UTR ncRNA elements that may direct post-transcriptional regulation in the D. melanogaster genome. We have improved the existing clustering pipeline by normalising the structural alignment scores through simulation and adopting the clique-finding style clustering algorithm. We performed benchmark tests against the LocARNA hierarchical clustering pipeline to demonstrate the performance improvement made by our new clustering method. Then we applied the improved clustering pipeline to 3′-UTR of the D. melanogaster genome and revealed 184 ncRNA element clusters. We identified two interesting clusters, where one cluster contains genes that are highly expressed in male Drosophila and the other contains genes that are essential for septate junction function in Drosophila. These findings have significantly enriched our current understanding of the 3′-UTR ncRNA elements and their correlation with post-transcriptional regulation.
Although structural conservation scored by RNAz indicates high clustering accuracy, it remains challenging to conduct functional analysis for the identified clusters. The mechanism of localisation can be very sophisticated, and 3′-UTR element may not be the only one that directs the regulation. For example, in Rabani et al.’s (2008) study, only nine conserved 3′-UTR RNA elements were identified from 94 sets of genes that are experimentally verified to be co-localised. We plan to apply this clustering pipeline to other genomic locations that may affect localisation, for example 5′-UTR, to discover more RNA elements. The difficulty of annotation is also due to the presence of many unannotated genes. For example, we tried to use functional enrichment analysis tools such as g:profiler (Reimand et al., 2007) and Ontologizer (Bauer et al., 2010), and pathway searching tools such as Ingenuity Pathway Analysis (IPA), to reveal potential correlations between the genes within a cluster. But most of the queries failed due to incomplete gene annotation. We also tried to map the gene clusters using experimental co-localisation data (Lecuyer et al., 2007), yet similarly, only a few of the genes appear to be well studied. As the functionalities of these genes are elucidated, we expect that more clusters can also be biologically explained. We also expect that researchers will refer and design experiments to confirm our predictions.
Finally, we observed that two issues still await to be solved to improve the existing clustering pipeline. First, the candidate regions for ncRNAs may be mispredicted, which will likely reduce the clustering accuracy. For example, RNAz is known to have a high false positive rate (Gruber et al., 2010), which may include many non-RNA elements in the candidate set and contaminate the clustering analysis. We can improve the clustering pipeline at this point by incorporating next-generation sequencing data, where the regions in the genome that are actively transcribed can be experimentally detected. Second, the computational bottleneck of the entire clustering process lies at the pairwise alignment of all candidate RNA elements. Existing alignment tools either have limited accuracy or satisfying accuracy but with a high computational overhead. To resolve this issue, we propose incorporating the sparse dynamic programming technique used in RNA folding (Wexler et al., 2007) and co-folding (Backofen et al., 2011; Ziv-Ukelson et al., 2010) to speed up existing alignment algorithms with high accuracy, and devise a more efficient alignment algorithm for clustering analysis. We anticipate that these improvements will enable clustering analysis on larger and more sophisticated data sets, and lead to further interesting discoveries.
Supplementary Material
Acknowledgements
The authors would like to thank Dr. Helen White-Cooper for allowing us to use the images registered in FlyTED. This work was supported by the University of Central Florida In-House Award and by the National Institute of General Medical Sciences of the National Institutes of Health (R01GM102515) (CZ and SZ).
Biographies
Biographical notes
Cuncong Zhong obtained his PhD and MS in Computer Science from the University of Central Florida. He also earned his BS in Computer Science and BS in Biotechnology from Huazhong University of Science and Technology, China. He is currently developing novel algorithms and software for metagenomic data annotation at the J. Craig Venter Institute as a post-doctoral fellow.
Justen Andrews received his PhD in Genetics from the University of Melbourne. He was an Associate Professor of Biology at the Indiana University Bloomington. Before joining IU, he was a postdoctoral researcher at the National Institutes of Health.
Shaojie Zhang received his PhD in Computer Science from the University of California, San Diego. He is currently an Associate Professor of Computer Science at the Department of Electrical Engineering and Computer Science at the University of Central Florida. His research is focused on bioinformatics, which includes ncRNA gene finding, RNA analysis, and computational genomics.
Contributor Information
Cuncong Zhong, Department of Electrical Engineering and Computer Science, University of Central Florida, Orlando, FL 32816, USA cczhong@eecs.ucf.edu.
Justen Andrews, Department of Biology, Indiana University, Bloomington, IN 47405, USA jandrew@bio.indiana.edu.
Shaojie Zhang, Department of Electrical Engineering and Computer Science, University of Central Florida, Orlando, FL 32816, USA; shzhang@eecs.ucf.edu.
References
- Altschul SF, Erickson BW. Significance of nucleotide sequence alignments: a method for random sequence permutation that preserves dinucleotide and codon usage. Molecular Biology and Evolution. 1985;2:526–538. doi: 10.1093/oxfordjournals.molbev.a040370. [DOI] [PubMed] [Google Scholar]
- Auld VJ, Fetter RD, Broadie K, Goodman CS. Gliotactin, a novel transmembrane protein on peripheral glia, is required to form the blood-nerve barrier in Drosophila. Cell. 1995;81:757–767. doi: 10.1016/0092-8674(95)90537-5. [DOI] [PubMed] [Google Scholar]
- Backofen R, Tsur D, Zakov S, Ziv-Ukelson M. Sparse RNA folding: time and space efficient algorithms. Journal of Discrete Algorithms. 2011;9:12–31. [Google Scholar]
- Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Barreau C, Benson E, Gudmannsdottir E, Newton F, White-Cooper H. Post-meiotic transcription in Drosophila testes. Development. 2008;135:1897–1902. doi: 10.1242/dev.021949. [DOI] [PubMed] [Google Scholar]
- Bauer S, Gagneur J, Robinson PN. GOing Bayesian: model-based gene set analysis of genome-scale data. Nucleic Acids Research. 2010;38:3523–3532. doi: 10.1093/nar/gkq045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Dor A, Shamir R, Yakhini Z. Clustering gene expression patterns. Journal of Computational Biology. 1999;6:281–297. doi: 10.1089/106652799318274. [DOI] [PubMed] [Google Scholar]
- Besse F, Ephrussi A. Translational control of localized mRNAs: restricting protein synthesis in space and time. Nature Reviews Molecular Cell Biology. 2008;9:971–980. doi: 10.1038/nrm2548. [DOI] [PubMed] [Google Scholar]
- Bron C, Kerbosch J. Finding all cliques of an undirected graph. Communications of the ACM. 1973;16:575–579. [Google Scholar]
- Chintapalli VR, Wang J, Dow JA. Using FlyAtlas to identify better Drosophila melanogaster models of human disease. Nature Genetics. 2007;39:715–720. doi: 10.1038/ng2049. [DOI] [PubMed] [Google Scholar]
- Coventry A, Kleitman DJ, Berger B. MSARI: multiple sequence alignments for statistical detection of RNA secondary structure. Proceedings of the National Academy of Sciences USA. 2004;101(33):12102–12107. doi: 10.1073/pnas.0404193101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crucs S, Chatterjee S, Gavis ER. Overlapping but distinct RNA elements control repression and activation of nanos translation. Molecular Cell. 2000;5:457–467. doi: 10.1016/s1097-2765(00)80440-2. [DOI] [PubMed] [Google Scholar]
- di Bernardo D, Down T, Hubbard T. ddbRNA: detection of conserved secondary structures in multiple alignments. Bioinformatics. 2003;19:1606–1611. doi: 10.1093/bioinformatics/btg229. [DOI] [PubMed] [Google Scholar]
- Dominski Z, Marzluff WF. Formation of the 3′ end of histone mRNA. Gene. 1999;239:1–14. doi: 10.1016/s0378-1119(99)00367-4. [DOI] [PubMed] [Google Scholar]
- Drysdale R. FlyBase: a database for the Drosophila research community. Methods in Molecular Biology. 2008;420:45–59. doi: 10.1007/978-1-59745-583-1_3. [DOI] [PubMed] [Google Scholar]
- Eddy SR. A memory-efficient dynamic programming algorithm for optimal alignment of a sequence to an RNA secondary structure. BMC Bioinformatics. 2002;3:18. doi: 10.1186/1471-2105-3-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddy SR, Durbin R. RNA sequence analysis using covariance models. Nucleic Acids Research. 1994;22:2079–2088. doi: 10.1093/nar/22.11.2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fasano A. Regulation of intercellular tight junctions by zonula occludens toxin and its eukaryotic analogue zonulin. Annals of the New York Academy of Sciences. 2000;915:214–222. doi: 10.1111/j.1749-6632.2000.tb05244.x. [DOI] [PubMed] [Google Scholar]
- Firth JA. Endothelial barriers: from hypothetical pores to membrane proteins. Journal of Anatomy. 2002;200(6):541–548. doi: 10.1046/j.1469-7580.2002.00059.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genova JL, Fehon RG. Neuroglian, Gliotactin, and the Na+/K+ ATPase are essential for septate junction function in Drosophila. Journal of Cell Biology. 2003;161(5):979–989. doi: 10.1083/jcb.200212054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graveley BR, Brooks AN, Carlson JW, Duff MO, Landolin JM, Yang L, Artieri CG, van Baren MJ, Boley N, Booth BW, Brown JB, Cherbas L, Davis CA, Dobin A, Li R, Lin W, Malone JH, Mattiuzzo NR, Miller D, Sturgill D, Tuch BB, Zaleski C, Zhang D, Blanchette M, Dudoit S, Eads B, Green RE, Hammonds A, Jiang L, Kapranov P, Langton L, Perrimon N, Sandler JE, Wan KH, Willingham A, Zhang Y, Zou Y, Andrews J, Bickel PJ, Brenner SE, Brent MR, Cherbas P, Gingeras TR, Hoskins RA, Kaufman TC, Oliver B, Celniker SE. The developmental transcriptome of Drosophila melanogaster. Nature. 2011;471:473–479. doi: 10.1038/nature09715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths-Jones S, Bateman A, Marshall M, Khanna A, Eddy SR. Rfam: an RNA family database. Nucleic Acids Research. 2003;31:439–441. doi: 10.1093/nar/gkg006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber AR, Findeiss S, Washietl S, Hofacker IL, Stadler PF. RNAZ 2.0: improved noncoding RNA detection. Pacific Symposium on Biocomputing. 2010;15:69–79. [PubMed] [Google Scholar]
- Hofacker IL, Bernhart SH, Stadler PF. Alignment of RNA base pairing probability matrices. Bioinformatics. 2004;20:2222–2227. doi: 10.1093/bioinformatics/bth229. [DOI] [PubMed] [Google Scholar]
- Hofacker IL, Fontana W, Stadler PF, Bonhoeffer LS, Tacker M, Schuster P. Fast folding and comparison of RNA secondary structures. Monatshefte für Chemie. 1994;125:167–188. [Google Scholar]
- Jansen RP. mRNA localization: message on the move. Nature Reviews Molecular Cell Biology. 2001;2:247–256. doi: 10.1038/35067016. [DOI] [PubMed] [Google Scholar]
- Kaczkowski B, Torarinsson E, Reiche K, Havgaard JH, Stadler PF, Gorodkin J. Structural profiles of human miRNA families from pairwise clustering. Bioinformatics. 2009;25:291–294. doi: 10.1093/bioinformatics/btn628. [DOI] [PubMed] [Google Scholar]
- Karlin S, Altschul SF. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proceedings of the National Academy of Sciences USA. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karunanithi S, Barclay JW, Brown IR, Robertson RM, Atwood HL. Enhancement of presynaptic performance in transgenic Drosophila overexpressing heat shock protein Hsp70. Synapse. 2002;44(1):8–14. doi: 10.1002/syn.10048. [DOI] [PubMed] [Google Scholar]
- Lecuyer E, Yoshida H, Parthasarathy N, Alm C, Babak T, Cerovina T, Hughes TR, Tomancak P, Krause HM. Global analysis of mRNA localization reveals a prominent role in organizing cellular architecture and function. Cell. 2007;131:174–187. doi: 10.1016/j.cell.2007.08.003. [DOI] [PubMed] [Google Scholar]
- Lyne R, Smith R, Rutherford K, Wakeling M, Varley A, Guillier F, Janssens H, Ji W, Mclaren P, North P, Rana D, Riley T, Sullivan J, Watkins X, Woodbridge M, Lilley K, Russell S, Ashburner M, Mizuguchi K, Micklem G. FlyMine: an integrated database for Drosophila and Anopheles genomics. Genome Biology. 2007;8(7):R129. doi: 10.1186/gb-2007-8-7-r129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin KC, Ephrussi A. mRNA localization: gene expression in the spatial dimension. Cell. 2009;136:719–730. doi: 10.1016/j.cell.2009.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazumder B, Seshadri V, Fox PL. Translational control by the 3′-UTR: the ends specify the means. Trends in Biochemical Sciences. 2003;28:91–98. doi: 10.1016/S0968-0004(03)00002-1. [DOI] [PubMed] [Google Scholar]
- McCaskill JS. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
- Nawrocki EP, Kolbe DL, Eddy SR. Infernal 1.0: inference of RNA alignments. Bioinformatics. 2009;25:1335–1337. doi: 10.1093/bioinformatics/btp157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang H, Tang J, Chen SS, Tao S. Statistical distributions of optimal global alignment scores of random protein sequences. BMC Bioinformatics. 2005;6:257. doi: 10.1186/1471-2105-6-257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen JS, Bejerano G, Siepel A, Rosenbloom K, Lindblad-Toh K, Lander ES, Kent J, Miller W, Haussler D. Identification and classification of conserved RNA secondary structures in the human genome. PLoS Computational Biology. 2006;2(4):e33. doi: 10.1371/journal.pcbi.0020033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabani M, Kertesz M, Segal E. Computational prediction of RNA structural motifs involved in posttranscriptional regulatory processes. Proceedings of the National Academy of Sciences USA. 2008;105:14885–14890. doi: 10.1073/pnas.0803169105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimand J, Kull M, Peterson H, Hansen J, Vilo J. g:Profiler: a web-based toolset for functional profiling of gene lists from large-scale experiments. Nucleic Acids Research. 2007;35:193–200. doi: 10.1093/nar/gkm226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie W, Legendre M, Gautheret D. RNA stem-loops: to be or not to be cleaved by RNAse III. RNA. 2007;13:457–462. doi: 10.1261/rna.366507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas E, Eddy SR. Noncoding RNA gene detection using comparative sequence analysis. BMC Bioinformatics. 2001;2:8. doi: 10.1186/1471-2105-2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sambandan D, Carbone MA, Anholt RR, Mackay TF. Phenotypic plasticity and genotype by environment interaction for olfactory behavior in Drosophila melanogaster. Genetics. 2008;179(2):1079–1088. doi: 10.1534/genetics.108.086769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmucker D, Jackle H, Gaul U. Genetic analysis of the larval optic nerve projection in Drosophila. Development. 1997;124:937–948. doi: 10.1242/dev.124.5.937. [DOI] [PubMed] [Google Scholar]
- Sudhof TC. Neuroligins and neurexins link synaptic function to cognitive disease. Nature. 2008;455(7215):903–911. doi: 10.1038/nature07456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torarinsson E, Havgaard JH, Gorodkin J. Multiple structural alignment and clustering of RNA sequences. Bioinformatics. 2007;23:926–932. doi: 10.1093/bioinformatics/btm049. [DOI] [PubMed] [Google Scholar]
- Tseng HH, Weinberg Z, Gore J, Breaker RR, Ruzzo WL. Finding non-coding RNAs through genome-scale clustering. Journal of Bioinformatics and Computational Biology. 2009;7:373–388. doi: 10.1142/s0219720009004126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washietl S, Hofacker IL, Stadler PF. Fast and reliable prediction of noncoding RNAs. Proceedings of the National Academy of Sciences USA. 2005;102:2454–2459. doi: 10.1073/pnas.0409169102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waterhouse RM, Zdobnov EM, Tegenfeldt F, Li J, Kriventseva EV. OrthoDB: the hierarchical catalog of eukaryotic orthologs in 2011. Nucleic Acids Research. 2011;39:D283–D288. doi: 10.1093/nar/gkq930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wexler Y, Zilberstein C, Ziv-Ukelson M. A study of accessible motifs and RNA folding complexity. Journal of Computational Biology. 2007;14:856–872. doi: 10.1089/cmb.2007.R020. [DOI] [PubMed] [Google Scholar]
- Will S, Reiche K, Hofacker IL, Stadler PF, Backofen R. Inferring noncoding RNA families and classes by means of genome-scale structure-based clustering. PLoS Computational Biology. 2007;3:e65. doi: 10.1371/journal.pcbi.0030065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J, Klyne G, Benson E, Gudmannsdottir E, White-Cooper H, Shotton D. FlyTED: the Drosophila testis gene expression database. Nucleic Acids Research. 2010;38:D710–D715. doi: 10.1093/nar/gkp1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong C, Andrews J, Zhang S. Discovering non-coding RNA elements in Drosophila 3′ untranslated regions; Proceedings of the IEEE 2nd International Conference on Computational Advances in Bio and Medical Sciences (ICCABS); Las Vegas, NV. 2012.Feb 23-25, pp. 1–6. [Google Scholar]
- Ziv-Ukelson M, Gat-Viks I, Wexler Y, Shamir R. A faster algorithm for simultaneous alignment and folding of RNA. Journal of Computational Biology. 2010;17(8):1051–1065. doi: 10.1089/cmb.2009.0197. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.