Review and Perspective: Neuromechanical considerations for predicting muscle activation patterns for movement

Abstract

Muscle coordination may be difficult or impossible to predict accurately based on biomechanical considerations alone due to redundancy in the musculoskeletal system. Because many solutions exist for any given movement, the role of the nervous system in further constraining muscle coordination patterns for movement must be considered in both healthy and impaired motor control. Based on computational neuromechanical analyses of experimental data combined with modeling techniques, we have demonstrated several such neural constraints on the temporal and spatial patterns of muscle activity during both locomotion and postural responses to balance perturbations. We hypothesize that subject-specific as well as trial-by-trial differences in muscle activation can be parameterized and understood by a hierarchical and low-dimensional framework that reflects the neural control of task-level goals. In postural control, we demonstrate that temporal patterns of muscle activity may be governed by feedback control of task-level variables that represent the overall goal-directed motion of the body. These temporal patterns then recruit spatially-fixed patterns of muscle activity called muscle synergies that produce the desired task-level biomechanical functions that require multi-joint coordination. Moreover, these principles apply more generally to movement, and in particular to locomotor tasks in both healthy and impaired individuals. Overall, understanding the goals and organization of the neural control of movement may provide useful reduced dimension parameter sets to address the degrees-of-freedom problem in musculoskeletal movement control. More importantly, however, neuromechanical analyses may lend insight and provide a framework for understanding subject-specific and trial-by-trial differences in movement across both healthy and motor-impaired populations.

Introduction

Musculoskeletal modeling has been instrumental in understanding joint torque and muscle function during movements based on the physics of the musculoskeletal system. Because generating de novo muscle-actuated simulations of movement based on performance criteria is challenging due to both muscle redundancy and the stiffness of the solution space, particularly for unstable tasks such as walking [1], recorded movement kinetics and kinematics are often used to constrain solutions. Typically, inverse dynamics is used to estimate net joint torques [2], and muscle activation patterns sufficient to produce these net joint torques are then identified using static optimization algorithms that minimize cost functions related to total muscle activity, energetics, or effort [3,4,5,6,7,8]. Simulated muscle activation patterns can also be identified through data tracking approaches using forward dynamic simulations, in which the cost function is to match recorded kinetics, kinematics, and sometimes electromyographic (EMG) signals, perhaps approximated as on-off excitation timing [9,10,11,12]. The resulting simulations have provided much insight into the biomechanical basis of sometimes non-intuitive muscle activation patterns due to the multiarticular actions of muscles and interjoint coupling [7,13,14,15]. However, due to the biomechanical redundancy of the musculoskeletal system, the same movement can be produced by different muscle coordination patterns and may vary both across subjects as well as across trials [28]. Whereas solutions identified through optimization techniques typically predict the action of prime movers reasonably well, in many cases the activity of other muscles are not well-predicted from such optimization techniques [5,17,18], even if subject-specific data are successfully reproduced.

In addition to biomechanical considerations, understanding the principles by which the nervous system selects muscle activation patterns in a redundant space of solutions is also necessary to accurately predict muscle activity, internal forces, and the kinematics of movement. The specific muscle coordination patterns used by an individual may depend on factors other than energetics or even performance measures. Even after biomechanical constraints are fulfilled, the musculoskeletal system still offers a great deal of redundancy in the selection of spatiotemporal muscle activation patterns to achieve a task [16,19]. Other factors such as constraints of neural circuitry, the achievement of task-level goals, prior experience, or movement training can also affect how we move. Particularly in unstable tasks such as balance and locomotion [20], co-contraction of muscles for joint stability may also be an important factor in determining muscle activation patterns [21,22,23]. While co-contraction does not contribute to net muscle joint torques, it can profoundly change the internal loading forces acting on bones and joints. Correctly identifying joint loads is a current grand challenge in biomechanics and clinically relevant for progression of osteoarthritis [24]. Further, muscle activation patterns can be altered independent of limb mechanics depending upon the sensorimotor state and the implicit task-level goals of the nervous system [25,26]. Finally, individual differences in movement may arise from preferred movement patterns or strategies based on prior training or experience [27,28,29,30] that may lead to individual differences in motor control. In some cases the differences may be small but profound: for example, walking using a medial thrust gait does not change global measures such as foot placement or trunk motion but significantly alters contact forces [31] and joint torques associated with osteoarthritis progression [32]. This illustrates the flexibility afforded to the nervous system in attaining task-level goals, and the subtle differences in leg kinetics and kinematics that may emerge from altering muscle activation patterns.

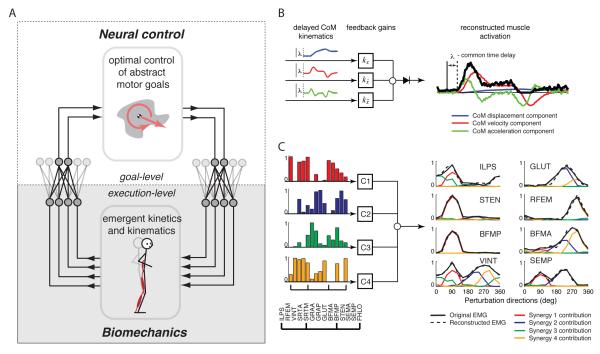
A neuromechanical approach is thus required to further advance our understanding of human movement. It is important to understand both the neural basis of muscle activation patterns, as well as the functional consequences of such patterns in a quantitative way. Here we present a high-level review of some of recent work demonstrating that muscle activation patterns may reflect a hierarchical and low-dimensional structure of neuromotor outputs that reflect control of task-level goals (Figure 1A). We have chosen to study standing balance control as a movement paradigm that can reveal general principles of how the nervous system may address muscle redundancy to achieve task-level goals. We define a task-level goal as a motor intention that cannot be directly mapped to a particular sensory input or a unique motor output. Rather, estimating the state of a task-level variable requires integration of a multiple sensory signals and cannot be inferred directly from local anatomical variables such as joint angles. Likewise, controlling a task-level variable cannot be achieved by controlling muscles, joint torques, or joint angles independently, but requires that they be coordinated in a task-specific way [33,34]. In balance control the task-level goal is well specified–i.e., to maintain the body center of mass (CoM) over the base of support (BoS) [35]–and this goal can be achieved by a number of different kinetic, kinematic, and EMG patterns [36]. We propose that the nervous system is hierarchically organized such that control of task-level goals governs the temporal patterns of muscle activity, which are then spatially distributed across many muscles to execute the movement (Figure 1A). We will present a review of research demonstrating that the temporal patterns of muscle activity in balance can be attributed to delayed neural feedback of CoM kinematics and not joint kinematics that can be described with a few feedback parameters (Figure 1B). We will then show that the temporal control of the CoM must then be translated into the appropriate spatial patterns of muscle activity via muscle synergies, which define fixed spatial patterns of multi-muscle activity producing consistent task-level biomechanical functions (Figure 1C). We will also present some examples where such principles generalize to the control of walking, and then illustrate the relevance of neural constraints on muscle activity in understanding impaired walking in people with post-stroke hemiparesis.

Figure 1.

A) Hierarchical neuromechanical framework for understanding muscle coordination. The low-dimensional structure of neuromotor outputs reflects the desired control of task-level goals. A dimensional reduction occurs in the multisensory integration mappings that use multiple afferent signals to estimate task-variables. B) In perturbed balance control, temporal patterns of muscle activity are governed by delayed feedback of CoM kinematic variables. Thus the entire timecourse of muscle activity can be compactly described using three feedback gain variables and a delay term. Each component of CoM motion is multiplied by a feedback gain at a common time delay and linearly added to produce a reconstructed muscle activation pattern or muscle synergy recruitment pattern. C) These temporal patterns reflecting task-level variables must then be mapped to a spatial distribution of muscles in order to generate execution-level motor commands to muscles. Muscle synergies allow task-level neural commands to be translated into execution-level muscle activation patterns. Spatially-fixed muscle synergies with variable recruitment patterns explain a wide variety of individual muscle activation patterns. Shown here are muscle synergies from cat responses to translation perturbations in 12 directions. Recorded muscles include Iliopsoas (ILPS), Rectus femoris (RFEM), Vastus intermedius (VINT), Anterior sartorius (SRTA), Medial sartorius (SRTM), Anterior gracilis (GRAA), Posterior gracilis (GRAP), Gluteus medius (GLUT), Anterior biceps femoris (BFMA), Posterior biceps femoris (BFMP), Semitendinosus (STEN), Anterior semimembranosus (SEMA), Posterior semimembranosus (SEMP), and Flexor hallucis longus (FHLO). The activation of an individual muscle results from adding the activation due to each muscle synergy. For 90° perturbations, the activation of SEMP is strictly co-activated with BFMP and STEN due to recruitment of the red muscle synergy. In contrast, for 270° activation of the same SEMP muscle is strictly coactivated with GLUT due to recruitment of the blue muscle synergy. Together our frameworks allow us to functionally decompose the multiple influences shaping the spatiotemporal patterns of muscle activation for task-level motor control.

Neural control of task-level variables governs temporal patterns of muscle activity

Evidence from our laboratory suggests that temporal patterns of muscle activity reflect neural control of task-level variables during balance. During postural perturbations to standing balance control, the temporal structure of muscle activation patterns is governed by delayed task-level feedback of CoM kinematics as opposed to local feedback control of joint kinematics. Thus, the entire timecourse of electromyographic (EMG) activity during recovery of balance in response to a perturbation of the support surface can be described using three feedback gains based on CoM kinematics (displacement, velocity, acceleration) acting at a common time delay (Figure 1B) which is based on the sensorimotor delays inherent in neural transmission and computation [37,38]. Further evidence that task-level and not joint-level feedback control governs temporal patterns is the robutstness of the CoM feedback model predictions in explaining the timecourse of lower limb and back muscles when differing joint-level postural strategies are employed (i.e. “ankle” and “hip” strategies) [39] and across long perturbations in which joint and CoM dynamics become uncorrelated [40]. Similarly, torque-level feedback models have revealed that each joint torque for balance control must be derived from sensory feedback arising from all other joints [41], such that local feedback mechanisms are insufficient to explain neural strategies for standing balance. Our feedback model describes the temporal pattern of activation of a muscle i, e_i(t) as follows:

$$e_i\left(t\right)=\lfloor k_{a,i}\ddot{x}(t-\lambda )+k_{\nu ,i}\stackrel{.}{x}(t-\lambda )+k_{d,i}x(t-\lambda )\rfloor ,i=1:N_{\mathit{MUS}}$$ (1)

where k_a,i’ k_v,i’ and k_d,i designate feedback gains on CoM acceleration, velocity, and displacement $\left(\ddot{x}\right(t),\stackrel{.}{x}(t)$, and x(t), respectively), λ designates a time delay associated with neural conduction and processing, and floor brackets ⌊·⌋ designate a threshold operator defined as:

$$\lfloor g\rfloor =\{\begin{array}{cc}g,\hfill & g>0,\hfill \\ 0,\hfill & g\le 0.\hfill \end{array}\phantom{\}}$$ (2)

The low-dimensional structure provided by the CoM feedback model allows us to characterize variations in muscle activation patterns for balance control across individuals, trials, and levels of impairment by varying a few parameters [37,38,39]. The robustness of the model in explaining inter-individual and inter-trial variations suggests that the nervous system does indeed modulate the control of task-level variables, and that such task-level representations can actually simplify computations for movement control. Across naïve subjects, inter-subject differences in the temporal patterns of muscle activation in postural responses can be characterized by variations in the magnitude of the three feedback gain parameters when perturbations are presented in randomized order [38,39]. However, when identical perturbations are presented serially and are thus predictable, patterns of muscle activity change [36,42]. These changes can be characterized by a gradual decrease in feedback gain magnitudes, converging toward an optimal solution that represents a tradeoff between CoM error and energetic cost [43]. The delayed CoM feedback model can equally predict temporal muscle activation patterns in cats, despite differences in biomechanical configuration compared to humans. Animals who are trained daily on a postural task over many months exhibit near-optimal temporal patterns [37]. Moreover, following large-fiber somatosensory loss, these animals converge toward a new optimal solution in which CoM acceleration feedback is absent. Together, these results suggest that the muscle activation patterns for balance control are governed by low-dimensional task-level control, but that the parameters characterizing movements within this structure may be continuously modified based on various and ever-changing factors such as energetics, stability, motor performance, or other goals.

Implications of temporal dimensional reduction and task-level control in musculoskeletal modeling

Task-level neural control has important implications for the musculoskeletal modeling community. Our results demonstrate that it is possible to interpret, as well as to predict, complex temporal patterns of muscle activity with only a small number of parameters based on task-level goals. This has the obvious computational advantage of limiting the search space for muscle activation patterns in dynamic simulations, since only a few feedback gains need to be identified for each muscle, rather than the comparatively large number of parameters necessary to specify an entire timecourse of muscle activation [cf. 1]. However, another implication of the predictive power of the concept of task-level neural control is that it suggests that bottom-up modeling approaches based only on joint-level feedback [44,45] may not be able to predict aspects of temporal patterns of muscle activity during realistic motor tasks that are believed to be governed by task-level control. Even in reactive tasks where short-latency motor responses may reflect joint-level feedback, the more substantial long-latency response to perturbations in both the upper and lower limbs reflect the control of task-level variables, such that muscle activity can be seen at joints that are not explicitly perturbed [46,47]. Thus the identification of task-level variables and the associated neural control structures are important in reactive tasks as well as voluntary tasks that involve pre-planning and anticipation. For reaching, task-level goals related to endpoint kinematics have been proposed [48]. For walking, task-level goals have been proposed such as energy exchange mechanisms [49,50,51,52] or the angular momentum of the body [53]. Understanding task-level goals can reveal the mechanisms underlying impaired locomotion; differences in amputee gait may result from their reduced ability to control angular momentum with a prosthetic limb [54]. Similarly, studies from computer animation have demonstrated that task-level control frameworks can be used to predict locomotor behaviors across a wide variety of biomechanical contexts [55].

Task-level recruitment of muscle synergies governs spatial patterns of muscle activity

In order to produce coordinated movements, low-dimensional task-level commands specifying temporal patterns must be mapped to multiple muscles distributed throughout the body. Spatial coordination of muscles across the body is required to reliably produce a given biomechanical function because individual muscles do not produce consistent biomechanical functions within the kinematically redundant and dynamically coupled musculoskeletal system [56,57,58]. In balance control we have experimentally identified muscle synergies that define fixed spatial activation patterns across multiple muscles (Figure 1C), and whose temporal recruitment varies as a function of the CoM feedback transformation described above [59]. Moreover, the structure and biomechanical functions of spatially-fixed muscle synergies appear to be consistent across a range of motor tasks. A consistent relationship between muscle synergy recruitment and endpoint force production was found in cats during balance control [60]; this direction of force production with respect to the limb axis was preserved across multiple postural configurations [61]. In humans, muscle synergy structure was consistent across postural configurations including narrow, wide, crouched, and single limb stance [62], as well as in a variety of postural responses such as hip, ankle, stepping, and feet in place [63]. Similarly, simulations in which muscle synergies constrain muscle activation patterns have reliably produced motor functions across variations in the motor task [64,65,66]. Moreover, altering the temporal recruitment of muscle synergies according to task-level demands can robustly produce a range of motor behaviors [64,67,68]. Thus, a range of motor behaviors may result from altering the temporal recruitment of a set of spatially-fixed muscle synergies.

In our work, we have operationally defined muscle synergies as muscle co-activation patterns in fixed ratios that we identify from experimental data. The use of such muscle synergies to map task-level to execution-level motor commands thus reduces the spatial dimensionality of muscular outputs. Therefore any matrix representing spatiotemporal patterns of muscle activity E(t) = [e₁(t); e₂(t); ⋯ e_NUMS(t)] with dimensions N_MUS × N_SAMP (corresponding to the number of muscles × the number of time samples) can be expressed as a linear combination of a matrix of fixed muscle synergy vectors W with dimensions N_MUS × N_SYN (the number of muscle synergies) and time-varying recruitment patterns C(t) ( N_SYN × N_SAMP) such that

$$E\left(t\right)=W\cdot C\left(t\right)$$ (3)

where element w_ij of W corresponds to the recruitment of the ith muscle in the jth synergy, and all elements of W and C are non-negative. To identify a set of muscle synergies ( W) from experimental data, we use non-negative matrix factorization (NMF) [69]. NMF produces additive components that are more physiologically interpretable than alternative approaches such as principal component analysis (PCA) [70]. For a detailed tutorial on extracting muscle synergies using NMF, please see http://www.neuro.gatech.edu/labs/ting/neuromechanics-tools/matlab-tutorial/ [70]. Although it is likely that muscle synergy structure could change over a period of training, we have demonstrated muscle synergies to be stable in the short-term, over days or weeks [28,61]. The temporal patterns of activation of each muscle synergy is determined by delayed feedback of CoM acceleration, velocity, and displacement:

$$c_{W_j}\left(t\right)=\lfloor k_{a,W_j}\ddot{x}(t-\lambda )+k_{\nu ,W_j}\stackrel{.}{x}(t-\lambda )+k_{d,W_j}x(t-\lambda )\rfloor$$ (4)

as in equation (1). We identify the feedback gains based on measured CoM kinematics [38,39,59].

Although there are varying ideas about the nature and organization of modularity in the nervous system, some of the alternate schemes cannot be feasibly implemented for reactive postural control. Reactions to perturbations are shaped by online feedback signals that are dependent upon the characteristics of the perturbation, and thus temporal patterns of muscle synergy recruitment cannot be generated using feedforward mechanisms that have been postulated in alternate hypotheses that may be more appropriate for locomotor tasks. For example, some studies examining modularity during locomotion have suggested that temporally-fixed patterns of muscle recruitment are coupled to spatially-varying muscle weightings [71,72,73]. Alternatively, in reaching, both spatiotemporal aspects have been proposed to be coupled such that preplanned temporal patterns are scaled to the desired reach amplitude and duration [74,75,76,77]. In contrast, studying reactive feedback tasks has allowed us to dissociate the control of spatial and temporal features of muscle activity, and we have explicitly demonstrated that temporally-fixed structures are insufficient to reproduce muscular variability in balance control [59]. Whereas the fixed temporal patterns for locomotion must be scaled as a whole, precluding online modification, in our scheme, the temporal structure is based on a low-dimensional sensorimotor feedback transformation for task-level feedback control of the CoM, which shapes motor patterns based on recent kinematic states. We propose that the control of temporal and spatial features of muscle activity are hierarchically controlled, each by independent low-dimensional control structures. This hypothesis is consistent with current models of locomotor central pattern generator circuits in which temporal rhythm generation is independent of and recruits structures that specify the spatial patterning of muscle activity [78]. Likewise, locomotor data has been robustly explained using spatially-fixed patterns of muscle activation, while allowing the temporal recruitment to vary according to the task demands [79,80]. Neurophysiological studies also support the hypothesis that fixed muscle synergies encoded in the spinal cord are differentially recruited by temporal patterns from higher neural centers [81,82,83].

Evidence that muscle synergies can characterize inter-subject and inter-trial variations in balance control further supports the idea that muscle synergies reflect the lowest level of functional organization in the motor repertoire. The spatially-fixed muscle synergies we have identified are specific to individual subjects, and also constrain the trial-by-trial variability observed within an individual [28,62]. Thus, using muscle synergies does not preclude variability in motor output or motor performance, but rather suggests that the variability reflects variations at the level of task-level neural control [84] rather than random noise in the excitation of individual muscles. Inter-trial variability in muscle activation patterns provides important information that is critical to identifying the common underlying structure in muscle synergies across movements. Averaging trials may thus obscure the underlying structure of motor outputs. Additionally, we observe different muscle activation patterns across individuals that may produce similar functions [61,63]. Each individual uses a unique set of muscle synergies that varies in both structure and number of muscle synergies, however this set is consistent across motor tasks and over a period of at least days and weeks [28,61,62,63]. While differences in anatomy may contribute to such differences in muscle synergies, it is likely that prior training and motor skill also influence subject-specific muscle synergies, which may lead to dissimilar kinetic and kinematic patterns for achieving an equivalent task-level goal. Using muscle synergies may contribute toward understanding inter-subject differences in movement, as well as explain a common motor structure governing intra-subject differences in motor performance.

The proposed hierarchical and modular organization of muscle activity may also underlie more dynamic behaviors such as walking and reaching. Cycle-by-cycle variations in walking patterns across walking speeds can be accounted for by four muscle synergies [80]. The recruitment of these muscle synergies appears to be related to function rather than a specific phase of the gait cycle [65,80,85]. For instance, each muscle synergy contributes to a function such as weight support, forward propulsion of the body, and deceleration of the leg [64,65]. Locomotor muscle synergies have also been found to be consistent across postural configurations and loading in cycling [79]. Similarly, in reaching tasks, muscle synergies are consistent across reaching directions [74,75] and differentially modulated during movements with changing target directions [76]. The same muscle synergies may also underlie reactive and voluntary tasks. During perturbed walking, muscle synergies for walking were recruited in atypical phases of the gait cycle in both a feedback manner in response to the perturbation as well as in anticipation of the perturbation [85]. This is consistent with neurophysiological evidence that spinally-encoded muscle synergies can be flexibly recruited from a variety of pathways, including the central pattern generator for walking, brainstem-mediated pathways used for balance control, as well as higher descending influences [81,82,86,87].

Implications of spatial dimensional reduction and task-level control in musculoskeletal modeling

Muscle synergies represent a feasible, neurally plausible control strategy for control of musculoskeletal models that may provide increased computational efficiency as well as improve predictions of muscle activity in simulations. Although the possibility exists that reducing the number of controlled variables from the number of muscles to the number of muscle synergies could limit the repertoire of possible motor behaviors [88], the feasibility of muscle synergy-based control strategies has been demonstrated in simulations of multiple motor tasks [64,65,66,68,89]. Moreover, the behavioral repertoire afforded by muscle synergy control has been shown to be similar to that provided by individual muscle control [67,90,91], although additional muscle synergies, or subdividing of muscle synergies may be necessary if task biomechanics diverge significantly [64,65]. These results are encouraging for modeling because they suggest that the search space of controlled variables for predicting natural movements may be reduced from the number of muscles to the number of muscle synergies, leading to speedups in computation time [67,91], particularly in the search for feasible, rather than optimal recruitment patterns [64]. Further, results from our laboratory suggest that muscle synergy control may also improve predictions of muscle co-activation in optimizations based on minimization of energetic cost [91]. However, it is also likely that true neural control of task-level variables is conditioned on degree of intrinsic stability of the musculoskeletal system from both muscle properties and local joint feedback circuits, which must be added to existing musculoskeletal models [20, 92].

Although modeling and experimental work define muscle synergies that are qualitatively similar, practical limitations complicate quantitative comparisons of modeled and experimentally determined muscle synergies. The muscles included in each muscle synergy are usually similar between models and experiments, particularly in the case of large, “prime mover” muscles [66,67]. In some cases, the muscles included in a modeled muscle synergy can be adjusted manually to better match experimentally identified muscle synergies [68], or experimentally-identified muscle synergies can be used as initial guesses in optimization procedures and modified somewhat to achieve simulation constraints [65]. However, muscle synergies in musculoskeletal models cannot typically be quantitatively compared to muscle synergies identified in EMG data because 1) the number of recorded muscles is typically fewer than the number of modeled muscles, and 2) normalization of EMG data, for example using maximum voluntary contraction, may be error-prone, and is often unavailable in studies involving animal models.

Because of these difficulties, simulating muscle synergy control presents additional challenges for musculoskeletal modeling in that muscle synergy vectors must often still be estimated using optimization approaches in concert with experimental kinetic and EMG data. Two main approaches have been used to address this problem. Some studies have estimated muscle synergies without relying on experimental data, for example, by approximating optimal solutions for the control of individual muscles with NNMF [90] or by identifying muscle synergies that can best span the input-output relationship of a musculoskeletal model identified through model order reduction techniques [67]. The disadvantage of these approaches is that they essentially suffer from the same complexities and weaknesses as using optimality principles to predict muscle activity, for example, requiring large-scale searches and other sophisticated computational techniques [1]. An alternative approach used in studies from our laboratory and others is to estimate muscle synergies by using experimentally-recorded force data as constraints in static optimization procedures [66,68,91,92]. We have found this approach to be advantageous because it is straightforward and predicts experimental data well. However, as described above it may be important to avoid averaging experimental data, as we have found that sets of muscle synergies identified in different experimental animals may make different predictions, even when an identical musculoskeletal model is used [91].

Hierarchical control of muscle synergies: applications to motor deficits

Understanding the control of muscle synergies may be critical to understanding movement deficits that originate from within the nervous system, such as stroke, cerebral palsy, and Parkinson’s disease. In particular, hemiparesis following stroke is due to disruption of descending neural pathways, with no direct effects on the musculoskeletal system or spinal circuitry. We found that the number of muscle synergies identified in muscle activation patterns during walking was reduced in the paretic limb compared to controls [80]. In both healthy subjects and in the nonparetic limb of stroke subjects, an average of 4 muscle synergies were recruited during forward walking across a range of speeds. In contrast, the number of muscle synergies identified in the paretic limb varied between 2 and 4 across subjects (n = 55). Moreover, the number of muscle synergies, a measure of the complexity of the neural output signal, was directly correlated to biomechanical measures of walking capacity, including walking speed, propulsive force, and gait asymmetry. The muscle synergies identified were frequently merged versions of those identified in the nonparetic limb and in control subjects. These results support the idea that muscle synergies allow the nervous system to robustly perform distinct biomechanical functions, and that independent recruitment of those functions are lost following stroke. Furthermore, examining the structure and recruitment of muscle synergies may also be useful for understanding peripheral deficits (i.e. amputation, loads, braces, orthotics, implants), because adaptation may be constrained by the muscle synergies.

The control of muscle synergies may be particularly relevant in musculoskeletal modeling of movement deficits because neural constraints on muscle activation may play an even larger comparative role in determining movements than the optimal control of the physics of the musculoskeletal system. Multiple modeling studies have found that in considering healthy populations, muscle synergy control may provide a good approximation of the primary features of the optimal control of individual muscles [67,91,93,94]. These studies suggest that approaches based on musculoskeletal modeling and optimization can predict muscle synergy structures as well as resulting behaviors. However, in stroke or other conditions with motor deficits, although the same underlying task-level control and muscle synergy structures may exist, evidence suggests that abnormal recruitment of muscle synergies may result in movements that are far from optimal. Because the same muscle synergies have been identified in conditions with motor deficits [80,81,82,95] it may not be possible to predict spatial muscle activation patterns in pathological movements based on optimization. However, it may be possible to simulate pathological movements by reducing the number of independently recruited muscle synergies. For example, reducing the number of independent muscle synergies in simulations of forward pedaling gaits that emulate those seen in hemiparesis where the crank may be advanced but the motion lacks smoothness, or it may not be possible to achieve the task [64]. Using muscle synergy analyses to better understand motor deficits is an emerging field and an ongoing priority in our research.

Conclusion

As biological movement results from neuromechanical interactions, furthering our understanding of subject-specific movements in healthy and motor-impaired individuals requires that both biomechanical and neural constraints governing movement be adequately represented in our models. While neural and biomechanical models have independently provided insights into the principles governing movement control that are common across subjects, future challenges require that we understand subject-specific differences in musculoskeletal anatomy, neural control mechanisms, as well as their interactions. Understanding generative mechanisms for movement will probably require the addition of 1) top-down approaches that consider task-level goals as the primary determinant of kinematic and kinetic variables [53,55,96], and 2) constraints on independent production of joint torques that mirror the divergent anatomy of interneurons that co-activate motoneurons [97,98]. Recent studies have demonstrated the potential power of such approaches in explaining and simulating movement during normal and impaired motor tasks; these studies emphasize the need for simulation platforms that facilitate exploration of the interactions between neural, muscular, and skeletal dynamics (see Bunderson et al., this issue and [99]). Once such mechanisms are in place, subject-specific and trial-by-trial differences in movement may be explored based on parametric differences in the costs and constraints associated with attainment of task-level goals. Such advances will be critical in understanding both healthy and impaired movements, as well as techniques for restitution of function via rehabilitation, prosthetics and orthotics, or assistive devices.