Dimensional reduction in sensorimotor systems: A framework for understanding muscle coordination of posture

Abstract

The simple act of standing up is an important and essential motor behavior that most humans and animals achieve with ease. Yet, maintaining standing balance involves complex sensorimotor transformations that must continually integrate a large array of sensory inputs and coordinate multiple motor outputs to muscles throughout the body. Multiple, redundant local sensory signals are integrated to form an estimate of a few global, task-level variables important to postural control, such as body center of mass position and body orientation with respect to Earth-vertical. Evidence suggests that a limited set of muscle synergies, reflecting preferential sets of muscle activation patterns, are used to move task variables such as center of mass position in a predictable direction following a postural perturbations.

We propose a hierarchal feedback control system that allows the nervous system the simplicity of performing goal-directed computations in task-variable space, while maintaining the robustness afforded by redundant sensory and motor systems. We predict that modulation of postural actions occurs in task-variable space, and in the associated transformations between the low-dimensional task-space and high-dimensional sensor and muscle spaces. Development of neuromechanical models that reflect these neural transformations between low and high-dimensional representations will reveal the organizational principles and constraints underlying sensorimotor transformations for balance control, and perhaps motor tasks in general. This framework and accompanying computational models could be used to formulate specific hypotheses about how specific sensory inputs and motor outputs are generated and altered following neural injury, sensory loss, or rehabilitation.

Postural control is a fundamental motor task ideally suited for investigating questions of sensorimotor integration and redundancy. The ability to maintain posture and balance are precursors to other voluntary movements such as reaching or walking over uneven terrain. Moreover, loss of balance is a clinically important problem, as falls are a primary cause of injury and accidental death in older adults (Minino et al., 2002). Yet, we currently have little understanding of the underlying neuromechanical principles that govern patterns of muscle activation during postural control or other basic motor behaviors.

Although technological advances allow the simultaneous measurement of multiple kinematic, kinetic, and electromyographic (EMG) data channels during behavioral experiments, we lack a framework for understanding how all of these measured variables are related to the control and performance of a functional task. Without this basic understanding, we cannot begin to understand or predict how patterns of muscle activation should be altered to perform novel tasks, nor can we understand the functional impact of disordered patterns of muscle activation in neurologically impaired individuals. In addition to making multiple measurements, advances in motor control must reveal why a particular pattern of muscle activation is chosen by the nervous system to achieve task goals. A quantitative framework for understanding the neuromechanical interactions and sensorimotor transformations during standing postural control is critical to unraveling the underpinnings of this important behavior.

A general framework will be presented that can be used to formulate specific hypotheses about sensorimotor transformations, and provide an organizational scheme for formulating computational and experimental studies of postural control. Computer simulations of the neuromechanical transformations from sensory input to motor output are critical for understanding the neural mechanisms underlying spatial and temporal patterns of muscle activation. Such simulations can also serve as a virtual test-bed for quantifying the functional impact of neurological disorders on postural control. Moreover, the framework has significant implications for understanding and evaluating experimentally-measured changes in muscle activation patterns due to learning, adaptation, injury, or disease. The general principle of dimensional reduction may be common to many motor control processes and can guide our approaches to understanding and improving motor dysfunction.

First, the fundamental “degrees of freedom” problem and its relevance to postural control will be reviewed. Then, experimental evidence that establishes the critical role of task-level sensorimotor integration processes during standing balance will be presented. Next, findings demonstrating that muscle activation patterns used during postural control can be simplified to combinations of a few muscle synergies--patterns of muscle activity used to control task-level biomechanical variables—will be discussed. Finally, a framework that integrates these observations of dimensional reduction in sensorimotor signals during postural control will be presented.

Degrees of freedom problem

To maintain standing balance, the nervous system must confront the classic “degrees of freedom” problem posed by Nikolai Bernstein (Bernstein, 1967), where many different solutions to a task are available due to the large number of elements that need to be controlled, or degrees of freedom, in the system. In postural control, muscles and joints across the limbs, trunk, and neck must be coordinated to maintain the body’s center of mass (CoM) over the base of support, typically formed by the feet. The many degrees of freedom afforded by the joints and muscles allows for multiple (i.e. redundant) solutions, allowing the nervous system flexibility in performing the postural task. This redundancy poses a problem to the nervous system: it must choose from a large set of possible solutions because the task requirements are not sufficient to uniquely specify how each muscle and joint must be controlled.

Bernstein proposed a neural strategy for simplifying the control of multiple degrees of freedom by coupling, or grouping, output variables at the kinematic level (Bernstein, 1967). This scheme was based on experimental observations that multiple joint angles appear to be controlled together, rather than independently, during motor tasks. For example, during running, the hip, knee, and ankle joints all flex and extend at the same time, suggesting that they are not controlled independently. This co-variation of joint angles has the effect of moving the CoM vertically in a simple motion that mimics the bouncing of a spring and mass system (Blickhan, 1989, Farley et al., 1993, McMahon and Cheng, 1990). In walking, the lower limb joint angles co-vary in a different pattern such that the overall motion of the CoM resembles that of an inverted pendulum (Cavagna et al., 1977, Minetti, 2001). Therefore, the overall effect of such joint angle co-variations, or kinematic synergies, may be to produce a predictable and simple motion of the task-variable at hand--in the case of locomotion, the trajectory of the CoM.

Yet, the strict co-variation of joint angles themselves does not appear to be the end-goal of the nervous system computation. Task-variables such as the CoM trajectory in postural control, or the finger trajectory in pointing movements, appear to be more precisely controlled by the nervous system than individual joint angles (Scholz and Schoner, 1999, Scholz et al., 2000), suggesting that the task-variables have special significance to the nervous system.

The neural principles and mechanisms underlying our ability to control task-variables within a high-degree of freedom system are still unknown and require further investigation into the specific sensorimotor transformations that facilitate these behaviors. While kinematic observations can identify important correlations and task variables controlled by the nervous system, they do not directly specify which muscle activation patterns should be used to produce the movements. This problem arises because Bernstein’s degrees of freedom problem also exists in the transformation between muscle activation patterns and kinematic patterns of movement. This additional redundancy in the musculature results not only because multiple muscles cross each joint, but also because the biomechanical equations of motion are such that different temporal patterns of muscle activation can lead to similar joint trajectories (Gottlieb, 1998). Therefore both spatial and temporal muscle activation patterns have a degree of redundancy that must be managed by the nervous system. To gain a deeper understanding of the underlying neural mechanisms for controlling task variables, the complex spatiotemporal coordination of multiple muscles and their effect on biomechanical task outputs must be considered.

We propose that the reduction of degrees of freedom observed at the biomechanical level reflects a reduction in degrees of freedom at the level of the neural circuits that activate muscles. Muscle synergies could be a mechanism through which nervous system achieves repeatable and correlated multi-joint coordination. We define muscle synergies to be a specific pattern of muscle co-activation. Each muscle synergy is presumed to be controlled by a single neural command signal, which modulates the overall magnitude of the patterns specified by a muscle synergy. Although muscle synergies simplify spatial coordination of muscles, temporal variations of the neural command signal must still be specified to achieve a motor task. We will address possible mechanisms for simplification of both spatial and temporal muscle activation patterns.

Postural responses to perturbations

The overall goal in standing equilibrium can be simply defined as maintaining the CoM over the base of support; however, there are multiple strategies for accomplishing this goal. For example, it is possible to extend the base of support by taking a step or using the hands to hold on to a stable object (Maki et al., 2003, Horak and Macpherson, 1996). The ability to choose an appropriate postural control strategy reflects complex and integrative sensorimotor processes. Successful balance control depends on having accurate knowledge of the entire body configuration in space, as well as the location of the body CoM relative to the line of gravity and the base of support. The activation of muscles in response to a perturbation results from integration of multiple sensory signals to properly estimate CoM displacement and earth-vertical. This role of local sensory signals in estimation of critical task-level variables is also illustrated by psychophysical experiments whereby perturbations to a single sensory channel create illusions of shifting earth-vertical, or the entire body orientation (Mergner and Rosemeier, 1998, Mergner et al., 2003, Hatzitaki et al., 2004, Hlavacka et al., 2001, Scinicariello et al., 2002). While postural responses themselves are thought to be integrated in the brainstem and cannot be voluntarily suppressed following a perturbation, postural strategy selection and postural response amplitude can depend on many different descending, cognitive, and emotional influences, such as habituation, divided attention, or fear (Woollacott and Shumway-Cook, 2002, Carpenter et al., 2006, Keshner et al., 1987).

Even within a specific postural response strategy, the rapid activation of muscles to stabilize the body CoM is finely tuned to the biomechanics of the perturbation, in particular, direction. When the support surface is translated in each of many directions in the horizontal plane, simulating a “slip”, multiple muscles across the body are activated by an amount related to the direction of the perturbation (Nashner, 1976, Henry et al., 1998, Horak and Macpherson, 1996, Macpherson, 1988a, Macpherson, 1988b). For example, a different set of muscles is activated in response to a forward perturbation versus a backward perturbation (Figure 1A). The directional sensitivity of the postural response can be represented as muscle tuning curves that illustrates the response amplitude as a function of direction and demonstrate that little co-contraction of antagonist muscles occurs (Figure 1B). Each muscle also has a unique tuning curve, demonstrating that postural responses are not fixed response patterns (Macpherson, 1988b, Horak and Macpherson, 1996, Ting and Macpherson, 2004, Ting and Macpherson, 2005). The tuning of muscle activation is already evident in the initial automatic postural response that begins 100 ms after the onset of platform motion in humans (Figure 1A), well before the CoM displacement reaches its maximum (Horak and Macpherson, 1996).

Figure 1. Muscle activity evoked following perturbations to the support-surface.

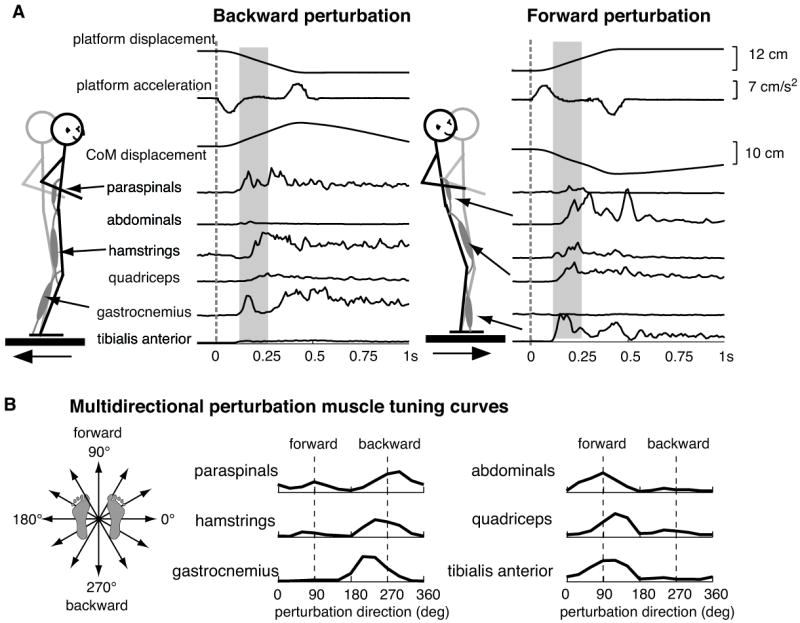
A) Backward perturbations of the support surface elicit activity in muscles on the posterior side of the body. Forward perturbations elicit activity in muscles on the anterior side of the body. The gray area represents the initial muscular response to perturbation, called the automatic postural response (APR). Note that at the onset of the APR, the amplitude of platform and center of mass displacement are quite small. B) The magnitude of the response during the APR varies as a function of direction and can be plotted as a tuning curve. Each muscle has a unique tuning curve, suggesting that each muscle is activated by a separate neural command signal.

Multisensory integration for postural control

Directional tuning in postural responses reflects integration of multiple sensory inputs to arrive at an estimate of the CoM displacement--the task-variable that must be controlled by the nervous system. This has been deduced from several studies showing that the spatial patterns of muscle activation during the postural response cannot be consistently correlated to any single sensory signal (Allum et al., 1998, Allum and Carpenter, 2005, Carpenter et al., 1999, Ting and Macpherson, 2004, Horak and Macpherson, 1996, Inglis and Macpherson, 1995, Runge et al., 1998, Keshner et al., 1988). Only the direction of CoM displacement can accurately predict the muscle activation patterns used in response to a perturbation (Gollhofer et al., 1989, Nashner, 1977, Ting and Macpherson, 2004, Carpenter et al., 1999). Since CoM motion is due to movement of all body segments, a combination of multiple sensory signals, including visual, vestibular, proprioceptive, and cutaneous signals, which encode local variables such as head motion in space or joint angle, must be considered to explain accurate directional tuning of postural responses. This means that no single sensory modality can accurately predict the direction of CoM movement caused by a perturbation.

As an example, support surface rotations in pitch and roll can elicit similar patterns of muscle activation to support surface translations in the horizontal plane as long as the net motion of the CoM induced by the perturbation is the same (compare Figure 2A and 2C). However, these conditions impose opposite changes in local joint angle displacements and head acceleration, and therefore opposite proprioceptive, vestibular, as well as visual cues (Nardone et al., 1990, Diener et al., 1983, Carpenter et al., 1999, Ting and Macpherson, 2004). Depending upon postural perturbation characteristics, short-latency responses can be evoked, but they do not provide any appreciable torque for stabilizing the body, and in some cases may be destabilizing (Nashner, 1976, Carpenter et al., 1999). The short-latency responses occur in muscles that are stretched and reflect local monosynaptic spinal circuits whereas, the longer-latency automatic postural response is multisynaptic and reflects both the direction of impending CoM destabilization and the postural strategy selected. In translation perturbations, short-latency responses occur in the same muscles as do the longer-latency postural response (Figure 2A), but in rotation perturbations, the short- and long-latency responses occur in opposite muscles (Figure 2B, 2C). Thus, if local variables such as muscle stretch were used to generate postural responses an incorrect response would occur in the case of rotations (Figure 2B).

Figure 2. Illustration demonstrating that local muscle stretch cannot predict postural responses.

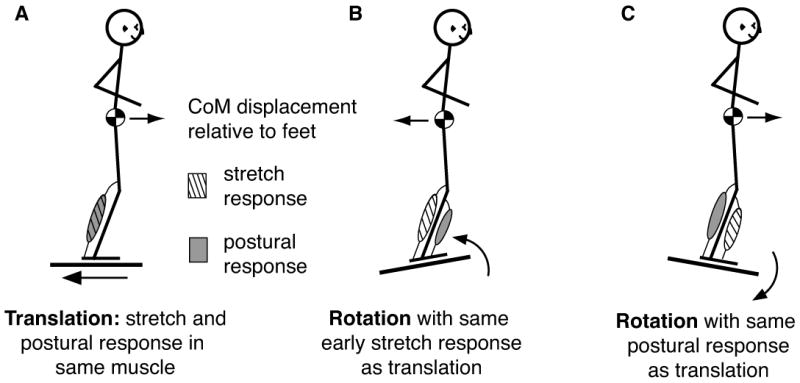
A) In translation perturbations of the support surface, the muscle stretch and postural response occur in the same muscles—in the case of backward perturbations, the triceps surae. B) In rotation perturbations of the support surface, the muscle stretch and the postural response occur in the opposite muscles. In the case of a toes-up rotation, the triceps surae is stretched, but the postural response occurs in the antagonist, the tibialis anterior. Therefore, the short-latency stretch response is possibly destabilizing. C) In toes-down perturbations of the support surface, the postural response occurs in the triceps surae muscle, the same as in the backward translation in A. In both cases, the center of mass is displaced in the forward direction relative to the base of support, requiring triceps surae activation. The direction of this more global, task-level variable that is not directly detected by any one sensory modality is the best predictor of muscle activation patterns during postural responses. (Illustration after Nashner 1976)

Neurophysiological, psychophysical, and biomechanical studies all demonstrate that estimates of body position and motion in space are achieved by combining multiple sensory information through an internal model and not through a simple summation of sensory inputs (Merfeld et al., 1999, Zupan et al., 2002, Kuo, 2005, Mergner et al., 2003). Supporting this idea, perturbations to a particular sensory organ through experimental manipulations tend to alter the global perception of vertical rather than the more local variables of head orientation in space, or ankle angle, respectively (Lackner et al., 2000, Sorensen et al., 2002, Popov et al., 1986, Tardy-Gervet and Severac-Cauquil, 1998, Park et al., 2006, Bisdorff et al., 1996, Gurfinkel and Levick, 1991, Maurer et al., 2001). It is not clear where in the nervous system multisensory integration occurs. There is evidence that task-level variables such as leg length, orientation, velocity, and end-point force are already represented in ascending afferent pathways originating from the spinal cord (Bosco and Poppele, 2001, Bosco et al., 1996, Bosco and Poppele, 1997, Lemay and Grill, 2004).

Synergy organization of motor outputs in posture

While each muscle’s directional tuning curve is unique, the control of muscles for posture appears to be simplified by the activation of a limited set of muscle synergies. We define a muscle synergy to be a muscle activation pattern with consistent spatial and temporal characteristics. Each muscle synergy is presumed to be controlled by a single neural command signal that modulates the magnitude of the muscle activation pattern specified by the synergy.

Older concepts of muscle synergies were restrictive in specifying a small set of fixed postural response patterns. Clinically, the term synergy sometimes refers to an inflexibility in motor patterns, such as the abnormal co-activation of flexors or of extensors seen in hemiplegia associated with stroke (Bourbonnais et al., 1989). In postural control, the idea of muscle synergies arose from the observation of distinct and mutually exclusive muscle activation patterns in response to two opposite directions of perturbation of the support surface, forward and backward (Figure 1A, after Nashner, 1977). In this early conception, the two identified muscle synergies define just two possible muscle activation patterns that specify strict correlations across multiple muscles (Figure 3A and Figure 4). Moreover, each muscle belongs to only one synergy, and only a single synergy can be activated during any given postural response. However, when the experimental paradigms for investigating postural control were expanded to include multiple perturbation directions in the horizontal plane, muscle activation patterns were not found to be strictly correlated across all directions in both cats and humans (E.g. Figure 1B and Figure 3B, Macpherson, 1988b, Henry et al., 1998), and the question of whether muscle synergies were a useful or physiological concept was debated (Macpherson, 1991).

Figure 3. Comparison of “fixed” versus “flexible” muscle synergy concepts.

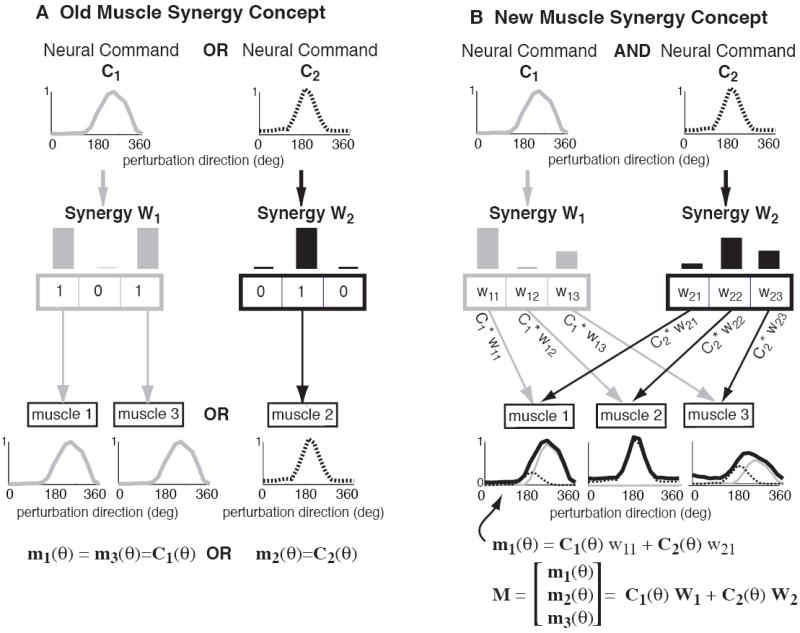
A) In the original muscle synergy concept, only one muscle synergy was elicited at a time, and muscles could only be activated by one synergy. Therefore, all muscles activated by the same synergy would have the same tuning curve, determined by the neural command, C_i, that activated it. B) In the new concept, more than one synergy can be activated at a time. Further, muscles can participate in multiple synergies, and have different weightings in each synergy. Each muscle’s tuning curve is a weighted average of the two tuning curves of each muscle synergy. This allows flexibility in muscle tuning curves while also reducing the dimension of the neural control task.

Figure 4. Two postural strategies for controlling the center of mass in response to backward perturbations of the support surface.

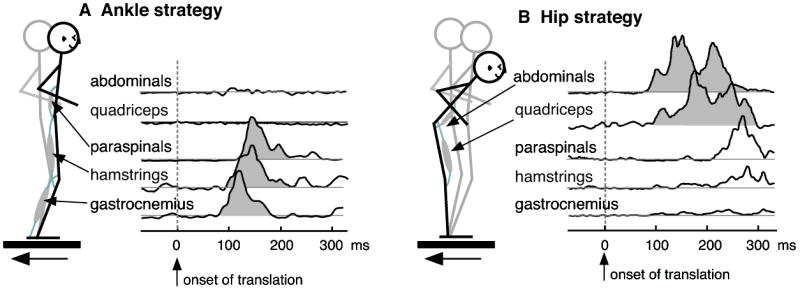
The two postural strategies are characterized by different joint motions and muscle activation patterns. A) In the ankle strategy, motion is restricted to the ankle joint, and muscles on the posterior side of the body are activated. B) In the hip strategy, the hip is flexed and muscles on the anterior side of the body are activated, but at longer latencies than in the ankle strategy. These two strategies represent extremes of a continuum, and a mixture of the two strategies can be observed in most postural responses (Creath et al., 2005, Runge et al., 1999).

In more recent formulations, it has been recognized that a limited number of muscle synergies can give rise to a continuum of postural responses. Although muscle activation patterns may not be strictly correlated across all perturbation directions, the set of postural responses has a lower dimension than the number of perturbation directions or muscles controlled, and can be accounted for by the flexible “mixing” of a limited set of muscle synergies (Figure 3B), as well as the fact that muscles can participate in more than one muscle synergy. In the example shown, the amplitudes of neural commands c₁ and c₂ can be varied independently, resulting in three different muscle tuning curves (Figure 3B).

When analyzing a set of muscle activation patterns measured experimentally, the muscle synergies used to generate that set can be identified using matrix factorization techniques (Tresch et al., 1999, Tresch et al., 2006). Mathematically, each muscle activation pattern is hypothesized to be a linear combination of a few (n) muscle synergies W_i, whose elements, w_ij, specify the pattern of muscle activity defined by that muscle synergy (Figure 3B, bar plots). Each muscle synergy is activated by one neural command, c_i, which can vary as a function of experimental condition such as perturbation direction, θ. C_i(θ) is a vector where each element specifies the level of the neural command over a range of perturbation directions, θ (Figure 3B, top). The net muscle activation pattern vector for any muscle over a range of perturbation direction, m_i is therefore hypothesized to take the form:

$${\mathbf{m}}_{\mathbf{i}}\left(\mathrm{\theta }\right)={\mathbf{C}}_{\mathbf{1}}\left(\mathrm{\theta }\right){\mathrm{w}}_{1\mathrm{i}}+{\mathbf{C}}_{\mathbf{2}}\left(\mathrm{\theta }\right){\mathrm{w}}_{2\mathrm{i}}+\dots .+{\mathbf{C}}_{\mathbf{n}}\left(\mathrm{\theta }\right){\mathrm{w}}_{\mathrm{ni}}$$

Where w_1i is the i’th element of synergy 1, W₁ and so on. Similarly, the overall muscle activation pattern for any given perturbation direction can be expressed a vector where each element is the resulting level of activation in each muscle:

$$\mathbf{m}\left({\mathrm{\theta }}_{\mathrm{\kappa }}\right)={\mathrm{c}}_{1\mathrm{k}}{\mathbf{W}}_{\mathbf{1}}+{\mathrm{c}}_{2\mathrm{k}}{\mathbf{W}}_{\mathbf{2}}+\dots .+{\mathrm{c}}_{\mathrm{nk}}{\mathbf{W}}_{\mathbf{n}}$$

Where c_1k represents the k’th element of C₁(θ), corresponding to the particular perturbation θ_κ. The matrix M is a concatenation of responses in all muscles across different experimental conditions, where each row represents a muscle, and each column an experimental condition such that:

$$\mathbf{M}={\mathbf{C}}_{\mathbf{1}}\left(\mathrm{\theta }\right){\mathbf{W}}_{\mathbf{1}}+{\mathbf{C}}_{\mathbf{2}}\left(\mathrm{\theta }\right){\mathbf{W}}_{\mathbf{2}}+\dots .+{\mathbf{C}}_{\mathbf{n}}\left(\mathrm{\theta }\right){\mathbf{W}}_{\mathbf{n}}$$

Each element of W_i takes a value between 0 and 1, representing the relative contribution of each muscle to that muscle synergy. In postural responses, this analysis has been used to investigate the initial response in a single time window, where the columns of M represent different perturbation directions. However, the muscle synergies can also be viewed as being modulated by a set of independent time-varying neural commands, c_i(t), where each time point is treated as a condition in the columns of M (Ivanenko et al., 2005, Ivanenko et al., 2003, Ivanenko et al., 2004). Several mathematical analysis techniques such as principal components analysis (PCA), independent components analysis (ICA), and factor analysis (FA) can be used to find muscle synergies (Tresch et al., 2006). Another such technique, non-negative matrix factorization (NMF), allows complex data sets to be more successfully partitioned into meaningful parts (Lee and Seung, 1999, Ting and Macpherson, 2005, Tresch et al., 2006).

Because the number of muscle synergies is smaller than the number of muscles, the spectrum of muscle activation patterns that can be generated using muscle synergies is still more limited than the case where muscles are controlled independently. Multiple muscle synergies may exist even for a single postural perturbation. In backward translation of the support surface in humans, two types of responses can be elicited (Nashner, 1976). One is called the “ankle strategy”, where the body remains upright and most of the motion occurs around the ankle joint. The other is called the “hip strategy”, where the trunk tilts forwards and the hip angle motion is most predominant (Figure 4). Each strategy can be defined by a distinct spatiotemporal pattern of muscle activation (Figure 4) and a specific pattern of joint torques (Runge et al., 1999, Alexandrov et al., 2001a, Alexandrov et al., 2001b, Alexandrov et al., 2005). Muscle synergy analysis of human postural responses demonstrates that each strategy corresponds to an independently modulated muscle synergy (Torres-Oviedo et al., 2005, Torres-Oviedo and Ting, 2006). This is consistent with studies at the joint torque and joint motion level suggesting that hip and ankle strategies represent two biomechanical response modes which are combined to form a continuum of postural responses (Creath et al., 2005, Runge et al., 1999). The flexible combination of two different synergies may underlie variations in the automatic postural response that have been shown to occur with perturbation amplitude, prior experience, and anticipation (Woollacott and Shumway-Cook, 2002, Carpenter et al., 2006, Keshner et al., 1987, Brown et al., 2002, Maki et al., 1991, Carpenter et al., 2004). Muscle synergy analysis might therefore provide a method to quantitatively compare postural responses with variable contributions from the two strategies. If so, this would suggest that muscle synergies are mechanisms by which descending influences can affect postural strategy selection (Park et al., 2004, Kuo, 1995, Horak et al., 1997).

The robustness of muscle synergies has been most thoroughly demonstrated in cat postural responses using different experimental conditions (Torres-Oviedo et al., 2006). The muscle synergies extracted from translation perturbation responses represent coordinated patterns of muscle activity across the entire limb (Figure 5A). These patterns are roughly grouped by anatomical function, but the patterns are not strictly predictable from muscle moment arms alone. In quiet standing, only one muscle synergy, dominated by extensor muscles, is active (Figure 5B, red). Following a perturbation, each muscle synergy has a distinctive tuning curve, which represents the purported neural command, c_i, to each muscle synergy for each perturbation direction (Figure 5B, lower). These muscle synergies are robust in that they are used under multiple biomechanical configurations that produce changes in the muscle tuning curves (Figure 5) as well as the active forces for stabilization. For example, when stance distance is changed, the neural commands to some of the muscle synergies change, while others remain relatively constant (Figure 5B). These changes can explain the variations in muscle tuning curves in the hindlimb muscles (Figure 6, black lines). Each muscle tuning curve is the sum of all the synergies activating a given muscle. Therefore, a change in any of the synergy commands will result in a change in the overall muscle tuning curve. Thus, the contribution of each muscle synergy to each tuning curve can explain the different tuning curve changes with stance distance in each muscle (Figure 6, colored lines). The robustness of the synergy structure is further demonstrated by the fact that the same muscle synergies can account for the postural responses to two very different types of perturbation. For example, the same set of synergies account for muscle tuning curves from postural responses to both translations and rotations, where, as explained in the previous section, the sensory inputs from the two types of perturbation vary dramatically. This further demonstrates that the muscle synergies reflect a motor output mechanism that is distinct from local or central processing of afferent information.

Figure 5. Muscle synergies robustly produce endpoint forces in cat postural control.

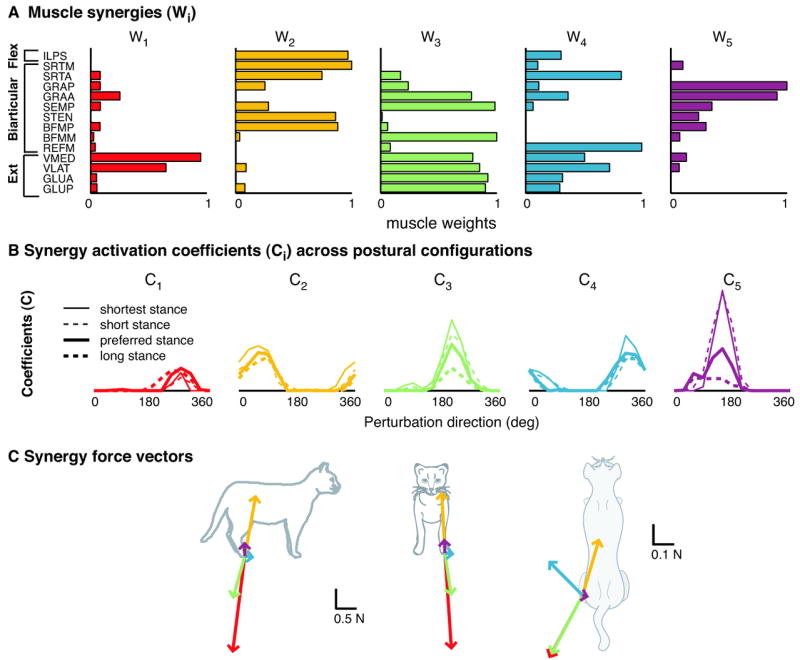
A) Five muscle synergy vectors, W_i, extracted from postural responses to support surface translation at the preferred stance distance in cat Bi. These five muscle synergies account for over 96% of the total variability accounted for in the preferred stance. Each bar represents the relative level of activation for each muscle within the synergy. Note that muscles can contribute to multiple muscle synergies. B) Activation coefficients, C_i, representing the purported neural commands to each muscle synergy during postural responses in four different postural configuration. Upper traces show background activity of each muscle synergy during the quiet stance period before perturbations. Lower traces show the synergy tuning curves in response to support surface translations. Changes in muscle tuning curves at different stance distances are due to variations in the amplitude of the neural commands to the various muscle synergies. Some muscle synergies (e.g. red, yellow) are relatively constant amplitude across all conditions, whereas others (e.g. green, purple) are highly modulated. C) Endpoint force vectors produced by each muscle synergy (same color coding), in the sagittal, frontal, and horizontal planes. Vectors are expressed as forces applied by the limb against the support surface. The amplitude of each the force vectors in any postural response is directly modulated by the amplitude of the neural command to each muscle synergy. (Adapted from Torres-Oviedo et al. 2006.)

Figure 6. Muscle tuning curves reconstructed using the same set of muscle synergies in four different postural configurations.

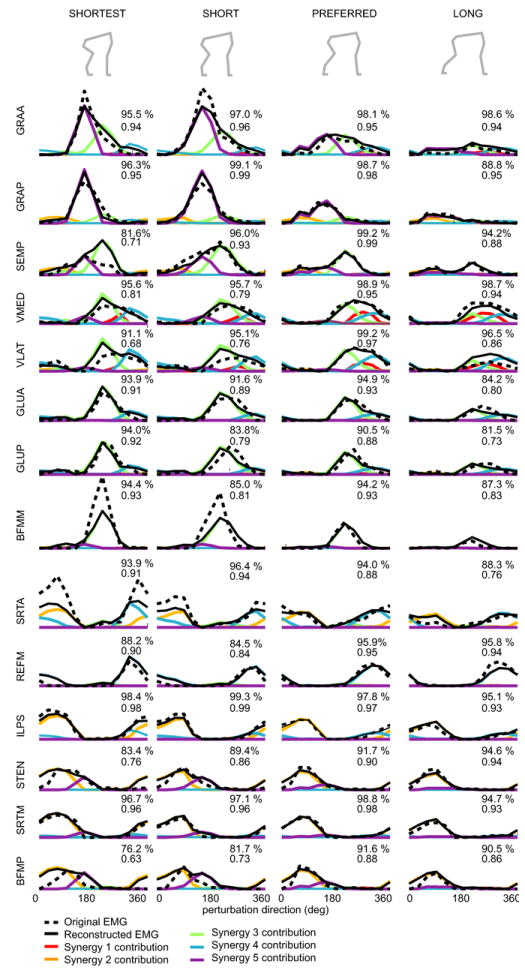
Muscle tuning curves vary across postural responses to support surface perturbation when postural configuration is varied. These variations can be reconstructed using the set of muscle synergies extracted from the preferred stance configuration. The original data are shown by the dashed black line, and the reconstructed data by the solid black line. The contribution from each synergy to the reconstruction is shown by the corresponding colored line. This is computed by multiplying each functional synergy vector W by its activation coefficient C. (Adapted from Torres-Oviedo et al. 2006.)

Muscle synergies have a direct functional effect, as demonstrated in cats where modulation of the neural commands to each muscle synergy changes the biomechanical output produced during postural responses. Each muscle synergy was correlated to the production of a specific active force vector at the endpoint of the hindlimb (Figure 5C); this relationship is consistent across all of the different postural conditions discussed above. Therefore changes in muscle activation and forces produced during postural response in different stance configurations (Macpherson, 1994, Torres-Oviedo et al., 2006) can be explained by simply changing the proportion of contribution of each muscle synergy.

These findings suggest that muscle synergies could be a functional mechanism by which descending neural commands related to the desired control of task-level variables are transformed into specific patterns of muscle activation that affect those task-level variables. This type of direct mechanism for motor coordination is appealing in that higher-level computations in the nervous system can occur in the context of task-level variables rather than in local afferent or efferent signals. Moreover, selection of muscle synergies would not require online forward or inverse computation of the muscle activation to motor output transformation. The muscle synergy pattern itself can be thought of as an element in a look-up table of the muscle activation to motor output transformation. Therefore each person’s motor outputs would be defined by the repertoire of muscle synergies available, which could exceed the number of muscles or degrees of freedom in the body.

Hierarchal feedback model of postural control

How can the many experimental and theoretical findings in postural control be unified in a coherent framework? By studying the nature of the dimensional reduction in sensorimotor systems, it may be possible to explain the apparent tension between the commonalities versus variations in postural behaviors observed across individuals. Frequently, individual variations deviate from general characterizations of muscle activation patterns during postural responses to perturbation. Are there common organizational themes underlying muscle activation patterns across tasks and individuals that can be used to guide our approaches to understanding postural control?

Rather than using the muscle activation patterns themselves as the primary determinant of postural strategies, we propose that the nature of the dimensional reduction within an experimental data set can be better used to characterize and compare motor outputs across trials and across individuals. Because of redundancy in the musculoskeletal system, even muscle activation patterns associated with a common task-variable can differ across individuals. For example, in cat postural control, the same number of muscle synergies were found across several cats (Torres-Oviedo et al., 2006). These muscle synergies were found to have similar tuning curves and produce similar force directions in different animals (Figure 7). This suggests that the neural commands to the muscle synergies and the motor output generated by the muscle synergies in response to perturbations are similar across cats. Postural responses in different individuals are probably modulated by disturbances in similar task-level variables, which by definition are independent of individual variations in morphometry, or postural configuration. But, muscle synergy composition differs significantly across individuals (Figure 7). Therefore, the exact muscle synergy mapping from task-variable to muscle activation patterns appears to be specific to each individual. Likewise, the sensory mappings leading to the estimation of the relevant task-variables are also likely to be individual-specific. Therefore, individuals are more similar in terms of the task-variables that are controlled, and not to specific sensorimotor patterns.

Figure 7. Example of similar dimensional-reduction and task-variable encoding across individuals.

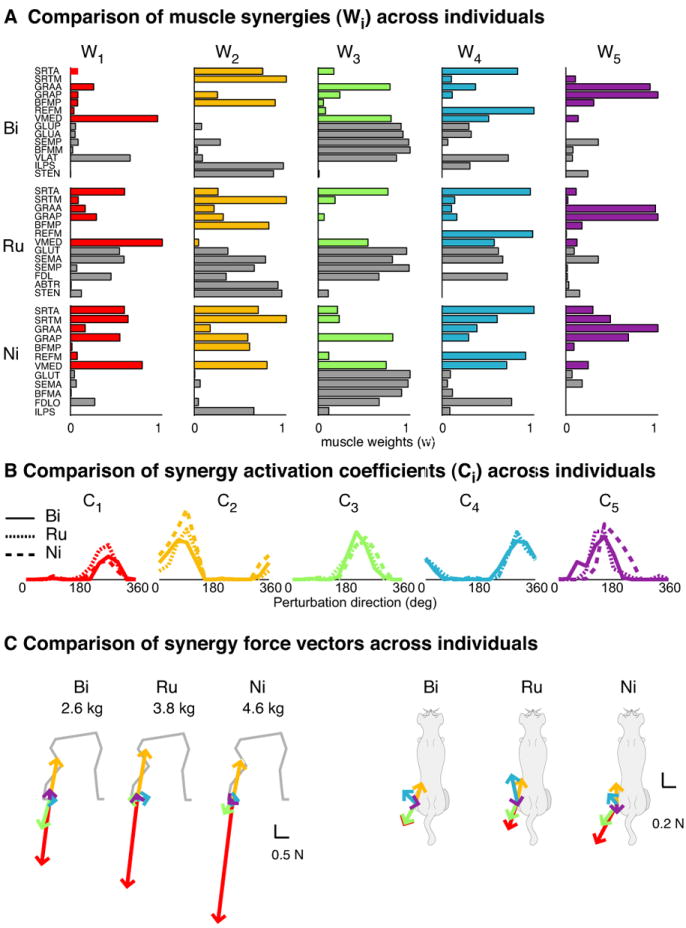
In all cats, 5 synergies accounted for >96% of the variability in response to translation at the preferred stance. A) Muscle synergies for each individual. Colored bars indicate muscles that were measured across all individuals. Gray bars indicate the remaining muscles collected for each individual. While there are general similarities in the most highly activated muscles in each synergy, substantial variation in muscles contributing to the synergies exist across individuals. B) Activation coefficients across animals are similar, indicating that they are activated in similar perturbation directions. C) Force vectors produced by each synergy are also quite similar. Taken together, this data demonstrates that neural commands encoding force-vector directions are quite similar across individuals, but the specific muscle synergy mapping used can vary. (Adapted from Torres-Oviedo et al. 2006.)

In this view, the number of muscle synergies and their corresponding neural commands carry more information than the activation pattern of individual muscles because they reflect the task-variables that are sensed and regulated by the nervous system. Changes in muscle activation patterns might then be thought of in terms of either changes in the activation patterns of a consistent set of muscle synergies, changes in the number of muscle synergies recruited, or changes in the composition of muscle synergies. This leads to a general framework in which processes causing variability due to influences at all levels of the nervous system can be explained using concepts of dimensional reduction in sensorimotor transformations during postural control (Figure 8).

Figure 8.

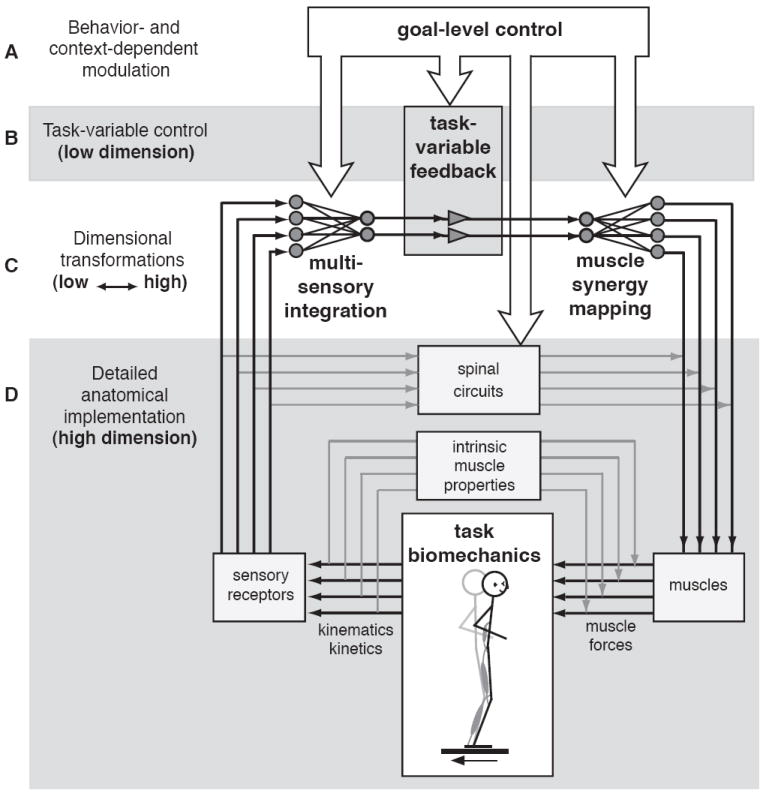
General framework for understanding dimensional reduction in muscle coordination of posture. The framework consists of a nested set of hierarchal feedback loops with much lower dimensionality at the higher levels than the lower levels. A) Goal-level modulation of postural responses occurs in task-variable space. Therefore behavioral or cognitive-level modulation can alter the task-variables attended to, as well as the way they are estimated and regulated by B) low dimensional feedback in the case of postural control. C) Mappings between low- and high-dimensional spaces are necessary for estimation and control of task-level variables. A dimensional reduction occurs in the multisensory integration mappings that use multiple afferent signals to estimate task-variables. Once the desired effect on the task-level variable is determined, a dimensional expansion occurs via muscle synergy mappings, allowing the action to be implemented in D) specific anatomical details. At this level there are many nonlinearities and state-dependent effects that can influence the eventual biomechanical output produced through the activation of a muscle synergy. However, some of these factors, such as spinal circuits, may be used to make the system more controllable by the reduced-dimension controller, and are also influenced by higher-level centers. This general framework can be used to make specific hypotheses about the characteristics of changes in muscle activation patterns in postural responses due to changes at all levels in the nervous system. In addition, it can be used to guide computational studies focused on understanding mappings to and from the low-dimensional space where movement is controlled by the nervous system.

The general framework for understanding muscle coordination is presented in terms of understanding sensorimotor transformations in postural responses, but can also be applied to most sensorimotor processes. The framework consists of a nested set of hierarchal feedback loops with much lower dimensionality at the higher levels than the lower levels. At the highest level, the relevant task-variables depend on the goal-level decisions in the nervous system (Figure 8A,B). For successful task performance, these goals must also be nominally matched to biomechanical constraints, and can be regulated in a feedback manner (Figure 8B). The estimate of the relevant task-variables depends upon sensory transformations that integrate high-dimensional multisensory signals; these transformations can also be influenced by behavioral goals (Figure 8C). Muscle synergies perform the symmetric function of transforming the desired control of task-variables into high-dimensional multiple muscle activations (Figure 8C). Muscle synergy activation patterns ultimately interact with spinal circuits and intrinsic muscle properties to produce biomechanical outputs (Figure 8D). Simultaneously, these biomechanical outputs induce sensory signals in afferents across the body that are then mapped onto task-variable estimates in the nervous system (Figure 8D,C). While the role of descending influences is primarily at the level of the relatively low-dimensional task-variable space, it can also affect the state of lower-level circuits in the spinal cord that ultimately will affect task performance (Figure 8D). This framework can be used to make predictions about how changes in muscle activation patterns are regulated by the nervous system and then suggest how computational studies can be used to substantiate the hypothesis.

In this framework, descending influences primarily modulate the relatively low-dimensional task-variable space. It has been hypothesized that a simple, linear neural control mechanism might sit at the top of a complex hierarchy of sensorimotor feedback loops used for movement control (Scott, 2004, Todorov, 2000). The control of task-level variables ultimately has to be considered and implemented in a high-dimensional space. It is possible that the role of the motor cortex is to perform this translation between task-level and local variables, perhaps by selecting the appropriate muscle synergies. Neuronal populations in the motor cortex reflect a wide array of both task-level variables and local variables (Scott, 2003). Moreover, long train stimulation of sites in the motor cortex generates coordinated movement of the limb to a common, final posture regardless of initial position, suggesting encoding of higher-order movement parameters (Graziano, 2006).

Changes in motor output due to descending, goal-level control affecting postural strategy selection can be thought of as changes in muscle synergy selection. For example, behavior-dependent modulation could influence the selection and modulation of appropriate sensory and motor mappings, consistent with the “strategy selection centers” proposed for postural control (Kuo, 2005, Park et al., 2004, Kuo, 1995, Horak et al., 1997). Different postural strategies could be preferentially selected by altering the selection of muscle synergies. Changes in postural responses due to descending influcences could therefore be due to changing the threshold for selection of an ankle or hip synergy. Such changes would be represented in terms of variations in the neural commands to muscle synergies, or preferential activation of particular muscle synergies within a given set, rather than changes in the muscle synergy patterns themselves. It has been shown that variability in locomotor behaviors can be explained by differences in the activation of muscle synergies and not random variability in the activation of each muscle (d’Avella and Bizzi, 2005, Tresch et al., 1999). We predict that variability in postural response also arises due to variations in the relatively low-dimensional set of neural commands.

The dimensional reductions occurring in the sensory and motor systems appear to be symmetric processes that serve the function of controlling task-level variables for motor behaviors. The ability to sense and to control relevant task-variables must match in order for feedback regulation of task-variables to occur. The sensory and motor mappings are independent but related processes in that both must resolve similar issues of sensorimotor redundancy in mapping between low-dimensional task-variables and high-dimensional anatomical details (Figure 8D). The redundancy allows flexibility in the mappings, ensuring that the control of task-level variables is not directly or immutably linked to any particular afferent or efferent pathway. This is consistent with recent studies demonstrating substantial non-uniqueness in neural circuits mapping sensory inputs into sparse neural representations in the production of motor outputs (Leonardo, 2005, Prinz et al., 2004).

In postural control, this concept is consistent with the fact that CoM kinematics cannot be reliably derived from any single sensory afferent population (Nashner, 1977) and that direct feedback of sensory signals does not explain human postural behaviors, particularly in situations of sensory conflict where an erroneous sensory signal must be ignored (Kuo, 2005, Nashner, 1977). The sense of verticality can be derived from multiple sensory systems, and the contributions of each sensory organ can be dynamically re-weighted under various experimental conditions (Peterka, 2002, Peterka and Loughlin, 2004, Mergner et al., 2003, Jeka et al., 2006, Carver et al., 2006).

Conversely, the control of task-variables is achieved through the inverse transformation to muscle activations encoded by the muscle synergies. In this case the muscle synergy defines one of many possible muscle activation patterns that has the desired effect on the task-variable at hand. Despite the numerous possibilities for affecting task-variables, it has been shown that individuals use the same muscle synergies across a wide range of tasks across days and weeks (Torres-Oviedo et al., 2006). Therefore, while the sensory and motor transformations are roughly optimal in the sense that they are comparable to solutions derived from optimization techniques (Kurtzer et al., 2006, Kuo, 1995, Kuo, 2005, Scott, 2004, Todorov and Jordan, 2002, Todorov, 2004), these mappings do not appear to be updated on a rapid trial-by-trial time scale. In tasks that are relatively uncommon in the experience of an individual, the nominal set of muscle synergies may not be optimal, and can result in less effective biomechanical outputs. This appears to be the case in the relaxation of the force constraint strategy for postural control at shorter stance distances (Ting, 2006, McKay and Ting, 2005, Macpherson, 1994, Torres-Oviedo et al., 2006).

Thus, the formation of muscle synergies and sensory transformations is considered to be a separate process from the goal-level decisions influencing their regulation and selection. In this framework, the sensory transformations and muscle synergies represent a relatively fixed set of preferred mappings, influenced by each individual’s experiences and motor training as well as the biomechanics of the task. If the formation of these mappings is influenced by experience, it may not be possible to directly compare muscle synergies across individuals in terms of their exact composition, but only on the task-level variables they encode. Similarities are inevitable because of the constraints imposed by task biomechanical constraints; however, redundancies in the sensory and motor systems allow for substantial individual variation. It is possible that such variations give rise to individual movement characteristics, as movement styles that nonetheless conform to physical constraints can be encapsulated through patterns of joint torque weightings in computer simulations for animation (Liu et al., 2005, Liu and Popovic, 2002).

Most individuals have reasonably consistent movement patterns, but muscle synergy number or composition could be altered through experience and training, in particular due to neural or musculoskeletal injury or disease. New muscle synergies might form after extended experience with a new motor task—such as with skiing or bicycling. It has also been shown that dancers have postural responses that tend to emphasize the orientation and alignment of the body, as compared to non-dancers who simply maintaining the CoM within the base of support (Mouchnino et al., 1993, Mouchnino et al., 1992). Likewise, the environment in which an individual is raised also affects sensory integration mappings (Wallace et al., 2006, Wallace and Stein, 2006). Orienting responses to a stimulus are enhanced when visual and auditory cues are congruent. However, animals raised in the dark experience no such enhancement (Wallace et al., 2004).

In speech, an instructive example can be found that demonstrates a process of dimensional reduction in sensorimotor systems that can be thought of as an experience-dependent “interpretation” of the relevant task variables (Kuhl, 1994, Kuhl, 2004). A similar phenomenon of matched dimensional reduction in sensory and motor processing occurs in the perception and production of speech sounds. The native language of each individual shapes their ability to both distinguish and produce speech sounds (Kuhl et al., 1997, Zhang et al., 2005). Essentially, a reduction in dimension occurs that is based on the native language of an individual. Idealized templates of speech sounds are formed in the nervous system that can be thought of as “sensorimotor synergies”—these synergies underlie the characteristic accents of individuals speaking a foreign language. Sensorimotor synergies in language are so strong that sounds considered to be very distinct in one language may not be perceivable, much less producible by native speakers of a different language. While there are similar characteristics of these synergies across a native-language population, they are also specific to each individual and can change through experience-dependent processes like intensive speech training. Therefore, sensorimotor transformations that map between low-dimensional task-variables and high-dimensional anatomical variables underlie individual speech or movement characteristics allowing us to recognize distinctive features of a person even when performing a novel task because of each individual’s distinctive set of “building blocks”, or sensorimotor synergies. Clearly we have dedicated circuits for language production, as well as motor behaviors, and yet these structures do not specify the exact synergy patterns in individuals, but facilitate the formation and general applicability of sensorimotor synergies in sensorimotor processes.

While the use of reduced dimension task-level control is appealing, the reality is that movements must be implemented in complex, nonlinear dynamic systems that are not easily controlled. The long latencies that exist between descending commands and peripheral action add further challenges to task performance, particularly for standing postural control in an unstable, bipedal postural configuration. It has been proposed that physiological “linearization” mechanisms may exist that allow a low-dimensional hierarchal feedback architecture to work, but the nature of this mechanism has not been discussed. However, there are many candidate components of the neuromuscular system that could are modifiable through descending and neuromodulatory influences. Intrinsic muscle properties provide instantaneous stabilizing influences, which can be influenced by activation level, or the motion history of the muscles. Spinal heterogenic stretch reflex circuits coordinate the limb (Nichols et al., 1999, Nichols, 1994, Wilmink and Nichols, 2003), but more importantly their strength can be altered by the state of the spinal network such that the online processing of afferent and efferent signals is altered. Neuromodulatory effects on motoneuron excitability can be affected by joint angle (Hyngstrom et al., in press). But, influence of these state-dependent changes in the spinal cord extends far beyond mono- or poly- synaptic reflex loops, and can alter the influence of a descending commards on the activation of single muscles, as well as the strength of ascending afferent signals. It is therefore likely that the context-dependent modulation of spinal circuits through descending control as well as neuromodulator release works in tandem with descending muscle synergy commands in order to produce predictable, stable movements. Therefore the spinal circuitry is an essential component of the implementation of the “simple” hierarchal control architecture, although it may not be responsible for specifying the muscle synergies used in postural control.

Future directions

This framework that links low- and high-dimensional representations of movement is an overarching hypothesis that lends itself to testing through computer simulations. Our philosophy is that neither a simple conceptual model nor a complex anatomical model in isolation can effectively elucidate principles of motor coordination. Current models of posture and movement are formulated either in the low-dimensional task-space, or in the high-dimensional anatomical details where individual muscles and joints are considered. Each has its strengths and weaknesses that cannot alone be used to understand neural mechanisms of movement. The neural mechanisms through which musculoskeletal systems exhibit “collapses in dimension” must be explicitly studied (Holmes et al., 2006). But to date, the sensorimotor transformations between low- and high-dimensional spaces have only been addressed by a few studies demonstrating that a muscle synergy organization is sufficient to control the task-variables (Loeb et al., 2000, Raasch and Zajac, 1999, Valero-Cuevas et al., 1998, Valero-Cuevas, 2000).

In posture, simplified feedback control models of posture have been used to explain how task-level variables are regulated by sensorimotor mechanisms (Bortolami et al., 2003, van der Kooij et al., 1999, Kuo, 1995, Peterka, 2002, Peterka, 2000). These models have been instructive in understanding the importance of various sensory channels on postural control (van der Kooij et al., 2001, Kuo et al., 1998, Peterka, 2002) but are not sufficient for understanding muscle activation patterns. On the other hand, current musculoskeletal models can explain individual muscle activations in a specific motor task (Pandy, 2001, Neptune, 2000, Zajac et al., 2003). But, in the absence of feedback loops, a small change in the pattern of muscle activation can completely destabilize the simulated system (Risher et al., 1997), allowing only the analysis of explicitly modeled conditions. Because these models lack sensorimotor mechanisms that allow them to respond to perturbations, they cannot yet be used to understand the neuromechanical principles coordinating muscles.

To bridge the gap between concepts about task-variable control and its implementation at the level of individual muscle activation patterns, novel methods for complementary and parallel development of simple and complex musculoskeletal models of posture must be developed (Full and Koditschek, 1999). The framework presented demonstrates why both low-dimensional and high-dimensional models alone can be used to produce reasonable simulations of movement. However, the functional relevance of a simple model of postural control to multiple joint motions depends critically on its integration with more complex musculoskeletal models. The future challenges in computational studies will be to incorporate relevant dimensional reduction mechanisms in the control of multiple muscles. As an example, six muscle synergies can be used to produce a range of natural pedaling behaviors in simulations, such as slow, fast, smooth, jerky and backwards pedaling (Zajac et al., 2003, Raasch et al., 1997, Raasch and Zajac, 1999). These simulations were found to predict phase changes in muscle activation patterns that were unexpected based on prior hypotheses (Ting et al., 1999). Moreover, when the model used only flexor and extensor synergies it was unable to advance the limb through the transition from extension to flexion (Raasch and Zajac, 1999). Similarly, stroke patients limited to flexion and extension synergies (Bourbonnais et al., 1989) have difficulties through the same phase transition (Brown et al., 1997). A similar model for understanding postural control would be critical to understanding the functional consequences of neural impairments that lead to balance disorders. Recent steps in this direction include models demonstrating reduced dimension in feedback control of posture. “Eigenmovements” that couple joint motions in multiarticular models of standing posture, can be used to reduce the dimension of the feedback parameters required for postural control (Alexandrov et al., 2005). Consistent with the eigenmovement hypothesis, at the level of muscle activation patterns, simulations demonstrate the need for coordinated control of multiple muscles to achieve task-variable control (Bunderson et al., 2006, Van Antwerp et al., 2006, Van Antwerp and Ting, 2006). Moreover, it has been shown that multiple muscle activation patterns in both cats and humans are regulated by simple feedback control laws (Lockhart, 2005, Welch and Ting, 2005), suggesting that a feedback control system might act at the level of the neural commands to muscle synergies.

The integration of simple and complex models may also be clinically relevant. The ability of patients to conform to overall control principles may be more important than the enforcement of specific synergies or detailed movement patterns. In cerebral palsy subjects with hemiplegia, different patterns of joint angle changes and EMGs are observed in each leg. These differences are difficult to interpret through direct comparison of the multiple variables. However, the overall mechanics and energy exchange mechanisms in the unaffected and affected limbs can be characterized by two simple models of gait: an inverted pendulum and a spring-mass model, respectively (Fonseca et al., 2004, Fonseca et al., 2001). Therefore, more insight is gained from understanding the control of task-level variables versus local variables. These conceptual frameworks can inform the analysis of data and design of new experiments and complex models, and may explain why prior attempts to enforce specific muscle activation patterns in clinical rehabilitation were unsuccessful. Development of computational models that can predict the functional consequences of muscle activation patterns in postural control may be more effective at predicting how postural function could improve in individuals with specific impairments. The resulting muscle activation patterns may not resemble a “normal” pattern, but take advantage of the capabilities of the individual.

Finally, the framework presented calls for more computationally sophisticated methods of data analysis that reflect the hypothesized neural organization principles. The framework suggests that a relatively low number of parameters can be used to describe complex changes in muscle activation patterns. Therefore, understanding low-dimensional task-level variables can lead to a better understanding of changes in local variables. For example, cats with large-fiber peripheral sensory neuropathy that destroys afferents from muscle spindles and Golgi tendon organs exhibit postural instability and delayed postural responses (Stapley et al., 2002). Application of a simple feedback model demonstrates that changes in the entire timecourse of multiple muscle activations can be described as a decrease in the feedback gain associated with CoM acceleration (Lockhart et al., 2005, Ting et al., 2005). This change can explain the apparent delay in the response through a change in only one of four feedback parameters. Further, since muscle directional tuning remains intact (Stapley et al., 2002), it is likely that the muscle synergy patterns in these animals is unaffected by the sensory loss. The framework further predicts that nominal changes in postural behaviors from goal- or task-level control due to changes in mental state, such as anticipation, adaptation, fear, or divided attention (Woollacott and Shumway-Cook, 2002, Carpenter et al., 2006, Keshner et al., 1987, Brown et al., 2002, Maki et al., 1991, Carpenter et al., 2004) would occur only in the modulation and selection of postural synergies. However, more changes due to disease or injury might result in the inability to activate particular muscle synergies, such as in Parkinson’s disease (Dimitrova et al., 2004), or an inappropriate activation of muscle synergies, as in cerebellar loss (Timmann and Horak, 1997), or a reorganization of muscle synergies themselves. The ability to differentiate these different mechanisms of changes may lead to greater insight into the neurological underpinnings of motor dysfunctions and the development of potential interventions.

Abbreviations

APR

Automatic postural response

CoM

Center of mass

EMG

Electromyographic

Muscle abbreviations used in figures

BFMA

Anterior biceps femoris

BFMM

Medial biceps femoris

BFMP

Posterior biceps femoris

EDL

Extensor digitorum longus

FDL

Flexor digitorum longus

GLUT

Gluteus medius

GLUP

Posterior gluteus medius

GLUA

Anterior gluteus medius

GRAA

Anterior gracilis

GRAP

Posterior gracilis

ILPS

Iliopsoas

LGAS

Lateral gastrocnemius

MGAS

Medial gastrocnemius

PLAN

Plantaris

REFM

Rectus femoris

SEMA

Anterior semimembranosus

SEMP

Posterior semimembranosus

SOL

Soleus

SRTA

Anterior sartorius

SRTM

Medial sartorius

STEN

Semitendinosus

TIBA

Tibialis anterior

TFL

Tensor fasciae lata

VLAT

Vastus lateralis

VMED

Vastus medialis