Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Aug 5;4:5949. doi: 10.1038/srep05949

Versatile, kinetically controlled, high precision electrohydrodynamic writing of micro/nanofibers

YongAn Huang 1,a, Yongqing Duan 1, Yajiang Ding 1, Ningbin Bu 1, Yanqiao Pan 1, Nanshu Lu 2, Zhouping Yin 1,b
PMCID: PMC4121616  PMID: 25091829

Abstract

Direct writing of hierarchical micro/nanofibers have recently gained popularity in flexible/stretchable electronics due to its low cost, simple process and high throughput. A kinetically controlled mechanoelectrospinning (MES) is developed to directly write diversified hierarchical micro/nanofibers in a continuous and programmable manner. Unlike conventional near-field electrospinning, our MES method introduces a mechanical drawing force, to simultaneously enhance the positioning accuracy and morphology controllability. The MES is predominantly controlled by the substrate speed, the nozzle-to-substrate distance, and the applied voltage. As a demonstration, smooth straight, serpentine, self-similar, and bead-on-string structures are direct-written on silicon/elastomer substrates with a resolution of 200 nm. It is believed that MES can promote the low-cost, high precision fabrication of flexible/stretchable electronics or enable the direct writing of the sacrificial structures for nanoscale lithography.

Micro/nanofibers composed of electrically conductive, semiconducting, photoelectric, piezoelectric or dielectric materials have been extensively explored as light-emitters, energy harvesters, supercapacitors and sensors1,2,3. If the electrically functional or active micro/nanofibers can be directly written on flexible substrates at low temperature, low cost flexible/stretchable electronics are expected to be fabricated without conventional photolithography processes. The direct-writing of smooth microstructures with viscous ink has attracted considerable attention in flexible/stretchable electronics4. Near-field electrospinning (NFES) can write smooth micro/nanofibers in a direct, continuous manner5, to fabricate nanowire electronics, piezoelectric devices and so on, using functional or sacrificial inks6,7,8,9. It overcomes the drawbacks of established ink-jet technique (applying heat or piezoelectric actuator to “push” a droplet of ink10,11,12) which include limited printing resolution (20 μm13), incompatibility with high-viscosity electronic ink14,15, and rugged structures due to discrete droplets. However, it is humdrum to just write straight micro/nanofibers. To write in a variety of patterns, the control of the position, resolution, and morphology of electrospun micro/nanofibers should be improved.

Here, we present a mechanoelectrospinning (MES) process that is kinetically controlled and high resolution. It utilizes the combination of electrical and mechanical forces, rather than purely electric field in NFES or thermal/acoustic energy in traditional ink-jet printing, to drive the viscous ink for the direct-writing of high-resolution, customizable microstructures. In addition to the features of ink-jet techniques such as large-area printing, low-cost operation, and customized flexibility16,17,18, the MES has some unique advantages such as: 1) resolution tunable from micrometre to nanometre using nozzles of diameters larger than 100 μm, which are not easy to be jammed, 2) compatibility with inks of broad ranges of viscosity that cannot be used in established ink-jet printing or photolithography techniques, 3) simultaneous control on the position and morphology of the deposited structures, and 4) direct deposition of smooth hierarchical structures such as island-bridge structures, serpentine structures, self-similar structures, and multi-level dot-array. The writing resolution, position, morphology, and patterns can be readily tuned by digitally controlled motion stage (substrate holder), nozzle-to-substrate distance, and applied voltage. It is hence a highly versatile and low cost method to direct-write solution-based materials for large-scale flexible/stretchable electronics and soft nanolithography.

Principles and Implementation

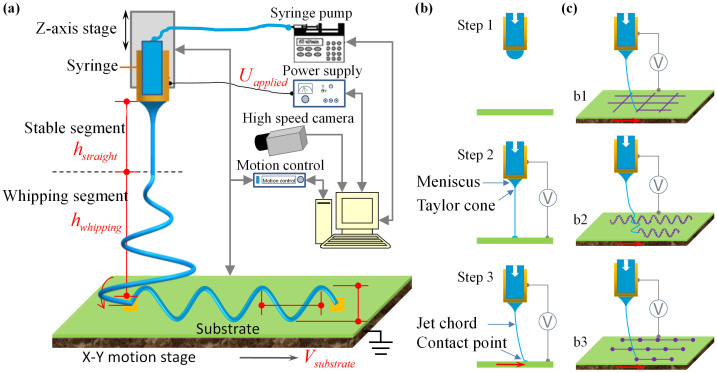
Figure 1a shows the schematic of MES direct-writing system that merges several disparate concepts. First, MES process is able to precisely manipulate the position, size, and morphology of each electrospun micro/nanofiber by adjusting the combination of mechanical drawing force and electrical field. The mechanical drawing force is determined by the velocity of substrate holder. When the optimal combination is achieved, sub-micrometer structures can be well written. Second, the nozzle-to-substrate distance, hz-axis = hstraight + hwhipping, is tunable from 0.5 mm to 10 mm, to fully explore the different dynamics of jetting fibers. Third, the applied voltage Uvoltage first gradually increases to a critical value to jet the ink from the apex of the Taylor cone, then decreases to a lower voltage just to stabilize the Taylor cone. Fourth, the motion stage where the substrate rests on is digitally controlled and hence stretches the jetting fiber in programmable manner. The four features make MES a versatile direct-writing technique, to fabricate abundant microstructures such as fiber array, serpentine structures and bead-on-string structures.

Figure 1. Schematic of multifunctional MES direct-writing process.

Figure 1

Open in a new tab

(a) Experimental setup and mechanism of MES direct-writing process. (b) Broken-down steps of MES direct-writing: ink is first filled in the nozzle and a drop forms at the end of the nozzle; when voltage is applied, the end drop is jetted from the nozzle and a Taylor cone is formed; when substrate starts to move, a fine ‘jet chord’ is formed between the meniscus and the contact point on the substrate. (c) Three modes of MES direct-writing process: the mapped direct-writing of straight structures, helix direct-writing of serpentine structures, and leap direct-writing of bead-on-string structure.

Figure 1b illustrates the MES process: filling nozzle with functional ink → increasing applied voltage to a high value, such as 2 kV → stretching the jetting fiber → decreasing applied voltage to a lower voltage such as 0.8 ~ 1 kV. The jetting fiber is analogous to the soft ladders dropping from helicopter, in the sense that it is impossible to control the landing point. The NFES tries to enhance positioning accuracy by shortening the nozzle-to-substrate distance. Here, an idea to achieve more precise positioning is borrowed from the kite that flies when dragged by a running person through a string. The ground position is controlled by the person, regardless of the position of the kite or the rigidity of the kite. A digitally controlled motion stage is adopted as the “person” to draw the jet micro/nanofiber. Three key processing parameters can tune the dynamic behavior of the jet fiber: 1) the translational speed, νsubstrate, which controls the mechanical drawing force and hence the fiber diameter or ribbon width, 2) the nozzle-to-substrate distance, hz-axis, which controls the cross-sectional geometry (i.e. circular or rectangular) as well as the shape (i.e. linear or serpentine) of the written structure, and 3) the applied voltage, Uvoltage, which dictates the dynamic behavior of jetting, as well as the fiber diameter. The tunable mechanical drawing force plays a critical role in improving the control over fiber position and morphology. It is helpful for controlling the bending instability of jet fibers6, and can reliably generate finer and longer fibers19. It is the primary cause that the electrical field of MES (about 2 × 105 V/m) is far lower than that of NFES (about 1 × 107 V/m)5. As a result, it helps avoid the electrical breakdown of the polymer substrates of flexible electronics during direct-writing.

The drawing force acting on the jetting fiber can be determined by the slope of the fiber θ, which increases with the translational speed (captured by a high-speed camera, see supplementary Figure S1). hz–axis ranges from 0.5 ~ 10 mm, far smaller than 15 ~ 30 cm in traditional electrospinning20,21, but larger than ~0.5 mm used inNFES5. In traditional electrospinning, the jet fiber completely solidifies when reaching the substrate whereas NFES adopts a solid tip, rather than a needle, to dip in a concentrated solution and then deposit a solid fiber. Adopting 0.5 mm < hz–axis < 10 mm gives the following advantages: 1) solution with a wide range of concentration may be supplied continuously by a needle for large-area nonstop printing; 2) the deposited micro/nanofiber can be tuned from solid to liquid, to control the cross-sectional geometry; and 3) the jetting velocity can be easily tuned to be comparable to the motion stage, yielding reasonable mechanical drawing force.

Several variants of MES are developed by coordinating the above process parameters. 1) The mapped direct-writing (MDW) mode is developed by introducing the “near-field” method to shorten the hz-axis within the range of the length of stable segment hstraight (e.g. hstraight = 5 mm), as shown in Figure 1a. The deposited micro/nanofibers are the mapping results of relative motion of the nozzle and substrate. 2) The leap direct-writing (LDW) mode is based on the competition between the mechanical drawing force, the electric force and the viscoelastic force, and works when 0.5 mm < hz-axis < 2 mm and νsubstrate <150 mm/s in experiments. It is utilized to fabricate bead-on-string structures in a programmable manner. 3) The helix direct-writing (HDW) mode is resulted from the whipping/buckling effect of electrospinning, where hstraight < hz-axis < hstraight + hwhipping (e.g. 15 mm < hz-axis < 45 mm), where hwhipping is the height of the first phase of instability. Serpentine structures can thereby be direct-written via linear translations of the motion stage. Complex micro-structures can be generated out of the different writing modes, including large-scale straight fiber array, multi-level wavy structures, in-plane/out-of-plane buckled structures, and bead-on-string structures, as illustrated in Figure 1c. All the experiments were performed under the room temperature and relative humidity of about 25%.

Results and Discussion

Mapped direct-writing of straight micro/nanofiber and their self-assembly to form dot arrays

Mapped direct-writing mode can deposit microstructures with controllable morphology and precise position. hz-axis controls the dynamic behavior as well as the phase change of fibers. If νsubstrate > 150 mm/s, straight liquid ribbons and solid micro/nanofibers can be direct-written when 0.5 mm < hz-axis < 2 mm and 2 mm < hz-axis < 5 mm, respectively. The degree of solidification can be tuned continuously, so that the cross-sectional geometry can gradually change from thin film to circle. In experiment, the ink is polyethylene oxide (PEO, Mw = 300 000) solution dissolved in distilled water with the weight concentration of 6 wt%. When hz-axis < 2 mm, there is not enough time for the solvent to completely evaporate before the ink reaches the substrate, hence liquid ink will rest and spread on the substrate to form a ribbon.

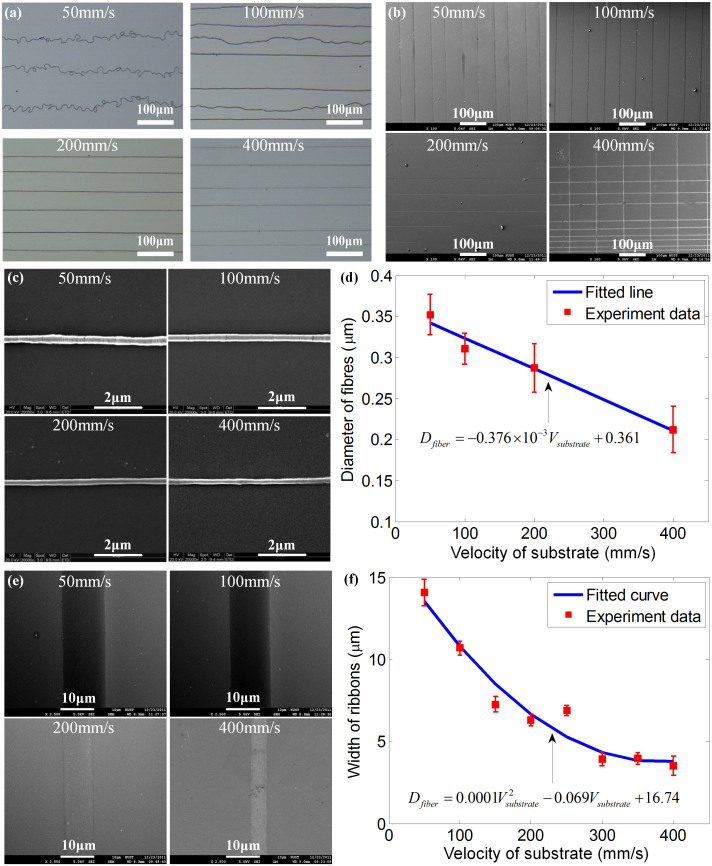
It is found that νsubstrate has significant influence on the positioning of electrospun micro/nanofibers. When νsubstrate is much lower than the speed of jetting, νjetting, (e.g. νjetting ≈ 170 mm/s when the flow rate is 50 nl/min, the applied voltage is 1 kV, and hz-axis = 5 mm), MDW is unable to deposit linear, aligned microstructures even if the motion stage moves linearly (see Figure 2a). The oscillation is resulted from air turbulence or buckling of solid micro/nanofibers. When νsubstrate is close to νjetting, the “chord” is tightened and the deposited fibers become straight due to the mechanical drawing force. When νsubstrate exceeds νjetting, fiber diameter or ribbon width can be tuned by νsubstrate. Linear arrays of micro/nanofibers with a 50-μm spacing (Figure 2b) are fabricated to demonstrate the relationship between νsubstrate and micro/nanofibers feature size.

Figure 2.

Figure 2

Open in a new tab

The dependence of fiber-diameter or ribbon-width on the velocity of the substrate: (a) optical micrographs of direct-written fibers at speeds of 50 mm/s, 100 mm/s, 200 mm/s and 400 mm/s with 5 mm nozzle-to-substrate distance; (b) SEM images of direct-written fibers at speeds of 50 mm/s, 100 mm/s, 200 mm/s and 400 mm/s with 2 mm nozzle-to-substrate distance; (c) SEM images of aligned fiber with 5 mm nozzle-to-substrate distance at speeds of 50 mm/s, 100 mm/s, 200 mm/s and 400 mm/s; (d) Correlation between fiber-diameter and the velocity of substrate; (e) are similar with (c), but with 2 mm nozzle-to-substrate distance, and the direct-written structures are ribbons; (f) Correlation between ribbon-width and the velocity of substrate.

hz–axis also plays an important role in positioning in addition to tuning the degree of solidification. Comparing Figures 2a and 2b, the fibers are written with nozzle-to-substrate distances of 5 mm and 2 mm, respectively. At hz-axis = 5 mm (Figure 2a), straight fibers can only be direct-written when νsubstrate > νjetting, whereas the solid fibers will buckle when νsubstrate < νjetting. Inversely, at hz-axis = 2 mm, the positionability of jetting fiber is free of νsubstrate, and the straight ribbon can be deposited even with very slow speed, such as 50 mm/s, even to 5 mm/s in leap direct-writing discussed behind. The fiber cross-section can continuously tuned by changing applied voltage, substrate speed and nozzle-to-substrate distance (Supplementary Figure S2). It benefits from the in situ accumulation of liquid fiber, does not exist the buckling behavior of solid fiber. The speed may improve the uniformity of the ribbon. Additionally, νjetting is a function of hz-axis that a larger hz-axis allows longer acceleration time for the jetting fiber under the electric force and the mechanical drawing force.

Fiber diameters are found to vary from 350 nm to 200 nm when νsubstrate increases from 50 mm/s to 400 mm/s, as shown by zoomed in SEM images in Figure 2c. Figure 2d shows the relationship between the fiber diameter Dfiber and the substrate speed νsubstrate with the fitted relation Dfiber = −0.376 × 10−3 Vsubstrate + 0.361. When hz-axis increases from 2 mm to 5 mm, the cross-sectional geometry and size of the deposited structures also change. Namely, the fibers become ribbons in the case of small hz-axis, and the width of ribbons is much larger than the diameter of fibers. The main reason is that the liquid fiber spreads on the substrate before it is fully stretched. Figure 2e shows the direct-written ribbon in various speeds of substrate. Figure 2f shows the relationship between the ribbon width Dfiber and the substrate speed νsubstrate with the fitted relation 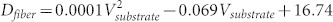Inline graphic.

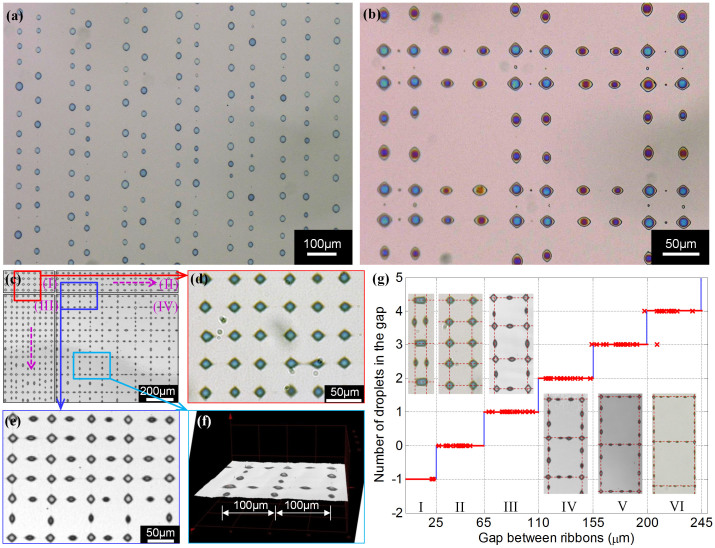
The highly aligned micro/nanofibers can be used as a template for the controllable self-assembly of large-scale dot array, in addition to as critical components in flexible energy conversion devices22, stretchable sensors23 or as sacrificial structures of nanofabrication8,24. Self-assembled dot arrays are widely applicable in microchemical reaction25, DNA detection26, and bio-sensing27, and MDW is a highly robust and relevant method. For instance, in microchemical reaction, one can direct-write different materials in two perpendicular directions. After self-assembly, two materials can form dots at the intersections, to prepare microchemical reaction. The dots can be controlled precisely, and the registration of two materials can be avoided. Further, based on the multi-level dot array, one can easily compare the results before and after microchemical reaction. Free self-assembly has demonstrated the capability to cut fibers into fragments and form dots28. Such dynamic behavior is governed by surface tension and Plateau–Rayleigh instability29,30. The challenges to transform from free self-assembly to controllable self-assembly are to precisely control the liquid line width, length, and ends, all of which can be addressed by the direct-written ribbon-lattice. A dot array can be direct-written in the following steps. First, MDW is applied to direct-write a parallel array of straight ribbons with uniform width. The width is the sole tunable parameter for free self-assembly to control the dot density (supplementary Figure S3). Second, the pattern is placed into a moist environment. As the solid ribbons uptake enough water vapor, it returns liquid, and periodic neckings will appear because the surface instabilities are activated. Finally, the fragmented segments contract longitudinally and grow laterally to form droplets and hence the array of parallel ribbons self-assemble into an array of small dots as the solvent continues evaporating. Therefore the three key steps of the self-assembly include necking, fragmenting, and contracting. Figure 3a shows a large-scale dot-array formed from straight parallel fibers in free self-assembly, and Figure 3b shows the controllable self-assembly of multi-level dot-array. Dot arrays self-assembled out of ribbon lattices with different width and gap (Figure 3c–f), to show that the finer the fibers are, the higher the density is. Figure 3g shows that there exists an obvious relationship between the number of droplets and the ribbon gap. In Region I there is no necking and two nearest intersections merge into one dot. It suggests that the ribbon lattices are unable to self-assemble when the lattice periodicity is smaller than 25 μm for bribbon ≈ 10.7 μm. In Region II, the dots are exactly located at the intersections of the ribbon lattice. Highly ordered and uniform microarrays can be fabricated, meanwhile the dot array periodicity can be continuously tuned from 25 μm to 65 μm. In Region III, there is one intermediate dot in each gap, indicating hierarchical microdot arrays can be generated. The dot array periodicity can be determined by halving the lattice periodicity (65/2 μm = 32.5 μm, 110/2 μm = 55 μm). When the ribbon lattice periodicity is larger than 65 μm, a new droplet will be added every 45 μm. The dot size and position are dominated by the lattices, so an arbitrary dot-array can be self-assembled in a controllable manner.

Figure 3.

Figure 3

Open in a new tab

Large-scale dot-array generated by MDW assisted self-assembly techniques: (a) large-scale dot-array of free self-assembly; (b) large-scale multi-level dot-array of controllable self-assembly based on ribbon-lattice two different diameters; (c) a large-scale dot-array self-assembled out of ribbon-lattices of different periodicity, (d) and (e) are the planar enlarged details, and (f) is the 3-dimensional image of microarray obtained by laser scanning confocal microscope; (g) the relationship between the number of droplets and the gap distance.

Helix direct-writing of serpentine structures

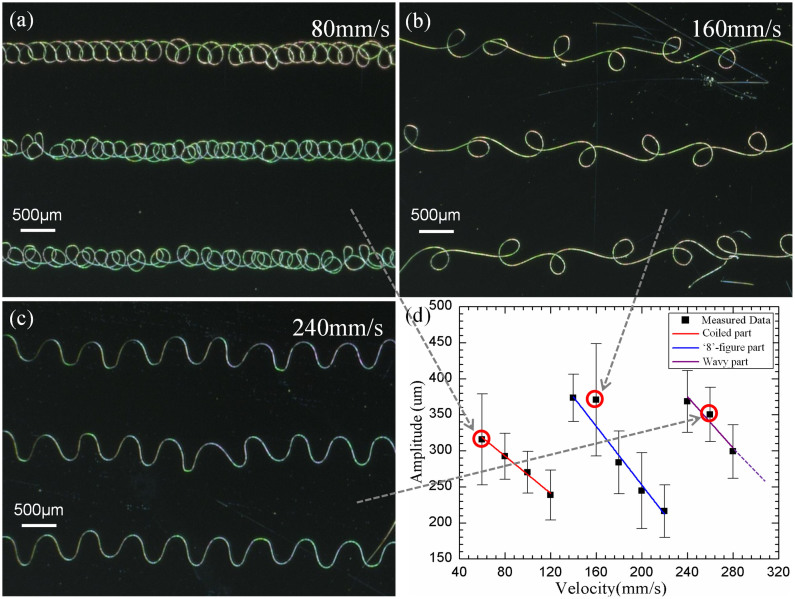
Serpentine structures are widely used in stretchable electronics to enhance the stretchability31 and reduce the stiffness32 of stiff electronic materials. Helix direct-writing can write serpentine structures in direct, continuous and controllable manners when 15 mm < hz-axis < 45 mm. The ink often exhibits complex dynamics, such as the ‘whipping/buckling’ instability so that the ink “dances” at a distance not far from the motion stage, hwhipping, as shown in Fig. 1a4,33,34. The first occurrence of non-axisymmetric instability locates at hstraight < hz-axis < hstraight + hwhipping. We take advantage of the instability to direct-write serpentine structures by linear translation of the motion stage (see supplementary Figure S4). When 15 mm < hz-axis < 45 mm, the unstable ‘whipping/buckling’ behavior is able to be controlled, and the unstable jet fiber can be positioned on the substrate by the combined control of substrate speed and nozzle-to-substrate distance, and applied voltage. Complex microstructures we have successfully written are coils (Figure 4a), “8”-shaped “vines” (Figure 4b), and sinuous (Figure 4c). The former two microstructures, except the sinuous microstructures, can also be direct-written by melt electrospinning35. However the sinuous microstructures is more important in enhancing the deformability of stretchable electronics.

Figure 4. Single-level serpentine fiber structures: (a) coiled structures; (b) ‘8’-figure structures; (c) wavy-shaped structures; and (d) relationship between the amplitude of serpentine and the velocity of substrate.

Figure 4

Open in a new tab

The νsubstrate can digitally control the layout of deposited fibers, from coils to serpentines, to straight lines, with the increase of νsubstrate, as shown in Figure 4. When νsubstrate > νjetting, HDW converts to MDW, with less control of position due to the larger nozzle-to-substrate distance. In experiment (the solution is PVDF (Polyvinylidene fluoride) with 16% concentration (Dimethylformamide: acetone = 6:4), and Uapplied = 2.2 kV, hz–axis = 25 mm, Qflow = 600 nl/min), three critical speeds are observed to divide the patterns into four kinds of shapes: coiled, “8”-shaped, serpentine and straight structures, where the transition speeds are about 130 mm/s, 230 mm/s and 330 mm/s. Thus, it indicates that the breaking point between the meandering and straight patterns is the onset of the fiber buckling. The structural period linearly decreases with νsubstrate. Due to small substrate speed, the fiber is only stretched by electrical field, and the mechanical drawing force only plays a guiding role in positioning the fibers along the motion direction. The shape of deposited structure is determined by the relative velocity and the instability of jetting, when other processing parameters are fixed.

The Uvoltage plays a critical and complex role in controlling the dynamic behavior of electrospinning. It may influence the jetting speed νjetting, fiber diameter and stable length hstraight simultaneously (Figure 1a). A series of experiments were carried out, where hz–axis = 25 mm, and Uvoltage from 1.7 kV to 3.3 kV with the incremental interval of 0.2 kV. The jetting speed increases monotonically with the applied voltage. It can be observed at the speed of 200 mm/s that only straight fibers can be deposited on the substrate at 1.7 kV, whereas serpentine fibers are deposited at 1.9 kV. That is to say the jetting speed exceeds the substrate speed, namely νjetting > νsubstrate, when Uvoltage increases from 1.7 kV to 1.9 kV. On the other hand, the rotation speed of helix motion also progressively increases with Uvoltage. It explains that only coiled fibers can be deposited when Uvoltage ≥ 2.1 kV, and the space of coiled fibers decreases monotonically with Uvoltage.

The hz–axis serves two critical purposes. One role is to differentiate HDW (for complex curvy fibers) from MDW (for straight fibers). When hz–axis < hstraight, HDW decays back to MDW. The other role of hz–axis is to determine the radius of the conical helix of whipping segment, to control the serpentine amplitude and wavelength. The rotation radius at the bottom increases monotonically with hz–axis. Serpentine structure with large amplitude and small wavelength can be formed by digitally tuning hz–axis and νsubstrate, to improve the stretchability of electronic devices. Furthermore, the ratio of amplitude and wavelength can be increased by depositing fiber onto uniaxially prestrained substrate.

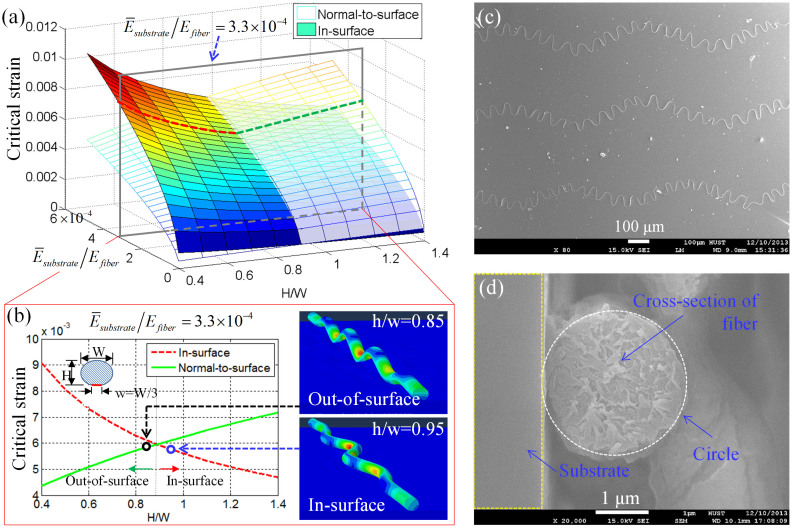
We adopt HDW to fabricate self-similar serpentine structures that are used in stretchable devices. The self-similar serpentine structures will increase the stretchability significantly, and are useful for stretchable electronic devices which are composed of large areas of undeformable components, especially avoiding out-of-surface deformation at stretching36,37,38. This process contains three main steps (supplementary Figure S5): 1) HDW direct-writes the first-level serpentine structures on Si substrate; 2) the transfer printing is utilized to transfer the serpentine structures from Si substrate to a prestrained rubber substrate; and 3) the buckling of serpentine structures occurs to form the hierarchical buckling structures, when the prestrained substrate is released from the prestrain εprestrain, which has to be larger than the critical buckling strain. Two different buckling modes are observed in experiments: in-surface buckling and out-of-surface buckling. We have confirmed the critical conditions for in- and out-of-surface buckling theoretically and experimentally23. The critical strains for in- and out-of-surface buckling are related to the fiber cross-section and the Young's moduli of the fiber and the rubber substrate. 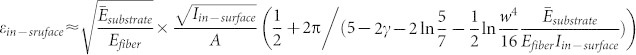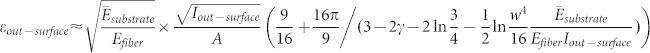The critical strains for in-surface and out-of-surface buckling modes are Inline graphic and Inline graphic, respectively, where Iin–surface and Iout–surface are the moment of inertia of the fiber along the in-surface and normal-to-surface directions. The buckling mode can be predicated comparing εprestrain with the critical strains of in-/out-of-surface buckling. When εprestrain < min(εout–surface, εin–surface), the fiber gets compressed without any buckling. If εprestrain < min(εout–surface, εin–surface), the in-surface buckling occurs when εout–surface > εin–surface, and the out-of-surface buckling occurs when εout–surface > εin–surface.

Figure 5 shows the critical strains for in- and out-of-surface buckling of deposited fibers with elliptical cross-section. The Young's modulus ratio has a significant effect on the critical strains of each buckling mode, but very little contribution to in- and out-of-surface buckling mode transformation. The critical point is mainly determined by the cross-section of deposited fiber. Figure 5b is the case that the Young's modulus ratio 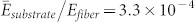Inline graphic, and we get the critical point is H/W ≈ 0.9. The right of Figure 5b is the finite element simulation of the buckling mode for different elliptical cross-sections. Figure 5c is an SEM figure of self-similar serpentine structure with hierarchical serpentine structures, and more can be seen in supplementary Figure S6. The cross-section is close to a circle (Figure 5d), which guarantees in-surface buckling of the first-order serpentine structures.

Figure 5. Critical strain for in-surface buckling and out-of-surface buckling.

Figure 5

Open in a new tab

(a) The semi-elliptical cross-section's critical strain for both in-plane and out-of-plane buckling. (b) The specific is 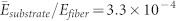Inline graphic, and the finite element simulation of in-surface and out-of-surface buckling. (c) The SEM figure of self-similar serpentine structures. (d) The circular cross-section of the self-similar structures.

Leap direct-writing of bead-on-string structures

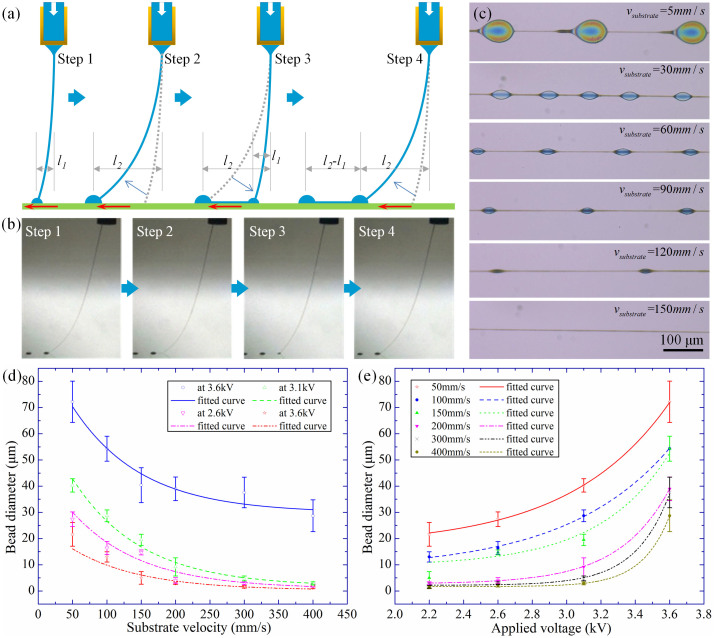
Leap direct-writing can digitally deposit the bead-on-string structures when 0.5 mm < hz-axis ≤ 2 mm and νsubstrate ≤ 120 mm/s, as schematically shown in Figure 6a. There are four key steps involved in LDW. In Step 1, the ink is jetted from the attached Taylor cone, and a fiber links the nozzle and substrate. When hz-axis = 2 mm, the fiber remains liquid when reaching the substrate. The liquid fiber accumulates at the contact point, forming a big drop if the substrate stays quiescent, in a sense similar with aerial refueling. In Step 2, when the substrate starts to move slowly, the jet fiber will gradually slope to match the substrate speed. In Step 3, the jet fiber jumps to the next point at a critical distance (at the speed of <120 mm/s), and the next identical cycle begins in Step 4. The formation of bead-on-string microstructures is composed of anchoring of contact point, stretching of liquid jet fiber, and skipping to the next contact point. The corresponding experimental steps are captured by high-speed camera (Figure 6b). These phenomena are mainly resulted from the competition of the viscoelastic strength of jet fiber with the combination of mechanical drawing force and electrical field force39. The manufacturing mechanism is intrinsically different from free self-assembly which demonstrates weaker control in positioning40.

Figure 6.

Figure 6

Open in a new tab

The leap direct-writing technique: (a) the schematic diagram of leap direct-writing: the ink first accumulates at contact point and then gets stretched by mechanical drawing force. At a critical distance, the ink leaps to the next contact point, and gets stretched again; (b) the leap direct-writing is captured by high-speed camera, similar with (a); and (c) different structures are deposited in the condition of applied voltage (1 kV), nozzle-to-substrate distance (2 mm), flow rate (50 nl/min). (d) and (e) show the effects of substrate speed and voltage on bead diameter. (d) The color lines are fitting curves at different applied voltage. The error bars present the standard deviation to the average values of 10 measurement results. (e) The color lines are fitting curves at different substrate speed. Supply rate, nozzle-to-substrate distance and nozzle diameter are 1200 nl/min, 7.5 mm and 145 μm, respectively.

The substrate speed controls the bead size and the string length, when hz-axis and Uvoltage are fixed. The accumulation time for the bead gets shorter with higher substrate speed, so that the bead diameter gradually decreases to the line width, and the string becomes longer and longer when the substrate speed reaches that of line writing. Additionally, the mechanical drawing force applied on the liquid fiber increases as the viscosity of the polymer solution enhances. Different bead-on-string structures obtained when varying substrate speeds from 5 mm/s to 120 mm/s are shown in Figure 6c, with the flow rate of 50 nl/min and Uvoltage = 1.25 kV. The beads are large at slow speed, and completely disappear when the speed reaches >150 mm/s. To further control the size of each bead, the substrate speed should be programmed to tune the time for ‘aerial refueling’. We also fabricate arrays of silicon nozzles to direct-write bead-on-string structures41. The microstructures are captured by confocal laser scanning microscopy (Supplementary FigureS7), with Uvoltage = 2.2 kV fixed. Fine fibers can be written when substrate speed is 400 mm/s, hz-axis = 7.5 mm, and flow rate is 1200 nl/min. It indicates that the silicon nozzle array is suitable for large-scale printing of bead-on-string structures. The experiment results show that the critical speed νcritical to transform from bead-on-string mode to fiber mode is between 150 mm/s and 200 mm/s. Figure 6d shows the bead size changes with the substrate speed at different applied voltage. When νsubstrate < νcritical, bead-on-string microstructures are fabricated. When νsubstrate < νcritical, the accumulation effect disappears, and LDW decays into MDW, where the fiber will be continuously pulled by the mechanical drawing force, and only line structures are fabricated.

Figure 6e shows that the applied voltage can also tune the size of bead-on-string structures. Si-nozzle was adopted to study the dependence, and four groups of experiments were carried out: 3.6 kV, 3.1 kV, 2.6 kV, and 2.2 kV, where the flow rate and nozzle-to-substrate distance kept constant (6 wt% PEO at 1200 nl/min, hz-axis = 7.5 mm). In each experiment, the substrate speed νsubstrate changes from 50 mm/s to 400 mm/s. It can be found that the bead enlarges monotonically with applied voltage at a constant substrate speed. It can also be noted that the critical voltage for the spurt of bead size growth is located between 3.1 kV and 3.6 kV.

Conclusion

A versatile MES direct-writing technique that can directly write high-viscosity ink on flexible substrates, in a continuous, high-resolution, noncontact, and low-temperature manner is developed to fabricate micro/nano-structures of various morphology and resolution by digitally tuning three key processing parameters: the substrate speed, the nozzle-to-substrate distance, and the applied voltage. The mechanical drawing force controlled by the substrate speed plays a critical role in the improvements over NFES techniques in terms of the resolution, positioning, and alignment of micro/nanofibers. The various micro/nano-structures will serve as the building blocks of a flexible or stretchable electronics. Arrayed structures can potentially be written simultaneously by multiply nozzles, which represents a viable solution for high-throughput manufacture using MES.

Author Contributions

Y.A.H. and Z.P.Y. designed the experiments and wrote the manuscript. Y.A.H., Y.Q.D. and Y.J.D. performed the direct-writing experiments. Y.A.H., N.B.B., Y.Q.P. and N.S.L. analyzed the data, and discussed the results. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep05949-s1.pdf (712.9KB, pdf)

Acknowledgments

The authors acknowledge supports from the National Natural Science Foundation of China (51322507, 51175209, 51121002) and the Fundamental Research Funds for the Central Universities (2013TS019). The general characterization facilities were provided through the National Laboratory.

References

  1. Li Y., Fu Z.-Y. & Su B.-L. Hierarchically Structured Porous Materials for Energy Conversion and Storage. Adv. Funct. Mater. 22, 4634–4667 (2012). [Google Scholar]
  2. Yang H. F., Lightner C. R. & Dong L. Light-Emitting Coaxial Nanofibers. Acs Nano 6, 622–628 (2012). [DOI] [PubMed] [Google Scholar]
  3. Gumennik A. et al. All-in-Fiber Chemical Sensing. Adv. Mater. 24, 6005–6009 (2012). [DOI] [PubMed] [Google Scholar]
  4. Huang Y. et al. Electrohydrodynamic direct-writing. Nanoscale 5, 12007–12017 (2013). [DOI] [PubMed] [Google Scholar]
  5. Sun D., Chang C., Li S. & Lin L. Near-Field Electrospinning. Nano Lett. 6, 839–842 (2006). [DOI] [PubMed] [Google Scholar]
  6. Chang C., Limkrailassiri K. & Lin L. W. Continuous near-field electrospinning for large area deposition of orderly nanofiber patterns. Appl. Phys. Lett. 93, 123111 (2008). [Google Scholar]
  7. Wang X. et al. Fabrication of nanochannels via near-field electrospinning. Appl. Phys. A-mater. 108, 825–828 (2012). [Google Scholar]
  8. Min S. Y. et al. Large-scale organic nanowire lithography and electronics. Nat. Commun. 4, 1773 (2013). [DOI] [PubMed] [Google Scholar]
  9. Agarwal S., Greiner A. & Wendorff J. H. Electrospinning of Manmade and Biopolymer Nanofibers-Progress in Techniques, Materials, and Applications. Adv. Funct. Mater. 19, 2863–2879 (2009). [Google Scholar]
  10. Yin Z. P., Huang Y. A., Bu N. B., Wang X. M. & Xiong Y. L. Inkjet printing for flexible electronics: Materials, processes and equipments. Chin. Sci. Bull. 55, 3383–3407 (2010). [Google Scholar]
  11. Calvert P. Inkjet printing for materials and devices. Chem. Mater. 13, 3299–3305 (2001). [Google Scholar]
  12. Chung S. et al. Inkjet-printed stretchable silver electrode on wave structured elastomeric substrate. Appl. Phys. Lett. 98, 153110 (2011). [Google Scholar]
  13. Sirringhaus H. et al. High-resolution inkjet printing of all-polymer transistor circuits. Science 290, 2123–2126 (2000). [DOI] [PubMed] [Google Scholar]
  14. Yun Y. H. et al. A Glucose Sensor Fabricated by Piezoelectric Inkjet Printing of Conducting Polymers and Bienzymes. Anal. Sci. 27, 375–379 (2011). [DOI] [PubMed] [Google Scholar]
  15. Jung H. C., Cho S. H., Joung J. W. & Oh Y. S. Studies on inkjet-printed conducting lines for electronic devices. J. Electron. Mater. 36, 1211–1218 (2007). [Google Scholar]
  16. Forrest S. R. The path to ubiquitous and low-cost organic electronic appliances on plastic. Nature 428, 911–918 (2004). [DOI] [PubMed] [Google Scholar]
  17. Park J. U. et al. High-resolution electrohydrodynamic jet printing. Nat. Mater. 6, 782–789 (2007). [DOI] [PubMed] [Google Scholar]
  18. de Gans B. J., Duineveld P. C. & Schubert U. S. Inkjet Printing of Polymers: State of the Art and Future Developments. Adv. Mater. 16, 203–213 (2004). [Google Scholar]
  19. Li D., Ouyang G., McCann J. T. & Xia Y. N. Collecting electrospun nanofibers with patterned electrodes. Nano Lett. 5, 913–916 (2005). [DOI] [PubMed] [Google Scholar]
  20. Li D. & Xia Y. Electrospinning of nanofibers: Reinventing the wheel? Adv. Mater. 16, 1151–1170 (2004). [Google Scholar]
  21. Greiner A. & Wendorff J. H. Electrospinning: A fascinating method for the preparation of ultrathin fibres. Angew. Chem. Int. Ed. 46, 5670–5703 (2007). [DOI] [PubMed] [Google Scholar]
  22. Chang C. E., Tran V. H., Wang J. B., Fuh Y. K. & Lin L. W. Direct-Write Piezoelectric Polymeric Nanogenerator with High Energy Conversion Efficiency. Nano Lett. 10, 726–731 (2010). [DOI] [PubMed] [Google Scholar]
  23. Duan Y., Huang Y., Yin Z., Bu N. & Dong W. Non-wrinkled, highly stretchable piezoelectric devices by electrohydrodynamic direct-writing. Nanoscale 6, 3289–3295 (2014). [DOI] [PubMed] [Google Scholar]
  24. Khudiyev T., Huseyinoglu E. & Bayindir M. Non-resonant Mie scattering: emergent optical properties of core-shell polymer nanowires. Sci. Rep. 4, 4607 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Xu B. B., Zhang Y. L., Wei S., Ding H. & Sun H. B. On-Chip Catalytic Microreactors for Modern Catalysis Research. Chemcatchem 5, 2091–2099 (2013). [Google Scholar]
  26. Shigeta K. et al. Functional Protein Microarrays by Electrohydrodynamic Jet Printing. Anal. Chem. 84, 10012–10018 (2012). [DOI] [PubMed] [Google Scholar]
  27. Arrabito G. & Pignataro B. Solution Processed Micro- and Nano-Bioarrays for Multiplexed Biosensing. Anal. Chem. 84, 5450–5462 (2012). [DOI] [PubMed] [Google Scholar]
  28. Huang Y., Wang X., Duan Y., Bu N. & Yin Z. Controllable self-organization of colloid microarrays based on finite length effects of electrospun ribbons. Soft Matter 8, 8302–8311 (2012). [Google Scholar]
  29. Brochardwyart F. & Redon C. Dynamics of Liquid Rim Instabilities. Langmuir 8, 2324–2329 (1992). [Google Scholar]
  30. Kondic L., Diez J. A., Rack P. D., Guan Y. F. & Fowlkes J. D. Nanoparticle assembly via the dewetting of patterned thin metal lines: Understanding the instability mechanisms. Phys. Rev. E 79, 026302 (2009). [DOI] [PubMed] [Google Scholar]
  31. Kim D. H. et al. Materials and noncoplanar mesh designs for integrated circuits with linear elastic responses to extreme mechanical deformations. Proc. Natl. Acad. Sci. 105, 18675–18680 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kim D. H. et al. Epidermal Electronics. Science 333, 838–843 (2011). [DOI] [PubMed] [Google Scholar]
  33. Duan Y., Huang Y. & Yin Z. Transfer printing and patterning of stretchable electrospun film. Thin Solid Films 544, 152–156 (2013). [Google Scholar]
  34. Huang Z. M., Zhang Y. Z., Kotaki M. & Ramakrishna S. A review on polymer nanofibers by electrospinning and their applications in nanocomposites. Compos. Sci. Technol. 63, 2223–2253 (2003). [Google Scholar]
  35. Brown T. D., Dalton P. D. & Hutmacher D. W. Direct Writing By Way of Melt Electrospinning. Adv. Mater. 23, 5651–5657 (2011). [DOI] [PubMed] [Google Scholar]
  36. Su Y. et al. Postbuckling analysis and its application to stretchable electronics. J. Mech. Phys. Solids 60, 487–508 (2012). [Google Scholar]
  37. Fan J. A. et al. Fractal design concepts for stretchable electronics. Nat. Commun. 5, 3266 (2014). [DOI] [PubMed] [Google Scholar]
  38. Xu S. et al. Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems. Nat. Commun. 4, 1543 (2013). [DOI] [PubMed] [Google Scholar]
  39. Bu N. B., Huang Y. A., Deng H. X. & Yin Z. P. Tunable bead-on-string microstructures fabricated by mechano-electrospinning. J. Phys. D. Appl. Phys. 45, 405301 (2012). [Google Scholar]
  40. Tian X. L., Bai H., Zheng Y. M. & Jiang L. Bio-inspired Heterostructured Bead-on-String Fibers That Respond to Environmental Wetting. Adv. Funct. Mater. 21, 1398–1402 (2011). [Google Scholar]
  41. Pan Y. Q., Huang Y. A., Bu N. B. & Yin Z. P. Fabrication of Si-nozzles for parallel mechano-electrospinning direct writing. J. Phys. D. Appl. Phys. 46, 255301 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep05949-s1.pdf (712.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES