Accuracy of forecasts in strategic intelligence

Significance

Forecasting is a vital part of strategic intelligence, offering policy makers indications about probable future conditions and aiding sound decision making. Nevertheless, there has not been a concerted effort to study the accuracy of intelligence forecasts over a large set of assessments. This study applied quantitative measures of forecasting accuracy commonly used in other areas of expert forecasting to over 1,500 strategic intelligence forecasts spanning approximately 6 y of intelligence production by a strategic assessment unit. The findings revealed a high level of discrimination and calibration skill. We also show how calibration may be improved through postforecast transformations. The study illustrates the utility of proactively applying scoring rules to intelligence forecasts as a means of outcome-based quality control.

Abstract

The accuracy of 1,514 strategic intelligence forecasts abstracted from intelligence reports was assessed. The results show that both discrimination and calibration of forecasts was very good. Discrimination was better for senior (versus junior) analysts and for easier (versus harder) forecasts. Miscalibration was mainly due to underconfidence such that analysts assigned more uncertainty than needed given their high level of discrimination. Underconfidence was more pronounced for harder (versus easier) forecasts and for forecasts deemed more (versus less) important for policy decision making. Despite the observed underconfidence, there was a paucity of forecasts in the least informative 0.4–0.6 probability range. Recalibrating the forecasts substantially reduced underconfidence. The findings offer cause for tempered optimism about the accuracy of strategic intelligence forecasts and indicate that intelligence producers aim to promote informativeness while avoiding overstatement.

Strategic intelligence assists high-level decision makers, such as senior government leaders, in understanding the geopolitical factors shaping the world around them. Such intelligence can help decision makers anticipate future events, avoid strategic surprises, and make informed decisions. Policy-neutral intelligence that is timely, relevant, and accurate can be of significant value to decision makers (1). Although not all intelligence is predictive, forecasts are an important part of intelligence, serving to reduce uncertainty about future events for decision makers (2). Forecasts compose a substantial part of the type of judgment that Sherman Kent (widely regarded as the father of modern intelligence analysis) identified as most informative—namely, judgments that go beyond the information given (3). A question arising, then, is how good are intelligence analysts at forecasting geopolitical events?

The answer to that question should be of value to multiple stakeholders. First, intelligence consumers should want to know how good the forecasts they receive actually are. This should guide the weight they assign to them and the trust they place in their sources. Second, intelligence managers directly accountable for analytic quality control should want to know how well their analysts are doing. An objective scorecard might mitigate accountability ping-pong pressures in which the intelligence community reactively shifts its tolerance levels for false-positive and false-negative errors to “now get it right” (4). Third, analysts, an intellectually curious breed, should want to know how good their forecasts are. Beyond satisfying curiosity, receiving objective performance feedback on a regular basis can encourage adaptive learning by revealing judgment characteristics (e.g., overconfidence) that would be hard to detect from case-specific reviews (5). Finally, citizens should want to know how well the intelligence community is doing. Not only does personal security depend on national security, intelligence is a costly enterprise, running into the tens of billions each year in the United States (6).

Despite good reasons to proactively track the accuracy of intelligence forecasts, intelligence organizations seldom keep an objective scorecard of forecasting accuracy (7). There are many reasons why they do not do so. First, analysts seldom use numeric probabilities, which lend themselves to quantitative analyses of accuracy (8). Many analysts, including Kent’s poets (3), are resistant to the prospect of doing so (9). Second, intelligence organizations do not routinely track the outcomes of forecasted events, which are needed for objective scorekeeping. Third, only recently have behavioral scientists offered clear guidance to the intelligence community on how to measure the quality of human judgment in intelligence analysis (10–13). Finally, there may be some apprehension within the community regarding what a scorecard might reveal.

Such apprehension is understandable. The intelligence community has been accused of failing to connect the dots (14), which would seem to be a requisite skill for good forecasting. Nor does literature on human forecasting accuracy inspire high priors for success. It has long been known that people are miscalibrated in their judgment (15), tending toward overconfidence (16). Tetlock’s study of political experts’ forecasts showed that although experts outperformed undergraduates, even the best human forecasters—the Berlinian foxes—were left in the dust compared with the savvier statistical models he tested (17), recalling earlier studies showing how statistical models outperform human experts’ predictions (18, 19).

Nevertheless, it would be premature to draw a pessimistic conclusion about the accuracy of intelligence forecasting without first-hand, quantitative examination of a sufficient number of actual intelligence forecasts. In addition, some experts, such as meteorologists (20, 21) and bridge players (22), are very well calibrated. Intelligence analysts share some similarities with these experts. For instance, their forecasts are a core product of their expertise. This is not true of all experts, not even those who make expert probabilistic judgments. For instance, physicians may be overconfident (23), but if their patients recover, they are unlikely to question their forecasts. The same is true for lawyers and their clients (24). In these cases, the success of experts’ postforecast interventions will matter most to clients. However, analysts do not make policy decisions or intervene directly. Their expertise is shown directly by the quality of their policy-neutral judgments.

Here we report the findings of a long-term field study of the quality of strategic intelligence forecasts where each forecast was expressed with a numeric probability of event occurrence (from 0/10 to 10/10). We examined an extensive range of intelligence reports produced by a strategic intelligence unit over an approximate 6-y period (March 2005 to December 2011). From each report, every judgment was coded for whether it was a forecast, given that not all judgments are predictive (e.g., some are explanatory). The judgments were generally intended to be as specific as possible, reflecting the fact that the intelligence assessments were written to assist policy makers in reaching decisions. Examples of actual forecasts (edited to remove sensitive information) include the following: “It is very unlikely [1/10] that either of these countries will make a strategic decision to launch an offensive war in the coming six months” and “The intense distrust that exists between Country X and Group Y is almost certain [9/10] to prevent the current relationship of convenience from evolving into a stronger alliance.” In cases, such as the latter example, where a resolution time frame is not specified in the forecast itself, it was inferable from the time frame of the report.

Subject matter experts were used to track the outcomes of the forecasted events, enabling us to quantify several aspects of forecast quality. Those aspects are roughly grouped into two types of indices. The first, discrimination [also called resolution (25)], refers to how well a forecaster separates occurrences from nonoccurrences. The second, calibration [or reliability (25)], refers to the degree of correspondence between a forecaster’s subjective probabilities and the observed relative frequency of event occurrences. We use multiple methods for assessing discrimination and calibration, including receiver operating characteristic (ROC) curve analysis (26), Brier score decomposition (25, 27, 28), and binary logistic models for plotting calibration (29, 30), thus allowing for a wide range of comparison with other studies.

We examined discrimination and calibration for the overall set of forecasts and whether forecast quality was influenced by putative moderating factors, including analyst experience, forecast difficulty, forecast importance, and resolution time frame, all of which were coded by experts. Would senior analysts forecast better than junior analysts? The literature offers mixed indications. For example, although expertise benefitted the forecasts of bridge players (22), it had no effect on expert political forecasters (17). Would easier forecasts be better than harder forecasts? Calibration is often sensitive to task difficulty such that harder problems yield overconfidence that is attenuated or even reversed (producing underconfidence) for easier problems—what is commonly termed the hard–easy effect (31). Would forecast quality be better for forecasts assessed by expert coders as more (versus less) important for policy decision making? This question is of practical significance because although intelligence organizations strive for accuracy in all their assessments, they are especially concerned about getting it right on questions of greatest importance to their clients. Finally, would accuracy depend on whether the resolution time frame was shorter (0–6 mo) or longer (6 mo to about 1 y). Longer time frames might offer better odds of the predicted event occurring, much as a larger dartboard would be easier than a smaller one to hit.

In addition to these descriptive aims, we were interested in the possible prescriptive value of the work. Prior research has shown that forecasting quality may be improved through postforecast transformations. Some approaches require the collection of additional forecasts. For example, using small sets of related probability estimates, Karvetski, Olson, Mandel, and Twardy (32) were able to improve discrimination and calibration skill by transforming judgments so that they minimized internal incoherence. Other studies have shown that calibration can be improved through transformations that do not require collecting additional judgments (33–35). To the extent that forecasts in this study were miscalibrated, we planned to explore the potential benefit and usability of transformations that do not require the collection of additional forecasts.

Results

Discrimination.

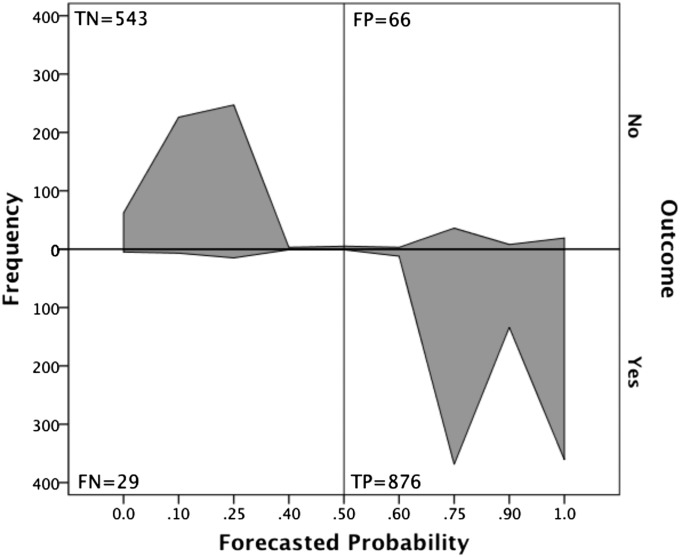
Fig. 1 shows a discrimination diagram of the forecast–outcome cross-tabulation data. The data are arrayed such that the four quadrants of the diagram show the frequency of true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN) when forecast probabilities ≤0.5 indicate event nonoccurrence and probabilities >0.5 indicate event occurrence. Fig. 1 shows that most forecasts (94%) were correctly classified as either TP or TN cases. As well, few cases were in the middle (0.4–0.6) range of the probability scale. This is advantageous because such high-uncertainty forecasts are less informative for decision makers.

Fig. 1.

Discrimination diagram. FN, false negatives; FP, false positives; TN, true negatives; TP, true positives.

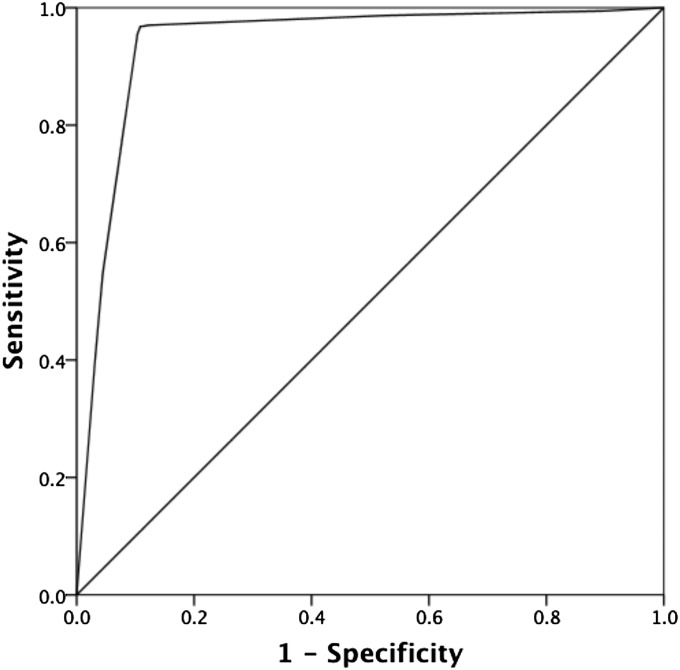
Fig. 2 shows the ROC curve, plotting the TP rate (sensitivity) as a function of the FP rate (1 − specificity). A useful measure of discrimination skill is the area under the ROC curve, A (25), the proportion of the total area of the unit square defined by the two axes of the ROC curve. A can range from 0.5 (i.e., the area covered by the 45° no-discrimination line) to 1.0 (perfect discrimination). A was 0.940 (SE = 0.007), which is very good.

Fig. 2.

ROC curve.

To assess the effect of the putative moderators, A_i was compared across levels of each moderator using the following Z-score equation (36):

$$Z=\frac{A_1-A_2}{\sqrt{{\text{SE}}_{A_1}^2+{\text{SE}}_{A_2}^2}}.$$ [1]

Discrimination was significantly higher for senior analysts (A₁ = 0.951, SE = 0.008) than for junior analysts (A₂ = 0.909, SE = 0.017), Z = 2.24, P = 0.025. Likewise, discrimination was higher for easier forecasts (A₁ = 0.966, SE = 0.010) than for harder forecasts (A₂ = 0.913, SE = 0.011), Z = 3.57, P < 0.001. Discrimination did not differ by importance or resolution time frame (P > 0.25).

Finally, discrimination was also very good when the forecast probabilities were taken into account using Brier score decomposition. The Brier score, B, is the squared deviation between a forecast and the outcome coded 0 (nonoccurrence) or 1 (occurrence). The mean Brier score is a proper scoring rule for probabilistic forecasts:

$$\overline{B}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(f_i-o_i\right)}^2,$$ [2]

where N is the total number of forecasts (1,514 in this study); f_i is the subjective probability assigned to the ith forecast; and o_i is the outcome of the ith event, coded 0 or 1. However, because $\overline{B}$ is affected not only by forecaster skill but also by the uncertainty of the forecasting environment, it is usually decomposed into indices of variance (VI), discrimination (DI), and calibration (CI):

$$\overline{B}=\text{VI}-\text{DI}+\text{CI},$$ [3]

where

$$\text{VI}=\overline{o}\left(1-\overline{o}\right),$$ [4]

$$\text{DI}=\frac{1}{N}{\displaystyle \sum }_{k=1}^K{N}_k{\left({\overline{o}}_k-\overline{o}\right)}^2,$$ [5]

and

$$\text{CI}=\frac{1}{N}{\displaystyle \sum }_{k=1}^K{N}_k{\left(f_k-{\overline{o}}_k\right)}^2.$$ [6]

In Eqs. 4–6, $\overline{o}$ is the base rate or overall relative frequency of event occurrence, K is the number of forecast categories (9 in this study), N_k is the number of forecasts in category k, f_k is the subjective probability assigned to forecasts in category k, and ${\overline{o}}_k$ is the relative frequency of event occurrence in category k. In this study, $\overline{B}$ = 0.074, VI = 0.240, and DI = 0.182. Because DI is upper-bounded by VI, it is common to normalize discrimination:

$${\eta }^2=\text{DI}/\text{VI}\text{.}$$ [7]

An adjustment is sometimes made to this measure (27). However, it had no effect in this study. Normalized discrimination was very good, with forecasts explaining 76% of outcome variance, η² = 0.758.

Calibration.

The calibration index, CI, which sums the squared deviations of forecasts and the relative frequencies of event occurrence for each forecast category, is perfect when CI = 0. In this study, CI = 0.016. An alternative measure of calibration called calibration-in-the-large (28), CI_L, is the squared deviation between the mean forecast and the base rate of event occurrence over all categories:

$${\text{CI}}_L=\overline{f}-\overline{o}.$$ [8]

Calibration in the large was virtually nil, CI_L = 3.60e−5. Thus, both indices showed that forecasts were well calibrated.

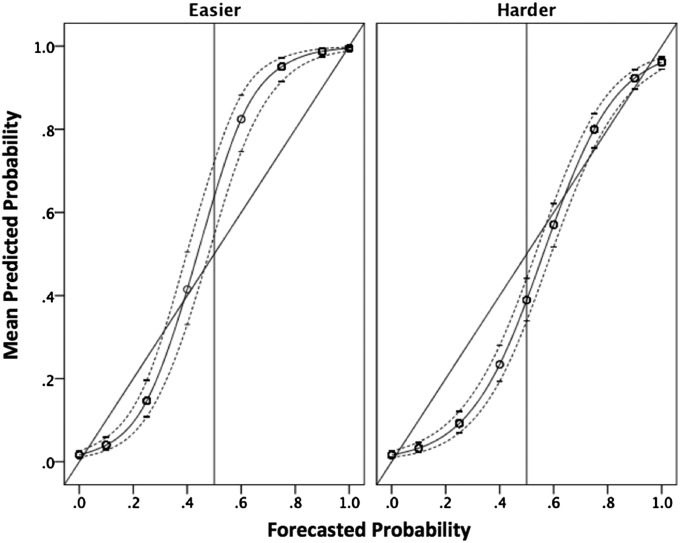
Calibration curves were modeled using a generalized linear model with a binary logistic link function. Event outcomes were first modeled on forecast, difficulty, importance, experience, resolution time frame, and all two-way interactions with forecast. Two predictors were significant: forecast and the forecast × difficulty interaction. Using forecast and difficulty as predictors, the model fit for forecast only and forecast with the interaction term were compared using Akaike information criterion (AIC) (37). The model including the interaction term improved model fit (AIC = 118.14) over the simpler model (AIC = 148.47). Fig. 3 shows the calibration curves plotting mean predicted probability of the event occurring as a function of forecast and difficulty. It is evident that in both the easier and harder sets of forecast, miscalibration was mainly due to underconfidence, as revealed by the characteristic S-shape of the curves. This pattern of calibration is also referred to as underextremity bias because the forecasts are not as extreme as they should be (38). In the easier set, underconfidence is more pronounced for forecasts above 0.5, whereas underconfidence is more pronounced for forecasts below 0.5 in the harder set.

Fig. 3.

Model-based calibration curves. Dotted lines show 95% confidence intervals.

A signed calibration of confidence index (39), CCI, was computed as follows, such that negative values indicated underconfidence and positive values indicated overconfidence:

$$\text{CCI}=\frac{1}{N}\left({\displaystyle \sum }_{k=1}^K{N}_k\left({\overline{o}}_k-f_k\right)\text{iff}\hspace{0.17em}{f}_k<0.5+{\displaystyle \sum }_{k=1}^K{N}_k\left(f_k-{\overline{o}}_k\right)\text{iff}\hspace{0.17em}{f}_k>0.5\right).$$ [9]

This measure omits the small number of cases where f_k = 0.5. In this study, CCI = −0.076 (s = 0.096), therefore indicating underconfidence. The 99% confidence interval on the estimate ranged from −0.082 to −0.070, placing zero well outside its narrow range. Given the nonnormality of subsample distributions of underconfidence, we examined the effect of the moderators on underconfidence using Mann–Whitney u tests. There was no effect of experience or resolution time frame (P > 0.15). However, underconfidence was greater for harder forecasts (median = −0.106) than for easier forecasts (median = −0.044), Z = −13.39, P < 0.001. Underconfidence was also greater for forecasts of greater importance (median = −0.071) rather than lesser importance (median = −0.044), Z = −4.49, P < 0.001. Given that difficulty and importance were positively related (r = 0.17, P = 0.001), we tested whether each had unique predictive effects on underconfidence using ordinal regression. Both difficulty (b = 1.26, SE = 0.10, P < 0.001) and importance (b = 0.32, SE = 0.12, P = 0.007) predicted underconfidence, together accounting for roughly an eighth of the variance in underconfidence (Nagelkerke pseudo-R² = 0.124).

Sensitivity.

The high degree of forecasting quality raises questions about the sensitivity of the results to excluded cases. There were two types of exclusions we explored: cases with ambiguous outcomes and cases without numeric probabilities. The first type accounted for about 20% of numeric forecasts and typically occurred when the event in question was not defined crisply enough to make an unambiguous determination of outcome. In such cases, the coders either assigned partial scores indicating evidence in favor of occurrence or nonoccurrence, or else an unknown code. We dummy coded partial nonoccurrences as 0.25, unknown cases as 0.50, and partial occurrences as 0.75 and recomputed the mean Brier score. The resulting value was 0.090. A comparable analysis was undertaken to assess the effect of excluding the roughly 16% of forecasts that did not have numeric probabilities assigned. In these cases, terms such as could or might were used, and these were deemed to be too imprecise to assign numeric equivalents. For the present purpose, we assume that such terms are likely to be interpreted as being a fifty-fifty call (40), and accordingly, we assign a probability of 0.50 to those cases. The recomputed mean Brier score was 0.097. Given that both recomputed Brier scores are still very good, we can be confident that the results are not due to case selection biases.

Recalibration.

Given that forecasts exhibited underextremity bias, we applied a transformation that made them more extreme. Following ref. 33–35, which draw on Karmarker’s earlier formulation (41), we used the following transformation:

$$t=\frac{f^a}{f^a+{\left(1-f\right)}^a},$$ [10]

where t is the transformed forecast and a is a tuning parameter. When a > 1, the transformed probabilities are made more extreme. We varied a by 0.1 increments from 1 to 3 and found that the optimal value for minimizing CI was 2.2. Fig. S1 plots CI as a function of a. Fig. S2 shows the transformation function when a = 2.2. Recalibrating the forecasts in this manner substantially improved calibration, CI = 0.0018. To assess the degree of improvement, it is useful to consider the square root of CI in percentage format, which is the mean absolute deviation from perfect calibration. This value is 12.7% for the original forecasts and 4.2% for the transformed forecasts, a 66.9% decrease in mean absolute deviation.

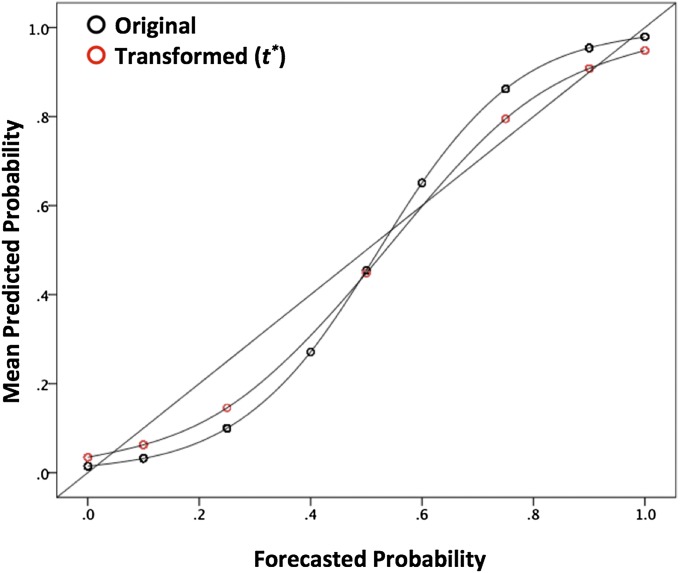
Although the Karmarker transformation improved calibration, the resulting forecast probabilities have no analog on the numeric scale used by the intelligence unit that we studied. To assess whether a more feasible recalibration method that uses the original scale points may be of value, the transformed values were mapped onto their closest original scale point, resulting in a remapping of the original forecasts, f_k, to the new transformed forecasts, t*_k as follows for [ f_k, t*_k]: [0, 0], [0.1, 0], [0.25, 0.1], [0.4, 0.25], [0.5, 0.5], [0.6, 0.75], [0.75, 0.9], [0.9, 1], and [1, 1]. With this feasibility adjustment, CI = 0.0021. The mean absolute deviation from perfect calibration was 4.6%, a slight difference from the optimized Karmarker transformation. Fig. 4 shows the calibration curve for the 1,514 forecasts before and after remapping, whereas Fig. S3 shows the curves before and after the Karmarker transformation was applied. The calibration curves for the transformed forecasts shown in the two figures are almost indistinguishable.

Fig. 4.

Calibration curves before and after recalibration to t*.

Discussion

Our findings warrant tempered optimism about the quality of strategic intelligence forecasts. The forecasts fared exceptionally well in terms of discrimination and calibration, and these results were not particularly sensitive to case exclusions. The results provide a stark comparison with Tetlock’s (17) findings. Whereas the best political forecasters in his sample explained about 20% of the outcome variance, forecasts in this study explained 76% of the variance in geopolitical outcomes. Likewise, the mean absolute deviation from perfect calibration (the square root of the calibration index) was 25% smaller in our study than in Tetlock’s, reflecting better calibration. Experience had no effect in his study, but analytic experience led to a practically beneficial improvement in discrimination in this study. Not only did senior analysts discriminate better than junior analysts, they produced 68% of the forecasts despite constituting less than half of the analyst sample (Materials and Method). Finally, whereas experts in Tetlock’s study showed overconfidence, forecasts in this study were underconfident. Although unbiased confidence is optimal, the cost of overconfidence in intelligence will usually outweigh that of underconfidence. Underconfident forecasting occurs when analysts discriminate better than they think they can. Although underconfidence reduces informational value for decision makers by expressing forecasts too timidly, it signals good judgment. Overconfidence, in contrast, indicates that forecasts are communicated with unwarranted certainty, implying that they are more error-prone than experts predict.

Several of the findings suggest that intelligence producers adhere to a professional norm of promoting informativeness while avoiding overstatement. First, there were few uninformative forecasts near maximum uncertainty (probabilities of 0.4–0.6). If analysts were only concerned with playing it safe, we would likely have seen a bulge rather than a trough in that region. Second, underconfidence was more pronounced when the issues were relatively complex and more important for policy makers. These variations are consistent with a norm of caution, which both difficulty and consequence of judgment should heighten. Indeed, the effect of difficulty may otherwise appear surprising given that harder problems usually produce greater overconfidence (30). As well, this pattern (greater underconfidence for harder forecasts) does not support the explanation that underconfidence in this study was mainly due to easy forecasting problems. A norm of caution may serve the intelligence community well in the absence of systematic feedback on the forecasting quality. With such feedback, adjustments to cautionary normative pressure could lead to crisper indications as analysts and their managers become aware of characteristics such as good discrimination (5). That would, in turn, better serve the aim of reducing uncertainty in the mind of the decision maker (2).

A deeper account of the present findings might trace normative pressures for cautious, yet informative assessments to analysts’ accountability to multiple, skeptical audiences. Accountability pressure has been shown to reduce overconfidence in predicting personality attributes (42), reduced overattribution bias (43), deeper information processing (44), and better awareness of the informational determinants of one’s choices (45). As Arkes and Kajdasz (46) have already noted about a preliminary summary of our findings presented to the National Research Council Committee on Behavioral and Social Science Research to Improve Intelligence Analysis for National Security, the strategic analysts who made the forecasts studied here had much more severe accountability pressures than experts in Tetlock’s (17) study and in other academic research. Experts in such studies know that their forecasts will be anonymously analyzed in the aggregate. In contrast, analysts are personally accountable to multiple, skeptical audiences. They have to be able to defend their assessments to their managers. Together with those managers, they need to be able to speak truth to power. Analysts are acutely aware of the multiple costs of getting it wrong, especially on the most important issues. The flipside of accountability pressure is feedback, which may also benefit accuracy. Given that analysts assessments must be vetted by managers and may receive input from peers, they may also benefit from the underlying team process, as has recently been verified in a controlled geopolitical forecasting tournament (47).

As noted earlier, underconfidence, as a source of miscalibration, is the lesser of two evils. It is also to a large extent correctable. We showed that miscalibration could be attenuated postforecast in ways that are organizationally usable. Using the Karmarker transformation as a guide, we remapped forecasts to the organizational scale value that had come closest to the transformed value. This procedure yielded a substantial 63.8% decrease in mean absolute deviation from perfect calibration. If intelligence organizations were able to discern stable biases in forecasting, such corrective measures could potentially be implemented between forecast production and finished intelligence dissemination to consumers.

Of course, recalibration, like any model-fitting exercise, requires caution. Aside from the philosophical matter of whether the transformed values still represent subjective probabilities (48), care ought to be taken not to overfit or overgeneralize the approach. This is especially likely in cases where the recalibration rules are based on small sets of forecasts or where attempts are made to generalize to other contexts. Accordingly, we would not advise a different intelligence organization to similarly make their forecasts more extreme without having first studied their own forecast characteristics. A further complication may arise if intelligence consumers have already learned to recalibrate a source’s forecasts. For instance, if policy makers know that the forecasts they receive from a given source tend to be underconfident, they may intuitively adjust for that bias by decoding the forecast in more extreme terms (33). Thus, a change in procedure that resulted in debiased forecasts would somehow have to be indicated to consumers so that they do not continue to correct the corrected forecasts. What this work suggests, however, is that at least in principle, such correctives are doable.

Materials and Methods

Forecast data were acquired from internal versions of intelligence reports produced by 15 strategic intelligence analysts that composed the analytic team of the Middle East and Africa Division within the Intelligence Assessment Secretariat (IAS) over the study period. IAS is the Canadian government’s strategic intelligence analysis unit, providing original, policy-neutral assessments on foreign developments and trends for the Privy Council Office and senior clients across government. The analysts were subject matter experts, normally with postgraduate degrees and in many cases extensive experience working or traveling in their regions of responsibility (especially for senior analysts).

The internal versions of reports included numerical probabilities assigned to unconditional forecasts, which could take on values of 0, 1, 2.5, 4, 5, 6, 7.5, 9, or 10 (out of 10). Such numbers were only assigned to judgments that were unconditional forecasts and they were not included in finished reports. Analysts within the division over the period of examination made the initial determination of whether their judgments were unconditional forecasts, conditional forecasts (e.g., of the form “if X happens, then Y is likely to occur”), or explanatory judgments (e.g., judgments of the probable cause of a past or ongoing geopolitical event), and those were subsequently reviewed and, if necessary, discussed with the analyst’s manager, who had the final say. Typically, each page of an intelligence report will contain several judgments of these various types, and these judgments represented a wide range of unique events or situations.

In cases, where the same judgment appeared multiple times, only the first judgment was entered into the database. For example, if a forecast appeared as a key judgment (i.e., a select set of judgments highlighted at the start of a report) and was then repeated later in the report, only the first appearance was counted. Moreover, a single analyst initially would produce a given forecast, which would subsequently be reviewed by the analyst’s manager. The drafting process also normally involves extensive consultation with other experts and government officials. Thus, the forecasts that appear in intelligence reports are seldom the result of a single individual arriving at his or her judgment in isolation. It is more accurate to regard an analytical forecast as an organizational product reflecting the input of the primary analyst, his or her manager, and possibly a number of peer analysts.

From a total set of 3,881 judgments, classifications were as follows: 59.7% (2,315) were unconditional forecasts, 15.0% were conditional forecasts, and 25.3% were explanatory judgments. From the unconditional forecasts, on which we focus, 83.8% (1,943) had numeric probabilities assigned. The remaining cases were not assigned numeric probabilities, because the verbal expressions of uncertainty used were deemed too imprecise to warrant a numeric translation.

Two subject matter experts unaffiliated with the division coded outcomes. Each coder handled a distinct set of forecasts, although both coded the same 50 forecasts to assess reliability, which was at 90% agreement. Although having unambiguous, mutually exclusive and exhaustive outcome possibilities for all forecasts is desirable (17), such control was impossible here. In 80.4% (i.e., 1,562/1,943) of cases, forecasts were articulated clearly enough that the outcome could be coded as an unambiguous nonoccurrence or occurrence. In the remaining cases, however, the outcome was ambiguous, usually because the relevant forecast lacked sufficient precision and actual conditions included a mix of pro and con evidence. In such cases, outcomes were assigned to “partial nonoccurrence,” “partial occurrence,” or “unknown” categories, depending on the coders’ assessments of the balance of evidence. However, the primary analyses are restricted to the unambiguous set. Note that outcomes themselves could represent either commissions and affirmed actions (e.g., President X will be elected) or omissions and negated actions (e.g., President X will not be elected). We further excluded 30 forecast cases that were made by teams of analysts and additional 18 cases for which full data on the coded moderator variables were unavailable. The final set of cases thus included 1,514 forecasts (Dataset S1).

Experts also coded the four moderating variables examined here. A.B. coded analyst experience, assigning the analyst to either a junior or senior category. In general, analysts with 0–4 y of experience as an analyst in the IAS were coded as junior, and those with more than 4 y of experience were coded senior. However, this was modified on occasion if other factors were in play, such as whether the analyst had prior experience in a similar strategic assessment unit or extensive experience working or traveling in their region of responsibility. Among the 15 analysts, seven were coded as senior (accounting for 1,027 or roughly 68% of the forecasts), and two of those became senior over the course of the study (those two thus contributed to both the junior and senior groupings). Expert coders coded the remaining three variables: forecast difficulty (easier/harder), forecast importance (lesser/greater), and resolution time frame (less than/greater than 6 mo). A.B. reviewed the codes and discrepant assignments were resolved by discussion. Further details on the procedures for coding these variables are available in Supporting Information.