Charge transport and rectification in molecular junctions formed with carbon-based electrodes

Significance

Single-molecule circuits represent an ultimate limit of device size and control, where function relates to intrinsic molecular properties. Here, we introduce a new paradigm for such circuits. Instead of using precious metals that have smooth densities of states around the Fermi energy, we introduce a hybrid device structure with the molecule trapped across a gold/graphite gap. These junctions rectify and have among the highest rectification ratios reported for a molecular junction. Using quantitative and predictive calculations, we explain our results as directly emanating from a nonuniform voltage drop and a nonconstant graphite density of states near the Fermi level. This work introduces the electrode as a tunable variable for realizing nonlinear device phenomena in hybrid junctions formed with layered two-dimensional materials.

Abstract

Molecular junctions formed using the scanning-tunneling-microscope–based break-junction technique (STM-BJ) have provided unique insight into charge transport at the nanoscale. In most prior work, the same metal, typically Au, Pt, or Ag, is used for both tip and substrate. For such noble metal electrodes, the density of electronic states is approximately constant within a narrow energy window relevant to charge transport. Here, we form molecular junctions using the STM-BJ technique, with an Au metal tip and a microfabricated graphite substrate, and measure the conductance of a series of graphite/amine-terminated oligophenyl/Au molecular junctions. The remarkable mechanical strength of graphite and the single-crystal properties of our substrates allow measurements over few thousand junctions without any change in the surface properties. We show that conductance decays exponentially with molecular backbone length with a decay constant that is essentially the same as that for measurements with two Au electrodes. More importantly, despite the inherent symmetry of the oligophenylamines, we observe rectification in these junctions. State-of-art ab initio conductance calculations are in good agreement with experiment, and explain the rectification. We show that the highly energy-dependent graphite density of states contributes variations in transmission that, when coupled with an asymmetric voltage drop across the junction, leads to the observed rectification. Together, our measurements and calculations show how functionality may emerge from hybrid molecular-scale devices purposefully designed with different electrodes beyond the so-called “wide band limit,” opening up the possibility of assembling molecular junctions with dissimilar electrodes using layered 2D materials.

Recent interest in understanding charge transport in molecular-scale devices and at metal/organic interfaces has led to innovations in both experimental and theoretical techniques designed to probe such devices (1, 2). Molecular junctions in a metal–molecule–metal motif using a variety of metals including Au, Ag, Pt, Al, and Cu have been studied extensively (3–7), contributing significantly to our understanding of the fundamental principles required to realize molecular-scale electronic components such as rectifiers or switches (8–14). However, the nanogap electrodes using such metals are mechanically unstable due to the high atomic mobility of metal atoms (15–18) and all except for Au oxidize easily under ambient conditions (6). Furthermore, the electrode density of states near the Fermi energy is typically nearly energy independent. This results in molecular junctions formed with metals having rather smooth and featureless transmission probabilities around the Fermi energy, limiting their applications. Carbon-based electrodes such as graphite have remarkable mechanical strength as well as a nonconstant highly dispersive density of states near its Fermi energy (19). In addition, molecules can be bonded covalently to carbon-based materials and can also bind through a van der Waals-based π–π stacking interaction (20). However, to date, such materials have not been used to create molecular junctions using the scanning-tunneling-microscope–based break-junction technique (STM-BJ). All-carbon electrodes have been used in the past, including carbon nanotubes and graphene (21–23); however, such devices are not easy to fabricate and characterize electronically with a statistically significant method. Moreover, there have been no computational studies on such junctions aimed at understanding the relation between charge transport and electrode properties.

Here, we measure the conductance of a series of graphite/amine-terminated oligophenyl/Au molecular junctions using the STM-BJ technique (4). We show that the conductance of this series decays exponentially with molecular backbone length with a decay constant that is essentially the same as that for measurements with Au electrodes. We show further that these molecular junctions rectify (14, 24), due to an asymmetry in the coupling of the molecule with the Au and graphite electrodes. The nature and magnitude of the rectification is directly connected to the nonconstant density of states of graphite near the Fermi level. The trends from self-energy–corrected density functional theory calculations are in agreement with our experimental results; specifically, we find that junction conductance decreases as the junction is elongated, as the angle between the molecule and the graphite substrate increases. These measurements and calculations together demonstrate new classes of molecular junctions with dissimilar electrodes using layered 2D electrodes.

Results and Discussion

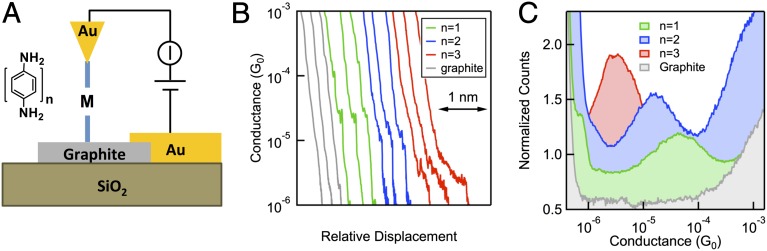
We use the STM-BJ technique to measure the conductance of a series of graphite/amine-terminated oligophenyl/Au molecular junctions as illustrated in Fig. 1A and detailed in Methods (4, 25) and in Fig. S1. Fig. 1B shows individual conductance versus displacement traces measured when no molecules are present (gray traces). No steplike conductance plateaus are seen in these traces, in contrast to measurements carried out using an Au tip and an Au substrate (Fig. S2) (25). Furthermore, the conductance does not exceed much beyond 10⁻¹ G₀ where G₀ = 2e²/h is the quantum of conductance, even if the tip–sample distance is compressed an additional 5 nm, indicating that this conductance corresponds to the contact conductance of sharp Au tip on a graphite substrate. Sample conductance vs. displacement traces measured with benzenediamine (BDA; green, n = 1), biphenyldiamine (DBDA; blue, n = 2), and terphenyldiamine (TBDA; red, n = 3) are shown in Fig. 1B. As a control, if the same tip is brought into contact with the Au contact pad on the side, conductance traces such as those shown in Fig. S3 are seen, indicating that this molecule-deposition method yields measurements analogous to those made in molecular solutions (25). The clear features seen below 10⁻⁴ G₀ when measurements are made on the graphite flake are due to the formation of stable graphite/molecule(s)/Au junctions. These features are sloped, indicating that junction conductance decreases with elongation. We attribute this to a change in the molecular-junction structure arising from an increase in the angle between molecular backbone and the graphite. We will return to a discussion of this later in the paper. We create one-dimensional conductance histogram of all measured traces (over 5,000 traces) using logarithm bins. These are compared in Fig. 1C, where a clear peak at a conductance value that decreases exponentially with molecule length is seen. Although we cannot determine the exact number of molecules in these junctions, the trends in plateau lengths and the fact that the same tip can be used to form single-molecule junctions on the Au electrode support the possibility that we have one or a few molecules between the tip and graphite substrate.

Fig. 1.

Schematic and conductance data for graphite/molecule/Au junctions. (A) Schematic of the junctions studied in this work. (Inset) Molecular structure. (B) Sample conductance versus displacement traces measured with BDA (green, n = 1), DBDA (blue, n = 2), and TBDA (red, n = 3). Control measurements without molecules are shown in gray. Traces are offset laterally for clarity. (C) Conductance histograms generated from over 5,000 traces for each junction type. Histograms are created using logarithm bins (100 bins/decade) and are normalized to the number of traces included. Measurements are carried out applying a −0.5 V to the substrate and measuring current through the tip.

Fig. 2 shows the normalized 2D conductance-displacement histograms and conductance plots for three molecules (n = 1–3) measured with a graphite electrode. All measured conductance traces are aligned along the displacement axis at a conductance of 10⁻² G₀. The conductance axis uses logarithmic bins and the displacement axis uses linear bins. The gray overlays are the conductance profiles created from 2D histograms of conductance traces measured for the graphite/Au junction without any molecule (Fig. S2). We find that the molecular-conductance features are clearly sloped for all three molecules compared with results measured with Au electrodes (Fig. S4) (6), and extend over a length that increases with the molecular length indicating that longer molecules can sustain a greater junction elongation (26). Because the junction conductance decreases with junction elongation we can distinguish the conductance at the start and the end of the molecular junction. To quantify this, we average the 2D histogram over a 0.1-nm width at the locations indicated by the arrows in Fig. 2 A–C to obtain a start and end conductance distribution. Fig. 2 A–C, Insets shows these distributions along with Gaussian fits (dashed curves) the peak values of which determine a start and end conductance for each junction type. In Fig. 2D we compare the end conductance for Au/molecule/graphite junctions (gray squares) with those from Au/molecule/Au electrodes (yellow squares) on a semilog scale. The dashed lines are exponential fits to these data, $G\mathrm{\sim }{e}^{\mathrm{-}\beta N}$, where β is the decay constant and N is the number of benzene rings in the backbone. The measured conductance decays exponentially with molecular backbone length with a decay constant that is essentially the same for Au/molecule/graphite (1.79 ± 0.15) and Au/molecule/Au (1.74 ± 0.05) electrodes. Extrapolating these fits to zero length gives an effective contact resistance. We find that the contact resistance for the Au/molecule/graphite junctions is ∼200 MΩ, and that of the Au/molecule/Au junctions is almost three orders of magnitude lower (∼360 kΩ). This difference indicates that the molecule/graphite electronic coupling is rather weak. That the decay constant does not depend significantly on the metal work function is consistent with previous findings (6, 27, 28).

Fig. 2.

2D conductance-displacement histograms. (A–C) The 2D histograms created by aligning all conductance traces at 0.01 G₀. The bins have a width of 0.002 nm along the displacement axis and 100/decade along the conductance axis. The start and end of the molecular conductance feature is indicated by arrows in the image. The gray trace is the conductance profile determined from a 2D histogram generated for graphite/Au traces measured without molecules. Inset shows the conductance distribution at the two displacements indicated by the arrows corresponding to the start and end of the molecular junction. (D) Conductance of fully elongated Au/molecule/Au and graphite/molecule/Au junctions plotted against number of benzene groups in the molecular backbone. Line fits show that both systems have a similar decay constant.

To compute junction-binding energetics and conductance of Au/BDA/graphite junction, we use first-principles calculations with a self-energy-corrected, parameter-free nonequilibrium Green’s function approach-based density functional theory (DFT+Σ) as detailed in Methods (29–32). Our van der Waals-corrected DFT calculations indicate that, at equilibrium, the molecule is almost flat on the graphite surface, forming an angle θ between the molecular backbone and the graphite surface of 3°. The upper nitrogen atom is at 3.64 Å above the graphite surface, and the lower nitrogen atom is above a hollow site, approximately centered on a six-member carbon ring. In our model junction geometries, we vary the distance between graphite surface and the nitrogen atom bonded to Au in 0.25-Å intervals, up to 6.39 Å, and relax the positions of other atoms. This gives 12 different junction geometries with an angle θ that ranges between 3° and about 33°. Fig. 3C shows the binding energy as a function of this angle (black trace).

Fig. 3.

Calculated structure, transmission curves, and binding energy. (A) Sample optimized geometry used to compute the transmission through a graphite/BDA/Au junction with a molecule–graphite angle θ is 20°. (B) Calculated DFT+Σ transmission curves for graphite/BDA/Au junctions with θ ranging from 3° to 21.8°. (C) Junction-binding energy (right axis) and conductance (left axis) determined from the transmission averaged between −0.2 and +0.3 eV plotted against the angle θ.

The DFT+Σ transmissions for these BDA junctions are shown in Fig. 3B. The main resonance responsible for transmission at E_F is associated with the highest occupied molecular orbital (HOMO) of BDA, whose peak energy lies between 1.5 and 2 eV below E_F. The HOMO resonance peak-transmission values are significantly less than unity and decrease as θ increases, indicating that the electronic coupling to the Au and graphite electrodes is highly asymmetric and becomes more so as θ increases. The features in transmission curves around E_F are due to the highly energy-dependent graphite density of states (33), and are responsible for the magnitude of the rectification of the junction, as detailed below.

To compare with measurements carried out by applying a −0.5-V bias voltage to the substrate, we compute the conductance (34) from a Landauer-like expression for the current at zero temperature (see Supporting Information for details). To determine the current, we compute how the voltage drops across the graphite/molecule/Au junction with ab initio transport calculations at finite bias (Supporting Information, Fig. S5). We find that 60% of the voltage drops at the graphite/molecule interface, and 40% of the voltage drops at the molecule/Au interface. Using these values, we integrate the transmission over a 0.5-eV energy window between −0.2 and +0.3 eV, and compute the conductance by dividing the calculated current by the applied voltage. Our calculated conductance values (green trace in Fig. 3C) are in excellent agreement with the conductance range obtained experimentally as delineated by dashed lines in Fig. 3C. Note that using the linear-response conductance value G=2e²/h T(E_F) determined from the DFT+Σ calculation, as is typical for comparing to experiments, leads to a significant underestimate relative to the values measured here at 0.5 V (Fig. S6).

We now turn to an aspect of these Au/molecule/graphite junctions, which elucidates the effect of the nonconstant, highly dispersive density of states of graphite near E_F and the asymmetry in the voltage drop across the junction. In determining the current, we may either integrate between −0.2 and +0.3 eV, or between −0.3 and +0.2 eV. These two choices correspond to reverse and forward bias polarities, respectively, and for these Au/molecule/graphite junctions, the two integrations yield significantly different results for conductance, implying rectification. We measure the conductance of Au/TBDA/graphite junction at two different bias polarities (+0.5 and −0.5 V applied to the substrate). We show in Fig. 4A the 1D conductance histogram with forward (light red line, +0.5V) bias and reverse (solid red line, −0.5 V) bias (see Fig. S7 for additional data). We see that the conductance is clearly larger when a positive bias is applied to the graphite electrode. To understand this result, we show a schematic energy-level diagram for these junctions in Fig. 4B. Changing the bias polarity changes the chemical potential, μ (red and light red lines) of graphite electrode relative to the Au electrode. Due to bias-induced changes in the electronic structure of the molecule, there is also a small shift in the peak energies of the HOMO and lowest unoccupied molecular orbital resonances as indicated in the figure. Because the electronic coupling at the molecule/Au interface is much larger than that at the molecule/graphite interface and conduction is through the HOMO, the conductance is higher when the graphite chemical potential is closer to the HOMO, i.e., when a positive bias is applied to the graphite, as illustrated in Fig. 4B.

Fig. 4.

Rectification in graphite/TBDA/Au junctions. (A) Histograms created from conductance traces measured with TBDA while applying a negative (dark red, reverse bias) and positive (light red, forward bias) bias to the graphite substrate. (B) A schematic diagram indicating the molecular orbital levels relative to the Au and graphite chemical potentials under forward and reverse bias conditions. (C) Conductance profiles determined from 2D conductance-displacement histograms for TBDA junctions measured under forward and reverse-bias conditions. Inset shows the rectification ratio as a function of displacement for these junctions. (D) DFT+Σ transmission curves for graphite/TBDA/Au junctions for two different molecule/graphite angles. The shaded areas indicated the region under the transmission curve that needs to be integrated to determine the conductance under forward (−0.3 to +0.2 eV) and reverse (−0.2 to +0.3 eV) bias conditions. Dark shaded regions highlight the difference between forward and reverse bias. (Inset) Energy-optimized junction structures used for these two calculations.

We show, in Fig. 4C, conductance profiles determined from 2D histograms of conductance traces measured at both polarities for TBDA junctions (see Fig. S8 for the 2D histograms). The conductance profile measured under forward bias (light red) shows a higher conductance compared with that measured under the reverse bias (dark red) at all displacement. The range of conductance values measured under forward bias is also larger than that under reverse bias explaining the wider 1D conductance histogram peak seen for the latter case. Fig. 4C, Inset, shows the ratio of the forward to reverse-bias conductance determined from the 2D histogram profile. This rectification ratio is a function of the displacement, and it is significantly higher at the junction formation point (∼3) than that at full extension (∼1.5). Because the start of the junction corresponds to a molecule that is less vertical than a fully extended junction, our measurements indicate that the rectification ratio is greater for junctions where the molecule is better coupled to the substrate.

To compare these experimental results to calculations, we show in Fig. 4D, the transmission functions for two different TBDA binding geometries, with the molecule at 20° (red line) and 70° (brown line) angle to the graphite substrate. These two transmission curves show a clear molecular resonance around −1.7 eV; however, the widths of these resonances are different. The more vertical geometry has a narrower resonance due to a weaker graphite/molecule coupling. This results in the vertical junction having a much lower transmission around zero bias, especially at energies below E_F. At energies above E_F the difference between the two transmission curves is much smaller as this is far off resonance, and the transmission is dictated by the nonlinear density of states of graphite. Integrating the area under these transmission functions for bias ranges from −0.2 to +0.3 V (reverse bias) and −0.3 to +0.2V (forward bias) illustrates the origin for the difference in the rectification ratio for the two geometries. The ratio of area is higher for the transmission curve of 20° (light red area/red area) than that of 70° (light brown/brown), yielding a theoretical rectification ratio of ∼2.5 for 20° and ∼1.7 for 70°, in good agreement with experiment.

In summary, we have developed an experimental and theoretical platform for studying molecular junctions created with a layered 2D material as an electrode. We have applied our methods to a series of junctions formed with amine-terminated oligophenyls between a graphite substrate and an Au tip. We find that the conductance of this series decays exponentially with molecular backbone length with a decay constant that is essentially the same as that for measurements with Au electrodes. More importantly, we show that these molecular junctions rectify due to an asymmetry in the coupling to the two electrodes. These experimental results are in good quantitative agreement with self-energy-corrected density functional theory calculations.

Methods

Experimental Details.

These measurements are carried out using graphite flakes (∼70 nm height and 40 × 20 μm in size) as the bottom electrode and a cut Au wire (99.998% purity) as a tip. The graphite flakes are mechanically transferred onto a SiO₂/Si substrate using standard exfoliation techniques. An electrical contact to the edge of this flake is then fabricated by depositing the Au film using a stencil mask technique. This resist-free fabrication prevents surface contaminations (Fig. S1) (35, 36). For the break-junction measurements, the Au tip is brought into contact with the graphite flake to achieve a conductance of ∼10⁻¹ G₀ − 10⁻² G₀. The tip is then withdrawn from the substrate at a speed of 18 nm/s while the conductance is recorded with voltage of −0.5 V applied to the graphite substrate. Measurements in the presence of molecules are made by first dipping the Au tip wire in a 1,2,4-trichlorobenzene molecular solution, drying the tip under N₂ before bringing the tip in contact with the graphite flake.

Theoretical Details.

We construct model junction geometries from BDA (or TBDA) contacting six graphite (0001) layers on one side and seven Au (111) layers on the other as illustrated in Fig. 3A (see Supporting Information for details of the junction geometry.) Following prior work (31), BDA (or TBDA) is contacted to Au via an undercoordinated adatom binding motif. To determine representative BDA–graphite binding geometries, we optimize the atomic positions of individual molecules on graphite (0001) slabs with DFT that includes van der Waals (vdW) dispersion interactions through the vdW–DF2 functional which is known to capture these interactions between aromatic molecules and surfaces (37). A nonequilibrium Green’s function formalism, implemented within the TranSiesta package (29) with the Perdew–Burke–Ernzerhof (PBE) functional (38), is used to compute zero-bias transmission of each junction. DFT+Σ (30, 31) is used to correct inaccurate PBE junction level alignment (Supporting Information).