Genetic information transfer promotes cooperation in bacteria

Significance

Bacteria often cooperate through the production of public goods that change their environment. These processes can affect human health by increasing virulence or antibiotic resistance. Public good production is costly, making cooperation susceptible to invasion by nonproducing “cheater” individuals. Bacteria also readily share genes, even among distinct species. Our experiments and models converge to show that when both cheating and cooperative genes are transferred, cooperators win against cheaters because transfer increases assortment among alleles, favoring cooperation. This can explain why genes for cooperation are often mobile, and suggests that, in addition to reducing antibiotic resistance spread, preventing gene mobility could reduce cooperative virulence.

Abstract

Many bacterial species are social, producing costly secreted “public good” molecules that enhance the growth of neighboring cells. The genes coding for these cooperative traits are often propagated via mobile genetic elements and can be virulence factors from a biomedical perspective. Here, we present an experimental framework that links genetic information exchange and the selection of cooperative traits. Using simulations and experiments based on a synthetic bacterial system to control public good secretion and plasmid conjugation, we demonstrate that horizontal gene transfer can favor cooperation. In a well-mixed environment, horizontal transfer brings a direct infectious advantage to any gene, regardless of its cooperation properties. However, in a structured population transfer selects specifically for cooperation by increasing the assortment among cooperative alleles. Conjugation allows cooperative alleles to overcome rarity thresholds and invade bacterial populations structured purely by stochastic dilution effects. Our results provide an explanation for the prevalence of cooperative genes on mobile elements, and suggest a previously unidentified benefit of horizontal gene transfer for bacteria.

Microorganisms produce a multitude of secreted factors, such as signaling, resource scavenging, virulence, or anticompetitor molecules (1). These so-called “public good” molecules are costly to produce but are accessible and potentially beneficial not just to the secreting organisms but to their neighbors as well. The production of the molecular public goods increases the fitness of neighboring individuals and can thus be considered as a cooperative behavior (2). The maintenance of cooperation is generally threatened by the spread of individuals that benefit from cooperation without paying the costs, so-called “nonproducers” or “cheaters.” Social evolution theory predicts that cooperation can be maintained when its benefits are directed preferentially to organisms carrying cooperation genes. Several mechanisms that bias the partner association in cooperative interactions have been proposed (3, 4) and the recent application of sociobiology theories to microorganisms has opened them to experimental tests (5, 6). For example, limited dispersal of clone mates (7) or homophillic receptor binding (8) can generate a positive assortment among individuals carrying cooperative genes, which can be quantified by relatedness statistics (9). Assortment could additionally be modified at the gene level by the frequent and peculiar forms of sex in bacteria that make their genomes extremely plastic (10): genes often transfer within and between bacterial lineages, mainly by association with mobile genetic elements such as plasmids or phages (11). Strikingly, genes coding for cooperative traits, such as extracellular antibiotic degradation (12) or cholera toxicity (13), are often located on mobile elements (14, 15) suggesting a link between social behaviors and horizontal transfer.

Two mechanisms can explain the localization of cooperative genes on mobile elements. First, sufficiently high levels of horizontal transfer may promote mobile genetic elements purely as molecular parasites, despite their potential fitness cost to host cells (16). Mobility could then allow accessory genes to persist in the environment, even in the absence of continued positive selection (17). In the specific case of public good encoding genes, horizontal transfer of a cooperative producer allele could convert a recipient from nonproducer into a producer and thus enforce cooperation by infection (18). However, cooperation maintenance via infection enforcement is predicted to be unstable (14, 19), as a noncooperative allele will still displace a cooperative allele when both transfer horizontally. Second, horizontal transfer could modify the patterns of relatedness (gene assortment) in a population. Theoretical work suggests that horizontal gene transfer will increase relatedness at mobile loci, because the local spread of mobile alleles will increase the probability that neighboring individuals bear the same allele, favoring investment in cooperative traits at these loci (14, 20). However, experimental evidence that transfer can significantly modify the selective pressures acting on cooperative behaviors through either of these mechanisms is lacking. Here, for the first time to our knowledge, we experimentally investigate the effects of horizontal transfer on cooperation.

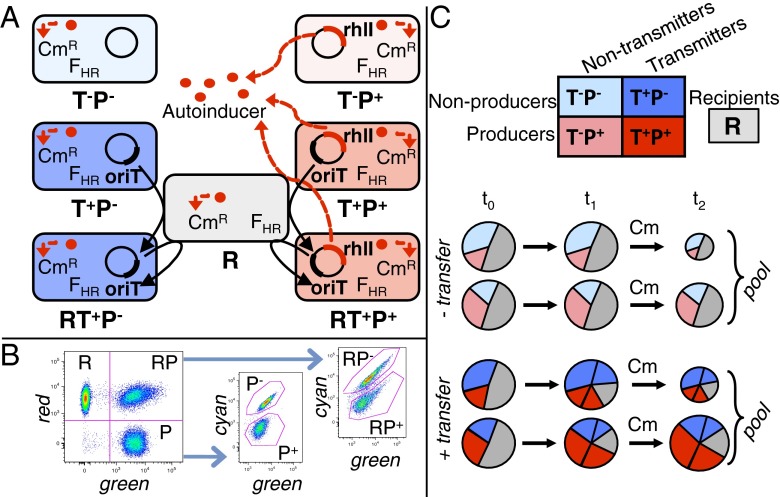
We developed a synthetic system in Escherichia coli with independent control of cooperation and conjugation. The cooperative trait is the secretion of a public good, namely the Pseudomonas aeruginosa quorum-sensing molecule C₄-HSL (21). The molecule is costly to produce but provides faster growth to both producer and nonproducer cells in the presence of the antibiotic chloramphenicol (Cm), by activating the expression of a chromosomal resistance gene. Using the conjugation machinery of the F plasmid (22), we constructed a helper F plasmid which enables the transfer of the mobilizable (T⁺) plasmids with (producer, P⁺) or without (nonproducer, P⁻) C₄-HSL public good gene, but does not transfer nonmobilizable (T⁻) plasmids (Fig. 1A). Initial plasmid-free cells (recipients, R), P⁺ and P⁻ plasmids are marked with distinguishable fluorescent proteins to enable monitoring of strain and plasmid dynamics using flow cytometry (Fig. 1B and Fig. S1). This synthetic approach allows us to study the effect of horizontal transfer in a biologically realistic setting without interference from plasmid–host coadaptation.

Fig. 1.

Experimental system. (A) Synthetic system for conjugation and cooperation. P⁺ cells express the synthase RhlI that produces C₄-HSL (Rhl autoinducer, red dots), which diffuses (red arrows) and activates expression of Cm resistance (Cm^R) in all cells within a subpopulation. F_HR plasmid expresses F conjugation machinery and mobilizes plasmids bearing oriT (T⁺) to recipient cells (black arrows), leading to RP⁺ and RP⁻, whereas plasmids without oriT (T⁻) are not mobilized. (B) Flow cytometry. Recipients are marked with RFP, plasmids with YFP (P⁺) or GFP (P⁻). Initial plasmid bearers (P) and recipients without (R) or with (RP) plasmids are first distinguished with green and red filters, followed by separation of P⁺ and P⁻ using green and cyan filters. (C) Experiment design. Public good producers (P⁺, red) and nonproducers (P⁻, blue) are mixed at t₀ with recipients (R) in subpopulations with varying ratios of P⁺ to P⁻. T⁻ plasmids (T⁻P⁺ and T⁻P⁻, pale colors) cannot be transmitted. T⁺ plasmids (T⁺P⁺ and T⁺P⁻, bright colors) can be transmitted to recipients, yielding new plasmid bearers (respectively, P⁺ and P⁻). At t₁ subpopulations are diluted in medium containing Cm and grown until t₂, when they are pooled.

We implemented a simple metapopulation, consisting of subpopulations (demes) founded with different initial proportions of producers and nonproducers, and linked by migration (21) (Fig. 1C and SI Text). Previous work has shown that the higher growth rate of producer-rich populations in the presence of Cm can lead to a seemingly paradoxical statistical effect known as “Simpson's paradox” (21): although decreasing in proportion in individual populations, the overall number of producers across the metapopulation increases because producer-rich subpopulations have more individuals than producer-poor ones. In parallel, we built mathematical models parametrized using experimentally obtained values for the cost and benefit of public good production and cost and rates of transfer (Materials and Methods and SI Text). By numerically solving the models, we quantify cooperation dynamics in scenarios with different plasmid transfer rates within demes and migration rates among demes.

Results

Enforcement of Cooperation Is Unstable in a Well-Mixed Population.

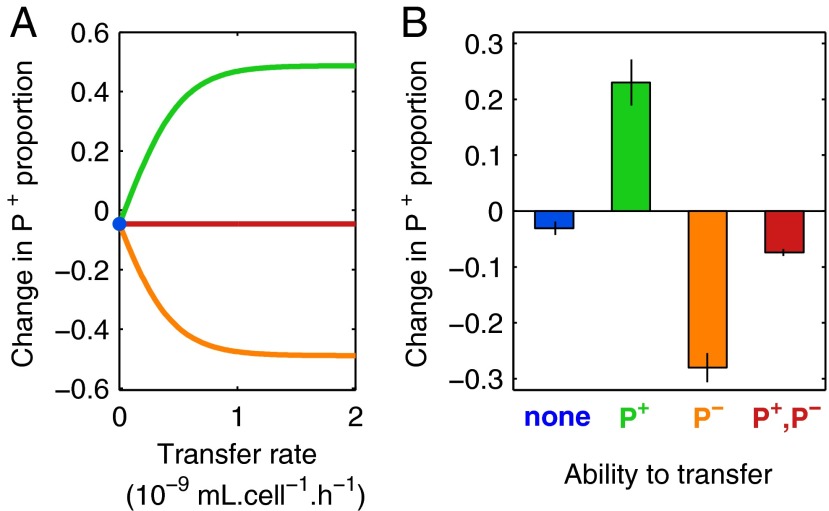
We first model (Fig. 2A) and test experimentally (Fig. 2B) the effect of horizontal transfer in a single well-mixed population where initially the majority of cells (97.5%) are recipients. In the absence of transfer (Fig. 2, blue), cooperation is not maintained. Producer plasmids pay the cost of public good production and are slightly outcompeted by nonproducer plasmids (3% decrease in P⁺ ratio, P = 0.02). As expected (18), the transmissible producer plasmid (T⁺P⁺) outcompetes the nontransmissible nonproducer (T⁻P⁻) plasmid thanks to the invasion of recipients (23% increase in P⁺ ratio, Fig. 2B, green; P = 0.004), leading to enforcement of cooperation because infectious transfer outweighs the cost of public good production for P⁺-bearing cells. However, when P⁻ plasmids are transferable (T⁺P⁻), they outcompete both a nontransmissible P⁺ plasmid (28% decrease in P⁺ ratio, Fig. 2B, orange; P = 5 × 10⁻⁶) and a P⁺ plasmid transferring at the same rate (7% decrease in P⁺ ratio, Fig. 2B, red; P = 3 × 10⁻⁶). In the latter case, the benefit of transfer cancels out, and T⁺P⁻ beats T⁺P⁺ by saving on production costs. Thus, as predicted by theory (19) and our models (Fig. 2A), transfer is not sufficient to maintain cooperation in a well-mixed population if both producer and nonproducer alleles are mobile.

Fig. 2.

Transfer favors producers as well as nonproducers in a well-mixed population. Initial proportions are 1.25% P⁺, 1.25% P⁻, and 97.5% R. The change in proportion of P⁺ among all plasmids P⁺/(P⁺+P⁻) is computed in the absence of public good benefits (no Cm, t₀ to t₁). (A) Simulated change in P⁺ proportion as a function of transfer rate, given different population composition. Blue point represents the population with plasmids T⁻P⁻ and T⁻P⁺ (no transfer), green line the population of T⁻P⁻ and T⁺P⁺ (only P⁺ transfer), orange line the population of T⁺P⁻ and T⁻P⁺ (only P⁻ transfer), red line the population of T⁺P⁻ and T⁺P⁺ (both P⁻ and P⁺ transfer). (B) Experimental change in P⁺ proportion in absence of transfer, or when one or both plasmids can transfer (color scheme the same as in A), shown as means ± SEM (n = 9). Statistically significant difference from zero was determined using a one-tailed t test.

Transfer Promotes Cooperation in a Structured Population.

To study the competition between producer and nonproducer transmissible plasmids in a structured population, we implemented a simple metapopulation consisting of two subpopulations with different initial ratios of P⁺ to P⁻ and identical proportions of plasmid-free recipients (Fig. 1C). The subpopulations grow separately in two distinct phases: transfer phase (no public goods benefit, no Cm, until t₁) and competition phase (public goods benefit, with Cm, from t₁ to t₂). At t₂ the two populations are mixed, mimicking a migration phase with global competition, and the relative success of the producer allele is measured as the change in P⁺ proportion relative to P⁻. In simulations, we also calculated an alternative metric, the absolute increase in P⁺ proportion, including plasmid-free recipient cells (Fig. S2).

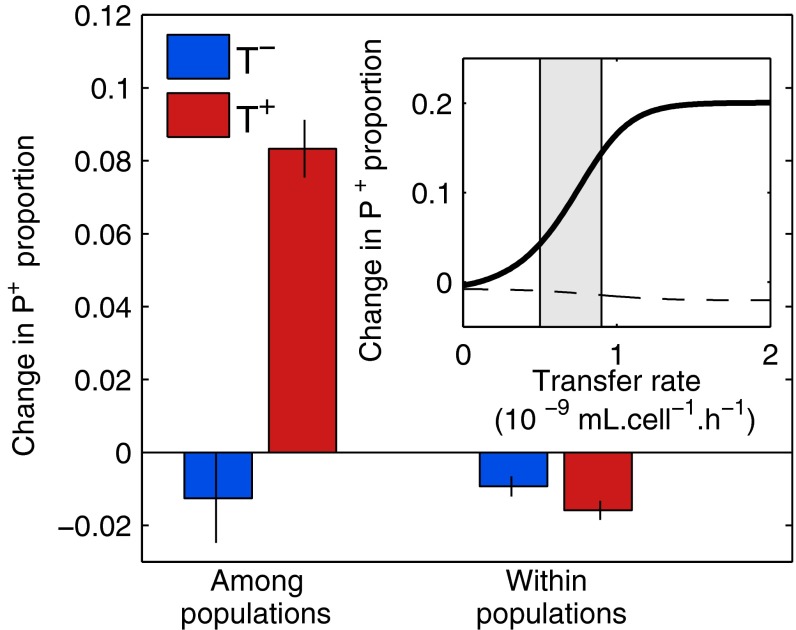
Our simulations predict that unlike in the single well-mixed population scenario, transmissibility of both P⁺ and P⁻ plasmids does select for cooperation in a structured metapopulation, increasing the global proportion of P⁺; cooperation is still disfavored when all plasmids are immobile (Fig. 3, Inset and Fig. S2). Our experiments confirm the result: producers are outcompeted in the absence of transfer (blue bar, Fig. 3, Left), but outcompete nonproducers when both plasmids can transfer (red bar, Fig. 3, Left). When the population is structured, transfer reverses the direction of the selective pressure and increases the global proportion of P⁺ by 10% (P = 6 × 10⁻⁶).

Fig. 3.

Transfer selects for cooperation in structured populations. The metapopulation consists of two subpopulations, with 97.5% recipients and initial P⁺/P⁻ ratios of 1:4 and 4:1. The change in proportion of P⁺ among all plasmids P⁺/(P⁺+P⁻) is computed during the competition phase (from t₁ to t_2, in the presence of Cm) without (blue) and with (red) transfer of both P⁺ and P⁻ plasmids and shown as means ± SEM (n = 9). (Inset) Simulated change in P⁺ proportion as a function of transfer rate, among (solid line) and within (dashed line) populations, the shaded area indicating estimated experimental transfer rates.

The difference we observe can arise from either within- or among-population dynamics. Transfer does not increase the ratio of P⁺ to P⁻ within each subpopulation (Fig. 3), as in the case of a well-mixed population. Thus, we can conclude that there is no direct infectious benefit of P⁺ plasmids. However, the global P⁺ proportion at the metapopulation level (Y_m) is disproportionally affected by within-population proportions (Y₁ and Y₂), based on each population’s contribution to the total plasmid count. Let a be the bias in Y_m due to subpopulation growth differences. The effect of subpopulation size on Y_m can then be captured by the following relationship: $Y_m=\left[(1-a)Y_1+(1+a)Y_2\right]/2$ (SI Text). In our experiments a increases with transfer from 0.08 to 0.37 (P = 4 × 10^-5), effectively amplifying Simpson’s paradox and promoting cooperation. The effect is well captured by our simulations. In the presence of Cm, the subpopulation initially enriched in producer cells grows more rapidly than the other subpopulation (Fig. S3A). In the presence of transfer both populations grow more rapidly, but the size of the one with higher initial P⁺ proportion increases more, exacerbating subpopulation size difference. Growth during the competition phase positively correlates with the amount of producers present after the transfer phase (Fig. S3B): the increase in population size differences is linked to an increased variation in P⁺ abundance across populations, following plasmid transfer.

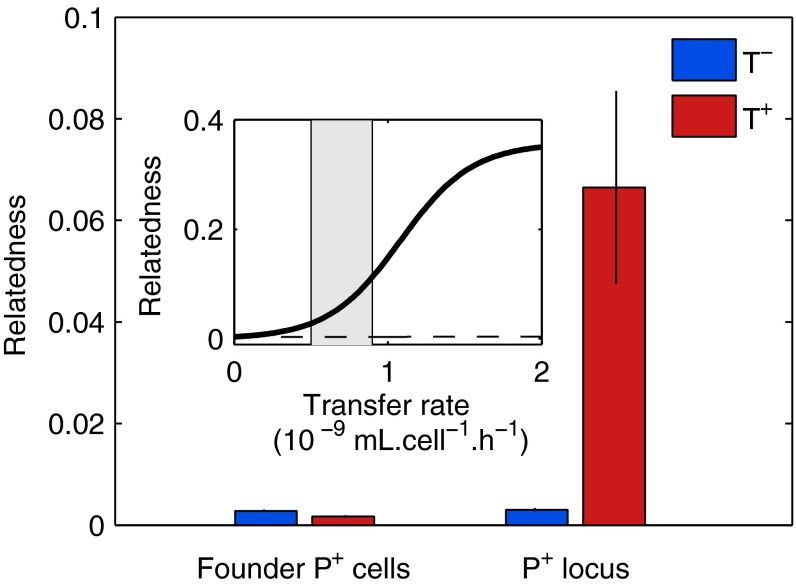
The effect of transfer on population genetic structure (due to both gene transfer and demographic effects) can be measured by relatedness. We calculate the producer relatedness (${\beta }_{G,g}^p$; Materials and Methods and SI Text) following transfer, before cooperation becomes beneficial (at t₁; Fig. 1C). Transfer strongly increases relatedness in both simulations and experiments, but only for the mobile allele (P = 0.004, Fig. 4). The increase in relatedness is equivalent to an increase in the proportion of variance in producer frequencies among subpopulations (23, 24), which occurs because horizontal transfer spreads the cooperative allele locally, amplifying variations among subpopulations. To test if transfer acts on cooperation through its effect on assortment, we prevent it from increasing assortment in our simulations by implementing a global mixing of all transferred plasmids across populations after the transfer phase (Fig. S4, dashed line vs. plain line). Subsequently, P⁺ proportion decreases despite no change in either costs or benefits of cooperation, or in the total rise in number of P⁺ and P⁻ plasmids with transfer. Thus, our results indicate that transfer leads to a metapopulation-scale increase in cooperation via an increase in assortment among cooperators.

Fig. 4.

Transfer selects for cooperation by increasing assortment among P⁺ alleles. Parameters are the same as in Fig. 3. Assortment is evaluated by measuring relatedness, computed at t₁, without (blue columns) and with (red columns) transfer, shown as mean ± SEM (n = 9). Transfer significantly increases relatedness for the mobile allele (considering P⁺ locus in all cells, P = 0.004) and slightly decreases relatedness for a nonmobile allele (considering only founder P⁺ cells, P = 0.005). The decrease of relatedness considering only founder P⁺ cells is due to a decrease in frequency of these cells during the transfer phase (t₀ to t₁) in the presence of transfer. (Inset) Simulated relatedness function of transfer rate for mobile (solid line) and nonmobile (dashed line) loci, the shaded area indicating estimated experimental transfer rates.

Transfer Effect on Cooperation Is Robust to Low Rates of Migration.

Subpopulation differences supporting cooperation may be suppressed by migration, which homogenizes the genotype proportions across subpopulations. To investigate such a scenario, we introduce into our model an additional exchange of cells between subpopulations after transfer has occurred, but before subpopulations first encounter Cm (t₁; Fig. 1C). Both in the absence and presence of transfer, migration decreases the selection for P⁺ (Fig. S5A), as it decreases the assortment among P⁺ cells (Fig. S5B), and brings the metapopulation closer to a well-mixed population, partially avoiding the Simpson's paradox. For low rates of migration, transfer still promotes the selection of P⁺. Horizontal transfer and migration have opposite effects on assortment, and sufficiently high migration effectively eliminates any increase in assortment due to transfer, highlighting that the effect of transfer is based on the existence of population structure. We should note that cooperation may still be maintained with high migration rates, if the mixing happens after the selection for cooperation has time to act (e.g., at t₂), exactly as we have implemented it in our experimental and modeling setup.

Cooperation Is Enhanced by Epidemic Spread Among Recipients.

The effect of transfer relies on the presence of recipients and we expect that it will be affected by their abundance and properties. In our simulations, increasing the proportion of plasmid-free recipients decreases the strength of selection for producers in the absence of transfer (Fig. 5, black arrows). When producers are diluted by nonproducing cells, they benefit less from their own public good production and are therefore counterselected. Increased plasmid transfer (Fig. 5, red arrows) effectively opposes the producer scarcity by allowing plasmids to invade recipients, restoring selection of producers. The transfer-driven epidemic spread of producers has a stronger effect on producer proportion when the initial plasmid population is small and the number of plasmid-free recipients is high.

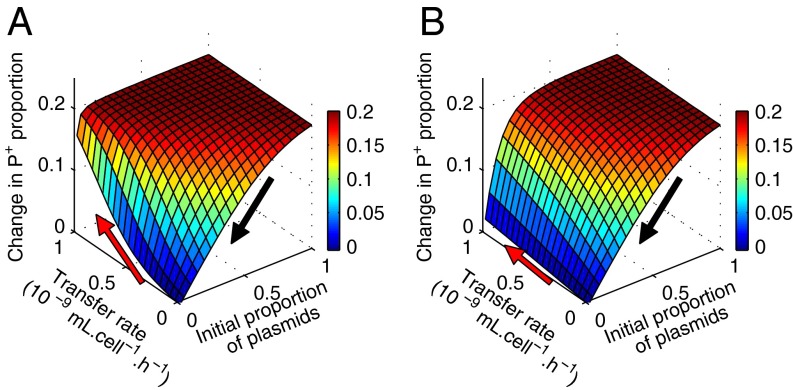
Fig. 5.

Stronger transfer effect when recipients are abundant and amplify transfer. The metapopulation consists of two subpopulations, with initial P⁺/P⁻ ratios of 1:4 and 4:1. Surfaces represent the change in proportion of P⁺ among all plasmids, P⁺/(P⁺+P⁻), during the competition phase (from t₁ to t_2, in the presence of Cm), as a function of transfer rate and initial proportion of plasmids in the population, (P⁺+P⁻)_t0. (A) Change in P⁺ proportion when recipients can also transfer plasmids. (B) Change in P⁺ proportion when recipients cannot transfer plasmids. Black arrows indicate increasing proportion of plasmid-free cells, red arrows indicate increasing transfer rates.

The plasmid epidemic also depends on the recipient's subsequent transfer ability. We simulate two extreme situations: (i) once infected, the recipients can also transfer plasmids (as is the case in our experiments), and (ii) recipients cannot transfer. Recipient transfer ability augments the effect of transfer on cooperator proportion (Fig. 5A vs. Fig. 5B) especially when the initial proportion of plasmids is low. Without secondary transfer, even at high transfer rates, the plasmids cannot spread fast enough to greatly modify the cooperative dynamics.

Transfer Can Promote Cooperation in Natural Scenarios.

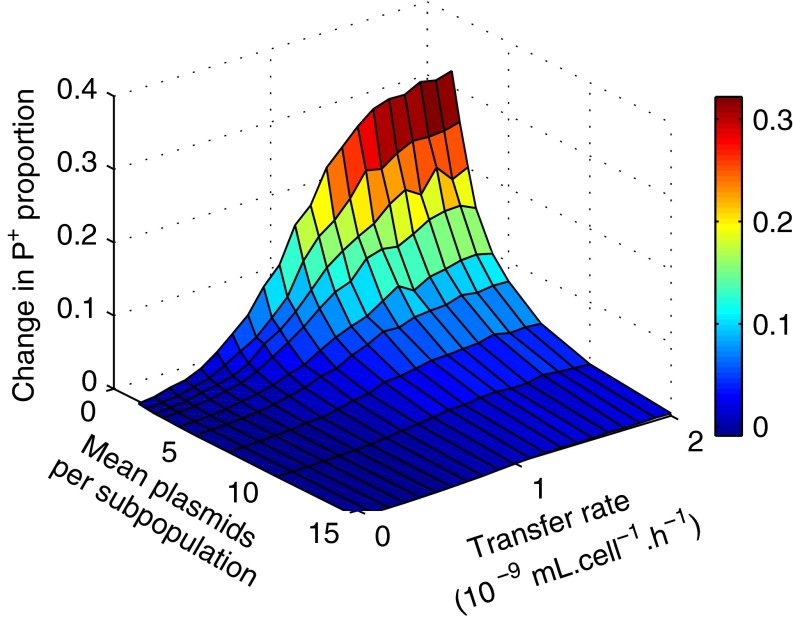
In our experiments, transfer does not create the initial variation, but only amplifies it. Variation in producer proportions could arise in nature when only a few plasmid-bearing cells colonize multiple populations of recipients. Because of the resulting low producer assortment among founder cells, we expect that the establishment of cooperation will depend on the presence of transfer. To simulate this scenario we implement strong dilutions leading to stochastic, Poisson-distributed number of founder cells (21). By varying both the founder cell dilution factor and the plasmid transfer rate we show that producers are selected only under strong dilution and high plasmid transfer conditions (Fig. 6). Weak dilution does not provide sufficient stochastic variation in the number of founder cells, and thus in producer proportions across populations, necessary for the rise in cooperation. Similarly, in the absence of transfer, the producers remain too rare to support cooperation. Transfer selects for cooperation by simultaneously amplifying the variation and overcoming the scarcity of cooperators created by the dilution. Notably, producer as well as nonproducer plasmids invade recipients thanks to horizontal transfer, but producers outcompete nonproducers thanks to their ability to exploit the increasing assortment, generating the Simpson's paradox.

Fig. 6.

Transfer allows rare producer genes to invade a bacterial metapopulation. The simulated metapopulation consists of 96 subpopulations initiated from a strongly diluted mix of (1%P⁺, 1%P⁻, 98%R), giving rise to Poisson distribution of P⁺ and P⁻ across populations. The change of P⁺ proportion among all plasmids, P⁺/(P⁺+P⁻), during the competition phase (from t₁ to t_2, in the presence of Cm), is shown as a function of the transfer rate and the initial mean number of plasmid-bearing cells per subpopulation, averaged over 20 simulations.

Discussion

Through qualitative and quantitative agreement between experiments and simulations, we demonstrate the two previously suggested ways in which horizontal transfer can favor public good production. We first show that infectious transfer can increase cooperation in nonstructured populations (16, 18), but the effect is short-lived. Transfer directly benefits any allele, including nonproducer ones, which would take over the plasmid population (19). In contrast, we show that in structured populations, horizontal transfer specifically favors public good production by increasing the feedback of public goods benefits preferentially to producer alleles (14). This study thus provides, to our knowledge, the first experimental demonstration of the maintenance of a cooperative behavior through transfer of genetic information: plasmid conjugation modifies both allele frequencies and population structure enough to favor cooperation. Transfer and public good production interact in the way predicted by theory (18, 19), as confirmed by our experimental measurements and simulation tests of assortment, and with no interference from other biological processes. Our simulations further show that the effect of transfer in structured populations requires three conditions: variation in initial producer proportion, an abundance of plasmid-free cells, and low to intermediate migration during the transfer phase.

The assumptions about the population structure, composition, and dynamics we have made throughout our experiments and models are based on realistic real-world situations. For example, in our simulations, the initial stochastic variation in producer proportions arises through strong dilution. Consider the epidemic spread of a bacterial disease whose growth strongly depends on a bacterial public good (for instance a secreted toxin). In such a scenario, the founder variance would be repeatedly created when new hosts are infected by a low number of plasmid-bearing cells, and migration between hosts is likely to remain rare during infection. In each host, existing microbiome bacteria can act as recipients and amplify the production of the public good (25). Moreover, huge variability exists in plasmid presence and abundance across bacterial isolates (26). Naturally varying environments can change rapidly, altering plasmid costs and benefits (27), repeatedly leading to plasmid loss ensuring the formation of plasmid-free populations that will allow transfer to take place. Finally, our results rely on a sufficiently high transfer rate allowing plasmids to invade a significant part of a recipient population. The naturally observed rates are comparable (28), heterogeneous (29), and increased by mechanisms such as transient transfer derepression (30), leading to amplification of plasmid spread. Overall, we expect that the conditions for the dynamics we describe will be regularly encountered in nature.

In conclusion, our study shows that horizontal transfer can extend the parameter space where cooperation is favored, by both infectious propagation of cooperation and an increase in producer allele assortment. In our experimental setup, assortment is initially controlled by population structure, as the probability of interactions between producer cells depends on their distribution among groups. Here we show that initially low relatedness is amplified by plasmid transfer, as suggested by theory (20). Horizontal transfer amplifies assortment because it acts at a local scale: conjugation requires cell contact and is thus necessarily local. Based on its effect on population structure, conjugation resembles other clustering mechanisms like multicellularity (31, 32), range expansion (33), budding dispersal (34), or group formation (35). However, it affects only specific genes carried on the infectious mobile genetic element, leading to different degrees of assortment for different genes from the same genome (36). We show experimentally that horizontal transfer strongly increases relatedness within a few generations because it is decoupled from and can happen faster than vertical transmission. Increasing relatedness at mobile loci (Fig. 4) improves the cost–benefit analysis for investment in the reproduction of neighboring cells (Fig. 3), as these cells are more likely to also carry cooperation genes due to infectious transfer. Gene assortment in the presence of mobile elements could be complicated by possible superinfections, where different competing plasmids inhabit the same cell (37), which would affect both the relatedness metric calculation and the cell phenotypes. However, superinfections are generally thought to be rare, due to widespread entry exclusion (38) and long-term segregation of incompatible plasmids (39). Our conclusions primarily concern the natural scenarios of epidemic spread in largely plasmid-free populations, rather than strong plasmid competition in nearly fully infected populations, where superinfection may evolve (37).

By demonstrating a link between infectious gene transfer (conjugation) and cooperation, our work has consequences for the understanding and management of bacterial communities. First, our results can explain the observed overrepresentation of cooperative genes (coding for secreted proteins) on mobile genetic elements (14, 15), as these genes will especially benefit from increased assortment. Additionally, mobile genetic elements are often associated with biofilm formation, another way of cell clustering that is physically induced by conjugation (40, 41). Biofilms could thus be another way for mobile elements to increase assortment which would not be gene-specific, but would still favor cooperation genes. Biofilms are themselves favorable to horizontal gene transfer (41), and could increase its gene-specific effect on relatedness. Second, our work suggests that by selecting for cooperation, horizontal transfer could provide adaptive benefits to host bacteria, shaped in turn by the degree of intragenomic conflict over directing benefits to neighboring cells (14). Plasmid-encoded cooperation may therefore modify selection for bacterial horizontal transfer mechanisms and contribute to the observed diversity in plasmid transfer rates among bacterial isolates (29). In bacteria, cooperation could represent an indirect selection pressure for sex, defined as any process selected by the benefits of genetic exchange (42), in addition to any direct advantage plasmids gain from transferring themselves. Finally, besides directly decreasing the spread of virulence and antibiotic resistance genes, targeting conjugation mechanisms (43) could hinder cooperative behaviors involved in the virulence of pathogenic bacteria by decreasing the range of conditions favoring the persistence of cooperative alleles.

Materials and Methods

Plasmids and Strains.

The background strain is JC1191, an E. coli strain that can grow in low concentrations of Cm in the presence of C₄-HSL, thanks to the addition of Pseudomonas quorum sensing machinery (21). P⁺ plasmid carries an artificial operon of yellow fluorescent protein (YFP) and rhlI under control of the strong promoter P_R. RhlI autoinducer synthase produces the Rhl autoinducer C₄-HSL (21). P⁻ plasmids carry green fluorescent protein (GFP) under control of P_R. Recipients bear pSB3K3-RFP plasmid expressing the mRFP1 (red fluorescent protein) gene.

To provide transfer ability, cells bear the helper plasmid F_HR, a mutant of pOX38::Tc (44) with reduced mobilization efficiency by the F relaxase (1,000-fold reduction compared with F), and a deletion of the traS gene involved in entry exclusion. Recipient cells bearing F_HR are able to receive plasmids efficiently and behave as secondary donors. The F_HR plasmid provides efficient mobilization of T⁺ plasmids present in the donor cell, which carry the wild-type origin of transfer oriT sequence of F plasmids, but no mobilization of T⁻ plasmids without oriT. Both P⁺ and P⁻ plasmids have T⁺ versions with oriT. Genotypes and relevant phenotypes of competitor plasmids are summarized in Fig. S1, and details about strains and plasmids are provided in SI Text.

Growth and Experiment Conditions.

Details about the growth media are provided in SI Text. Experiments were conducted under well-mixed conditions. For the transfer phase of the experiments, strains were mixed at various ratios (vol/vol) and first grown from a 1:10 dilution (t₀; Fig. 1C) into medium lacking Cm, up to an optical density of 3. Strains were grown at 35 °C because F transfer is strongly reduced at 30 °C. When the initial proportion of P⁺ and P⁻ plasmid-bearing cells was low, this step was repeated with maximum two successive dilutions into medium lacking Cm to increase plasmid transfer. Cultures were then diluted 1:10 and grown until stationary phase (t₁; Fig. 1C) at 30 °C, which allows preinduction of Cm resistance by C₄-HSL in nonproducer as well as producer cells and enhances the fluorescence signal. Finally, for experiments involving cooperation, cultures were diluted 1:100 into medium containing 6.25 μg/mL Cm (at t₁; Fig. 1C) and grown for 12–16 h at 30 °C until t₂ (Fig. 1C), where they were pooled. Cultures were analyzed for strain and plasmid proportions by flow cytometry (SI Text).

Relatedness.

Relatedness ${\beta }_{G,g}$ quantifies genetic assortment by measuring how an individual’s social environment G covaries with the individual’s genotype g. Relatedness can be calculated as the linear regression coefficient connecting an individual’s genotype (specifically, genetic value underlying the focal trait, here g = 1 if producer and 0 otherwise) with the genotype of its interactants (G is then the proportion of producers in the subpopulation of a focal individual) (9). Here, we focus on the relatedness of P⁺, ${\beta }_{G,g}^p$, considering that the social environment of an individual corresponds to the local population it belongs to (see SI Text for details). Relatedness computed at the P⁺ locus describes how much the benefits of public goods produced by P⁺ will affect preferentially P⁺-bearing cells because of population structure.

Model.

We model the dynamics of producer (P⁺) and nonproducer (P⁻) alleles, carried on horizontally transmitted, incompatible plasmids (see SI Text for details). Plasmids can only be transferred to plasmid-free recipient cells (R). Producer cells (that bear P⁺ plasmid) pay a cost of cooperation c. Transfer follows a mass-action law (45): the number of transfer events is proportional to the product of plasmid-bearing (P⁺ and P⁻) and plasmid-free (R) cell densities in the local population. To mimic experimental conditions (growth limited by carrying capacity of the culture media), rates of transfer and growth follow a logistic function and decrease with the progressive consumption of resources until stationary phase at carrying capacity K. With the basal growth rate of ψ and basal rates of transfer of ${\gamma }_{P^{+}}$ and ${\gamma }_{P^{\mathrm{-}}}$ for P⁺ and P⁻, respectively, the equations for growth and transfer are as follows:

$$\frac{d{P}^{+}}{dt}=\left[\psi \left(1\mathrm{-}c\right)+{\gamma }_{P^{+}}R\right]P^{+}\left(1\mathrm{-}\frac{n_{tot}}{K}\right),$$

$$\frac{d{P}^{\mathrm{-}}}{dt}=\left[\psi +{\gamma }_{P^{\mathrm{-}}}R\right]P^{\mathrm{-}}\left(1\mathrm{-}\frac{n_{tot}}{K}\right),$$

$$\frac{dR}{dt}=\left[\psi \mathrm{-}\left({\gamma }_{P^{+}}{P}^{+}+{\gamma }_{P^{\mathrm{-}}}{P}^{\mathrm{-}}\right)\right]R\left(1\mathrm{-}\frac{n_{tot}}{K}\right).$$

We explicitly follow the experimental protocol by modeling the transfer and competition phases. From t₀ to t₁, preinduction of Cm resistance and transfer happen until stationary phase, without beneficial effects of public goods. From t₁ to t₂, the growth rate depends on the public good concentration, assumed to be proportional to the proportion of producing cells in the local population. For equations modeling initial and secondary plasmid bearers separately, Fig. 5B, see SI Text.

We model two types of metapopulations: a simple one with 2 separate subpopulations (all simulations except Figs. 2 and 6), and a metapopulation with 96 subpopulations arising from Poisson dilution of an initial cell mix (Fig. 6). Subpopulations grow separately until t₂, when they are pooled. For Figs. S4 and S5, we modeled additional migration between the two subpopulations at t₁ (see SI Text for details).