Hierarchical random walks in trace fossils and the origin of optimal search behavior

Significance

How best to search for food in heterogeneous landscapes is a universal problem facing mobile organisms. Diverse modern animals use a random search strategy called a Lévy walk, composed of many small move steps interspersed by rare long steps, which theoretically is optimal for locating sparse resources. Here, we find the first evidence, to our knowledge, that extinct animals, in this case 50 My-old sea urchins, used a Lévy-like search strategy. Our results are important because they indicate Lévy walks likely have an ancient origin and may arise from simple behaviors observed in much older fossil trails. This foraging strategy may have adapted in response to decreased food availability after productivity collapse associated with past climate change and mass extinctions.

Abstract

Efficient searching is crucial for timely location of food and other resources. Recent studies show that diverse living animals use a theoretically optimal scale-free random search for sparse resources known as a Lévy walk, but little is known of the origins and evolution of foraging behavior and the search strategies of extinct organisms. Here, using simulations of self-avoiding trace fossil trails, we show that randomly introduced strophotaxis (U-turns)—initiated by obstructions such as self-trail avoidance or innate cueing—leads to random looping patterns with clustering across increasing scales that is consistent with the presence of Lévy walks. This predicts that optimal Lévy searches may emerge from simple behaviors observed in fossil trails. We then analyzed fossilized trails of benthic marine organisms by using a novel path analysis technique and find the first evidence, to our knowledge, of Lévy-like search strategies in extinct animals. Our results show that simple search behaviors of extinct animals in heterogeneous environments give rise to hierarchically nested Brownian walk clusters that converge to optimal Lévy patterns. Primary productivity collapse and large-scale food scarcity characterizing mass extinctions evident in the fossil record may have triggered adaptation of optimal Lévy-like searches. The findings suggest that Lévy-like behavior has been used by foragers since at least the Eocene but may have a more ancient origin, which might explain recent widespread observations of such patterns among modern taxa.

The specific pattern of searching movements used by an organism to locate food relative to the food’s distribution closely determines the number of successful encounters (1–3). The evolution of optimal search patterns is predicted because natural selection favors individuals that are best able to find resources critical to survival (4). It is recognized, however, that the natural environment is too complex for evolution to produce a behavior pattern that is optimal across all scales and contexts (5). Rather, simple rules probably will evolve that, on average, perform well in their natural environment (5). Such rules are exemplified in the different movement modes that tend to characterize behavior across different spatiotemporal scales. For instance, simple deterministic foraging searches, such as Archimedean spirals (6) or area-restricted searching (7), that are driven by sensory and cognitive abilities are efficient where food distributions are known, easily detected, or predictable. However, these patterns are inefficient when food resources are sparsely or patchily distributed and the forager has incomplete information on resource location; under these conditions, probabilistic searches such as Lévy walks become advantageous (1–3).

Theory predicts that Lévy walk search strategies should be optimal where food is sparse and distributed unpredictably (1), whereas Brownian walks are sufficiently efficient for locating abundant prey (2). A Lévy walk search pattern comprises displacements (move steps) drawn from a probability distribution with a heavy power-law tail that results in a fractal pattern of “walk clusters” with no characteristic scale, such that P(l) ∼ l^−µ, with 1 < µ ≤ 3, where l is the move step length between turns and µ the power-law exponent. Over many iterations, a Lévy walk will be distributed much further from its starting position than a Brownian walk of the same length [hence is termed superdiffusive (8)], because small-step walk clusters are interspersed by long “steps” to new locations, with this pattern repeating across all scales. It has been demonstrated that a Lévy walk with exponent µ ∼2 is optimal when the search targets are not depleted or rejected once visited but instead may be revisited profitably, either because they replenish overtime or because targets are distributed patchily (1, 2). Importantly, Lévy searches with µ ∼2 are optimal for a very broad range of target densities and distributions (9). In the very low-density regime, Lévy strategies remain the optimal solution with the optimal exponent 1 < µ_opt ≤ 2 dependent on specific environmental properties, such as the degree of spatial landscape heterogeneity or temporal target revisitability (10, 11). Consequently, optimal Lévy searches result in more predictable target encounters during foraging in otherwise unpredictable environments (9). Because Lévy walks can optimize search efficiencies in this way, it is proposed that natural selection should have led to adaptations for Lévy walk foraging [the Lévy flight foraging (LFF) hypothesis] (1–3). The apparent ubiquity of Lévy patterns among extant organisms, including humans (1–3, 12–18), suggests that searches that approximate them have evolved naturally (3). It has been hypothesized that behavioral adaptations to changes in environmental resources cue the switching between localized Brownian and Lévy random searching (2, 3, 13) or that sensory interactions with heterogeneous environments may give rise to Lévy movement patterns (an emergent phenomena) (19); however, the origins of such potential mechanisms remain elusive.

The fossilized records of animal movements preserved as trails and burrows (trace fossils) are the only direct record of extinct organisms’ behavior and may provide a means to understand the evolution of search strategies in ancient landscapes, including during dramatic environmental changes (6, 20, 21). At intervals throughout evolutionary history, organisms have faced large-scale collapses of primary productivity due to abiotic environmental changes, such as volcanism and global warming, that often are associated with mass extinctions of species (22, 23). This raises the possibility that random search patterns such as Lévy walks, with characteristic long steps to new locations, might have acted to increase the likelihood of ancient organisms finding scarce resources, as the search time to find distant patches is minimized in this movement strategy compared with Brownian motion (2). Nevertheless, so far, only localized foraging patterns based on simple taxes have been identified in trace fossils (6, 20, 21).

An early computer simulation (20) showed that the patterns recorded by many trace fossils could be reconstructed in model foragers by using three simple “rules”: “phobotaxis,” which forbids an individual from crossing its own trail; “thigmotaxis,” which compels an individual to stay close to an existing trail; and “strophotaxis,” which is the propensity for making U-turns and which may be cued innately or triggered by the presence of an obstruction or other discontinuity. These three basic patterns of behavior now underlie most theories of spiral and meandering trace fossils (24). A general characteristic of many fossil trails is that they resemble self-avoiding random walks, as there is minimal recrossing of existing tracks (24). This resemblance is more than superficial, because some trace fossils from deep-water turbidite fan settings are fractal (25, 26), and have fractal dimensions typically estimated to be between 1.5 and 1.6 (25), which span the fractal dimension (1.55) of a self-avoiding random walk. This suggests that trace fossils also may be modeled as Lévy walks, because they share with self-avoiding random walks the same range of fractal dimensions and so exhibit, on average, the same number of subclusters per cluster with change of scale (27). However, to our knowledge, no previous study investigated the possibility of Lévy behavior occurring in ancient organisms.

Results and Discussion

We used numerical simulations to examine whether Lévy walks may result from simple taxes, namely phobotaxis, thigmotaxis, and strophotaxis (Materials and Methods). In our simulations, model organisms move between nodes on a regular square lattice containing randomly distributed “obstructions.” The modeled obstructions may represent natural discontinuities encountered by an organism, such as its own trail, an absence of food, meeting a competitor, detecting a predator, or an innately cued change of direction. Each node visited is marked so that a trail is laid, with the organism following previously laid trails using a “wall-following algorithm” that captures the combined effects of thigmotaxis and phobotaxis. Upon encountering an obstruction, strophotaxis is implemented by switching the handedness of the wall-following algorithm. Thus, our model captures key behaviors, and although it is not intended to be realistic in every detail, it introduces interactions between the organism and its environment, or motivational changes within an organism, which are complexities that were absent from early models (20).

Simulation outputs show that before encountering an obstruction, the model organism spirals outward, forming an Archimedes spiral (Fig. 1A) characteristic of some early fossil traces (6). After encountering obstructions, random looping patterns appear (Fig. 1A). The presence of starting spirals and, in particular, clusters of localized “walks” are common in meandering trace fossils, such as in Cosmorhaphe (Fig. 1B). Our simulation shows that initial spiraling becomes less evident as the number of obstructions increases (Fig. 1C). In the presence of sufficiently numerous obstructions, model parameter estimation using maximum likelihood estimation (MLE) and Akaike information criteria weights (wAIC) for best-fit model selection (Materials and Methods) favors a power-law over an exponential (Brownian) model as being the better model of the step-length distribution, i.e., the distribution of distances traveled between consecutive turns. Power-law scaling characteristic of Lévy walks is evident across all scales of the movement pattern, from the shortest to the longest steps (Fig. 1D). The MLE estimate for the power-law exponent is 2.14, which is close to the optimum for Lévy search (1, 3, 13). Therefore, Lévy power-law scaling emerging from the simple rules of behavioral taxes seen in fossil trails when interacting with a heterogeneous environment (e.g., food patchiness) predicts the presence of fossil trails with Lévy patterns.

Fig. 1.

Simple fossil behavior may give rise to Lévy patterns. (A) Simulated self-avoiding, trail-following random walk and (B) an example of a self-avoiding fossil trail, Cosmorhaphe, from the Lower Eocene (Beloveža Beds, sample UJTF77; Table S1). (C) The same simulation as in A but with introduced strophotaxis (U-turns) in response to randomly distributed obstructions or innate cues. Note the similarity in trail form between B and C. (D) Cumulative frequency distribution of move step lengths between turns (○) for the simulation exemplified in C shows a model best fit to a truncated power law with µ = 2.14 (red line) compared with the exponential (blue line). In A and C, track intersections are evident, as occasionally a self-avoiding walker traps itself and is forced to cross (intersect) itself. The trajectories in A and C are random, although this becomes clear only for very long tracks.

To test for the presence of heavy-tailed movement patterns, including Lévy walks, we analyzed fossil trails made by benthic marine animals in deep-sea, turbidite fan habitats (“flysch”) from the Late Cretaceous and Eocene epochs (Table S1 and Fig. S1). One potential limitation we encountered when undertaking individual path analysis is that many trace fossil specimens are too short (21) to support the type of robust statistical analysis that is applied to modern trails (15) because of issues related to collection, preservation, and rock exposure in the field. We approached this problem in two ways: First, we focused our analysis on the longest, most complete fossil trails recorded during targeted fieldwork (Table S1). Second, we used a novel path analysis technique (28) that identifies move step lengths in 2D trajectories objectively, is very resilient to gaps in a track, and gives reliable results, even for a trail composed of relatively few steps. Unambiguous identification of turning points in trajectories is crucial for accurate estimation of move step lengths (28). The advantage of our method is that by analyzing two dimensions separately, there is a very high likelihood of detecting a Lévy walk (power law) if it is present, because a scale-free Lévy walk remains unchanged (the exponent will not vary) regardless of the dimension in which it is viewed, which is not the case for other simple distributions (3, 28). This leads to a clear prediction: an ideal Lévy walk is described by a similar power law on both axes, whereas a scale-dependent walk, e.g., Brownian walk, will not satisfy this criterion. Testing the LFF hypothesis is concerned mainly with power-law (Pareto–Lévy) and exponential distributions of move step lengths, because the LFF predicts that Lévy (power-law) searching optimizes location of sparse food, whereas simple Brownian (exponential) movements are expected where food is abundant (1, 15). In addition to power-law and exponential models, we also tested truncated power laws, because animal movements are naturally bounded (13), as well as the truncated exponential, log-normal (a heavy-tailed distribution), and gamma distributions. We also compared trace fossil step-length distributions with three composite Brownian (CB) walk distributions comprising proportions of two, three, and four exponential distributions (28), because these distributions may have parameters “fine-tuned” to a Lévy walk (28–31). Rather than CB walks being an alternative, competing model of movement pattern data resembling Lévy walks—because most CB walks will not resemble a Lévy walk so will not be “mistaken” for them—they instead provide a means by which an organism can approximate a Lévy walk and give insights into the underlying mechanism producing Lévy walk patterns (27, 30).

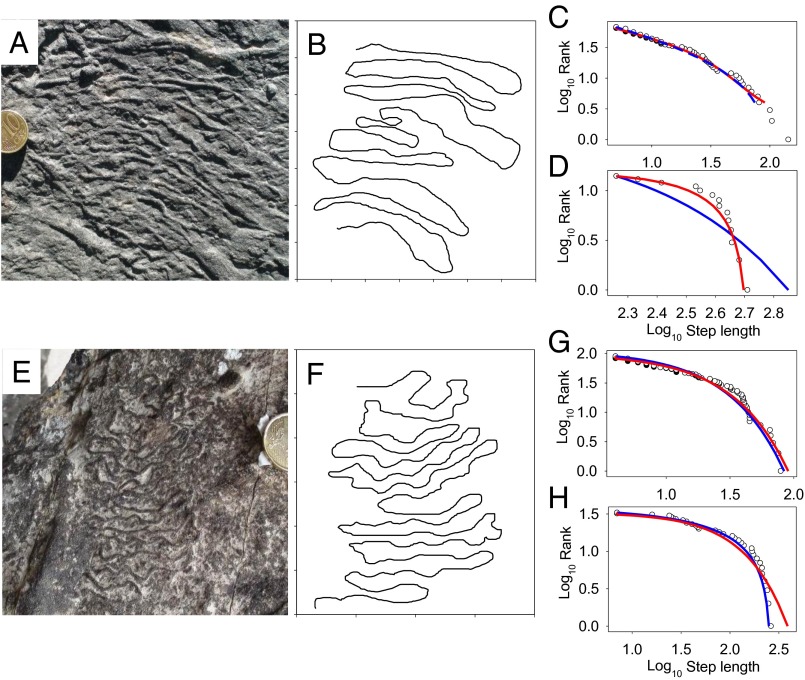
The specimens analyzed comprised (i) meandering trace fossils produced by unknown, worm-like trace makers and classified in the ichnogenera Cosmorhaphe and Helminthorhaphe (n = 3 from Poland; n = 4 from the Spanish Pyrenees), and (ii) trace fossils of deposit-feeding, irregular echinoids (known as heart urchins) (Atelostomata; probably Spatangoida) classified broadly in the ichnogenus Scolicia but including examples of the preservational variants Paleobullia and Taphrhelminthopsis (n = 7 trails from Eocene strata of northern Spain) (Table S1 and Fig. S1). Cosmorhaphe and Helminthorhaphe all were formed as surficial grooves or near-surface open tunnels as the animals moved through the sediment, which then were preserved by fine sand deposited on top, filling in the grooves or burrows. The Scolicia specimens comprise two types: those that were formed as surficial grooves, as above, and others that formed as deeper burrows that were excavated and filled in by the animal as it moved through the sediment. In both cases, the sediments then turned to rock. Helminthorhaphe comprises first-order meanders with strong trail-following and self-avoiding tendencies (Fig. 2 A and B). Cosmorhaphe are distinctive as self-avoiding second-order meanders (Fig. 2 E and F), and Scolicia are self-avoiding but comprise more complex, higher-order meanders, in which longer, straighter move steps sometimes separate sequences of shorter steps, with this pattern occurring at different scales (Figs. 3 A and B and 4 A, B, D, and E).

Fig. 2.

Brownian walks in trails of Eocene worm-like animals. Trace fossils of (A and B) Helminthorhaphe flexuosa and (E and F) Cosmorhaphe tremens (samples D1L2 and D2L6, respectively; Table S1 and Fig. S1) and the digitized trails. For scale: coin diameter, 19.75 mm. MLE with wAIC shows model fits for H. flexuosa to a (C) two-exponential CB distribution on the x axis (red line, CB best fit; blue line, truncated power law) and (D) a truncated power law fitting only the tail of the data (red line) on the y axis vs. an exponential (blue line). For C. tremens, model best fits (G and H) to a CB with two and three exponentials on the x and y axes, respectively (red lines), compared with a truncated power law.

Fig. 3.

Hierarchically nested random walks in fossil echinoid trails. (A) Scolicia specimen (MBA-3d) from the Lower Eocene Higuer–Getaria Formation (coin diameter, 20 mm) and (B) the digitized trail. (C and D) Model best fits to truncated Pareto–Lévy power laws (red line) for the move step-length distributions in both x and y axes compared with exponential fits (blue line). (E and F) Marginally better fits to four-exponential CB distributions (red line) in both x and y axes vs. truncated power laws (blue line) indicate very similar fits to empirical move step data and, therefore, that a multimodal or CB walk of this Scolicia specimen is finely tuned to a Lévy walk.

Fig. 4.

Scolicia trails reflect sparse and abundant resource landscapes. (A and B) A spatially extensive Scolicia trail (MBA-1) 6.2 meters long shows (C) similar model fits of a truncated Lévy power law (blue line) and a CB walk (red line), with many long, ballistic move steps characteristic of movement responses to resource scarcity. Gray box in B denotes photographed area in A. (D and E) Scolicia specimen (MBA-4a) from a different location within the Lower Eocene Higuer–Getaria Formation shows more intensive walk clusters at several different scales. (Scale: acetate sheet length, 29.7 cm.) (F) A model best fit to a CB distribution with three exponentials (red line; y-axis steps shown) and strong fits to truncated Lévy distributions in both axes also were found (blue line, y-axis steps shown; Table S3), indicating fine-tuning of multimodal Brownian walks to a Lévy walk that is optimal in a patchy resource environment. (G) Putative assemblage of many individual self-avoiding Scolicia trails from the same formation may represent aggregation in an abundant food patch. Area shown, 1.85 × 1.16 m.

The specimens of Helminthorhaphe that show phobotaxis, thigmotaxis, and strophotaxis are highly localized with steps between turns in distinct modes. As a result, trace fossils with compact, thigmotactic localized searches were best approximated in one dimension by a CB distribution (Fig. 2C) and in the second dimension by more weakly supported distributions of various forms (Fig. 2D) (Table S2). Cosmorhaphe also were consistent with CB walks described by two or three exponentially distributed step-length clusters in both x and y dimensions for all three specimens (Fig. 2 G and H), indicating support for paths with hierarchical walk clusters. The empirical results for Helminthorhaphe and Cosmorhaphe are predicted from our simulation results showing deterministic local searches, which for Cosmorhaphe extends to random looping across at least two spatial scales (i.e., exhibiting turns within larger turns) (Figs. 1B and 2B). Strong fits to truncated (Lévy) power laws were not found in both dimensions for any individual Helminthorhaphe or Cosmorhaphe (Table S2).

In contrast, the studied specimens of Scolicia were more spatially extensive, showing little or no trail following (thigmotaxis) but evidence for path self-avoidance (Fig. 3 A and B). We found that 11 of 14 step-length distributions from Scolicia specimens (x and y dimensions for each of seven specimens) were best fitted by truncated Lévy-like (power-law) distributions with power-law exponents between 0.94 and 1.67 (mean μ = 1.21 ± 0.22 SD). Model selection showed strongest support for the truncated Pareto–Lévy distribution in these trails (wAIC range 0.70–1.0) (Table S3). Notably, five (of seven) individual specimens were best fit by truncated power laws in both x and y spatial dimensions (Fig. 3 C and D and Table S3), suggesting resemblance to a Lévy walk for these particular examples. Other Lévy power-law features also were evident: self-similarity at different scales (e.g., Fig. 3B) and scaling across more than two orders of magnitude of the data (e.g., Fig. 3 C and D). However, when the CB walk distributions were included in the model set, there was a small improvement over truncated Lévy best fitting to Scolicia single-dimension step distributions by second-, third-, or fourth-order CB distributions in 57% of cases (8 of 14 distributions) (e.g., Fig. 3 E and F and Table S4). For three Scolicia specimens, there was stronger support (least worst) for one or either of the more complex CB models (CB3 or CB4) on both axes (Table S4). This indicates that the CB walks are finely tuned to a Lévy walk, as shown, for example, by the similarity between the truncated Lévy and four-exponential CB model fits in Fig. 3 E and F. For the remaining six distributions, two still showed strongest support for truncated Lévy patterns and two showed no clear support for CB over truncated power-law distributions, whereas for a single specimen (x and y distributions), there was no clear support for any one model (Table S4). Overall this suggests that the search patterns exhibited by Eocene deposit-feeding, irregular echinoids were hierarchical walk clusters described by Lévy walks or by CB walks finely tuned to Lévy walks.

It is unsurprising that the CB walk distributions approximated fossil echinoid trail patterns as well as, if not better than, Lévy walks in most cases, because fitting requires optimized proportions of two to four exponential distributions and, hence, a greater number of parameters than a truncated Lévy distribution. Improved fits are expected with greater numbers of parameters, and it has been argued that the most parsimonious model in this context is the one with fewest parameters (28, 29). Nonetheless, an improved fitting of CB walks over Lévy walks to movement paths has generated debate (31) because it questions the strength of support for Lévy behavior in some species, such as marine mussels (14, 29). However, our results argue for this contention to be reconsidered in light of the emergent patterns generated by the simple behaviors of trace fossils. Our simulations show that Lévy walks may emerge from simple taxes displayed by fossil animals: a change in movement pattern may appear without an organism changing its behavior or selecting a preferred search strategy. Moreover, our analysis of trace fossils from the Eocene demonstrates that ancient movement patterns can be described as hierarchically nested Brownian walk clusters that converge to a truncated Lévy walk. It is striking that the CB walks were finely tuned to theoretically optimal Lévy walks, suggesting selection pressure for Lévy walk characteristics (27, 30).

Trace fossils appear to predate the basic plan for the vertebrate nervous system that probably was established within 100 My of the initial Cambrian explosion (32). It has been hypothesized that Lévy walks evolved early because of their widespread occurrence in the behavior of taxonomically well-separated groups—for example among fish, reptiles, insects, and birds (3, 12, 13, 15)—and in human cognition and mobility (17, 33). Our results confirm that search patterns that are driven by simple behaviors and approximate theoretically optimal Lévy walks may have an ancient origin. The earliest such fossil trails comprise patterns that often cross themselves and indicate relatively crude foraging behaviors (34). More complex traces in the form of surface trails or shallow burrows that meander or spiral and are self-avoiding are first recorded in the Lower Cambrian trace fossil record, ∼540 Ma (34). Numerical simulations of Darwinian evolution of behavioral programming suggest that in environments with homogenous food supply, competition between individuals should favor trails with maximum coverage and minimal recrossing of existing tracks (35). The trace fossil Cosmorhaphe is known from the Lower Silurian (∼443–433 Ma), in the aftermath of the Late Ordovician mass extinction event (23), through to the present day (36). Although resembling a self-avoiding random walk, Cosmorhaphe has been interpreted as a shallow infaunal burrow system constructed as a “microbe farm” or trap, similar to the burrows of Paraonis (36, 37). Our findings suggest, however, that the Cosmorhaphe specimens analyzed in this study are quantitatively similar to Helminthorhaphe and to the simple Brownian random walks that approximate short-range, localized foraging movements of extant animals (13, 15), supporting the traditional view (24) that these are the fossil burrows of foragers. Such self-avoiding behavior persists in modern taxa, being observed directly in grazing trails of the isopod Chiridotea coeca and in the movements of the owl limpet Lottia gigantea (27). Taken together, this suggests the interesting possibility that spatially intensive foraging by Cosmorhaphe described by low-domain hierarchical (CB) random walks (e.g., Cosmorhaphe tremens; Fig. 2 E and F and Table S2) may have occurred as early as the Silurian Period.

The self-avoiding trail typified by an Archimedes spiral and the localized movements of simple Brownian walks are efficient search patterns for food distributed homogeneously where encounters are more predictable, and these adequately describe the trails of Helminthorhaphe and Cosmorhaphe. However, the specimens of Scolicia we analyzed exhibit more complex patterns that indicate foraging adaptations linked to changes in food availability. We found support for hierarchical walk clusters and evidence of ballistic, straight-line movements (mean µ = 1.21) of several meters by ∼3-cm–long echinoids (Figs. 3 A and B and 4 A, B, D, and E), which are analogous to Lévy walks with lower exponents (µ → 1) that are optimal for finding isolated resource targets (1, 2, 15, 16). One interpretation of these spatial patterns, and one that is predicted by the LFF hypothesis, is that these echinoids responded to resource-poor conditions by adapting more extensive, ballistic searches to locate sparse food patches further away (2, 13, 16). Our modeling results are consistent with this interpretation, because an increased occurrence of locations without food (i.e., obstructions), in addition to trail self-avoidance, will yield longer steps, characteristic of Lévy walks with lower exponents. In further support, we found, in addition to solitary individual tracks (Figs. 3 A and B and 4 A, B, D, and E), bedding planes with many crisscrossing Scolicia specimens (Fig. 4G), which appear similar to area-restricted search patterns seen in modern foragers when dense food patches are encountered (7). Given that self-avoiding trails are common, the paths likely were made by different individuals within a limited area, presumably attracted by a rich resource patch. Hierarchical walk clusters, Lévy-like movement patterns, extensive ballistic steps, and locally, dense assemblages of Scolicia indicate that benthic detritus probably was not homogeneously distributed in the Eocene deep-sea turbidite fans of the studied locations. Indeed, spatially and temporally heterogeneous (patchy) distributions of organic matter are seen in modern (38) deep-sea floor settings, and have been suggested for ancient settings (39). Thus, our method of analyzing trace fossils may provide insights into the distribution of food resources in ancient ecosystems. Furthermore, sparse food in patchy resource environments predicts the adaptation of Lévy searches, patterns that minimize the time to locate distant patches (1, 40).

Dramatic reductions in primary production are thought to have characterized major mass extinction episodes in the past (22) and episodes of climate change, such as the more recent interglacials (41). During the end-Cretaceous extinction event, changes in ocean nutrient supply may have been a crucial factor in driving echinoid extinction because of the preferential survival of deposit-feeding taxa such as spatangoids (42). Our analysis of Scolicia trace fossils indicates that descendants of these survivors inhabiting Eocene deep-sea settings displayed Lévy-like movement patterns with low power-law exponents that describe more ballistic trajectories, which are considered theoretically optimal for finding isolated food items (1). Therefore, we hypothesize that in the past, extreme climate change and productivity collapse associated with extinctions might have triggered the evolution of foraging adaptations converging on optimal Lévy walks conferring increased survival rates. Similarly, animals already using such strategies because they lived in habitats with highly sparse, patchily distributed food perhaps were preadapted to survive such events. This empirical “Lévy survival strategy” (LSS) hypothesis is informed by theoretical model simulation studies showing that in environments with very low resource densities at the edge of extinction, normal diffusive searchers rapidly die, but superdiffusive foragers—described by Lévy walks with lower exponents (1 < µ ≤ 2)—can survive for long periods without nearing extinction (9, 43–45). The singular advantage of extensive, ballistic Lévy-like searching for increasing survival rates in very low-density resource environments implies its early evolution in animals. An ancient origin might explain widespread recent observations of Lévy behavior in diverse extant taxa (3, 12–19, 27–29, 33, 40) and suggestions that it is an intrinsic behavior (3, 40, 46) for optimal random foraging in a broad range of heterogeneous landscapes (9). Our identification of Lévy-like movements in Eocene echinoids is a first step in reconstructing the evolution of this optimal search behavior, perhaps from origins in the Silurian or earlier. To explore these ideas further and to test the LSS hypothesis, our approach and method (28) may be applied to any type of fossil trail and trackway of sufficient length for understanding extinct foraging patterns and environmental resource distributions.

Materials and Methods

Simulations.

For simulating searches, model foragers moved between nodes on a regular square lattice according to a wall-following algorithm, the best-known rule for traversing mazes, which also is known as either the “left-hand rule” or the “right-hand rule.” This algorithm (47) captures both thigmotaxis and phobotaxis as model organisms move forward while keeping a set distance to the left or right of a previous trail. Randomly introduced strophotaxis simulated encounters with obstructions whereupon the handedness of the wall-following algorithm was reversed.

Movement Analysis.

Fossil trails were recorded in the field by tracing them directly onto acetate sheets that later were digitized, and the x and y coordinates were calculated using custom-written software. MLE was used to fit model parameters to simulated or empirical step-length distributions according to the methods described in Humphries et al. (28), with model selection by wAIC, where a weight of 1.0 provides strongest support and 0 weight no support.

Fossil Locations and Stratigraphy.

Visits to European museums housing major trace fossil collections showed that almost all curated specimens were of insufficient length and lacked the minimum number of steps required for robust analysis. Thus, field surveys were conducted to find longer specimens. Two areas in northern Spain known to expose fossiliferous, Eocene rocks containing abundant trace fossils were surveyed by R.J.T. and B.M.: (i) the classic outcrops of the Lower Eocene Higuer–Getaria Formation at Zumaia and near Getaria (26) and (ii) outcrops of the Lower–Middle Eocene Hecho Group in the Pyrenees, north of Jaca (48) (Table S2).