Abstract
All neuroimaging packages can handle group analysis with t-tests or general linear modeling (GLM). However, they are quite hamstrung when there are multiple within-subject factors or when quantitative covariates are involved in the presence of a within-subject factor. In addition, sphericity is typically assumed for the variance–covariance structure when there are more than two levels in a within-subject factor. To overcome such limitations in the traditional AN(C)OVA and GLM, we adopt a multivariate modeling (MVM) approach to analyzing neuroimaging data at the group level with the following advantages: a) there is no limit on the number of factors as long as sample sizes are deemed appropriate; b) quantitative covariates can be analyzed together with within- subject factors; c) when a within-subject factor is involved, three testing methodologies are provided: traditional univariate testing (UVT)with sphericity assumption (UVT-UC) and with correction when the assumption is violated (UVT-SC), and within-subject multivariate testing (MVT-WS); d) to correct for sphericity violation at the voxel level, we propose a hybrid testing (HT) approach that achieves equal or higher power via combining traditional sphericity correction methods (Greenhouse–Geisser and Huynh–Feldt) with MVT-WS.
To validate the MVM methodology, we performed simulations to assess the controllability for false positives and power achievement. A real FMRI dataset was analyzed to demonstrate the capability of the MVM approach. The methodology has been implemented into an open source program 3dMVM in AFNI, and all the statistical tests can be performed through symbolic coding with variable names instead of the tedious process of dummy coding. Our data indicates that the severity of sphericity violation varies substantially across brain regions. The differences among various modeling methodologies were addressed through direct comparisons between the MVM approach and some of the GLM implementations in the field, and the following two issues were raised: a) the improper formulation of test statistics in some univariate GLM implementations when a within-subject factor is involved in a data structure with two or more factors, and b) the unjustified presumption of uniform sphericity violation and the practice of estimating the variance–covariance structure through pooling across brain regions.
Introduction
In the research endeavor towards addressing a specific hypothesis, conventional voxel-wise FMRI group analysis is a vital step that allows the investigator to make a general statement at the population level. In the typical methodology for such a leap of generalization from individual results to the group level one takes the effect estimates from individual subject analysis and treats them as raw data in a general linear model (GLM), with an underlying assumption that those effect estimates are either equally reliable across all subjects or with negligible within-subject variability relative to the between-subjects counterpart. The effect estimates are regression coefficients (usually referred to as β values) or linear combinations. And the GLMs traditionally include Student’s t-tests (including paired, one-and two-sample versions), multiple regression, and AN(C)OVA.
The difficulty of modeling multi-way AN(C)OVA
For categorical variables, the dichotomy of between-subjects and within-subject factors is necessary because the levels (or groups) of the former can be considered independent while this is generally not true for the latter. Such differentiation necessitates accounting for the correlations among the levels of a within-subject factor, and leads to the different treatments between two-sample and paired t tests as well as numerous types of AN(C)OVA in terms of the number of explanatory variables and their types (categorical or quantitative, between-or within-subject). The computations for Student's t-tests and multiple regression are quite straightforward and economical. In contrast, under the conventional ANOVA platform with rigid data structure (i.e., equal numbers of subjects across groups and no missing data), one calculates the sum of squares (SS) for each effect term through simplified formulas, and then obtains their respective ratios as F-statistics for significance testing. The process is computationally efficient through the SS formulas, but each ANOVA formulation with different factor types or with an extra factor leads to a different model framework because of the unique variance partitioning involved. This can become very tedious especially when unique random effects have to be accounted for in the case of within-or intra-subject (repeated-or longitudinal-measures) factors. For example, a two-way within-subject ANOVA is more complicated than its one-way counterpart in formulating the F-statistics. Because of this limitation, the ANOVA methodology adopted in AFNI (Cox, 1996) is currently constrained to up to four fixed-effects factors through separate programs 3dANOVA, 3dANOVA2, 3dANOVA3, and GroupAna.
As an alternative, GLM is more flexible than the ANOVA platform at the cost of additional computation complexity. For example, GLM can accommodate unequal numbers of subjects across groups. However, unlike the efficient SS computation under the ANOVA framework, each categorical variable under GLM is dummy coded by multiple indicators. The complication of the coding process occurs when a within-subject factor is involved, and the subjects are also required to be entered in the model through dummy coding, to account for the random effects (intercepts). If more than one within-subject factor is formulated under GLM, all the possible interactions between those within-subject factors and subjects except the one with the highest order are also required. It is because of this complication that the GLM implementations in both FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki) and SPM (http://www.fil.ion.ucl.ac.uk/spm) can properly handle only one within-subject factor, and statistical tests involving any between-subjects factors cannot be validly performed in the same model because of the complexity in variance partitioning. Even if the software allows for more than one within-subject factor (e.g., two-or three-way within-subject ANOVA), the results would be incorrect as no differentiation in error partition is implemented. In addition, it is invalid under their GLM implementations to test the effect at a specific factor level (e.g., male group, positive condition, or negative condition of the female group) or a level combination whose weights do not sum to zero (e.g., sum of positive and negative conditions) because the residuals are used in variance estimation. In contrast, GLM Flex (McLaren et al., 2011) is a Matlab-based package that allows the handling of such cases without the inflated false positive rate (FPR) for group comparisons that occurred with the previous alternative Flexible Factorial Design in SPM and its comparable implementation within the General Linear Model setup in the group analysis scheme FEAT of FSL. In addition, GLM Flex can model interactions among up to five fixed-effects variables that users encode with dummy variables.
Sphericity violation
The traditional approach to handling a within-subject factor with more than two levels (e.g., one-way within-subject ANOVA) is susceptible to the violation of a correlational assumption: sphericity or compound symmetry. The compound symmetry assumption requires that the variances and covariances of the different levels of the within-subject factor are homogeneous (identical), while the sphericity assumption, an extension of the homogeneity of variance assumption in between-subjects ANOVA, states that all the variances of the level differences are equal. Note that compound symmetry is also known as uniformity, intraclass correlation model, or exchangeable correlation structure, and sphericity is sometimes referred to as circularity. Although sphericity is the necessary and sufficient condition for the validity of the F-statistics in traditional within-subject ANOVAs, compound symmetry is much easier to verify, and is a special case of the sphericity assumption, thus is a sufficient but not necessary condition: If compound symmetry is satisfied, then sphericity is met. On the other hand, sphericity almost means compound symmetry: it is possible, but rare, for data to violate compound symmetry even when sphericity is valid.
Data variability and correlations across conditions at the group level arise because of neurological basis and intrinsic heterogeneity across subjects. For example, a subject who responds more strongly than the group average to the positive condition may also have a higher response to the negative or neutral condition. However, the correlation (proportion of shared or overlapping variance) between the positive and negative conditions is not necessarily the same as between positive and neutral conditions, and between negative and neutral conditions. The deviation from sphericity could lead to inflated significance. However, the traditional correction through adjusting for the degrees of freedom has never been adopted in the neuroimaging packages. Instead one proposed method was to estimate the correlations through pooling across all the “active” voxels in the whole brain (Glaser and Friston, 2007), which has been adopted at both individual and group levels in SPM. However, the presumption of a global correlation structure has not been systematically validated.
The difficulty of modeling quantitative covariates together with within-subject factors
Due to experimental constraints, samples (trials or subjects) are not always randomly manipulable. For example, it is unrealistic to expect each subject to respond to all trials with the same reaction time (RT) or to have the same average RT. The resulting variability can be modeled through amplitude correlation (or parametric modulation) at the individual trial level, while across-subjects variations can be controlled or accounted for in group analysis through the incorporation of relevant quantitative covariates (e.g., age, IQ, RT, etc.).On other occasions, the association itself between the brain response and a quantitative covariate is of interest, and necessitates considering it as an explanatory variable.
If a model contains only quantitative covariates or if the only categorical explanatory variables are between-subjects factors, modeling quantitative covariates is relatively easy and straightforward through a univariate regression or general linear model (GLM). On the other hand, the classical ANCOVA usually includes at least one between-subjects factor as well as one or more quantitative covariates. It is of note that the historical incarnation of ANCOVA emphasizes additivity and does not consider any interactions between factors and quantitative covariates. This is the reason for the notion of homogeneity or parallelism of slopes, which is totally unnecessary when the interactions are included. Furthermore, the concept of ANCOVA is basically subsumed under GLM; if not for the legacy usage, the ANCOVA nomenclature can be fully abandoned to avoid confusion. When a within-subject factor is involved, the situation becomes complicated under the univariate modeling framework, and so far no neuroimaging software has the capability to do this except via the linear mixed-effects modeling (LME) approach (Chen et al., 2013). Here we will explore the possibility of modeling a quantitative covariate in the presence of a within-subject factor under the multivariate framework.
A motivational example
Tomotivate the present exposition of the MVM approach, we present a real FMRI group study to demonstrate a typical design that accounts for a confounding effect, varying age across subjects. Briefly, the experiment involved one between-subjects factor, group (two levels: 21 children and 29 adults) and one within-subject factor (two levels: congruent and incongruent conditions). Stimuli were large letters (either “H” or “S”) composed of smaller letters (“H” or ”S”). For half of the stimuli, the large letter and the component letters were congruent (e.g., “H” composed of “H”s) and for half they were incongruent (e.g., “H” composed of “S”s). Parameters for the whole brain BOLD data on a 3.0 T scanner were: voxel size of 3.75 × 3.75 × 5.0mm3, 24 contiguously interleaved axial slices, and TR of1250 ms (TE=25 ms, FOV=240 mm, flip angle= 35°). Six runs of EPI data were acquired for each subject, and each run lasted for 380 s with 304 brain volumes. The task followed an event-related design with six runs of 96 trials each, three global runs interleaved with three local runs (order counterbalanced across subjects). Subjects used a two-button box to identify the large letter during global runs and the component letter during local runs. Trials lasted 2500 ms: the stimulus was presented for 200 ms, followed by a fixation point for 2300 ms. Inter-trial intervals were jittered with a varying number of TRs. This allowed for a trial-by-trial analysis of how the subject’s BOLD response varied with changes in RT.
The EPI time series went through the following preprocessing steps: slice timing and head motion correction, spatial normalization to a Talairach template (TT_N27) at a voxel size of 3.5 × 3.5 × 3.5 mm3, smoothing with an isotropic FWHM of 6 mm, and scaling by the voxel-wise mean value. The scaling step during preprocessing enables one to interpret each regression coefficient of interest as an approximate estimate of percent signal change relative to the temporal mean. To capture the subtle BOLD response shape under a condition, each trial was modeled with 10 basis (tent or piecewise linear spline) functions, each of which spanned one TR (or 1.25 s). In addition, the subject’s RT at each trial was incorporated as a modulation variable. In other words, two effects per condition were estimated in the time series regression at the individual level: one reveals the response curve associated with the average RT while the other shows the marginal effect of RT (response amplitude change when RT increases by 1 s) at each time point subsequent to the stimulus. In addition, the following confounding effects were included in the time series regression model for each subject: third-order Legendre polynomials accounting for slow drifts, incorrect trials (misses), censored time points with extreme head motion, and the six head motion parameters.
At the group level, it is the RT marginal effects that are of most interest, and the four explanatory variables considered are: a) one between-subjects factor, Group (two levels: children and adults), b) two within- subject factors: Condition (two levels: congruent and incongruent) and Component (10 time points where the profile of RT marginal effects were estimated), and c) one quantitative covariate: age. This is seemingly a relatively simple experimental design, but none of the FMRI packages except for the linear mixed-effects (LME) modeling approach implemented into program 3dLME in AFNI can analyze this situation simply because of the difficulty of modeling a quantitative covariate in the presence of a within-subject factor.
Preview
The layout of the paper is as follows. First, we review the modeling platforms for ANOVA and GLM, and elaborate their limitations. The MVM platform is then introduced to overcome some of those limitations. Second, simulation data were generated to reveal how the MVM methodology performs in terms of controllability for false positives and false negatives relative to alternative approaches, and the implementation of MVM strategy in AFNI was applied to the experimental dataset. Finally, we discuss the limitations of MVM, compare the strategy with other methodologies and its limitations, and raise some questions about the current practice and implementations in group analysis. Our contributions here are fourfold: a) The MVM method allows for any number of explanatory variables; b) Quantitative covariates can be modeled in the presence of within-subject factors; c) The MVM platform provides a convenient venue for voxel-wise correction for sphericity violation; d) With our open-source program 3dMVM in AFNI, main effects, interactions and post hoc tests can be performed through symbolic labels, relieving the user of the burden from tedious dummy coding.
Throughout this article, regular italic letters (e.g., α) stand for scalars, boldfaced italic letters in lower (a) and upper (X) case for column vectors and matrices respectively, and words in monospaced font (3dMVM) for program names. It is of note that the word multivariate is used here in the sense of treating the effect estimates from the same subject or from the levels of a within-subject factor as the instantiations of simultaneous response (or outcome) variables. This usage differs from the popular connotation in the FMRI field when the spatial structure (multiple voxels) is modeled as the simultaneous response variables. Those cases include multivariate pattern analysis (Haxby, 2012), independent component analysis, and machine learning methods such as support vectormachine. Major acronyms used in the paper are listed in Appendix F.
MVM platform
In contrast to the univariate GLM (Appendix A), the levels of a within-subject factor can be treated as multiple simultaneous response variables under MVM. That is, each ANOVA design can be subsumed as a special case of MVM. Furthermore, the extension also allows the handling of simultaneous variables that are of different nature, unlike the scenario of a within-subject factor under the ANOVA scheme where the same type of measurement (e.g., BOLD response in FMRI) is acquired under different conditions (e.g., positive, negative and neutral emotions). For example, daily caloric intake, heart rate, body mass and height in behavioral study, or correlation (or connectivity) measure under resting state, fractional anisotropy, gray-matter volume, and task-related BOLD response from MRI data, can be formulated in a four-variate model.
A multivariate GLM includes multivariate regression and MAN(C) OVA as special cases, and can be expressed from a subject-wise perspective, , or through the variable-wise pivot, bj = Xaj + dj, or in the following concise form,
| (1) |
The n rows of the response matrix represent the data from the n subjects while the m columns correspond to the levels of within-subject factor(s). When multiple within-subject factors occur, all their level combinations are flattened or unfolded from a multi-dimensional space onto a one-dimensional row of B. For example, two within-subject factors with a and b levels respectively are represented with an ab-variate model under MVM with m = ab in Eq. (1). Unlike UVM, the within-subject factors are coded in B on the left-hand side of Eq. (1), and only between-subjects variables such as subjects-grouping factors (e.g., sex, genotypes), subject-specific measures (e.g., age, IQ) and their interactions are treated as explanatory variables on the right-hand side. The same linear model is applied to all the m response variables, which share the same model (or design) matrix X = (xih) = (x1, x2,…, xn)T.Without loss of generality, X is assumed of full column-rank q. Each column of the regression coefficient matrix A = (α hj) corresponds to a response variable, and each row is associated with an explanatory variable. Lastly, the error matrix D = (δij)n × m = (δ1, δ2,…, δn)T = (d1, d2,…, dm) is assumed nm-dimensional Gaussian: vec (D) ~ N (0, In ⊗ Σ), where vec and ⊗ are column stacking and direct (or Kronecker) product operator respectively. As in UVM, the assumptions for Eq. (1) are linearity, normality and homogeneity of variance–covariance structure (same Σ across all the between-subjects effects). A striking feature of coefficients Eq. (1) is that Σ embodies the correlations among the m error terms as well as the m simultaneous variables and is estimated from the data instead of being presumed of sphericity as in UVM.
The matrix representation of MVM in coefficients Eq. (1) vis-à-vis the vector counterpart of GLM coefficients (Eq. (9) in Appendix A) is reflected in most properties and testing statistics as well as the solutions for coefficients Eq. (1) (Appendix B), which require
| (2) |
That is, the total number of measuring units (e.g., subjects) cannot be less than the total number of explanatory and simultaneous variables. Similarly, a counterpart exists in partitioning the variability sources: the total sum of squares and cross products (SSP) can be partitioned under the multivariate GLM into one SSP term for regression and the other for the errors. The specific effect for a subject-grouping factor, quantitative covariate or an interaction, corresponds to one or more columns in the model matrix X of coefficients Eq. (1), and is represented in one or more rows of regression coefficients matrix A. Also similar to UVM, significance testing for the hypothesis about a specific effect can be formulated as SSPH against SSPE, with the former being the incremental or marginal SSP between the reduced model under the hypothesis and the full model and the latter being the SSP for the errors. In general, one may perform general linear testing (GLT) as functions of the elements of A,
| (3) |
where the hypothesis matrix L, through premultiplying, specifies the weights among the rows of A that are associated with groups or quantitative covariates, and the response transformation matrix R, through postmultiplying, formulates the weighting among the columns of A that correspond to the m response variables. It is assumed that L and R are full of row- and column-rank respectively, and u < q, v < m. The matrix L (or R) plays a role of contrasting or weighted averaging among the groups of a between-subjects factor (or the levels of a within-subject factor). Without loss of generality, the constant matrix C is usually set to 0.
The GLT formulation Eq. (3), sometimes referred to as double linear or bilinear hypothesis, provides a convenient form for effect testing including any effect associated with a within-subject factor. For example, main effects and interactions can be considered as special cases of GLTs with associated L and R. When R = 1m × 1, the hypothesis (Eq. (3) solely focuses on between-subjects explanatory variables (columns in X) while effects among the levels of the within-subject factors are averaged (or collapsed). In contrast, hypotheses regarding a within-subject factor can be constructed via specifying the columns of R. Four MVT statistics can be constructed (Appendix B) for Eq. (3) based on HE−1, a “ratio” between the SSPH matrix H for the hypothesis (Eq. (3)) against the SSPE matrix E for the errors in the full model (Eq. (1)). Under the null hypothesis, HE−1 = I. Without loss of generality, the effects discussed here are limited to main effect of an explanatory variable and interactions among two or more explanatory variables. Other effects can be treated as main effects or interactions under a sub-model, or estimated through post hoc testing. For an effect not associated with any within-subject factor, its testing can be performed by setting R = 1, and is essentially equivalent to the counterpart under the univariate GLM. Complications occur in making inference in regard to an effect associated with one or more within-subject factors, and there are three possible testing approaches: a) strict multivariate testing (MVT) in MAN(C)OVA, b) within-subject multivariate testing (MVT-WS), and c) univariate testing (UVT) under the MVM platform. Here we only discuss the latter two situations as they directly pertain to the univariate GLM.
Within-subject multivariate testing (MVT-WS)
Under the conventional MVM one can test the centroid in Rm at the group level, and such centroid testing is composed of joint tests in the sense that the same hypothesis is tested across the m response variables (Appendix C). However, when a within-subject factor with m levels is modeled under UVM, the hypothesis about the centroid is typically not of direct interest. Instead, the focus under MVM is usually on the main effect of the factor (or the equality of the m levels) and the interactions between the factor and other explanatory variables, and the testing strategy is typically referred to as within-subject multivariate testing (MVT-WS), repeated-measures MA(C)OVA, or profile analysis. When only one within-subject factor with m levels is involved, its associated R can be derived from the corresponding effect coding matrix, converting the original m response variables into m − 1 unique deviations each of which represents the difference between a level and the average across all levels. And the testing for the main effect now pertains to the (m − 1)-dimensional centroid of those deviations. When there are k within-subject factors present (k > 1), the R for each effect associated with one or more within-subject factors can be computed through the Kronecker product,
| (4) |
where R(i) takes the effect coding matrix if the i th within-subject factor is involved in the effect, otherwise R(i) = 1ni, where ni is the number of levels for the i th within-subject factor (i = 1, 2, ⋯, k) (Appendix C).
In summary, the MVM framework allows one to perform multivariate testing for the main effect of a within-subject factor and its interactions with other variables. Unlike its counterpart under the univariate GLM, the MVT-WS strategy estimates the variance–covariance matrix based on the data instead of presuming a specific structure (e.g., sphericity). At the cost of degrees of freedom and with a higher demand for sample sizes as shown in Eq. (2), it bypasses the stringent sphericity assumption made in the univariate GLM, and can accommodate any possible variance–covariance structure. The choice of effect coding here is for interpretation convenience and consistency, but it should be emphasized that infinite coding methods exist. If a coding method is chosen so that the columns of R(i) are orthonormal, the transformed variance–covariance matrix is diagonal with equal variance and thus spherical. However, different coding strategies in R(i) do not matter in terms of hypothesis testing because of the invariance property.
Univariate testing (UVT) under the MVM platform
Even though the levels of a within-subject factor are treated as simultaneous response variables under the MVM framework (Eq. (1)), UVT can still be performed under MVM thanks to the pivotal role played by the response transformation matrix R in Eq. (3). Furthermore, if the dataset can also be analyzed under the univariate GLM, the UVT statistics from MVM are exactly the same as they would be obtained through the univariate approach. More importantly, MVM offers more UVT capability (e.g., unequal numbers of subjects across groups, quantitative explanatory variable in the presence of within-subject factor) and provides the option of correction for sphericity violation. Specifically, for an effect of a between-subjects factor (or quantitative covariate) or their interaction, the formulation of its F-statistic with H and E through L and R is done in the same way for MVT-WS, and R essentially plays the role of averaging or collapsing among the levels of each within-subject factor (if present). In fact H and E in this case correspond to the SS terms under the corresponding UVT, leading to the same F-statistic as in the associated UVM. For an effect that involves at least one within- subject factor, the UVT F-statistic is different from the situation with MVT-WS. Once the associated R in Eq. (4) is constructed, under the sphericity assumption its SS term and the corresponding SS term for errors can be obtained (Fox et al., 2013) as tr(H (RTR)−1) and tr(E (RTR)−1). Under alternative coding schemes that render an orthonormal transformation matrix R, unique portions of variance among the transformed response variables can be captured, and the SS terms simplify to tr(H) and tr(E).
The two kinds of explanatory variables are differentially coded in the MVM formulation (Eq. (1)) as follows. The within-subject factors are flattened and mapped onto R1 as the columns in the data matrix B, the parameter matrix A and the residual matrix D. On the other hand, the between-subjects factors and quantitative covariates are coded as the columns in the model matrix X with the corresponding effect parameters expressed as the rows in A, and each subject is associated with a row in B, X and D. It is of note that subjects are not explicitly represented among the columns of X in Eq. (1), unlike the univariate GLM(Appendix A) in which all the response values form a column vector and subjects are coded as columns for the random effects in the model matrix. The separate coding for the two variable types in MVM is also reflected in the roles of L and R in formulating each hypothesis, and provides a simpler solution in pairing the SS terms for each effect than the univariate GLM. It is this separate treatment that not only makes its extended modeling capabilities and advantages possible but also leads to elegant implementations. Unlike the univariate GLM where the difficulty lies in the pairing for the denominator of each F-statistic, the SSPE matrix E is fixed, and the UVT formulation under MVM hinges on the construction of the SSPH matrix H, which translates to formulating the response transformation matrix R. As R in Eq. (4) is either the coding matrix for a within-subject factor or the Kronecker product of multiple coding matrices, it is much simpler than the pairing process in the univariate GLM.
For example, the UVT for a factorial two-way within-subject ANOVA (Appendix C) demonstrates that the flattened within-subject factors under MVM can be restored through constructing a proper R in Eq. (3). The transformation provides a convenient hinge with which any number of within-subject factors is multiplicatively flattened onto the left-hand side of an MVM system, and later allows for the restoration of significance testing for main effects and interactions in the UVM style. This process in and of itself is of little theoretical value; rather, the appealing property of the transformation lies in the computational or algorithmic perspective. The implementation advantage is that the user interface only involves symbolic representations of all variables and factor levels without any direct specification through dummy coding. In addition, the easy pairing for SS terms in the F-statistic of each effect relieves one of the manual pairing process in the univariate GLM so that the number of within-subject factors is no longer a limitation in implementation. Furthermore, the sphericity verification and the correction for its violation (Appendix D) become an intrinsic step for UVT under MVM because they depend on the transformation matrix R and the SSPE matrix E.
Another appealing feature of MVM is in modeling quantitative covariates in the presence of a within-subject factor. If such a covariate is at the subject level (i.e., between-subjects covariate) and does not vary across the within-subject factor levels, treating the within-subject factor levels as simultaneous response variables in MVM allows separate effect modeling of the covariate for each factor level. In other words, a within-subject factor with m levels is estimated with m different slopes for the quantitative covariate, which cannot be handled under UVM. The significance testing for the m slopes can be performed under UVT through the framework (Eq. (3)) or under MVT-WS. A quantitative covariate that varies across the within-subject factor levels (i.e., within-subject covariate) cannot be modeled under MVM, but can be analyzed through LME (Chen et al., 2013).
Implementation of MVM in AFNI
To recapitulate, the MVM framework includes AN(C)OVA and multiple regression as special cases. In addition to the capability of MVT-WS, it lends us extended options when performing UVT compared to the traditional approaches such as ANOVA and univariate GLM. For example, as each subject occupies one or more rows in the model formulation, the impact of unequal numbers of subjects across groups would be limited on the degrees of freedom and the orthogonality of variance partitioning, but not on modeling capability. Subject-specific quantitative explanatory variables can be easily incorporated in the model matrix X, even in the presence of within-subject factors. The construction of effect testing through the hypothesis matrix L and the response transformation matrix R in Eq. (3) allows for easy implementation with any number of explanatory variables, and the user is relieved from having to deal with dummy coding. The Mauchly test for sphericity violation and the correction for the inflatedl F-tests can be readily established.
The MVM framework has been implemented in the AFNI program 3dMVM in the open source statistical language R (R Core Team, 2013), using the MVM function aov.car() in the R package afex (Singmann, 2013). In addition to the capability of modeling quantitative covariates at the subject (and the whole brain) level, 3dMVM can also handle quantitative covariates at the voxel level (e.g., signal-to-fluctuation-noise ratio). Post hoc t-tests are represented through symbolic representations based on R package phia (De Rosario-Martinez, 2012), and they include pair-wise comparisons between two levels of a factor, linear combinations (e.g., trend analysis) among multiple levels of a factor (weights not having to sum to zero), and interactions among multiple factors that involve one or two levels of each factor. For example, in a 3 × 3 × 3 ANOVA, all the 2 × 2 and 2 × 2 × 2 interactions are essentially t-tests, which can be performed in 3dMVM. Parallel computing on multi-core systems can be invoked using R package snow (Tierney et al., 2013). Effect coding was adopted for factors so that the intercept represents the overall average effect across all factor levels and at the center of each quantitative covariate. Runtime varies from minutes to hours, depending on data size, model complexity, and computing power.
The F-statistic for an effect that only involves between-subject variables (factors or quantitative covariates) under MVM is uniquely determined because of the absence of sphericity issue and is the same as would be obtained under UVM. In contrast, for any effect that is associated with at least one within-subject factor, 3dMVM provides four versions of F-statistic: a) within-subject multivariate testing (MVT-WS), b) univariate testing without sphericity correction (UVT-UC), c) univariate testing with sphericity correction (UVT-SC) through contingencies based on the Greenhouse–Geisser and Huynh–Feldt corrections (Appendix D) (Girden, 1992),
and, d) hybrid testing (HT) that extends the UVT-SC approach,
| (5) |
The two correction methods above, UVT-SC and HT, adopted at the voxel level in 3dMVM, are similar to statistical packages such as car in R (Fox et al., 2013), GLM in IBM SPSS Statistics (IBM Corp., 2012) and REPEATED statement in PROC GLM of SAS (SAS Institute Inc., 2011) except that contingent schemes are adopted here. In addition, instead of directly adjusting the degrees of freedom for sphericity correction, we opt to keep the original degrees of freedom (constant across the brain) but change the F-value to match the adjusted p-value, and this allows us to simplify the bookkeeping and visualization of the output.
The variables and input data are specified through the long format of data frame, a standard data structure in R. In keeping with AFNI’s interface for coding convention, variable type declaration and general linear hypothesis tests in 3dMVM are specified through variable names (e.g., condition) and symbolic labels (e.g., pos, neg, and neu). This is considerably more appealing and less error-prone than manually dummy-coding the categorical variables and model formulations. Neuroimaging data can be in AFNI or NIfTI format. The F-statistics for individual explanatory variables and their interactions are automatically generated instead of the user specifying regressors or assigning weights among the regressors as in FSL, SPM, and GLM Flex. The Pillai–Bartlett trace is adopted as the default for MVT-WS although the other three multivariate statistics are available as options. Two types of F-statistic formulations are available, partially sequential and marginal (types II and III in the SAS terminology). The user can request for post hoc tests through symbolic coding, and both the amplitude and t-statistic are provided as output. A scripting template for running 3dMVM is demonstrated in Appendix E.
Applications and results
Among the four approaches in testing an effect associated with a within-subject factor, MVT-WS is considered the most effective when the response variables are moderately correlated (e.g., between 0.4 and 0.7) (Tabachnick and Fidell, 2013)with the following rationale: If the correlation is too low, the response variables are loosely independent of each other and the variance–covariance structure is close to sphericity, thus the MVM approach becomes inefficient and may lose power compared to the univariate methods; on the other hand, when the correlation becomes high, the response variables can be considered the same variable, and MVM would be costly in wasting high degrees of freedom. To effectively compare these testing methods in light of power and controllability for false positive rate (FPR), simulations and applications are needed.
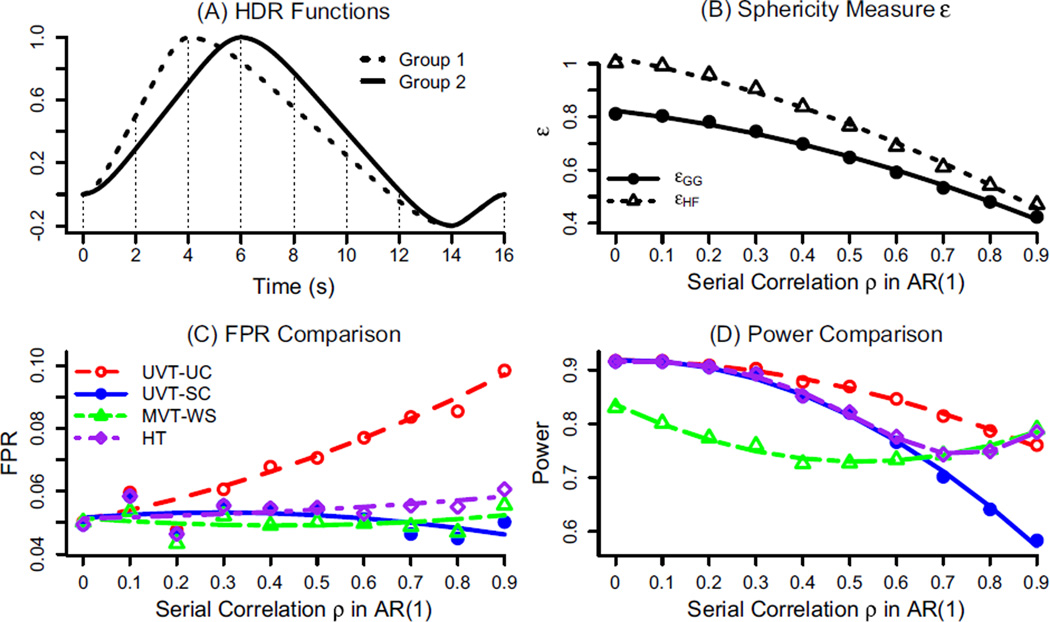
Simulations of group analysis with 3dMVM Simulated data were generated with the following parameters in a typical FMRI group analysis: two groups with 15 subjects in each, and their hemodynamic response (HDR) functions lasting for 12 s but with a 2 s difference in peak location (Fig. 1A). The HDRs are presumably estimated through 7 basis functions (e.g., TENT in AFNI) at the individual subject level to capture the shape differences. Each effect component βij estimated from the i th subject in the j th group (i = 1, 2,‥, 7; j = 1, 2) corresponds to the response amplitudes at TR grids, and are assumed to follow a multivariate Gaussian distribution with a first order autoregressive AR(1) structure for the variance-covariance matrix
where σ = 0.3, and 10 equally-spaced values ρ = 0.0, 0.1,…, 0.9 were chosen to simulate the extent of sphericity violation, ranging from none to high severity. Infinite correlation structures exist as long as the matrices are symmetric positive semi-definite. The AR(1) choice was based on two considerations, the nature of the data structure (HDR estimates at consecutive time points) and the full spectrum of sphericity violation subject it spans: The severity is a monotone increasing function of ρ (Fig. 1B). 5000 datasets were generated, each of which was analyzed through 3dMVM with two explanatory variables, Group (2 levels) and Component (7 effect estimates associated with the basis functions). This is essentially a two-way mixed-design factorial ANOVA with one between- and one within-subject factor. FPR and power were assessed through counting the datasets with the perspective F-statistic surpassing the threshold corresponding to the nominal significance level of 0.05.
Fig. 1.
Simulation data and results for the interaction Group:Component. (A) The presumed HDR functions with a post stimulus undershoot for the two groups, with a difference of 2 s in shifted peak location, were generated by a convolution program waver in AFNI, and sampled at TR=2 s (shown with vertical dotted lines). (B) Average sphericity measure ε across 5000 simulations for the two methods, GG and HF. Notice that 1/6 ≤ εGG ≤ εHF ≤ 1 (Appendix D). (C) Controllability for false positives in univariate testing (UVT) of Group:Component without correction (UVT-UC) (red) is poor when the serial correlation becomes high. The traditional sphericity correction (UVT-SC) (blue), within-subject multivariate testing (MVT-WS) (green), and hybrid testing (HT) are well behaved. (D) UVT-SC (blue) pays the cost in power relative to UVT-UC (red). Compared to UVT-SC (blue), MVT-WS (green) underperforms when ρ < 0.65 but excels when ρ≥ 0.65. Even though mostly worse than UVT-UC in power, HT (purple) achieves a detection rate that is approximately the higher one between MVT-WS and UVT-SC. The curves in (B), (C) and (D) were fitted to simulated results (plotting symbols) through loess smoothing with the second order of local polynomials.
As a reference, UVT-UC for the main effect (or coincidence) of between-subjects factor Group (whether the two groups have different areas under the curve, , without involving sphericity violation because of a scalar variance–covariance, shows an FPR very close to the nominal significance level of 0.05 (not shown here). In contrast, UVT-UC for the interaction Group:Component (parallelism in profile analysis, testing whether the HDR curves are commensurate or parallel with each other: H0 : β11 − β12 = … = β71 − β72) has a reasonable control for FPR when ρ < 0.2 (no ormild sphericity violation), but becomes increasingly out of control with higher ρ or more severe sphericity violation (Fig. 1C). On the other hand, MVT-WS, UVT-SC and HT perform well in FPR control (Fig. 1C) throughout the whole range of ρ.
With regard to power, all four tests for the interaction effect shows a decreasing trend as ρ (and sphericity violation severity) becomes high (Fig. 1D), which is not unexpected because higher serial correlation leads to more difficulty in untangling the components. UVT-SC achieves roughly the same power when ρ < 0.2, but its power loss worsens with a large ρ. On the other hand, there is a large power disadvantage for MVT-WS even when ρ = 0 compared to UVT-UC and UVT-SC. Its underperformance gradually deteriorates with a large ρ but improve with ρ > 0.3. Around ρ = 0.65, MVT-WS overtakes UVT-SC, and its outperformance expands further and finally exceeds UVT-UC around ρ = 0.87. As HT is conditionally defined in Eq. (5) based on the sphericity measure εHF, its power performance is roughly the higher one between MVT-WS and UVT-SC.
The main effect of Component (or first-order interaction) indicates whether the average HDR curve between the two groups is a flat line or constancy (H0 : β11 + β12 = … = β71 + β72), a special case of hypothesis of parallelism (the average HDR curve parallel to the null). Its simulated results show a similar pattern (not illustrated here) to the second-order interaction effect, Group:Component, in both FPR control and power.
It is of note that our simulation results with an AR(1) correlation structure are not consistent with the previous notion that MANOVA is most powerful when the correlations among the response variables are in the range of (0.4, 0.7) (Tabachnick and Fidell, 2013). Instead MVT-WS underperforms compared to UVT-SC when ρ < 0.65, but MVT-WS (and HT) overtakes UVT-SC in power when ρ ≥ 0.65. In other words, UVT-SC is preferred when the sphericity violation is moderate (e.g., εHF < 0.65), but MVT-WS outperforms UVT-SC when sphericity is severely violated (εHF ≥ 0.65).
Applying 3dMVM to real data
How do the testing approaches (UVT-UC, UVT-SC,MVT-WS, and HT) perform when applied to real data? What does a real dataset reveal about the heterogeneity of the variance–covariance structure in the brain? Does MVT-WS identify any significant regions that would not be detected under UVT? To address these questions, we applied MVM to the data presented in the Introduction section with n =50 (2 groups: 21 children and 29 adults), m = 20 (2 conditions with each having 10 estimates of RT marginal effect) and design matrix X of q = 4 columns in Eq. (1): all ones (intercept or average effect across groups), effect coding for the two groups, the average age effect between the two groups, and the interaction Group:Age (or group difference in age effect). The age values were centered within each group so that the group effect can be interpreted as the difference between the two groups at their respective average age. Runtime was about 90 min using 12 processors on a Linux system (Fedora 14) with Intel® Xeon® X5650 at 2.67 GHz.
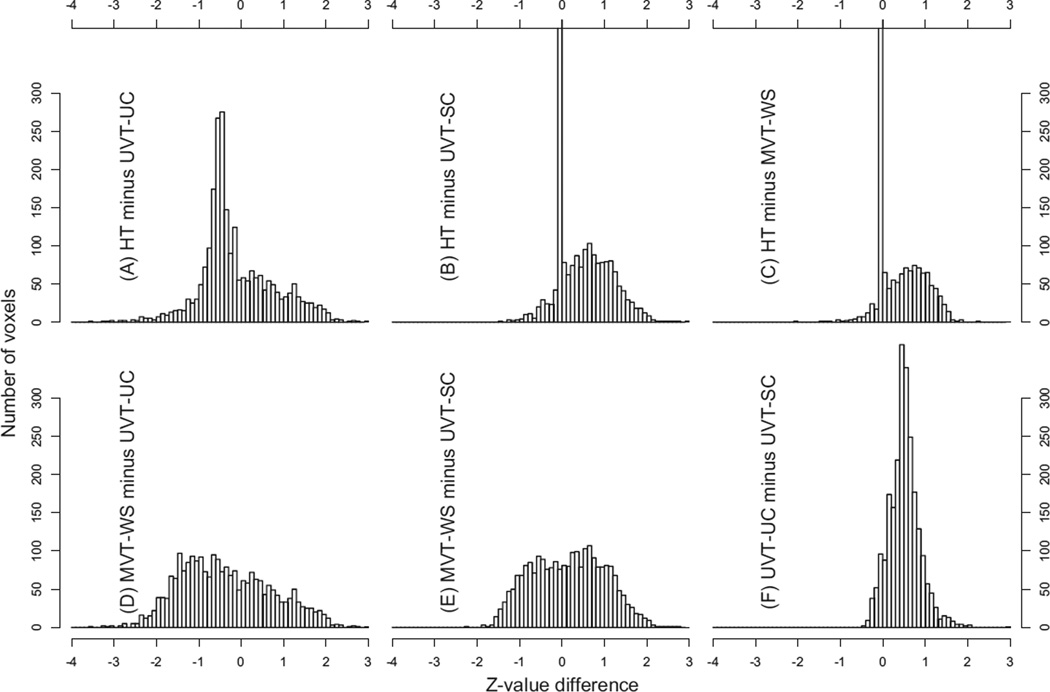
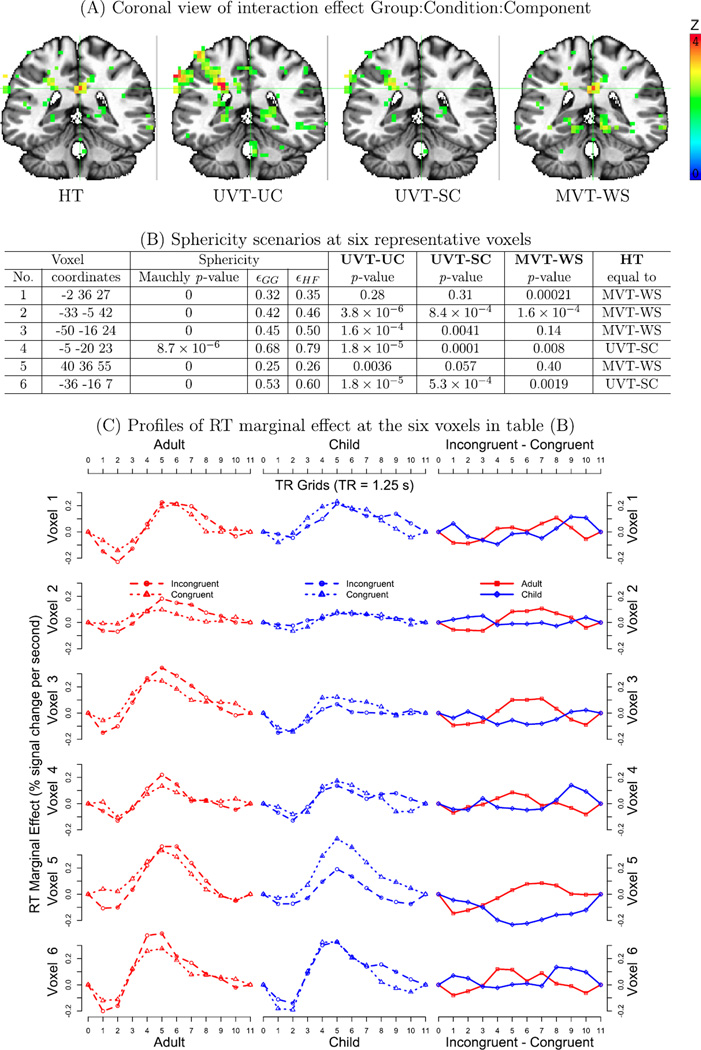
We focused on the three-way interaction Group:Condition:Component that indicated whether the two groups had the same or parallel profile of RT marginal effect differences between the two conditions. Four F-statistics, UVT-UC, UVT-SC, MVT-WS, and HT, for the interaction were obtained and then, due to different degrees of freedom, converted to Z-values for direct comparisons. Their overall performance can be assessed through histograms of pair-wise differences in Z-value (Fig. 2) and a slice of significance map in a coronal view (Fig. 3A). In general, UVT-UC, at the cost of poor control for FPR, showed the highest power among all four tests in almost all regions (A, D, F in Fig. 2). Some exceptions exist; for example, MVT-WS rendered significant results at regions where other tests failed, as shown at the region (crosshair) in Fig. 3A and Voxel 1 in Figs. 3(B and C). The outperformance of MVT-WS is also seen in the voxel count in Figs. 2(D and E). With FPR well-controlled, it is not unexpected to see that UVT-SC achieved lower power than UVT-UC (Fig. 2F; Voxels 2–5 in B and C of Fig. 3). On the other hand, UVT-SC achieved higher power than MVT-WS at some regions (Fig. 2E, Voxels 3–5 in B and C of Fig. 3) while at other regions MVT-WS outperformed (Fig. 2E; Voxels 1 and 2 in Figs. 3(B and C)). HT largely takes its statistical value from either UVT-SC or MVT-WS based on the severity of sphericity violation in the contingency table (Eq. (5)). However, as indicated at Voxels 2, 3, and 5 in Figs. 2(B and C) and in Figs. 3(B and C), the significance level of HT is not always the higher value between the two. Even though the simulations indicated that HT had equal or higher power than UVT-SC and MVT (Fig. 1), it does not necessarily render equal or higher significance when applied to each specific dataset due to the nature of randomness. The voxels in Fig. 3 were selected from clusters, not isolated voxels, that survived a liberal voxel-level significance of 0.05. In addition to statistical significance, the spatial extent and the profile patterns of the RT colorbar marginal effects were consistent across voxels within each cluster (not shown here) as well as across regions (Fig. 3C), providing additional evidence for the existence of the effects under investigation. One observation of interest is that, when the sample size is proper, MVT and UVT usually converge; however, discrepancies of significance inference between UVT and MVT typically occur when the sphericity violation is severe (e.g., εHF < 0.55) as shown at Voxels 1, 3, and 5. This revelation underscores the importance of combining both UVT and MVT in data analysis.
Fig. 2.
Histograms of Z -value differences at 2383 voxels (resolution: 3.5 × 3.5 × 3.5 mm3) that reached the voxel-wise significance level of 0.05 for HT. The Z-values were converted from the original F-values with different degrees of freedom. Six pairwise comparisons are shown: (A) HT and UVT-UC, (B) HT and UVT-SC, (C) HT and MVT-WS, (D) MVT-WS and UVT-UC, (E) MVT-WS and UVT-SC, (F) UVT-UC and UVT-SC. Cell width is 0.1 in Z -value difference. The spikes in (B) and (C), with a height of 958 and 1437 voxels respectively, were chopped off for a comparable representation among the histograms, and they indicate that little difference existed between the two tests at most voxels.
Fig. 3.
(A) Four tests are illustrated on a coronal slice (Z = 27) with colored voxels at the 0.05 level. No multiple testing correction or cluster-level thresholding was applied. Voxel 1 in (B) and (C) is located at the crosshair. The left brain is shown on the right. (B) The Mauchly test, sphericity measures (εGG and εHF) and the four testing statistics are shown at six voxels from the three-way interaction. The extent of sphericity violation is broad among the six voxels. (C) RT marginal effects in condition comparisons (first two columns) and in the three-way interaction are plotted at the six voxels in (B) with each profile spanning over 11 TRs or 13.75 s. In addition to the statistical significance presented in (B), the RT marginal effect profiles of each group at both conditions and the three-way interactions provided strong evidence for the existence of the associated effects at these voxels.
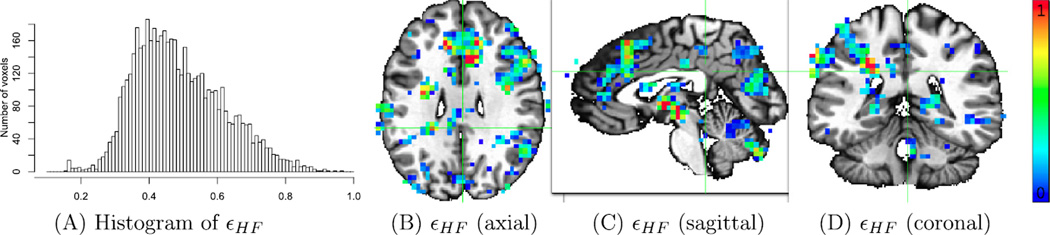
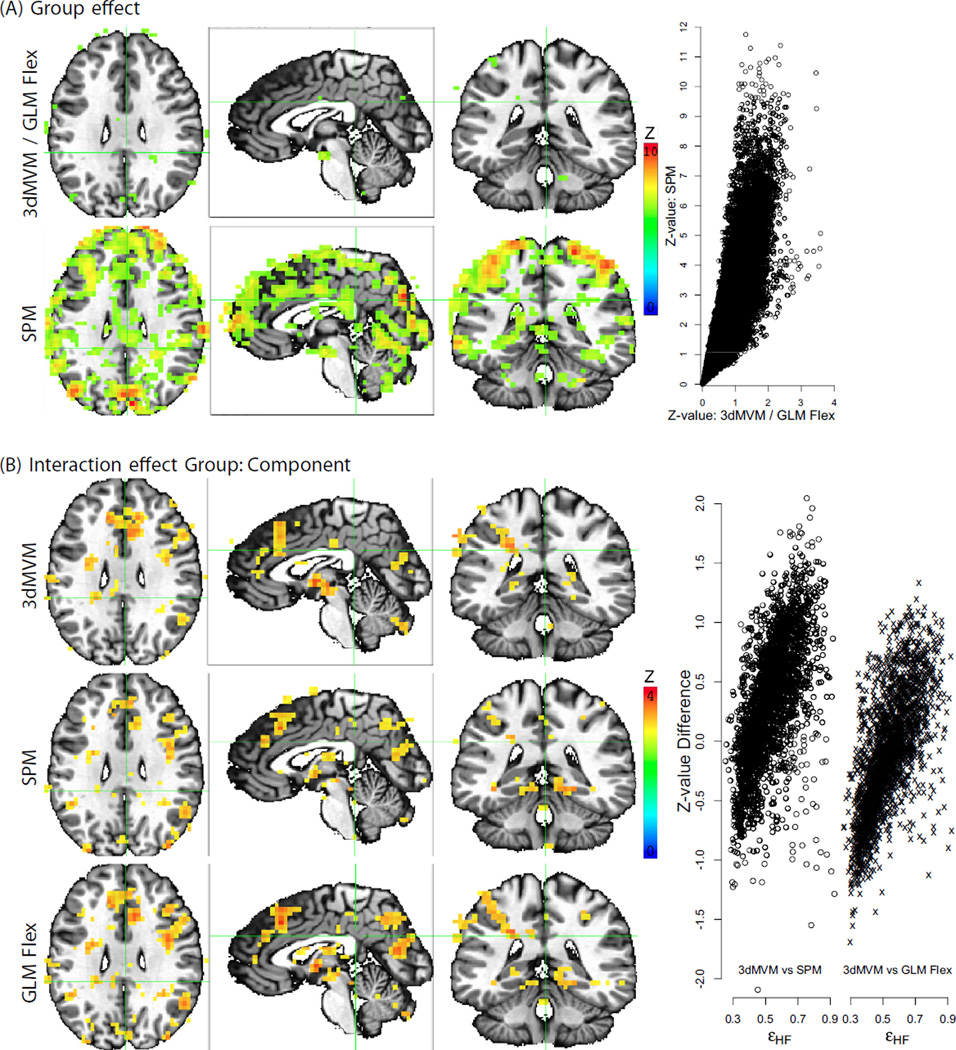
One popular practice in correcting for sphericity violation is to assume a uniform correlation structure within and across the brain regions, and thus the structure could be estimated by pooling all the voxels among those regions that reach some level of significance (Glaser and Friston, 2007). However, to our knowledge the uniformity assumption has not been empirically tested. With MVM and our empirical data, we found substantially broad variations in the violation severity from the perfect sphericity (Fig. 3B; Fig. 4) both within and across regions, raising questions about the brain-wide pooling strategy. Per reviewer's request, we performed direct comparisons of the MVM approach to the modeling strategies adopted in SPM and GLM Flex. To do so, we had to reduce the original model by removing two explanatory variables, quantitative covariate RT and within-subject factor Condition, through averaging the two conditions. In such a mixed two-way ANOVA with one between-subjects factor Group and one within- subject factor Component, we compared the three omnibus tests: main effects for Group and Component, and their interaction. As shown in Fig. 5A, 3dMVM and GLM Flex provided identical Group effect except for differences ascribable to numerical roundoff errors. However, SPM's Flexible Factorial Design returned largely inflated statistical significance values resulting from the incorrect implementation of the F-statistic for the between-subjects effect (McLaren et al., 2011) with a smaller denominator (MSS (A) instead of MSBS (A)) as well as larger number of degrees of freedom (432 instead of 48) for the F-statistic of the group effect (the between-subjects factor A in Eq. (7) of Appendix A). On the other hand, the three programs rendered similar interaction effect Group:Component (Fig. 5B) at a liberal voxel-wise significance level of 0.05. However, closer comparisons show that the effect significance differed between MVM and the other two programs. This is the result of the differing assumptions about the spatial distribution of the variance–covariance structure. The amount and direction of bias were strongly correlated with the extent of sphericity violation relative to the average as demonstrated in the scatterplot of Fig. 5B.
Fig. 4.
Spatial in homogeneity of εHF values is illustrated through a histogram (A), an axial (X= − 2) (B), a sagittal (Y = 36) (C) and a coronal (Z = 27) view (D) at 5192 voxels (resolution: 3.5 × 3.5 × 3.5 mm3) that reached the significance level of 0.05 for UVT-UC. Cell width in (A) is 0.01. The distribution of εGG (not shown here) is similar. Notice that 1/9 ≤ εGG ≤ εHF ≤ 1 (Appendix D), mean(εGG) = 0.439, sd (εGG) = 0.105, mean (εHF) = 0.488, sd(εHF) = 0.130. Coronal view (D) and the colored clusters are the same as in Fig. 3A. Red, green and blue in (B) and (C) correspond to no, mild, and severe violation of sphericity assumption. A substantial amount of variability in εHF exists within and across brain regions; that is, the severity of sphericity violation is spatially heterogeneous.
Fig. 5.
Performance comparisons on a two-way ANOVA with one between-subjects (Group) and one within-subject (Component) factor among three modeling strategies: 3dMVM in AFNI, Flexible Factorial Design in SPM (SPM8 v5236), and Matlab package GLM Flex. The original F-statistic values with different degrees of freedom were converted to Z -values for direct comparisons. The color-coded Z -value maps are thresholded at the voxel-wise significance level of 0.05 and shown at the same focus point of (X, Y, Z) = (−2, 36, 27) as in Figs. 3A and 4. (A) 3dMVM and GLM Flex rendered virtually identical group effect while Flexible Factorial Design dramatically inflated the significance due to the incorrect formulation of F-statistic for the between-subjects effect: both the denominator (MSS (A) versus MSBS (A) for factor A in Eq. (7) of Appendix A) and the associated degrees of freedom (432 versus 48) were impropriate. The inflation is also demonstrated in the scatterplot of the Z -values in the brain on the right-hand side. (B) The three programs gave similar interaction effect, but the subtle differences lie in the biases of Flexible Factorial Design and GLM Flex on the significance. UVT-SC was adopted here in 3dMVM for comparisons. As shown in the scatterplot of Z-value differences, the biases at each voxel are positively correlated with the deviation of sphericity violation from the average among the selected voxels. The slight differences between Flexible Factorial Design and GLM Flex were likely due to different selected voxels for the pooling process of the correlation structure.
Discussion
Group analysis is an essential part of neuroimaging investigations to make generalizations. As a routine step, most studies can be analyzed through Student’s t-tests or simple ANOVAs. The majority of researchers are trained in the conventional ANOVA-style, and are thus familiar with such procedures. In some situations, it might be more straightforward to adopt a piecemeal strategy and parse the individual Student’s t-tests than to utilize one full model. Under other circumstances, Student’s t-tests and simple ANOVAs no longer meet the needs as they did in the early days of neuroimaging, and sophisticated modeling strategies are needed. Nowadays a longitudinal study scenario would not be farfetched with seven explanatory variables, including four between-subjects factors: sex (male and female), disease (patient and control), genotypes (two homo-and one hetero-zygote), multiple sites/scanners; two within-subject factors: condition (positive, negative and neutral stimuli), clarity (clear and vague); and one quantitative covariate: age. Even if this scenario could be analyzed through a piecemeal fashion (without modeling the age effect), one would be inundated by the sheer number (~200) of individual t-tests.
There are some reasons why it is advantageous to adopt the traditional approach of one integrative model that incorporates all the explanatory variables. When numerous explanatory variables are involved, the omnibus F-test for an intersection (or global null) hypothesis regarding a main or interaction effect offers the safeguard of weak family-wise error (FWE) rate control, a minimum requirement in such a multiple comparison scenario relative to the strong FWE correction for the post hoc tests. In addition, the omnibus F-statistic provides a search guide for particular comparisons without exhaustively enumerating all possible combinations. Another benefit is that, compared to the piecemeal tests involving one group, merging all the data into one comprehensive model may increase statistical power by enlarging or borrowing sample sizes across groups. Lastly, due to sampling constraints or other reasons, it is sometimes desirable to control or account for confounding effects such as age and IQ, and such quantitative covariates are easier and more economical (with lower cost in degrees of freedom) to handle in a full model than the piecemeal fashion. Traditional ANOVAs, as adopted in 3dANOVA, 3dANOVA2, 3dANOVA3 and GroupAna in AFNI, are performed through frugal computations of SS terms for the numerator and denominator of each F formulation. Their applications are limited from the following perspectives: A) Each specific model is associated with a unique set of F-ratios based on the numbers of factors and factor types (between- or within-subject), which is a considerable deterrent when extending the modeling scope; B) Quantitative covariates cannot be incorporated; C) A rigid data structure requires an equal number of subjects across groups; D) Sphericity testing and correction for its violation are generally not available under the SS computation schemes. In contrast, the univariate GLM approach offers a more versatile and inclusive platform for a full model strategy. In addition to being capable of seamlessly incorporating quantitative covariates, GLM has the potential to analyze cases with a large number of explanatory variables. This modeling strategy has been implemented in programs such as 3dRegAna in AFNI, GLM of FEAT in FSL, Full and Flexible Factorial Design in SPM, and the stand-alone programGLM Flex. However, their applications are hindered by three limitations. The pairing of numerator and denominator in each F-statistic is tedious, and depends on the variable type (between- or within-subject factor, or quantitative covariate) as well as on the number of explanatory variables. This UVM limitation prevents the strategy from extending to an arbitrary number of variables. Furthermore, there is no direct correction available for sphericity violation under the univariate GLM. Lastly, it is difficult to model a quantitative covariate with a within-subject factor.
In the literature, modeling a quantitative covariate is usually restricted to standard multiple regression (in the absence of between-subjects factors) or ANCOVA with between-subjects factors but no within-subject factors. It is rare to see discussions about modeling a quantitative variable in the presence of one or more within-subject factors. One suggestion (Rutherford, 2001) is that one can break down, for example, a mixed two-way factorial ANCOVA (one between-and one within-subject factor plus a quantitative covariate) into two separate analyses. As the quantitative variable would not have any impact on the comparisons among the levels of the within-subject factor, it would be unnecessary to consider modeling such a quantitative covariate when testing the within-subject factor effects. However, the inclusion of a quantitative explanatory variable is not just important for improving a specific effect estimate, but also for increasing the statistical power by accounting for knowable source of variability. On the other hand, if the correlation between the levels and the quantitative covariate is not a nuisance but a goal, a workaround solution proposed was to reduce the within-subject factor into multiple pairwise comparisons among the levels, and then run traditional ANCOVAs on each comparison. However, such practice presumes that the correlation between each level and the quantitative covariate is constant across all levels, a presumption that may not necessarily hold unless tested, unlike in MVM where each level is treated as a response variable with a separate covariate effect. Lastly, the piecemeal approach is suboptimal and may become unbearably cumbersome as the number of variables increases.
Due to some flaws in software design or implementation, misuses or outright model misspecification is often seen even in seemingly simple analyses (McLaren et al., 2011). For example, effect estimates from multiple runs or sessions from each subject are easily and incorrectly entered as independent samples in t-tests; two-sample t-tests and between-subjects ANOVAs (e.g., "full factorial design") are mistakenly used to handle situations involving a within-subject factor; a mixed ANOVA with one between-and one within-subject factor implemented in univariate GLM (e.g., "flexible factorial design") is inappropriately adopted to make inferences about the effect of the between-subjects factor or the effect at a specific factor level; improper analysis for a two-or three-way within-subject ANOVA is performed in GLM (e.g., "flexible Factorial Design") where no error differentiation is considered. In contrast, an interface that requires the user to explicitly specify the structural model for the data in terms of the explanatory variables (in symbolic form) has the potential to force clarity into the statistical analysis choice.
Overview of the MVM methodology
Multivariate GLM, as a progenitor of the theory of algebraic invariants, has been available for over 50 years, but its wide applications are generally discouraged (Tabachnick and Fidell, 2013). A few reasons have contributed to its unpopularity in general. Compared to UVM, MVM’s theory is less tractable, and is generally not covered in basic statistics education. In addition, most multivariate models can also be formulated under the univariate platform, but the multivariate approach is generally considered not as powerful as the latter. Also, the various testing statistics under MVM are not as well-behaved or as simple as the popular t-and F-statistics. Its high computational cost is another hindering factor cramping its wide applicability. Nevertheless, the MVM provides two irreplaceable advantages, one in implementing the traditional UVT methodology, and the other in offering MVT as an auxiliary test. Its role as a scaffold allows for any number of within- subject factors under UVT and further augments the UVT by the capability to correct for sphericity violation. Its adaptive flexibility in capturing the correlations among the levels of a within-subject factor under MVT complements UVT. Specifically, the deviations among the levels of a within-subjects factor are traditionally entered into UVM as random effects, leading to a parsimonious assumption for the covariance structure. In contrast, in MVM those deviations are treated as simultaneous response variables, allowing for estimating the correlations.
We have implemented the MVM methodology as an alternative to the univariate GLM in the program 3dMVM in AFNI. A flattening process transforms the levels for each within-subject factor as well as the level combinations across multiple within-subject factors into simultaneous response variables, and separates the within-subject factors from the between-subjects variables on the two sides of the MVM system. The platform renders the same results as the univariate GLM when no within-subject factors are involved in the hypothesis. On the other hand, when an omnibus hypothesis is associated with one or more within-subject factors, two types of testing, MVT-WS and UVT, can be performed through a folding process. The former is constructed through proper specifications of L, R, and C in general linear hypothesis (Eq. (3)) in which the variance–covariance structure Σ is estimated instead of being assumed spherical. Similar to the univariate GLM, the impact of unequal numbers of subjects across groups would be limited by the degrees of freedom and the broken orthogonality, not by modeling capability. It is the separation between within-and between-subjects variables and the construction of the response transformation matrix R in Eq. (3) that allow for easy implementation with any number of explanatory variables, and the user is relieved of directly dealing with dummy coding. In addition, the Mauchly test for sphericity violation and the correction for over-liberal F-tests in UVT are readily incorporated. Among the four F-tests (UVT-UC, UVT-SC, HT, andMVT-WS) implemented in 3dMVM for each omnibus hypothesis that involves a within-subject factor, the latter three tests possess well-behaved control of FPR. Consistent with previous studies (O’brien and Kaiser, 1985; Maxwell and Delaney, 2004), our simulations and analysis results with real data indicated that there is no single preferable testing method that uniformly achieves the highest power. It is the combination of UVT and MVT that not only expands the modeling capabilities but also benefits in combined detection power (Barcikowski and Robey, 1984; Looney and Stanley, 1989). Their complementary role is evidenced by the situations when one test but not the other reveals significance, which usually occurs when sphericity is severely violated. For example, Voxel 1 in Fig. 3 illustrates the importance of significance detection through MVT-WS that would not be revealed through the univariate GLM or UVT.
It is more often the rule than the exception that the variance–covariance matrix Σ for a within-subject factor with more than two levels is not spherical. The data-driven approach of MVM for estimating Σ is more adaptive to allow for any correlation pattern, but pays the price in statistical power when sphericity violation is negligible or moderate; the power loss is reflected in the reduction of denominator degrees of freedom for the F-statistic (cf., the corresponding UVT F-statistic). On the other hand, MVT-WS is preferred when the violation is severe. In contrast, UVT makes a parsimonious assumption about spherical structure Σ, and produces the same results as the univariate GLM. However, UVT under the MVM platform excels in two aspects relative to the univariate GLM. First, sphericity testing is available, and the violation, if significant, can be corrected through adjustment in the degrees of freedom. Secondly, incorporating a quantitative explanatory variable in the presence of a within-subject factor is available under MVM but not under the univariate GLM.
In future work, we plan to extend the MVM framework to two situations. First, when the BOLD response shape is captured through multiple basis functions, MVM offers further detection power than what has been demonstrated here in the real data application. The second scenario is that multiple response variables in different modalities (or units) can be readily analyzed in the traditional MVT fashion. For example, connectivity measures of resting state at various seed regions are truly simultaneous response variables and can be formulated in an MVM system to test the centroid. Similarly, a correlation (or connectivity) measure under resting state, fractional anisotropy on the white matter tract, gray matter volume, and task-related BOLD response from MRI data would constitute a four-variate model.
Comparisons with other implementations in neuroimaging
For within-subject experiment designs, there are three modeling approaches: UVM, MVM, and linear mixed-effects modeling (LME). Theoretically, LME (e.g., as implemented in the AFNI program 3dLME) is considered the most inclusive platform, and UVM naturally generalizes to LME that is advantageous under several circumstances (Bernal-Rusiel et al., 2012; Chen et al., 2013), including missing data, modeling quantitative covariates that vary within-subject (e.g., RT measures under positive, negative and neutral conditions), and data with genetic information. However, the LME framework becomes lackluster in practice especially when dealing with conventional AN(C)OVAs for two reasons. First, its flexibility to model the variance–covariance structure excels in model building and comparison, but becomes impractical in the situation of massively univariate modeling. In addition, the difficulty in assigning degrees of freedom leads to its heavy reliance on asymptotic properties. When the sample size is not large enough, it is unrealistic to adopt numerical approximations such as bootstrapping and Markov Chain Monte Carlo (MCMC) simulation sampling for neuroimaging data analysis.
The Matlab package GLM Flex, FSL (GLM in FEAT) and SPM (Full and Flexible Factorial Design) all provide the univariate GLM methodology. Among them, GLM Flex is the closest in capability to 3dMVM with the following differences: a) 3dMVM canmodel quantitative covariates in the presence of within-subject factors; b) Symbolic representation for factor levels provides a more user-friendly interface for both input and output; c) 3dMVM provides voxel-wise sphericity correction instead of assuming one variance–covariance structure over the whole brain; d) No upper bound exists in 3dMVM upon the number of explanatory variables, provided that the sample size is appropriate (e.g., at least five observations per variable). By way of illustration, neither FSL nor SPM can analyze the dataset presented in the Applications and results section. In addition, their implementations are problematic when a within-subject factor is involved in a data structure with two or more factors due to the undifferentiated pairing for the F-statistic denominator that can lead to higher FPR than intended. Specifically, the SS for errors is adopted for all the omnibus F-statistic formulation, thus only the F-statistics for the effects associated with the highest order interaction among the within-subject factors are appropriately constructed. For instance, in the presence of a within-subject factor, inferences regarding a between-subjects factor are invalid (McLaren et al., 2011); similarly, a two-way within-subject ANOVA, when analyzed in SPM or FSL, would lead to inflated significance for the main effect for both factors. For the same reason, testing for most post hoc hypotheses under the SPM and FSL implementations is equally problematic (e.g., the effect of positive condition in the control group in a two-way mixed ANOVA).
Furthermore, perfect sphericity is assumed in FSL, while SPM and GLM Flex presume a uniform variance–covariance structure in the “activated” regions, which is estimated through pooling (Glaser and Friston, 2007). First, the spatial homogeneity presumption is unrelated to the formulation of F-statistics in UVT (McLaren et al. 2011). Even if the whole brain shares the same correlation structure, the denominator for the F-statistic of a between-subjects factor, as well as the degrees of freedom, should still be properly specified, as shown in Appendix A. Additionally, the power (or sensitivity) consideration in statistic selection should be based on a solid ground, not at the sacrifice of proper FPR controllability. Furthermore, if the sphericity violation is spatially homogeneous in the brain, this pooling method offers an economical approach. However, our empirical data suggested that such a presumption does not hold well (Fig. 4): substantial variability in sphericity violation exists within and across regions. If this violation in a region happens to be around the global average, the correction method may work reasonably well for that region. However, a cluster whose violation severity is much higher (mostly the warm colors in Figs. 4B–D and the scatterplot in Fig. 5) would suffer from an unnecessary penalty in power. On the other hand, those regions with much lower violation (mostly the blue voxels in Figs. 4B–D and the scatterplot in Fig. 5) would be unjustifiably rendered with inflated significance. The voxels selected in SPM and GLM Flex for spatially averaging of the variance–covariance structure are only limited to those whose significance reaches a threshold (e.g., 0.001), but the estimated variance–covariance structure is then applied to all the data, causing further biases across the whole brain. The biased statistical significance introduced by this procedure may impact the characteristics of clusters (e.g. peak, shape and size) as well as their survival for multiple testing correction – without extensive testing (beyond the scope of this paper) it is impossible to judge the import of this effect. Lastly, the smoothing process of the variance–covariance structure among the selected voxels is typically not accounted for in the FWE correction.
Our simulation results showed that the MVM approach is robust at the voxel level in terms of FPR control and power achievement, and the spatial extent of noise can be reasonably handled through the FWE correction. In the majority of FMRI packages, spatial smoothing during preprocessing is used to improve the signal-to-noise ratio, and the smoothness of the noise is taken into account in multiple testing corrections for FWE. Furthermore, paired t-tests (a special one-way within-subject ANOVA with a 2 × 2 variance–covariance matrix) are performed voxel-wise without taking into account the spatial structure in the brain among all packages. One may argue that the amount of noise embedded in the FMRI data justifies the pooling process under the presumption of uniform correlation structure across the brain. As the correlation structure demonstrates the extent of synchronization across the factor levels (e.g., a subject who responds stronger to the positive condition relative to the group average may also have a higher response to the negative and neutral conditions), the uniformity presumption boils down to the following question: is the synchronization the same across the whole brain? Even though our evidence of nonuniform correlation (Fig. 5) could be discounted by the fact that FMRI data are noisy, and it may well be nearly impossible to resolve with full certainty regarding the uniformity presumption in the absence of a gold standard with real data (How to measure the robustness? Are more identified blobs better or worse?), there is no compelling evidence to suggest the validity of the presumption. A large gap exists between the presumption and the fact that FMRI data are noisy: noisy data do not translate to a uniform correlation structure. We believe that the principle of parsimony (Occam's razor) favors a method with less stringent assumptions. In light of these considerations, we argue that the voxel-wise sphericity correction for UVT stands on firmer ground than one with a stronger presumption that is difficult to validate with real or simulated data (What spatial distribution should one assume about the correlation structure in simulations?). The associated computational cost is well worth it, to ensure reasonably accurate statistical inferences.
Current limitations of MVM
3dMVM is computationally inefficient compared to the SS method; most analyses take half an hour or more. In addition, there are other limitations. a)With the parsimonious assumption of sphericity, the univariate GLM pays a low price in degrees of freedom through pooling the variances across the levels of a within-subject factor. In contrast, those levels are treated as separate response variables under MVM with the requirement (Eq. (2)) dictating that the total number of subjects be at least greater than or equal to the total number of simultaneous and explanatory variables. For example, suppose that the BOLD response for each of three emotion conditions is modeled by 8 basis functions. With one group of subjects, the MVM platform needs at least 3 × 8 + 1=25 subjects. Such a stringent requirement is not needed in the univariate GLM. b) Within-subject quantitative covariates cannot be modeled in 3dMVM. For example, suppose that one considers the average RT under each of the three emotion conditions as an explanatory variable at the group level. Such a scenario would have to be handled through LME (Chen et al., 2013). c) Even though unequal numbers of subjects are not an issue under MVM, a subject with missing data would have to be abandoned in the analysis. For example, if one subject performed positive and neutral, but not negative, tasks, the subject’s available data could not be utilized with MVM but can be utilized with LME (Chen et al., 2013) or through data imputation. d) 3dMVM cannot handle LME models with sophisticated hierarchical data structures such as subjects of monozygotic or dizygotic twins, siblings, or parents from multiple families (Chen et al., 2013).
What if a cluster fails to survive rigorous corrections?
There are strong indications that a large portion of activations are likely unidentified at the individual subject level due to the lack of power (Gonzalez-Castillo et al., 2012). The detection failure (false negative rate) at the group level would probably be equally high, if not higher. Even though most scientific investigations place a heavily-lopsided emphasis on the FPR controllability, the sensitivity or power is the primary focus under some circumstances, such as pre-surgical detection where the efficiency is usually less than 10% (Button et al., 2013). Several possibilities may lead to a cluster not achieving the desired significance at the group level under a rigorous procedure: a) To reach a specific power level, a huge number of subjects are usually required, which most studies lack due to financial and/or time costs; b) Spatial alignment is composed of multiple steps including cross-TR, cross-session, cross-modality and cross-subject components, increasing the chance of misalignment. Suboptimal or even erroneous alignment procedure surely would have a big impact on the power performance at the group level; c) Variations in response magnitude or signal-to-noise ratio across regions as well as variations in spatial extent (region size) may lead to different efficiency in activation detection across regions. Intrinsically small response magnitudes or small regions, such as the amygdala, require a smaller voxel-wise p-value to survive multiple testing correction compared to their larger counterparts, which may not be always tenable. The small volume correction (SVC) method is not always a legitimate solution, especially when other regions are of interest at the same time. d) If a two-tailed test, when appropriate, is strictly performed instead of two one-tailed tests,1 or if both multiple testing correction for the same hypothesis and multiple comparisons correction for different hypotheses are rigorously executed at the same time, many studies would face the power deficiency issue.
Similarly, a region without sphericity correction (e.g., the cluster at the left inferior parietal lobule of Fig. 4D and UVT-UC in Fig. 3A) may survive the FWE correction while those tests under sphericity correction (UVT-SC, HT, and MVT-WS in Fig. 3A) may fail. In other words, the investigator could face a difficult situation between two choices: a statistically rigorous approach leads to results that fail to reach the cluster-level significance, and another approach with invalid presumption (uniform or perfect sphericity) renders easy result reporting. We recommend that the investigator perform the appropriate and rigorous correction, and in the meantime consider the less rigorous results. If clusters that do not survive rigorous corrections do agree with prior evidence (particularly from other modalities) or have substantial effect sizes (e.g., in percent signal change), then the results can be reported with the caveat that they would not survive the proper correction. Such results are still of suggestive value and provide a benchmark for future confirmation. In contrast to the omnipresence, over-obsession and distorted impression of lopsided focus on statistic values only (e.g., color-coded blobs of t-values) in the field, the response magnitude should be presented, providing a solid ground for cross-region comparisons, cross-examinations, replicability, power analysis, and meta analysis across studies (Sullivan and Feinn, 2012). Our suggestion of reporting effect magnitudes is aligned with and complementary to a recent proposal to avoid the misinterpretations of significance maps (Engel and Burton, 2013). For example, as manifested in Fig. 3B, Voxel 5 in the left inferior parietal lobule of Fig. 4D and UVT-UC in Fig. 3A was statistically significant only under UVT-UC at a p-value of 0.0036, marginally significant under UVT-SC (p = 0.057), and not significant under MVT-WS (p = 0.40). The cluster where Voxel 5 resided had a spatial extent of 155 voxels (6646 mm3) at the voxel-wise significance level of 0.05, and it would not survive an FWE correction at the whole brain level based on Monte Carlo simulations, which requires a minimum cluster size of 247 voxels (10,590 mm3) with an FWHM of 10 mm. One could easily dismiss the reliability of the cluster purely based on the stringent statistical thresholding as well as the fact that sphericity correction was not performed. However, if one examines the substantial effect magnitude and the similar profiles and patterns with other regions (Fig. 3C), it is hard to fully deny the suggestive value of reporting the cluster together with its effect sizes and profiles.
Conclusion
The MVM scheme provides a unified and inclusive platform that enables us to offer a comprehensive alternative to univariate GLM typically encountered in neuroimaging group analysis with four tests: within-subject multivariate testing, univariate testing with and without sphericity correction, and hybrid testing. Our implementation of MVM provides a unique program 3dMVM with modeling capabilities beyond the current packages. Its interface is easy-to-use, and allows the user to specify models and data structure through symbolic representations. In addition to handling the traditional univariate GLM, it can analyze the situations where there are a large number of explanatory variables or when a quantitative covariate is involved in the presence of one or more within-subject factors. As the severity of sphericity violation is usually inhomogeneous across the brain, 3dMVM offers a rigorous correction method at the voxel level.
Highlights.
AN(C)OVA can be analyzed via multivariate modeling.
There is no limit on the number of explanatory variables.
Quantitative covariates can be modeled in the presence of a within subject factor.
Sphericity violation can be corrected at the voxel level.
Model and all tests can be specified via symbolic labels.
Acknowledgments
Our work benefited significantly from the statistical computational language and environment R, its many packages, and the support of the R community. All the plots were created in R using the base graphics library. Special thanks are due to Henrik Singmann for his assistance in the technical details of the R package afex.We would also like to thank Donald McLaren for his help in running SPM and the GLM Flex package. The research and writing of the paper were supported by the NIMH and NINDS Intramural Research Programs of the NIH/HHS, USA.
Appendix A. UVM approach to AN(C)OVA through GLM
The univariate modeling (UVM) approach for AN(C)OVA or GLM involves one response variable, which is the brain response magnitude in the context of neuroimaging data analysis. Suppose that one is interested in teasing apart the effects on the BOLD response among q quantitative covariates, one between-subjects factor A, and one within-subject factor B. The relevant effects can be formulated as a cell means model,
| (6) |
where βi(j)k is the i th subject’s effect estimate (e.g., BOLD response) at the j th level (group) of factor A and k th level of factor B, xi(j)h and αh are the i th subject’s value of the h th explanatory variable and its associated group effect, , and are respectively the fixed effect at the j th level of factor A, the fixed effect at the k th level of factor B, and their interaction effect, bi(j) is a random effect term, indicating the deviation of the i th subject at the j th level of factor A from all the fixed effects, and δi(j)k represents the random error associated with the i th subject at the j th level of factor A and the k th level of factor B. The index notation i(j) emphasizes that each subject is nested within a specific group. For simplicity, we assume a balanced design with equal number of subjects across groups. i = 1, 2,…, n ; j = 1, 2,…, a ; k = 1, 2,…, b.
Subjects in the model (Eq. (6)) are sometimes considered the levels of a random factor S. There are no random effects associated with those between-subjects variables (factors or quantitative measures) because each subject takes only one value for each such explanatory variable. In contrast, each subject is measured as many times as the number of levels for each within-subject factor; therefore, the random term, bi(j), indicates the deviation of the i th subject from the respective fixed effects, , and . It is noteworthy that no direct random effect is included for because such an interaction effect between factor B and subjects S cannot be differentiated from the residual term δi(j)k, unless there are multiple measures from each combination.
Without the presence of quantitative covariates (q = 1 and xi(j)1 = 1), the model (Eq. (6)) is traditionally called a mixed factorial two-way ANOVA. To obtain the F-statistic for each fixed effect in the ANOVA frame-work, one pairs an appropriate variance source as numerator with another as denominator. Each variance source can be explicitly expressed as the mean squares (MS), which is the sum of squares (SS) for the errors associated with each fixed effect, adjusted by their respective degrees of freedom. More specifically, the F-statistics for main effects of factors A and B and their interaction in a mixed factorial two-way ANOVA (Eq. (6) with q =1) can be constructed as (Neter et al., 1996)
| (7) |
where
| (8) |
In the absence of multiple measures from each combination, MSBS(A) is the same as MSE, the mean squares of the errors. The nice feature about the explicit expression of the MS terms is that they can be numerically hard-coded into a program through the summation of data and their squares respectively, leading to highly efficient computations involving only simple and direct SS terms. This scheme has been adopted into programs 3dANOVA, 3dANOVA2, 3dANOVA3, and GroupAna in AFNI, and their runtime for FMRI group analysis is typically in seconds. For example, a mixed factorial two-way ANOVA can be analyzed with 3dANOVA3-type 5.
However, the limitations for the direct computation of SS terms are quite obvious. This calculation requires a rigid data structure, and cannot deal with an unbalanced design (unequal numbers of subjects across groups) or missing data. Any quantitative covariates cannot be analyzed under the framework either. The number of factors that can be incorporated in the model is programatically limited. To expand the applicability of the ANOVA platform, one can transform the cell means model (Eq. (6)) into a regression counterpart in which an effect (fixed or random) for a categorical variable is typically dummy coded in the model (or design)matrix. For the convenience of interpretation, we choose effect coding (sum-to-zero or orthogonal contrast) in which the reference (or base) level is set to −1 so that each level other than the reference takes 1 in its associated regressor and 0 otherwise. The intercept α1 is associated with xi(j)1 = 1; when a quantitative covariate is present, α1 illustrates the effect associated with the center value of the variable. Furthermore, α1 can be interpreted as the average effect across the factor levels including subjects. Each other regression coefficient, or bi(j), reveals the corresponding effect relative to the group average, thus effect coding is also called deviation coding. For example, the ANCOVA model (Eq. (6)) can be represented and extended to a GLM or Gauss-Markov setup,
| (9) |
where b is the stacking of all the response variable values. X is assumed of full column rank, and its columns are associated with two categories. First, they include the regressors for the fixed effects. For example, the ANCOVA model (Eq. (6)) can be expressed in Eq. (9) with the fixed-effects columns in X coded by intercept (xi(j)1 = 1), quantitative covariates xi(j)h (h = 2, 3,… q), m − 1 columns for the M groups (levels of factor A), l − 1 columns for the l levels of within-subject factor B, (m − 1)(l − 1) columns for the interaction between factors A and B. Secondly, they may contain the regressors for the random effects: each group is represented through effect coding with as many as the number of subjects in that group minus 1. d is the stacking of error terms that are confounded with the random effects of interaction between factor B and subjects. Another natural extension is that the GLM formulation (Eq. (9)) can be expressed as a special case of LME model (Chen et al., 2013).
Instead of direct computations in the cell means model (Eq. (6)), each SS term can be obtained by solving the full GLM (Eq. (9)) through ordinary least squares (OLS) against the respective reduced model. Specifically, the SS term for the errors for the full GLM (Eq. (9)) is expressed as
| (10) |
where P = X(XTX)−1XT is the orthogonal projection matrix of b onto the space spanned by the columns of X, and In is an identity matrix of size n × n. SSE in Eq. (10) characterizes the data variability in the L2-space that cannot be accounted for by the explanatory variables (or the columns of X) in the full model. When the columns associated with a specific effect (e.g., factor A) are removed from X, the resultant SSE for the reduced (or restricted) model would be higher than the one from the full model, and the incremental (or marginal) SSE captures the contribution in SS attributable to the corresponding effect (e.g., factor A). That is, each of the SS terms (e.g., SSA, SSB, SSAB, and SSS (A)) can be computed using Eq. (10) but with the coding columns (e.g., for A, B, AB, and S respectively) removed from X and then subtracting the SSE for the full model. Such computations in Eq. (10) are apparently not as efficient as the direct formulas (Eq. (8) in Appendix A), and thus the GLM runtime is usually in the order of minutes or longer. However, one advantage of GLM over the direct SS computations is the availability of modeling unbalanced designs. It is of note that, with equal numbers of subjects across groups and with no missing data, model regressors are orthogonal, and the additivity of the SS terms (Eq. (8)) holds for the model (Eq. (6)); that is, the total SS equals the sum of all individual SS terms. Equivalently, the additivity is translated to the orthogonality of the regressors in the GLM (Eq. (9)). An unbalanced data structure (as is the case with missing data) leads to the loss of orthogonality, and the additivity of the SS terms is broken, leading to the sensitivity of the SS terms and thus the F-statistics to the variable orders in the model. This is the source of diverse and controversial adoption of schemes: sequential, hierarchical or partially sequential, and marginal SS computations, also known as types I, II, and III respectively. A second advantage is that quantitative covariates can be modeled in the absence of within-subject factors under the GLM framework, and Eq. (9) reduces to multiple regression or ANCOVA. Within the AFNI package, this is the approach adopted in programs such as 3dttest++ and 3dRegAna. The third advantage of GLM is the flexible choice of explanatory variables and their interactions. For example, if the highest order interaction in the model is deemed nonexistent, it can be removed from the model. The downside of the flexibility is that, similar to the situation of unbalanced design, it leads to the loss of additivity and orthogonality of the SS terms. In contrast, ANOVA is rigid in the sense that all main effects and interactions have to be included in the model and computation even if some effects are deemed not present.
For a two-way mixed factorial ANOVA without multiple measures (cf. Eq. (6) with q = 1 and xi(j)1 = 1), the denominator for the F-statistics of B and AB is the mean squares of errors (MSE), which can be directly computed as in Eq. (10). However, the proper denominator for the F-statistic of the between-subjects factor A is not MSE but MSS (A). Mistakenly using MSE instead of MSS (A) as the denominator creates inflated significance for factor A as clearly demonstrated by McLaren et al. (2011). Such an artificial inflation also occurs when making a post hoc inference for the effect of a specific factor level or the linear combination of multiple levels when their weights do not add up to zero. As the number of within-subject factors increases, each extra factor requires a separate model with unique random effects and separate variance partitioning. Consequentially the pairing for the denominators of F-statistics becomes numerically tedious and even unwieldy for both the direct SS computations and the GLM scheme. It is this challenge that leads to the upper bound of four within-subject factors in the AFNI ANOVA suite. For GLM implementations, only the Matlab package GLM Flex allows for more than one within-subject factor with the capability of modeling up to five fixed-effects variables, and properly handles omnibus testing for between-subjects factors as well as post hoc inferences.
As the complexities of FMRI experiment design and the resultant group analysis deepen, the limitation on the number of variables will become paramount. Another challenge under the UVM platform (both direct SS computations and GLM) is that quantitative covariates cannot be directly modeled in the presence of a within-subject factor. Further- more, whenever there are more than two levels for a within-subject factor, the F-statistics for the main and interaction effects are by default constructed under the sphericity assumption for the variance–covariance matrix and thus inflated. No correction is currently provided in the AFNI ANOVA suite or in FSL. Only SPM and GLM Flex deal with the issue by estimating the variance–covariance matrix under the assumption that all “activated” voxels and regions (e.g., under the voxel-wise significance of 0.001) share the same correlation structure. Such an assumption would only hold if no heterogeneity exists across voxels and regions, and may become questionable in reality. These limitations are some of the motivations that lead to our exploration of the MVM approach for FMRI group analysis.
Appendix B. MVM under a constraint and the associated testing statistics
Just as in univariate GLM, the least squares estimates (LSE) for A and E in the MVM system (Eq. (1)) are (Rencher and Christensen, 2012)
| (11) |
where the quadratic form Q = BT(I − P)B = BT (I − X(XTX)−1 XT)B = BT B ÂT XT B is the counterpart of residual sum of squares (RSS) in UVM, and also paralleling is that P = X(XTX)−1XT is the orthogonal projection matrix that is symmetric and idempotent. In other words, P projects Rn onto the space spanned by the columns of the design matrix X : PB = XÂ, and P(I − P) = 0.
To solve the MVM (Eq. (1)) under the constraint (Eq. (3)), we adopt a two-step procedure, which also demonstrates intuitively the transformation role of R in Eq. (3). First, we consider transforming the response data B in the original MVM system (Eq. (1)) through BR = BR, and solve a new MVM framework,
| (12) |
The resultant LSE solutions are
| (13) |
The original GLT (Eq. (3)) now serves as a constraint or general linear hypothesis,
| (14) |
for the new MVM (Eq. (12)). Following the same algebraic operations as in univariate GLM (Seber, 2008), we obtain the LSE solutions for the MVM system (Eq. (12)) under the constraint (Eq. (9)),
| (15) |
It can be further shown (Seber, 1984) that, under the hypothesis (Eq. (3)), the SSP matrices for the hypothesis and errors are respectively
where Wv (k, Δ) denotes a v-dimensional Wishart distribution with k degrees of freedom and parameter matrix Δ, a generalized version of χ2 (or more generally Γ) distribution. The diagonals of H and E are the SS terms for the hypothesis and errors respectively for the traditional univariate tests. An intuitive connection here based on the transformed system (Eq. (12)) is that H corresponds to the incremental variance–covariance matrix in Eq. (15) relative to Eq. (13) while E is associated with Σ̂R in Eq. (13).
Four versions of testing statistics (Rencher and Christensen, 2012) are typically adopted for the hypothesis (Eq. (3)) through the eigen-values λ1, λ2,…, λr of HE−1,
where det and tr are determinant and trace functions that summarize the sum of squares and the shared variances among the response variables into a scalar, often referred to as generalized sample variance. The Lawley–Hotelling trace can be viewed as the L1-norm of the eigenvalue vector or generalized entropy index GE(1). Roy’s largest root is the L∞-norm of the eigenvalue vector, GE(∞), the spectral or L2-norm ‖HE−1‖2. Wilks’ λ is GE(−1) on (1 + λ1, 1 + λ2,…, 1 + λr) up to a monotone transformation each.
The four multivariate testing statistics are exact tests, but are not equivalent with each other in general. However, when only two groups of subjects are involved, there is only one eigenvalue, so they become equivalent and reduce to Hotelling’s T2. For easier thresholding of significance testing, they can be approximated by F-statistic. As indicators of relationship between explanatory and response variables, they differ slightly in their approaches to aggregating the variabilities across the response variables accounted for by the explanatory variables or under Eq. (3). Roy’s largest root, as the union-interaction principle test, only considers the largest effect on the response variables (or largest loading on the associated eigenvector). The other three are compound tests that involve all the response variables. Equivalent to the likelihood ratio test, Wilks's λ is the most intuitively interpretable with a range between 0 and 1. For example, a small Wilks's λ indicates greater accountability. Specifically, 0 (or 1) means a perfect (or no) relationship between the explanatory and the response variables. And 1 minus Wilks's λ is the multivariate counterpart of coefficient of determination R2 in univariate GLM, showing the proportion of data variability in the response variables that is accounted for by the explanatory variables. The Pillai–Bartlett trace sums over the variances that can be explained by the discriminant variables (or the greatest separation of the explanatory variables), and is considered the most reliable among the four and provides the best protection against false positives when the sample size is relatively small. The Lawley–Hotelling trace represents the most significant linear combination of the response variables. When the sample is reasonably large, the latter three MVT statistics render similar results.
When R = I, the general linear hypothesis (Eq. (3)) corresponds to the conventional multivariate testing (Appendix B). In addition, the eigenvectors associated with λ1, λ2,…, λr are orthogonal with each other, and are the linear combinations of the response variables. Each eigenvalue indicates the amount of variability that can be accounted for by the associated eigenvector.
Appendix C. Examples of formulating GLT matrices
We start with two special scenarios that are the multivariate versions of one- and two-sample t-tests. In the first case of multivariate one-sample test, each subject is measured in Rm, X = 1 n × 1, and A is of size 1 × m. An m-variate analog of univariate one-sample hypothesis can be expressed under Eq. (3) as,
| (16a) |
| (16b) |
This is a one-sample Hotelling’s T2-test, the multivariate analog of the univariate one-sample t-test. The null hypothesis (Eq. (16a)) states that the group centroid is at the origin of Rm.
In the multivariate two-sample case, X and A are of size n × 2 and 2 × m respectively. With effect coding, the hypothesis for group comparison in Rm and its testing formulation under Eq. (3) are respectively,
| (17a) |
| (17b) |
The hypothesis (Eq. (17a)) compares the centroid in Rm between the groups, and its associated test is a two-sample Hotelling’s T2, the multivariate analog of the univariate two sample t-test. One may also perform testing for each group’s effect with respectively
The within-subject MVT (MVT-WS) hypothesis of interest parallel to Eq. (16a) is the factor main effect in one-way within-subject ANOVA,
| (18a) |
| (18b) |
Notice that the response transformation matrix R5 is essentially the effect coding matrix for the within-subject factor under UVM with each column representing the contrast between the first and last levels. This representation also embodies the transformation from the centroid hypothesis (Eq. (16a)) to the main effect hypothesis (Eq. (18a)). Alternatively the namesake for R5 has another perspective: Eq. (18a) can be formulated by transforming the original m response variables to m − 1 variables with each of the first m − 1 response variables subtracting the m-th variable. In other words, after the transformation, Eq. (18a) under the new MVM with m − 1 response variables becomes a conventional multivariate hypothesis with R = Im − 1 for an Rm − 1 centroid: (α1 − αm, α2 − αm,…, αm − 1 − αm) = 01× (m − 1). A generic derivation for the transformation can be found in Appendix B.
Similarly, the MVT-WS hypothesis of interest parallel to Eq. (17a) is the interaction between the factor and the two groups in the mixed factorial two-way ANOVA,
It should be easy now to formulate the MVT-WS version of main effect hypothesis for the within-subject factor (α․1 = α․2= … = α․m) and for the groups (α1․ = α2․) throughL = (1,0), R = R5 and L = (0, 1), R = 1m × 1 respectively. The center dot (·) here in the effect parameter index notations indicates the averaging or collapsing among the levels of the corresponding factor.
The above cases can be naturally extended to the situations with more explanatory variables. For example, a two-way between-subjects ANOVA is a trivial case because of the absence of within-subject factors. Thus the response transformation matrix is scalar, R = 1, and the multivariate model reduces to a UVM system.
For a mixed factorial two-way ANOVA (model (1) with q =1)with between-subjects factor A of a levels and within-subject factor B of b levels, the main effects for factors A and B and their interaction A:B can be tested under MVM through Eq. (3) with the following
where is the effect coding matrix for factor B. And the F-statistics from the above GLTs are equivalent to Eq. (7) if the data structure is balanced.
For a factorial two-way within-subject ANOVA with factors A and B of a and b levels respectively, one can similarly analyze the data under the MVM framework and obtain the MVT-WS results via Eq. (3) with
where and RA : B = R(A) ⊗ R(B) are the effect coding matrices for factor A and interaction A : B respectively.
Appendix D. The Mauchly test and sphericity corrections
The Mauchly test for sphericity verifies whether Σ in Eq. (1) is proportional to identity matrix, and can be performed through (Timm, 2002)
where Ẽ = R̃T ER̃, R̃ is an orthogonormal matrix whose columns are normalized orthogonal columns of the response transformation matrix R in Eq. (3), E is the SSP matrix for the errors, and v is the number of columns in R. W is close to 1 if Ẽ is approximately a diagonal matrix, and – ln W can be approximated by χ2-distribution with a scaling factor. Furthermore, the Greenhouse-Geisser and Huynh-Feldt measures of sphericity can be computed as well under UVM (Keselman et al., 2001),
where 1/v ≤ εGG ≤ εHF ≤ 1 and perfect sphericity corresponds to the upper bound εGG = εHF = 1 and the lower bound instantiates the case when there is one dominating eigenvalue (thus the data can be approximated in one-dimension). The correction for sphericity violation can be performed through multiplying both the numerator and denominator degrees of freedom in the original F-statistic by either εGG or εHF. The Greenhouse-Geisser measure tends to be over-conservative when the violation is not severe while the Huynh-Feldt modification is too liberal when sphericity is significantly violated.
Appendix E
Interface for running 3dMVMProgram 3dMVM is run, for example, on a tcsh terminal with a command script as the following. As in the notional convention in R, the operator * between the variables a and b means a * b = a + b + a : b, while + and : represent addition and interaction among the variables. As in most AFNI program, the specific usage and the options can be found in command 3dMVM -help at the terminal.
| 3dMVM | -prefix | OutputFile | -jobs 8 | \ | ||
| -bsVars | ’Group*Age’ | -wsVars | ’Cond*Component’ | \ | ||
| -qVars | ’Age’ | -SC | -MV | -num_glt 40 | \ | |
| - | ||||||
| -dataTabel | \ | |||||
| Subj | Group | Age | Cond | Component | InputFile | \ |
| S1 | Child | 2.3 | Con | tent1 | S1_Con_t1+tlrc | \ |
| S1 | Child | 2.3 | Con | tent2 | S1_Con_t2+tlrc | \ |
| - | ||||||
| S1 | Child | 2.3 | Con | tent10 | S1_Con_t10+tlrc | \ |
| - | ||||||
| S50 | Adult | −1.9 | Inc | tent1 | S50_Con_t1+tlrc | \ |
| S50 | Adult | −1.9 | Inc | tent2 | S50_Con_t2+tlrc | \ |
| - | ||||||
| S50 | Adult | −1.9 | Inc | tent10 | S50_Con_t10+tlrc |
Appendix F. List of acronyms used in the paper
AN(C)OVA
analysis of (co)variance
- FPR
false positive rate
- FWE
family-wise error
- GLM
general linear model
- GLT
general linear testing
- HDR
hemodynamic response
- HT
hybrid testing defined in Eq. (5)
- LSE
least squares estimate
- MAN(C)OVA
multivariate analysis of (co)variance
- MLE
linear mixed-effects modeling
- MSE
mean squares of errors
- MVM
multivariate modeling
- MVT
multivariate testing
- MVT-WS
multivariate testing for a within-subject effect
- SS
sum of squares
- SSP
sum of squares and product
- SSPE
sum of squares and product for errors
- SSPH
sum of squares and product for the hypothesis
- UVM
univariate modeling
- UVT
univariate testing
- UVT-SC
univariate testing with sphericity correction
- UVT-UC
univariate testing with sphericity uncorrected
Footnotes
Unless the directionality of a contrast is a priori known, the commonly practiced one tailed t-tests are problematic especially when both directions are considered simultaneously in the same study. The Bonferroni method for multiple comparison corrections with two simultaneous one-tailed t-tests is essentially the same as running a two-tailed t-test. The software should not make a decision for the user in terms of one-versus two sided testing, nor should it preclude the user from the proper testing options.
References
- Barcikowski RS, Robey RR. Decision in a single group repeated measures analysis: statistical tests and three computer packages. Am. Stat. 1984;38:248–250. [Google Scholar]
- Bernal-Rusiel JL, Greve DN, Reuter M, Fischl B, Sabuncu MR for the Alzheimer’s Disease Neuroimaging Initiative. Statistical analysis of longitudinal neuroimage data with Linear Mixed Effects models. NeuroImage. 2012;66C:249–260. doi: 10.1016/j.neuroimage.2012.10.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Button KS, Ioannidis JPA, Mokrysz C, Nosek BA, Flint J, Robinson ESJ, Munafò MR. Power failure: why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 2013;14:365–376. doi: 10.1038/nrn3475. [DOI] [PubMed] [Google Scholar]
- Chen G, Saad ZS, Britton JC, Pine DS, Cox RW. Linear mixed-effects modeling approach to fMRI group analysis. NeuroImage. 2013;73:176–190. doi: 10.1016/j.neuroimage.2013.01.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput. Biomed. Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. ( http://afninimhnihgov). [DOI] [PubMed] [Google Scholar]
- De Rosario-Martinez H. phia: post-hoc interaction analysis. R package version 0.1–0. 2012 http://CRANR-projectorg/package=phia. [Google Scholar]
- Engel SA, Burton PC. Confidence intervals for FMRI activation maps. PLoS ONE. 2013;8(12):e82419. doi: 10.1371/journal.pone.0082419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. The correlation between relatives on the supposition of Mendelian inheritance. Philos. Trans. R. Soc. Edinb. 1918;52:399–433. [Google Scholar]
- Fox J, Friendly M, Weisberg S. Hypothesis tests for multivariate linear models using the car package. R J. 2013;5(1):39–52. [Google Scholar]
- Girden E. ANOVA: Repeated Measures. Newbury Park, CA: Sage; 1992. [Google Scholar]
- Glaser D, Friston KJ. Covariance components. In: Friston KJ, editor. Statistical Parametric Mapping. Academic Press; 2007. [Google Scholar]
- Gonzalez-Castillo J, Saad ZS, Handwerker DA, Inati SJ, Brenowitz N, Bandettini PA. Whole-brain, time-locked activation with simple tasks revealed using massive averaging and model-free analysis. PNAS. 2012;109(14):5487–5492. doi: 10.1073/pnas.1121049109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenhouse SW, Geisser S. On methods in the analysis of profile data. Psychometrika. 1959;24:95–112. [Google Scholar]
- Hancock GR, Klockars AJ. The quest for α: developments in multiple comparison procedures in the quarter century since games: (1971) Rev. Educ. Res. 1996;66:269–306. [Google Scholar]
- Haxby JV. Multivariate pattern analysis of fMRI: the early beginnings. NeuroImage. 2012;62(2):852–855. doi: 10.1016/j.neuroimage.2012.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huynh H, Feldt LS. Estimation of the Box correction for degrees of freedom from sample data in randomised block and split-plot designs. J. Educ. Stat. 1976;1:69–82. [Google Scholar]
- IBM Corp. IBM SPSS Statistics for Windows. Armonk, NY: IBM Corp.; 2012. [Google Scholar]
- Keselman HJ, Algina J, Kowalchuk RK. The analysis of repeated measures designs: a review. Br. J. Math. Stat. Psychol. 2001;54:1–20. doi: 10.1348/000711001159357. [DOI] [PubMed] [Google Scholar]
- Looney SW, Stanley WB. Exploratory repeated measures analysis for two or more groups: review and update. Am. Stat. 1989;43:220–225. [Google Scholar]
- Mauchly JW. Significance test for sphericity of a normal n-variate distribution. Ann. Math. Stat. 1940;11(2):204–209. [Google Scholar]
- Maxwell SE, Delaney HD. Designing Experiments and Analyzing Data: A Model Comparison Perspective. 2nd ed. Mahwah, NJ: Lawrence Erlbaum; 2004. [Google Scholar]
- McLaren DG, Schultz AP, Locascio JJ, Sperling RA, Atri A. Repeated-measures designs overestimate between-subject effects in fMRI packages using one error term. 17th Annual Meeting of Organization for Human Brain Mapping; 26–30 June 2011; Quebec City, Canada. 2011. ( http://mrtoolsmghharvardedu/indexphp/GLM_Flex). [Google Scholar]
- Neter J, Kutner M, Wasserman W, Nachtsheim C. Applied Linear Statistical Models. 4th ed. Irwin: McGraw-Hill; 1996. [Google Scholar]
- R Core Team. Vienna, Austria: R Foundation for Statistical Computing; 2013. R: A Language and Environment for Statistical Computing. ( http://wwwR-projectorg/). [Google Scholar]
- Rencher AC, Christensen WF. Methods of Multivariate Analysis. 3rd ed. Wiley; 2012. [Google Scholar]
- Riley RD. Multivariate meta-analysis: the effect of ignoring within-study correlation. J. R. Stat. Soc. Ser. A. 2009;172:789–811. [Google Scholar]
- Roy SN. On a heuristic method of test construction and its use in multivariate analysis. Ann. Math. Stat. 1953;24:220–238. [Google Scholar]
- Rutherford A. Introducing ANOVA and ANCOVA: A GLM Approach. SAGE Publications Ltd; 2001. [Google Scholar]
- SAS Institute Inc. Base SAS® 9.3 Procedures Guide. Cary, NC: SAS Institute Inc.; 2011. [Google Scholar]
- Seber GAF. Multivariate Observations. Wiley; 1984. [Google Scholar]
- Seber GAF. A Matrix Handbook for Statisticians. Wiley; 2008. [Google Scholar]
- Singmann H. afex: analysis of factorial experiments. R package version 0.5–71. 2013 http://CRANR-projectorg/package=afex. [Google Scholar]
- Sullivan GM, Feinn R. Using effect size - or why the P value is not enough. J. Grad. Med. Educ. 2012;4(3):279–282. doi: 10.4300/JGME-D-12-00156.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabachnick BG, Fidell LS. Using Multivariate Statistics. 6th ed. Pearson: 2013. [Google Scholar]
- Tierney L, Rossini AJ, Li N, Sevcikova H. Snow: Simple Network of Workstations. R package version 0.3–12. 2013 http://CRANR-projectorg/package=snow. [Google Scholar]
- Timm NH. Applied Multivariate Analysis. Springer; 2002. [Google Scholar]