Abstract
Background
A simple risk score to predict long-term mortality after percutaneous coronary intervention (PCI) using pre-procedural risk factors is currently not available. In this study, we created one by simplifying the results of a Cox proportional hazards model.
Methods and Results
A total of 11,897 patients who underwent PCI from October through December 2003 in New York State were randomly divided into derivation and validation samples. Patients’ vital statuses were tracked using the National Death Index through the end of 2008. A Cox proportional hazards model was fit to predict death after PCI using the derivation sample, and a simplified risk score was created. The Cox model identified 12 separate risk factors for mortality including older age, extreme body mass indexes, multivessel disease, a lower ejection fraction, unstable hemodynamic state or shock, a number of comorbidities (cerebrovascular disease, peripheral vascular disease, congestive heart failure, chronic obstructive pulmonary disease, diabetes, and renal failure), and a history of coronary artery bypass graft surgery. The C statistics of this model when applied to the validation sample were 0.787, 0.785, and 0.773 for risks of death within 1, 3, and 5 years after PCI, respectively. In addition, the point-based risk score demonstrated good agreement between patients’ observed and predicted risks of death.
Conclusions
A simple risk score created from a more complicated Cox proportional hazards model can be used to accurately predict a patient's risk of long-term mortality after PCI.
Keywords: PCI, follow-up study, mortality, risk score
A number of statistical models and simple risk scores using patient pre-procedural risk factors have been created to predict procedural mortality after percutaneous coronary intervention (PCI) in the hope of being able to risk stratify patients prior to the procedure.1-9 However, no simple risk scores have been created to predict long-term mortality following PCI. Two complicated statistical models have been created in previous studies,10, 11 but in part because of their complexity, they are seldom used clinically. While complex statistical models can be used to predict a patient's risk of death, simple risk scores are more intuitive to clinicians and patients alike for optimal education and procedural recommendations.
In a previous study, we created a simple bedside risk score for predicting in-hospital mortality after PCI.2 In this study, we sought to develop a statistical model and an accompanying simplified risk score to predict long-term mortality following PCI. This risk score for long-term mortality can be easily used to predict a patient's risk of long-term mortality after PCI, and this information is useful in the process of informed consent and as an aid along with other considerations (e.g., patient preferences, CAD burden), in determining the appropriate intervention for patients who are candidates for both PCI and CABG surgery.
METHODS
Databases
The main database used in this study was the New York State's Percutaneous Coronary Intervention System (PCIRS). Established in early 1990s, the PCIRS registers all PCI procedures performed in non-federal hospitals in the State of New York. For each PCI performed, registry data include patient demographics, pre-procedural risk factors, type of procedures and devices, post-procedural complications, and discharge status that are reported by hospitals’ data coordinators to the New York State Department of Health. Submitted data are matched to the State's hospital discharge data to evaluate the completeness of data reporting. In addition, samples of patients’ medical records are reviewed to evaluate the accuracy of patient risk factors and hospitals are asked to resolve any inconsistency identified in the review process
The National Death Index, which records all death certificates in the United State, was used to identify vital status after discharge. Patients’ social security numbers were used to match patients in the PCIRS and the National Death Index. This project was approved by the Institutional Review Boards at the University at Albany, State University of New York and the Pennsylvania State University College of Medicine.
Study Population and Outcome
The study population included all patients who underwent PCI in the 45 hospitals performing the procedures in New York between October 1 and December 31, 2003. This period was chosen because by October 2003 the majority of the PCI patients were treated with DES and long enough follow-up could be achieved. The outcome of interest was mortality after PCI in a follow-up period through December 31, 2008, which was the latest year of data available to us at the time of analysis.
Statistical Analysis
Developing a prediction model
First, the study population was randomly divided into 2 groups, the derivation (n=5948) and validation (n=5949) samples. The data in the derivation sample were used to identify predictors of long-term mortality after PCI using Cox proportional hazards modeling. The candidate variables included demographics, body surface area, body mass index (BMI), left main coronary disease (stenosis ≥ 50%), number of diseased coronary arteries (stenoses ≥ 70% in the left anterior descending artery, left circumflex artery, and right coronary artery or a major branch of those vessels), ejection fraction, history of myocardial infarction (MI), hemodynamic stability, comorbidities (cerebrovascular disease, peripheral arterial disease, congestive heart failure, malignant ventricular arrhythmia, chronic obstructive pulmonary disease, diabetes, and renal failure), history of open heart surgery and PCI and the presence of stent thrombosis (The definitions of the significant risk factors for long-term mortality identified in later steps are listed in Appendix 1). Body surface area, BMI, and ejection fraction were treated as categorical variables by dividing patients into clinical meaningful groups.
For each risk factor, a Cox proportional hazard model was fit using that risk factor as the only predictor in the model. Robust sandwich estimators for standard errors of regression coefficients were obtained to account for the clustering of patients. The significant (P<0.05) predictors in bivariate analyses were then used as candidate variables to develop a multivariable Cox proportional hazards model to identify significant (P<0.05) predictors using a backward-selection approach.12 In this model, the best function of age was determined by testing age as a continuous linear variable and as a spline function. Body surface area, BMI and ejection fraction were treated as categorical variables to make the model more clinically meaningful. Missing values for ejection fraction were first tested as a separate category, and then combined with the reference group since there was no increased risk of death associated with missing values. In addition to the significant risk factors’ independent effects, interactions between age and other significant predictors were tested for significance and none was found to be significant.
Assessing the performance of the prediction model
The data from the validation sample were used to assess the performance of the derivation model. The discrimination of the model was evaluated by calculating C statistics when it was used to predict patients’ risks of death at years 1, 3, and 5 after PCI.13 In addition, the receiver operating characteristics (ROC) curves for the predictions of 1-, 3- and 5-year mortality using the final Cox proportional hazards model applied to the validation sample were plotted and compared to the ROC curves derived using the derivation sample. The calibration of the derivation model was assessed by comparing the observed and predicted mortality rates at years 1, 3, and 5 for each of 10 groups of patients divided equally by the predicted risk of death.14, 15
Then, the discrimination of the final Cox proportional hazards model developed in the previous steps was compared to that of a series of more complicated Cox proportional hazards models developed also using the derivation sample that accounted for possible time-dependent effects of risk factors. This comparison was performed using the data of the validation sample. These time-dependent models consisted of a number Cox proportional hazards models initially fitted for a series of time periods, within 30 days of the procedure, 31 days to 6 months, and every 6-month interval until 5 years after PCI. The period-specific models with similar regression coefficients of risk factors were then combined and the final time-dependent models included 3 time periods, within 30 days, 31 days to 1 year, and later than 1 year after procedure. The C statistics of the final single Cox proportional hazards model were 0.787, 0.785, and 0.773 at years 1, 3, and 5 after procedure, which were similar to their counterparts of 0.779, 0.782, and 0.772 for the more complicated 3 period-specific models. Therefore, it was deemed appropriate to use the simpler model in our analyses.
Developing a risk score
The method suggested by Sullivan et al16 was then used to create a simplified risk score for predicting long-term mortality after PCI. Using the regression coefficient of age in the final Cox proportional hazards model developed from the derivation sample, the constant of the risk score was defined as 5 times the regression coefficient of age (0.0536 × 5 = 0.2680). Then the regression coefficient for each level of every risk factor was divided by the constant (0.2680) to compute its weights for the risk score. In the next step, age was divided into conventional groups. These weights for risk factors were referred as points and were rounded to the nearest non-zero integers. For each patient, the point total was the sum of the points of all risk factors that for the patient. Then, the predicted risk of death for each possible point total at years 1, 3, and 5 after procedure was calculated as . In this formula, S0(t) was the survival rate at the mean values of all risk factors at each time point (t) of years 1 (0.9757), 3 (0.9319) and 5 (0.8792); and 0.2680 was the constant in the risk score. Also, was the sum of the products of the regression coefficient and the mean value of every risk factor in the final Cox proportional hazards model.
Evaluating the accuracy of the risk score
The discrimination of the risk score was evaluated using the data from the validation sample by calculating C statistics when the risk score was used to predict patients’ risks of death at years 1, 3, and 5 after PCI.13 The accuracy of predicting the risks of death 1, 3, and 5 years after PCI using the simplified risk score was also evaluated by examining the agreements between the predicted and observed mortality rates in 10 groups of patients separated according to the distribution of the point totals and the clinical importance of the predicted risks of death. For a given group of patients at a specific time point, if the average predicted risk of death was within the 95% confidence interval of the observed risk, the agreement between predicted and observed risks was deemed as good.
All statistical analyses were conducted in SAS version 9.3 (SAS Institute, Cary, NC).
RESULTS
Study population
We identified 11,897 patients who had undergone PCI in 45 NYS hospitals between October 1 and December 31, 2003; 1,966 had died prior to December 31, 2008. The respective 1, 3 and 5-year mortality rates were 4.0%, 9.8% and 16.1%. Patient characteristics of the entire study population, the derivation and the validation samples were presented in Table 1. Overall, patient characteristics were similar between the derivation and the validation samples.
Table 1.
Distribution of baseline risk factors.*
| Risk Factor | Total Population (n=11897) | Derivation Sample (n=5948) | Validation Sample (n=5949) |
|---|---|---|---|
| Mean age (y) | 64.6 ± 12.1 | 64.6 ± 12.1 | 64.6 ± 12.0 |
| Age group (y), n (%) | |||
| <50 | 1411 (11.9) | 718 (12.1) | 693 (11.6) |
| 50-59 | 2721 (22.9) | 1341 (22.5) | 1380 (23.2) |
| 60-69 | 3315 (27.9) | 1652 (27.8) | 1663 (28.0) |
| 70-79 | 3083 (25.9) | 1551 (26.1) | 1532 (25.8) |
| ≥80 | 1367 (11.5) | 686 (11.5) | 681 (11.4) |
| Female sex, n (%) | 3852 (32.4) | 1914 (32.2) | 1938 (32.6) |
| Race, n (%) | |||
| Hispanic | 901 (7.6) | 467 (7.9) | 434 (7.3) |
| Non-Hispanic white | 9456 (79.5) | 4702 (79.1) | 4754 (79.9) |
| Non-Hispanic black | 928 (7.8) | 454 (7.6) | 474 (8.0) |
| Non-Hispanic other race | 612 (5.1) | 325 (5.5) | 287 (4.8) |
| Body surface area (m2) | 2.02 ± 0.26 | 2.02 ± 0.26 | 2.02 ± 0.26 |
| Body mass index (kg/m2), n (%) | |||
| <25.0 | 2726 (22.9) | 1361 (22.9) | 1365 (22.9) |
| 25.0 - 39.99 | 8636 (72.6) | 4311 (72.5) | 4325 (72.7) |
| ≥40 | 535 (4.5) | 276 (4.6) | 259 (4.4) |
| Left main coronary artery disease (stenosis ≥ 50%), n (%) | 461 (3.8) | 245 (4.1) | 216 (3.6) |
| Number of diseased vessels (stenosis ≥ 70%), n (%) | |||
| 3 | 1822 (15.3) | 895 (15.0) | 927 (15.6) |
| 2 | 3666 (30.8) | 1827 (30.7) | 1839 (30.9) |
| 0 or 1 | 6409 (53.9) | 3226 (54.2) | 3183 (53.5) |
| Ejection fraction, n (%) | |||
| <20% | 100 (0.8) | 55 (0.9) | 45 (0.8) |
| 20-29% | 426 (3.6) | 196 (3.3) | 230 (3.9) |
| 30-39% | 897 (7.5) | 427 (7.2) | 470 (7.9) |
| 40-49% | 1899 (16.0) | 977 (16.4) | 922 (15.5) |
| ≥50% | 7747 (65.1) | 3879 (65.2) | 3868 (65.0) |
| Missing | 828 (7.0) | 414 ( 7.0) | 414 (7.0) |
| Previous myocardial infarction, n (%) | |||
| <6 hours before treatment | 669 (5.6) | 328 (5.5) | 341 (5.7) |
| 6-11 hours before treatment | 234 (2.0) | 128 (2.2) | 106 (1.8) |
| 12- 23 hours before treatment | 362 (3.0) | 195 (3.3) | 167 (2.8) |
| 1-7 days before treatment | 1527 (12.8) | 777 (13.1) | 750 (12.6) |
| 8-20 days before treatment | 172 (1.5) | 86 (1.4) | 86 (1.4) |
| ≥21 days before treatment | 2334 (19.6) | 1157 (19.5) | 1177 (19.8) |
| No previous myocardial infarction | 6599 (55.5) | 3277 ( 55.1) | 3322 (55.8) |
| Hemodynamic state, n (%) | |||
| Shock | 28 (0.2) | 12 (0.2) | 16 (0.3) |
| Unstable | 72 (0.6) | 31 (0.5) | 41 (0.7) |
| Stable | 11797 (99.2) | 5905 (99.3) | 5892 (99.0) |
| Cerebrovascular disease, n (%) | 908 (7.6) | 454 (7.6) | 454 (7.6) |
| Peripheral arterial disease, n (%) | 769 (6.5) | 358 (6.0) | 411 (6.9) |
| Congestive heart failure, n (%) | |||
| At current admission | 671 (5.6) | 355 (6.0) | 316 (5.3) |
| Before current admission | 351 (3.0) | 172 (2.9) | 179 (3) |
| None | 10875 (91.4) | 5421 (91.1) | 5454 (91.7) |
| Malignant ventricular arrhythmia, n (%) | 62 (0.5) | 33 (0.6) | 29 (0.5) |
| Chronic obstructive pulmonary disease, n (%) | 693 (5.8) | 351 (5.9) | 342 (5.7) |
| Diabetes, n (%) | 3486 (29.3) | 1740 (29.3) | 1746 (29.3) |
| Renal failure, n (%) | |||
| Requiring dialysis | 213 (1.8) | 110 (1.8) | 103 (1.7) |
| Creatinine >2.5 mg/dl (220 μmol/liter) | 154 (1.3) | 72 (1.2) | 82 (1.4) |
| No renal failure | 11530 (96.9) | 5766 (96.9) | 5764 (96.9) |
| Previous percutaneous coronary intervention, n (%) | 3791 (31.9) | 1863 (31.3) | 1928 (32.4) |
| Previous coronary artery bypass graft surgery, n (%) | 2140 (18.0) | 1021 (17.2) | 1119 (18.8) |
| Stent thrombosis (as the indication for PCI), n (%) | 15 (0.1) | 7 (0.1) | 8 (0.1) |
Plus–minus values are means±SD. Because of rounding, percentages may not total 100.
† Mortality rate was calculated using Kaplan-Meier method.
Univariate regression analysis: derivation sample
The unadjusted associations between patients’ clinical, anatomic and procedural characteristics and long-term (5-year) risk of death are presented in Appendix 2. Higher risk of death was related to older age, female sex, non-Hispanic black race, extreme values of BMI, left main coronary artery disease, multivessel disease, lower values of ejection fraction, history of MI, unstable hemodynamic state or shock, the presence of a number of comorbidities (cerebrovascular disease, peripheral arterial disease, congestive heart failure, malignant ventricular arrhythmia, chronic obstructive pulmonary disease, diabetes and renal failure) and history of coronary artery bypass graft surgery.
Multivariable regression analysis: derivation sample
Multivariable analysis identified 12 separate risk factors for mortality (Table 2). These risk factors were older age, BMI < 25 kg/m2 or BMI ≥ 40kg/m2, multivessel disease, lower values of ejection fraction, unstable hemodynamic state or shock, a number of comorbidities (cerebrovascular disease, peripheral vascular disease, congestive heart failure, chronic obstructive pulmonary disease, diabetes and renal failure), and history of coronary artery bypass graft surgery. Age was the only risk factor used as a continuous variable (number of years > 50); the other risk factors were represented as categorical variables. Table 2 shows that each 1-year increase in age after 50 years was associated with a 6% increase in the chance of dying (adjusted hazard ratio=1.06, P<0.0001). For the categorical risk factors, the hazard ratios for death ranged from 1.13 for BMI < 25 kg/m2 (compared to 25.0-39.99 kg/m2) to 21.03 for shock (compared to stable hemodynamic state).
Table 2.
Final Cox proportional hazard model for death developed using the derivation sample.
| Risk Factor | Coefficient | Standard Error | Hazard Ratio (95% Confidence Interval) | P-Value |
|---|---|---|---|---|
| Age: Number of years > 50 | 0.0536 | 0.0032 | 1.06 (1.05, 1.06) | <0.0001 |
| Body mass index (kg/m2) | ||||
| <25.0 | 0.1254 | 0.0488 | 1.13 (1.03, 1.25) | 0.01 |
| 25.0 - 39.99 | - | Reference | - | |
| ≥40 | 0.6479 | 0.1232 | 1.91 (1.50, 2.43) | <0.0001 |
| 2 or 3 diseased vessels (stenosis ≥ 70%) | 0.2654 | 0.0629 | 1.30 (1.15, 1.48) | <0.0001 |
| Ejection fraction | ||||
| <20% | 0.9292 | 0.1847 | 2.53 (1.76, 3.64) | <0.001 |
| 20-29% | 0.7762 | 0.1560 | 2.17 (1.60, 2.95) | <0.001 |
| 30-39% | 0.4812 | 0.0834 | 1.62 (1.37, 1.91) | <0.001 |
| 40-49% | 0.2970 | 0.0718 | 1.35 (1.17, 1.55) | <0.001 |
| ≥50%* | - | - | Reference | - |
| Hemodynamic state | ||||
| Shock | 3.0460 | 0.5045 | 21.03 (7.82,56.54) | <0.001 |
| Unstable | 0.7586 | 0.3174 | 2.14 (1.15, 3.98) | 0.02 |
| Stable | - | - | Reference | - |
| Cerebrovascular diseases | 0.3546 | 0.0678 | 1.43 (1.25, 1.63) | <0.001 |
| Peripheral arterial diseases | 0.4254 | 0.1036 | 1.53 (1.25, 1.88) | <0.001 |
| Congestive heart failure | ||||
| At current admission | 0.5524 | 0.0912 | 1.74 (1.45, 2.08) | <0.001 |
| Before current admission | 0.4480 | 0.1303 | 1.57 (1.21, 2.02) | 0.0006 |
| None | - | - | Reference | - |
| Chronic obstructive pulmonary diseases | 0.4548 | 0.1262 | 1.58 (1.23, 2.02) | 0.0004 |
| Diabetes | 0.3467 | 0.0618 | 1.41 (1.25, 1.60) | <0.0001 |
| Renal failure | ||||
| Requiring dialysis | 1.6845 | 0.1306 | 5.39 (4.17, 6.96) | <0.0001 |
| Creatinine >2.5 mg/dl (220 μmol/liter) | 1.0243 | 0.1947 | 2.79 (1.90, 4.08) | <0.0001 |
| No renal failure | - | - | Reference | - |
| Previous coronary artery bypass graft surgery | 0.2983 | 0.0770 | 1.34 (1.15, 1.55) | 0.0001 |
Including missing ejection fraction.
Validation of the Cox proportional hazards model
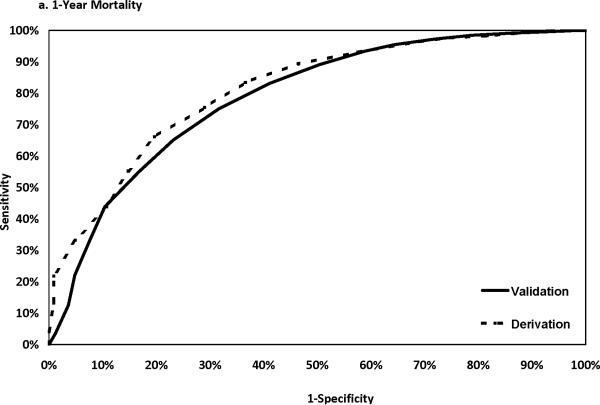
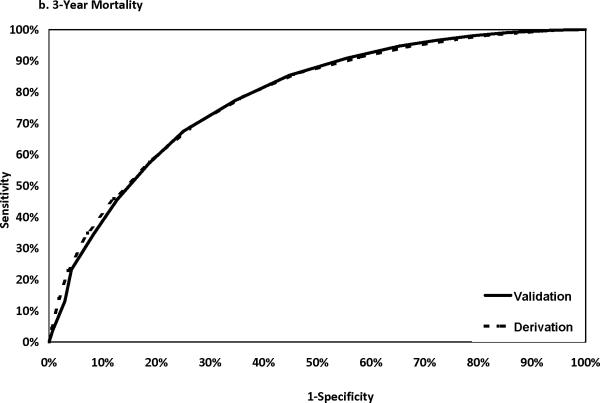
The discriminatory power of the Cox model was assessed using data from the validation sample. The C statistics were 0.787, 0.785, and 0.773 for risks of death within 1, 3, and 5 years after PCI, respectively. The corresponding C statistics using the derivation sample data were 0.809, 0.786 and 0.782 respectively. Figure 1 shows that the ROC curves developed using the derivation and the validation samples were closer to each at 3 and 5 years than at year 1 after PCI. The calibration of the model was good as shown in Appendix 3, in which the observed and predicted mortality rates were close to each other for each of the 10 deciles at 1, 3 and 5 years after PCI.
Figure 1.
ROC curves in the derivation and the validation samples.
Point-based risk score
The integer points for each characteristic found to be associated with death in the Cox proportional hazards model are listed in Table 3. The points associated with all reference categories were assigned a value of 0; the highest point value for any characteristic associated with death was 11 for shock. The possible point totals for patients ranged from 0 to a possible high of 39.
Table 3.
Points assigned to each risk factor (derivation sample)
| Risk Factor | Points |
|---|---|
| Age (y) | |
| ≤50 | 0 |
| 51-59 | 1 |
| 60-69 | 3 |
| 70-79 | 5 |
| ≥80 | 7 |
| Body mass index (kg/m2) | |
| <25.0 | 1 |
| 25.0 - 39.99 | 0 |
| ≥40 | 2 |
| Number of diseased vessels (stenosis ≥ 70%) | |
| 2 or 3 | 1 |
| 0 or 1 | 0 |
| Ejection Fraction, % | |
| <30 | 3 |
| 30-39 | 2 |
| 40-49 | 1 |
| ≥50 | 0 |
| Hemodynamic state | |
| Shock | 11 |
| Unstable | 3 |
| Stable | 0 |
| Cerebrovascular diseases | 1 |
| Peripheral arterial diseases | 2 |
| Congestive heart failure | 2 |
| Chronic obstructive pulmonary diseases | 2 |
| Diabetes | 1 |
| Renal failure | |
| Requiring dialysis | 6 |
| Creatinine >2.5 mg/dl (220 μmol/liter) | 4 |
| No renal failure | 0 |
| Previous coronary artery bypass graft surgery | 1 |
Possible range of point total is 0 to 39.
For every possible point total, the predicted risks of death at 1, 3, and 5 years after PCI are presented in Table 4. The predicted 1-year risk of death ranged from 0.58% for a point total of 0 to a >60% mortality for a point total of at least 19. The 5-year risk of death ranged from 2.98% for a point total of 0 to >99% for a point total of at least 19.
Table 4.
Predicted mortality rates associated with individual point totals (derivation sample)
| Predicted Mortality (%) | ||||
|---|---|---|---|---|
| Point Total | Percentage of Patients (%) | 1 y | 3 y | 5 y |
| 0 | 3.97 | 0.58 | 1.64 | 2.98 |
| 1 | 8.77 | 0.75 | 2.14 | 3.88 |
| 2 | 8.28 | 0.98 | 2.79 | 5.04 |
| 3 | 11.09 | 1.28 | 3.64 | 6.54 |
| 4 | 10.46 | 1.67 | 4.73 | 8.46 |
| 5 | 11.13 | 2.18 | 6.14 | 10.91 |
| 6 | 10.69 | 2.84 | 7.94 | 14.02 |
| 7 | 9.32 | 3.70 | 10.26 | 17.92 |
| 8 | 7.98 | 4.81 | 13.19 | 22.75 |
| 9 | 6.05 | 6.24 | 16.89 | 28.64 |
| 10 | 3.97 | 8.07 | 21.48 | 35.68 |
| 11 | 3.11 | 10.42 | 27.10 | 43.83 |
| 12 | 1.82 | 13.40 | 33.85 | 52.96 |
| 13 | 1.04 | 17.15 | 41.74 | 62.69 |
| 14 | 0.96 | 21.80 | 50.66 | 72.44 |
| 15 | 0.50 | 27.50 | 60.29 | 81.46 |
| 16 | 0.22 | 34.32 | 70.10 | 88.95 |
| 17 | 0.24 | 42.28 | 79.37 | 94.39 |
| 18 | 0.20 | 51.25 | 87.30 | 97.68 |
| ≥19 | 0.20 | > 60 | > 93 | > 99 |
* The highest observed total risk score was 23 in the derivation sample.
Agreements between the observed and predicted risks
The agreements between the observed and predicted risks of death using the simplified risk score at years 1, 3, and 5 after PCI are assessed in Figure 2 (Panels 2a – 2c) across 10 groups of point totals. Among 30 pairs of observed and predicted risks examined, only 2 pairs (for point total of 2 at year 3 and for point totals of at least 11 at year 5) had the predicted risk of death outside the 95% CI of the corresponding observed risk of death. The respective C statistics for the risks of death within 1, 3, and 5 years after PCI were 0.787, 0.782, and 0.768.
Figure 2.



Observed (with 95% confidence interval) and predicted mortality rates by point total in the validation sample.
DISCUSSION
The most important finding in the study is that we were able to modify a Cox proportional hazards model to produce a simplified risk index for 5-year mortality following discharge after PCI such that the predicted mortality was in very good agreement with what was observed in New York State. The clinical, anatomic and procedural characteristics that we identified to estimate 5 year mortality among patients discharged alive after a PCI include older age, extreme values (both high and low) of BMI, multivessel disease, lower values of ejection fraction, unstable hemodynamic state or shock, several comorbidities (cerebrovascular disease, peripheral vascular disease, congestive heart failure, chronic obstructive pulmonary disease, diabetes, and renal failure) and history of CABG surgery.
Comparison with prior studies
Female sex has been reported as a risk factor for in-hospital mortality in our logistic regression for in-hospital mortality,2 it was not a predictor for long-term mortality in this study. All of these risk factors identified in our study have also been found to be significant predictors of long-term mortality for PCI in other studies in which complex models or longer term mortality were derived.10, 11
One major differences between this study and the only 2 prior studies that developed prediction models for long-term mortality after PCI is that those studies produced complex models, whereas this study we created a simple risk score that can be used to quickly estimate longer-term mortality. Furthermore, in the MacKenzie study,patients analyzed had undergone PCI between 1992 through 2001, prior to the introduction of drug-eluting stents10 and the Weintraub study enrolled only Medicare beneficiaries who were at least 65 years old in the drug-eluting stent era.11 Therefore, this study is more representative of the experience of all PCI patients in the current, drug-eluting stent era. A total of 7728 (65.0%) of the patients in our study received at least one drug-eluting stent. Moreover, in this study we created a simple risk score that can be conveniently used to predict a patient's risk of long-term (up to 5-year) mortality based on pre-procedural risk factors.
Although it is true that statistical models can now be programmed using computers to calculate the predicted risk of death, a simple clinical risk score remains an attractive risk stratification tool for both clinicians and patients. Risk scores are much more likely to be adopted by clinicians than their corresponding statistical models despite of the availability of computer programs. Another difference between prior studies and the current study is that instead of fitting 3 separate Cox proportional hazards models for 3 different time periods (as was done in both prior studies,10, 11 we fit one model that showed similar discrimination as a group of 3 more complicated models for 3 time periods, i.e., within 30 days, 31 days to 1 year, and later than 1 year after PCI. The C statistics at years 1, 3, and 5 on the validation data set were 0.787, 0.785, and 0.773, respectively, using the simple model and their counterparts using the 3 period-specific models were 0.779, 0.782, and 0.772. It is worth noting that although C statistics for short-term PCI models are frequently very close to 0.9, the C statistics for longer-term models do not have that high discrimination. For example, the C statistic for 5-year mortality in the MacKenzie et al.10 study was 0.81, and the C statistic for 2-year mortality in the Weintraub et al.11 study was 0.78.
Using a combination of procedural and long-term mortality
The application of this risk score for long-term mortality after PCI readily lends itself to be used in conjunction with existing risk scores for procedural mortality, including (although not limited to) the procedural risk score developed by our group.1-9 For example, our risk score for in-hospital mortality includes 9 risk factors (age, female sex, left main disease, hemodynamic instability or shock, ejection fraction, history of MI, peripheral arterial disease, congestive heart failure, and renal failure) and can be easily used to predict the risk of in-hospital death.2 Simply combining the risk of in-hospital mortality in our earlier risk index and the risk of death after procedure using this risk index provides the combined risk of procedural and long term death of patients for whom PCI is being considered.
More importantly, for patients rated as appropriate for revascularization by the Appropriate Use Criteria issued by the American College of Cardiology Foundation and other professional societies,17 this long-term risk score in conjunction with New York's previously developed short-term PCI risk score2 can be used to compare short- and longer term PCI outcomes with CABG outcomes obtained from New York's short-term and longer-term risk scores for isolated CABG surgery.18,19 Although there are other reasons for choosing a procedure (e.g., complications, recovery difficulty and period, quality of life), this comparative information should be valuable to clinicians and patients in choosing a procedure.
High-Risk Patients
Note that for a small number of patients (0.4%), there is an expected mortality rate in excess of 50%. Although this rate is very high, it is likely to be high with competing interventions. For patients appropriate for revascularization, the short- and long-term PCI mortality rate for these patients should be compared with the expected short- and long-term mortality raters for CABG surgery (see paragraph above).4,18,19
Application to significantly different patient populations
This risk score for long-term mortality after PCI can be recalibrated for a different patient population to account for the possible difference in long-term survival from the study population. Recalibration can perhaps best be performed using the method applied by D’Agostino and colleagues.20 This method uses the same equation described in the methods section to calculate the predicted risks of death for each point total in the risk score in Table 4, but uses the prevalence of the risk factors and the average survival rates at years 1, 3, and 5 after PCI in the new population of interest. With recalibration, this risk score can be readily used to estimate long-term survival in other patient populations.
Limitations
There are a few important limitations of our study. First, these data preceded the introduction of second-generation drug-eluting stents. Some (though not all) studies suggest that long-term mortality may differ following receipt of a second vs. first generation DES. If the 5 year mortality does indeed differ with second generation stents, the data might be less accurate when applied to patients receiving such stents. Second, to achieve long-term follow-up for mortality, we had to rely on the data of past patients. However, the accuracy of this risk score when applied to more recent patients could not be evaluated in this study because of the lack of long-term mortality data for such patients. We encourage other investigators to validate this risk score in different settings using newer patient data with long enough follow-up. Third, in this study the overall atherosclerotic burden was measured using the number of vessels diseased. More accurate but complicated measures such as SYNTAX score21 or Friesinger score22 are not available in this study. However, adding such variables may improve the accuracy of the prediction model for long-term validity. Fourth, in the PCIRS database, many risk factors, e.g., congestive heart failure, chronic obstructive pulmonary and renal failure disease are categorical variables with no more than 3 categories. Having such variables defined with more categories may also improve the accuracy of the prediction model. Fifth, some known risk factors for long-term mortality, e.g., metastatic cancer and frailty, were not available in our data and the absence of this information could limit the accuracy of our predictions. Sixth, while it is important to examine the accuracy of the developed risk score in very high-risk patients, there were not enough patients with point totals of 11 and higher to be confident about the precise risk of mortality for these patients. Finally, there was a slight over-prediction of mortality by the risk score in the validation sample, particularly at 5 years. This highlights the need for recalibration when the model is used for other populations.
Conclusions
We have created a simple, easy to use risk score for predicting long-term mortality after PCI using a population-based registry. This may be a useful risk stratification tool for clinicians and patients.
Supplementary Material
Acknowledgments
We thank the New York State Cardiac Advisory Committee for their encouragement and support of this study; and Kimberly Cozzens, Cynthia Johnson, and the cardiac catheterization laboratories of the participating hospitals for their tireless efforts to ensure the timeliness, completeness, and accuracy of the registry data.
Sources of Funding: This work was supported by the NIH grant RC1HL099122.
Footnotes
Disclaimer: The views expressed are those of the authors and do not necessarily reflect those of the New York State Department of Health.
Disclosure: None.
Contributor Information
Chuntao Wu, Penn State Hershey College of Medicine, Hershey, PA.
Fabian T. Camacho, Penn State Hershey College of Medicine, Hershey, PA.
Spencer B. King, III, St. Joseph's Health System, Atlanta, GA.
Gary Walford, Johns Hopkins Medical Center, Baltimore, MD.
David R. Holmes, Jr, Mayo Clinic, Rochester, MN.
Nicholas J. Stamato, United Health Services, Binghamton, NY.
Peter B. Berger, Geisinger Health System, Danville, PA.
Samin Sharma, Mt. Sinai Medical Center, New York, NY.
Jeptha P. Curtis, Yale University School of Medicine, New Haven, CT.
Ferdinand J. Venditti, Albany Medical College, Albany, NY.
Alice K. Jacobs, Boston Medical Center, Boston, MA.
Edward L. Hannan, University at Albany State University of New York, Albany, NY.
References
- 1.Peterson ED, Dai D, DeLong ER, Brennan JM, Singh M, Rao SV, Shaw RE, Roe MT, Ho KKL, Klein LW, Krone RJ, Weintraub WS, Brindis RG, Rumsfeld JS, Spertus JA. Contemporary mortality risk prediction for percutaneous coronary intervention: results from 588,398 procedures in the National Cardiovascular Data Registry. J Am Coll Cardiol. 2010;55:1923–1932. doi: 10.1016/j.jacc.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu C, Hannan EL, Walford G, Ambrose JA, Holmes DR, Jr., King SB, 3rd, Clark LT, Katz S, Sharma S, Jones RH. A risk score to predict in-hospital mortality for percutaneous coronary interventions. J Am Coll Cardiol. 2006;47:654–660. doi: 10.1016/j.jacc.2005.09.071. [DOI] [PubMed] [Google Scholar]
- 3.Ellis SG, Weintraub W, Holmes D, Shaw R, Block PC, King SB. Relation of operator volume and experience to procedural outcome of percutaneous coronary revascularization at hospitals with high interventional volumes. Circulation. 1997;95:2479–2484. doi: 10.1161/01.cir.95.11.2479. [DOI] [PubMed] [Google Scholar]
- 4.Moscucci M, Kline-Rogers E, Share D, O'Donnell M, Maxwell-Eward A, Meengs WL, Kraft P, DeFranco AC, Chambers JL, Patel K, McGinnity JG, Eagle KA. Blue Cross Blue Shield Michigan C. Simple bedside additive tool for prediction of in-hospital mortality after percutaneous coronary interventions. Circulation. 2001;104:263–268. doi: 10.1161/01.cir.104.3.263. [DOI] [PubMed] [Google Scholar]
- 5.O'Connor GT, Malenka DJ, Quinton H, Robb JF, Kellett MA, Shubrooks S, Bradley WA, Hearne MJ, Watkins MW, Wennberg DE, Hettleman B, O'Rourke DJ, McGrath PD, Ryan T, VerLee P. No New England Cardiovasc Dis Study G. Multivariate prediction of in-hospital mortality after percutaneous coronary interventions in 1994-1996. J Am Coll Cardiol. 1999;34:681–691. doi: 10.1016/s0735-1097(99)00267-3. [DOI] [PubMed] [Google Scholar]
- 6.Qureshi MA, Safian RD, Grines CL, Goldstein JA, Westveer DC, Glazier S, Balasubramanian M, O'Neill WW. Simplified scoring system for predicting mortality after percutaneous coronary intervention. J Am Coll Cardiol. 2003;42:1890–1895. doi: 10.1016/j.jacc.2003.06.014. [DOI] [PubMed] [Google Scholar]
- 7.Resnic FS, Ohno-Machado L, Selwyn A, Simon DI, Popma JJ. Simplified risk score models accurately predict the risk of major in-hospital complications following percutaneous coronary intervention. Am J Cardiol. 2001;88:5–9. doi: 10.1016/s0002-9149(01)01576-4. [DOI] [PubMed] [Google Scholar]
- 8.Shaw RE, Anderson HV, Brindis RG, Krone RJ, Klein LW, McKay CR, Block PC, Shaw LJ, Hewitt K, Weintraub WS. Development of a risk adjustment mortality model using the American College of Cardiology National Cardiovascular Data Registry (ACC-NCDR) experience: 1998-2000. J Am Coll Cardiol. 2002;39:1104–1112. doi: 10.1016/s0735-1097(02)01731-x. [DOI] [PubMed] [Google Scholar]
- 9.Singh M, Lennon RJ, Holmes DR, Bell MR, Rihal CS. Correlates of procedural complications and a simple integer risk score for percutaneous coronary intervention. J Am Coll Cardiol. 2002;40:387–393. doi: 10.1016/s0735-1097(02)01980-0. [DOI] [PubMed] [Google Scholar]
- 10.MacKenzie TA, Malenka DJ, Olmstead EM, Piper WD, Langner C, Ross CS, O'Connor GT. Northern New England Cardiovascular Disease Study G. Prediction of survival after coronary revascularization: modeling short-term, mid-term, and long-term survival. Ann Thorac Surg. 2009;87:463–472. doi: 10.1016/j.athoracsur.2008.09.042. [DOI] [PubMed] [Google Scholar]
- 11.Weintraub WS, Grau-Sepulveda MV, Weiss JM, Delong ER, Peterson ED, O'Brien SM, Kolm P, Klein LW, Shaw RE, McKay C, Ritzenthaler LL, Popma JJ, Messenger JC, Shahian DM, Grover FL, Mayer JE, Garratt KN, Moussa ID, Edwards FH, Dangas GD. Prediction of long-term mortality after percutaneous coronary intervention in older adults: results from the National Cardiovascular Data Registry. Circulation. 2012;125:1501–1510. doi: 10.1161/CIRCULATIONAHA.111.066969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lin DY, Wei LJ. The robust inference for the Cox proportional hazards model. J Am Stat Assoc. 1989;84:1074–1078. [Google Scholar]
- 13.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 14.Hosmer DW, Lemeshow S. Applied Logistic Regression. John Wiley and Sons; New York, NY: 1989. [Google Scholar]
- 15.Hosmer DW, Lemeshow S, May S. Applied survival analysis: Regression modeling of time to event data. Wiley-Interscience; Hoboken, NJ: 2008. [Google Scholar]
- 16.Sullivan LM, Massaro JM, D'Agostino RB., Sr Presentation of multivariate data for clinical use: The Framingham Study risk score functions. Stat Med. 2004;23:1631–1660. doi: 10.1002/sim.1742. [DOI] [PubMed] [Google Scholar]
- 17.Patel MR, Dehmer GJ, Hirshfeld JW, Smith PK, Spertus JA. ACCF/SCAI/STS/AATS/AHA/ASNC 2009 appropriateness criteria for coronary revascularization: a report of the American College of Cardiology Foundation Appropriateness Criteria Task Force, Society for Cardiovascular Angiography and Interventions, Society of Thoracic Surgeons, American Association for Thoracic Surgery, American Heart Association, and the American Society of Nuclear Cardiology. Circulation. 2009;119:1330–1352. doi: 10.1161/CIRCULATIONAHA.108.191768. [DOI] [PubMed] [Google Scholar]
- 18.Hannan EL, Farrell LJS, Wechsler A, Jordan D, Lahey SJ, Culliford AT, Gold JP, Higgins RSD, Smith CR. The New York risk score for in-hospital/30-day mortality for coronary artery bypass graft surgery. Annals of Thoracic Surgery. 2013;95:46–52. doi: 10.1016/j.athoracsur.2012.08.047. [DOI] [PubMed] [Google Scholar]
- 19.Wu C, Camacho FT, Wechsler AS, Lahey S, Culliford AT, Jordan D, Gold JP, Higgins RSD, Smith CR, Hannan EL. A risk score for predicting long-term mortality following coronary artery bypass graft surgery. Circulation. 2012;125:2423–2430. doi: 10.1161/CIRCULATIONAHA.111.055939. published online April 30, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.D'Agostino RB, Sr., Grundy S, Sullivan LM, Wilson P, Group CHDRP Validation of the Framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. JAMA. 2001;286:180–187. doi: 10.1001/jama.286.2.180. [DOI] [PubMed] [Google Scholar]
- 21.Sianos G, Morel MA, Kappetein AP, Morice MC, Colombo A, Dawkins K, van den Brand M, Van Dyck N, Russell ME, Mohr FW, Serruys PW. The SYNTAX Score: an angiographic tool grading the complexity of coronary artery disease. EuroIntervention. 2005;1:219–227. [PubMed] [Google Scholar]
- 22.Friesinger GC, Page EE, Ross RS. Prognostic significance of coronary arteriography. Trans Assoc Am Physicians. 1970;83:78–92. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.