Digital Inline Holographic Microscopy (DIHM) of Weakly-scattering Subjects

Abstract

Weakly-scattering objects, such as small colloidal particles and most biological cells, are frequently encountered in microscopy. Indeed, a range of techniques have been developed to better visualize these phase objects; phase contrast and DIC are among the most popular methods for enhancing contrast. However, recording position and shape in the out-of-imaging-plane direction remains challenging. This report introduces a simple experimental method to accurately determine the location and geometry of objects in three dimensions, using digital inline holographic microscopy (DIHM). Broadly speaking, the accessible sample volume is defined by the camera sensor size in the lateral direction, and the illumination coherence in the axial direction. Typical sample volumes range from 200 µm x 200 µm x 200 µm using LED illumination, to 5 mm x 5 mm x 5 mm or larger using laser illumination. This illumination light is configured so that plane waves are incident on the sample. Objects in the sample volume then scatter light, which interferes with the unscattered light to form interference patterns perpendicular to the illumination direction. This image (the hologram) contains the depth information required for three-dimensional reconstruction, and can be captured on a standard imaging device such as a CMOS or CCD camera. The Rayleigh-Sommerfeld back propagation method is employed to numerically refocus microscope images, and a simple imaging heuristic based on the Gouy phase anomaly is used to identify scattering objects within the reconstructed volume. This simple but robust method results in an unambiguous, model-free measurement of the location and shape of objects in microscopic samples.

Download video file ^{(21.6MB, mp4)}

Introduction

Digital inline holographic microscopy (DIHM) allows fast three-dimensional imaging of microscopic samples, such as swimming microorganisms^1,2 and soft matter systems^3,4, with minimal modification to a standard microscope setup. In this paper a pedagogical demonstration of DIHM is provided, centered around software developed in our lab. This paper includes a description of how to set up the microscope, optimize data acquisition, and process the recorded images to reconstruct three-dimensional data. The software (based in part on software developed by D.G. Grier and others⁵) and example images are freely available on our website. A description is provided of the steps necessary to configure the microscope, reconstruct three-dimensional volumes from holograms and render the resulting volumes of interest using a free ray tracing software package. The paper concludes with a discussion of factors affecting the quality of reconstruction, and a comparison of DIHM with competing methods.

Although DIHM was described some time ago (for a general review of its principles and development, see Kim⁶), the required computing power and image processing expertise has hitherto largely restricted its use to specialist research groups with a focus on instrument development. This situation is changing in the light of recent advances in computing and camera technology. Modern desktop computers can easily cope with the processing and data storage requirements; CCD or CMOS cameras are present in most microscopy labs; and the requisite software is being made freely available on the internet by groups who have invested time in developing the technique.

Various schemes have been proposed for imaging the configuration of microscopic objects in a three-dimensional sample volume. Many of these are scanning techniques^7,8, in which a stack of images is recorded by mechanically translating the image plane through the sample. Scanning confocal fluorescence microscopy is perhaps the most familiar example. Typically, a fluorescent dye is added to a phase object in order to achieve an acceptable level of sample contrast, and the confocal arrangement used to spatially localize fluorescent emission. This method has led to significant advances, for example in colloid science where it has allowed access to the three-dimensional dynamics of crowded systems^9-11. The use of labeling is an important difference between fluorescence confocal microscopy and DIHM, but other features of the two techniques are worth comparing. DIHM has a significant speed advantage in that the apparatus has no moving parts. The mechanical scanning mirrors in confocal systems place an upper limit on the data acquisition rate - typically around 30 frames/sec for a 512 x 512 pixel image. A stack of such images from different focal planes can be obtained by physically translating the sample stage or objective lens between frames, leading to a final capture rate of around one volume per second for a 30 frame stack. In comparison, a holographic system based on a modern CMOS camera can capture 2,000 frames/sec at the same image size and resolution; each frame is processed `offline' to give an independent snapshot of the sample volume. To reiterate: fluorescent samples are not required for DIHM, although a system has been developed that performs holographic reconstruction of a fluorescent subject¹². As well as three-dimensional volume information, DIHM can also be used to provide quantitative phase contrast images¹³, but that is beyond the scope of the discussion here.

Raw DIHM data images are two-dimensional, and in some respects look like standard microscope images, albeit out of focus. The main difference between DIHM and standard bright field microscopy lies in the diffraction rings that surround objects in the field of view; these are due to the nature of the illumination. DIHM requires a more coherent source than bright field - typically an LED or laser. The diffraction rings in the hologram contain the information necessary to reconstruct a three-dimensional image. There are two main approaches to interpreting DIHM data; direct fitting and numerical refocusing. The first approach is applicable in cases where the mathematical form of the diffraction pattern is known in advance^3,4; this condition is met by a small handful of simple objects like spheres, cylinders, and half-plane obstacles. Direct fitting is also applicable in cases where the object's axial position is known, and the image can be fitted using a look-up table of image templates¹⁴.

The second approach (numerical refocusing) is rather more general and relies on using the diffraction rings in the two-dimensional hologram image to numerically reconstruct the optical field at a number of (arbitrarily spaced) focal planes throughout the sample volume. Several related methods exist for doing this⁶; this work uses the Rayleigh-Sommerfeld back propagation technique as described by Lee and Grier⁵. The outcome of this procedure is a stack of images that replicate the effect of manually changing the microscope focal plane (hence the name `numerical refocusing'). Once a stack of images has been generated, the position of the subject in the focal volume must be obtained. A number of image analysis heuristics, such as local intensity variance or spatial frequency content, have been presented to quantify the sharpness of focus at different points in the sample¹⁵. In each case, when a particular image metric is maximized (or minimized), the object is considered to be in focus.

Unlike other schemes that seek to identify a particular focal plane where an object is 'in focus', the method in this work picks out points that lie inside the object of interest, which may extend across a wide range of focal planes. This approach is applicable to a broad range of subjects and is particularly suitable for extended, weakly-scattering samples (phase objects), such as rod-shaped colloids, chains of bacteria or eukaryotic flagella. In such samples the image contrast changes when the object passes through the focal plane; a defocused image has a light center if the object is on one side of the focal plane and a dark center if it is on the other. Pure phase objects have little to no contrast when they lie exactly in the focal plane. This phenomenon of contrast inversion has been discussed by other authors^16,17 and is ultimately due to the Gouy phase anomaly¹⁸. This has been put on a more rigorous footing in the context of holography elsewhere, where the limits of the technique are evaluated; the typical uncertainty in position is of the order of 150 nm (approximately one pixel) in each direction¹⁹. The Gouy phase anomaly method is one of the few well-defined DIHM schemes for determining the structure of extended objects in three dimensions, but nevertheless some objects are problematic to reconstruct. Objects that lie directly along the optical axis (pointing at the camera) are difficult to reconstruct accurately; uncertainties in the length and position of the object become large. This limitation is in part due to the restricted bit depth of the pixels recording the hologram (the number of distinct gray levels that the camera can record). Another problematic configuration occurs when the object of interest is very close to the focal plane. In this case, the real and virtual images of the object are reconstructed in close proximity, giving rise to complicated optical fields that are difficult to interpret. A second, slightly less important concern here is that the resulting diffraction fringes occupy less of the image sensor, and this coarser-grained information leads to a poorer-quality reconstruction.

In practice, a simple gradient filter is applied to three-dimensional reconstructed volumes to detect strong intensity inversions along the illumination direction. Regions where intensity changes quickly from light to dark, or vice versa, are then associated with scattering regions. Weakly-scattering objects are well described as a noninteracting collection of such elements²⁰; these individual contributions sum to give the total scattered field which is easily inverted using the Rayleigh-Sommerfeld back propagation method. In this paper, the axial intensity gradient technique is applied to a chain of Streptococcus cells. The cell bodies are phase objects (the species E. coli has a refractive index measured²¹ to be 1.384 at a wavelength λ=589 nm; the Streptococcus strain is likely to be similar) and appear as a high-intensity chain of connected blobs in the sample volume after the gradient filter has been applied. Standard threshold and feature extraction methods applied to this filtered volume allow the extraction of volumetric pixels (voxels) corresponding to the region inside the cells. A particular advantage of this method is that it allows unambiguous reconstruction of an object's position in the axial direction. Similar methods (at least, those that record holograms close to the object, imaged through a microscope objective) suffer from being unable to determine the sign of this displacement. Although the Rayleigh-Sommerfeld reconstruction method is also sign-independent in this sense, the gradient operation allows us to discriminate between weak phase objects above and below the focal plane.

Protocol

1. Setup and Data Acquisition

1. Grow a culture of Streptococcus strain V4051-197 (smooth swimming) cells in KTY medium from frozen stock²². Incubate in a rotary shaker overnight at 35 °C and 150 rpm, to saturation.

2. Inoculate 10 ml of fresh KTY medium with 500 µl of the saturated culture. Incubate for a further 3.5 hr at 35°C and 150 rpm until the cells reach an optical density of approximately 1.0 at λ=600 nm (approximately 5 x 10⁸ cells/ml).

3. Dilute 1:400 in fresh media to obtain the final concentration of motile cells.

4. On a microscope slide, make a ring of grease (e.g. from a syringe filled with petroleum jelly) around 1 mm in height and place a drop of the sample solution in the center. Place a cover glass on top and press lightly at the edges to seal, ensuring that liquid is in contact with both slide and cover glass. The resulting sample chamber should be around 100-200 µm in depth.

5. Place the sample chamber in the microscope with the cover glass facing down, and carefully, to prevent the formation of air bubbles in the oil between glass and lens.

6. Focus the microscope on the bottom surface of the sample chamber, and bring the condenser to focus.

7. Switch off the standard illumination and place the LED head behind the condenser aperture of the microscope. Set the LED power supply to maximum output.

8. Close the condenser aperture to its fullest extent, and if necessary, nudge the LED in its mount until the illumination is centered on the objective lens aperture.

9. Switch on the computer and camera, and redirect all light to the microscope's camera port. Adjust the frame rate and the image size in the image acquisition software.

10. Make the frame exposure time as short as possible while still retaining good contrast. Check an image intensity histogram to ensure that the image is not saturated or under-exposed.

11. If necessary, refocus the microscope so that object of interest is slightly defocused (typically by 10-30 µm). The object and the focal plane should be in the same medium (i.e. the focal plane should lie inside the sample chamber).

2. Reconstruction

The first step of processing data is to numerically refocus a video frame at a series of different depths, producing a stack of images. User-friendly software for doing this may be found here: http://www.rowland.harvard.edu/rjf/wilson/Downloads.html along with example images (acquired using an inverted microscope, and a 60X oil immersion objective lens) and a scene file for ray traced rendering.

1. Input the frame of interest and its respective background as separate image files, in the relevant boxes on the interface. A background image is a frame that fairly represents the background of the video, in the absence of the hologram, and will be used to suppress any fixed-pattern noise that could interfere with the hologram localization and analysis.

2. Enter values into the global settings boxes on the left hand side of the screen before running the program. The first three are output stack parameters: Axial position of the first frame ('Start focus'); number of slices in the reconstructed stack ('Number of steps'); axial distance between each slice in the stack ('Step size').

3. In order to reconstruct objects with the correct proportions, the step size should be the same size as the lateral pixel spacing. Enter the camera's lateral sampling frequency (1/pixel spacing) in the 'Pixel/micron' box, the illumination wavelength and medium refractive index in the last two boxes. The program's default values are appropriate for reconstructing the example data.

4. Press the 'Flip Z-gradient' button if the center of the object is dark in the hologram (see example frame 2005 and the discussion section for more details).

5. Check the bandpass filter on/off state (default is on). This optional bandpass filter, located in a box below the gradient-flip switch, is responsible for suppressing the contribution from noisy pixels. The bandpass filter is applied to each image slice immediately after generation.

6. Check the intermediate output switch on/off states (default is on). Intermediate analysis steps are written in two output videos, as uncompressed .avi files: the first is the refocused stack (file name ending in '_stack.avi'), the second is the stack after the axial gradient operation (file name ending in '_gradient.avi'). Ideally, this second stack will contain the object of interest highlighted as a bright object against a dark background.

7. After setting all parameters, press 'Run' in the main window. The selected frame will appear in the main box of the software.

8. Use the magnifying glass tool found on the toolbar to the left of the image to zoom in (left click) and zoom out (shift+left click). Use the rectangle tool on the toolbar to select a region of interest (ROI). Capture as many of the hologram's fringes as possible inside the rectangle, as this will optimize the reconstruction.

9. Press the 'Process' button to generate the two image stacks. Inspect the resulting stacks using ImageJ (which can be obtained for free at http://rsb.info.nih.gov/ij/). If the object of interest can be clearly seen in the gradient image stack, proceed to the next step to extract the object coordinates.

3. Rendering

1. Besides frame refocusing, this program can locate the x, y, z coordinates for each voxel in the object of interest. Press the 'Feature Extraction' button to enable this function.

2. Enter a path, including extension (for example: c:\home\output.inc), for the output coordinates file. Select 'POV-Ray style' in the 'output coordinate style' box. This causes the program to write an object file that can be visualized using the free POV-Ray raytracing software package (which can be obtained from http://www.povray.org/).

3. Reprocess the images as in section 2 above. The program will provide a series of (x, y ,z) coordinates in the selected ROI, written to the file name in the 'Output coordinate' box. Extraction of object coordinates takes significantly longer than stack generation.

4. Make sure that the sample POV-Ray file (supplied with the reconstruction code) is in the same folder as the coordinates file just generated. Edit the sample .pov file and replace the file name in inverted commas on the line #include "MYFILE.inc" with the name of the data file generated by the reconstruction code.

5. Click the 'Run' button in POV-Ray to render a bitmap image. The camera position, lighting and texture options are just a few of the customizations possible in POV-Ray; see the online documentation for details.

Representative Results

To demonstrate the capabilities of DIHM, experiments were performed on a chain of Streptococcus bacteria. The chain itself measured 10.5 mm long, and was composed of 6-7 sphero-cylindrical cells (two of the cells in the chain are close to dividing) with diameters in the range 0.6-1 μm. Figures 1a and 1b show the main interface of the reconstruction and rendering software. Examples of the numerical refocusing procedure are seen in Figure 2, where a spatial bandpass filter has been applied. Figure 3 shows the effect of the gradient filter on the images in Figure 2. The raw data used to construct both of these images are bundled with the code download as example frame 108. Lastly, Figure 4 shows the effect of good and poor quality data on the reconstructed geometry. Both frames in this last figure were taken from a video of the same chain of cells (a different chain to the one in the first two figures). A good reconstruction is possible in most cases, but when the chain is oriented end-on the reconstruction fails, giving a large round object at the focal plane. This failure mode is characteristic of objects oriented along the optical axis. For scale, in the computer rendered images, the checks on the floor are 1 µm on a side. For a more detailed discussion of the precision and accuracy of this method, readers should consult Wilson and Zhang¹⁹.

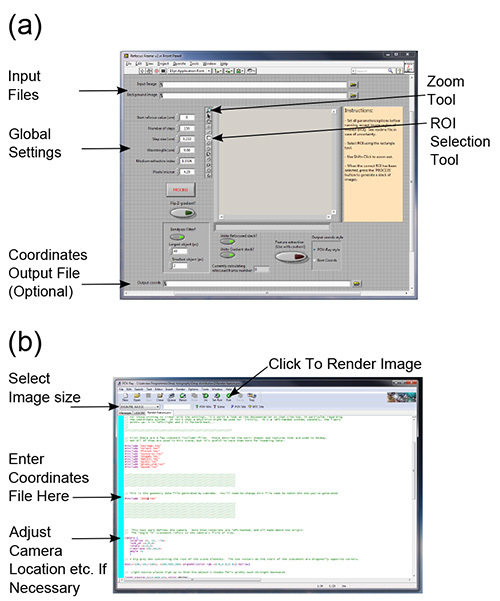Figure 1. Software interfaces. The main interface of the reconstruction software is shown in panel (a), where the file input boxes, global settings parameters and other important features referred to in the text have been highlighted. Panel (b) shows the example scene file for POV-Ray, in the program's default scene editor. The file name between inverted commas on the line indicated should be set to the output file from the reconstruction software. It may be necessary to change the camera's location and direction (relevant section indicated) in order to properly visualize the reconstruction. See the online POV-Ray documentation for further instructions. Click here to view larger image.

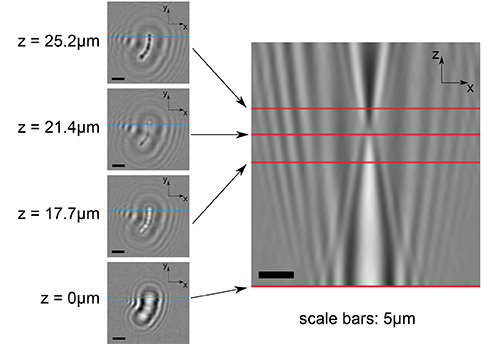Figure 2. Examples of numerically refocused images. The figure panels in the left-hand column show numerically refocused (x, y) planes at a variety of heights within the reconstructed volume (as indicated). The bottom left-hand image shows the original hologram data, divided through by the background data. The large panel on the right shows an (x, z) slice through the same stack. The point of contrast inversion along the z-axis can be clearly seen at about one-third of the way from the top of the image. The red lines on the larger image show where this plane (x, z) intersects the (x, y) planes to the left. Similarly, the blue lines in the smaller panels show the intersection of the (x, z) slice. Click here to view larger image.

Figure 3. Examples of gradient-filtered images. This image shows the effect of applying the gradient filter to the data in Figure 2. Note that the object of interest is highlighted as a symmetrical bright spot. Click here to view larger image.

Figure 4. Examples of data that lead to good and poor rendered images. The two images in panels (a) and (c) were taken from the same video of a tumbling chain of cells. The data in panel (a) are representative of most frames in this series, in which the chain is not oriented directly along the optical axis. The shape and position of the object are faithfully reproduced in the rendering in panel (b). In the case of panel (c), the chain was momentarily oriented end-on to the focal plane; objects in this configuration are difficult to reconstruct, and typically yield a 'blob' close to the focal plane, as seen in panel (d). Click here to view larger image.

Discussion

The most important step in this experimental protocol is the accurate capture of images from a stable experimental setup. With poor background data, high fidelity reconstruction is next to impossible. It is also important to avoid objective lenses with an internal phase contrast element (visible as a dark annulus when looking through the back of the objective), as this can degrade the reconstructed image. The object of interest should be far enough from the focal plane that a few pairs of diffraction fringes are visible in its image (a suitable heuristic is that the defocused pattern should appear to have 10 times the linear dimension of the focused object - see example data). Objects too close to the focal plane suffer from twin-image and sampling artifacts, as previously described. It is also important to have a good characterization of the camera's pixel spacing, as this is a critical factor in correctly determining refocus distances. Often, camera documentation will list 'pixel size' in the specifications; this can be a little ambiguous, because certain types of camera (CMOS cameras in particular) can have significant areas of the space between pixels that are not sensitive to light. The most reliable way to obtain this information is to use a standard calibration target, such as a USAF 1951 resolution chart, and measure the sampling frequency (number of pixels per micrometer) directly from an image.

In the limit of monochromatic illumination, the resolution of a DIHM system is ultimately set by the numerical aperture of the objective lens (NA) and the wavelength of illumination (λ)^23,24. Laterally separated points should lie at least a distance Δ_lat='λ'/2NA apart if they are to be separately resolved. Similarly, the axial resolution limit in the ideal case is given by 'Δ'_ax=λ/2(NA)². When using an LED in DIHM, there is a limit to the depth of the volume that may be imaged; this is ultimately determined by the optical system and the coherence of the illumination. A typical depth of this 'sensitive volume' is around 100-200 µm for an LED, though a detailed account of this type of effect can be found elsewhere²⁵. The sensitive volume is limited in the other two directions by the size of the image. Although the software is fairly robust, certain operations are rather memory-hungry. Reconstructing an image stack and obtaining the intensity gradient are both fairly conservative, but extracting the coordinates of a feature of interest from a gradient stack can consume a lot of memory (several hundred megabytes to several gigabytes). To this end, it is advisable to restrict the reconstructed volume of interest to 100-150 pixels in each dimension. This restriction can be eased somewhat if the code is run on a 64 bit operating system with more than 4 GB of RAM (the software was written on a machine with 12 GB), although computation time can become prohibitive.

To examine a larger system, the LED light source can be replaced by a laser, which allows reconstruction of objects lying at a much greater depth from the focal plane - easily up to millimeters - and at lower magnification. Preliminary experiments with such a setup, using a laser diode coupled to a single-mode optical fiber, allowed reconstructed depths up to 10 mm using a 10X microscope objective. This increased depth of field comes at a cost, however; the laser's large coherence length leads to image noise, particularly reflections from various surfaces in the optical train (the walls of the sample chamber, lens surfaces, etc.) These effects are offset somewhat when the apparatus is stable enough to get a good background image. However, extraneous reflections have an unknown distribution of phases, so if their magnitude is comparable to that of the reference wave (unscattered light), reconstruction can become impossible. Other authors have modified the coherence of a laser light source, for example, by modulating the laser driving current²⁶ or using a rotating ground glass screen to reduce coherence²⁷.

From a troubleshooting point of view, most problems encountered while using the holographic reconstruction software are best resolved by inspecting the interim stages of data analysis. In the case of the reconstructed image stack, the objects should 'deblur' symmetrically as they come into focus. If the diffraction fringes look strongly asymmetrical, a poor or offset background image is often to blame. If the image for reconstruction has been taken from a stack of similar images, for example a frame from a video sequence of a moving object, a background image can sometimes be obtained by averaging (by mean or median) pixel values across all of the video frames. If the subject moves substantially during the video sequence, its contribution to any one pixel value is small and the dominant contribution will come from the unaltered background frames in which the subject was absent. In the case where an object's coordinates are not properly returned, the gradient image stack can be a useful diagnostic. If the object is seen as a void surrounded by a bright ring in the gradient image stack, the gradient filter should be flipped and the image reprocessed. As mentioned in the introduction, the Rayleigh-Sommerfeld reconstruction method is insensitive to the sign of an object's distance from the focal plane. If two weakly-scattering objects are the same distance from the focal plane but on opposite sides, they would come into focus at the same position in the reconstructed image stack. However, their axial intensity patterns would be reversed. The center of the object originally found above the focal plane (with respect to the inverted microscope geometry) changes from light to dark on passing through the in-focus position, whereas the object below the focal plane changes from dark to light. The gradient-flip option therefore extracts either objects above the focal plane (default) or below the focal plane (with gradient-flip set to 'on'), giving an unambiguous axial coordinate. Note that this strictly holds only for weakly-scattering objects; the method works very well for polystyrene microspheres up to 1 µm in diameter, but less well for larger polystyrene particles. Biological samples typically exhibit much weaker scattering, as their refractive indices are closer to that of the surrounding medium (polystyrene has a refractive index close to 1.5), so larger objects can be studied.

In terms of future directions, this software could be extended to process multiple frames in a video, to enable tracking of swimming microorganisms or colloidal particles in three dimensions. The high frame rate that the technique affords is well suited to tracking even the fastest swimmers, such as the ocean-dwelling Vibrio alginolyticus, which swims at speeds up to 150 µm/sec²⁸. The microscopic swimming trajectories of single cells were first tracked some time ago²⁹, but this usually requires specialized apparatus. The Gouy phase anomaly approach not only lends itself to simple tracking of single cells over long distances, but affords the opportunity to examine correlations between the swimming behavior of different individuals. This depends specifically on three-dimensional geometry, data that has hitherto been inaccessible for technical reasons.

As mentioned in the introduction, a comparison with fluorescence confocal microscopy is not ideal, but the ubiquity of confocal systems makes a comparison of the three-dimensional imaging aspect worthwhile. In fact, DIHM is complementary to confocal microscopy; there are comparative advantages and disadvantages of both. DIHM allows much faster data acquisition rates: several thousand volumes per second is routine, given a fast enough camera. This allows tracking of (for example) multiple swimming bacteria, which is beyond the capability of slower confocal systems. Even with a fast camera, DIHM is an order of magnitude cheaper than confocal microscopy, and the data for a three-dimensional volume can be stored in a single two-dimensional image, reducing demands on data storage and backup. DIHM is more easily scalable in the sense that working with lower magnifications, larger samples and longer working distances is trivial. Confocal microscopy still has the upper hand in dense or complex samples, however. For example, in a dense colloidal suspension, multiple scattering makes holographic reconstruction practically impossible; a confocal system in either fluorescent emission or reflection mode would be better suited to studying such systems⁹. Moreover, confocal microscopy is a more natural choice for experimental systems in which fluorescent labeling is of central importance. Although fluorescence holography has been shown to work with a range of test subjects³⁰ the collection efficiency is currently far below that of a good confocal system. Furthermore, such experimental systems currently require specialist optical apparatus and experience to operate; hopefully they will become more widely available with further development.

In summary, DIHM is unparalleled in its ability to acquire high-resolution three-dimensional images of microscopic objects, at high speeds. We provide user-friendly software that makes this technique accessible to the nonspecialist with minimal modifications to an existing microscope. Furthermore, the reconstruction software integrates easily with freely available computer rendering software. This allows intuitive visualization of microscopic subjects, viewable from any angle. Given the three-dimensional nature of many fast microscopic processes involving weakly-scattering objects (e.g. beating eukaryotic flagella or cilia, swimming bacteria, or diffusing colloids), this technique should be of interest across a wide range of fields.

Disclosures

The authors declare that they have no competing financial interests.