Finite-volume WENO scheme for viscous compressible multicomponent flows

Abstract

We develop a shock- and interface-capturing numerical method that is suitable for the simulation of multicomponent flows governed by the compressible Navier-Stokes equations. The numerical method is high-order accurate in smooth regions of the flow, discretely conserves the mass of each component, as well as the total momentum and energy, and is oscillation-free, i.e. it does not introduce spurious oscillations at the locations of shockwaves and/or material interfaces. The method is of Godunov-type and utilizes a fifth-order, finite-volume, weighted essentially non-oscillatory (WENO) scheme for the spatial reconstruction and a Harten-Lax-van Leer contact (HLLC) approximate Riemann solver to upwind the fluxes. A third-order total variation diminishing (TVD) Runge-Kutta (RK) algorithm is employed to march the solution in time. The derivation is generalized to three dimensions and nonuniform Cartesian grids. A two-point, fourth-order, Gaussian quadrature rule is utilized to build the spatial averages of the reconstructed variables inside the cells, as well as at cell boundaries. The algorithm is therefore fourth-order accurate in space and third-order accurate in time in smooth regions of the flow. We corroborate the properties of our numerical method by considering several challenging one-, two- and three-dimensional test cases, the most complex of which is the asymmetric collapse of an air bubble submerged in a cylindrical water cavity that is embedded in 10% gelatin.

1. Introduction

The present work is motivated by the pervasive nature of multicomponent flows in practical applications. These flows often feature bubbles [1, 2] and/or droplets [3, 4] and develop rich dynamics as material interfaces deform and interact with other flow features such as shockwaves [5]. Interactions between material interfaces and shockwaves present unique challenges for the numerical method, which should satisfy three important criteria. It should maintain discrete conservation of the total mass, momentum and energy to correctly identify the position of important flow features. It should not generate spurious oscillations across either shockwaves or material interfaces to preserve numerical stability. And finally, for efficiency, it should be high-order accurate in smooth regions of the flow, away from discontinuities. Attempts at designing numerical schemes that satisfy these criteria can be classified into two categories based on the treatment of material interfaces. They are the interface-tracking and the interface-capturing methods.

Interface-tracking methods have the distinct advantage of treating material interfaces in a natural way, as sharp discontinuities. Arbitrary Lagrangian-Eulerian [6], free-Lagrange [7], front-tracking [8–11] and level set/ghost fluid [12–20] schemes all belong in this category. Their sharp treatment of material interfaces enables two fluids sharing an interface to have starkly different equations of state (EOS) and while at mechanical equilibrium, generally avoid the onset of spurious oscillations at the interface. They also have the advantage of rendering the implementation of any interfacial physics rather straightforward. Their primary drawback, however, is that they are typically not discretely conservative at material interfaces, which may lead them to incorrectly predict their position, as well as those of shockwaves, if the two flow features happen to interact during the computation.

Achieving discrete conservation in interface-capturing methods, on the other hand, is relatively simple. It is sufficient to solve the continuity, momentum and energy equations in conservative form, while relaxing the sharp character of material interfaces and thus allowing them to numerically diffuse over a small but finite region [21–31]. This numerical diffusion, unfortunately, gives rise to unphysical mixtures of fluids during computations, which, if not treated in a thermodynamically consistent manner and evolved in a fashion that is consistent with the continuity, momentum and energy equations, can lead to spurious oscillations at material interfaces. As a result, interface-capturing methods make the implementation of EOS that strongly differ from one another across material interfaces challenging and further, make it nontrivial to simulate a material interface that is simultaneously in mechanical equilibrium and void of spurious oscillations. Attempts to achieve the latter have even led some authors to sacrifice discrete conservation [32–35]. The implementation of interfacial physics also becomes more difficult, as it is not immediately clear how such effects can consistently be applied across a diffused material interface.

For both interface-tracking and interface-capturing methods, solutions to the aforementioned problems do exist. Discretely conservative interface-tracking methods have been developed in the past [6–8, 19, 20] and requirements to consistently treat mixtures of fluids while maintaining oscillation-free material interfaces and discrete conservation in interface-capturing methods are well-understood [29–31]. It has also been shown possible to implement interfacial physics in the latter, as recently demonstrated for heat transfer [25] and surface tension [27]. In this study, we prefer to develop an interface-capturing framework because achieving discrete conservation in it is straightforward and robust strategies for the treatment of mixtures of fluids and suppression of spurious oscillations at interfaces separating them are readily available. In the future, we are also interested in implementing surface tension and relaxing the assumption of immiscibility to include phase change. The inclusion of such interfacial physics, though more difficult in interface-capturing methods, is shown to be possible. Lastly, we choose to develop an interface-capturing scheme because they generally are more efficient than interface-tracking methods and their complexity does not increase with increasing simulation dimensionality or with the number of fluids.

To simultaneously achieve a discretely conservative, high-order and non-oscillatory interface-capturing scheme, several requirements must be satisfied. As previously mentioned, discrete conservation is the easiest to obtain and merely requires that the mass, momentum and energy equations be solved in conservative form. An oscillation-free behavior, on the other hand, is the most challenging. Foremost, it requires that material interfaces be evolved with an advection equation that is written in non-conservative form and is consistent with the conservation equations for mass, momentum and energy [29]. Mass fractions, volume fractions or specific functions of the EOS parameters are typically evolved. An oscillation-free interface-capturing method also requires that these equations of motion be closed by a thermodynamically consistent set of mixture rules, which are typically derived by assuming that mixtures are in mechanical equilibrium [28]. Care must then be taken when solving the resulting governing equations. They must be cast in a finite-volume framework and discretized with a non-oscillatory spatial and temporal method, with the primitive state variables, rather than the conservative ones, spatially reconstructed [30]. In order to achieve high-order accuracy while maintaining nearly non-oscillatory behavior, WENO spatial reconstructions [36–39] and TVD RK time-steppers [40] have been shown to perform well.

An interface-capturing scheme that meets nearly all of the above requirements was developed by Johnsen and Colonius [30] and applied to a compressible multicomponent flow model first introduced by Shyue [21]. The model consists of the Euler system of equations coupled with two advection equations, one for each function of the stiffened gas EOS parameters. To solve it, the numerical scheme of Johnsen and Colonius utilizes a fifth-order finite-volume WENO spatial reconstruction [37], an HLLC approximate Riemann solver [41] and a third-order TVD RK time-stepper [40]. The numerical method is discretely conservative and non-oscillatory but unfortunately, despite being advertised as such, is not formally high-order accurate. The authors fail to identify the propagation of a second-order spatial error that arises from the procedure utilized to obtain the cell average primitive variables from their conservative counterparts prior to reconstruction. The problem goes unnoticed in the convergence analysis as a consequence of considering a nearly linear test case. In our study, we propose a fix and extend their numerical framework to a more general compressible multicomponent flow model, three dimensions and include viscous effects. The new system of governing equations was first introduced by Massoni et al. [25] and Allaire et al. [28], and is more general than that of Shyue in that it conserves the mass of each fluid in the flow, rather than just the total mass, and advects the volume fraction of each fluid, rather than functions of the stiffened gas EOS parameters. We choose it because it has the distinct advantage of explicitly tracking each fluid in the flow, which facilitates the treatment of mixtures composed of more than two fluids and the future implementation of interfacial physics. In order to extend the numerical scheme for this model to three dimensions, we follow the work of Titarev and Toro [42] on finite-volume WENO schemes for three-dimensional conservation laws. Finally, we include the effects of viscosity based on the work of Perigaud and Saurel [27].

For the remainder of this paper, we proceed as follows. In Sec. 2, we introduce the viscous and compressible multicomponent flow equations. In Sec. 3, we describe the steps that are necessary to adapt and extend the numerical scheme of Johnsen and Colonius [30] to this model and three dimensions. We then present several benchmark problems in one, two and three dimensions in Sec. 4. These numerical tests validate our numerical method and corroborate its high-order accuracy, discrete conservation and oscillation-free behavior. Finally, in Sec. 5, we summarize our results and provide concluding remarks alongside suggestions for future work.

2. Governing equations

2.1. Five-equation model

We describe viscous and compressible multicomponent flows with the five-equation model first introduced in its inviscid form by Allaire et al. [28] and Massoni et al. [25] and subsequently extended to include viscous effects by Perigaud and Saurel [27]. The model was originally written for two fluids and is given in Eqs. (1)–(5). It consists of two continuity equations, Eqs. (1) and (2), a momentum and an energy equation, Eqs. (3) and (4), respectively, and an advection equation for the volume fraction of one of the two fluids, Eq. (5):

$$\frac{\partial ({\alpha }_1{\rho }_1)}{\partial t}+\nabla ·({\alpha }_1{\rho }_1\mathbf{u})=0,$$ (1)

$$\frac{\partial ({\alpha }_2{\rho }_2)}{\partial t}+\nabla ·({\alpha }_2{\rho }_2\mathbf{u})=0,$$ (2)

$$\frac{\partial (\rho \mathbf{u})}{\partial t}+\nabla ·(\rho \mathbf{uu}+\rho \mathbf{I}-\mathbf{T})=\mathbf{0},$$ (3)

$$\frac{\partial E}{\partial t}+\nabla ·((E+p)\mathbf{u}-\mathbf{T}·\mathbf{u})=0,$$ (4)

$$\frac{\partial {\alpha }_1}{\partial t}+\mathbf{u}·\nabla {\alpha }_1=0,$$ (5)

where ρ is the density, u = (u, v, w)^T is the velocity, p is the pressure, E is the total energy, α is the volume fraction, T is the viscous stress tensor and the subscripted variables indicate those quantities which are specific to the individual fluids. The viscous stress tensor is given by

$$\mathbf{T}=2\mu \left(\mathbf{D}-\frac{1}{3}(\nabla ·\mathbf{u})\mathbf{I}\right),$$ (6)

where μ is the shear viscosity and

$$\mathbf{D}=\frac{1}{2}\left(\nabla \mathbf{u}+{(\nabla \mathbf{u})}^{\mathrm{T}}\right)$$ (7)

is the deformation rate tensor. Note that to simplify the discussion, we have presently ignored the effects of bulk viscosity and further take the shear viscosity of each fluid to be constant. Both assumptions, however, can readily be generalized. Though the five-equation model is written for two fluids, it may easily be extended to account for additional fluids by supplementing the equations of motion with a continuity equation and a volume fraction advection equation for each new fluid that is added. For the sake of conciseness, however, we only consider the model for two fluids in our discussion and comment as necessary about extensions to the more general case.

We choose the five-equation model because it meets several key criteria, foremost of which is that it is cast in a quasi-conservative form that ensures that when using standard shock-capturing schemes, the required physical quantities are conserved, while spurious oscillations at the material interfaces are avoided, see Allaire et al. [28]. The compressible Navier-Stokes equations, Eqs. (1)–(4), which govern the flow of each fluid, are written in conservative form and conserve the mass of each fluid, as well as the total momentum and energy. The advection equation for the volume fraction on the other hand, Eq. (5), which specifies the position of the material interfaces between the two fluids, is not written in conservative form. This choice, along with that of the transported quantity, ensures that the advection equation is consistently coupled with the compressible Navier-Stokes equations so to lead to an oscillation-free behavior at material interfaces.

There are multiple alternatives to the five-equation model that meet the above criterion. The differences between these models and the current equations of motion range from conserving the total mass of the two fluids, versus the mass of each, to transporting alternate scalar quantities, most notably functions of the EOS parameters, versus the volume fraction [21–24, 29]. However, in interface-capturing methods, the former difference will typically lead to mass transfer between the supposedly immiscible fluids, while advecting functions of the EOS parameters not only leads to the dependence of the complexity of the equations of motion on the EOS, but can also result in a non-uniquely defined material interface position [31]. The latter two issues are further exasperated when more intricate EOS are considered and/or there are more than two fluids in the flow. We therefore find it preferable to build a numerical scheme around the more general five-equation model.

2.2. Stiffened gas EOS

The closure of the five-equation model is in part achieved with the stiffened gas EOS, which has widely been utilized in compressible multicomponent flow applications to describe pure gases, liquids and solids, such as air, water, copper and even uranium, to name a few [22, 43, 44]. This thermodynamic relationship was first introduced by Harlow and Amsden [45] and is given by

$$p=(\gamma -1)\rho \epsilon -\gamma {\pi }_{\infty },$$ (8)

where ε is the specific internal energy, with $\rho \epsilon =E-\frac{1}{2}\rho \mathbf{uu}$, and γ and π_∞ are fitting parameters. The associated sound speed is given by $c=\sqrt{\gamma (p+{\pi }_{\infty })/\rho }$. We note that the fitting parameters for a particular material are typically determined from its shockwave Hugoniot data. The fitting procedure is described in detail by Cocchi et al. [43], while an extensive database of shockwave Hugoniot data for different materials has been assembled by Marsh [46].

Though the shockwave Hugoniot database of Marsh [46] has been extensively utilized in literature to fit the stiffened gas EOS parameters, we do not use it here for two reasons. One, we are interested in compressible multicomponent flow applications at low pressures, (10²) MPa, and the database was assembled for materials tested at extremely high pressures, 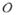(10) GPa. Two, for water, which we are interested in modeling with the stiffened gas EOS, authors utilizing the database have obtained fitting parameters that result in a physically incorrect sound speed at ambient conditions, see for example [9, 22, 27, 43]. We resolve both of these issues by using the shockwave Hugoniot data of Gojani et al. [47]. For materials of interest, the stiffened gas EOS parameters fitted from the latter, along with the density and sound speed, are listed in Table 1. For completeness, the properties of air are also included in the table. Air obeys the ideal gas law, a special case of the stiffened gas EOS when π_∞ = 0 Pa and γ is the ratio of specific heats.

Table 1.

Properties of air, helium, water and 10% gelatin at normal temperature and pressure. These include the density, ρ, the sound speed, c, and the stiffened gas EOS fitting parameters, γ and π_∞.

Fluid	ρ [kg/m3]	c [m/s]	γ	π∞ [Pa]
Air	1.204	343	1.40	0
Helium	0.166	1008	1.67	0
Water	1000	1450	6.12	3.43 × 108
10% Gelatin	1030	1553	6.72	3.70 × 108

2.3. Mixture rules

To complete the closure of the five-equation model, a set of rules governing the properties of mixtures of fluids must be established. The mixtures are artifacts of the numerical scheme and occur in narrow regions surrounding material interfaces as a result of numerical diffusion inherent to all interface-capturing methods. It is common practice to define the following rules for the mixture volume fraction, Eq. (9), density, Eq. (10), and internal energy, Eq. (11):

$$1={\alpha }_1+{\alpha }_2,$$ (9)

$$\rho ={\alpha }_1{\rho }_1+{\alpha }_2{\rho }_2,$$ (10)

$$\rho \epsilon ={\alpha }_1{\rho }_1{\epsilon }_1+{\alpha }_2{\rho }_2{\epsilon }_2.$$ (11)

Two additional rules may then be derived by assuming that each pure fluid composing the mixture is at the same pressure. This is referred to as the isobaric assumption and it is consistent with the modeled flow physics in that in the absence of surface tension, the pressure across an isolated material interface should not vary, see Allaire et al. [28] for a more rigorous consistency analysis. Combining Eqs. (8) and (11) with the isobaric assumption yields the mixture rules for two functions of the stiffened gas EOS parameters:

$$\mathrm{\Gamma }={\alpha }_1{\mathrm{\Gamma }}_1+{\alpha }_2{\mathrm{\Gamma }}_2,$$ (12)

$${\mathrm{\Pi }}_{\infty }={\alpha }_1{\mathrm{\Pi }}_{\infty ,1}+{\alpha }_2{\mathrm{\Pi }}_{\infty ,2},$$ (13)

where Γ = 1/(γ − 1) and Π_∞ = γπ_∞/(γ − 1). The closure of the equations of motion is finalized by defining a mixture rule for the coefficient of shear viscosity. Following Perigaud and Saurel [27], we choose

$$\mu ={\alpha }_1{\mu }_1+{\alpha }_2{\mu }_2.$$ (14)

Note that all of the above properties of a mixture are obtained through the linear combination of the analogous properties of the pure fluids composing it. As such, extending Eqs. (9)–(14) to account for additional fluids is straightforward.

It is worth mentioning at this time that although Eqs. (9)–(11) and (14) appropriately describe any mixture of fluids, depending on the choice of the EOS or if the fluids composing the mixture are each governed by a different EOS, it may not be possible to derive analytical expressions for the remaining mixture relationships, e.g. Eqs. (12) and (13), in order to complete the closure of the five-equation model. In such cases, the isobaric constraint can be utilized within an iterative procedure to determine the remaining mixture properties. This procedure, along with analytical expressions for some other common EOS, such as the van der Waals and Mie-Gruneisen laws, are provided in detail by Allaire et al. [28].

3. Numerical method

3.1. Spatial discretization

The five-equation model is a hyperbolic and quasi-conservative system of equations [28] and is well suited for numerical approximation by Godunov-type schemes. The latter are reconstruct-evolve-average methods and rely on reconstructed values of the cell averages of the solution at the cell faces for the determination of the average fluxes at the cell faces, which are subsequently utilized to evolve the cell averages of the solution in time [41, 48]. We seek to design such a method for the five-equation model and have it satisfy three important criteria: high-order accuracy, discrete conservation and non-oscillatory behavior. We begin by spatially discretizing the equations of motion in their conservation-law form:

$$\frac{\partial \mathbf{q}}{\partial t}+\frac{\partial {\mathbf{f}}^{\mathrm{a}}(\mathbf{q})}{\partial x}+\frac{\partial {\mathbf{g}}^{\mathrm{a}}(\mathbf{q})}{\partial y}+\frac{\partial {\mathbf{h}}^{\mathrm{a}}(\mathbf{q})}{\partial z}=\frac{\partial {\mathbf{f}}^{\mathrm{d}}(\mathbf{q})}{\partial x}+\frac{\partial {\mathbf{g}}^{\mathrm{d}}(\mathbf{q})}{\partial y}+\frac{\partial {\mathbf{h}}^{\mathrm{d}}(\mathbf{q})}{\partial z}+\mathbf{s}(\mathbf{q}),$$ (15)

where q is the vector of state variables, f, g and h are vectors of fluxes, s is the vector of source terms and the superscripts “a” and “d” denote advective and diffusive fluxes, respectively, see Appendix A for details. Note that the transport equation for the volume fraction takes a different but mathematically equivalent form in Eq. (15) compared to in Eq. (5):

$$\frac{\partial {\alpha }_1}{\partial t}+\nabla ·({\alpha }_1\mathbf{u})={\alpha }_1\nabla ·\mathbf{u}.$$ (16)

This form was introduced by Johnsen and Colonius [30] and is necessary to later adapt the HLLC approximate Riemann solver to the advection equation. Eq. (15) is discretized on a finite-volume Cartesian grid by considering an arbitrary cell in the grid and integrating Eq. (15) over its control volume, I_i,j,k, denoted by

$$I_{i,j,k}=\left[x_{i-1/2},x_{i+1/2}\right]\times \left[y_{j-1/2},y_{j+1/2}\right]\times \left[z_{k-1/2},z_{k+1/2}\right],$$ (17)

where i, j and k are the indices of the cell in the x-, y- and z-directions, respectively, and x_i±1/2, y_j±1/2 and z_k±1/2 are the positions of the cell faces. The result of the spatial integration, simplified by the application of the divergence theorem, yields the following semi-discrete form of Eq. (15):

$$\begin{array}{l}\frac{\mathrm{d}{\mathbf{q}}_{i,j,k}}{\mathrm{d}t}=\frac{1}{\mathrm{\Delta }{x}_i}\left[\left({\mathbf{f}}_{i-1/2,j,k}^{\mathrm{a}}-{\mathbf{f}}_{i+1/2,j,k}^{\mathrm{a}}\right)-\left({\mathbf{f}}_{i-1/2,j,k}^{\mathrm{d}}-{\mathbf{f}}_{i+1/2,j,k}^{\mathrm{d}}\right)\right]\\ +\frac{1}{\mathrm{\Delta }{y}_j}\left[\left({\mathbf{g}}_{i,j-1/2,k}^{\mathrm{a}}-{\mathbf{g}}_{i,j+1/2,k}^{\mathrm{a}}\right)-\left({\mathbf{g}}_{i,j-1/2,k}^{\mathrm{d}}-{\mathbf{g}}_{i,j+1/2,k}^{\mathrm{d}}\right)\right]\\ +\frac{1}{\mathrm{\Delta }{z}_k}\left[\left({\mathbf{h}}_{i,j,k-1/2}^{\mathrm{a}}-{\mathbf{h}}_{i,j,k+1/2}^{\mathrm{a}}\right)-\left({\mathbf{h}}_{i,j,k-1/2}^{\mathrm{d}}-{\mathbf{h}}_{i,j,k+1/2}^{\mathrm{d}}\right)\right]+{\mathbf{s}}_{i,j,k},\end{array}$$ (18)

where the state variables and the source term are now averages over the cell volume, while the flux vectors are averages over the cell faces. These spatial averages take the following form:

$${\mathbf{q}}_{i,j,k}=\frac{1}{V_{i,j,k}}{\int }_{z_{k-1/2}}^{z_{k+1/2}}{\int }_{y_{j-1/2}}^{y_{j+1/2}}{\int }_{x_{i-1/2}}^{x_{i+1/2}}\mathbf{q}(x,y,z,t)\mathrm{d}x\mathrm{d}y\mathrm{d}z,$$ (19)

$${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{a}}=\frac{1}{\mathrm{\Delta }{y}_j\mathrm{\Delta }{z}_k}{\int }_{z_{k-1/2}}^{z_{k+1/2}}{\int }_{y_{j-1/2}}^{y_{j+1/2}}{\mathbf{f}}^{\mathrm{a}}(\mathbf{q}(x_{i+1/2},y,z,t))\mathrm{d}y\mathrm{d}z,$$ (20)

$${\mathbf{s}}_{i,j,k}=\frac{1}{V_{i,j,k}}{\int }_{z_{k-1/2}}^{z_{k+1/2}}{\int }_{y_{j-1/2}}^{y_{j+1/2}}{\int }_{x_{i-1/2}}^{x_{i+1/2}}\mathbf{s}(\mathbf{q}(x,y,z,t))\mathrm{d}x\mathrm{d}y\mathrm{d}z,$$ (21)

where Δx_i = x_i+1/2 − x_i−1/2, Δy_j = y_j+1/2 − y_j−1/2, Δz_k = z_k+1/2 − z_k−1/2 and V_i,j,k = Δx_iΔy_jΔz_k. Note that only the form of one flux vector is provided, as the form of the remaining ones is analogous. Eq. (18) is the end result of the spatial discretization of Eq. (15). It remains, however, an exact relationship and must now be numerically approximated.

We proceed by first numerically approximating the right-hand side (RHS) of Eq. (18). To do so, the surface integrals of the fluxes, e.g. Eq. (20), and the volume integral of the source term, Eq. (21), need to be estimated. Titarev and Toro [42] suggest utilizing a two-point, fourth-order, Gaussian quadrature rule, as it offers a good balance between accuracy and computational cost when paired with a high-order WENO spatial reconstruction scheme. Then, applying the two-point Gaussian quadrature rule to Eq. (20), we get

$${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{a}}\approx \frac{1}{4}\sum _{m=1}^2\sum _{l=1}^2{\mathbf{f}}^{\mathrm{a}}\left(\mathbf{q}\left(x_{i+1/2},y_{j_l},z_{k_m},t\right)\right),$$ (22)

where y_jl and z_km are the y- and z-coordinates of the Gaussian quadrature points and are given by

$$y_{j_l}=y_j+(2l+1)\frac{\mathrm{\Delta }{y}_j}{2\sqrt{3}}\text{and}{z}_{k_m}=z_k+(2m+1)\frac{\mathrm{\Delta }{z}_k}{2\sqrt{3}},$$ (23)

with the indices j_l and k_m defined as

$$j_l=j+(2l+1)\frac{1}{2\sqrt{3}}\text{and}{k}_m=k+(2m+1)\frac{1}{2\sqrt{3}}.$$ (24)

Note that the surface integrals of the remaining fluxes are treated analogously. Next, we seek to apply the two-point Gaussian quadrature rule to the volume integral of the source term. In doing so, however, we must ensure that the velocity utilized in the numerical integration of the source term is consistent with that utilized in the numerical integration of the fluxes. To satisfy this requirement for the source term of the advection equation, we follow the work of Johnsen and Colonius [30] in approximating its volume integral with a midpoint rule and the divergence of the velocity therein with a centered scheme. As a result, we get

$${({\alpha }_1\nabla ·\mathbf{u})}_{i,j,k}\approx {\alpha }_{1_{i,j,k}}\left[\frac{1}{\mathrm{\Delta }{x}_i}\left(u_{i+1/2,j,k}-u_{i-1/2,j,k}\right)+\frac{1}{\mathrm{\Delta }{y}_j}\left(v_{i,j+1/2,k}-v_{i,j-1/2,k}\right)+\frac{1}{\mathrm{\Delta }{z}_k}\left(w_{i,j,k+1/2}-w_{i,j,k-1/2}\right)\right],$$ (25)

which utilizes the same velocity as Eq. (18) does to evaluate the fluxes. We note that though Eq. (25) is formally only second-order accurate, the error is zero everywhere except near material interfaces, which are not resolvable beyond first-order accuracy in any case. The above simplification now requires us to numerically integrate the source term as a surface integral, rather than a volume one. Specifically, we must now apply the two-point Gaussian quadrature rule to the surface integrals of the velocity components in Eq. (25). In doing so, we get

$$u_{i+1/2,j,k}\approx \frac{1}{4}\sum _{m=1}^2\sum _{l=1}^{2}u\left(\mathbf{q}\left(x_{i+1/2},y_{j_l},z_{k_m},t\right)\right),$$ (26)

with the remaining velocity components treated analogously.

The last step to finalizing the numerical approximation of the RHS of Eq. (18) is to reconstruct the state variables at the Gaussian quadrature points on every cell face in order to be able to evaluate the quadrature rule for all of the fluxes, e.g. Eq. (22), and the velocity components in the source term, e.g. Eq. (26). To obtain high-order accuracy spatially and avoid introducing spurious oscillations, we utilize a fifth-order WENO scheme to reconstruct the state variables from both the left and the right side of each cell face. An appropriate monotone function of the dual values of the state variables is then utilized to evaluate the fluxes, e.g.

$${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{a}}\approx \frac{1}{4}\sum _{m=1}^2\sum _{l=1}^2{\widehat{\mathbf{f}}}^{\mathrm{a}}\left({\mathbf{q}}_{i+1/2,j_l,k_m}^{\mathrm{L}},{\mathbf{q}}_{i+1/2,j_l,k_m}^{\mathrm{R}}\right),$$ (27)

and the velocity components in the source term, e.g.

$$u_{i+1/2,j,k}\approx \frac{1}{4}\sum _{m=1}^2\sum _{l=1}^2\widehat{u}\left({\mathbf{q}}_{i+1/2,j_l,k_m}^{\mathrm{L}},{\mathbf{q}}_{i+1/2,j_l,k_m}^{\mathrm{R}}\right),$$ (28)

where “L” and “R” denote the state variables reconstructed from the left and the right side of a cell face, respectively, and the hat superscript indicates the monotone function counterpart of the superscripted variable. The choice of a monotone function enables us to compute a singular value of the fluxes at each cell face and achieve the familiar telescoping property of the fluxes [41, 48], which guarantees that the numerical method is discretely conservative. Further details on the WENO reconstruction may be found in Appendix C, while those on the choice of a monotone function are provided in the overview of the HLLC approximate Riemann solver, in Appendix D.

3.2. Reconstructed variables

The choice of the reconstructed state variables is not unique and in practice, it is preferable not to reconstruct the conservative variables as this will introduce spurious oscillations near material interfaces, as well as in regions where discontinuities of different characteristic fields interact [49, 50]. In order to avoid introducing spurious oscillations near material interfaces, Johnsen and Colonius [30] showed that the primitive variables should be reconstructed. They further demonstrated that by projecting the primitive variables onto the characteristic fields prior to the reconstruction and thus reconstructing the characteristic variables, the introduction of spurious oscillations in regions where discontinuities of different characteristic fields interact could also be avoided.

Recall, however, that at the beginning of each time-step, only the cell average conservative variables are available. To remedy this, Johnsen and Colonius [30] suggest obtaining a second-order accurate estimate of the cell average primitive variables by directly computing them from the conservative ones. They argue that a WENO interpolation of this second-order accurate approximation will nevertheless result in a high-order accurate reconstruction. But, as we illustrate in Sec. 4.4, this is in general not the case and in fact, usually reduces the formal order of the spatial accuracy of the numerical method to second-order. We recover a high-order accurate scheme by discretizing the volume integral of the primitive variables, v, i.e.

$${\mathbf{v}}_{i,j,k}=\frac{1}{V_{i,j,k}}{\int }_{z_{k-1/2}}^{z_{k+1/2}}{\int }_{y_{j-1/2}}^{y_{j+1/2}}{\int }_{x_{i-1/2}}^{x_{i+1/2}}\mathbf{v}(\mathbf{q}(x,y,z,t))\mathrm{d}x\mathrm{d}y\mathrm{d}z,$$ (29)

with the two-point Gaussian quadrature rule to get a fourth-order accurate estimate of the cell average primitive variables:

$${\mathbf{v}}_{i,j,k}\approx \frac{1}{8}\sum _{n=1}^2\sum _{m=1}^2\sum _{l=1}^2\mathbf{v}\left(\mathbf{q}\left(x_{i_l},y_{j_m},z_{k_n},t\right)\right),$$ (30)

where v is defined in Appendix B. Then, at the beginning of each time-step, in order to obtain the cell average primitive variables, the cell average conservative variables must first be reconstructed at the Gaussian quadrature points in the cell volume. The cell average primitive variables may subsequently be projected onto the characteristic fields by following the procedure outlined in Appendix B.

We note that in addition to the characteristic variables, the cell average of the gradient of the velocity must also be reconstructed at the Gaussian quadrature points of both the left and right side of each cell face. This is necessary in order to evaluate the viscous terms in the diffusive fluxes. We evaluate the cell average of the gradient of the velocity by applying the divergence theorem to the volume integral of each of its terms in order to obtain the following surface integral:

$$\nabla {\mathbf{u}}_{i,j,k}=\frac{1}{V_{i,j,k}}{\int }_{V_{i,j,k}}\nabla \mathbf{u}\mathrm{d}V=\frac{1}{V_{i,j,k}}{\int }_{\partial V_{i,j,k}}\mathbf{nu}\mathrm{d}A,$$ (31)

which may then be evaluated to obtain, for example, the first column vector of ∇u_i,j,k:

$$\frac{\partial {\mathbf{u}}_{i,j,k}}{\partial x}=\frac{{\mathbf{u}}_{i+1/2,j,k}-{\mathbf{u}}_{i-1/2,j,k}}{\mathrm{\Delta }x},$$ (32)

with the remaining column vectors, those for the spatial derivatives of the cell average velocity in the y- and z-direction, taking a similar form. Note from Eq. (32) that in order to obtain all of the elements of ∇u_i,j,k and reconstruct them at the cell faces, the average velocity at the cell faces must first be computed. In Appendix E, we outline all of the variables that must be reconstructed and the order in which their reconstruction must be carried out.

3.3. Temporal integration

To complete the design of the numerical method, the semi-discrete approximation of the equations of motion must now be temporally integrated. Since the latter is a system of ordinary differential equations, we choose an RK time-marching scheme to evolve the state variables in time. In particular, to achieve high-order accuracy temporally and avoid introducing spurious oscillations, we follow Johnsen and Colonius [30] and Titarev and Toro [42] in choosing the low-storage, third-order, TVD RK time-marching scheme of Gottlieb and Shu [40]:

$$\begin{array}{l}{\mathbf{q}}_{i,j,k}^{(1)}={\mathbf{q}}_{i,j,k}^n+\mathrm{\Delta }t\mathbf{L}\left({\mathbf{q}}_{i,j,k}^n\right),\hfill \\ {\mathbf{q}}_{i,j,k}^{(2)}=\frac{3}{4}{\mathbf{q}}_{i,j,k}^n+\frac{1}{4}{\mathbf{q}}_{i,j,k}^{(1)}+\frac{1}{4}\mathrm{\Delta }t\mathbf{L}\left({\mathbf{q}}_{i,j,k}^{(1)}\right),\hfill \\ {\mathbf{q}}_{i,j,k}^{n+1}=\frac{1}{3}{\mathbf{q}}_{i,j,k}^n+\frac{2}{3}{\mathbf{q}}_{i,j,k}^{(2)}+\frac{2}{3}\mathrm{\Delta }t\mathbf{L}\left({\mathbf{q}}_{i,j,k}^{(2)}\right),\hfill \end{array}\}$$ (33)

where L is the operator evaluating the numerically approximated RHS of Eq. (18), the superscripts (1) and (2) denote the intermediate time-stages between two consecutive time-steps, and the superscripts n and n + 1 denote the current and the subsequent time-steps, respectively. With the choice of time-stepper made, the design of the numerical scheme is now complete and overall, the algorithm satisfies the desired criteria previously outlined, i.e. it is high-order accurate, discretely conservative and non-oscillatory.

3.4. Stability

The stability of the numerical scheme is dictated by the Courant-Friedrichs-Lewy (CFL) number, C, and the diffusion number, D. Unfortunately, as a result of the nonlinear behavior of both the equations of motion and the WENO reconstruction, the stability bounds of either criterion are not readily obtainable by analytic methods. Though these bounds could be determined through extensive numerical experimentation, in practice, we find it simpler to guide our choice of a stable time-step by relying on the readily available stability results for a forward in time, centered in space, numerical scheme applied to the linear advection-diffusion equation, where 0 < C, 2D ≤ 1/N and N is the number of dimensions. We note, however, that since we are applying a linear stability result to a nonlinear problem, these bounds are not conservative and in general, a time-step smaller than that predicted is necessary to maintain stability. We also note that the strong time-step restriction imposed by the diffusion number can be removed by an implicit treatment of the viscous terms, by utilizing a semi-implicit Runge-Kutta method for example [51], as done in [52].

Of course, since the numerical scheme is not TVD due to the WENO reconstruction, even for a forbiddingly small choice of time-step, stability cannot be guaranteed in the long-term when evolving a general initial condition. This issue is particularly relevant to the simulation of flows featuring the interaction of shockwaves and material interfaces with high pressure and density ratios, respectively. In such cases, WENO may not be able to find a smooth stencil during reconstruction and may interpolate values for a variable that a) are outside its physical range, b) will be outside its physical range once it is updated and/or c) will result in other variables, which are computed from the one that is reconstructed, to lay outside their physical range. In the worst-case scenario, a simulation may have to be abruptly terminated. In our experience, this is typically the case when an unphysical sound speed is recovered.

Some authors have proposed partly alleviating this problem by either reducing the order of the reconstruction [42] or utilizing flux limiters [53–55] in the affected regions of the flow. This, however, may lead to excessive smearing of material interfaces as they evolve or, in the case that an interface-sharpening technique is employed as a remedy, a loss of discrete conservation [54]. Note that while it is true that discretely conservative interface-sharpening techniques do exist for diffuse interface methods [56], their robustness remains to be rigorously documented when applied to material interfaces with high density ratios and which are interacting with strong shockwaves.

To maintain the desired properties of our numerical scheme, we do not utilize any of the above methods. Instead, when necessary, we primarily increase stability by initially smearing material interfaces over a few cells, as well as reducing the number of WENO reconstructions per time-step near them. The latter is achieved by omitting all of the reconstructions at the Gaussian quadrature points. Note that this neither affects the formal order of accuracy near material interfaces, nor, in our experience, negatively impacts their smearing. We also utilize monotonicity preserving bounds for WENO near material interfaces to prevent the reconstruction of a variable outside its physical range [38]. Finally, for viscous simulations, we limit the coefficient of shear viscosity in mixture regions to the range established by the components composing the mixture in order to avoid the onset of anti-diffusion.

Note that though the above-proposed strategies are sufficient to maintain numerical stability in the challenging test cases considered in this study, it is difficult to predict a priori whether they will be adequate for an arbitrarily chosen initial condition since the numerical scheme remains non-TVD. In the case that they are not, reducing the order of the reconstruction or using flux limiters, as in [42, 53–55], may be inevitable to increase stability, in spite of the additional smearing of material interfaces. If necessary, these strategies can be implemented at relatively low computational cost and effort in the present numerical scheme.

4. Numerical results

In the sections that follow, we present one-, two- and three-dimensional test cases to validate and verify our numerical scheme. Specifically, we show that the present algorithm is high-order accurate in smooth regions of the flow, discretely conserves the mass of each component, along with the total momentum and energy, and does not generate spurious oscillations. Also note that unless it is specified otherwise, the properties of the fluids utilized in each test case may be found in Table 1.

4.1. Isolated interface advection

The onset of spurious oscillations at material interfaces can have a detrimental impact on both the quality and reliability of computed solutions. It can result in the pollution of fine flow features [31], the premature growth of physical instabilities [30] and the thickening of material interfaces [33]. Worse, it may even result in the computation of the wrong solution [14] or the fatal termination of the computation [33]. Of course, the severity of these problems will depend on the initial condition [29]. To illustrate some of these issues for a numerical scheme plagued by spurious oscillations and to confirm that the proposed numerical scheme does not experience them, we consider an initial condition relevant to many multicomponent flow computations – the advection of an isolated air/water interface.

In particular, we consider an air/water interface under atmospheric pressure, advected in a periodic domain and at a constant velocity. The initial condition for this problem, non-dimensionalized by the density and sound speed of water, is given by

$$({\alpha }_1{\rho }_1,{\alpha }_2{\rho }_2,u,p,{\alpha }_1)=\{\begin{array}{lll}(1.204\times {10}^{-3},0,0.01,4.819\times {10}^{-5},1)\hfill & \text{for}\hfill & \hfill -1\le x<0,\\ (0,1,0.01,4.819\times {10}^{-5},0)\hfill & \text{for}\hfill & \hfill 0\le x<1.\end{array}$$ (34)

It is evolved with a constant time-step, Δt = 5 × 10⁻³, on a uniform grid composed of 200 cells, for exactly one period, i.e. until the material interface has returned to its original position. Three different methods are utilized to compute the numerical solution. In the first, the conservative variables, instead of the primitive variables, are reconstructed at the cell boundaries in order to demonstrate how the onset of spurious oscillations at the material interface corrupts the numerical solution. In the second, following Johnsen and Colonius [30], the primitive variables are reconstructed from their second-order accurate cell averages in order to recover an oscillation-free material interface. Finally, the initial condition is also evolved with the present numerical scheme, where the primitive variables are reconstructed from their fourth-order accurate cell averages, to confirm that the oscillation-free character of the material interface, recovered by the previous method, is conserved.

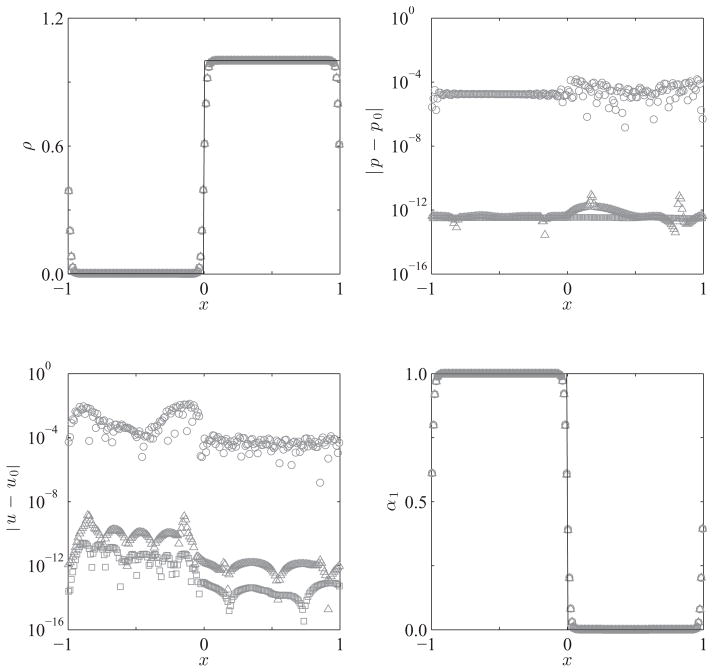
In Fig. 1, we compare the results obtained by all three methods, both to each other, as well as to the exact solution. We include the plots for density, velocity, pressure and the volume fraction. Note that in order to be able to visualize the spurious oscillations in velocity and pressure for all three methods, on the same plots, the absolute value of the difference between the approximate and exact solutions is plotted for these quantities, instead of the quantities themselves. The results in Fig. 1 are as expected. When the conservative variables are reconstructed, spurious oscillations are generated at the material interface. For the chosen initial condition, these are unacceptably large, at times matching, and even surpassing, the order of magnitude of the uniform velocity and pressure. As a result, though not shown, the pressure computed by this method often becomes negative, which is supported by the stiffened gas EOS, but is bound to mispredict a change in phase, if the latter physics were to be included. Nevertheless, the plots of density and volume fraction indicate that the position of the material interface, as well as the jump in these quantities across it, are correctly computed.

Figure 1.

Plots of density, magnitude of the error in velocity and pressure, and volume fraction for the isolated interface advection problem given by Eq. (34). The exact solution (—), along with three numerical solutions distinguished by the type and order of accuracy of the cell average variables that are reconstructed at the cell boundaries, are compared at t = 200. The latter include the conservative variables ( ), the second-order accurate primitive variables ( ), following Johnsen and Colonius [30], and the fourth-order accurate primitive variables ( ), following the present numerical scheme.

When the primitive variables are reconstructed from their second-order accurate cell averages, on the other hand, the spurious oscillations are reduced to the order of the round-off error. In the current case, for both the velocity and pressure, this corresponds to 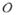(10⁻¹²), which is well below the order of magnitude of the corresponding uniform values. Note that reconstructing the primitive variables from their fourth-order accurate cell averages only marginally compromises this result, suggesting that the present numerical scheme conserves the oscillation-free character at material interfaces. Though not shown, comparable results were also obtained for other initial conditions. Finally, note that in both cases, the correct density and volume fraction profiles are also computed.

4.2. Shock-interface interaction

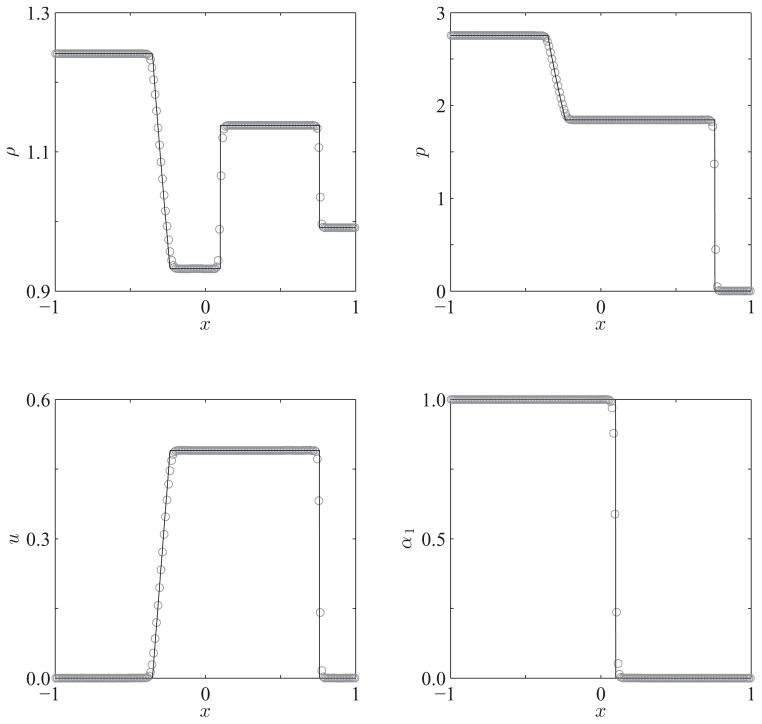
As previously indicated, the interaction between a shockwave and a material interface is a challenging problem for numerical schemes that have sacrificed discrete conservation at the material interface to either sharpen it or to avoid spurious oscillations. Most commonly, such methods will miscalculate the position and speed of the waves resulting from the interaction, with the error becoming increasingly worse with an increasing loss in conservation. To study the behavior of our numerical scheme when applied to such problems, we consider here the interaction between a strong shockwave in helium and an air/helium interface.

The original problem was studied by Liu et al. [15] and later, in modified form, by Johnsen [57]. As given by the latter, the problem consists of a Mach 8.96 shockwave traveling in helium toward a material interface with air, which is simultaneously moving toward the shockwave. Both the unprocessed helium and the air are at atmospheric pressure. The initial condition for this problem, utilizing the fluid properties and non-dimensionalization as in [57], is given by

$$({\alpha }_1{\rho }_1,{\alpha }_2{\rho }_2,u,p,{\alpha }_1)=\{\begin{array}{lll}(0.386,0,26.59,100,1)\hfill & \text{for}\hfill & \hfill -1\le x<-0.8,\\ (0.1,0,-0.5,1,1)\hfill & \text{for}\hfill & \hfill -0.8\le x<-0.2,\\ (0,1,-0.5,1,0)\hfill & \text{for}\hfill & \hfill -0.2\le x\le 1.\end{array}$$ (35)

The solution is evolved with a constant time-step, Δt = 10⁻⁴, on a uniform grid composed of 200 cells, and consists of the original shockwave partly transmitted into the air and partly reflected back into the helium.

In Fig. 2, the exact and numerical solutions for the density, velocity, pressure and volume fraction are given at t = 0.07. The numerical solution compares well to the exact one, correctly identifying the position and speed of all of the waves in the problem. Once again, no spurious oscillations at the material interface are observed. However, some oscillations in the wake of the reflected shockwave are present. These are a consequence of the high-order accuracy of the spatial reconstruction and, though not shown, disappear as the latter is reduced.

Figure 2.

Plots of density, velocity, pressure and volume fraction for the shock-interface interaction problem given by Eq. (35). The exact (—) and numerical ( ) solutions are compared at t = 0.07.

4.3. Gas-liquid Riemann problem

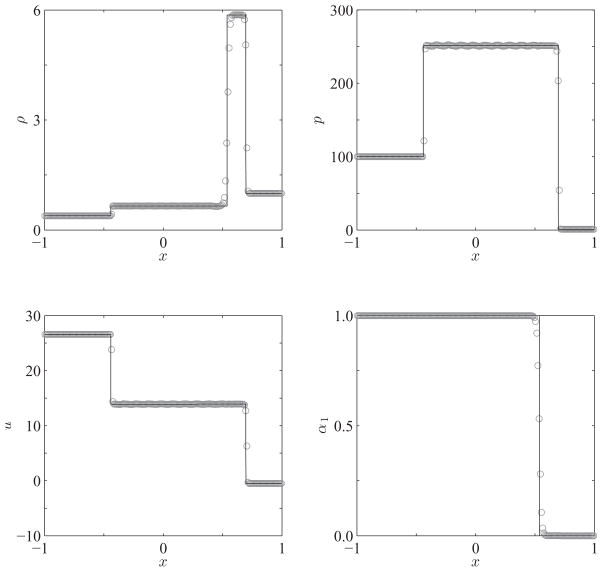
The last one-dimensional test case that we consider is a gas-liquid Riemann problem originally studied by Cocchi et al. [43], and subsequently by Shyue [21], as a model for underwater explosions. It is a challenging shock tube problem and provides an excellent test of the stiffened gas EOS. The left state of the problem consists of highly compressed air, while the right state is water at atmospheric pressure. The initial condition for this problem, utilizing the fluid properties and non-dimensionalization as in [43], is given by

$$({\alpha }_1{\rho }_1,{\alpha }_2{\rho }_2,u,p,{\alpha }_1)=\{\begin{array}{lll}(1.241,0,0,2.753,1)\hfill & \text{for}\hfill & \hfill -1\le x<0,\\ (0,0.991,0,3.059\times {10}^{-4},0)\hfill & \text{for}\hfill & \hfill 0\le x\le 1.\end{array}$$ (36)

It is evolved with a constant time-step, Δt = 10⁻³, on a uniform grid composed of 200 cells, and consists of a left-moving rarefaction wave and a right-moving shockwave and material interface.

In Fig. 3, the exact and numerical solutions for the density, velocity, pressure and volume fraction are given at t = 0.2. As in the previous test cases, the numerical solution compares well to the exact one and correctly identifies the position and speed of all of the waves in the problem. Moreover, there are no visible oscillations at the material interface or elsewhere in the solution.

Figure 3.

Plots of density, velocity, pressure and volume fraction for the gas-liquid Riemann problem given by Eq. (36). The exact (—) and numerical ( ) solutions are compared at t = 0.2.

4.4. Isentropic vortex

We consider next a two-dimensional problem governed by the Euler equations for which an analytical solution is readily available – the evolution of an isentropic vortex. The problem was studied by Balsara and Shu [38] and subsequently by Titarev and Toro [42] in order to assess the convergence properties of increasingly higher-order accurate WENO schemes for smooth solutions to the Euler equations. Similarly, we study this problem here to verify that the present numerical scheme achieves high-order accuracy away from shockwaves and material interfaces and also to demonstrate that the original method of Johnsen and Colonius [30] fails to do the same.

The isentropic vortex is a perturbation superimposed on the mean flow of an ideal gas and its initial condition may compactly be written in terms of the perturbed velocities, u′ and v′, and temperature, T′:

$$\begin{array}{l}{u}^{\prime }=\frac{\epsilon }{2\pi }exp\left[\alpha \left(1-r^2\right)\right]y,\hfill \\ v^{\prime }=-\frac{\epsilon }{2\pi }exp\left[\alpha \left(1-r^2\right)\right]x,\hfill \\ T^{\prime }=-\frac{(\gamma -1)}{16\alpha \gamma {\pi }^2}exp\left[2\alpha \left(1-r^2\right)\right],\hfill \end{array}\}$$ (37)

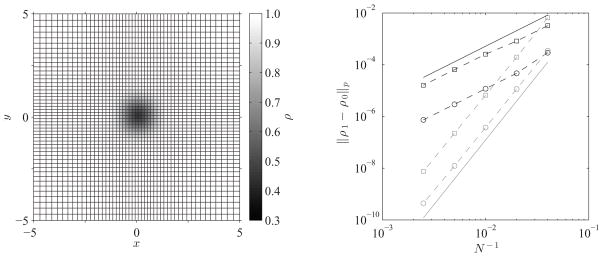
where ε is the strength of the vortex, α is its decay rate, r² = x² + y² and the usual primitive variables may be obtained from the ideal gas law, p = ρT, and the isentropic relationship p = ρ^γ. We note that it is typical to superimpose the vortex on a nonzero, but uniform, velocity field of air and to evolve the resulting initial condition on a domain with periodic boundary conditions. However, without any loss in the generality of the convergence study, we choose here quiescent air instead, (u, v, T) = (0, 0, 1), as well as extrapolation boundary conditions, in order to facilitate the extension of the study to nonuniform grids. We evolve the initial condition on a square domain, x, y ∈ [−5, 5], and choose the strength, ε = 5, and decay rate, α = 1, of the vortex such that it has compact support in this region. A fixed CFL number, C = 0.3, is selected for the convergence study and a fifth-order RK time-stepping scheme, with the coefficients of Cash and Karp [58], is provisionally utilized instead of the third-order TVD RK method to ensure that the order of accuracy of the temporal discretization does not mask that of the spatial discretization. The nonuniform grids are generated by a continuously differentiable hyperbolic tangent function and are stretched at the domain boundaries. In Fig. 4, the cell size distribution for the coarsest grid, 25 × 25 cells, is shown in the plot on the left. The numerical solution is computed on grid sizes up to 400 × 400 cells with an output time of t = 1. Note that since the isentropic vortex is stationary, the exact solution at the given output time is simply the initial condition to the problem and any discrepancy between the exact and numerical solutions is due to numerical diffusion.

Figure 4.

Plots of the density at t = 0, ρ₀, on the coarsest nonuniform grid, 25 × 25 cells (left) and p-norm of the error between the density at t = 0 and t = 1, ρ₁, as a function of the grid size, N × N (right), for the stationary isentropic vortex problem given by Eq. (37). The grid convergence of the L₁- and L_∞-norm is shown for both when the primitive variables are reconstructed at the cell boundaries from their second-order accurate cell averages (– – and – –, respectively), following Johnsen and Colonius [30], and their fourth-order accurate cell averages (– – and – –, respectively), following the present scheme. Reference slopes for the second-order (—) and fifth-order (—) convergence rates are also included.

The convergence study is performed on the density, for which the initial condition is shown in the left plot of Fig. 4. In the right plot of the same figure, the results of the study are presented. These include the L₁- and L_∞-norms of the error in density as a function of the grid size for both the present numerical scheme and that of Johnsen and Colonius [30]. The reference slopes for both the second- and fifth-order convergence rates are also included. The results indicate that reconstructing the primitive variables at the cell boundaries from their second-order accurate cell averages, contrary to the conclusions of Johnsen and Colonius, does not lead to a high-order accurate numerical scheme. Instead, the resulting method is second-order accurate at best, as indicated by the second-order convergence rate of the corresponding L₁- and L_∞-norms. On the other hand, the results show that the present numerical scheme, by reconstructing the primitive variables at the cell boundaries from their fourth-order accurate cell averages, recovers high-order accuracy. In this case, the corresponding L₁- and L_∞-norms achieve a fifth-order convergence rate. We note that this is higher than the optimal fourth-order convergence rate that is expected as a result of utilizing a two-point Gaussian quadrature rule. It agrees, however, with the results of the analogous convergence study by Titarev and Toro [42], who also observed superconvergence.

Finally, though its parameters and results are not detailed here, we have also performed a convergence study on the typical isentropic vortex problem, i.e. where the vortex is superimposed on a nonzero, but uniform, air flow, (u, v, T) = (1, 1, 1), and evolved on a domain with periodic boundary conditions. Uniform grids, with a range of sizes comparable to before, were utilized to study the convergence properties of only the present numerical scheme and with the third-order TVD RK time-stepping method. A little better than fourth-order convergence was achieved in both the L₁- and L_∞-norms, despite the third-order accuracy of the temporal discretization. We note that once more, this superconvergence is consistent with the results of Titarev and Toro [42].

4.5. Shock-bubble interaction

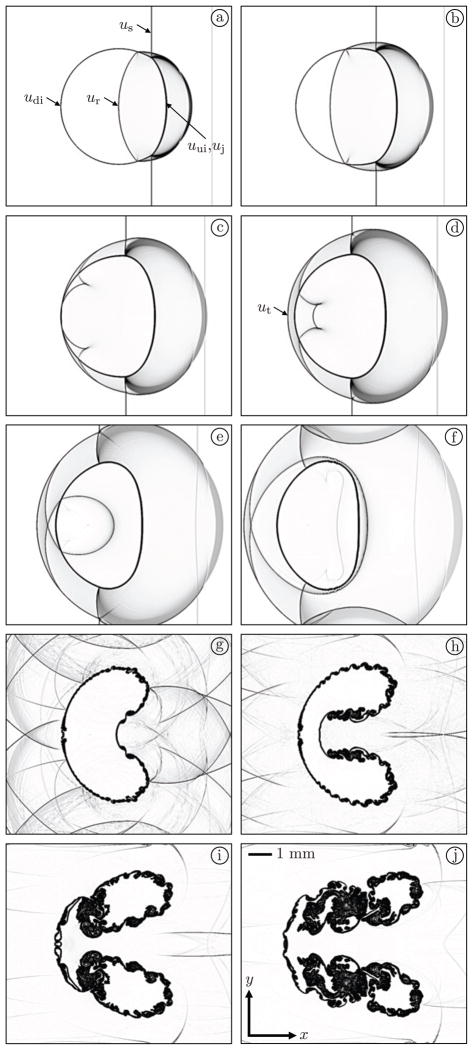
We consider next the two-dimensional interaction between a helium bubble and a weak shockwave in air. The problem was experimentally studied by Haas and Sturtevant [5] and subsequently often utilized as a validation case for multicomponent flow algorithms, see [11, 13, 16, 20, 26, 30, 34, 54, 56, 59] to name a few. It consists of a 5 cm in diameter bubble, vertically centered inside a shock tube and filled with helium. The helium in the bubble is not pure, but contaminated by the surrounding air, 28% by mass concentration. The bubble is impacted by a Mach 1.22 shockwave traveling in air at atmospheric pressure. A schematic of the initial condition for this problem is shown in Fig. 5 and the corresponding state variables are given by

Figure 5.

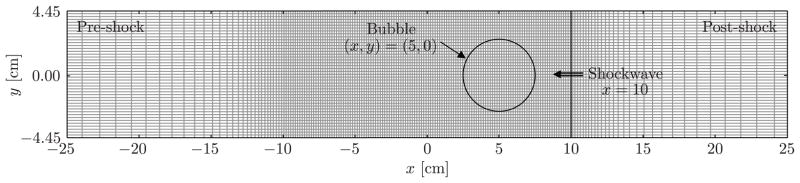
Schematic of the initial condition and the computational grid (only one of every forty cells shown) for the shock-bubble interaction problem. Note that as a result of the symmetry of the initial condition, only the top half of the displayed computational grid is utilized in the simulation.

$$({\alpha }_1{\rho }_1,{\alpha }_2{\rho }_2,u,v,p,{\alpha }_1)=\{\begin{array}{lll}(0,1.204,0,0,101325,0)\hfill & \text{for}\hfill & \text{Pre}-\text{Shock},\hfill \\ (0,1.658,-114.49,0,159060,0)\hfill & \text{for}\hfill & \text{Post}-\text{shock},\hfill \\ (0.158,0.061,0,0,101325,0.95)\hfill & \text{for}\hfill & \text{Bubble},\hfill \end{array}$$ (38)

where the densities, velocities and pressures are in kg/m³, m/s and Pa, respectively.

As illustrated in Fig. 5, we utilize a 6000 × 890 nonuniform computational grid to evolve the initial condition. A reflective boundary condition is used along the top of the grid, to model the shock tube wall, while a symmetry boundary condition is employed along its lengthwise centerline for computational efficiency. Inflow and outflow boundary conditions are implemented on the right and left of the grid, respectively, and are smoothly stretched away from the shock-bubble interaction region to prevent any reflections off of these boundaries from polluting the solution. The grid in the shock-bubble interaction region, x ∈ [−10, 10] cm, on the other hand, is uniform with Δx = Δy = 50 μm. The solution is evolved at a fixed CFL number, C = 0.4, and until t = 983 μs. The latter is measured from the moment the shockwave impacts the bubble and is the last time at which Haas and Sturtevant [5] report shadowgraph images from the experiment.

In Fig. 6, as a qualitative form of validation of our numerical scheme, we provide numerical Schlieren images of the shock-bubble interaction at approximately the same times that Haas and Sturtevant [5] obtain their shadowgraphs. The numerical Schlieren images depict the configuration of the waves resulting from the shock-bubble interaction, as well as the eventual involution of the bubble to form a jet and subsequently a vortex ring. The results of the simulation compare very well to those of the experiment, though for conciseness, we do not include the latter here. We note that there are no visible spurious oscillations in the numerical Schlieren images, despite the fact that they accentuate small fluctuations in density. A common startup error, however, is generated by the shockwave and is visible in nearly every image [60]. Fortunately, since it is nearly stationary and outside the region where the shockwave and bubble interact, it bears no adverse dynamic effect on the numerical solution.

Figure 6.

Following the numerical Schlieren imaging technique of Quirk and Karni [34], the temporal snapshots for the shock-bubble interaction problem at a) 26, b) 37, c) 52, d) 62, e) 80, f) 102, g) 245, h) 427, i) 674 and j) 983 μs. See Table 2 for information regarding the labeled flow features.

We validate our numerical scheme quantitatively by comparing the experimental velocity measurements of key flow features, as obtained by Haas and Sturtevant [5], to those obtained in the simulation. The flow features include the incident shock, refracted shock, transmitted shock, upstream interface, downstream interface and jet, and are annotated in the numerical Schlieren images a) and d) of Fig. 6. In Table 2, a side-by-side comparison of the experimental and simulation results is made. The velocity measurements from the simulation are all within the 10% experimental error associated with the measurements of Haas and Sturtevant and in general, fall within 5% of the experimental mean values. Note that though we do not report the uncertainty in the velocity measurements from the simulation, we expect it to be small and solely a function of the grid resolution. Indeed, since all conserved variables are conserved within round-off error, (10⁻¹²) in this case, we expect that all flow features move with the correct velocities.

Table 2.

Comparison between the present simulation and the experiment of Haas and Sturtevant [5] of the velocities of various flow features for the shock-bubble interaction problem. These include, along with the time interval in the simulation over which they were averaged, the velocities of the incident shock, u_s [−60, 0], refracted shock, u_r [0, 52], transmitted shock, u_t [52, 240], upstream interface, u_ui [10, 52], downstream interface, u_di [140, 240], and jet, u_j [140, 240]. Note that the velocities and time intervals are given in m/s and μs, respectively, and the corresponding flow features are identified in Fig. 6. All measurements are taken along the x-axis.

Data	us	ur	ut	uui	udi	uj
Simulation	420	945	379	173	145	230
Experiment	410 ± 41	900 ± 90	393 ± 39	170 ± 17	145 ± 15	230 ± 23

Lastly, we compare the present results to those of recent numerical simulations performed at a higher or comparable resolution. These include the work of Hejazialhosseini et al. [59], who utilized a level set method on wavelet-adapted grids with an effective resolution of Δx = Δy = 6 μm, and the work of So et al. [56], who utilized a diffuse interface method with interface sharpening on a uniform grid with Δx = Δy = 63 μm. Their results are consistent with ours, as we recover qualitatively similar large- and small-scale flow features. In particular, the Kelvin-Helmholtz instability that develops along the interface of the bubble and is clearly visible in numerical Schlieren images g)–j) of Fig. 6 is in good agreement. The instability is triggered at an earlier time in the simulations of Hejazialhosseini et al. and So et al., however, primarily because the ongoing diffusion of the material interface in the present simulation acts to regularize the material interface and delays the growth of the instability.

4.6. Taylor-Green vortex

We verify our numerical scheme for the Navier-Stokes equations by studying the evolution of a three-dimensional Taylor-Green vortex. The latter is a typical test problem for high-order methods and one of the simplest in which the production of small scales can be studied. The initial condition for the Taylor-Green vortex is given by

$$\begin{array}{l}u=u_{0}sin\left(\frac{x}{L}\right)cos\left(\frac{y}{L}\right)cos\left(\frac{z}{L}\right),\hfill \\ v=-u_{0}cos\left(\frac{x}{L}\right)sin\left(\frac{y}{L}\right)cos\left(\frac{z}{L}\right),\hfill \\ w=0,\hfill \\ p=p_0+\frac{{\rho }_0{u}_0^2}{16}\left(cos\left(\frac{2x}{L}\right)+cos\left(\frac{2y}{L}\right)\right)\left(cos\left(\frac{2z}{L}\right)+2\right),\hfill \end{array}\}$$ (39)

where L, ρ₀, u₀ and p₀ are the reference length scale, density, velocity and pressure in the problem, respectively. The fluid in which the vortex propagates is air, initially at uniform reference temperature, T₀, such that the initial condition for the density field is obtained from that for the pressure field using the ideal gas law. We evolve the vortex at a relatively low Reynolds number, Re = ρ₀u₀ L/μ = 100, an effectively incompressible Mach number, M₀ = u₀/c₀ = 0.1, and in a periodic domain, x, y, z ∈ [−πL, πL]. The domain is discretized by a uniform grid with 200 × 200 × 200 cells and we enforce fixed CFL and diffusion numbers, C = 0.15 and D = 0.10, to maintain stability throughout the simulation.

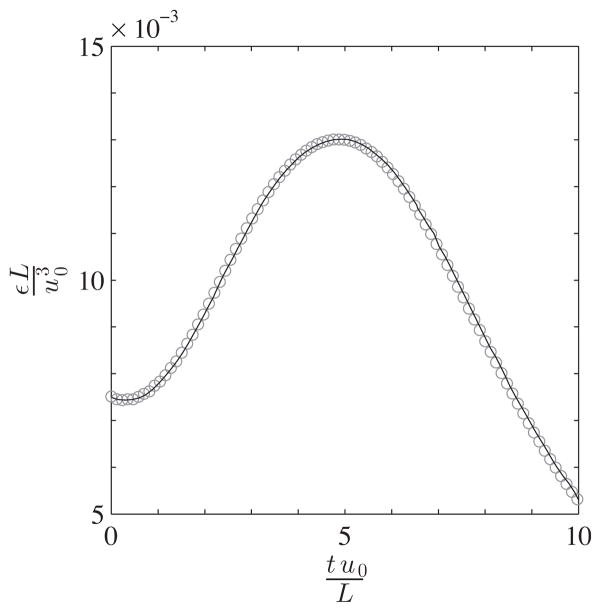
We evolve the Taylor-Green vortex until non-dimensional time tu₀/L = 10 in order to capture both the generation of the small scales, which result from three-dimensional vortex stretching, and their subsequent dissipation, which are due to viscous damping. In Fig. 7, we depict the former process with a plot of the isosurfaces of the z-component of the non-dimensional vorticity, ω_zL/u₀, at the initial and final moments of the simulation, where the vorticity is given by ω = ∇ × u. In Fig. 8, both processes are illustrated with a plot of the rate of dissipation of the non-dimensional kinetic energy, $\epsilon L/u_0^3$, as a function of the non-dimensional time. The rate of dissipation of the kinetic energy is computed over the entire volume of the computational domain, V, by

Figure 7.

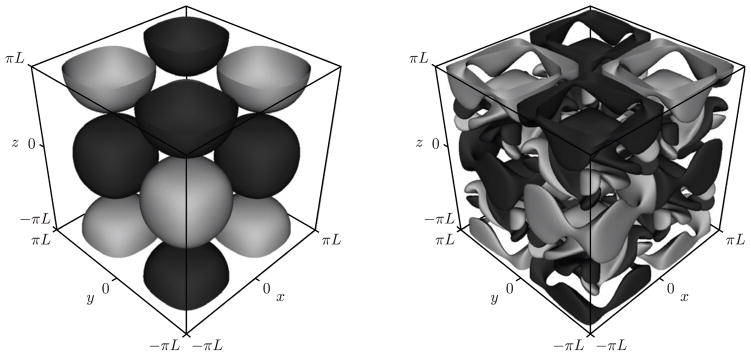
Plot of the isosurfaces of the z-component of the non-dimensional vorticity, ω_z L/u₀, for the Taylor-Green vortex problem at non-dimensional times tu₀/L = 0 (ω_z L/u₀ = ±0.33, left) and tu₀/L = 10 (ω_z L/u₀ = ±0.67, right). Note that the negative and positive isosurfaces of ω_z L/u₀ are colored in black and gray, respectively.

Figure 8.

The rate of dissipation of the non-dimensional kinetic energy as a function of the non-dimensional time for the Taylor-Green vortex problem. The solution from the present numerical scheme ( ) is compared to the direct spectral numerical solution of Brachet et al. [61] (—).

$$\epsilon =-\frac{1}{{\rho }_{0}V}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_V\frac{1}{2}\rho \mathbf{uu}\mathrm{d}V.$$ (40)

From Fig. 8, we can see that the strength of the vortex stretching initially grows, until tu₀/L ≈ 5, when the effects of viscous dissipation begin to dominate. The present numerical solution compares well to the direct spectral numerical solution of Brachet et al. [61], which is also included in the figure. Though not shown, we note that the Taylor-Green vortex eventually decays away, due to the absence of forcing.

4.7. Shock-vessel-bubble interaction

The last test case that we consider is the interaction between a shockwave and a bubble inside a vessel. The study of this problem is most notably relevant to understanding how vascular injury due to cavitation is initiated during the treatment of kidney stones by shockwaves in lithotripsy [62]. However, we primarily study it here to illustrate the ability of the present numerical scheme to handle flows that feature high density, pressure and viscosity ratios, as well as components with starkly different stiffened gas EOS parameters. Note that the problem we consider here is highly idealized; [52, 57, 62, 63] should be consulted for detailed justifications of the physical modeling.

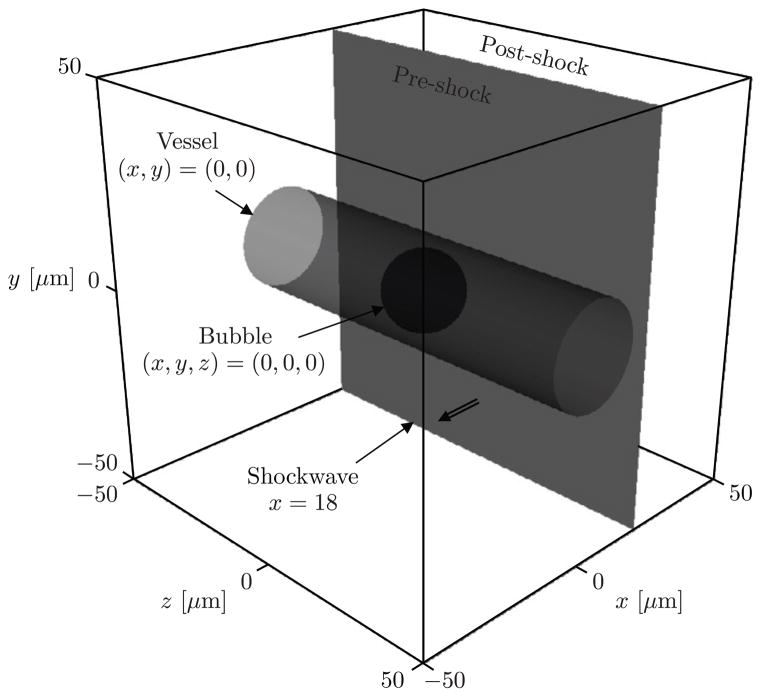
A schematic of the initial condition and computational domain is given in Fig. 9. It consists of a 20 μm in diameter air bubble that is centered inside a 26 μm in diameter vessel. The vessel is a cylindrical cavity that is filled with water, which models blood, and is embedded in 10% gelatin, a fluid that models tissue. The bubble and vessel are initially in equilibrium, at atmospheric pressure, until they are processed by a 40 MPa shockwave. The state variables corresponding to the initial condition are given by

Figure 9.

Schematic of the initial condition and the computational domain for the shock-vessel-bubble interaction problem. Note that as a result of the symmetry of the initial condition, only a quarter of the displayed computational domain is utilized in the simulation.

$$({\alpha }_1{\rho }_1,{\alpha }_2{\rho }_2,{\alpha }_3{\rho }_3,u,v,w,p,{\alpha }_1,{\alpha }_2)=\{\begin{array}{lll}(0,0,1030,0,0,0,101325,0,0)\hfill & \text{for}\hfill & \text{Pre}-\text{shock},\hfill \\ (0,0,1046,-24.20,0,0,4\times {10}^7,0,0)\hfill & \text{for}\hfill & \text{Post}-\text{shock},\hfill \\ (0,1000,0,0,0,0,101325,0,1)\hfill & \text{for}\hfill & \text{Vessel},\hfill \\ (1.204,0,0,0,0,0,101325,1,0)\hfill & \text{for}\hfill & \text{Bubble},\hfill \end{array}$$ (41)

where the densities, velocities and pressures are in kg/m³, m/s and Pa, respectively. We treat the air inside the bubble and the water inside the vessel as inviscid, μ₁ = μ₂ = 0 Pa·s, and consider the 10% gelatin to be highly viscous, μ₃ = 0.4 Pa·s. We take 10% gelatin to be significantly more viscous than the other fluids based on recent findings that indicate that viscous effects may play an important role in suppressing bubble dynamics in tissue [52, 63]. Then, based on the density in the post-shock region, the jump in pressure across the shockwave and the initial diameter of the bubble, the Reynolds numbers, $Re=\sqrt{\rho \mathrm{\Delta }p}D/\mu$, corresponding to these viscosities are given by Re₁, Re₂ → ∞ and Re₃ = 10. Note that by taking Re₁, Re₂ → ∞, we merely imply that the physical viscosity is zero since, of course, a small grid-dependent numerical viscosity will be present in the simulation.

We utilize a 400 × 200 × 200 uniform computational grid to evolve the initial condition. Extrapolation boundary conditions are utilized in the x-, y- and z-directions, while symmetry boundary conditions are applied along the x-y and x-z planes that intersect the x-axis in order to reduce the computational cost of the simulation. We enforce fixed CFL and diffusion numbers, C = 0.10 and D = 0.10, to maintain stability numerical stability. We end the simulation at t = 79 ns, shortly after the collapse of the bubble and the subsequent impact of the liquid jet into the wall of the vessel. Note that the time is measured from the moment the transmitted shockwave impacts the bubble.

The numerical solution to this problem is characterized by the shock-induced collapse of the bubble inside the vessel, which results from the impact of the incoming shockwave that is partially transmitted from the 10% gelatin into the water. The collapse of the bubble is followed by the formation of a liquid jet, which pierces its distal side, i.e. that furthest from the incoming shockwave, and impinges onto the wall of the vessel. The jetting of the bubble leads to the formation of a vortex ring, which further propagates into the tissue. The interaction between the bubble and vessel is illustrated in Fig. 10 with snapshots of the solution along the x-z plane at important times during the lifecycle of the bubble. These include a) the instant the proximal side of the bubble, i.e. that closest to the incoming shockwave, first involutes, b) when the minimum bubble volume is reached, c) when the vortex ring first forms and d) the last time at which the solution is computed. In Fig. 11, we also provide snapshots of the fully three-dimensional shape of the bubble at the final simulated time. Note that to illustrate the effects of tissue viscosity, the results for Re₃ → ∞ are included in both figures for comparison.

Figure 10.

Temporal snapshots of the flooded contours of the volume fractions of air (black), water (white) and 10% gelatin (gray) in the x-z plane of the three-dimensional shock-vessel-bubble interaction problem. The contour colors are saturated for volume fractions greater than 0.5. Results are shown for Re₃ → ∞ (top), at a) 45, b) 53, c) 70 and d) 79 ns, and Re₃ = 10, at a) 51, b) 55, c) 71 and 79 ns.

Figure 11.

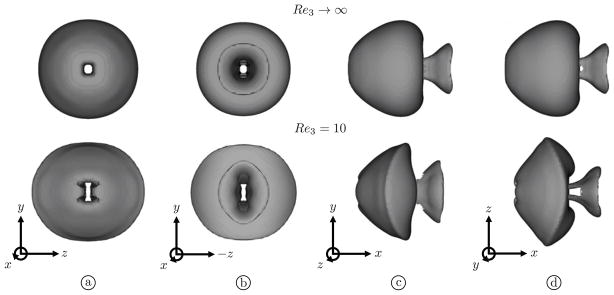
The a) front, b) back, c) side and d) top views of the shape of the bubble at t = 79 ns for the shock-vessel-bubble interaction problem. The shape is given by the 0.5 isosurface of the volume fraction of air. Results are shown for Re₃ → ∞ (top) and Re₃ = 10 (bottom).

As expected, a large tissue viscosity inhibits the deformation of the vessel and also, but perhaps more surprisingly, noticeably alters the shape of the bubble throughout its lifecycle compared to the inviscid case. As the bubble collapses it seeks to draw fluid in, predominantly along the paths of least resistance. The latter lie along the primary axis of the vessel, while the paths of highest resistance are perpendicular to this axis and require the deformation of the vessel walls, which is resisted by the large tissue viscosity. In particular, it is most difficult for the bubble to draw fluid in along its centerline, on its proximal side, as the wall of the bubble at that location is closest to the wall of the vessel, as measured in the direction of the propagation of the shockwave. This leads to a lag in the involution of the proximal bubble wall along the centerline and therefore the onset of a protrusion at this location in the early stages of the collapse, which is visible in Fig. 10, snapshots a) and b) of Re₃ = 10, but not in the analogous snapshots of Re₃ → ∞. The protrusion eventually vanishes as the liquid jet forms and impacts the distal vessel wall, at which point the distal side of the bubble not only begins to deform the wall of the vessel but must also conform to its geometry due to the large tissue viscosity. The latter results in an oblong shape of the distal bubble wall, elongated in the direction of the primary axis of the vessel, which may be observed in Fig. 11, in the snapshots of Re₃ = 10. The same snapshots show the proximal side of the bubble to be elongated in an exactly perpendicular direction. This is not all that surprising and is simply a consequence of the retarded involution of the bubble walls along that direction during collapse, which is due to the previously discussed increased resistance in the fluid flow along paths perpendicular to the primary axis of the vessel. Note on the other hand that the analogous snapshots of Re₃ → ∞ show the final shape of the bubble to be nearly axisymmetric, despite the difference in the acoustic impedance between water and 10% gelatin.

Finally, we observe that in addition to inhibiting the deformation of the vessel and altering the shape of the bubble, a large tissue viscosity also delays the onset of critical moments in the lifecycle of the bubble compared to the inviscid case, as illustrated in Fig. 10. This same behavior is observed for bubbles collapsing in an increasingly viscous fluid, see Liu et al. [64], and so should not entirely be unexpected here, despite the decreased level of confinement offered by the vessel. The work of Liu et al. further suggests that an increase in tissue viscosity will lead to additional delay in the collapse of the bubble. We expect that an increase in vascular confinement will have the same effect. Naturally, increasing either tissue viscosity or vascular confinement will also further alter the shape of the bubble, while increasing the tissue viscosity will additionally suppress the deformation of the vessel. A similar behavior was also observed in the work of Freund et al. [52], who numerically studied the shock-induced collapse of a bubble near a viscous layer.

5. Conclusions

We have developed a shock- and interface-capturing numerical scheme for the simulation of multicomponent flows governed by the Navier-Stokes equations. The numerical scheme is high-order accurate, discretely conserves the mass of each component in the flow, along with the total momentum and energy, and does not generate spurious oscillations. It is capable of handling flows that feature large density, pressure, and viscosity ratios, as well as components with significantly different stiffened gas EOS parameters. Future improvements of the numerical scheme will include the addition of surface tension and phase change.

Appendix A. State variables, fluxes and source terms

The vectors of state variables, q, fluxes, f, g and h, and source terms, s, of the conservation-law form of the five-equation model, Eq. (15):

$$\begin{array}{c}\mathbf{q}=\left(\begin{array}{c}{\alpha }_1{\rho }_1\\ {\alpha }_2{\rho }_2\\ \rho u\\ \rho v\\ \rho w\\ E\\ {\alpha }_1\end{array}\right),{\mathbf{f}}^{\mathrm{a}}=\left(\begin{array}{c}{\alpha }_1{\rho }_{1}u\\ {\alpha }_2{\rho }_{2}u\\ \rho u^2+p\\ \rho vu\\ \rho wu\\ (E+p)u\\ {\alpha }_{1}u\end{array}\right),{\mathbf{g}}^{\mathrm{a}}=\left(\begin{array}{c}{\alpha }_1{\rho }_{1}v\\ {\alpha }_2{\rho }_{2}v\\ \rho uv\\ \rho v^2+p\\ \rho wv\\ (E+p)v\\ {\alpha }_{1}v\end{array}\right),{\mathbf{h}}^{\mathrm{a}}=\left(\begin{array}{c}{\alpha }_1{\rho }_{1}w\\ {\alpha }_2{\rho }_{2}w\\ \rho uw\\ \rho vw\\ \rho w^2+p\\ (E+p)w\\ {\alpha }_{1}w\end{array}\right),\mathbf{s}=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ {\alpha }_1\nabla ·\mathbf{u}\end{array}\right),\\ {\mathbf{f}}^{\mathrm{d}}=\left(\begin{array}{c}0\\ 0\\ {\tau }_{xx}\\ {\tau }_{xy}\\ {\tau }_{xz}\\ {\tau }_{xx}u+{\tau }_{xy}v+{\tau }_{xz}w\\ 0\end{array}\right),{\mathbf{g}}^{\mathrm{d}}=\left(\begin{array}{c}0\\ 0\\ {\tau }_{yx}\\ {\tau }_{yy}\\ {\tau }_{yz}\\ {\tau }_{yx}u+{\tau }_{yy}v+{\tau }_{yz}w\\ 0\end{array}\right),{\mathbf{h}}^{\mathrm{d}}=\left(\begin{array}{c}0\\ 0\\ {\tau }_{zx}\\ {\tau }_{zy}\\ {\tau }_{zz}\\ {\tau }_{zx}u+{\tau }_{zy}v+{\tau }_{zz}w\\ 0\end{array}\right),\end{array}\}$$ (A.1)

where τ is an element of the viscous stress tensor, Eq. (6), and the superscripts “a” and “d” denote advective and diffusive fluxes, respectively.

Appendix B. Characteristic decomposition

To illustrate the projection of the primitive variables onto the characteristic fields, we begin by rewriting the conservation-law form of the equations of motion, Eq. (15), in its equivalent quasi-linear form and as a function of the primitive variables. In the process, we neglect the viscous terms, as they will not impact the sought-after result, and once again consider the advection equation for the volume fraction in its original form, see Eq. (5). Eq. (15) then becomes

$$\frac{\partial \mathbf{v}}{\partial t}+\mathbf{A}(\mathbf{v})\frac{\partial \mathbf{v}}{\partial x}+\mathbf{B}(\mathbf{v})\frac{\partial \mathbf{v}}{\partial y}+\mathbf{C}(\mathbf{v})\frac{\partial \mathbf{v}}{\partial z}=\mathbf{0},$$ (B.1)

where v is the vector of primitive variables and A = ∂_vF, B = ∂_vG and C = ∂_vH are Jacobian matrices. The individual components of these vector and matrix variables are given by

$$\begin{array}{c}\mathbf{v}=\left(\begin{array}{c}{\alpha }_1{\rho }_1\\ {\alpha }_2{\rho }_2\\ u\\ v\\ w\\ p\\ {\alpha }_1\end{array}\right),\mathbf{A}=\left(\begin{array}{ccccccc}u& 0& {\alpha }_1{\rho }_1& 0& 0& 0& 0\\ 0& u& {\alpha }_2{\rho }_2& 0& 0& 0& 0\\ 0& 0& u& 0& 0& {\rho }^{-1}& 0\\ 0& 0& 0& u& 0& 0& 0\\ 0& 0& 0& 0& u& 0& 0\\ 0& 0& \rho c^2& 0& 0& u& 0\\ 0& 0& 0& 0& 0& 0& u\end{array}\right),\\ \mathbf{B}=\left(\begin{array}{ccccccc}v& 0& 0& {\alpha }_1{\rho }_1& 0& 0& 0\\ 0& v& 0& {\alpha }_2{\rho }_2& 0& 0& 0\\ 0& 0& v& 0& 0& 0& 0\\ 0& 0& 0& v& 0& {\rho }^{-1}& 0\\ 0& 0& 0& 0& v& 0& 0\\ 0& 0& 0& \rho c^2& 0& v& 0\\ 0& 0& 0& 0& 0& 0& v\end{array}\right),\mathbf{C}=\left(\begin{array}{ccccccc}w& 0& 0& 0& {\alpha }_1{\rho }_1& 0& 0\\ 0& w& 0& 0& {\alpha }_2{\rho }_2& 0& 0\\ 0& 0& w& 0& 0& 0& 0\\ 0& 0& 0& w& 0& 0& 0\\ 0& 0& 0& 0& w& {\rho }^{-1}& 0\\ 0& 0& 0& 0& \rho c^2& w& 0\\ 0& 0& 0& 0& 0& 0& w\end{array}\right).\end{array}\}$$ (B.2)

Now in order to obtain the characteristic variables from the primitive ones, Eq. (B.1) must be decomposed along its characteristics. However, since the characteristic decomposition is only applied in one coordinate direction at a time, we illustrate the procedure for the x-direction with the understanding that the procedure for the remaining coordinate directions is entirely analogous. We begin by solving the eigenvalue decomposition problem for A:

$$\mathbf{A}={\mathbf{Q}}_{\mathrm{A}}{\mathbf{\Lambda }}_{\mathrm{A}}{\mathbf{Q}}_{\mathrm{A}}^{-1},$$ (B.3)

where Q_A is a matrix whose columns are the right eigenvectors of A and Λ_A is a matrix whose diagonal elements are the corresponding eigenvalues:

$${\mathbf{Q}}_{\mathrm{A}}=\left(\begin{array}{ccccccc}-\frac{{\alpha }_1{\rho }_1}{2c}& 1& 0& 0& 0& 0& \frac{{\alpha }_1{\rho }_1}{2c}\\ -\frac{{\alpha }_2{\rho }_2}{2c}& 0& 1& 0& 0& 0& \frac{{\alpha }_2{\rho }_2}{2c}\\ \frac{1}{2}& 0& 0& 0& 0& 0& \frac{1}{2}\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ -\frac{\rho c}{2}& 0& 0& 0& 0& 0& \frac{\rho c}{2}\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right),{\mathbf{\Lambda }}_{\mathrm{A}}=\left(\begin{array}{ccccccc}u-c& 0& 0& 0& 0& 0& 0\\ 0& u& 0& 0& 0& 0& 0\\ 0& 0& u& 0& 0& 0& 0\\ 0& 0& 0& u& 0& 0& 0\\ 0& 0& 0& 0& u& 0& 0\\ 0& 0& 0& 0& 0& u& 0\\ 0& 0& 0& 0& 0& 0& u+c\end{array}\right).$$ (B.4)

Then, by assuming that Q_A is spatially and temporally frozen, the variable transformation v = Q_Aw_A, along with Eq. (B.3), can be substituted into Eq. (B.1) to yield the dimensionally split characteristic equation for the x-direction:

$$\frac{\partial {\mathbf{w}}_{\mathrm{A}}}{\partial t}+{\mathbf{\Lambda }}_{\mathrm{A}}\frac{\partial {\mathbf{w}}_{\mathrm{A}}}{\partial x}=\mathbf{0},$$ (B.5)

where w_A is the vector of characteristic variables obtained from the projection of the primitive variables onto the characteristic fields in the x-direction:

$${\mathbf{w}}_{\mathrm{A}}={\mathbf{Q}}_{\mathrm{A}}^{-1}\mathbf{v}.$$ (B.6)

The variable transformation in Eq. (B.6) may now be utilized to convert the cell average primitive variables into the cell average characteristic variables so that the latter may be reconstructed. Note, however, that since Eq. (B.6) was obtained based on a characteristic decomposition in the x-direction, the reconstruction of the resulting characteristic variables must be carried out on cell faces normal to that direction. Then, applying Eq. (B.6) to the cell average primitive variables in a given cell, we get

$${\mathbf{w}}_{{\mathrm{A}}_{i,j,k}}={\mathbf{Q}}_{{\mathrm{A}}_{i+1/2,j,k}}^{-1}{\mathbf{v}}_{i,j,k},$$ (B.7)

where the frozen projection matrix, ${\mathbf{Q}}_{\mathrm{A}}^{-1}$, is to be evaluated at state v_i+1/2,j,k. However, the latter is not known prior to reconstruction, so that typically a Roe or arithmetic average of v_i,j,k and v_i+1,j,k is utilized instead. We prefer computing the arithmetic average, as it is less computationally expensive than and performs equally well in our tests as the Roe average. Once the characteristic variables have been reconstructed at the Gaussian quadrature points of both the left and right side of the cell faces normal to the x-direction, the primitive variables may be recovered by projecting the characteristic variables back onto the physical fields:

$$\begin{array}{l}{\mathbf{v}}_{i+1/2,j_l,k_m}^{\mathrm{L}}={\mathbf{Q}}_{{\mathrm{A}}_{i+1/2,j,k}}{\mathbf{w}}_{{\mathrm{A}}_{i+1/2,j_l,k_m}}^{\mathrm{L}},\hfill \\ {\mathbf{v}}_{i+1/2,j_l,k_m}^{\mathrm{R}}={\mathbf{Q}}_{{\mathrm{A}}_{i+1/2,j,k}}{\mathbf{w}}_{{\mathrm{A}}_{i+1/2,j_l,k_m}}^{\mathrm{R}}.\hfill \end{array}\}$$ (B.8)

Note that the procedure described by Eqs. (B.7) and (B.8) does not affect the formal order of the spatial accuracy of the numerical method and has readily been utilized in the past with high-order methods for conservation laws, see [30, 42, 49, 50] to name a few.

Appendix C. WENO reconstruction

Our WENO scheme is primarily a generalization of the original fifth-order method of Liu et al. [36] to nonuniform grids. To our knowledge, the building blocks of such a scheme, i.e. the polynomials, weights and smoothness indicators, have only been reported in literature once before and in a limited capacity. Specifically, Johnsen [57] provided them for a reconstruction at the cell boundaries, but not at the quadrature points. In this section, we thus briefly overview the procedure by which the generalized WENO building blocks of an arbitrarily high-order reconstruction at a given point may be obtained and document those for a fifth-order reconstruction, at both the cell boundaries and quadrature points.

Following the notes of Shu [65], a (2k − 1)^th-order WENO reconstruction in cell I_i consists of the convex combination of k polynomials of k^th-order, which are defined on candidate stencils

$$S_r(i)=\{x_{i-r},\dots ,x_{i-r+k-1}\},r=0,\dots ,k-1.$$ (C.1)

The Lagrange form of each polynomial is given by

$$f^{(r)}(x)=\sum _{m=0}^k\sum _{j=0}^{m-1}{f}_{i-r+j}\mathrm{\Delta }{x}_{i-r+j}\left(\frac{{\displaystyle \sum _{\begin{array}{l}l=0\\ l\ne m\end{array}}^k}{\displaystyle \prod _{\begin{array}{c}q=0\\ q\ne m,l\end{array}}^k}\left(x-x_{i-r+q-1/2}\right)}{{\displaystyle \prod _{\begin{array}{l}l=0\\ l\ne m\end{array}}^k}\left(x_{i-r+m-1/2}-x_{i-r+l-1/2}\right)}\right),$$ (C.2)

where f is an arbitrary function whose pointwise approximation is to be obtained in cell I_i from its cell averages in the candidate stencils. Without any loss in the generality of the methodology, we can then write the convex combination of the candidate polynomials for a reconstruction at the right cell boundary of cell I_i, x_i+1/2, as follows:

$$f_{i+1/2}=\sum _{r=0}^{k-1}{\omega }_{i+1/2}^{(r)}{f}_{i+1/2}^{(r)}=f(x_{i+1/2})+O\left(\mathrm{\Delta }{x}_i^{2k-1}\right),$$ (C.3)

where the nonlinear weights, ω, satisfy

$${\omega }_{i+1/2}^{(r)}\ge 0,\sum _{r=0}^{k-1}{\omega }_{i+1/2}^{(r)}=1,$$ (C.4)

for stability and consistency, and are specially designed to achieve a (2k − 1)^th-order reconstruction in smooth regions of f and an essentially non-oscillatory one in regions containing discontinuities.

The nonlinear weights depend on both the cell size distribution and the smoothness of the interpolated function. They are derived from the so-called ideal weights, d, which are only a function of the former and for which the relationships in Eq. (C.3) and (C.4) also hold, i.e.

$$f_{i+1/2}=\sum _{r=0}^{k-1}{d}_{i+1/2}^{(r)}{f}_{i+1/2}^{(r)}=f(x_{i+1/2})+O\left(\mathrm{\Delta }{x}_i^{2k-1}\right)$$ (C.5)

and

$$d_{i+1/2}^{(r)}\ge 0,\sum _{r=0}^{k-1}{d}_{i+1/2}^{(r)}=1.$$ (C.6)

The ideal weights are obtained by matching the coefficients of the convex combination of the k^th-order polynomials with those of a (2k − 1)^th-order polynomial generated by Eq. (C.2) and centered about cell I_i. Though the ideal weights also achieve a (2k − 1)^th-order reconstruction in smooth regions of f, they produce oscillatory behavior for reconstructions in regions containing discontinuities.

The nonlinear weights are derived from the ideal weights by taking into account the smoothness of f. The latter is characterized by the smoothness indicators of Jiang and Shu [37], β:

$${\beta }^{(r)}=\sum _{l=1}^{k-1}{\int }_{x_{i-1/2}}^{x_{i+1/2}}\mathrm{\Delta }{x}_i^{2l-1}{\left(\frac{{\mathrm{d}}^l{f}^{(r)}(x)}{{\mathrm{d}}^{l}x}\right)}^2\mathrm{d}x,$$ (C.7)

which are utilized to first rescale the ideal weights:

$${\alpha }_{i+1/2}^{(r)}=\frac{d_{i+1/2}^{(r)}}{{({\beta }^{(r)}+\epsilon )}^2},$$ (C.8)

and subsequently normalize them so to obtain the nonlinear ones:

$${\omega }_{i+1/2}^{(r)}=\frac{{\alpha }_{i+1/2}^{(r)}}{{\displaystyle \sum _{s=0}^{k-1}}{\alpha }_{i+1/2}^{(s)}}.$$ (C.9)

ε in Eq. (C.8) is a small parameter that is utilized to avoid division by zero. Typically, it is set to 10⁻⁶ to avoid deteriorating the formal order of accuracy of the reconstruction near critical points of f. In practice, we remove this restriction and set ε to machine precision by means of an additional mapping of the nonlinear weights, see Henrick et al. [39] for details.

Note that the above-described methodology is analogous for the reconstruction at any other point within cell I_i. In addition, the resulting WENO scheme is no more expensive than one developed on a uniform grid, as all grid-dependent coefficients that appear in the polynomials, weights and smoothness indicators can be computed prior to simulation. Next, we document the building blocks of a fifth-order WENO reconstruction. For conciseness, we utilize the square bracket notation to denote the usual jump in a quantity, e.g. ${[x]}_{i-1/2}^{i+1/2}=x_{i+1/2}-x_{i-1/2}$.

A.1. Polynomials

x = x_i+1/2

$$\begin{array}{l}{f}_{i+1/2}^{(0)}=f_i+\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+5/2}\right)}{{[x]}_{i-1/2}^{i+3/2}{[x]}_{i-1/2}^{i+5/2}}{[f]}_i^{i+1}-\frac{{[x]}_{i-1/2}^{i+1/2}{[x]}_{i+1/2}^{i+3/2}}{{[x]}_{i-1/2}^{i+5/2}{[x]}_{i+1/2}^{i+5/2}}{[f]}_{i+1}^{i+2}\hfill \\ f_{i+1/2}^{(1)}=f_i+\frac{{[x]}_{i-1/2}^{i+1/2}{[x]}_{i+1/2}^{i+3/2}}{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-3/2}^{i+3/2}}{[f]}_{i-1}^i+\frac{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-1/2}^{i+1/2}}{{[x]}_{i-3/2}^{i+3/2}{[x]}_{i-1/2}^{i+3/2}}{[f]}_i^{i+1}\hfill \\ f_{i+1/2}^{(2)}=f_i-\frac{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-1/2}^{i+1/2}}{{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-5/2}^{i+1/2}}{[f]}_{i-2}^{i-1}+\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-5/2}^{i+1/2}+{[x]}_{i-3/2}^{i+1/2}\right)}{{[x]}_{i-5/2}^{i+1/2}{[x]}_{i-3/2}^{i+1/2}}{[f]}_{i-1}^i\hfill \end{array}\}$$ (C.10)

x = x_i−1/2

$$\begin{array}{l}{f}_{i-1/2}^{(0)}=f_i-\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i-1/2}^{i+5/2}\right)}{{[x]}_{i-1/2}^{i+3/2}{[x]}_{i-1/2}^{i+5/2}}{[f]}_i^{i+1}-\frac{{[x]}_{i-1/2}^{i+1/2}{[x]}_{i-1/2}^{i+3/2}}{{[x]}_{i-1/2}^{i+5/2}{[x]}_{i+1/2}^{i+5/2}}{[f]}_{i+1}^{i+2}\hfill \\ f_{i-1/2}^{(1)}=f_i+\frac{{[x]}_{i-1/2}^{i+1/2}{[x]}_{i-1/2}^{i+3/2}}{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-3/2}^{i+3/2}}{[f]}_{i-1}^i+\frac{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-1/2}^{i+1/2}}{{[x]}_{i-3/2}^{i+3/2}{[x]}_{i-1/2}^{i+3/2}}{[f]}_i^{i+1}\hfill \\ f_{i+1/2}^{(2)}=f_i-\frac{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-1/2}^{i+1/2}}{{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-5/2}^{i+1/2}}{[f]}_{i-2}^{i-1}+\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-5/2}^{i+1/2}+{[x]}_{i-3/2}^{i+1/2}\right)}{{[x]}_{i-5/2}^{i+1/2}{[x]}_{i-3/2}^{i+1/2}}{[f]}_{i-1}^i\hfill \end{array}\}$$ (C.11)

$x=x_{i+1/(2\sqrt{3})}$

$$\begin{array}{l}{f}_{i+1/(2\sqrt{3})}^{(0)}=f_i+\frac{{[x]}_{i-1/2}^{i+1/2}\left(2{[x]}_{i-1/2}^{i+3/2}+{[x]}_{i-1/2}^{i+5/2}+{[x]}_{i+1/2}^{i+5/2}\right)}{2\sqrt{3}{[x]}_{i-1/2}^{i+3/2}{[x]}_{i-1/2}^{i+5/2}}{[f]}_i^{i+1}-\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+3/2}\right)}{2\sqrt{3}{[x]}_{i-1/2}^{i+5/2}{[x]}_{i+1/2}^{i+5/2}}{[f]}_{i+1}^{i+2}\hfill \\ f_{i+1/(2\sqrt{3})}^{(1)}=f_i+\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+3/2}\right)}{2\sqrt{3}{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-3/2}^{i+3/2}}{[f]}_{i-1}^i+\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-3/2}^{i-1/2}+{[x]}_{i-3/2}^{i+1/2}\right)}{2\sqrt{3}{[x]}_{i-3/2}^{i+3/2}{[x]}_{i-1/2}^{i+3/2}}{[f]}_i^{i+1}\hfill \\ f_{i+1/(2\sqrt{3})}^{(2)}=f_i-\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-3/2}^{i-1/2}+{[x]}_{i-3/2}^{i+1/2}\right)}{2\sqrt{3}{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-5/2}^{i+1/2}}{[f]}_{i-2}^{i-1}+\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-5/2}^{i-1/2}+{[x]}_{i-5/2}^{i+1/2}+2{[x]}_{i-3/2}^{i+1/2}\right)}{2\sqrt{3}{[x]}_{i-5/2}^{i+1/2}{[x]}_{i-3/2}^{i+1/2}}{[f]}_{i-1}^i\hfill \end{array}\}$$ (C.12)

$x=x_{i-1/(2\sqrt{3})}$

$$\begin{array}{c}{f}_{i-1/(2\sqrt{3})}^{(0)}=2f_i-f_{i+1/(2\sqrt{3})}^{(0)}\\ f_{i-1/(2\sqrt{3})}^{(1)}=2f_i-f_{i+1/(2\sqrt{3})}^{(1)}\\ f_{i-1/(2\sqrt{3})}^{(2)}=2f_i-f_{i+1/(2\sqrt{3})}^{(2)}\end{array}\}$$ (C.13)

A.2. Ideal weights

x = x_i+1/2

$$\begin{array}{c}{d}_{i+1/2}^{(0)}=\frac{{[x]}_{i-5/2}^{i+1/2}{[x]}_{i-3/2}^{i+1/2}}{{[x]}_{i-5/2}^{i+5/2}{[x]}_{i-3/2}^{i+5/2}}\\ d_{i+1/2}^{(2)}=\frac{{[x]}_{i+1/2}^{i+3/2}{[x]}_{i+1/2}^{i+5/2}}{{[x]}_{i-5/2}^{i+3/2}{[x]}_{i-5/2}^{i+5/2}}\end{array}\}$$ (C.14)

x = x_i−1/2

$$\begin{array}{c}{d}_{i-1/2}^{(0)}=\frac{{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-3/2}^{i-1/2}}{{[x]}_{i-5/2}^{i+5/2}{[x]}_{i-3/2}^{i+5/2}}\\ d_{i-1/2}^{(2)}=\frac{{[x]}_{i-1/2}^{i+3/2}{[x]}_{i-1/2}^{i+5/2}}{{[x]}_{i-5/2}^{i+3/2}{[x]}_{i-5/2}^{i+5/2}}\end{array}\}$$ (C.15)

$x=x_{i+1/(2\sqrt{3})}$

$$\begin{array}{r}\hfill d_{i+1/(2\sqrt{3})}^{(0)}=\{{[x]}_{i-1/2}^{i+1/2}\left(\sqrt{3}{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2-6{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-5/2}^{i-1/2}+{[x]}_{i-3/2}^{i-1/2}\right)-18{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-3/2}^{i-1/2}\right)\\ \hfill +6{[x]}_{i-1/2}^{i+3/2}\left({\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+3{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-5/2}^{i-1/2}+{[x]}_{i-3/2}^{i-1/2}\right)+6{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-3/2}^{i-1/2}\right)\}\\ \hfill ÷\left\{18{[x]}_{i-5/2}^{i+5/2}{[x]}_{i-3/2}^{i+5/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+3/2}\right)\right\}\\ \hfill d_{i+1/(2\sqrt{3})}^{(2)}=\{-\left(6+\sqrt{3}\right){\left({[x]}_{i-1/2}^{i+1/2}\right)}^3-6{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2\left(2{[x]}_{i-3/2}^{i-1/2}-2{[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+5/2}\right)\\ \hfill -18{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i+1/2}^{i+5/2}\left({[x]}_{i-3/2}^{i-1/2}-{[x]}_{i-1/2}^{i+3/2}\right)-{[x]}_{i-3/2}^{i-1/2}{[x]}_{i-1/2}^{i+3/2}\right)\\ \hfill +36{[x]}_{i-3/2}^{i-1/2}{[x]}_{i-1/2}^{i+3/2}{[x]}_{i+1/2}^{i+5/2}\}\\ \hfill ÷\left\{18{[x]}_{i-5/2}^{i+3/2}{[x]}_{i-5/2}^{i+5/2}\left({[x]}_{i-3/2}^{i-1/2}+{[x]}_{i-3/2}^{i+1/2}\right)\right\}\end{array}\}$$ (C.16)

$x=x_{i-1/(2\sqrt{3})}$

$$\begin{array}{l}{d}_{i-1/(2\sqrt{3})}^{(0)}=d_{i+1/(2\sqrt{3})}^{(0)}-\frac{{\left({[x]}_{i-1/2}^{i+1/2}\right)}^3}{3\sqrt{3}{[x]}_{i-5/2}^{i+5/2}{[x]}_{i-3/2}^{i+5/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+3/2}\right)}\\ d_{i-1/(2\sqrt{3})}^{(2)}=d_{i+1/(2\sqrt{3})}^{(2)}+\frac{{\left({[x]}_{i-1/2}^{i+1/2}\right)}^3}{3\sqrt{3}{[x]}_{i-5/2}^{i+3/2}{[x]}_{i-5/2}^{i+5/2}\left({[x]}_{i-3/2}^{i-1/2}+{[x]}_{i-3/2}^{i+1/2}\right)}\end{array}\}$$ (C.17)

A.3. Smoothness indicators

$$\begin{array}{r}\hfill {\beta }^{(0)}=4{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2(\frac{10{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+5/2}\right)+{\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+5/2}\right)}^2}{{\left({[x]}_{i-1/2}^{i+3/2}{[x]}_{i-1/2}^{i+5/2}\right)}^2}{\left({[f]}_i^{i+1}\right)}^2\\ \hfill -\frac{19{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2-{[x]}_{i-1/2}^{i+1/2}{[x]}_{i+1/2}^{i+5/2}+2{[x]}_{i-1/2}^{i+3/2}\left({[x]}_{i-1/2}^{i+3/2}+{[x]}_{i+1/2}^{i+5/2}\right)}{{[x]}_{i-1/2}^{i+3/2}{[x]}_{i+1/2}^{i+5/2}{\left({[x]}_{i-1/2}^{i+5/2}\right)}^2}{[f]}_i^{i+1}{[f]}_{i+1}^{i+2}\\ \hfill +\frac{10{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+{[x]}_{i-1/2}^{i+1/2}{[x]}_{i+1/2}^{i+3/2}+{\left({[x]}_{i+1/2}^{i+3/2}\right)}^2}{{\left({[x]}_{i-1/2}^{i+5/2}{[x]}_{i+1/2}^{i+5/2}\right)}^2}{\left({[f]}_{i+1}^{i+2}\right)}^2)\\ \hfill {\beta }^{(1)}=4{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2(-\frac{{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-3/2}^{i-1/2}+20{[x]}_{i-1/2}^{i+1/2}\right)+{[x]}_{i-1/2}^{i+3/2}\left(2{[x]}_{i-3/2}^{i-1/2}+{[x]}_{i-1/2}^{i+1/2}\right)}{{[x]}_{i-3/2}^{i+1/2}{[x]}_{i-1/2}^{i+3/2}{\left({[x]}_{i-3/2}^{i+3/2}\right)}^2}{[f]}_i^{i+1}{[f]}_i^{i+1}\\ \hfill +\frac{10{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+{[x]}_{i-1/2}^{i+1/2}{[x]}_{i+1/2}^{i+3/2}+{\left({[x]}_{i+1/2}^{i+3/2}\right)}^2}{{\left({[x]}_{i-3/2}^{i+1/2}{[x]}_{i-3/2}^{i+3/2}\right)}^2}{\left({[f]}_{i-1}^i\right)}^2\\ \hfill +\frac{10{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+{[x]}_{i-3/2}^{i-1/2}{[x]}_{i-1/2}^{i+1/2}+{\left({[x]}_{i-3/2}^{i-1/2}\right)}^2}{{\left({[x]}_{i-3/2}^{i+3/2}{[x]}_{i-1/2}^{i+3/2}\right)}^2}{\left({[f]}_i^{i+1}\right)}^2)\\ \hfill {\beta }^{(2)}=4{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2(\frac{12{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+3{[x]}_{i-1/2}^{i+1/2}\left({[x]}_{i-5/2}^{i-1/2}+{[x]}_{i-3/2}^{i-1/2}\right)+{\left({[x]}_{i-5/2}^{i-1/2}+{[x]}_{i-3/2}^{i-1/2}\right)}^2}{{\left({[x]}_{i-5/2}^{i+1/2}{[x]}_{i-3/2}^{i+1/2}\right)}^2}{\left({[f]}_{i-1}^i\right)}^2\\ \hfill -\frac{19{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2-{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-1/2}^{i+1/2}+2{[x]}_{i-3/2}^{i+1/2}\left({[x]}_{i-5/2}^{i-1/2}+{[x]}_{i-3/2}^{i+1/2}\right)}{{[x]}_{i-5/2}^{i-1/2}{[x]}_{i-3/2}^{i+1/2}{\left({[x]}_{i-5/2}^{i+1/2}\right)}^2}{[f]}_{i-2}^{i-1}{[f]}_{i-1}^i\\ \hfill +\frac{10{\left({[x]}_{i-1/2}^{i+1/2}\right)}^2+{[x]}_{i-3/2}^{i-1/2}{[x]}_{i-1/2}^{i+1/2}+{\left({[x]}_{i-3/2}^{i-1/2}\right)}^2}{{\left({[x]}_{i-5/2}^{i-1/2}{[x]}_{i-5/2}^{i+1/2}\right)}^2}{\left({[f]}_{i-2}^{i-1}\right)}^2)\end{array}\}$$ (C.18)

Appendix D. Numerical flux

The methodology to obtain the solution to a Riemann problem with the HLLC solver is identical for quadrature points on cell faces normal to the same direction and is analogous between quadrature points on orthogonal cell faces. As a result, to illustrate the solution procedure, we temporarily drop the indicial notation used in the previous sections and consider a Riemann problem in the x-coordinate direction comprised of left and right states, q_L and q_R, respectively. The advective numerical flux is then given by the HLLC solver as

$${\widehat{\mathbf{f}}}^{\mathrm{a}}=\frac{1+sgn(s_{\ast })}{2}\left[{\mathbf{f}}_{\mathrm{L}}^{\mathrm{a}}+s_{-}({\mathbf{q}}_{\ast \mathrm{L}}-{\mathbf{q}}_{\mathrm{L}})\right]+\frac{1-sgn(s_{\ast })}{2}\left[{\mathbf{f}}_{\mathrm{R}}^{\mathrm{a}}+s_{+}({\mathbf{q}}_{\ast \mathrm{R}}-{\mathbf{q}}_{\mathrm{R}})\right],$$ (D.1)

where the state in the intermediate star region, with K = L or R, is given by

$${\mathbf{q}}_{\ast \mathrm{K}}=\left(\frac{s_{\mathrm{K}}-u_{\mathrm{K}}}{s_{\mathrm{K}}-s_{\ast }}\right)\left(\begin{array}{c}{({\alpha }_1{\rho }_1)}_{\mathrm{K}}\\ {({\alpha }_2{\rho }_2)}_{\mathrm{K}}\\ {\rho }_{\mathrm{K}}{s}_{\ast }\\ {\rho }_{\mathrm{K}}{v}_{\mathrm{K}}\\ {\rho }_{\mathrm{K}}{w}_{\mathrm{K}}\\ E_{\mathrm{K}}+(s_{\ast }-u_{\mathrm{K}})\left({\rho }_{\mathrm{K}}{s}_{\ast }+\frac{p_{\mathrm{K}}}{s_{\mathrm{K}}-u_{\mathrm{K}}}\right)\\ {\alpha }_{1_{\mathrm{K}}}\end{array}\right).$$ (D.2)

The advective numerical flux is fully determined once the wave speeds, s, have been estimated. Following Einfeldt et al. [66], we choose

$$\begin{array}{l}{s}_{-}=min(0,s_{\mathrm{L}}),\hfill \\ s_{+}=max(0,s_{\mathrm{R}}),\hfill \end{array}\}$$ (D.3)

and

$$\begin{array}{l}{s}_{\mathrm{L}}=min(\overline{u}-\overline{c},u_{\mathrm{L}}-c_{\mathrm{L}}),\hfill \\ s_{\mathrm{R}}=max(\overline{u}+\overline{c},u_{\mathrm{R}}+c_{\mathrm{R}}),\hfill \end{array}\}$$ (D.4)

where ū and c̄ are averages computed from the left and right states of the Riemann problem and may be obtained from either a Roe or an arithmetic averaging procedure. In practice, however, we once again find that the two averaging methods yield nearly identical numerical results and so choose to compute arithmetic averages since they are more computationally efficient. Finally, to estimate the wave speed in the star region, we follow Batten et al. [67] in choosing

$$s_{\ast }=\frac{p_{\mathrm{R}}-p_{\mathrm{L}}+{\rho }_{\mathrm{L}}{u}_{\mathrm{L}}(s_{\mathrm{L}}-u_{\mathrm{L}})-{\rho }_{\mathrm{R}}{u}_{\mathrm{R}}(s_{\mathrm{R}}-u_{\mathrm{R}})}{{\rho }_{\mathrm{L}}(s_{\mathrm{L}}-u_{\mathrm{L}})-{\rho }_{\mathrm{R}}(s_{\mathrm{R}}-u_{\mathrm{R}})}.$$ (D.5)

Note that the above choice of wave speeds will result in the exact resolution of isolated shockwaves and contact waves by the HLLC solver [67].

With the advective numerical flux computed, we may now evaluate the numerical source term velocity and diffusive flux. In both cases, for consistency, the same velocity as in the advective numerical flux must be utilized [27, 30]. The component of the numerical velocity in the x-direction is given by

$$\widehat{u}=\frac{1+sgn(s_{\ast })}{2}\left[u_{\mathrm{L}}+s_{-}\left(\frac{s_{\mathrm{L}}-u_{\mathrm{L}}}{s_{\mathrm{L}}-s_{\ast }}-1\right)\right]+\frac{1-sgn(s_{\ast })}{2}\left[u_{\mathrm{R}}+s_{+}\left(\frac{s_{\mathrm{R}}-u_{\mathrm{R}}}{s_{\mathrm{R}}-s_{\ast }}-1\right)\right],$$ (D.6)

and is derived from the advective numerical flux of the advection equation. The remaining velocity components, on the other hand, may simply be written as

$$\widehat{v}=\frac{1+sgn(s_{\ast })}{2}{v}_{\mathrm{L}}+\frac{1-sgn(s_{\ast })}{2}{v}_{\mathrm{R}},$$ (D.7)

$$\widehat{w}=\frac{1+sgn(s_{\ast })}{2}{w}_{\mathrm{L}}+\frac{1-sgn(s_{\ast })}{2}{w}_{\mathrm{R}}.$$ (D.8)

Note that in the solution procedure of a Riemann problem in the x-direction, only û is necessary to evaluate the numerical source term velocity, while all of the velocity components are needed to compute the numerical diffusive flux. In addition, the latter also requires that a value of the velocity gradient be available at the interface of the Riemann problem. Following Perigaud and Saurel [27], we choose

$$\overline{\nabla \mathbf{u}}=\frac{1}{2}[{(\nabla \mathbf{u})}_{\mathrm{L}}+{(\nabla \mathbf{u})}_{\mathrm{R}}].$$ (D.9)

Appendix E. Algorithm

To facilitate the implementation of the proposed numerical scheme, we proceed next by illustrating how its building blocks are assembled to evolve the cell average conservative variables in time. We omit, however, discussing the time-marching scheme itself, since it is explicit and straightforward to implement. Instead, we provide the steps necessary to evaluate the RHS of the semi-discrete form of the equations of motion in Eq. (18), which is represented by the L operator in the time-stepper in Eq. (33), and must be evaluated at least once at each time-stage. We begin with the cell average conservative variables, q_i,j,k:

1. From q_i,j,k, build the primitive variables, v_i,j,k:

   1. Reconstruct q_i,j,k in the x-direction to get q_il,j,k.

   2. Reconstruct q_il,j,k in the y-direction to get q_il,jm,k.

   3. Reconstruct q_il,jm,k in the z-direction to get q_il,jm,kn.

   4. Convert q_il,jm,kn into v_il,jm,kn.

   5. Average v_il,jm,kn to get v_i,j,k.

2. To evaluate the RHS contribution of the advective fluxes and source term in the x-direction, from v_i,j,k, build ${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{a}}$ and u_i+1/2,j,k, respectively:

   1. Project v_i,j,k onto the characteristic fields to get w_i,j,k.

   2. Reconstruct w_i,j,k in the x-direction to get ${\mathbf{w}}_{i+1/2,j,k}^{\mathrm{K}}$.

   3. Reconstruct ${\mathbf{w}}_{i+1/2,j,k}^{\mathrm{K}}$ in the y-direction to get ${\mathbf{w}}_{i+1/2,j_l,k}^{\mathrm{K}}$.

   4. Reconstruct ${\mathbf{w}}_{i+1/2,j_l,k}^{\mathrm{K}}$ in the z-direction to get ${\mathbf{w}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$.

   5. Project ${\mathbf{w}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$ onto the physical fields to get ${\mathbf{v}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$.

   6. Convert ${\mathbf{v}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$ into ${\mathbf{q}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$.

   7. Compute ${\widehat{\mathbf{f}}}_{i+1/2,j_l,k_m}^{\mathrm{a}}$ and û_i+1/2,jl,km from ${\mathbf{q}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$ with the Riemann solver.

   8. Average ${\widehat{\mathbf{f}}}_{i+1/2,j_l,k_m}^{\mathrm{a}}$ and û_i+1/2,jl,km to get ${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{a}}$ and u_i+1/2,j,k.

3. To evaluate the RHS contribution of the advective fluxes and source term in the y- and z-directions, build ${\mathbf{h}}_{i,j+1/2,k}^{\mathrm{a}}$ and v_i,j+1/2,k, and ${\mathbf{g}}_{i,j,k+1/2}^{\mathrm{a}}$ and w_i,j,k+1/2, respectively, by following a procedure similar to that in Step 2.

4. From the velocities ${\mathbf{u}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$, build the spatial derivative of the velocity in the x-direction, ∂_xu_i,j,k:

   1. Average ${\mathbf{u}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$ to get u_i+1/2,jl,km.

   2. Average u_i+1/2,jl,km to get u_i+1/2,j,k.

   3. Compute ∂_xu_i,j,k from u_i+1/2,j,k with the divergence theorem.

5. Build ∂_yu_i,j,k and ∂_zu_i,j,k by following a procedure similar to that in Step 4.

6. To evaluate the RHS contribution of diffusive fluxes in the x-direction, from û_i+1/2,jl,km and ∇u_i,j,k, build ${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{d}}$:

   1. Reconstruct ∇u_i,j,k to get $\nabla {\mathbf{u}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$ by following a procedure similar to that in Step 2, (b)–(d).

   2. Average $\nabla {\mathbf{u}}_{i+1/2,j_l,k_m}^{\mathrm{K}}$ to get ∇u_i+1/2,jl,km.

   3. Compute ${\widehat{\mathbf{f}}}_{i+1/2,j_l,k_m}^{\mathrm{d}}$ from û_i+1/2,jl,km and ∇u_i+1/2,jl,km directly.

   4. Average ${\widehat{\mathbf{f}}}_{i+1/2,j_l,k_m}^{\mathrm{d}}$ to get ${\mathbf{f}}_{i+1/2,j,k}^{\mathrm{d}}$.

7. To evaluate the RHS contribution of diffusive fluxes in the y- and z-directions, thus completing the evaluation of the RHS, build ${\mathbf{g}}_{i,j+1/2,k}^{\mathrm{d}}$ and ${\mathbf{h}}_{i,j,k+1/2}^{\mathrm{d}}$, respectively, by following a procedure similar to that in Step 6.