Abstract
Many studies that gather social network data use survey methods that lead to censored, missing, or otherwise incomplete information. For example, the popular fixed rank nomination (FRN) scheme, often used in studies of schools and businesses, asks study participants to nominate and rank at most a small number of contacts or friends, leaving the existence of other relations uncertain. However, most statistical models are formulated in terms of completely observed binary networks. Statistical analyses of FRN data with such models ignore the censored and ranked nature of the data and could potentially result in misleading statistical inference. To investigate this possibility, we compare Bayesian parameter estimates obtained from a likelihood for complete binary networks with those obtained from likelihoods that are derived from the FRN scheme, and therefore accommodate the ranked and censored nature of the data. We show analytically and via simulation that the binary likelihood can provide misleading inference, particularly for certain model parameters that relate network ties to characteristics of individuals and pairs of individuals. We also compare these different likelihoods in a data analysis of several adolescent social networks. For some of these networks, the parameter estimates from the binary and FRN likelihoods lead to different conclusions, indicating the importance of analyzing FRN data with a method that accounts for the FRN survey design.
Keywords: censoring, latent variable, marginal likelihood, missing data, ordinal data, ranked data, network, social relations model
1 Introduction
Relating social network characteristics to individual-level behavior is an important application area of social network research. For example, in the context of adolescent health, many large-scale data-collection efforts have been undertaken to examine the relationship between adolescent friendship ties and individual-level behaviors, including the PROSPER peers study (Moody et al., 2011), the School Study of the Netherlands Institute for the Study of Crime and Law Enforcement (NSCR) (Weerman & Smeenk, 2005), and the National Longitudinal Study of Adolescent Health (Add Health) study (Harris et al., 2009). These and other studies have reported evidence for relationships between friendship network ties and behaviors such as exercise (Macdonald-Wallis et al., 2011), smoking and drinking behavior (Kiuru et al., 2010), and academic performance (Thomas, 2000).
A common approach to the statistical analysis of such relationships is via a statistical model relating the observed social network data to a set of explanatory variables via some unknown (multidimensional) parameter to be estimated. Often the network data are represented by a sociomatrix S, a square matrix with a missing diagonal where the (i, j)th element si,j describes the relationship from node i to node j. In cases where si,j is the binary indicator of a relationship from i to j, the sociomatrix can be viewed as the adjacency matrix of a directed graph. A popular class of models for such data are exponential random graph models (ERGMs), typically having a small number of sufficient statistics chosen to represent effects of explanatory variables and other important patterns in the graph (Frank & Strauss, 1986; Snijders et al., 2006). Another class of models includes latent variable or random effects models. These models assume a conditional dyadic independence in that each dyad {si,j, sj,i} is assumed to be independent of other dyad {sk,l, sl,k}, conditional on some set of unobserved latent variables. The latent variables are often taken to be node-specific latent group memberships (Nowicki & Snijders, 2001; Airoldi et al., 2008) or latent factors (Hoff et al., 2002; Hoff, 2005), which can represent various patterns of clustering or dependence in the network data.
While statistical models such as these can often be very successful at representing the main features of a social network or relational dataset, they generally ignore contexts or constraints under which the data were gathered. In particular, these models generally assume the relational dataset is fully observed, and that the support of the probability model is equal to the set of sociomatrices that could have been observed. As a simple example where such an assumption is not met, consider the analysis of the well-known “Sampson’s monastery” dataset (Sampson, 1969; Breiger et al., 1975) using a binary random graph model. These data include relations among 18 monks, each of which was asked to nominate and rank-order three other monks whom they liked the most, and three other monks whom they liked the least. The relations reported by each monk thus consist of a partial rank ordering of all other monks in the monastery. Since a binary random graph model does not accommodate rank data, analysis of these data with such a model typically begins by reducing all positive ranked relations to “ones,” and all negative ranked relations to “zeros,” leaving unranked relations as zeros as well. Such a data analysis essentially throws away some of the information in the data. Furthermore, the support of most binary random graph models consists of all possible graphs on the node set. In contrast, the data collection scheme used by Sampson (1969) was censored, as no graph with more than three outgoing edges per node could have been observed.
The ranked nomination scheme used to gather Sampson’s (1969) monastery data is not exceptional. Ranked nomination methods were among the first to be used for the collection of respondent-provided sociometric data (Moreno, 1953, 1960) and have been used extensively in both research and applied settings ever since. They remain quite common in studies of work environments and children in classrooms, and are recommended in Sherman’s (2002) widely used online resource “Sociometry in the Classroom.” Several large-scale studies of adolescent health and behaviors have used variations on ranked-nomination schemes, including the PROSPER, NCSD, and Add Health studies mentioned above. However, statistical analyses of data from these studies generally ignore the ranked and censored nature of the data, as in Currarini et al. (2010), Weerman (2011), and Fletcher & Ross (2012). In an attempt to mitigate the effects of censoring, Goodreau et al. (2009) coarsen the data further by converting ranked and censored relational data from the Add Health study to binary indicators of reciprocated ties. Recent work by Handcock & Gile (2010) develops a framework for ERGM estimation from incompletely observed networks, but the focus is on data sampled from egocentric surveys and link tracing designs.
A data analysis goal of these and many other social network studies is to quantify the relationships between ranked friendship nominations and individual-level attributes, such as grade level, ethnicity, academic performance, and smoking and drinking behavior. Quantification of these relationships is of interest for a variety of reasons, including identification of at-risk youth, or to aid in the development of adolescent health programs, which often have components based on peer interventions. Statistical evaluations of the relationships are often made by modeling the network outcome si,j for each pair of individuals (i, j) as depending on (among other things) a linear predictor βT xi,j, where xi,j is a vector of observed characteristics and contextual variables specific to the pair, and β is an unknown regression parameter to be estimated. In particular, data analysis based on both ERGMs and variety of latent variable models mentioned above allow for estimation of such regression terms from complete and fully observed network data.
In this paper, we develop a type of likelihood that accommodates the ranked and censored nature of data from fixed rank nomination (FRN) surveys, and allows for estimation of the type of regression effects described above. In addition, we show that the failure to account for censoring in such data can lead to biased inferences for certain types of regression effects, in particular, the effects of any characteristics specific to the nominators of the relations. In the next section, we introduce the FRN likelihood, which accommodates both the ranked nature of FRN data and the constraint on the number of nominations. We relate this likelihood to three other likelihood functions that are in use or may be appropriate for related types of network data collection schemes: a “binary” likelihood based on a probit model appropriate for unranked, uncensored binary network data; a variant of the binary likelihood that accounts for the censored nature of the data; and a likelihood based solely on the information in the ranks. We show how the Bayesian parameter estimates based on these likelihood functions can be obtained via a very general Markov Chain Monte Carlo (MCMC) algorithm. In Section 3 we provide both an analytical argument and a simulation study that suggests that the binary likelihood may provide misleading inference for some model parameters, in particular those that estimate the effects of the nominator’s characteristics on network relations. We also compare the performance of the censored binary and rank likelihoods with the FRN likelihood. The similarities and differences among the likelihoods are illustrated further in an analysis of several adolescent social networks from the Add Health study, in which we model the friendship preferences of students as a function of individual and pair-specific explanatory variables based on characteristics such as grade, grade point average, ethnicity, and smoking and drinking behavior. A discussion follows in Section 5.
2 Likelihoods based on fixed rank nomination data
In this section we develop a type of likelihood function that is appropriate for modeling data that come from FRN surveys. The likelihood is derived by positing a relationship between the observed relational data S and some underlying relational data Y that the ranks are representing. In some situations, such a Y is reasonably well defined. For example, the ith row of S may record the top email recipients for individual i. In this case, the observed data S is a coarsened version of the sociomatrix Y of email counts. In other situations a definition of Y is less precise, as with surveys that ask people to nominate their “top five friends.” For either case, the likelihood developed below provides a statistical model for the ranked nomination data that makes full use of the rank information and accounts for the constraint on the number of nominations that may be made. We contrast this likelihood to other likelihood functions that do not make use of the rank data and/or do not account for the nomination constraint.
2.1 Set-based likelihoods for ranked nomination data
Let Y = {yi,j : i ≠ j} denote a sociomatrix of numerical or ordinal relationships among a population of n individuals so that yi,j > yi,k means that person i’s relationship with person j is in some sense stronger, of more value, or larger in magnitude than their relationship with person k. Observation of Y would allow for an analysis of the relationship patterns in the population, perhaps via a statistical model {p(Y|θ) : θ ∈ Θ}, where θ is an unknown parameter to be estimated.
As discussed in the Introduction, many surveys of social relations record only incomplete representations of such a sociomatrix Y. In positive FRN schemes, each individual provides an ordered ranking of people with whom they have a “positive” relationship up to some limited number, say m. One representation of such data is as a sociomatrix of scores S = {si,j : i ≠ j}, coded so that si,j = 0 if j is not nominated by i, si,j = 1 if j is i’s least favored nomination, and so on. Under this coding, si,j > si,k if i scores j “more highly” than k, or if i nominates j but not k. Letting ai = {1, …, n} \ {i} be the set of individuals whom person i may potentially nominate, each observed outdegree di ≡ Σj∈ai 1(si,j > 0) satisfies di ≤ m.
In order to make inference about θ from the observed scores S, the relationship between S and the unobserved relations Y must be specified. The entries of S, as described above, can be written as an explicit function of Y as follows:
| (1) |
where ranki(yi,j) is the rank of yi,j among the values in the ith row of Y, from high to low. These scores can be viewed as a coarsened and censored function of the relations Y, or in other words, the sociomatrix S is a many-to-one function of Y. Some intuition can be gained by describing this function in terms of its inverse, defined by the following three associations:
| (2) |
| (3) |
| (4) |
The first association follows from the definition of ranked individuals as those with whom there is a positive relationship. The second association follows from {si,j : j ∈ ai}, the elements in the ith row of S, having the same order as {yi,j : j ∈ ai}, the elements in the ith row of Y. The third association is a result of the censoring of the ranks: If person i did not nominate person j (si,j = 0) but could have (di < m), then their relationship with j is not positive (yi,j < 0). On the other hand, if di = m then person i’s unranked relationships are censored, and so yi,j could be positive even though si,j = 0. In this case, all that is known about yi,j is that it is less than yi,k for any person k that is ranked by i.
Given a statistical model {p(Y|θ) : θ ∈ Θ} for the underlying social relations Y, inference for the parameter θ can be based on a likelihood derived from the observed scores S. The likelihood is, as usual, the probability of the observed data S as a function of the parameter θ. To obtain this probability, let F(S) denote the set of Y-values that are consistent with S in terms of associations (2)–(4) above. Since the entries of S are the observed scores if and only if Y ∈ F(S), the likelihood is given by
where μ is a measure that dominates the probability densities {p(Y|θ) : θ ∈ Θ}. We refer to a likelihood of this form, based on a set F(S) defined by Equations (2)–(4), as an FRN likelihood, as it is derived from the probability distribution of the data obtained from a FRN survey design.
The FRN likelihood can be related to other likelihood functions that are used for ordinal or binary data. For example, consider the set R(S) = {Y : si,j > si,k ⇒ yi,j > yi,k}, defined by association (3) alone. The likelihood given by LR(θ : S) = Pr(Y ∈ R(S)|θ) is known as a rank likelihood for ordinal data, variants of which have been used for semiparametric regression modeling (Pettitt, 1982) and copula estimation (Hoff, 2007). Use of a rank likelihood for FRN data is valid in some sense, but not fully informative: By the way the sets are defined, we have F(S) ⊂ R(S), as the information about Y that R(S) provides incorporates only one of the three conditions that defines F(S). This rank likelihood thus uses accurate but incomplete information about the value of Y as compared with the information used by the FRN likelihood.
Another type of likelihood often used to analyze relational data is obtained by relating S and Y as follows:
| (2) |
| (5) |
Letting B(S) = {Y : si,j > 0 ⇒ yi,j > 0, si,j = 0 ⇒ yi,j ≤ 0}, the corresponding likelihood is given by LB(θ: S) = Pr(Y ∈ B(S)|θ). We refer to this as a binary likelihood, as probit and logistic models of binary relational data use this type of likelihood. To see this, note that the set B(S) contains information only on the presence (si,j > 0) or absence (si,j = 0) of a ranked relationship. As with probit or logit models, the presence or absence of a relationship corresponds to a latent variable (here yi,j) being above or below some threshold (zero). Such a likelihood for FRN data is neither fully informative nor valid: Not only does it discard the information that differentiates among the ranked individuals, it also ignores the censoring on the outdegrees that results from the restriction on the number of individuals that any one person may nominate. In particular, F(S) ⊄ B(S) generally, and so the binary likelihood is based on the probability of the event {Y ∈ B(S)}, subsets of which we know could not have occurred. We note that the information about Y provided by S via Equations (2) and (5) corresponds to the commonly used representation of a relational dataset as an edge list, i.e., a list of pairs of individuals between which there is an observed relationship. Such a representation ignores any information in the ranks, ignores the possibility of missing data, and does not by itself convey any information about censored relationships.
A final likelihood we consider is formed by recognizing the censoring but ignoring the order of the si,j’s beyond noting who is and is not ranked. To account for the censoring, we infer that person i does not positively rate person j (yi,j ≤ 0) if they do not rank them (si,j = 0) and person i has unfilled nominations (di < m). Our modified set of allowable Y-values can then be described by the conditions
| (2) |
| (4) |
| (6) |
Restrictions (2) and (4) are two of the three restrictions used to form the FRN likelihood. Restriction (6) is similar to restriction (3) of the FRN likelihood in that it recognizes a preference ordering between ranked and unranked individuals, but unlike the FRN likelihood it does not recognize differences among ranked individuals. Letting C(S) be the set of Y-values consistent with Equations (2), (4), and (6), we refer to
as the censored binomial likelihood. As the censored binomial likelihood recognizes the censoring in FRN data, we expect it to provide parameter estimates that do not have the biases of the binomial likelihood estimators. On the other hand, LC ignores the information in the ranks of the scored individuals, and so we might expect it to provide less precise estimates than the FRN likelihood. In particular, note that if Y satisfies condition (6) then it also satisfies condition (4), but the converse does not hold. This implies that F(S) is a proper subset of C(S) and so, like the rank likelihood, LC uses accurate but incomplete information about the value of Y as compared with the information used by the FRN likelihood.
The FRN likelihood LF is an “ordinary” likelihood in the sense that it is simply the probability of the observed data S as a function of the parameter θ. The rank and censored binary likelihoods LR and LC can be viewed as marginal likelihoods based on LF (Severini, 1991, Section 8.3): Since F(S) ⊂ R(S), for example, LF can be written as
where the second equality is true because F(S) ⊂ R(S). This shows LR(θ : S) to be a marginal probability in the decomposition of the probability Pr(Y ∈ F(S)|θ) into marginal and conditional parts. Similarly, since F(S) ⊂ C(S), LC (θ: S) is also a marginal likelihood. In contrast, LB is not a marginal likelihood based on LF since F(S) is not generally a subset of B(S).
Finally, we note that the FRN and rank likelihoods implicitly allow for ties in the observed scores S, and therefore can accommodate ordinal relational data such as weighted graphs. For example, suppose the score si,j is on a categorical Likert scale. The observation that si,j1= si,j2> si,k tells us that i prefers j1 and j2 to k, and so yi,j1 and yi,j2 are both larger than yi,k, but that i’s preferences for j1 and j2 are of the same category, and so there is no information about the relative ordering of yi,j1 and yi,j2. This is the same ordering information included in the FRN and rank likelihoods: Given si,j1= si,j2> si,k, both likelihoods presume that yi,j1 and yi,j2are larger than yi,k, but neither presume an ordering of yi,j1 and yi,j2.
2.2 Bayesian estimation with set-based likelihoods
The FRN, rank, and binary likelihoods can each be expressed as the integral of p(Y|θ) over a high-dimensional and somewhat complicated set of Y-values. These integrals are generally intractable, but interpreting the Y-values as latent variables suggests the possibility of parameter estimation via an expectation–maximization (EM) algorithm. However, for the models used in this paper, the E-step of such an algorithm would require the expectation of a complete-data log-likelihood with respect to a large number of correlated Y-values constrained to lie in one of the sets. The fact that the entries of Y are constrained and correlated makes obtaining such an expectation very difficult, and would typically require a separate MCMC approximation for each iteration of the EM algorithm (Geweke, 1991; Rodriguez-Yam et al., 2004). Alternatively, Bayesian inference for θ is reasonably straightforward to obtain using a single MCMC posterior approximation. Given the observed ranks S and a prior distribution p(θ) over the parameter space Θ, the joint posterior distribution with density p(θ, Y|S) can be approximated by generating a Markov chain whose stationary distribution is that of (θ, Y) given Y ∈ F(S), R(S), or B(S), depending on the likelihood being used. The values of θ simulated from this chain provide an approximation to the (marginal) posterior distribution of θ given by the information from S. One such MCMC algorithm is the Gibbs sampler, which iteratively simulates values of θ and Y from their full conditional distributions. Below we provide Gibbs samplers for the FRN, binary, and rank likelihoods that can be used with any model for Y that allows for simulation of each yi,j from p(yi,j |θ, Y−(i,j)) constrained to an interval, where Y−(i,j) denotes the entries of Y other than yi,j. If simulation from this distribution is not available, the algorithms below can be modified by replacing such simulations with the Metropolis–Hastings sampling schemes.
Given current values of (θ, Y), one step of the Gibbs sampler for the FRN likelihood proceeds by updating the values as follows:
Simulate θ ~ p(θ|Y).
-
For each i ≠ j, simulate yi,j ~ p(yi,j |θ, Y−(i,j), Y ∈ F(S)) as follows:
- If si,j > 0, simulate
if si,j = 0 and di < m, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j ≤ 0);
if si,j = 0 and di = m, simulate yi,j ~ p(yi,j|Y−(i,j), θ) × 1(yi,j ≤ min{yi,k : si,k > 0}).
In the above steps, “y ~ f(y)” means “simulate y from a distribution with density proportional to f(y).” For each ordered pair (i, j), step 2 of this algorithm will generate a value of yi,j from its full conditional distribution, constrained so that conditions (2)–(4) that define the FRN likelihood are met. Gibbs samplers for the rank, binary, and censored binary likelihoods are obtained by replacing step 2 of the above algorithm with different constrained simulation schemes. For the rank likelihood, step 2 is simply as follows:
simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(max{yi,k : si,k < si,j} ≤ yi,j ≤ min{yi,k : si,k > si,j}).
For the binary likelihood, step 2 becomes
if si,j > 0, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j > 0);
if si,j = 0, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j ≤ 0).
The procedure for the censored binary likelihood is a bit more involved:
-
If di < m (no censoring)
if si,j > 0, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j > 0);
if si,j = 0, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j ≤ 0).
-
If di = m (censoring)
if si,j > 0, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j > max{yi,k : si,k = 0});
if si,j = 0, simulate yi,j ~ p(yi,j |Y−(i,j), θ) × 1(yi,j ≤ min{yi,k : si,k > 0}).
It is also straightforward to extend this Gibbs sampler to accommodate certain types of missing data. For example, some students participating in the Add Health study were not included on their school’s roster of possible nominations. In this case, si,j is missing for each unlisted student j and every other student i. If the relations {yi,j : i ∈ {1, …, n} \ j} of the students to a particular student j are independent of whether or not student j is on the roster, the observed rankings S provide no information about {yi,j : i ∈ {1, …, n} \ j} and thus the full conditional distribution of yi,j is p(yi,j|yj,i, θ), unconstrained. Simulating yi,j from this distribution for each missing si,j allows for imputation of friendship nominations to unlisted students, and generally facilitates simulation of the parameter θ in the MCMC algorithm.
The above algorithms, or simple variants of them, are straightforward to implement for many statistical models of social networks and relational data. For example, latent variable models based on conditional dyadic independence will satisfy p(yi,j|Y−(i,j), θ) = p(yi,j|yj,i, θ), which makes step 2 of the above algorithms much easier. Such models include social relations models (SRMs) (Li & Loken, 2002), stochastic blockmodels (Nowicki & Snijders, 2001), mixed-membership models (Airoldi et al., 2008), latent space models (Hoff et al., 2002), and latent factor models (Hoff, 2005, 2009a). In addition, in these models the unobserved relations Y can be taken to be normally distributed, and so step 2 involves simulations from constrained normal distributions, which are fairly easy to implement. Furthermore, it is not necessary in step 1 that θ is simulated from its full conditional distribution. Instead, all that is necessary is that it is simulated in a way that makes the stationary distribution of the Markov chain equal to the posterior distribution p(θ, Y|S). This can be achieved with a block Gibbs sampler for different components of θ, or with the Metropolis–Hastings algorithm. The Metropolis–Hastings algorithm in this context would work by replacing step 1 of the above algorithm with the following procedure: Given a current value θ, propose a new value θ* from some distribution with density f(θ*| θ). The value θ* is accepted as the new value of θ with probability λ, where
If θ* is not accepted, then θ is unchanged. This procedure, when used iteratively with step 2 above, generates a Markov chain that can be used to approximate the target posterior distribution. This same type of procedure can be used if it is not possible to simulate yi,j directly from the distribution given in step 2 of the above algorithm. For more details on the Metropolis–Hastings algorithms and the Gibbs sampling for constrained latent variables, see for example, Hoff (2009b, Chapters 10 and 12).
3 Comparing likelihoods in social relations regression models
While we have argued that LB(θ : S), LC (θ : S), and LR(θ : S) may be inappropriate or incomplete for estimating θ from FRN data, in practice they may provide inference about approximates that are obtained from LF (θ : S), at least for some aspects of θ or under certain conditions. To explore this possibility, we consider inference under different likelihoods in the case where θ represents the parameters in the following standard regression model for relational data:
| (7) |
The additive row effect ai is often interpreted as a measure of person i’s “sociability,” whereas the additive column effect bi is taken as a measure of i’s “popularity.” The parameter ρ represents potential correlation between yi,j and yj,i. In a mixed-effects version of this model, the possibility that a person’s sociability ai is correlated with their popularity bi can be represented with a covariance matrix Σab. The covariance among the elements of Y = {yi,j : i ≠ j} induced by Σab and is called the SRM (Warner et al., 1979), and has been frequently used as a model for continuous relational data (Wong, 1982; Gill & Swartz, 2001; Li & Loken, 2002) as well as a component of a generalized linear model for binary or discrete network data (Hoff, 2005). For example, the binary likelihood used in tandem with the SRM amounts to a type of mixed-effects probit regression model. This model is very similar to the “p2” model of van Duijn et al., (2004), which is an extension of the well-known log-linear p1 model of Holland & Leinhardt, (1981). Like the SRM, the p2 model has row- and column-specific random effects and allows the network relationships to depend on regressors. We note that these models cannot represent commonly observed network patterns such as transitivity, clustering, or stochastic equivalence, unless these patterns can be captured by covariate effects. However, the set-based likelihoods and estimation scheme presented above can be applied to network models that do account for such patterns, as will be discussed in Section 5.
In what follows, we consider the estimation of parameters (β, a, b, Σε, Σab) in the SEM for the underlying relations Y, when the observed data include only the censored nomination scores S, given by Equation (1). As we will show, the likelihoods LR(θ : S) and LB(θ : S) are inappropriate for estimation of any row-specific effects, i.e., terms in the regression model (7) that are constant across the row index i, the index of the nominators of the relations. This limitation includes any nominator-specific regressors, as well as nominator-specific random effects. We first show this analytically, and then confirm the results with a simulation study. On the other hand, the simulation study suggests that LC provides estimates of the regression parameters that are similar to those provided by LF, particularly when the degree of censoring is high.
3.1 Estimation of additive row effects
In assessing the ability of LR(θ : S) and LB(θ : S) to estimate row-specific effects, it will be convenient to reparameterize the model to separate out these terms from the rest. We rewrite Equation (7) as
so that αi is equal to ai from Equation (7) plus any regression effects that are constant across rows (i.e., are based on any characteristics of the nominator of the tie), and now represents any other column- or dyad-specific regression terms, including the additive column effect bj.
We first show that the row-specific effects α = (α1, …, αn) are not estimable using the rank likelihood LR(θ : S). Recall that the rank likelihood is given by
where here we take θ = {α, β, σ2, ρ}. For a given row i, the likelihood only provides information on the relative ordering of yi,j ’s, and not their overall magnitude. To see why this precludes estimating row effects, note that the ordering of yi,j ’s within row i is unchanged by the addition of a constant, and so if Y ∈ R(S), so is Y + c1T for any vector c in IRn. Letting θ = (α, βcd, Σε), we have
for all c ∈ IRn, and so Pr(Y ∈ R(S)|θ = (α, βcd, Σε)) cannot be a function of α, and therefore cannot be used to estimate α.
Estimation of row effects is also problematic for the binomial likelihood LB(θ : S). Recall that the binomial likelihood is given by
Under the binomial likelihood, the data are essentially assumed to be coming from a probit regression model and the estimate of the row effect αi is largely determined by the number of nominations that person i will make, i.e., their observed outdegree di. This is appropriate in the absence of censoring, where di reflects the number of positive relations that person i has. However, in the presence of censoring, a person’s outdegree (and therefore their estimated row effect) may be controlled by the maximum number of nominations m they are allowed to make. For example, consider a person i having many more positive relations, say d̃i, than the number of allowed nominations m. In this case, di will equal m and the binomial likelihood will underestimate αi, reflecting the observed outdegree of m rather than person i’s actual outdegree d̃i. In addition, if d̃i is much higher than m for many individuals then many individuals will make the maximum number of nominations, and the variability in the observed outdegree will be low. Inference under the binomial likelihood will incorrectly attribute this to low variability among αi’s. As one component of the variability in αi’s is the variability in the row-specific regression effects , underestimated variability among αi’s will translate into an underestimated magnitude for βr.
We make this argument more concrete via an analytic comparison between the binomial and FRN likelihoods, showing that the binomial likelihood for the SRM is approximately equal to the FRN likelihood for a model with no row-specific variability. Unless there is actually no row-specific variability among the relations, this latter FRN likelihood is misspecified. The fact that the binomial likelihood gives approximately the same inference as this misspecified likelihood indicates the consequences of ignoring the censoring via the use of the binomial likelihood. For simplicity, we compare likelihoods based on the ranked nomination data from a single nominator who makes m nominations. Denote this individual’s unobserved relations to the other n − 1 individuals as y = {yj : j = 1, …, n − 1}, and the observed nomination scores as s = {sj : j = 1, …, n − 1}. From Equations (2)–(4), the FRN likelihood is the joint probability of the events A(s) = {y ∈ IRm−1 : y(m) > ···> y(1) > 0} and B(s) = {y ∈ IRm−1 : y(1) > max{yj : sj = 0}}, where y(k) denotes the nominator’s relationship to the person with the kth lowest non-zero score. For example, y(1) is the relation to the person j for which sj = 1.
Suppose we use this misspecified FRN likelihood with a model for y, where yj ’s are independent with , and contains no intercept (this would correspond to a model with no row-specific effects, when extended to a likelihood based on data from multiple nominators). Letting ϕ and Φ be the standard normal density and cumulative distribution function (CDF) respectively, the no-intercept FRN likelihood can be expressed as
| (8) |
since A(s) and B(s) are conditionally independent given y(1). Now Pr(B(s)|βcd, y(1)) is given by
| (9) |
which is the same as the contribution of “zeros” to a probit likelihood for binary data with linear predictor , where α = −y(1).
Using Bayes’ rule, we can write Pr(A(s)|βcd, y(1)) as
| (10) |
Note that the first term is equivalent to the contribution of the “ones” to a probit likelihood for binary data with linear predictor , where α = −y(1). Combining Equations (9) and (10) gives
where LB(α, βcd : s−(1)) is exactly the binomial likelihood, absent information from the lowest ranked nomination, under the probit model with linear predictor . Incorporating this expression into Equation (8) shows that relationship between the no-intercept FRN likelihood and this binomial probit likelihood is
where . A Laplace approximation to this integral gives
where α̂ is the maximizer in α of the integrand and c does not depend on βcd.
Proceeding heuristically, we generally expect LB(α, βcd : s−(1)) to be close to LB(α, βcd : s), the binary likelihood based on the nominator’s full set of scores, as the former is lacking only the information on one ranked individual. Furthermore, if n is much larger than m, then we expect that g will be relatively flat as a function of (α, βcd) as compared with LB, as the latter is a probit likelihood based on n ≫ m observations, and the former involves the conditional probability of a particular relative ordering among only m − 1 relations. As a result, the maximizer in α of log LB(α, βcd : s) + log g(α, βcd) should be close to the maximizer in α of log LB(α, βcd : s), and log g(α̂, βcd) should be relatively flat as a function of βcd compared with log LB(α̂, βcd). Combining these approximations suggests that
where α̂ is the maximizer in α of LB(α̂, βcd : s), and d is (roughly) constant in (α, βcd).
Extending this approximation to the case of ranked nominations from n individuals, we have
where d̃ is a constant and for convenience we have ignored the possibility of dyadic correlation between εi,j and εj,i. The result suggests that if most individuals make the maximum number of nominations then the binomial likelihood with row-specific effects α1, …, αn should give roughly the same fit to the data as the FRN likelihood lacking any such effects. Estimation using the latter likelihood is equivalent to setting any row-specific regression coefficients βr to zero, and setting the across-row variance of any random effects a1, …, an to zero as well. As the fit under the binomial likelihood will be similar, we expect it to provide underestimates of the magnitude of βr and the variance of ai’s. However, these results do not preclude the possibility of approximately correct inference for column- and dyad-specific effects, represented here by βcd.
3.2 Simulation study
We evaluated the above claims numerically with a simulation study, comparing parameter estimates for the SRM (7) obtained from the binomial, censored binomial, rank, and FRN likelihoods, hereafter referred to as LB, LC, LR, and LF. We generated relational data Y from an SRM as in Equation (7) with random row and column effects:
| (11) |
where our mean model had the following form:
In this model, xi,r and xj,c are individual-level characteristics of person i as a nominator and person j as a nominee, respectively, and could quantify things such as smoking behavior or grade point average of the individuals. The two dyad-specific characteristics xi,j,1 and xi,j,2 are specific to each pair of individuals, and could represent such things as the amount of time spent together, or an indicator of co-membership to a common group. For each Y generated from this model, we obtained the corresponding nomination scores under the FRN scheme using the relationship in Equation (1).
We generated 80 network datasets of n = 100 individuals each from this model, using the following parameter values:
β0 = −3.26, βr = βc = βd1 = βd2 = 1;
;
{x1,r, …, xn,r}, {x1,c, …, xn,c}, {xi,j,1 : i ≠ j} ~ i.i.d. N(0, 1),
xi,j,2 = zizj/.42, where z1, …, zn ~ i.i.d. binary(1/2).
The second dyadic characteristic xi,j,2 can be viewed as an indicator of co-membership to a common group, of which each individual is a member with probability 1/2. The product zizj is divided by 0.42 to give xi,j,2 a standard deviation of 1 so that it is on the same scale as other characteristics. The value of the intercept, β0 = −3.26, was chosen so that 15% of yi,j’s were greater than zero, making the average uncensored outdegree equal to 15.
The value of m, the maximum number of nominations, was varied among the 80 networks so that 20 networks were generated for each value of m ∈ {5, 15, 30, 50}. The value m = 5 resulted in a high degree of censoring, with 69% of uncensored outdegrees d̃i being greater than or equal to m. This censoring rate decreased with increasing m, with rates of 39%, 16%, and 4% under m = 15, 30, and 50, respectively.
For each dataset, we obtained posterior mean estimates and standard deviations under the four likelihoods using the MCMC approach based on the procedure described in Section 2.2. We ran the MCMC algorithms for 110,000 iterations each, dropped the first 10,000 iterations to allow for burn-in and saved parameter values every 25th iteration, resulting in 4,000 simulated values of each parameter from which to make inference. Effective sample sizes (an assessment of the MCMC approximation) on average across parameters were 1,111, 884, 309, and 1,025 for LB, LC, LR, and LF respectively.
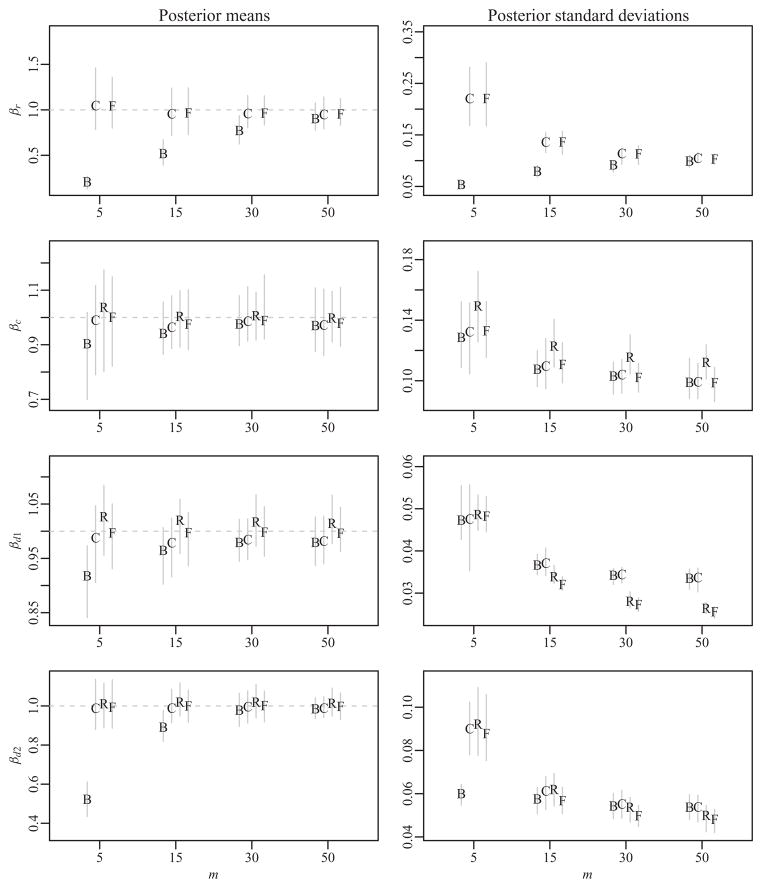
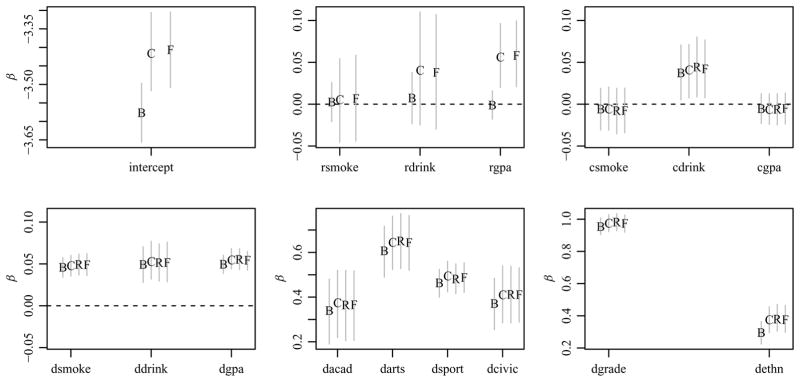
Posterior mean estimates and standard deviations for each of the regression parameters are summarized in Figure 1. The four rows of the figure correspond to the four parameters (βr, βc, βd1, βd2), and the first and second columns correspond to the parameter estimates and standard deviations, respectively. The plot in the second row and first column, for example, summarizes the estimates of βc across the 20 different datasets for each value of m, estimated using the four likelihoods. For each m ∈ {5, 15, 30, 50}, a 90% interval for the 20 estimates of βc for a given likelihood is shown with a vertical bar. The bars are grouped together for each m-value, representing LB, LC, LR, and LF from left to right. The height of the letter in the middle of each bar is the average of the estimates across the 20 datasets for that likelihood, and is an approximation to the expected value of the corresponding Bayes estimator. The other plots in the figure were constructed similarly. Note that the first row only displays results for βr under LB, LC, and LF, as LR does not provide an estimate of βr.
Fig. 1.
Ranges of posterior mean estimates and standard deviations of regression parameters across simulated datasets, likelihoods, and m-values. Within each plot, results for the binomial, censored binomial, rank, and FRN likelihoods are grouped from left to right for each value of m and labeled as B, C, R, and F, respectively.
Performance of the binomial likelihood
The results of these simulations are consistent with the discussion of the inadequacies of the binomial likelihood in the previous section. For example, the first row of the figure highlights potential problems with LB in terms of estimating regression coefficients of nominator-specific regressors. Such coefficients relate outdegree heterogeneity to individual-specific effects. When the amount of censoring is large, the heterogeneity of the censored outdegrees is low and so any nominator-specific regression coefficients will be erroneously estimated by LB as being low in magnitude as well. This degree of underestimation is reduced as the amount of censoring decreases with increasing m. In addition, the plot in the first row and second column shows that for low values of m, the posterior standard deviations of βr under LB are substantially smaller than those under LF. Taken together, these two plots indicate that inference under LB can lead not only to overconfident inference but also overconfidence in the wrong parameter values. The second and third plots in the first column suggest that binomial likelihood estimates of column- and dyad-specific regression coefficients βc and βd1, while not as accurate as those from other likelihoods, are not unreasonable. In contrast, the binomial likelihood estimates of βd2 perform poorly for low values of m. The difference between estimation of βd2 and βd1 is that, unlike X1 = {xi,j,1}, the matrix X2 = {xi,j,2} exhibits substantial row variability. Recall that xi,j,2 = zizj/0.42 is essentially the indicator of co-membership to a group. If individual i is not in the group, then the ith row of X2 is all zeros, whereas if they are in the group, then half the entries in the ith row are nonzero (as half of the population is in the group). By ignoring the censoring, the binomial likelihood underestimates the row variability in Y, and thus also the variability that can be attributed to the row variation in X2.
Information loss for the marginal likelihoods
The first column of the figure suggests that, compared with the binomial likelihood LB, the censored binomial and rank likelihoods, LC and LR, provide estimates that are similar to those provided by the FRN likelihood LF. However, recall that both LC and LR are marginal likelihoods derived from LF, and therefore are using a subset of the information used by LF. This is reflected somewhat in the second column of the figure, which shows the range of posterior standard deviations across simulated datasets, likelihoods, and m-values. Evaluating LC first, the first two plots in the second column suggest that there is not much information loss for estimating βr and βc in going from the FRN likelihood to the censored binomial likelihood, as the standard deviations under these likelihoods are quite similar. However, for βd1 and βd2, the differences between the standard deviations is more pronounced: The standard deviations from LC are generally larger than those under LF, and the differences tend to increase with increasing m, especially for βd1. This pattern makes sense, as there is more information about the ranks when m is large. The FRN likelihood makes full use of this information whereas the censored binomial likelihood only distinguishes between ranked and unranked individuals. Parameter uncertainty, as reflected by the posterior standard deviation, is therefore higher under LC. Standard deviations are also generally higher under LR than LF. As with LC, this can be explained by the fact that LR does not use the complete information in the data: The rank likelihood does not incorporate the information given by Equations (2) and (4), which state that ranked individuals have positive y-scores, and for uncensored nominators, unranked individuals have negative y-scores. Not using this information leads to a higher degree of parameter uncertainty as compared with the FRN likelihood.
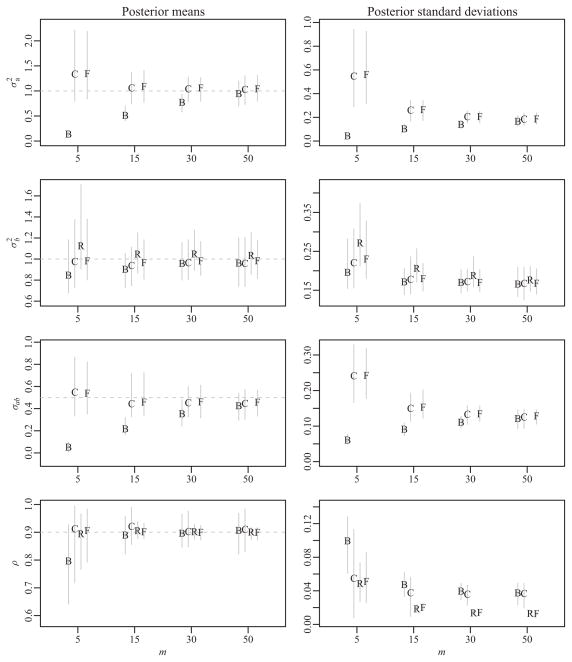
Inference for covariance terms
Estimation results for the covariance parameters , σab, and ρ are similarly summarized in Figure 2. Recall that LR does not provide estimates for any sender-specific effects, including and σab. The performances of different likelihoods for these parameters follow patterns similar to those described above for regression coefficients. In particular, the binomial likelihood confidently underestimates the heterogeneity in the sociability parameter ai, and therefore underestimates both and σab. The correctly specified FRN likelihood LF provides the most accurate parameter estimates, with the censored binomial likelihood LC providing estimates of roughly equal precision. One exception to this is in the estimation of the reciprocity parameter ρ, where both rank-based likelihoods LF and LR provide noticeably more precise inference than the binomial likelihoods LC and LB, particularly when m is large. This is presumably due to the relatively larger amount of information in the ranks for these values of m.
Fig. 2.
Ranges of posterior mean estimates and standard deviations of covariance parameters across the simulated datasets, likelihoods, and m-values. Within each plot, results for the binomial, censored binomial, rank, and FRN likelihoods are grouped from left to right for each m-value and labeled as B, C, R, and F, respectively.
To summarize, the results of the simulation study suggest that the binomial likelihood LB provides generally biased inference for model parameters in the presence of censoring. In contrast, the FRN likelihood LF provides estimators that do not appear to have substantial bias. The marginal likelihoods LC and LR that are based on LF also appear to have small bias, although seem to provide less precise inference as compared with LF. This is likely due to the fact that marginal likelihoods use less data information than the full likelihoods upon which they are based. However, for LC we note that this loss in precision does not appear to be appreciable until m is a quarter to a third of the number n of individuals in the network. These results suggest that for FRN surveys where m is substantially smaller than n, the majority of the information about the regression parameters comes from distinguishing between ranked and unranked individuals, and that the relative ordering among the ranked individuals provides at most a modest amount of additional information. For such surveys, the censored binomial likelihood may provide an adequate approximation to inferences that would be obtained under the FRN likelihood.
4 Analysis of add health data
As described in the Introduction, one component of the Add Health study included FRN surveys administered to a national sample of high schools. Within each school, each participating student was asked to nominate and rank up to five same-sex friends and five friends of the opposite sex. Students were also asked to provide information about a variety of their own characteristics, such as ethnicity, academic performance, smoking and drinking behavior, and extra-curricular activities. To describe the relationships between an individual’s characteristics and the friendship nominations they send and receive, we fit the social relations regression model (11), with a mean model given by
where βr, βc, and βd are vectors of unknown regression coefficients, corresponding to row-, column-, and dyad-specific regressors. We fit such a model to both male–male and female–female FRN networks of seven schools from the Add Health study, where the schools were chosen based on their high within-school survey participation rates. Based on an initial exploratory data analysis of these 14 FRN networks, the following row, column, and dyadic regressors were selected:
A description of the variables is as follows:
Behavioral characteristics: Self-reported Grade Point Average (GPA) and smoking and drinking activity were ranked among all students of a given sex within a school and converted to normal z-scores via a quantile transformation. These z-scores were included as both row-specific regressors (rsmoke, rdrink, rgpa) and column-specific regressors (csmoke, cdrink, cgpa), and formed the basis of dyadic interaction terms (dsmoke, ddrink, dgpa). For example, dsmokei,j = rsmokei × csmokej.
Extracurricular activities: Participation in school-sponsored extracurricular activities was categorized by activity type (academic, artistic, sports, civic). The number of activities of each type jointly participated in by pairs of students was included as dyadic regressors (dacad, darts, dsports, dcivic). For example, dsportsi,j is the number of sports in which both students i and j participated.
Demographic characteristics: For each pair of students (i, j), a binary indicator of the same grade (dgrade) and a measure of ethnic similarity (dethn) were included as dyadic regressors. The ethnic similarity variable was calculated using the Jaccard index, and is the ratio of the number of ethnic groups shared by the members of a dyad divided by the total number of ethnic groups claimed by the either member.
As the data were obtained using an FRN study design, it seems most appropriate to estimate the regression coefficients β = (βr, βc, βd) using the FRN likelihood described in Section 2. Also of interest is a comparison of such estimates with those obtained using the binomial, censored binomial, and rank likelihoods, in order to see whether the relationships between the estimates are similar to those seen in the simulation study in Section 3.2. To this end, we obtained parameter estimates and confidence intervals of β for each of the 14 FRN networks and each of the four likelihoods. In the interest of brevity, we give details of the data and results for the male–male and female–female networks for only one school, and briefly summarize the results for the remaining 12 networks.
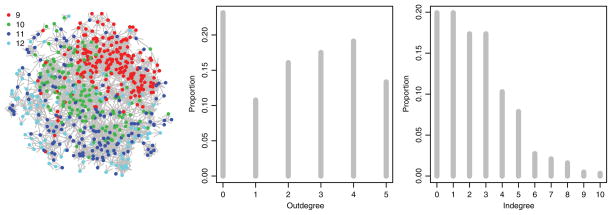
Graphical descriptions of the male–male and female–female FRN networks of the largest of the seven schools are presented in Figures 3 and 4 respectively. The networks are based on the data from 622 male and 646 female study participants. The first plot in each row consists of a graph with edges representing the friendship nominations and nodes representing the students, color-coded by grade. The second and third plots give the degree distributions, i.e., the empirical distributions of the number of nominations made to other survey participants (outdegree) and the number of nominations received by other survey participant (indegree). All outdegrees are less than or equal to 5, reflecting the fact that each student was allowed to make at most five nominations. A substantial number of students also report 0 friendships to other survey participants, but this should not be taken to mean that they have zero friendships: A substantial fraction of friendship nominations of the survey participants were with the students in the school who did not participate in the survey (22% for this school), or with individuals entirely outside the school. As no information is available for these out-of-survey individuals, we cannot include them in the model directly. However, the FRN and censored binomial likelihoods can be modified to accommodate this additional form of censoring by recognizing that the number of out-of-survey friendship ties alters how within-survey ties are censored: If individual i makes out-of-sample nominations, they have remaining nominations to allocate to within-survey friendships. If individual i makes out-of-survey nominations and within-survey nominations, then they are indicating that they do not have any further positive within-survey relationships. In contrast, if then this individual’s relationships are censored and we do not have information on the presence or absence of additional within-survey relationships. Accounting for this censoring information can be made by modifying Equation (4), defining LF and LC to be
Fig. 3.
Male nomination network. (color online)
Fig. 4.
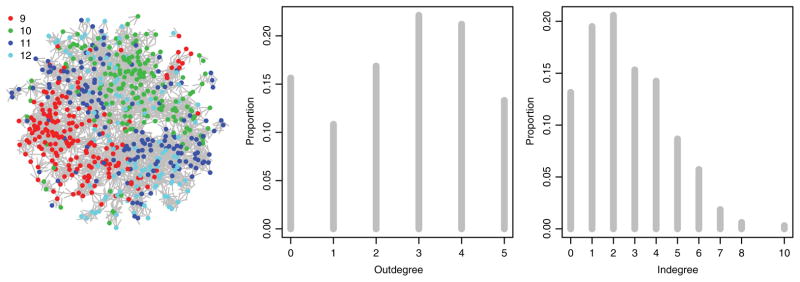
Female nomination network. (color online)
where the only change from Equation (4) is that the maximum (within-survey) outdegree is now the individual-specific value mi as opposed to being a common value m.
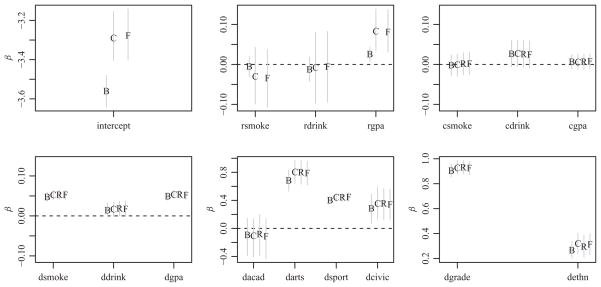
Using the MCMC algorithms described in Section 2.2, we obtained parameter estimates and confidence intervals of β for both male–male and female–female networks, using LB, LC, LR, and LF as likelihoods. The Markov chains appeared to converge very quickly. The Markov chains were run long enough so that the effective sample sizes (the equivalent number of independent iterations) were at least 500 for each school, sex, and likelihood, averaged across parameter values. Posterior medians and 95% confidence intervals for all regression parameters are shown in Figures 5 and 6. Point estimates and confidence intervals based on LF suggest that for both males and females, an individual’s GPA (rgpa) is positively associated with their evaluation of other individuals as friends, and that increased drinking behavior (cdrink) seems to be positively associated with an individual’s popularity. In addition, the dyadic effect estimates indicate that, on average, similarity between two individuals by just about any measure increases their evaluation of each other.
Fig. 5.
Parameter estimates and 95% confidence intervals for β in the male–male network. Each group of intervals represents from left to right the intervals obtained from the binomial (B), censored binomial (C), rank (R), and FRN (F) likelihoods, respectively. The rank likelihood does not provide parameter estimates for an intercept or for the row-specific effects rsmoke, rdrink, and rgpa.
Fig. 6.
Parameter estimates and confidence intervals for β in the female–female network.
Parameter estimates and confidence intervals based on other likelihoods generally provide similar conclusions about the effects, the exception being the intercept and row effects. Intercept estimates under LB are lower than those under LF, as they fail to recognize censoring in outdegree. For both males and females, coefficient estimates for the row effects are generally closer to zero under LB than LF, and the confidence intervals are substantially narrower. In particular, confidence intervals for rdrink and rgpa from LF in the female network (the second plot of Figure 6) are centered around positive values, whereas the corresponding intervals from LB are essentially centered around zero. These phenomena are similar to the patterns of bias seen in the simulation study in Section 3.2, and predicted by the analytical approximation in Section 3.1.
We fit the same model to the male–male and female–female networks of six additional schools (12 additional networks). Generally speaking, the same pattern of differences between different estimators appeared for these schools as for as the school analyzed above and in the simulation study: As compared with the FRN likelihood, the binomial likelihood estimated the intercept as being too low and the row effects as too close to zero with overly narrow confidence intervals. In addition, parameter estimates for dyadic effects that were not mean-centered (such as dgrade and dethn) were also too close to zero. These results are summarized in Table 1. For each effect type, we computed the (geometric) average ratio of the magnitude of the parameter estimate under LF to those under LB, LC, and LR. Besides giving larger (negative) intercept estimates than LF, LB generally gave estimates with smaller magnitudes, especially for the row effects and the non-mean-zero dyadic effects dgrade and dethn. We also computed the average ratio of the confidence interval widths under different likelihoods. Interval widths were generally similar across likelihoods, the main exception being that the interval widths for the row effects under LB were on average three times narrower than the intervals obtained from LF, similar to what was seen in the simulation study. In contrast, LC and LR provide parameter estimates and interval widths that are comparatively close to those from LF.
Table 1.
Average relative magnitudes of parameter estimates (first number) and confidence interval widths (second number) from the FRN likelihood LF as compared with the binomial (LB), censored binomial (LC), and rank (LR) likelihoods. The rank likelihood does not estimate an intercept or row effects.
| Likelihood | Effect type
|
||||
|---|---|---|---|---|---|
| Intercept | Row | Column | Mean-zero dyadic | Other dyadic | |
| LB | 0.89, 1.68 | 2.22, 2.95 | 1.02, 1.03 | 1.06, 1.06 | 1.20, 1.09 |
| LC | 1.00, 1.00 | 0.99, 1.00 | 0.98, 0.99 | 0.99, 1.00 | 0.99, 0.99 |
| LR | NA, NA | NA, NA | 1.05, 0.98 | 0.99, 0.99 | 1.06, 0.98 |
5 Discussion
Graphical representations of relational data often entail dichotomizations of non-binary numerical or ordinal relational data, and a loss of the context in which the data were gathered. Statistical methods based solely on the graphical representation of the data run the risk of being inefficient and misleading. In this paper, we have shown how a binary likelihood that uses only the graphical representation of an FRN dataset can provide incorrect inferences for a variety of model parameters. Specifically, in a social relations regression model, the binary likelihood can substantially underestimate the effects of regressors with variation among the nominators of relations. This includes characteristics of the nominators of ties, as well as dyadic indicators of group co-membership between the nominators and nominees.
Such problems can be avoided by use of a likelihood function based on the data collection scheme. In this paper, we have developed a likelihood that accounts for the censored and ordinal nature of FRN data. In a simulation study, parameter estimates based on this FRN likelihood were shown to lack the biases present in estimates based on the binary likelihood. In addition, the FRN likelihood was seen to provide more precise inference for the coefficients of dyadic-level regressors when the number of possible nominations was large. However, a modified binary likelihood that accounted for data censoring was seen to provide inference that was roughly as accurate as that provided by the FRN likelihood when the maximum number of nominations was small compared with the total number of individuals in the network. This result suggests that there may not be much information to be gained in FRN surveys by asking survey respondents to rank their nominations.
Our analytical and empirical comparisons were based on the social relations regression model, a model that does not explicitly represent network features such as transitivity, clustering, or stochastic equivalence. A popular class of statistical models that can capture a wider variety of patterns in uncensored, binary network relations are exponential random graph models (ERGMs) (Frank & Strauss, 1986; Wasserman & Pattison, 1996). In theory, ERGMs could be used to model censored relations by restricting attention to graphs with constrained outdegrees. While this is implemented in the R-package ergm, estimating parameters in such a framework can be computationally prohibitive. In addition, ERGMs are explicitly graph models for binary data, and do not accommodate valued, ranked relations. However, recent work by Krivitsky & Butts (2012) has extended the ideas behind ERGMs to a class of exponential family models for ranked relational data. Taken together with the recent work of Handcock & Gile (2010) for incompletely observed networks, these advances could allow for exponential family modeling using data from FRN and other ranked and censored sampling schemes.
An alternative to ERGMs is latent variable models that treat the data from each dyad as conditionally independent given some unobserved node-specific latent variables. Such models can capture patterns of stochastic equivalence, transitivity, and clustering often found in relational datasets, and also have a conditional independence structure that allows for estimation using the FRN likelihood within the MCMC framework described in Section 2.2 (with the addition of steps for updating values of latent variables). Such models extend the SRM given in Equation (7) as
| (12) |
where f is a known function and (u1, …, un) and (v1, …, vn) are sender- and receiver-specific latent variables. A version of the stochastic blockmodel (Nowicki & Snijders, 2001) follows when the latent variables take on a fixed number of categorical values. Alternatively, taking , with ui and vj being low-dimensional vectors, gives a type of latent factor model (Hoff, 2005, 2009a).
The simulation study and network analyses in this paper were implemented in the open source R statistical computing environment using the amen package, available at http://cran.r-project.org/web/packages/amen/. This package provides inference for the social relations latent variable model given by Equation (12), and under a variety of censoring mechanisms and data types. Replication code for the simulation study is available at the first author’s website, http://www.stat.washington.edu/hoff/.
Acknowledgments
This work was supported by NICHD grant R01 HD-67509.
Contributor Information
PETER HOFF, Email: pdhoff@uw.edu, Departments of Statistics and Biostatistics, University of Washington, Seattle, WA 98195, USA.
BAILEY FOSDICK, Email: bfosdick@samsi.info, Statistical and Applied Mathematical Sciences Institute, Research Triangle Park, NC 27709, USA.
ALEX VOLFOVSKY, Email: volfovsky@fas.harvard.edu, Department of Statistics, Harvard University, Cambridge, MA 02138, USA.
KATHERINE STOVEL, Email: stovel@u.washington.edu, Department of Sociology, University of Washington, Seattle, WA 98195, USA.
References
- Airoldi EM, Blei DM, Fienberg SE, Xing EP. Mixed membership stochastic blockmodels. Journal of Machine Learning Research. 2008;9:1981–2014. [PMC free article] [PubMed] [Google Scholar]
- Breiger RL, Boorman SA, Arabie P. An algorithm for clustering relational data with applications to social network analysis and comparison with multidimensional scaling. Journal of Mathematical Psychology. 1975;12(3):328–383. [Google Scholar]
- Currarini S, Jackson MO, Pin P. Identifying the roles of race-based choice and chance in high school friendship network formation. Proceedings of the National Academy of Sciences. 2010;107(11):4857–4861. doi: 10.1073/pnas.0911793107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher JM, Ross SL. Technical report. National Bureau of Economic Research; Cambridge, MA: 2012. Estimating the effects of friendship networks on health behaviors of adolescents. [Google Scholar]
- Frank O, Strauss D. Markov graphs. Journal of the American Statistical Association. 1986;81(395):832–842. [Google Scholar]
- Geweke J. Efficient simulation from the multivariate normal and student-t distributions subject to linear constraints and the evaluation of constraint probabilities. Computing Science and Statistics: Proceedings of the 23rd symposium on the interface. 1991:571–578. [Google Scholar]
- Gill PS, Swartz TB. Statistical analyses for round robin interaction data. Canadian Journal of Statistics. 2001;29(2):321–331. [Google Scholar]
- Goodreau SM, Kitts JA, Morris M. Birds of a feather, or friend of a friend? using exponential random graph models to investigate adolescent social networks*. Demography. 2009;46(1):103–125. doi: 10.1353/dem.0.0045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handcock MS, Gile KJ. Modeling social networks from sampled data. Annals of Applied Statistics. 2010;4(1):5–25. doi: 10.1214/08-AOAS221. Retrieved from http://dx.doi.org/10.1214/08-AOAS221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Halpern CT, Whitsel E, Hussey J, Tabor J, Entzel P, Udry JR. [December 15 2012 ];The national longitudinal study of adolescent health: Research design. 2009 Retrieved from http://www.cpc.unc.edu/projects/addhealth/design.
- Hoff PD. Bilinear mixed-effects models for dyadic data. Journal of the American Statistical Association. 2005;100(469):286–295. [Google Scholar]
- Hoff PD. Extending the rank likelihood for semiparametric copula estimation. Annals of Applied Statistics. 2007;1(1):265–283. [Google Scholar]
- Hoff PD. Multiplicative latent factor models for description and prediction of social networks. Computational and Mathematical Organization Theory. 2009a;15(4):261–272. [Google Scholar]
- Hoff PD. Springer Texts in Statistics. New York, NY: Springer; 2009b. A first course in bayesian statistical methods; p. ix.p. 270. EUR 64.15; SFR 99.50. [Google Scholar]
- Hoff PD, Raftery AE, Handcock MS. Latent space approaches to social network analysis. Journal of the American Statistical Association. 2002;97(460):1090–1098. [Google Scholar]
- Holland PW, Leinhardt S. An exponential family of probability distributions for directed graphs. Journal of the American Statistical Association. 1981;76 (373):33–50. [Google Scholar]
- Kiuru N, Burk WJ, Laursen B, Salmela-Aro K, Nurmi JE. Pressure to drink but not to smoke: Disentangling selection and socialization in adolescent peer networks and peer groups. Journal of Adolescence. 2010;33(6):801–812. doi: 10.1016/j.adolescence.2010.07.006. [DOI] [PubMed] [Google Scholar]
- Krivitsky PN, Butts CT. [December 15 2012];Exponential-family random graph models for rank-order relational data. 2012 Retrieved from http://arxiv.org/abs/1210.0493.
- Li H, Loken E. A unified theory of statistical analysis and inference for variance component models for dyadic data. Statistics Sinica. 2002;12(2):519–535. [Google Scholar]
- Macdonald-Wallis K, Jago R, Page AS, Brockman R, Thompson JL. School-based friendship networks and children’s physical activity: A spatial analytical approach. Social Science & Medicine. 2011;73(1):6–12. doi: 10.1016/j.socscimed.2011.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moody J, Brynildsen WD, Osgood DW, Feinberg ME, Gest S. Popularity trajectories and substance use in early adolescence. Social Networks. 2011;33(2):101–112. doi: 10.1016/j.socnet.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno JL. Who shall survive? Foundations of sociometry, group psychotherapy and socio-drama. Mustang, OK: Beacon House; 1953. [Google Scholar]
- Moreno JL. The sociometry reader. New York, NY: Free Press; 1960. [Google Scholar]
- Nowicki K, Snijders TAB. Estimation and prediction for stochastic blockstructures. Journal of the American Statistical Association. 2001;96(455):1077–1087. [Google Scholar]
- Pettitt AN. Inference for the linear model using a likelihood based on ranks. Journal of the Royal Statistical Society B. 1982;44(2):234–243. [Google Scholar]
- Rodriguez-Yam G, Davis RA, Scharf LL. Efficient Gibbs sampling of truncated multivariate normal with application to constrained linear regression. 2004 Unpublished manuscript. [Google Scholar]
- Sampson SF. Unpublished doctoral dissertation. Cornell University; Ithaca, NY: 1969. Crisis in a cloister. [Google Scholar]
- Severini TA. On the relationship between Bayesian and non-Bayesian interval estimates. Journal of the Royal Statistical Society B. 1991;53(3):611–618. [Google Scholar]
- Sherman L. [December 15 2012];Sociometry in the classroom: How to do it. 2002 Retrieved from http://www.users.muohio.edu/shermalw/sociometryfiles/sociointroduction.htmlx.
- Snijders TAB, Pattison PE, Robins GL, Handcock MS. New specifications for exponential random graph models. Sociological Methodology. 2006;36(1):99–153. [Google Scholar]
- Thomas SL. Ties that bind: A social network approach to understanding student integration and persistence. Journal of Higher Education. 2000;71:591–615. [Google Scholar]
- van Duijn Marijtje AJ, Snijders Tom AB, Zijlstra Bonne JH. p2: A random effects model with covariates for directed graphs. Statistica Neerlandica. 2004;58(2):234–254. [Google Scholar]
- Warner R, Kenny DA, Stoto M. A new round robin analysis of variance for social interaction data. Journal of Personality and Social Psychology. 1979;37:1742–1757. [Google Scholar]
- Wasserman S, Pattison P. Logit models and logistic regressions for social networks: I. an introduction to markov graphs and p. Psychometrika. 1996;61(3):401–425. [Google Scholar]
- Weerman FM. Delinquent peers in context: A longitudinal network analysis of selection and influence effects. Criminology. 2011;49(1):253–286. [Google Scholar]
- Weerman FM, Smeenk WH. Peer similarity in delinquency for different types of friends: A comparison using two measurement methods. Criminology. 2005;43(2):499–524. [Google Scholar]
- Wong GY. Round robin analysis of variance via maximum likelihood. Journal of the American Statistical Association. 1982;77(380):714–724. [Google Scholar]