Prediction of Periventricular Leukomalacia Occurrence in Neonates After Heart Surgery

Abstract

This paper is concerned with predicting the occurrence of Periventricular Leukomalacia (PVL) using vital and blood gas data which are collected over a period of twelve hours after neonatal cardiac surgery. A data mining approach has been employed to generate a set of rules for classification of subjects as healthy or PVL affected. In view of the fact that blood gas and vital data have different sampling rates, in this study we have divided the data into two categories: (i) high resolution (vital), and (ii) low resolution (blood gas), and designed a separate classifier based on each data category. The developed algorithm is composed of several stages; first, a feature pool has been extracted from each data category and the extracted features have been ranked based on the data reliability and their mutual information content with the output. An optimal feature subset with the highest discriminative capability has been formed using simultaneous maximization of the class separability measure and mutual information of a set. Two separate decision trees (DT) have been developed for the classification purpose and more importantly to discover hidden relationships that exist among the data to help us better understand PVL pathophysiology. The DT result shows that high amplitude twenty minute variations and low sample entropy in the vital data and the defined out of range index as well as maximum rate of change in blood gas data are important factors for PVL prediction. Low sample entropy represents lack of variability in hemodynamic measurement, and constant blood pressure with small fluctuations is an important indicator of PVL occurrence. Finally, using the different time frames of data collection, we show that the first six hours of data contain sufficient information for PVL occurrence prediction.

I. Introduction

Newborns with congenital heart disease are at high risk for different types of brain injury [1]–[3]. According to [4] patients with congenital heart disease (CHD) have increased rates of neurodevelopmental impairments. A study by Miller et al. [5] showed that pre-term newborns with CHD have widespread brain abnormalities before they undergo cardiac surgery.

Periventricular leukomalacia (PVL) is a particular type of brain injury that affects mostly premature infants. The condition occurs when immature cells in the white matter are exposed to low oxygen levels and low blood flow. The injury occurs most frequently in an arterial watershed zone that exists at the border of the lateral ventricles of the brain. The injury results in scarring, or gliosis, in the white matter and disruption of neuronal networks [6]. When severe, affected individuals exhibit motor control problems (cerebral palsy) or other developmental delays or epilepsy later in life [7], [8].

In order to identify and quantify PVL after neonatal heart surgery, PVL was defined as punctate periventricular white matter lesions associated with T1 hyperintensity, with or without restriction of water diffusion on diffusion-weighted imaging [9]. Furthermore, PVL lesions were manually segmented using ITK-SNAP Q8. User-guided 3-dimensional active contour segmentation of anatomic structures significantly improved efficiency and reliability [10]. PVL volumes were expressed in mm³.

Research has shown a high incidence of PVL both before and after cardiac surgery in full-term neonates with CHD [11]–[13]. Current observations suggest that hypoplastic left heart syndrome (HLHS) and transposition of great arteries (TGA) are two CHDs which have high correlation with occurrence of the PVL. Licht et al. [14] showed that, before surgery, term infants with hypoplastic left heart syndrome and transposition of the great arteries have brains that are smaller and structurally less mature than expected for full-term infants. They suggested that brain immaturity may increase the occurrence probability of periventricular leukomalacia in the preoperative, intraoperative, and postoperative periods.

Recently, there has been a growing interest in clinical research to aim to understand the progression and pathology of PVL, to develop protocols for the prevention of PVL development and to examine the trends in outcomes of individuals with PVL [15], [16].

Results of a study by Petit et al. [17] showed that pre-operative brain injury in neonates with transposition of the great arteries is associated with hypoxemia and longer time to surgery. The study of the relationship between preoperative cerebral blood flow and preoperative neurologic conditions has been carried out by Licht et al. [18]. Their findings indicated that the low cerebral blood flow values were associated with PVL. Deficiency in oxygen concentrations in the blood and low carbon dioxide concentrations (PCO₂) have also been suggested as important factors indicating PVL occurrence [19].

Despite advancement in research in the field of PVL, there are no treatments currently prescribed for PVL; furthermore, clinical prediction of PVL occurrence almost always has low accuracy [20]. This is due to fact that the origin of PVL and its physiology still remain to be clearly understood. Consequently, all treatments administered are in response to secondary pathologies, such as seizures, that develop as a consequence of the PVL [21]–[23].

A computer based decision making tool, also referred to as an Intelligent Patient Monitoring (IPM) Tool or as computer-aided diagnostics or clinical decision making systems, will help the care-givers aggregate different types of physiological data and discover the hidden knowledge or patterns in the data to quickly make the correct decision [24]–[28]. Most of the currently used IPM tools employ data driven techniques with data collected from an experiment. These techniques analyze the collected data using statistical or computational intelligence algorithms to arrive at a conclusion on the state of health of the patient. The IPM is comprised of a knowledge base data mining approach as well as patient-specific information to provide support for decision-making in patient care. A systematic review by Garg et al. [29], [30] of a hundred studies concluded that IPM improved practitioner performance in 64% of the studies and improved patient outcomes in 13% of the studies.

Computational intelligence (CI) techniques are potentially powerful tools for classification and prediction and are attracting increasingly more attention in the field of clinical decision making [19], [24], [31]–[38]. The CI techniques include data mining algorithms and techniques like decision tree (DT) [37], [39], neural networks (NN) [19], support vector machine (SVM) [35], [36], [40], adaptive neuro-fuzzy inference system (ANFIS) [34], [41], etc. Among the many different CI techniques, we have chosen DT for the task of PVL prediction in the current study. The main advantages of DT based approach that makes it a perfect fit for this study are the ability to discover hidden patterns in the data and generation of easily interpretable classification rules.

DT algorithms give reliable and effective results that provide high-classification accuracy with a simple representation of gathered knowledge, and are especially appropriate to support decision-making processes in medicine.

In this study, we investigate how DT can help the clinicians to predict the PVL occurrence after the neonatal heart surgery. By constructing a DT and extracting classification rules, the clinicians will be able to identify predictive factors for the occurrence of the PVL. As a result the goal in this paper is to classify patients with PVL from patients showing no sign of PVL after heart surgery. These rules will enable better management of the patient targeting the reduction of events, as well as, reduction of the cost of therapy, due to the expected restriction of interventions in necessary cases only.

II. Materials and Methods

A. Data Collection

Vital sign data from 44 neonates were collected according to a pre-specified protocol at the Children’s Hospital of Philadelphia (CHOP). Subjects of this study were limited to two heart diagnoses; hypoplastic left heart syndrome (HLHS) and transposition of great arteries (TGA), accounting for the fact that these two diseases are considered to have the highest likelihood of PVL occurrence as their postoperative effect. Demographic data collected includes sex, type of disease (HLHS or TGA), cardiopulmonary bypass (CPB) duration in minutes, aorta cross-clamp time (ACC) in minutes and deep hypothermic circulatory arrest (DHCA) duration in minutes. Clinical and demographic characteristics of the study cohort are shown in Tab. I.

TABLE I.

Demographic characteristics of the collected data

Male, %	59
Diagnosis, %HLHS	55
DHCA time, mean ± SD	27 ± 26
CPB time, mean ± SD	102 ± 31
CCD time, mean ± SD	61 ± 19
PVL, %	45
Extent, mean ± SD	94 ± 251

For each patient, vital sign data as well as blood gas measurements were collected for a 12 hour period immediately after surgery. The sampling time for the vital data varies both inter and intra-patient from 4 to 17 seconds. The blood gas data were also collected at irregular sampling intervals, and varying from 20 to 90 minutes. Tab. II lists the collected hemodynamic variables as well as their respective measurement reliability. Reliability number is qualitatively derived from expert opinions and knowledge of the test. Data that was captured directly from the patient (i.e., vital sign data) was highly reliable, while data that was calculated such as HCO₃ was considered to be less reliable.

TABLE II.

The collected vital and blood gas data at Children’s hospital of Philadelphia (CHOP) with their reliability. SR is the sampling rate.

Category	Data	Info.	Reliability
Vital	MAP (mmHg)	Irregular SR (3–20 sec)	1
	HR (bpm)		1
	RAP (mmHg)		1
	SpO2 (%)		1
Blood Gas	pH	Irregular SR (20–90 min)	1
	PaCO2 mmHg		1
	PaO2 mmHg		1
	HCO3 mmol/L		0.8
	O2Sat %		0.6
	Hgb g/dL		0.7
	K+ mmol/L		0.8
	Ca++ mmol/L		0.8
	Na+ mmol/L		0.8
	Hct %		0.7

B. Algorithm Design

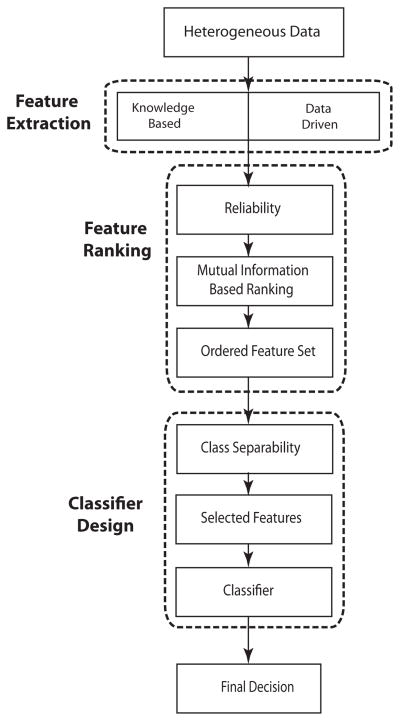
Next, we discuss the steps involved with the designed algorithm for the task of data classification and rule extraction. In Fig. (1) we provided a schematic overview of the proposed algorithm. As shown the algorithm consists of three main steps: feature extraction, feature ranking and classifier design. First, The patient data was collected at the hospital and was used to form the pool of features. A modified version of the mutual information method that takes into account the reliability of the collected data was then used for ranking the extracted features in the feature pool. After forming the ordered feature set the optimal feature subset that encapsulates the most critical features was selected by maximizing the class separability measure. The optimal feature subset was reduced in size compared to the original feature set; however, by maximizing the class separability measure, this subset can be expected to result in a higher accuracy in the final prediction. The selected features were then fed to the decision tree (DT).

Fig. 1.

Schematic of the proposed algorithm.

C. Feature Extraction

Since the resolution of the collected data is different for blood gas data and the vital data, we divide them into two categories of high resolution (vital data) and low resolution (blood gas data). Consequently two different feature pools will be developed for each category of the data. Table (III) shows the extracted features from different categories of the data.

TABLE III.

The extracted features from vital and blood gas data.

Category	Data
Vital	Extremes (min, max)
	mean, skewness, kurtosis
	Wavelet energy at 1,20, 120 minutes
	Sample entropy
Blood Gas	Extremes (min, max)
	Weighted mean
	Admission value
	Out of range index
	max rate of change
	max rate of change in upper range
	max rate of change in lower range

The minimum and maximum values of the data are important features for both vital and blood gas data, because they could potentially reveal mechanisms that are triggered in the body when a hemodynamic variable passes a certain threshold. Skewness and kurtosis are third and forth order statistical moments of a random variable. Statistical moments of a random variable x are defined using (1).

$$m_n(x)=E\{{(x-\mu )}^n\}$$ (1)

where, n is the order, μ is the mean value of the data and E is the expected value. Skewness is an indicator of probability density function asymmetry and kurtosis is an indicator of the invariability of a signal. Admission value is the first value of the recorded blood gas data. Our preliminary results [42] which were carried out using blood gas data collected every four hours showed the importance of admission recordings in PVL occurrence prediction.

It is known that hemodynamic variables fluctuate at different time scales consisting of seconds, minutes, hours, and possibly, days. These variations are presumably caused by different regulatory mechanisms. It is believed that these mechanisms are both affected by, and affect the PVL occurrence. In order to try to uncover regulatory mechanisms that are most actively involved with the occurrence of PVL, we use the continuous wavelet transform (CWT). We calculate the energy of the continuous wavelet transform coefficients of vital data at 1 minute, 20 minutes and 2 hour time scales. These time scales are selected in the way that represent the physiological phenomena that are occurring in different time scales. Since the sampling rate for data collection varies both in inter-patient and intra-patient, we first up-sample the data to the sampling rate of 1 second using linear interpolation, calculate the CWT coefficients at the desired time scales and then calculate the energy of the signal at each scale.

The CWT of signal x(t) is defined by (2):

$$X_{\omega }(a,b)=\frac{1}{\sqrt{\mid a\mid }}{\int }_{-\infty }^{\infty }x(t){\psi }^{\ast }(\frac{t-b}{a})\mathrm{d}t$$ (2)

where, a is the time scale, b is the transitional value and ψ* is the complex conjugate of the mother wavelet function ψ. In this study Morlet function is used as a mother wavelet function; it should be noted that the Morlet function is often used in literature in case of non-stationary signals [43]. The energy of the CWT at scale a is calculated by (3):

$$E(a)=\sum _{i=1}^N{\mid X_{\omega }(a,i)\mid }^2$$ (3)

The Morlet function is defined by (4):

$${\mathrm{\Psi }}_k(t)=C_k{\pi }^{-0.25}{e}^{-0.5t^2}(e^{\mathit{ikt}}-e^{-0.5k^2})$$ (4)

where, k allows a trade-off between time and frequency resolutions. Sample entropy (SampEn) is a measure of signal complexity and is the negative natural logarithm of the conditional probability of having a signal window with length N, having repeated itself within a tolerance r for m points, will also repeat itself for m + 1 points, without allowing self-matches [44]. SampEn is used in the literature to evaluate the cyclic behavior of heart rate variability (HRV) and blood pressure variability (BPV) [45], [46].

The collected blood gas data have very low resolution and are discontinuous. To overcome this limitation, and after confirmation by clinicians, we assumed that there are no sharp, unexpected variations in the data between samples. Hence it is reasonable to linearly interpolate the blood gas data. The weighted mean of blood gas data takes into the account the duration of time that the patient stays at a specific measurement. This feature is clinically more significant than the mean value of the data, because, from a clinical point of view the time duration of a blood gas reading is as important as its amplitude.

Time weighted mean is calculated using (5).

$$M_w(x)=\frac{{\sum }_{i=1}^m{t}_i{x}_i}{{\sum }_{i=1}^m{t}_i}$$ (5)

where, m is the number of measurements and x is the measured variable.

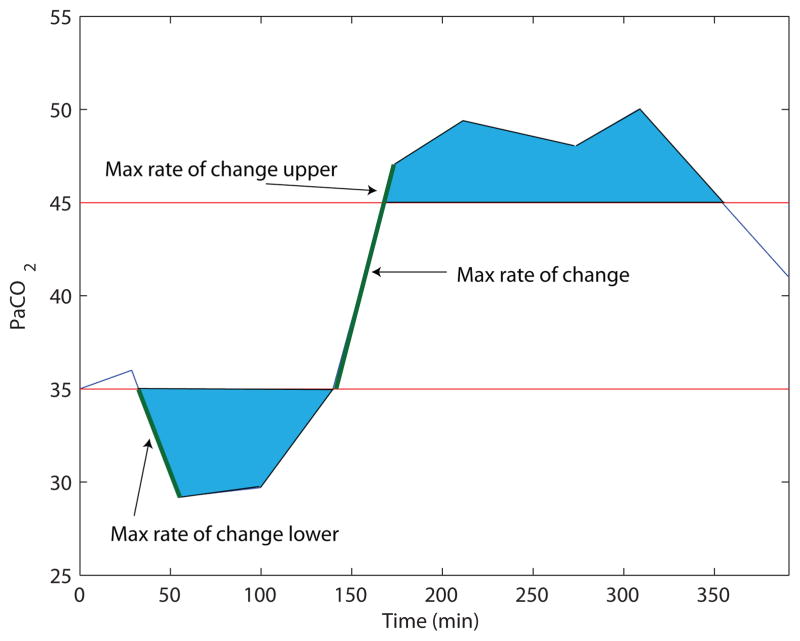
In addition, we define out of range index (ORI) as a new feature in this paper. Out of range index is a measure of both amplitude difference of a measurement within its normal range and the time that the measurement spent out of normal range. The normal range limits of the collected blood gas data are presented in Tab. IV. Figure (2) shows the defined feature for a data sample.

TABLE IV.

Normal Range of Blood Gas Data

Measurement	Lower Limit	Upper Limit
pH [47]	7.34	7.44
PaCO2	35	45
PaO2	75	100
HCO3	22	26
O2Sat	95	100
Hgb	14	16
K+	3.5	5
Ca++	8.5	10.5
Na+	135	145
Hct	36	44

Fig. 2.

Plot of features extracted from a sample blood gas measurement. The blue area is the ORI index of the PaCO₂ for a sample patient.

D. Feature Ranking

In this paper we apply the concept of mutual information to rank the features. Mutual information of two random variables is defined as a measure of their mutual dependence. Let x_i be the ith feature and p(x_i) be its corresponding probability density function. The mutual information is then defined as:

$$I(x_i;w_k)=\sum _{i\in X}\sum _{k\in \{\pm 1\}}p(x_i,w_k)log\frac{p(x_i,w_k)}{p(x_i)p(w_k)}$$ (6)

where, w_k represents the classes and p(x_i, w_k) is the joint probability distribution of x_i and w_k. To take into account the reliability of the collected data and to bolster the effect of the data with high reliability, we modified the mutual information technique by inserting coefficient of reliability into (6). The modified mutual information of feature x_i and class w_k is hence calculated using (7)

$$I_m(x_i;w_k)=c_{R}I(x_i;w_k)$$ (7)

where, c_R is a measure of the reliability of the collected data. The ordered feature set is not the best feature set, because we have not considered the mutual information between the features. To solve this problem we use the concept of mutual information of a set, which is defined in (8)

$$I(S;w_k)=\frac{1}{\mid S\mid }\sum _{x_i\in S}{I}_m(x_i;w_k)-\frac{1}{{\mid S-1\mid }^2}\sum _{x_i,x_j\in S}I(x_i;x_j)$$ (8)

where, |S| is size of the set S, I(S;w_k) is mutual information of set S and class w_k and I(x_i;x_j) is mutual information of features, x_i and x_j. By finding the set S_opt that maximizes (8), the algorithm is able to form the best ordered feature set. In this paper we use the algorithm proposed by Kappaganthu and Nataraj [48] to find the S_opt.

E. Class Separability Measure

Now that the optimal feature vector have been formed the next step is to find a subset of the feature matrix that has the maximum discriminative capacity. The subset with the highest discriminative capacity is the subset that will result in the highest classification accuracy. The class separability is a measure that has been defined as a measure of divergence between classes using the feature subset x_s,

$$d={\int }_{-\infty }^{\infty }(p(x_s\mid w_1)-p(x_s\mid w_2))ln\frac{p(x_s\mid w_1)}{p(x_s\mid w_2)}\mathrm{d}{x}_s$$ (9)

where p(x_s|w_i) is the conditional probability of x_s with respect to w_i. An optimal feature subset is the feature subset that maximizes the class separability and has a reduced dimensionality.

In this part, the algorithm to extract the optimal feature set using the class separability measure is explained. We intend to extract an optimal subset S_opt from the ordered feature set S obtained in the previous stages. The criterion for optimization is to achieve the maximum class separability measure using as few features as possible. We simply start with an empty feature set S_∅ and at each step we add a feature to the set and measure the class separability between the two classes that we have. The process will stop when the class separability index reaches its maximum. The algorithm for this is as follows.

1. Set S₀ = ∅

2. Initialize i = 1 and S_i = S(1).

3. Start loop

4. Measure class separability between the two classes (d_i) using Eq. (9)

5. If S_i = S Stop Loop and proceed to step 12, else continue.

6. i = i + 1

7. S_i = S_i ∩ S_i+1

8. Measure class separability for the S_i

9. If d_i > d_i−1

10. Return i and Stop the loop

11. Else continue

12. End loop

13. Obtain S_opt as S_i

F. Classifier Design

In this part of the algorithm, a machine learning type classifier is designed to classify PVL patients from healthy subjects. Decision Tree has been selected as the classifier. The DT algorithm uses a recursive partitioning technique to construct a tree based structure for generating a set of “if-then-else” rules in order to predict the desired event. Unlike almost all other techniques in data mining that construct a gray box model for classification, DT produces a very easy to interpret model. This characteristic is very useful in clinical settings because clinicians are not only interested in the final prediction, but are also interested in finding injury pathways for possible interventions to prevent the injury. The DT induction consists of two phases: construction and pruning. The Gini index has been used as splitting criterion for tree construction and Fisher’s exact test (FET) has been used for pruning the tree [49]. Moreover, the output data type has been chosen as categorical instead of as a numerical variable since it resulted in a more robust classification. The p-value threshold for pruning has been set to 0.05.

III. Results

Features that are mentioned in Tab. (III) have been extracted from the data and two separate feature pool, one for vital data and one for blood gas data, have been formed. The features have been ranked using the modified mutual information algorithm, the optimal feature set with maximized mutual information of set have been found and dimension of the feature pools have been reduced using the class separability measure. Table (V) lists the optimal feature subsets for both vital and blood gas data.

TABLE V.

Optimal subsets of the features extracted from vital and blood gas data which are used for designing the classifiers.

Category	Rank	Feature
Vital	1	2 hour variations in HR
	2	MAP sample entropy
	3	20 min variations in HR
	4	Kurtosis HR
	5	1 min variations in SpO2
	6	20 min variations in SpO2
	7	Kurtosis MAP
	8	1 min variations in MAP
	9	Min SpO2
	10	HR sample entropy
	11	2 hour variations in MAP
	12	RAP sample entropy
Vital	1	Max rate of change PaCO2
	2	K+ ORI
	3	HCO3 ORI
	4	Ca2+ ORI
	5	Max PaCO2
	6	Max rate of change in lower range Na+
	7	PaCO2 ORI
	8	Min PaO2
	9	Admission PaO2
	10	pH ORI
	11	Max rate of change K+
	12	Max rate of change HCO3
	13	Max rate of change PaO2
	14	Max rate of change in upper range Ca++
	15	Weighted mean Hgb
	16	Max rate of change in upper range PaCO2
	17	Admission Na+

Table (V) shows that the subset of 12 features out of 36 features extracted from the vital data will result in highest classification accuracy. For vital data, this table demonstrates that the energy of the wavelet coefficients, sample entropy and kurtosis are the most important features for PVL occurrence prediction. This table also shows that compared to other vital data, RAP contains the least amount of information for PVL occurrence prediction. Regarding the blood gas data, the table shows that the subset of 19 features out of 80 features extracted from the blood gas data will result in the highest classification accuracy. This table highlights the rule of the blood partial pressures of O₂ and CO₂ in occurrence of PVL after neonatal cardiac surgery. Moreover, it can be seen from Table (V) that the defined blood gas features, ORI and maximum rate of change in the upper and lower ranges are significant PVL predictors.

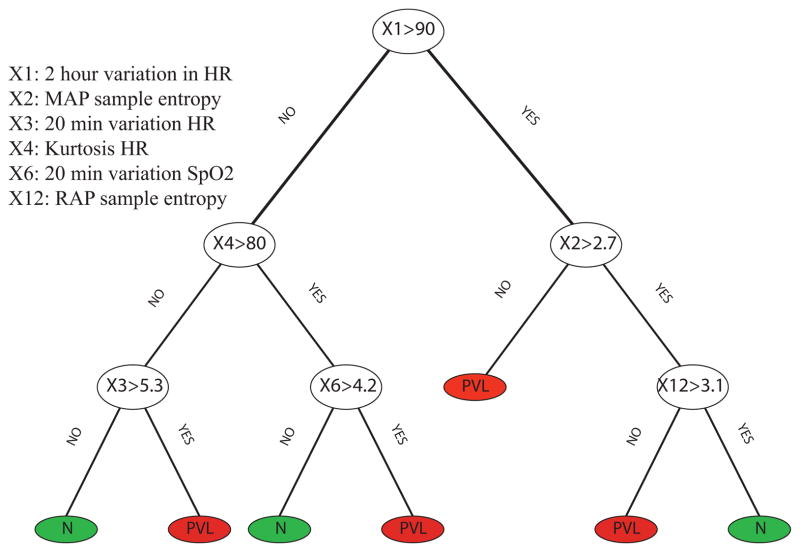
After deriving the optimal feature sets for both vital and blood gas data, a DT classifier has been generated for each category of the data. A DT that has been formed based on the vital data to predict the occurrence of the PVL is represented in Figure (3). Investigating the DT shows that generally high amplitude 20 minute variations and low sample entropy in the data are important factors for the prediction of PVL. Low sample entropy represents lack of variability in hemodynamic measurement, and constant blood pressure with small fluctuations is an important indicator of PVL occurrence.

Fig. 3.

DT shows that high amplitude 20 minute variations and low sample entropy in the data is an important factor for prediction of PVL.

In addition, a DT based on the features derived from blood gas data has been generated and is shown in Figure (4). Results show that among all blood gas measurements, CO₂ concentration in blood, and Ionized Potassium, Calcium, Sodium and Bicarbonate HCO₃ are the most valuable parameters for predicting PVL. This result further validates our previous suggestion presented in [42] which highlighted the role of blood CO₂ concentration as an important factor in the PVL prediction. This result also shows the importance of the rate of change in blood gas data as well as the defined out of range index as indicators of hemodynamic instability which could lead to PVL.

Fig. 4.

DT constructed based on optimal features set derived from blood gas data. Results show that among all blood gas measurements, CO₂ concentration in blood, and Ionized Potassium, Calcium and Sodium are the most valuable parameters for predicting PVL.

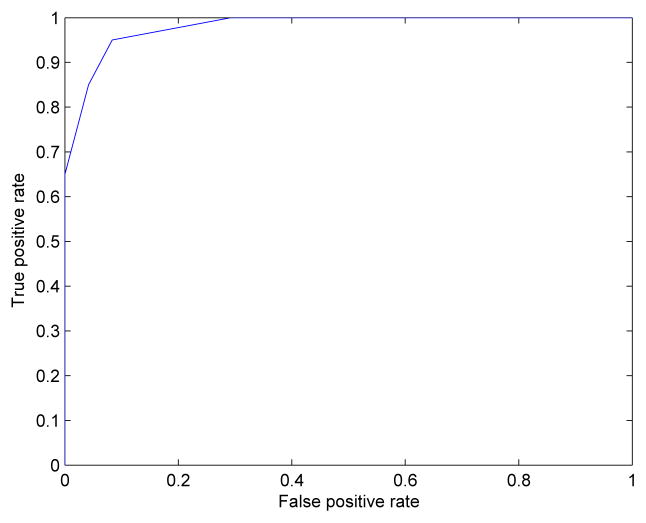
The classification accuracy of the designed classifier is shown using the receiver operating characteristic (ROC) curve. The higher area under the curve shows the higher classification accuracy. The plot shows high accuracy in classification although, the relatively small size of the data set makes it impossible to have a smooth curve.

In the final step, by using all of the extracted features from both vital data and blood gas data, we would like to predict the length of a data collection that would be sufficient for timely prediction of the PVL. To the best of our knowledge there has been no study carried out so far to find the optimum length of time needed for data collection after the neonatal heart surgery to be able to achieve positive PVL prediction. This could help to target time of intervention to prevent PVL, reducing injury, and reducing healthcare cost. To this end we trained and tested the DT with first 2, 4, 6 and 8 hours of the data and we compared the prediction results with the complete data. Table VI shows that six hours of the data contains sufficient information for reliable PVL prediction. Another way to interpret this result is that after 6 hours the opportunity to prevent PVL will decrease significantly.

TABLE VI.

Prediction accuracy for different length of data.

DATA	TP	FP	FN	TN	Se	PP	F-Score
All	19	2	1	22	95%	90%	0.93
8Hours	19	2	1	22	95%	90%	0.93
6Hours	18	1	2	23	90%	95%	0.93
4Hours	16	4	4	20	80%	80%	0.80
2Hours	15	4	5	20	75%	79%	0.76

IV. Discussion and Conclusions

In the clinical context, the area under the physiological measurement curve has been considered a more valuable predictor of the state of patients than extreme values. The results of this study show that this is a valid argument also in the case of PVL prediction.

The results of formulating a decision tree from vital data put emphasis on stationarity of both HR and blood pressures as strong predictors of PVL. Moreover, the maximum and minimum values of the rate of change of PaCO₂ are the most important parameters from the blood gas data. One of the main objectives of this study is to increase PVL prediction accuracy in order to help clinicians to plan possible treatments in a timely manner to avoid occurrence of the PVL. Our results show that 6 hours of the data contains sufficient information for reliable PVL prediction. This in fact is a very important result due to the fact that it shows a possible time frame for physiological interventions. It should be noted however that these results are preliminary and we are in the process of collecting additional patient data to further validate them.

While the findings of this study seem to be very interesting and important, it still needs explanation from a physiological point of view. Hence, the next step of the current study is to investigate the physiological reasons behind these findings. For example, questions that need investigating include: how does decreased uncertainty in MAP result in the PVL occurrence, what is the relationship between PVL and HR, and how does the CO₂ affect the PVL occurrence. Furthermore, additional data is needed to prove the robustness of the developed algorithm to measurement noise and application to special cases.

Fig. 5.

Receiver operating characteristic (ROC) curve (plot of true positive rate vs. false positive rate).

Biographies

Ali Jalali Ali Jalali received his M.Sc degree in mechanical engineering from K.N. Toosi University of Technology, Tehran, Iran. He is currently a PhD candidate at the Department of Mechanical Engineering at the Villanova University. His research interests include data analysis and biomedical diagnostics using machine learning techniques with applications in ICU outcome prediction, cardiopulmonary resuscitation research, arrhythmia detection and cardiovascular engineering.

Erin M. Buckley Dr. Erin M Buckley received her Ph.D. in physics from the University of Pennsylvania in 2011. She is currently a research fellow at the Athinoula A. Martinos Center for Biomedical Imaging. Her research focuses on the development and applications of diffuse optical spectroscopies applied to critically-ill neonatal populations.

Jennifer M. Lynch Jennifer M. Lynch received the M.Sc. degree in physics from the University of Pennsylvania in 2011, where she is currently working toward the Ph.D. degree in physics in the subfield of biomedical optics. Her research interests include employing diffuse optical spectroscopies to monitor cerebral hemodynamics in pediatric populations.

Jennifer M. Lynch Peter J. Schwab graduated from the University of Pennsylvania in 2011 with a B.A. in Philosophy. He has worked as a technician in Dr. Daniel Licht’s Neurovascular Imaging Lab at the Children’s Hospital of Philadelphia since 2011. His research interests include neurovascular imaging, brain-computer interfacing, neuroplasticity and philosophy of mind.

Daniel J. Licht Dr. Daniel J. Licht is the director of the Neurovascular Imaging Lab at The Children’s Hospital of Philadelphia and he is in charge of implementing and adapting novel instrumentation to answer important clinical questions. His research program is informed by his clinical responsibilities, which includes neurology consult liaison to the Cardiac Intensive Care Unit and a founding member of the CHOP Pediatric Stroke Program. To accomplish research goals he has employed all-optical devices for probing cerebral oxygenation (frequency domain NIRS) and cerebral blood flow (diffuse correlation spectroscopy) in infants and children with critical illness.

C. Nataraj Dr. C. Nataraj holds the Mr. and Mrs. Robert F. Mortiz, Sr. Endowed Chair Professorship in Engineered Systems at Villanova University. He has a B.S. in Mechanical Engineering from Indian Institute of Technology, and M.S. and Ph.D. in Engineering Science from Arizona State University. After getting his Ph.D. in 1987, he worked for a year as a research engineer and a partner with Trumpler Associates, Inc. He is currently the Chairman of the Mechanical Engineering Department at Villanova University. Dr. Nataraj was also the founding Director of the Center for Nonlinear Dynamics and Control (CENDAC) in the College Of Engineering. Dr. Nataraj has worked on various research problems in nonlinear dynamic systems with applications to mobile robotics, unmanned vehicles, rotor dynamics, vibration, control, and electromagnetic bearings. Dr. Natarajs current interest includes biomedical diagnostics and mathematical modeling of biological systems. His research has been funded by Office of Naval Research, National Science Foundation, National Institute of Health and many companies.