Abstract
Purpose
To estimate the ratio α/β of Prostate Cancer from the effect of dose of radiation on the long term rise of prostate specific antigen (PSA).
Materials and methods
Repeated measures of PSA from 5,093 patients treated for localized prostate cancer by external beam radiation therapy (EBRT) were analysed. Patients came from 6 large cohorts. A biphasic linear mixed model described the post-treatment evolution of PSA. The effect of the radiation dose schedule on the long term rate of rise of PSA was estimated from the model. The model adjusted for standard prognostic factors (T-stage, initial PSA and Gleason) and cohort specific effects.
Results
Adjusted for other factors, total dose of EBRT and sum of squared doses per fraction were associated with long term rate of change of PSA (respectively p=0.0017 and p=0.0003), an increase of each being associated with a lower rate of rise. The ratio α/β was estimated at 1.55 Gy with 95% confidence interval [0.46;4.52]. This estimate was robust to adjustment of the linear mixed model but varied according to which cohorts were included, especially the one bringing hypofractioned schemes.
Conclusions
Using more than 5,000 patients treated by EBRT and a method that accounts for all the repeated measures of PSA after end of treatment rather than only the time of biochemical recurrence, a very low and precise value for α/β was estimated. This result favors hypofractionated radiation therapy that could better control the tumor with a reduced late toxicity. However outcome data from EBRT studies using higher doses per fraction are still needed to validate this result.
Keywords: Prostate cancer, Prostate-specific Antigen, Radiation therapy, Alpha/beta, Radiosensitivity
Context
Fractionation sensitivity for Prostate cancer was widely investigated and discussed in the literature (see Daşu, 2007 for an overview). It is usually quantified by the ratio α/β that is derived from the linear-quadratic biological model for tumor control (Brenner, 2008). In contrast with other tumors for which α/β is around 10Gy, first estimates for prostate cancer were found between 1Gy and 3 Gy indicating a very high sensitivity to fractionation (e.g. Fowler, 2001 ; Brenner, 1999, Wang 2003). With such low values, the α/β for prostate cancer would be even lower than α/β for rectum tissues estimated between 3.6Gy to 6Gy (Fowler, 2003), rectum tissues being the late reacting normal tissues mostly affected by late complications due to toxicity in prostate cancer radiation therapies.
Hypofractionated therapy that aims at delivering fewer larger dose fractions is known to reduce the length of treatment with benefit both for the patient and for cost of treatment but its toxicity was mostly debated. Based on this low α/β, i.e. higher sensitivity to radiation for prostate tissue than for normal tissue, hypofractionated radiation therapy would in addition improve local control of the tumor and reduce late toxicity.
The first estimations of α/β for prostate cancer around 1.5Gy (and more generally less than 3Gy) were obtained by comparing two arms of treatment, brachytherapy and external beam radiation therapy (EBRT) (Brenner, 1999, Fowler, 2001, Wang, 2003). These estimates were criticized because of differences inherent to the two treatments that could have yielded to biases in the estimation (Brenner, 2003), and it was recommended that estimation be better derived from comparison of different EBRT therapies (Bentzen, 2005). So, comparison of hypofractionated EBRT and conventional EBRT were conducted that led to the same low estimates of α/β below 3Gy (Livsey, 2003 ; Bentzen, 2005 ; Kupelian, 2005 ; Yeoh 2006). However these studies usually reported similar (or a few times only significantly lower) rate of late complications, and similar tumor control as in the conventional therapy arm. They lacked of statistical power to bring any definitive conclusions (Daşu, 2007).
By reviewing 17 estimates of α/β in the literature, Daşu (2007) yielded to an averaged estimate of 1.85 Gy but emphasized the large uncertainty around some estimates that prevented them from validating low α/β ratio for prostate cancer, and thus validating the discussion in favour of hypofractionated therapy. The recent multicentric study including 3,756 patients of Williams (2007) illustrates the lack of precision with a low estimate of 3.7 Gy but very large confidence bands (95% confidence interval=[1.1, ∞]).
In these previous works, α/β was estimated using either binary end point such as biochemical recurrence (defined as nadir+2ng/mL according to ASTRO – Roach, 2006) at 5 years, or time-to-recurrence endpoint (biochemical or clinical recurrence). Yet, after end of radiation therapy, repeated measures of PSA are collected that can bring a lot more information about the progression of prostate cancer and biochemical recurrence. This evolution was described recently using a linear mixed model and dose of radiation was shown to be highly associated with long term rise of PSA (Proust-Lima, 2008). In that paper we provided a framework for evaluating prognostic and other factors that may be associated with disease progression. A finding was that the dose of radiation was associated with the pattern of post treatment PSA values, but that given the pattern of PSA the dose of radiation provided no further significant information about clinical recurrence. This provides a rationale for the approach in the current paper where we are investigating the effect of the radiation fractionation schedule on disease progression and we can do that by using just the linear mixed model approach focussing on the PSA values after treatment and not considering clinical recurrence.! ang2057
In this context, this paper aims at estimating the α/β not on a binary indicator or time-to-event indicator derived from the biochemical recurrence but directly on the rate of change of PSA after end of treatment. By using directly repeated measures of PSA, the statistical power should be enhanced and a better precision in the estimation of α/β is expected. More than 5000 patients from 6 different large cohorts were included in the analysis, all being treated by EBRT with either a hyperfractionated scheme, a conventional scheme or a hypofractionated scheme so that a wide range of radiation therapy schedules were considered.
Methods and Materials
Patient cohorts
Data for patients treated for prostate cancer by external beam radiation therapy (EBRT) came from 6 different cohorts: University of Michigan, Ann Arbor, Michigan (UM) (Taylor, 2005), Radiation Therapy Oncology Group (RTOG 9406) (Roach, 2004), Peter Mac Callum Cancer Center, Melbourne, Australia (PMCC), William Beaumont Hospital, Detroit, Michigan (WBH) (Kestin, 1999), Royal Brisbane Hospital, Brisbane, Australia (RBH) (Williams, 2004; Williams, 2007) and (which name ?) Vancouver, Australia (?). Those having planned neoadjuvant or adjuvant androgen deprivation therapy (ADT) were not included.
All patients had clinically localized prostate cancer of clinical stage T1 to T4 and were node and metastasis negative. All data were acquired under Institutional Review Board approval at the respective institutions and at UM, where the data were aggregated and analysed.
In summary, EBRT (either 2D or 3D conformal) was targeted to the prostate or prostate plus seminal vesicles depending on clinical risk. Whole pelvic radiotherapy was not routinely performed. All cases were required to have at least one year follow-up without clinical recurrence or salvage ADT and at least two PSA measurements before end of follow-up. All PSA measures collected after EBRT until the end of follow-up (minimum time to clinical recurrence or lost to follow-up) or initiation of salvage ADT were analysed. PSA measures were logarithmically transformed using ln(PSA+0.1 ng/mL) to satisfy the normality assumptions for inclusion in the statistical models.
Three prognostic factors were used in the analysis: the pre-treatment level of PSA at diagnosis (iPSA; transformed on the continuous scale to iPSA=ln(iPSA+0.1)), T-stage category (1, 2, 3-4) and Gleason score (<7, 7, >7). Dose of radiation D was defined as the sum of all fractional doses dj given during the J sessions of therapy. To evaluate the α/β ratio, squared dose D2 was defined as the sum of all squared fractional doses given during the therapy. From the linear-quadratic model (Brenner, 2008), the α/β is the ratio of the regression coefficients of D and D2. The mean dose per fraction was defined as the average dose per fraction received over sessions.
Statistical analysis
Distributions of prognostic factors over cohorts were compared using Kruskall-Wallis test for continuous variables and Chi-square test for categorical variables.
Change over time of PSA after end of radiation therapy was described using a linear mixed model (LMM) (Laird and Ware, 1982). Evolution of PSA has 3 components as described by Proust-Lima et al. (2008) and shown in figure 1: (1) post-treatment level of PSA, denoted as post-treatment PSA (ptPSA) ; (2) short term evolution during the first year after end of EBRT, approximated by f1(t)=((1+t)-1.5-1) and denoted as short term drop of PSA (stPSA) ; (3) long term rate of increase of PSA, described by a linear trend and denoted as long term rise of PSA (ltPSA).
Figure 1.
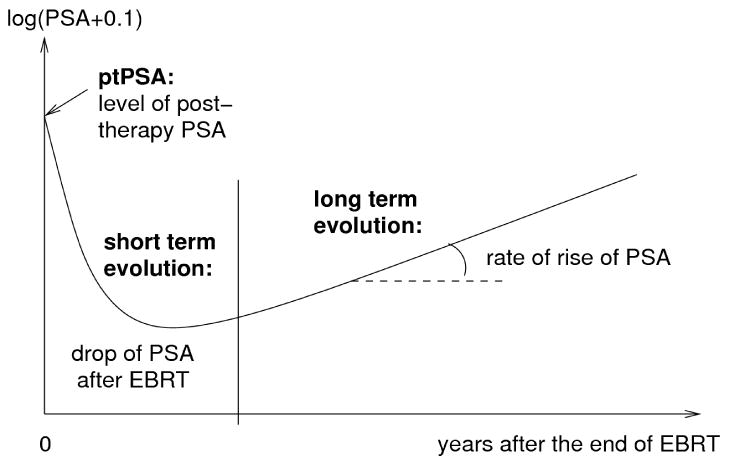
Evolution of PSA after end of radiation therapy: post-treatment level of PSA, short term drop of PSA and long term rise of PSA.
The linear mixed model accounted for inter-individual variability through individual correlated Gaussian random-effects for each component (ptPSA, stPSA and ltPSA), as well as intra-individual correlation through correlated errors (using a spherical spatial correlation structure) in addition to the independent Gaussian measurement errors. Details are given in Appendix.
The model was adjusted for iPSA, T-stage and Gleason score, and their interactions with short term drop and long term rise of PSA in order to obtain a complete adjustment. A more parsimonious adjustment proposed by Proust-Lima (2008) was also considered in a sensitivity analysis. It consisted in iPSA on post-treatment PSA, T-stage and iPSA on short term evolution, and Gleason, T-stage and iPSA on long term evolution.
Dose and squared dose effect were primarily evaluated on long term rise of PSA in order to compute the α/β ratio. However, estimates were adjusted for dose and squared dose effects on ptPSA and stPSA to avoid any confusion. Associations were tested using the Wald test and the likelihood ratio test (LRT).
When pooling the cohorts together, cohort-specific intercepts, short term drops and long term rises were included to correct for the heterogeneity between cohorts.
The ratio α/β was estimated as the ratio of the effect of dose and squared dose on long-term rise of PSA. Confidence bands were obtained using a profile of likelihood detailed in appendix. Statistical analyses were performed with SAS statistical software version 9.1.3 (SAS Institute, Cary, NC). Statistical tests were at the two-sided α=0.05 level of significance.
Results
Description of cohorts
The 6 cohorts are described in Table 1. A total of 5,093 patients were included in the analysis: 503 (9.9%) patients were from UM, 615 (12.1%) from RTOG, 395 (7.7%) from PMCC, 1268 (24.9%) from WBH, 1466 (28.8%) from RBH and 846 (16.6%) from Vancouver. The median time of follow-up was 4.7 years after end of treatment, with relatively shorter time of follow-up for UM and WBH (respectively a median of 4.1 and 3.7 years) and longer time for RBH with a median of 5.3 years. The median number of PSA measures per patient varied from 8 for UM, PMCC and WBH to 11 for RTOG. The prognostic factor distribution differed significantly over cohorts (p<0.0001 for each factor). Respectively 30% and 61.5% of patients had a T-stage of 1 and 2 over the cohorts. However, RTOG included more T-stage 1 (56.6%) and less T-stage 3 and 4 (2.3%) while PMCC and Vancouver included less T-stage 1 (respectively 18.7% and 21.8%) and more Tstage 3 and 4 (respectively 21.5% and 17.5%). The proportion of patients having a Gleason score of 7 varying from 19.9% for BM to 37.4% for UM, and strictly higher than 7 varying from 4.8% for PMH to 9.0% for BM with a proportion over cohorts of 23.1% of patients with a score of 7 and 6.9% of patients with a score greater than 7. Finally, the median level of pre-treatment PSA ranged from 7.4ng/mL for RTOG to 15.0ng/mL for RBH with a median level over cohorts of 9.3ng/mL.
Table 1.
Description of the six cohorts.
| UM (N=503) | RTOG (N=615) | PMCC (N=395) | WBH (N=1268) | RBH (N=1466) | Vanc (N=846) | Pooled (N=5093) | |
|---|---|---|---|---|---|---|---|
| Ann Arbor, MI, USA | Multicentric, USA | Melbourne, Australia | Detroit, MI, USA | Brisbane, Australia | Vancouver, Canada | ||
| Period of recruitment | 1988-2004 | 1994-2001 | 1997-2003 | 1987-2003 | 1990-1998 | 1994-2001 | |
| Number of PSA measures | 4607 | 6417 | 3285 | 11380 | 14636 | 7484 | 47809 |
| T-stage : 1 | 163 (32.4%) | 348 (56.6%) | 74 (18.7%) | 431 (34.0%) | 298 (20.3%) | 184 (21.8%) | 1498 (29.4%) |
| 2 | 290 (57.7%) | 253 (41.1%) | 236 (59.8%) | 792 (62.5%) | 1047 (71.4%) | 514 (60.7%) | 3132 (61.5%) |
| 3, 4 | 50 (9.9%) | 14 (2.3%) | 85 (21.5%) | 12 (3.5%) | 121 (8.3%) | 148 (17.5%) | 463 (9.1%) |
| Gleason <7 | 276 (54.9%) | 421 (68.5%) | 247 (62.5%) | 902 (71.1%) | 1466 (76.1%) | 605 (71.5%) | 3567 (70.0%) |
| =7 | 188 (37.4%) | 156 (25.4%) | 129 (32.7%) | 252 (19.9%) | 262 (17.9%) | 190 (22.5%) | 1177 (23.1%) |
| >7 | 39 (7.8%) | 38 (6.2%) | 19 (4.8%) | 114 (9.0%) | 88 (6.0%) | 51 (6.0%) | 349 (6.9%) |
| Clinical recurrence | 84 (16.7%) | 40 (6.5%) | 21 (5.3%) | 188 (14.8%) | NA | 146 (17.3%) | 479 (13.2%)* |
| SADT | 44 (8.8%) | 47 (7.6%) | 43 (10.9%) | 176 (13.9%) | 561 (38.3%) | 127 (15.0%) | 998 (19.6%) |
| Age (years) | 69.8 (56.2,79.7) | 69.0 (54.0,77.0) | 69.8 (58.5,76.7) | 73.0 (61.0,83.0) | 68.9 (57.7,77.3) | 72.0 (61.0,79.0) | 70.9 (58.0,79.0) |
| iPSA (ng/mL) | 8.2 (2.3,46.4) | 7.4 (2.6,19.2) | 10.5 (4.0,27.0) | 7.7 (2.3,38.2) | 15.0 (3.5,54.0) | 8.3 (1.8,26.1) | 9.3 (2.5,41.6) |
| # measures per patient | 8 (3,19) | 11 (4,17) | 8 (3,14) | 8 (3,19) | 9 (3,18) | 9 (3,15) | 9 (3,18) |
| Time of follow-up (years) | 4.1 (1.1,10.4) | 4.9 (1.4,8.9) | 4.6 (1.6,7.2) | 3.7 (1.1,9.5) | 5.3 (1.5,9.4) | 5.0 (1.1,9.9) | 4.7 (1.2,9.5) |
| Total dose (Gr) | 70.4 (66.0,77.8) | 78.0 (70.3,82.4) | 70.0 (66.0,74.0) | 66.6 (66.0,77.4) | 63.2 (52.5,66.0) | 66.0 (52.5,70.0) | 66.6 (52.6,79.2) |
| Dose per fraction (Gr) | 1.85 (1.80,2.00) | 2.02 (1.81,2.12) | 2.00 (2.00,2.00) | 1.80 (1.79,2.00) | 2.11 (2.00,2.63) | 2.00 (2.00,2.63) | 2.00 (1.80,2.63) |
NA=not available. Continuous data are depicted as median (5th and 95th percentiles), and categorical data are depicted as number (percentage)
excluding RBH
Total dose of EBRT and dose per fraction
A large range of total dose of EBRT was observed over cohorts with total dose varying from 50 Gy to 84.6 Gy. The median total dose was 66.6 Gy over cohorts but varied significantly across cohorts (p<0.0001) from a median of 63.2 Gy for RBH to a median of 78.0 Gy for RTOG (Table 1). The dose per fraction ranged from 1.70Gy to 2.77Gy with a median of 2.00Gy over all patients. The dose per fraction varied significantly over cohorts (p<0.0001) from a median of 1.80Gy for WBH to 2.11Gy for RBH. This wide range gave us the opportunity to explore the ratio α/β for Prostate cancer on the pooled dataset.
α/β estimation
Effects of dose and squared dose on the three components of the PSA pattern were estimated in the biphasic linear mixed model with adjustment for iPSA, T-stage, Gleason and cohort. Parameter regression for dose and squared dose are given in Table 2. Total dose of EBRT was associated with post-treatment initial level of PSA (p=0.0002), an higher total dose being associated with a lower post-treatment level of PSA. Squared dose was not associated with post-treatment PSA level (p=0.876). Neither dose nor squared dose were significantly associated with the short term drop of PSA (respectively p=0.135 and p=0.163). Finally dose and squared dose were highly associated with long term rise of PSA. Higher dose was associated with a lower long term rate of rise of PSA (p=0.0017) and increasing squared dose was associated with a lower long term rise of PSA (p=0.0003). This association led to an estimation of α/β =-0.0062/-0.0040=1.55 Gy. The 95% confidence interval was [0.46;4.52] using the profile likelihood method.
Table 2.
Regression parameters, standard-error and degree of significance for dose and squared dose of radiation therapy on post-treatment PSA level, short term drop of PSA and long term rise of PSA in the linear mixed model adjusted for iPSA, T-stage and Gleason.
| Estimate | Standard-error | p-value | |
|---|---|---|---|
| Post-treatment PSA: | |||
| Dose | -0.0116 | 0.0031 | 0.0002 |
| Squared Dose | 0.00027 | 0.0017 | 0.876 |
| Short term drop: | |||
| Dose | -0.0093 | 0.0063 | 0.135 |
| Squared Dose | -0.0048 | 0.0035 | 0.163 |
| Long term rise: | |||
| Dose | -0.0062 | 0.0020 | 0.0017 |
| Squared Dose | -0.0040 | 0.0011 | 0.0003 |
Robustness of the estimate to correlation structure and adjustment for prognostic factors
To evaluate whether this estimate of α/β from the long term rise was robust to the assumptions of the linear mixed model, we compared the estimate of α/β for different specifications of the statistical model. Using complete or parsimonious adjustment for prognostic factors iPSA, T-stage and Gleason did not change the estimate of α/β nor its 95% confidence interval (α/β=1.58, 95%CI=[0.46;4.69]). Accounting for the correlation between repeated measures of PSA improved markedly the fit of the data (log-likelihood improved by 3200 points). Estimate of α/β was slightly reduced if independent errors were assumed (α/β=1.15, 95%CI=[0.24;3.23]). Changing the adjustment for dose in the two first components of the model did impact slightly the estimate of α/β. Not adjusting for squared dose on post-treatment PSA or short term drop of PSA gave α/β=2.37 ([0.83;7.63]), while when adjusting only for dose on the post-treatment level of PSA, α/β=1.64 ([0.38;5.96]). While these estimates are all low, it does suggest that dose and fractionation on post-treatment level of PSA could slightly confound the effect of dose and fractionation on the long term rise of PSA, and hence highlights! s202057 the need for the complete adjustment as we used in the principal analysis.
Variability over cohorts
The large variability over cohorts due to their heterogeneity in recruitment, time period, countries and other unknown factors had to be accounted for. We chose to include cohort-specific mean trajectory parameters which were found to be of primary importance as they greatly improved the goodness-of-fit (by 108 points of log-likelihood). There were significant differences between cohorts in the initial post-treatment level, probably reflecting differences between the patient populations that were not accounted for by the other prognostic factors. There were also slight differences in the rate of rise of PSA. This adjustment did not change prognostic factors nor mean trajectory estimates but greatly impacted the α/β estimate (α/β=10.6 without adjustment). This result was expected as fractionation scheme greatly varied over cohorts. When investigating cohort influence in determining this estimate, only RBH cohort seemed to change the range of the estimate. Indeed, excluding this dataset led to α/β=3.16 with larger confidence bands (95%CI=[0.95;21.20]) while excluding one of the 5 other cohorts led to α/β from 1.14 to 1.53. However, firs! t, the estimate remained low and second it should be noted that mainly RBH cohort brought hypofractioned schemes of EBRT which is required to estimate precisely α/β (Williams et al., 2007). RBH had a median averaged dose per fraction of 2.11 Gy versus lower or equal to 2 Gy for other cohorts. Finally, to precise the α/β estimate, we accounted for interactions between prognostic factors and cohorts, and then accounted for the year of treatment that could have explained differences over cohorts, but the estimate of α/β remained in the same range as for the main analysis (with respectively α/β=1.47 and α/β=2.02).
α/β estimation per subgroups of prognostic factors
We evaluated whether the α/β was different when considering subpopulation of patients with different prognostic factors values : T-stage<2, T-stage=2 and T-stage>2 ; Gleason<7, Gleason=7 and Gleason>7 ; iPSA≤10ng/mL and iPSA>10ng/mL (10ng/mL was closed to the median value of 9.3ng/mL over the cohorts). The linear mixed model with complete adjustment for prognostic factors and correlated errors was estimated separately in the different subgroups of patients defined by these prognostic factors. The model was also adjusted for dose and squared dose on post-treatment PSA level and short term drop of PSA. Parameters associated with dose and squared dose on long term rate of rise of PSA and α/β estimates are given in Table 3. For some of the subgroups the effect of dose and dose squared are not statistically significant. This occurred in the smaller subgroups who tended to have more advanced disease, perhaps reflecting greater heterogeneity amongst these patients. Except for the Gleason>7 category, estimates of α/β remained very low varying from α/β=-0.90 to α/β=2.88. Among subjects with Gleason>7, α/β was estimated close to 20 but with a lack of precision (95% confidence bands ]-∞;+∞[). There was a slight tendency for the estimate of α/β to be higher (range 2.5 to 2.88) for patients with less advanced disease, although these estimates are not precise.ar
Table 3.
Regression parameter and degree of significance from the Wald test of dose and squared dose on long term rate of change of PSA adjusted for iPSA, T-stage and Gleason as well as dose and squared dose on post-treatment PSA and short term drop of PSA, and derived estimate of the α/β ratio with 95% confidence bands for subgroups of prognostic factors.
| Prognostic factor | Strate | Number of subjects (%) | Dose | Squared dose | α/β | 95% CI * |
|---|---|---|---|---|---|---|
| T-stage | <2 | 1498 (29.4%) | -0.00854 (p=0.004) | -0.00342 (p=0.011) | 2.55 | [0.53;17.95] |
| =2 | 3132 (61.5%) | -0.00422 (p=0.086) | -0.00449 (p=0.005) | 0.94 | [-0.20;5.67] | |
| >2 | 463 (9.1%) | -0.0210 (p=0.196) | -0.0150 (p=0.226) | 1.98 | ]-∞;∞[ | |
| Gleason | <7 | 3567 (70.0%) | -0.0103 (p<0.001) | -0.0040 (p<0.001) | 2.63 | [1.29;6.67] |
| =7 | 1177 (23.1%) | 0.0071 (p=0.261) | -0.0079 (p=0.020) | -1.22 | [-6.85;1.77] | |
| >7 | 349 (6.9%) | 0.0234 (p=0.1772) | 0.00123 (p=0.887) | 14.71 | ]-∞;∞[ | |
| iPSA | ≤10ng/mL | 2775 (54.5%) | -0.0074 (p<0.001) | -0.00257 (p=0.013) | 2.98 | [0.94;23.12] |
| >10ng/mL | 2318 (45.5%) | -0.00245 (p=0.547) | -0.0688 (p=0.006) | 0.29 | [-0.97;3.38] |
∞ was noted for bounds >1,000 or <1,000.
α/β estimation per dataset
The linear mixed model with complete adjustment for prognostic factors and correlated errors was estimated separately on each cohort. The model was also adjusted for dose and squared dose on post-treatment PSA level and short term drop of PSA. Table 4 gives the regression parameters associated with dose and squared dose on the long term rate of rise of PSA. Estimates of α/β varied greatly from cohort to cohort. However, except for RTOG and Vancouver that had relatively narrow 95% confidence intervals around low values of α/β (respectively -1.71 and 0.96), confidence bands allowed for extremely low value of α/β as well as infinitely large values. This shows that no conclusion regarding the value of α/β can be derived from an analysis of the cohorts separately. Indeed, some cohorts only include a few different doses per fraction or total dose so that estimation of the ratio is not possible. Only pooling the data provided a broad range of different doses per fraction and thus a precise estimate.
Table 4.
Regression parameter and degree of significance from the Wald test of dose and squared dose on long term rate of change of PSA adjusted for iPSA, T-stage and Gleason as well as dose and squared dose on post-treatment PSA and short term drop of PSA, and derived estimate of the α/β ratio with 95% confidence bands per dataset.
| Dose | Squared dose | α/β | 95% CI * | |
|---|---|---|---|---|
| UM | -0.0052 (p=0.75) | -0.0013 (p=0.89) | 4.12 | [-1.91;+∞[ |
|
| ||||
| RTOG | 0.0117 (p=0.167) | -0.0068 (p=0.003) | -1.72 | [-2.83;1.86] |
|
| ||||
| PMCC | -0.185 (p=0.156) | 0.0901 (p=0.166) | -2.05 | ]-∞;+∞[ |
|
| ||||
| WBH | -0.0264 (p<0.001) | -0.0025 (p=0.541) | 10.68 | [1.17;+∞[ |
|
| ||||
| RBH | 0.00005 (p=0.99) | -0.00037 (p=0.94) | -0.143 | ]-∞;+∞[ |
|
| ||||
| Vancouver | -0.0098 (p=0.0014) | -0.0102 (p=0.027) | 0.959 | [0.36;7.53] |
∞ was noted for bounds >1,000 or <1,000.
Discussion
There exists a large literature on estimation of α/β for prostate cancer, with the consensus on a very low value of α/β around 1.5 Gy evoking a high sensitivity to fractionation of radiation therapy and a theoretical superiority of hypofractionated schemes (Daşu, 2007, Khoo, 2008, Brenner, 2003). However, previous studies were criticized in two directions. First, estimation was usually based on comparison of EBRT and brachytherapy while these two kinds of treatment are not necessarily directly comparable (Brenner, 2003). Secondly, estimation usually lacked of precision with very large confidence bands that made it impossible to conclude definitely on the extreme low value of the ratio (Williams, 2007).
In the present work, we considered more than 5,000 patients who were treated for a localized prostate cancer by external beam radiation therapy to estimate the α/β of Prostate cancer. First, this prevented us from possible biases due to different nature of treatment, and second, using data from 6 cohorts, a broad range of doses was considered with dose per fraction varying from 1.70Gy to 2.77Gy and total dose from 50 Gy to 84.6 Gy.
For the first time, the ratio α/β was directly estimated from the effect of dose on the long term rate of change of PSA rather than on an indicator of biochemical recurrence derived from the PSA post-treatment evolution so that all repeated measures of progression of cancer were used and the amount of information was maximised. The ratio was estimated at 1.55 Gy Gy with very narrow 95% confidence bands ([0.46;4.52] from the profile of likelihood). The estimate was robust to the specification of the model for covariates and correlation structure with estimations of α/β varying from 1.2 Gy to 2.3 Gy depending on the linear mixed model estimated. However, we found that accounting for cohort variability or not changed considerably the estimate. Indeed, each cohort had specific characteristics to account for but they also brought different ranges of EBRT total dose or doses per fraction so that, especially RBH data that informed on higher doses per fraction than other cohorts influenced the estimate.
The result of this paper should be interpreted with caution. Indeed, it is based on 5 observational cohorts and only one clinical trial. Second, patients were recruited at different periods of time which could have induced different guidance for scheme of radiation therapy, gravity of cases included and even possibly definitions of prognostic factors such as Gleason. Third, as observational cohorts, dose was administered according to prognostic factors of the patient and possibly other factors that we ignore. As a result, a close adjustment for cohort variability was the only way to provide an estimate of the ratio α/β that was adjusted at best for this heterogeneity over cohorts but we cannot prevent the estimate from other unknown influential factors.
In conclusion, the model we provided gave the best adjustment for cohort variability and the best fit of the 6-cohort data so that this analysis, based on biochemical recurrence of cancer defined as the continuous long term rise of PSA rather than a binary endpoint, does suggest a low value of α/β with narrow confidence bands. This result is in accordance with previous estimations in the literature. It shows a very high sensitivity of prostate tissue to radiation that would favor hypofractionated trials to evaluate if larger doses per fraction give a better control of Prostate tumor with a reduced late toxicity. However, the authors recommend that this analysis be still validated on other cohorts and especially clinical trials that include high doses per fraction as RBH dataset does.
Acknowledgments
This research was supported by grant CA110518 from the US National Cancer Institute.
Appendix
Linear mixed model
For subject i (i=1,…,N) and occasion j (j=1,…,ni), PSA(tij) is the level of PSA measured at time tij after the end of EBRT and PSA*(tij)=log(PSA(tij)+0.1) is the level of PSA in the logarithm scale. Evolution of PSA* over time was described using the following linear mixed model proposed in Proust-Lima et al. (2008) to simply describe post-treatment PSA kinetics:
Evolution of PSA* after end of EBRT was described in three phases (see Figure 1): the post-therapy level; short term evolution in the first year after RT using f1(t)=(1+t)-1.5 -1, and long term evolution using the linear trend.
The mean PSA* evolution in the population was described by the intercepts μ0, μ1 and μ2 associated with each phase as well as covariate effects X0iβ0, X1iβ1 and X2iβ2 where X0i, X1i and X2i were potentially different vectors of covariates (including T-stage, Gleason, iPSA, dose and dose squared). The individual departure from the mean evolution was described by a Gaussian vector of random-effects ui=(u0i,u1i,u2i)T with mean vector 0 and variance-covariance matrix B. The independent Gaussian errors εi(tij) were centered at zero with variance σ2. Correlated errors wi(tij) were added to account for correlation between repeated measures of a same patient. Correlated errors were centered at zero with spherical spatial structure of variance covariance: . Spherical spatial structure gave the best fit to the data among the spatial covariance structures proposed by SAS proc MIXED.
To account for heterogeneity over cohorts, cohort-specific fixed effects were added so that became for cohort k (k=1,…,K). The SAS MIXED procedure was used to estimate the parameters using maximum likelihood.
Estimate of α/β and 95% confidence bands
The and required for the linear quadratic model are respectively the estimated coefficients of total dose and sum of squared dose per fraction on long term PSA in X2i. From this the ratio is estimated as. However, no direct estimate of the variance can be derived from the linear mixed model so we used a profile of likelihood. This method consists in finding the interval of values of the ratio for which the log-likelihood is greater than the maximum of log-likelihood obtained for minus 1.96. For a grid of fixed values of the ratio r, total nominal dose is computed as, the linear mixed model including this covariate on long term rise of PSA is estimated, and the log-likelihood is calculated.
Footnotes
Conflict of interest notification: no actual or potential conflicts of interest exist.
References
- Bentzen SM, Ritter MA. The alpha/beta ratio for prostate cancer: what is it, really? Radiother Oncol. 2005 Jul;76(1):1–3. doi: 10.1016/j.radonc.2005.06.009. [DOI] [PubMed] [Google Scholar]
- Brenner DJ, Hall EJ. Fractionation and protraction for radiotherapy of prostate carcinoma. Int J Radiat Oncol Biol Phys. 1999 Mar 15;43(5):1095–101. doi: 10.1016/s0360-3016(98)00438-6. [DOI] [PubMed] [Google Scholar]
- Brenner DJ, Martinez AA, Edmundson GK, Mitchell C, Thames HD, Armour EP. Direct evidence that prostate tumors show high sensitivity to fractionation (low alpha/beta ratio), similar to late-responding normal tissue. Int J Radiat Oncol Biol Phys. 2002 Jan 1;52(1):6–13. doi: 10.1016/s0360-3016(01)02664-5. [DOI] [PubMed] [Google Scholar]
- Brenner DJ. Hypofractionation for prostate cancer radiotherapy--what are the issues? Int J Radiat Oncol Biol Phys. 2003 Nov 15;57(4):912–4. doi: 10.1016/s0360-3016(03)01456-1. [DOI] [PubMed] [Google Scholar]
- Brenner DJ. The linear-quadratic model is an appropriate methodology for determining isoeffective doses at large doses per fraction. Semin Radiat Oncol. 2008 Oct;18(4):234–9. doi: 10.1016/j.semradonc.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daşu A. Is the alpha/beta value for prostate tumours low enough to be safely used in clinical trials? Clin Oncol (R Coll Radiol) 2007 Jun;19(5):289–301. doi: 10.1016/j.clon.2007.02.007. Epub 2007 Mar 9. Review. [DOI] [PubMed] [Google Scholar]
- Fowler J, Chappell R, Ritter M. Is alpha/beta for prostate tumors really low? Int J Radiat Oncol Biol Phys. 2001 Jul 15;50(4):1021–31. doi: 10.1016/s0360-3016(01)01607-8. [DOI] [PubMed] [Google Scholar]
- Fowler JF, Ritter MA, Chappell RJ, Brenner DJ. What hypofractionated protocols should be tested for prostate cancer? Int J Radiat Oncol Biol Phys. 2003 Jul 15;56(4):1093–104. doi: 10.1016/s0360-3016(03)00132-9. [DOI] [PubMed] [Google Scholar]
- Kestin LL, Vicini FA, Ziaja EL, et al. Defining biochemical cure for prostate carcinoma patients treated with external beam radiation therapy. Cancer. 1999;86(8):1557–1566. doi: 10.1002/(sici)1097-0142(19991015)86:8<1557::aid-cncr24>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- Kupelian PA, Thakkar VV, Khuntia D, Reddy CA, Klein EA, Mahadevan A. Hypofractionated intensity-modulated radiotherapy (70 gy at 2.5 Gy per fraction) for localized prostate cancer: long-term outcomes. Int J Radiat Oncol Biol Phys. 2005 Dec 1;63(5):1463–8. doi: 10.1016/j.ijrobp.2005.05.054. Epub 2005 Sep 19. [DOI] [PubMed] [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38(4):963–974. [PubMed] [Google Scholar]
- Livsey JE, Cowan RA, Wylie JP, Swindell R, Read G, Khoo VS, Logue JP. Hypofractionated conformal radiotherapy in carcinoma of the prostate: five-year outcome analysis. Int J Radiat Oncol Biol Phys. 2003 Dec 1;57(5):1254–9. doi: 10.1016/s0360-3016(03)00752-1. [DOI] [PubMed] [Google Scholar]
- Proust-Lima C, Taylor JMG, Williams SG, Ankerst DP, Liu N, Kestin LL, Bae K, Sandler HM. Determinants of change of prostate-specific antigen over time and its association with recurrence following external beam radiation therapy of prostate cancer. Int J Radiat Oncol Biol Phys. 2008 doi: 10.1016/j.ijrobp.2008.01.056. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach M, Winter K, Michalski JM, et al. Penile bulb dose and impotence after three-dimensional conformal radiotherapy for prostate cancer on RTOG 9406: findings from a prospective, multiinstitutional, phase I/II dose-escalation study. Int J Radiat Oncol Biol Phys. 2004;60(5):1351–1356. doi: 10.1016/j.ijrobp.2004.05.026. [DOI] [PubMed] [Google Scholar]
- Roach M, 3rd, Hanks G, Thames H, Jr, Schellhammer P, Shipley WU, Sokol GH, Sandler H. Defining biochemical failure following radiotherapy with or without hormonal therapy in men with clinically localized prostate cancer: recommendations of the RTOG-ASTRO Phoenix Consensus Conference. Int J Radiat Oncol Biol Phys. 2006 Jul 15;65(4):965–74. doi: 10.1016/j.ijrobp.2006.04.029. [DOI] [PubMed] [Google Scholar]
- Taylor JMG, Yu M, Sandler HM. Individualized predictions of disease progression following radiation therapy for prostate cancer. J Clin Oncol. 2005;23(4):816–825. doi: 10.1200/JCO.2005.12.156. [DOI] [PubMed] [Google Scholar]
- Wang JZ, Guerrero M, Li XA. How low is the alpha/beta ratio for prostate cancer? Int J Radiat Oncol Biol Phys. 2003 Jan 1;55(1):194–203. doi: 10.1016/s0360-3016(02)03828-2. [DOI] [PubMed] [Google Scholar]
- Williams SG, Duchesne GM, Millar JL, et al. Both pretreatment prostate-specific antigen level and posttreatment biochemical failure are independent predictors of overall survival after radiotherapy for prostate cancer. Int J Radiat Oncol Biol Phys. 2004;60(4):1082–1087. doi: 10.1016/j.ijrobp.2004.04.048. [DOI] [PubMed] [Google Scholar]
- Williams SG, Taylor JM, Liu N, Tra Y, Duchesne GM, Kestin LL, Martinez A, Pratt GR, Sandler H. Use of individual fraction size data from 3756 patients to directly determine the alpha/beta ratio of prostate cancer. Int J Radiat Oncol Biol Phys. 2007 May 1;68(1):24–33. doi: 10.1016/j.ijrobp.2006.12.036. [DOI] [PubMed] [Google Scholar]
- Yeoh EE, Holloway RH, Fraser RJ, Botten RJ, Di Matteo AC, Butters J, Weerasinghe S, Abeysinghe P. Hypofractionated versus conventionally fractionated radiation therapy for prostate carcinoma: updated results of a phase III randomized trial. Int J Radiat Oncol Biol Phys. 2006 Nov 15;66(4):1072–83. doi: 10.1016/j.ijrobp.2006.06.005. Epub 2006 Sep 11. [DOI] [PubMed] [Google Scholar]


