Biomarker Validation: Common Data Analysis Concerns

Statistical concerns such as confounding and multiplicity, for which solutions have existed for years, are common in biomarker validation studies; however, published validation studies may not address these issues. By not only raising the issues but also describing possible solutions, this discussion may help decrease false discovery and enhance the reproducibility of validation study findings.

Abstract

Biomarker validation, like any other confirmatory process based on statistical methodology, must discern associations that occur by chance from those reflecting true biological relationships. Validity of a biomarker is established by authenticating its correlation with clinical outcome. Validated biomarkers can lead to targeted therapy, improve clinical diagnosis, and serve as useful prognostic and predictive factors of clinical outcome. Statistical concerns such as confounding and multiplicity are common in biomarker validation studies. This article discusses four major areas of concern in the biomarker validation process and some of the proposed solutions. Because present-day statistical packages enable the researcher to address these common concerns, the purpose of this discussion is to raise awareness of these statistical issues in the hope of improving the reproducibility of validation study findings.

Implications for Practice:

Statistical concerns such as confounding and multiplicity, for which solutions have existed for years, are common in biomarker validation studies; however, published validation studies may not address these issues. By not only raising the issues but also describing possible solutions, this discussion may help decrease false discovery and enhance the reproducibility of validation study findings.

Introduction

The fundamental goal of a large number of statistical analyses is to identify factors important to the outcome. Whether using a simple two-sample t test, a more complex generalized linear model, or multivariate analysis methods (e.g., principal components analysis, factor analysis, and discriminant analysis), the goal is to determine whether the outcome is affected by measurable covariates. For oncology research, biomarkers have become an important covariate because biomarker identification can lead to targeted therapy and thus become the first step to personalized cancer treatment. Because biomarkers are explored as prognostic and predictive factors of clinical outcome, it is important to understand the common statistical issues of biomarker validation.

Biomarker validation, like any other confirmatory process based on statistical methodology, must discern associations that occur by chance from those reflecting true biological relationships. As noted by Genser et al., most researchers use a statistical significance level to decide whether the result of an analysis (i.e., the p value) is likely to be the result of chance [1]. Intrapatient correlation and multiplicity are two major factors to address in calculating the appropriate p value for an analysis and thus are two important factors of biomarker validation. Multiplicity can be an issue due to the investigation of several potential biomarkers or due to the investigation of multiple endpoints or measures of response. Studies with multiple endpoints require multiple testing corrections of the per-comparison significance levels, prioritization of the outcomes, or development of a composite endpoint. Many studies used to assess the prognostic or predictive value of biomarkers are retrospective case-control studies that carry the typical baggage inherent to retrospective observational studies, such as selection bias. The aim of this paper is to discuss these four important statistical issues that should be addressed in the design and analysis of biomarker studies.

Methods

Clinical references contained in this review were identified through queries of the PubMed and Medline databases. Only articles published in English were considered. The search was conducted with the term “biomarker validation” cross-referenced with “issue” and/or “limitation.” The literature was also queried with respect to “multiplicity,” “selection bias,” “multiple endpoints,” and “intra-class correlation.”

Discussion

The primary statistical concerns about biomarker validation, for the most part, are not new to data analysis. Assessing whether an individual biomarker is associated with a clinical outcome such as tumor response is no different than assessing whether smoking is associated with lung cancer and thus possess many of the same inherent issues. Retrospective biomarker studies may suffer from selection bias, the same as any retrospective observational study. Longitudinal biomarker studies (i.e., multiple observations per subject) require the same attention to within-subject correlation as any other statistical modeling exercise. Unique nuances, however, arise because multiplicity may not only be the typical inferential multiplicity caused by multiple comparisons due to subset analyses but also be caused by the investigation of a large number of candidate biomarkers. The number of candidate genes is quite large in the biomarker-discovery phase and is in the tens of thousands. As the number of genes investigated in the discovery phase has increased, the number of candidate genes for biomarker validation has increased, and the line between discovery and validation may be blurred as studies attempt to discover and validate biomarkers in small samples. Biomarkers are used not only as prognostic and predictive factors but also as surrogate endpoints. Because agents are developed with the goal of inhibiting specific cellular and molecular targets, it is appropriate to consider the use of biomarkers that reflect the proposed mechanism of action of the agent being studied as surrogate endpoints in clinical trials [2]. Surrogate endpoints may be useful when the pathophysiology of the disease and the mechanism of action of the intervention are thoroughly understood [3]. Change in the expression level of a pharmacodynamic biomarker could be used as a surrogate for clinical benefit. Are biomarkers differentially expressed at different levels of the clinical endpoint? Do patients with pathologic complete response exhibit a higher or lower level of biomarker expression than patients with stable disease or patients experiencing disease progression? The validation of a biomarker as a surrogate endpoint requires proof that the biomarker correlates well with clinical benefit (or lack thereof). The question is, how does one define clinical benefit (e.g., overall survival, disease- or progression-free survival, tumor response)? Surrogate-endpoint studies must address this issue if multiple clinical endpoints are considered.

Within-Subject Correlation

When multiple observations of the same metric (unordered repeated measures) are collected from the same subject, there is a distinct possibility of correlated results. Often this occurs when specimens from multiple tumors are obtained from individual patients. Within-subject correlation (or intrapatient correlation) is a form of intraclass correlation. The earliest attempts to quantify intraclass correlation were modifications of Pearson’s product-moment correlation coefficient. Fisher’s discovery of analysis of variance is a byproduct of his work to obtain linear equations composed of the variance components required to estimate the intraclass correlation from a completely randomized design [4]. The within-subject correlation is the proportion of the total variance attributable to the random subjects that is explained by the variance between subjects and is typically estimated by dividing the estimate of the between-subject variance by the sum of the estimates of the between- and within-subject variances.

Bartley et al. investigated the complex patterns of altered microRNA (miRNA) expression during the adenoma-adenocarcinoma sequence of 69 matched specimens from 21 colorectal patients [5]. They found that 36 of 230 miRNAs identified were significantly differentially expressed for four tissue-type pairwise comparisons (mucosa vs, adenocarcinoma, mucosa vs. high-grade dysplasia, mucosa vs. low-grade dysplasia, and low-grade dysplasia vs. adenocarcinoma) along the entire sequence to adenocarcinoma. However, they found that none of the 36 miRNAs was significantly differentially expressed when analyzed for stage of disease after adjustment for within-patient correlation. Such studies underscore the need to account for within-subject correlation when analyzing biomarker data. Anti-5-hydroxymethyl-2′-deoxyuridine antibody shows, for example, stability and low intraindividual variance with data from individuals rarely crossing over values of other subjects in a study by Hu et al. [6]. They noticed an intraclass correlation of 0.99 in their data when analyzing this potential cancer risk biomarker, signifying nearly complete dependence of measurements within patient. Analyzing such data assuming independent observations will almost surely inflate the type I error rate and result in spurious findings of significance. The use of mixed-effects linear models, which account for a dependent variance-covariance structure within subject, to analyze biomarker data are becoming more common in the literature [7, 8]. Comparisons based on the generalized estimating equations generated by these mixed-effects models produce more realistic p values and confidence intervals. In the biomarker validation process, researchers should not hesitate to make the most of the potential of their data and embrace more sophisticated statistical approaches when warranted.

O’Conner et al. developed biomarkers of tumor microvasculature from pretreatment dynamic contrast-enhanced magnetic resonance images [9]. Their study consisted of 10 patients with 26 colorectal cancer liver metastases. A linear model was used to model the percentage of remaining tumor volume at the end of treatment cycle 5. Because some patients had more than one tumor, a mixed-effects model was used to explore potential within-patient correlation. Because none was observed, the tumors were subsequently treated independently [9]. Intra- and interobserver variability of computed tomography measurements and their use as imaging biomarkers in oncology was studied by McErlean et al. [10]. A linear model with a random subject effect was fitted to their data to account for multiple lesions from a single patient. These authors’ willingness to explore the potential dependence of within-patient measurements underscores the evolution of data analysis in the clinical literature and their realization of the potential impact of ignoring such correlation.

Multiplicity

It is common for clinical researchers to use a statistical significance level to decide whether the result of an analysis is likely due to chance. Concerns about multiplicities in biomarker validation must be addressed to improve the reproducibility of the findings. The probability of concluding that there is at least one statistically significant effect across a set of tests (subset analyses) when in fact no effect exists increases with each additional test; therefore, it is necessary to control or limit the type I error rate (i.e., false discovery) [11]. A wealth of articles have been dedicated to the conduct of planned and unplanned subset analyses and addressing multiple testing issues [12–16].

As Berry noted, controlling for false-positive results may increase the rate of false negatives [17]. His thorough discussion of the issues of multiple testing in empirical studies includes what he describes as silent multiplicities (unreported and unrecognized comparisons) and such may be particularly relevant for biomarker validation. Biomarker validation studies typically involve multiple variables, multiple potential outcomes or markers of clinical benefit, and multiple subsets of patients in the investigation to study possible associations and biological relationships. The null hypothesis for biomarker validation is that the measured characteristic has no relevance or effect on prognoses, predictive power for therapeutic response, biological process, and so forth. Multiplicities are not just the spawn of data dredging; we know they arise from well-planned subset and interim analyses that require multiple comparisons of the data. However, Berry noted that silent multiplicities may exist and are potentially problematic because many comparisons may go unreported in the literature [17].

Biomarker validation studies are sensitive to false positives because the list of potential markers is characteristically extensive. Although one must be sensitive to methodology that increases potential false negatives, it is essential to attempt to limit false discovery so that the literature is not burdened with unreproducible biomarker findings. The primary goal when multiple simultaneous comparisons are conducted should be to control false discovery while maximizing power to detect meaningful associations. As multiple-comparison methodology evolved, controlling the family-wise error rate was of primary importance [11]. The medical literature is replete with the use of the methods of Tukey, Bonferroni, Scheffe, and others that attempt to do just that: control false discovery at the experiment or study level rather than the individual-comparison level. The analysis of microarray data led to a rethinking of the approach to controlling the type I error rate. Because the number of simultaneous hypotheses considered matches the number of genes, the probability of a false-positive finding is likely. Benjamini and Hochberg pioneered the approach to controlling the false discovery rate used in biomarker studies [18]. Their less stringent, more powerful approach controls the proportion of false discoveries rather than controlling the family-wise type I error rate. Today, the major statistical analysis packages include several approaches to handling multiplicities and should be a common part of biomarker validation.

Biomarker validation studies are sensitive to false positives because the list of potential markers is characteristically extensive. Although one must be sensitive to methodology that increases potential false negatives, it is essential to attempt to limit false discovery so that the literature is not burdened with unreproducible biomarker findings.

Brand et al. noted that serum biomarker-based screening for pancreatic cancer could greatly improve survival in appropriately targeted high-risk populations [19]. Their study of 83 biomarkers was composed of 333 patients with histologically diagnosed pancreatic ductal adenocarcinoma (PDAC), 144 patients with benign pancreatic conditions, 227 healthy controls, and 203 patients diagnosed with other cancers. Their analysis made use of two techniques to control for multiplicities. Pairwise differences were investigated among the groups within each of the 83 biomarkers using Tukey’s range test. In order to identify serum biomarkers that discern those with PDAC from healthy controls, the false discovery rate method developed by Benjamini and Hochberg was then applied to the 83 Tukey-adjusted p values for comparing PDAC and healthy controls across all biomarkers. Similarly, important biomarkers for distinguishing PDAC from benign disease were determined [19]. This process controlled the analysis not only for multiple pairwise comparisons of groups (e.g., PDAC to healthy controls, PDAC to benign disease) but also for the investigation of multiple biomarkers.

Multiple Clinical Endpoints

Multiple endpoints can lead to multiplicities. As Berry suggested, there may be silent multiplicities because analyses of uncorrelated endpoints may go unreported [17]. It is not unusual to see studies reported in the literature that investigate several metrics of clinical benefit such as overall survival, progression-free survival, duration of response, complete response rate, objective response rate (complete and partial), and clinical benefit rate (complete and partial response plus stable disease) simultaneously with no correction for multiplicity. The evaluation of multiple endpoints in a search for a relationship that yields a “significant” p value greatly inflates the risk of a false-positive finding and, at the very least, requires some adjustment for multiple testing [20, 21]. The problem of multiple endpoints may be aggravated by multiple start dates for the time-to-event endpoints. Overall survival may be reported starting from the date of diagnosis, the start date of neoadjuvant therapy, or the date of surgery. Under such conditions, how can one reach a consensus as to the validity of a biomarker? What is the decision as to a biomarker’s validity when the results of the analyses of two endpoints are contradictory?

Pocock et al. offered, as a possibility, the selection of a single primary endpoint for formal statistical inference, adjusting the analysis of each endpoint for multiple testing and deriving an appropriate global test, considering that the endpoints are possibly biologically related and positively correlated [21]. Several approaches have been proposed in the literature to create a univariate outcome by combining multiple clinical endpoints [22–25]. A possible issue of composite endpoints is the fact that often they are not of equal clinical importance. Consequently, simple composite metrics such as overall rates and averages that, by definition, give equal weight to each component may not mirror clinical behavior. Weighted measures can be used, but the weighting function must be appropriately accounted for in the calculation of standard errors and such that it accurately determines significance levels. A very intuitive approach to the multiple-endpoint problem for the comparison of two samples was suggested by Buyse [26]. His idea is to compare the two samples based on the endpoint of highest priority first, and if—and only if—no winner can be determined with respect to this endpoint, would one move to the endpoint of the next highest priority. This very instinctive algorithmic approach would continue until either a winner were declared or all candidate endpoints were considered. Rauch et al. gave a thorough treatment of the pros and cons of using prioritization in confirmatory studies to contend with the existence of multiple clinical endpoints of interest [27].

A possible issue of composite endpoints is the fact that often they are not of equal clinical importance. Consequently, simple composite metrics such as overall rates and averages that, by definition, give equal weight to each component may not mirror clinical behavior.

A composite endpoint should be clinically relevant and merge individual endpoints coherently. Rather than investigate several endpoints, such as overall survival, time to progression, time to toxicity, and time to treatment discontinuation, a primary analysis of one composite endpoint such as event-free survival (EFS) may be reasonable. Cheson et al. suggested defining EFS as the time from study entry to any treatment failure, including disease progression, or discontinuation of treatment for any reason (e.g., disease progression, toxicity, patient preference, initiation of new treatment without documented progression, or death) [28]. Psyrri et al. evaluated the correlation between tissue biomarker expression (measured by automated quantitative protein analysis) and clinical outcome for an Eastern Cooperative Oncology Group phase II trial of induction chemotherapy with weekly cetuximab, paclitaxel, and carboplatin followed by chemoradiation with the same regimen in patients with operable stage III/IV head and neck squamous cell carcinoma. The authors of this study chose EFS as the primary endpoint; however, they also report overall and progression-free survival. This study is a prime example of a mixed message because overall and progression-free survival are statistically significant for extracellular signal-regulated kinase (ERK) status (high vs. low); however, ERK status is not significant for EFS. Retinoblastoma protein status (high vs. low) is significant for EFS but not for overall and progression-free survival [29]. It is imperative that we do not overtest. We must decide on an endpoint and accept the findings based on said endpoint if we ever expect to achieve reproducibility and consistency in research.

Selection Bias

The typical study design in molecular epidemiology is case control for reasons of feasibility, that is, retrospective data tend to be more readily available. However, there are inherent limitations of cross-sectional data collected retrospectively in such approaches. In particular, the assignment of causality generally eludes observational studies. As Spivack et al. indicated, a note of caution should be sounded in examining the correlations noted by analyses of retrospective observational data [30]. As the list of genes studied during the biomarker-discovery phase grows, the need to validate their prognostic and predictive power intensifies. The greatest potential to validate these biomarkers may lie in retrospective studies due to the wealth of data that exist. The time required to conduct a time-to-event study with an endpoint such as progression-free or overall survival is greatly reduced for retrospective trials compared with prospective trials. However, as researchers identify biomarker strata (e.g., normal vs. overexpressed), these strata may not be homogeneous with respect to other potential predictors of clinical outcome. It may not be fair to call this problem “selection bias,” but it is bias and the same techniques that are used to address selection bias must be applied to the biomarker validation process.

The fact that other predictors of clinical benefit are most likely not to be balanced between the levels of the biomarker strata represents a huge inferential problem. Such confounding limits the researcher’s ability to comfortably determine the prognostic and predictive power of individual biomarkers. Using a multivariate model to address this issue is common. For example, the literature is full of proportional hazards regressions used to compare the impact of biomarker status on survival endpoints that are adjusted for age, stage, treatment, and so forth. But these models only attempt to assess the biomarker’s impact by simultaneously adjusting for the other known predictors of survival. Care must be taken such that adjustment is made only for covariates that are related to both the biomarker level and the outcome of interest so that the relationship of biomarker expression and any of the covariates is not driven by the biological process. If the relationship is not just chance selection but in fact the model controls for what are known as “intermediate variables,” the effect of biomarker expression on the outcome will be underestimated. Assume, for example, that clinical benefit is being measured by overall survival and we have measured both age at diagnosis and biomarker expression level (normal vs. overexpressed). If the age distribution is not homogeneous between the two levels of biomarker expression, this could lead to inaccurate findings. One might adjust a proportional hazards model for age; however, the assumption is that there is no natural association between the age of the patient and the expression level, that is, the observed imbalance was just chance. Now consider a similar scenario, only instead of age, the researcher measures tumor stage. Further assume that as stage increases, so does expression level, not just by chance but as a natural relationship. By adjusting the model for stage, the impact of expression level of the biomarker may be completely masked. Consequently, using forms of linear models to account for confounding is not a perfect solution.

Matched samples are a possible solution to selection bias or confounding. The first step is to identify the important factors on which to match (i.e., the factors that need to be balanced). The same care taken to identify linear-model covariates should be given to the matching process to avoid what is known as “overmatching,” which causes bias. What is known as “hard matching” finds pairs of individuals in each strata of biomarker expression that match (or nearly match) on each of the factors to be balanced. Propensity score matching can also be used to attempt to produce balanced samples between the overexpressed and normal-level biomarker groups. Austin provides a comprehensive introduction to using propensity score methods to reduce the effects of confounding in observational studies and provides a strategy for assessing covariate balance postmatching [31]. Use of a quasi-experimental design such as propensity score matching allows the researcher to mimic the characteristics of a randomized controlled trial, which is the gold standard for estimating factor effects. As Austin discusses, matched samples require the researcher to use statistical methodologies that are relevant to dependent samples [31]. A concern among researchers is the loss of data. Not all subjects from the overexpressed-biomarker group will have a suitable match in the normal-level biomarker group and vice versa, thus these unmatched individuals would be excluded from the analysis. Another method to address imbalance between the normal-level and overexpressed biomarker groups is to use the inverse of the propensity score to weight each observation in the overexpressed group and 1 minus the inverse of the propensity score (i.e., the propensity of not being in the overexpressed group) in the normal group. Using weighting allows the researcher to include all of the data and does not depend on random sampling, thus providing for reproducibility while controlling for confounding [32].

Janin et al. investigated whether serum 2-hydroxyglutarate would predict the presence of IDH1/2 mutations at diagnosis and provide a marker of minimal residual disease for acute myeloid leukemia patients. Their study concludes that a significant difference in overall survival exists between patients with and without NPM1 mutations among 53 patients with acute myeloid leukemia with IDH mutations [33]. However, patient characteristics such as age, sex, white blood cell level, percentage of circulating blasts, and bone marrow blasts are not balanced between patients with and without NPM1 mutations. One cannot know whether the effect is real or an artifact of the confounders. Although the study methods discuss the use of a multivariate Cox model to determine significant predictors of survival, the multivariate model is focused on determining the significant predictors among the set of biomarkers (IDH1 R132, IDH2 R140Q, FLT3-ITD, and NPM1 mutations). Only age is accounted for in the analysis of the individual biomarkers and only when the non-age-adjusted comparison is significant. What if the imbalance is the reason the comparison is insignificant? Addressing the patient-characteristic imbalance between the two groups using inverse propensity score weighting or a multivariable-model approach would strengthen the analysis.

Conclusion

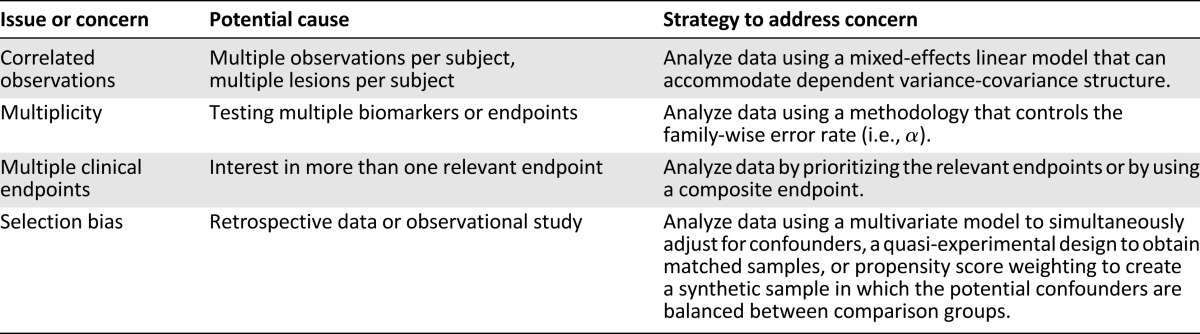
Major statistical issues present in biomarker validation are addressable. This article has attempted to discuss four major issues that are easy to manage with present-day statistical packages but are not always addressed in the literature. Table 1 summarizes these concerns. If multiple specimens are obtained from individual patients, the researcher must account for the intrapatient correlation that may be present. Only a minor reduction in power is experienced when using a model that accounts for intraclass correlation when no within-subject correlation is present. However, not accounting for intraclass correlation when it is present may greatly overestimate the significance of the findings. Regardless of whether the researcher chooses to control the family-wise error rate or the false discovery rate, some attempt to limit false discovery as part of the biomarker validation process is warranted. We should not “throw the baby out with the bathwater” by overzealously controlling false discovery to the point of limiting discovery and producing false negatives. Reproducibility depends on a reasonable approach to the issue of multiplicity. The literature is full of examples of biomarker validation studies with multiple endpoints, yet many ignore the problem. Addressing this issue is critical if we want the literature to be awash with reproducible findings. To address the issue of multiple endpoints in the process of biomarker validation, the researcher must (a) agree to adjust the comparisons for multiplicity, thus lowering the power of the study; (b) create a composite endpoint that fairly reflects clinical behavior; or (c) use an algorithm such as a prioritization that a priori clearly decides how a winner will be determined. Although randomized controlled trials are considered the gold standard approach for estimating factor effects, there is growing interest in using observational studies due to feasibility that manifests as cost savings in both time and money. Issues of covariate confounding must be addressed to ensure reproducibility. Although concerns are present in biomarker validation, most can be resolved with present statistical methodologies that are readily available through common analysis packages.

Table 1.

Potential biomarker validation study issues and strategies

Disclosures

The author indicated no financial relationships.