Abstract
We propose a principal stratification approach to assess causal effects in non-randomized longitudinal comparative effectiveness studies with a binary endpoint outcome and repeated measures of a continuous intermediate variable. Our method is an extension of the principal stratification approach by Lin et al. [10,11], originally proposed for a longitudinal randomized study to assess the treatment effect of a continuous outcome adjusting for the heterogeneity of a repeatedly measured binary intermediate variable. Our motivation for this work comes from a comparison of the effect of two glucose-lowering medications on a clinical cohort of patients with type 2 diabetes. Here we consider a causal inference problem assessing how well the two medications work relative to one another on two binary endpoint outcomes: cardiovascular disease related hospitalization and all-cause mortality. Clinically, these glucose-lowering medications can have differential effects on the intermediate outcome, glucose level over time. Ultimately we want to compare medication effects on the endpoint outcomes among individuals in the same glucose trajectory stratum while accounting for the heterogeneity in baseline covariates (i.e., to obtain “principal effects” on the endpoint outcomes). The proposed method involves a 3-step model estimation procedure. Step 1 identifies principal strata associated with the intermediate variable using hybrid growth mixture modeling analyses [13]. Step 2 obtains the stratum membership using the pseudoclass technique [17,18], and derives propensity scores for treatment assignment. Step 3 obtains the stratum-specific treatment effect on the endpoint outcome weighted by inverse propensity probabilities derived from Step 2.
Keywords: Causal inference, Comparative effectiveness studies, Growth mixture model, Principal stratification, Propensity score
1 Introduction
Conducting comparative effectiveness research is a way to investigate what treatment works for which patients under what circumstances [1]. Here we consider comparative effectiveness studies (CES’s) that aim at assessing whether treatment effects on the endpoint outcome differ due to the heterogeneity of an intermediate variable in a prospective longitudinal cohort derived from existing databases. Findings of such CES’s (e.g., outcome prediction models) can be integrated into future clinical practices to provide timely recommendation to each patient regarding the treatment that yields better clinical outcome(s) given the patient’s baseline covariates and the intermediate variable observed [2–4]. The motivating example of this paper arises from a longitudinal CES in a clinical cohort of patients with type 2 diabetes mellitus (T2DM) who received medical care in the Veteran Administration Health Care System (VAHCS) during FY1999–FY2006. In this clinical cohort, some of patients characteristics prior to the baseline (e.g., age and comorbidity) may affect the glucose-lowering medication prescribed as well as the outcomes of interest: cardiovascular diseases (CVD) and mortality. Further, glucose response (intermediate variable) may vary among patients within the same glucose-lowering medication group, which can potentially modify the medication effect on CVD and mortality. Our interest here is to assess the differential effects of two glucose-lowering medications on CVD and mortality (separately) conditioning on the intermediate glucose trajectory while accounting for heterogeneity in patients’ baseline characteristics. For a practical reason, the heterogeneity of longitudinal glucose pattern will be characterized in terms of glucose response strata (e.g., patients within the same stratum have clinically similar glucose levels over time [5]). In particular, the method proposed in this paper capitalizes on the fact that glucose levels are routinely collected in clinical practice for patients with T2DM, and this information can be useful for assessing patients’ intermediate medication response. Depending on patients’ intermediate medication response (i.e., glucose response), the treatment effect on CVD and mortality may vary. For example, suppose that one of the medication is more effective among those with greater insulin resistance (indicated by higher glycosylated hemoglobin A1c or HbA1c levels). Then there may exhibit greater differential medication effect on CVD in the stratum with higher HbA1c levels (see the analysis results in Section 3).
The methodological challenges for causal modeling of the longitudinal CES described above include the following. (I) Unlike a randomized controlled trial (RCT), the comparison groups in a non-randomized CES may not be compatible at the baseline, which can potentially confound the treatment-outcome association (e.g., in Table 3, age is associated with both medication prescription and the endpoint outcomes). Thus deriving causal inference for a non-randomized CES often requires adjusting for baseline differences between treatment groups. This adjustment for baseline differences requires (i) balancing the treatment groups based on complete covariates used for treatment assignment but not involving the outcome, and (ii) sufficient overlap between comparison groups on these key covariates [6]. (II) A CES like an RCT, there may exhibit heterogeneity in post-treatment intermediate variables (e.g., glucose response in our application example), which may alter the treatment effect on the outcome of interest [7–13]. The principal stratification (PST) technique has been developed to advance causal modeling by adjusting for post-treatment heterogeneity [8–13]. However, PST has mostly been applied to RCT’s, whereas treatment assignment in our example and many CES’s is nonrandom. To counter these complications and to enhance the credibility of causal inference drawn from CES’s, a simultaneous consideration of pre-treatment and post-treatment heterogeneity is necessary [2–4]. (III) An additional challenge in the longitudinal CES setting to be tackled here is that the intermediate variable is continuous and repeatedly measured. Characterizing principal strata associated with repeated measures of a continuous intermediate variable based on growth mixtures model (GMM) analyses appears to be promising in RCT’s [12,13]. However, much research is needed to understand when (conditions under which) GMM can be utilized in non-randomized studies to derive causally interpretable results.
Table 3.
GMM Analysis Results of the Application Example
| Estimation Procedu Reference Group |
3-step Hybrid RSG |
3-Step Hybrid SU+MET |
3-Step – |
|---|---|---|---|
| Poor Control Stratum (22%) | Estimate & 95% CI | ||
| Baseline HbA1c | 8.55 (8.42,8.68) | 8.41 (8.33,8.49) | 8.45 (8.30,8.60) |
| Post-treatment HbA1c | 8.60 (8.41,8.78) | 8.38 (8.25,8.50) | 8.49 (8.27,8.71) |
| RSG Effect on HbA1c | 0.36 (0.00,0.72) | 0.23 (−0.08,0.54) | −0.07 (−0.36,0.22) |
| RSG Effect on CVD (Odds Ratio) | 0.28 (0.09,0.83) | 0.35 (0.15,0.83) | 0.37 (0.16,0.85) |
| RSG Effect on Death (Odds Ratio) | 0.66 (0.28,1.51) | 0.70 (0.36,1.37) | 0.84 (0.44,1.61) |
| Better Control Stratum (78%) | Estimate & 95% CI | ||
| Baseline HbA1c | 7.23 (7.20,7.25) | 7.17 (7.14,7.19) | 7.18 (7.14,7.22) |
| Post-treatment HbA1c | 7.00 (6.96,7.03) | 6.95 (6.92,6.98) | 6.96 (6.92,7.01) |
| RSG Effect on HbA1c | 0.09 (0.01,0.16) | 0.09 (0.01,0.17) | 0.07 (−0.01,0.15) |
| RSG Effect on CVD (Odds Ratio) | 0.76 (0.55,1.06) | 0.77 (0.55,1.08) | 0.77 (0.55,1.07) |
| RSG Effect on Death (Odds Ratio) | 1.18 (0.88,1.57) | 1.19 (0.88,1.60) | 1.15 (0.86,1.56) |
This paper proposes a modeling framework that integrates GMM [14], PST [8,9], and propensity score (PSC) [2] techniques to assess causal effects for non-randomized longitudinal CES’s in the presence of imbalanced baseline covariates between treatment groups and heterogeneity in a repeatedly measured continuous intermediate variable M. Our method is drawn on the potential outcome framework, which allows an explicit specification of causal effects based on the outcome distribution under all treatment conditions [15,16]. In the context of PST, the (causal) treatment effect is drawn based on the difference in outcome Y under all possible treatment conditions within the same study subject conditioning on the potential outcomes of post-treatment intermediate variable(s) M [8,9].
Regarding PST analyses, we propose a modeling approach differing from that of Frangakis and Rubin [8,9]. In Frangakis and Rubin [8,9], the definition of each principal stratum is pre-specified based on the potential outcomes of M (e.g., there could exist up to four strata based on the combination of whether the value of M is above or below a pre-specified threshold under control vs. treatment condition). In contrast, we consider an exploratory PST approach similar to that of Lin et al. [10,11], where principal strata are determined jointly by the data, underlying distributional assumptions, and substantive knowledge. More specifically, our PST approach uses GMM to derive principal strata based on the likelihood of repeatedly measures of a continuous intermediate variable under plausible assumptions (see Section 2.4). GMM assumes that the study population originates from a finite number of distinct strata such that the repeatedly measured intermediate variable (under all treatment conditions) for individuals in each stratum follows a distinct multivariate normal distribution, while the means/covariance within each stratum can differ by treatment condition. These stratum membership in GMM however are not pre-defined nor observed, and they are derived by identifying statistically distinct strata while appropriate model constraints can be imposed to ensure substantive plausibility (e.g., restricting subjects of the same stratum to have the same baseline regardless of the treatment condition, or null treatment effect in certain strata). Under certain assumptions (see Section 2.4), the strata derived from the proposed GMM will meet the principal strata property.
There are several aspects that set this study apart from [10,11] and other related studies in terms of the study design, the type of data targeted in the analysis, and modeling approach. First, instead of using the latent class modeling technique by [10,11] which identifies principal strata based on repeated measures of a binary intermediate variable in an RCT, we employ a hybrid GMM technique [13] to identify principal strata based on repeated measures of a continuous intermediate variable in a CES (see Section 2). Second, regarding model estimation, under the randomization assumption of a RCT, Lin et al. [10,11] derived causal effects on a continuous outcome based on the joint likelihood of the potential outcomes of the intermediate variable and the observed endpoint outcome. In our case with a non-randomized CES, we employed a 3-step estimation procedure. Step 1: identify principal strata empirically based on GMM analyses. Step 2: achieve balance in baseline covariates among treatment groups within each stratum through pseudoclass [17,18] and propensity score techniques. Step 3: calculate causally interpretable stratum-specific treatment effects on the endpoint outcome using separate logistic regression analyses for each stratum, where the inverse stratum-specific propensity scores are incorporated as weights.
The organization of this paper follows: Section 2 describes the GMM approach of PST analyses, model assumptions and constraints required, and estimation procedure. Section 3 applies the proposed methods to a CES example involving treatments for type 2 diabetes. Section 4 summarizes the paper.
2 Method
2.1 Notation
We introduce a causal model for our problem in terms of potential outcomes terminology. Let Zi denote the treatment condition (e.g., prescribed medication in our application example) for individual i, where Zi = 1, ⋯, p. For each individual i, xi denotes the corresponding time-independent baseline covariates. Let Y be the generic binary endpoint outcome of interest. Denote Yi(*) = (Yi(1), …, Yi(p)) for the potential endpoint outcome of individual i under p distinct treatment conditions. If Y for individual i is observed under treatment condition Zi = a, we write . Similarly, denote Mi(*) = (Mi(1), ⋯, Mi(p)) for the potential outcome of the continuous intermediate variable measured repeatedly from individual i under p distinct treatment conditions. We write if M for individual i is observed under treatment condition Zi = a. Let Si denote the principal stratum membership of individual i, which depends on Mi(*), such as {Si = s : Mi(*) ∈ Ωs} with distinct and nonoverlapping subsets {Ωs : s = 1, ⋯, K}, or Mi(*) of each stratum arising from a different p.d.f. fs(m) and Pr(Mi(*) ∈ Ω|S = s) = ∫Ω fs(m)dm for any measurable set (also see Section 2.2 for details). In our setting (similar to that of our application example as described in Section 3), the first element of Mi(a), denoted by Mi1(a), measures the intermediate variable for individual i under treatment Zi = a during the time period between treatment assignment and the time point when treatment effect start to be revealed by M (e.g., it is approximately a 3-month time window in our application example), and the remaining elements of Mi(a) contain the measure(s) of the intermediate variable for individual i during the rest post-treatment follow-up period (e.g., our application example deals with the scenario with Mi(a) = (Mi1(a), Mi2(a)). Under this setting, the distribution of Mi1(a) is identical for all values of a among those in the same stratum. As discussed in Section 2.4, having Mi1(․) as described above is useful (although not necessary) for model identifiability under the GMM framework.
Our notations M and S correspond to the notations C (for repeated measures of compliance status) and U (for principal strata associated with compliance over time) in [11]. Throughout, we focus on situations where the treatment condition of each individual (or the realization of Zi) does not change during the study period (which holds in our application example). However, our proposed model allows Zi to be influenced by baseline covariates xi, including treatment(s) used prior to the baseline. Thus our method is suitable for assessing the effect of the current treatment conditioning on prior treatment history and intermediate response to the current treatment.
2.2 A Stratification Strategy
PST involves a categorization of study subjects in terms of their potential values of the post-treatment intermediate variable under all treatment conditions, {Mi(*) : i = 1, ⋯, n}. The main goal of PST analyses is to assess the differential treatment impact on the endpoint outcome Y across strata.
Typically, one characterizes principal stratum membership S in terms of {Si = s : Mi(*) ∈ Ωs} with distinct and nonoverlapping subsets {Ωs : s = 1, ⋯, K} (see [8,9]). Since Mi(*) is only known up to the observed in practice (i.e., if Zi = a), Si is identifiable up to a mixture of strata that contains . This stratification approach based on a pre-specified rule of the potential outcome Mi(*) is suitable for situations when there is sufficient information about {Ωs : s = 1, ⋯, K} with respect to Mi(*).
Strata Derived from Growth Mixture Modeling
For longitudinal studies with multiple measures of M yet with limited knowledge regarding the specification of {Ωs : s = 1, ⋯, K}, one may consider a more exploratory approach – GMM which characterizes principal strata in terms of a latent mixture distribution: Pr(Mi(*) ∈ Ω) = Σs ∫Ω fs(m|xi)π(s|xi)dm for any measurable set Ω (e.g., [12,13]), where π(s|xi) = Pr(S = s|xi) and s = 1, ⋯, K. The GMM approach assumes that the population arises from a finite mixture of distinct subpopulations, with each Mi(*) in stratum s following a distribution fs. In this framework, since the number of strata (say K and K < ∞) and the stratum distribution ({fs : s = 1, ⋯, K}) usually can not be completely pre-specified, they are estimated from the empirical data. It is possible to incorporate substantive knowledge into the GMM analysis to identify principal strata by imposing constraints on model parameters. For example, among individuals of the same stratum who receive the same treatment, it is sensible to restrict the mean of Mi1(zi) (M measured prior to the activation of a treatment) and the mean rate of change in M to be the same [12]. It is also sensible to restrict the mean of Mi1(zi) to be the same across all treatment groups in the same stratum [12].
In our application example shown in Section 3, we conducted PST analyses using the GMM approach to characterize the glucose control stratum membership based on {fs : s = 1, ⋯, K} derived from repeated measures of blood glucose level. The GMM approach characterizes an individual’s glucose control stratum membership through quantifying his or her likelihood of being ‘good” or “poor” control based on the observed glucose (e.g., HbA1c) levels over time (e.g., characterized by a growth curve). This probabilistic characterization of glucose control stratum membership based on GMM, compared to the cutpoint approach (e.g., a single measure of HbA1c < 7% vs. HbA1c ≥ 7%), seems to be more clinically sensible as explained below. The 7% cutpoint of HbA1c is known as the threshold associated with an increased risk of microvascular diseases. However, there is no clear HbA1c cutpoint identified for increased CVD risk. Also note that the relationship between HbA1c and complications is subject to variation (or departure from the mean association) across individuals [19]. Thus clinical decisions made based on the same cutpoint for all individuals is likely to be suboptimal. In addition, HbA1c levels vary over time making this a time-dependent variable. This temporal variation is not accounted for by the cutpoint approach. In contrast, GMM identifies distinct glucose response strata based on HbA1c trajectory over time, that is, it characterizes each individual’s glucose response in terms of the probability of glucose response stratum membership given the individual’s glucose measures. A recent study has shown that GMM analyses can be used to derive clinically meaningful glucose control strata based on repeated measures of HbA1c over time [5].
2.3 Model
Below we establish a causal modeling framework in the context of longitudinal CES with a repeatedly measured continuous intermediate variable M and a binary endpoint outcome Y. The goal is to assess the treatment effect on Y with a causal interpretation while accounting for heterogeneity in M over time and imbalance in baseline covariates between treatment groups. To this end, our proposed model integrates the PST, the latent variable mixture modeling (GMM), and propensity score techniques.
We use the GMM below to derive principal strata associated with M:
| (1) |
| (2) |
where esi ~ N(0, Σs), with being the vector of elements in , and π(Si = s|xi) = Pr(Si = s|xi). In (1), T denotes the time covariate matrix associated with M (e.g., T = [1, t] for linear growth trajectory with t being the vector of time points at with M is measured); is the matrix of covariate effects on growth factors in stratum s with row j elements of , denoted by , being the covariate effects on the jth growth factor; is the matrix of the treatment effects on growth factors in stratum s for subject i with , the element on row j and column a of , being the jth growth factor under treatment a for subject i; and di is the vector associated with treatment condition for subject i with the ath element being 1 and the rest elements being 0 when Zi = a. In (2), denotes the covariate effect on the log-odds of stratum s relative to the reference stratum s0. For some situations, may be sufficient to explain the variation of M due to X. Then it is appropriate to set like in our application example.
The propensity score model of the treatment received for a subject i given Si = s is assumed to follow a (binomial/multinomial) logistic regression model,
| (3) |
with for the covariate effect on the log-odds of Zi = a relative to Zi = a0 under stratum s, where a0 denotes the reference treatment group. Note that , the log-odds of Zi = a associated with xi, is independent of Si based on assumption (A3) as described in Section 2.4. Later in Section 4, we discuss the implication of allowing the log-odds of Zi = a to depend on both Si and xi.
Finally, the endpoint binary outcome variable Yi given Si = s is assumed to follow a logistic regression model,
| (4) |
with being the covariate effects on the log-odds of Y, and the ath element of , denoted by , being the log-odds of Y = 1 under treatment a.
The model for potential outcomes (Y (*), M(*)) described in (1), (2), and (4) above corresponds to the model for observed outcomes (Yobs, Mobs) as follows:
Thus the stratum-specific treatment effect on the log-odds of Y = 1 can be assessed by the estimate of () for a ≠ a′ and s = 1, ⋯, K.
2.4 Model Assumptions
Identifying causal effects under the potential outcome modeling framework is intimately related to the underlying assumptions, primarily regarding the unobserved counterfactual outcomes. Five default assumptions posited in this paper are listed below.
-
(A1)
Balanced Propensity Score for Treatment Assignment assumes [Zi|Si = s, xi] = [Zi|Si = s, ηsi], where ηsi = Pr(Zi|xi, Si).
-
(A2)
SUTVA or stable unit treatment value assumption, originally coined by Rubin [16], here in the context of PST analysis refers to the assumption that once we condition on Si and covariates xi, the potential outcomes Yi(*) of a study subject i is independent of the treatment assignment of any other study subject.
-
(A3)
Treatment Ignorability consists of two components: (i) conditional treatment ignorability assuming (Yi(*), Mi(*)) ⊥ Zi|Si, xi, and (ii) Si ⊥ Zi|xi.
-
(A4)
Conditional Mutual Ignorability assumes Yi(*) ⊥ Mi(*)|Si, xi, or conditional independence between Yi(*) and Mi(*) given covariates xi and stratum membership Si. This also implies [Yi(*)|Mi(*), xi] = [Yi(*)|Si, xi].
-
(A5)
Conditional normality assumes that Mi(*)|Si follows a multivariate normal distribution.
Remark. For the longitudinal CES considered herein, assumptions (A3)–(A5) are posited to ensure that the strata S′s identified by GMM analyses as described in Section 2.5 will meet the property of principal strata [9]. In particular, (A4) is posited to ensure unbiased estimation of the distribution of M(*) under the stepwise estimation procedure proposed in Section 2.5, where are not involved in parameter estimation associated with M. Therefore, assumptions (A1)–(A5) are sufficient for our proposed PST analyses of longitudinal CES.
Plausibility of Assumptions (A1)–(A5)
Assumption (A1) means that conditioning on Si, all the systematic variation associated with the assignment of Zi due to observed covariates xi is the same as that due to the propensity score ηsi. This assumption assures that propensity scores obtained are adequate to balance baseline covariates between treatment groups within each stratum [6,20,21]. It is more general than [Zi|xi] = [Zi|ηi] since besides xi, it also allows the propensity score to depend on Si – an inherent characteristic of an individual that is captured by the stratum membership associated with a post-treatment intermediate variable. Assumption (A1) is quite plausible in our application example because it was derived from existing databases containing adequate baseline covariates that predict treatment assignment as well as intermediate variable(s) for estimating Si.
Assumption (A2) could be quite reasonable in studies where for subjects within the same stratum, the treatment condition for one subject does not depend on the potential outcomes Yi(*) of any other subject in the same stratum. Should (A2) hold true, it implies the exchangeability among {Yi(*) : i = 1, ⋯, n} conditioning on Si and xi.
Assumption (A3) is plausible under RCT’s where the treatment condition of an individual i is independent of both the corresponding potential outcomes (Yi(*), Mi(*)) and Si given xi. The first component of (A3), conditional treatment ignorability assumption, (Yi(*), Mi(*)) ⊥ Zi|Si, xi, could be realistic in some observational studies where the treatment assignment depends on subjects’ potential intermediate response category Si rather than the actual value of the intermediate outcome. For example, in some clinical practices (such as the practices in the VA health Care System considered in our application example), physicians often take into account the uncertainty/variation when predicting patients’ potential intermediate response to the medication at the time of prescribing the medication. The second component of (A3), Si ⊥ Zi|xi, corresponds to the property of principal strata [9], which is not always plausible in observational studies. Nevertheless, as shown in our simulations (see Section 4), the violation of Si ⊥ Zi|xi appears to have a limited impact on the estimation of the principal effect.
Assumption (A4) is posited to ensure unbiased estimation of causal effects on Y in our stepwise estimation procedure for non-randomized CES’s (see Section 2.5). It is appropriate for situations where conditioning on stratum Si and covariates xi, the potential outcome Yi(*) is not affected by the actual values of potential outcome Mi(*). Instead, given xi, Yi(*) depends on Mi(*) only through Si. Under GMM analyses, this assumption can be met by imposing appropriate model constraints, e.g., by restricting the within-stratum variation of Mi(*) such that conditioning on x and S, Y is independent of the within-stratum variation of M.
Assumption (A5) is posited since the underlying parametric assumption of each mixture component of a GMM is pivotal for determining principal strata associated with the continuous M. That is, the validity of our exploratory method of principal stratification relies on the knowledge about the distribution of M in a homogeneous population (i.e., within a stratum). In our application example with M being the glucose measure HbA1c (%), it is appropriate to assume that M follows a mixture of (multivariate) normals in patients with T2DM as suggested in the prior literature [22,23]. Note that even though assuming (A5) is scientifically valid, the normality assumption can be violated in a fitted GMM that misspecifies the number of strata (such as being informed by residual diagnostics) [18]. In the context of PST analyses, misspecifying the number of strata in GMM can affect the estimation of principal strata and principal effects (see Scenarios III and IV in Section 4 and Tables 4 and 5.).
Table 4.
GMM Parameters for Simulated Data
| Scenario Assumption violation |
I - |
II (A4) |
III (A3) & (A5) |
IV (A3)–(A5) |
|
|---|---|---|---|---|---|
| β10 | 0.15 | 0.15 | 0.15 | 0.15 | |
| −0.15 | −0.15 | −0.15 | −0.15 | ||
| α1 | 0.00 | 0.30 | 0.00 | 0.30 | |
| β20 | 0.40 | 0.40 | 0.40 | 0.40 | |
| −0.20 | −0.20 | −0.20 | −0.20 | ||
| α2 | 0.00 | 0.80 | 0.00 | 0.80 | |
| N(7, .225) | N(7, .225) | 0.8 * N(7, .225) | 0.8 * N(7, .225) | ||
| 0.2 * N(6, .225) | 0.2 * N(6, .225) | ||||
| N(7, .225) | N(7, .225) | N(7, .225) | N(7, .225) | ||
| N(.1, .01) | N(.1, .01) | N(.1, .01) | N(.1, .01) | ||
| N(0, .01) | N(0, .01) | N(0, .01) | N(0, .01) | ||
| N(8, .225) | N(8, .225) | N(8, .225) | N(8, .225) | ||
| N(8, .225) | N(8, .225) | N(8, .225) | N(8, .225) | ||
| N(.2, .01) | N(.2, .01) | N(.2, .01) | N(.2, .01) | ||
| N(0, .01) | N(0, .01) | N(0, .01) | N(0, .01) | ||
Table 5.
Simulation Results: Biases and Coverage of Model Estimates
| Scenario Assumption Violation |
I - |
II (A4) |
III (A3) & (A5) |
IV (A3)–(A5) |
|
|---|---|---|---|---|---|
| β1z (s.e.) | 0.009 (0.049) | 0.004 (0.063) | −0.012 (0.029) | 0.008(0.027) | |
| coverage | 0.888 | 0.826 | 0.914 | 0.888 | |
| β2z (s.e.) | −0.014 (0.072) | −0.014 (0.073) | −0.040 (0.034) | −0.025 (0.038) | |
| coverage | 0.794 | 0.726 | 0.714 | 0.728 | |
| 0.016 | −0.014 | −0.222 | −0.233 | ||
| −0.007 | 0.006 | 0.077 | 0.080 | ||
| 0.003 | −0.002 | −0.074 | −0.075 | ||
| 0.006 | −0.008 | −0.066 | −0.071 | ||
| −0.005 | 0.006 | 0.008 | 0.011 | ||
| 0.005 | −0.006 | 0.006 | 0.007 | ||
| β1z | 0.005 (0.052) | 0.012 (0.055) | −0.005 (0.028) | −0.006 (0.047) | |
| coverage | 0.926 | 0.886 | 0.714 | 0.774 | |
| β2z | −0.030 (0.071) | −0.028 (0.079) | −0.043 (0.037) | −0.008 (0.057) | |
| coverage | 0.764 | 0.768 | 0.728 | 0.638 | |
| 0.007 | −0.004 | −0.210 | −0.220 | ||
| −0.002 | 0.001 | 0.070 | 0.074 | ||
| −0.001 | 0.002 | −0.071 | −0.072 | ||
| −0.002 | 0.0004 | −0.054 | −0.061 | ||
| 0.002 | −0.002 | 0.002 | 0.004 | ||
| −0.001 | 0.001 | 0.010 | 0.010 | ||
Compared to Assumptions in Lin et al. [11]
Assumption (A1) is not required in [11] due to the randomization study design. For CES’s, (A1) is needed to assure that the propensity score model for treatment group membership yields balancing scores to be adjusted for in the outcome model for deriving the stratum-specific causal effect (see Section 2.5).
Assumption (A2) is weaker than the SUTVA posited in [11] which assumes the same SUTVA as that in [16]. It seems more plausible in CES’s to assume that the non-interference of treatment assignment between study subjects holds within each stratum instead of across all study subjects.
Assumption (A3) is default in [11] due to the randomization study design. For CES’s, (A3) is assumed to assure that the stratum-specific treatment effect adjusting for the stratum-specific propensity scores is causally interpretable (see Section 2.5). Note that (A3) is not verifiable in either RCT or CES’s since the counterfactual outcomes are not observable.
Assumption (A4) is not required in [11] since the model estimation is derived based on PST analyses of the joint likelihood of () and (M1(*), ⋯, Mn(*)) (see equation (6) in [11]). We assume (A4) to ensure that the information contained in Y does not affect the estimation of S so that our stepwise estimation approach, which derives S based on the likelihood of (M1(*), ⋯, Mn(*)) (see Section 2.5), will result in consistent estimates of S.
Assumption (A5) is not relevant to the situation considered in [11] where principal strata were derived from binary intermediate outcomes using latent class model analyses.
Other Model Identifiability Assumptions (Optional)
Besides the assumptions (A1)–(A5) described above, additional data or further model constraints may be needed to identify stratum specific causal effects using our proposed GMM method.
For the longitudinal CES considered herein where there is a measure of the intermediate variable M at baseline (or during the time period between treatment assignment and the time point when treatment effect starts to be revealed by M), restricting this baseline across all treatment groups within the same stratum to have a common distribution (i.e., and for a ≠ a′ and s = 1, ⋯, K) is critical for the identification of principal strata. To see the rationale behind this, we note that principal stratum membership is considered as an inherent characteristic of study subjects [9]. Thus for subjects originating from the same principal stratum with similar covariates, at baseline, regardless of their treatment conditions, should share a common distribution (see [12]). On the other hand, if assessed at baseline of two individuals are significantly distinct, then they are likely to originate from different strata regardless of their treatment conditions. For situations like our application example as demonstrated in Section 3, where the baseline M′s are significantly distinct between different strata, for s ≠ s′ and a = 1, ⋯, p is usually sufficient to ensure strata identification.
In some situations, there may exist two distinct strata (say s and s′) with M at baseline having the same distribution (e.g., and for a ≠ a′ and s ≠ s′) but differing in other growth parameters (e.g., for some j > 1), then additional constraints on for j > 1 are needed for stratum identification. Three identifiability constraints inspired by the work of [7] are listed below.
-
(C1)
“Exclusion restriction in treatment effect on M” restricts the stratum-specific treatment effect on M to be the same across certain strata, where stratum-specific treatment effect is assessed by the treatment effect on the rate of change in M over time (i.e., the slope of M). That is to impose { : for certain s ∈ (1, ⋯, K)}, where denotes the slope associated with M under treatment a. A special case of (C1): {: for certain s ∈ (1, ⋯, K)}, would be reasonable for strata where the treatment effect on M is limited, such as “never responders” or “always responders” with respect toM under all treatment conditions (see Figure 6 of [12]). In the context of GMM, two distinct strata subject to (C1) are qualitatively different since the rate of change in M in each treatment group differs by strata (e.g., ). Thus their stratum-specific treatment effect on Y may differ even for stratum with .
-
(C2)
“Exclusion homogeneity in M” restricts the rate of change in M to be the same across strata under a subset of treatment conditions. That is to impose { : for some treatment a and {(s, ⋯, s′) ∈ (1, ⋯, K)}. Constraint (C2) differs from constraint (C1) in the sense that (C1) is a within-stratum constraint across treatment conditions, while (C2) is a between-stratum constraint for a certain treatment condition. Constraint (C2) would be reasonable for a treatment that has a similar effect on M across strata, such as the glucose-lowering effect of insulin at a given dose level.
-
(C3)
“Monotonicity in treatment effect on M” restricts the directionality of the treatment effect on M to be consistent across certain strata, but it allows the magnitude to differ across these strata. That is to impose {: for some (a, a′) and certain s ∈ {1, ⋯, K)}. This constraint limits the existence of strata such that the directionality of stratum-specific treatment effect on M to be the same across strata.
In general, model constraints posited to identify principal strata and causal effects should be scientifically plausible in the content area since they limit the choices of scientifically plausible strata. The main difference between (C1)–(C3) and those in [7] is that in our setup, the constraints do not involve Y.
2.5 Estimation
Under the randomization assumption (thus (A2) and (A3) hold), correct specification of the distribution and the number of strata associated with M (i.e., (A5) holds), and appropriate model identifiability constraints (if necessary), maximum likelihood estimates (MLE’s) of causal effects can be derived from the likelihood below:
| (5) |
However, since the randomization assumption is often violated in our CES setting, consequently, , and deriving model estimates based on (5) can result in biases (since even (A1)–(A5) hold, the imbalance in baseline covariates between treatment groups is not accounted for under (5)). As a remedy, we assume (A1)–(A5), and propose a 3-step estimation procedure as follows.
Step 1 derives principal strata based on (1) and (2) using the hybrid GMM approach by Jo et al. [13]. This hybrid GMM approach first conducts GMM analyses to identify distinct strata of M for individuals who receive the reference treatment, say Zi = zref. These distinct strata under the reference treatment condition are derived by computing MLE’s for the following likelihood:
| (6) |
where Sref denotes reference stratum membership, and Kref is the pre-specified number of reference strata in each GMM analysis with its optimal value being determined by model fit and substantive knowledge. Then the pseudoclass technique is used to obtain one pseudovalue of Sref for each individual in the reference treatment group. That is, for each subject i in the reference treatment group, the pseudo Sref membership, ŝref, is obtained by drawing a random sample from the multinomial distribution with probabilities {} (i.e., the estimated posterior probabilities of reference stratum membership from GMM analyses of the reference treatment group). To derive principal strata associated with Mi(*) based on Mobs and ŝref, we conduct subsequent GMM analyses of all treatment groups by deriving MLE’s from the following likelihood:
| (7) |
where the estimated ŝref is treated as the known Sref for the reference treatment group, Sref is missing-at-random in the non-reference treatment groups, and {P1, ⋯, PKref} is a partition of {1, ⋯, K} such that s ∈ Ph for sref = h for h = 1, ⋯, Kref (for example, Ph = {h} for h = 1, ⋯, K when Kref = K and S = Sref; or P1 = {1, 2} and P2 = {3, 4} correspond to Kref = 2, K = 4, Sref,i = 1 when Si = 1 or Si = 2, and Sref,i = 2 when Si = 3 or Si = 4). Under Assumptions (A3)–(A5) and the pseudoclass property [18], principal strata Si can be derived from the hybrid GMM analysis [13] by drawing a random sample from the multinomial distribution with probabilities {} (i.e., the estimated posterior probabilities of stratum membership).
In our GMM analyses, both Kref and K are pre-specified in each model estimation. The optimal Kref and K along with other model parameters are determined based on goodness-of-fit indices [24,25] and model diagnostics [18]. To ensure model identifiability given that each Mi(*) is observed only under the treatment received, certain constraints on model parameters may be required (see Section 2.5). The EM algorithm [26] implemented in the Mplus software [27] was used in this paper to carry out the ML-EM computation in Step 1. Under assumptions (A3)–(A5), the reference strata identified based on (6) will be coarse principal strata since they are distinct strata associated with M under the reference treatment condition. Then (7) incorporates the reference stratum membership (or coarse principal stratum membership) derived from (6) using the pseudoclass technique, the data from both treatment groups, and certain model constraints (as needed) to identify principal strata.
Step 2 calculates principal stratum specific propensity scores of treatment condition by modeling the log-odds of a treatment group membership relative to the reference treatment group membership as a linear function of baseline covariates x for each stratum (see (3)). In this step, each subject’s principal stratum membership is obtained using the pseudoclass technique [17,18] – for each subject i, the pseudostratum membership is obtained by drawing a random sample from the multinomial distribution with probabilities {} estimated from Step 1. Suppose that the distribution of Mi(*) is correctly specified. Then under (A1), the pseudostratum specific propensity score of treatment group membership will meet the balanced score criterion [6,20,21].
Step 3 conducts stratum specific logistic regression analyses based on (4) to assess the odds ratios of a binary endpoint outcome Y among the treatment groups while adjusting for stratum-specific propensity scores of treatment conditions. That is, for each s, the stratum-specific treatment effect is derived based on
| (8) |
Since we are interested in the treatment effect on Y in the population setting, propensity scores derived from Step 2 are incorporated as inverse probability weights (IPW) [2] in the estimation. However note that IPW can lead to instable estimates if there exist propensity scores that are very close to 0 or 1. In this case, propensity score matching is recommended, and the resulting causal effects are limited to those matching pairs.
Finally, according to the pseudoclass theory [18], hypothesis tests are derived based on an average of multiple independent repetitions of Steps 2 and 3 (100 repetitions was used throughout this paper): final estimates and standard errors being the averaged estimates and the square root of averaged variances from all repetitions. Under (A1)–(A5), the derived stratum specific IPW estimate of treatment effect is unbiased and causally interpretable. GMM validation is assessed by Akaike information criterion (AIC) [24], Bayesian information criterion (BIC) [25]), and residual diagnostics [18].
Table 1 below summarizes the 3-step estimation procedure described above, and an alternative 3-step estimation procedure. The only difference between the two procedures is in Step 1, where two different GMM approaches, [12] vs. [13], are used to derive principal strata. A comparison of these two procedures is demonstrated in the application example below.
Table 1.
GMM Analyses and Causal Effect Estimation
| Assumptions | Estimating Likelihood | Estimating Procedure |
|---|---|---|
| (A1)–(A5) | (1) & (2) | Step 1: Jo, Wang, Ialongo (2009) hybrid GMM |
| (3) | Step 2: stratum-specific propensity score | |
| (4) | Step 3: IPW logistic regression | |
| (A1)–(A5) | (1) & (2) | Step 1: Muthén and Brown (2009) GMM |
| (3) | Step 2: stratum-specific propensity score | |
| (4) | Step 3: IPW logistic regression | |
3 Application Example
The efficacy findings of rosiglitazone (RSG) on cardiovascular risk or mortality in T2DM assessed by randomized control trials have not been consistent [28]. As RSG was commonly used as an add-on oral glucose-lowering agent in clinical practices at the VAHCS, the objective of our analyses was to compare the effectiveness of RSG as an add-on oral agent to sulfonylureas plus metformin combination (RSG+SU+MET) relative to that of sulfonylureas plus metformin combination (SU+MET) conditioning on HbA1c trajectory strata using a VAHCS cohort during October 1, 2002 and May 31, 2006. Our primary outcomes were CVD related hospitalization and mortality, both being binary with 1 denoted for event occurrence and 0 for no event. The study cohort was limited to a well representative random sample of veterans who participated in the VA Large Health Survey (LHS) conducted in 1999 since LHS is the only VAHCS data source that contains diabetes duration, a potential predictor for both glucose-lowering medication prescribed and CVD outcome. Then using the inpatient and outpatient records in the VAHCS databases, we identified patients who had at least one primary care visit as well as a diagnosis of T2DM (ICD-9 code = 250.00 or 250.02) each year during FY1999–FY2000. We excluded patients who were not eligible for RSG use due to safety or tolerability concern (i.e., those who had previously diagnosed for CVD, liver or renal diseases). Those who had been prescribed insulin or pioglitazone during the study period were also excluded. To obtain a reliable measure (indicator) of newly use of SU+MET, we required each study subject to have had SU or MET as the mono class of glucose-lowering medication prior to SU+MET starting. Furthermore, to make sure an accurate measure of the CVD related hospitalization event during the study period, we required each patient to have had at least one outpatient visit to the VAHCS primary care clinics each year during the study period. The study cohort was comprised of 4,442 individuals who had prescription(s) of SU+MET combination for ≥ 90 days, among whom 830 had RSG for ≥ 90 days as an add-on to (SU+MET). The cutpoint of 90-day exposure was chosen to make sure that patients in each group have had sufficient exposure to the respective glucose-lowering medication.
The intermediate variable in this study was the HbA1c level. For each patient, two HbA1c measures were used in the analyses: the mean HbA1c within 90-days since the medication prescription as well as the accumulated mean during the remaining study period (due to limited measures of HbA1c in each patient during the post-treatment study period). Covariates adjusted for in the analyses included patients age, diabetes duration at the baseline, age-adjusted Charlson co-morbidity score, and race/ethnicity.
Verification of Model Assumptions
Assumption (A1) balanced propensity score for treatment assignment is plausible in this study using the well-validated VAHCS databases that contain critical baseline covariates for predicting treatment assignment as well as intermediate variable(s) for estimating Si. The first component of (A3) conditional treatment ignorability assumption would be plausible under no unmeasured confounding. In this study the glucose-lowering medication Zi chosen by the physician was typically based on VA clinical practice guideline regarding the recommendation for glucose-lowering medication [29] – the guideline recommended medication prescription based on patients’ baseline characteristics xi in terms of medication safety, tolerability, and efficacy. Since all study subjects met the safety and tolerability criteria, the primary factors (pertaining to efficacy) that could influence medication choice were patients’ demographics, previous medical history, and potential glucose-lowering response to the medication (i.e., Si), which were all adjusted for in our analyses. Although in diabetes research, patients’ behavioral factors (e.g., lifestyle and self-glucose monitoring) could be potential confounders, these factors that were available in the VA databases were found not to be significantly associated with the outcomes. Also note that in the general health care facilities, physicians experience and preference on treatment are more variable than those in the VA system, and they could be potential confounders to be adjusted for. The extent to which the departure from the first component of (A3) may affect model estimation is shown in our simulations under Scenarios III and IV (see Section 4). It is reasonable to assume that the potential glucose response to the medication is perceived by physicians as a categorical variable Si (instead of the actual glucose value). This is because that glucose measure HbA1c is subject to intra-assay, inter-assay [30], and seasonal variation [31]. Thus patients with glucose response falling within a similar range are more likely to be stratified into the same category and share similar clinical decision (e.g., prescription). The second component of (A3), Si ⊥ Zi|xi, may not be plausible in this observational study. Nevertheless, our simulation results in Section 4 suggest that departure from Si ⊥ Zi|xi seems to have limited impact on model estimation. Assumption (A2) conditional SUTVA could be quite reasonable in this study since the VAHCS promotes patient-centered care and evidence-based medicine, and therefore for patients within the same glucose-response stratum, the glucose-lowering medication Zi chosen by the physician for patient i should not be driven by the potential glucose levels or CVD outcome from any other patient in the same stratum. Assumption (A4) conditional mutual ignorability (or Yi(*) ⊥ Mi(*)|Si, xi) should be plausible for our situation here since each glucose response stratum identified by GMM is clinically sensible with appropriately bounded HbA1c and thus similar CVD/mortality outcomes (see Table 3). The normality assumption (A5) is plausible according to prior studies [22,23].
Estimation
In our primary analyses, Step 1 derived principal strata associated with the two repeated measures of HbA1c using a hybrid GMM approach [13]. We first explored the HbA1c strata under each treatment group using separate GMM [14] based on (6), which suggested two strata with two distinct baseline HbA1c under each treatment condition. The stratum-specific distribution of HbA1c at baseline is similar between the two treatment groups, which suggests K = Kref = 2. Then according to (A3), we derived HbA1c strata using both treatment groups jointly based on a GMM, where within each stratum, the intercepts for the two treatment groups are restricted to be the same but the slope can vary by treatment (this constraint also limits K = Kref = 2). As shown in columns 2–3 in Table 3, the estimated principal strata were robust to the choice of the reference treatment group in the hybrid GMM analyses of HbA1c trajectories. The purpose of conducting hybrid GMM analyses is to strike a balance between the empirical fit to the data and obtaining S that permits a causal interpretable GMM. Model fit of GMM was assessed by AIC [24], BIC [25], and residual diagnostics [18]. Under (A3)–(A5), these HbA1c strata derived from GMM are principal strata associated with HbA1c.
In Step 2, we first obtained the HbA1c stratum membership for each individual using the pseudoclass technique [17,18]. That is, we drew a random sample from the binomial distribution with probabilities equal to the posterior probabilities of stratum membership conditioned on each individual HbA1c values (i.e., {}). Then the stratum-specific propensity score of each treatment condition was derived by modeling the log-odds of receiving (SU+MET+RSG) vs. (SU+MET) as a linear function of baseline covariates x (including age, mean HbA1c prior to the medication prescription date, race/ethnicity, duration of T2DM, and comorbidity) for each stratum.
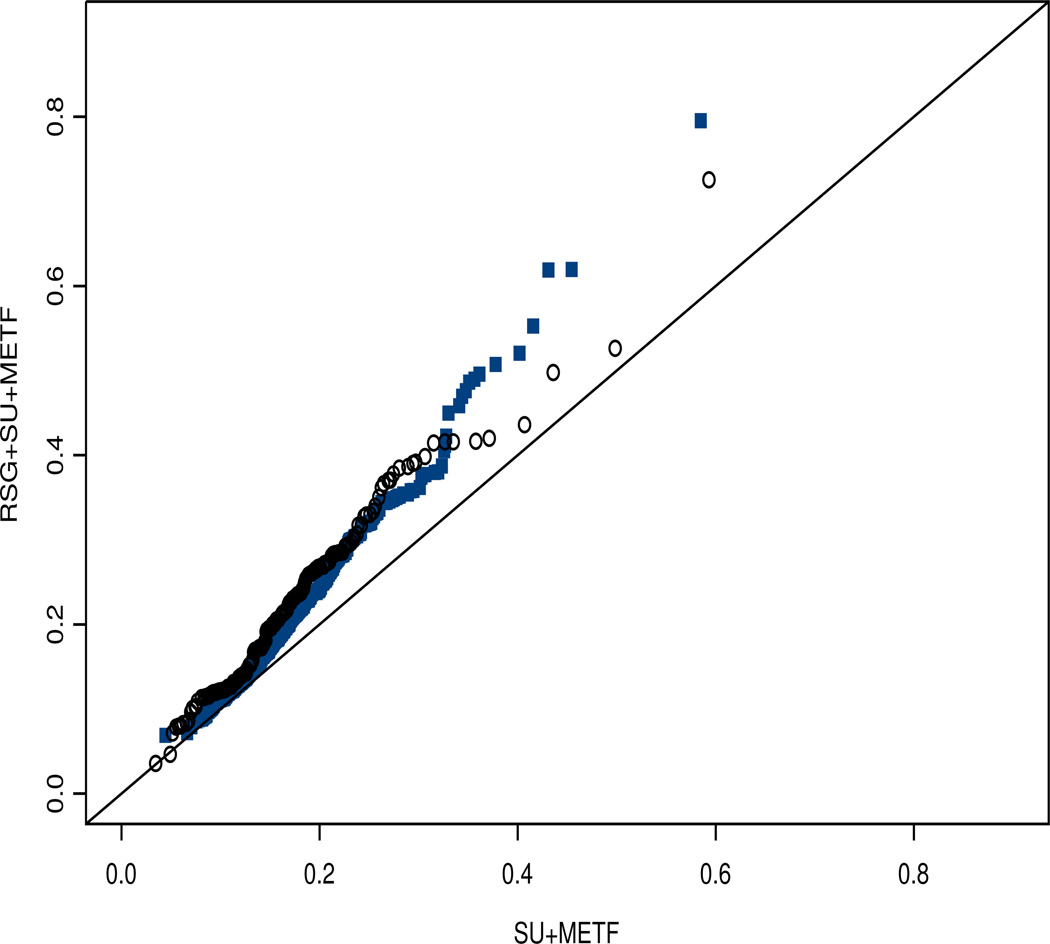
Step 3 calculated the odds ratios of a CVD (or mortality) event between the treatment groups for each stratum while adjusting for stratum-specific propensity scores of treatment conditions. The stratum membership obtained from Step 2 was used here. The stratum-specific propensity scores obtained from Step 2 were incorporated as inverse probability weights (or the reciprocal of the propensity scores were specified as the weights) in the logistic regression analysis based on (4). As shown in Figure 2, the IPW estimates are appropriate here since no extreme propensity score was found in the study.
Finally, following [18], we conducted model estimation and hypothesis testing of the RSG effect on CVD and mortality based on the average of the estimates and variances from 100 independent repetitions (pseudoclass draws) of Step 2 and Step 3: final estimates and the associated variances being the average of the estimates and variances from each repetition.
Result
The Step 1 hybrid GMM analyses, with the (SU+MET+RSG) group being the reference group, identified two HbA1c strata: poorer glycemic control stratum (22%) with means of HbA1c at baseline and post-treatment period being (8.55, 8.60) for the (SU+MET) group and (8.55, 8.96) for the (SU+MET+RSG) group, and better glycemic control stratum (78%) with means of HbA1c (7.23, 7.00) for the (SU+MET) group and (7.23, 7.09) for the (SU+MET+RSG) group. These glucose response strata identified by GMM appear to be clinically sensible: (i) the stratum with higher HbA1c levels is subject to greater variability compared to the stratum with lower HbA1c levels [30]; (ii) the stratum with lower HbA1c levels is clinically homogeneous; and (iii) the stratum with higher HbA1c levels could be subject to clinical heterogeneity, but the data was not powered to detect it statistically. Patient characteristics by the combination of medication group and glucose stratum membership are summarized in Table 2.
Table 2.
Descriptive Statistics (Means/Standard Deviation or %) by Medication Group and Glycemic Control Stratum in the Application Example
| Poorer Control (22%) | SU+METF | RSG+SU+METF |
| Baseline | ||
| Age | 56.76 (9.96) | 57.16 (9.04) |
| Black | 24.18% | 20.79% |
| Hispanic | 13.02% | 10.41% |
| Baseline HbA1c | 8.80 (1.20) | 9.11 (1.52) |
| Duration of diabetes > 10 years | 12.79% | 12.92% |
| Comorbidity Score | 3.09 (1.74) | 3.07 (1.33) |
| Endpoint Outcome | ||
| CVD | 3.02% | 0.56% |
| Mortality | 2.09% | 2.81% |
| Better Control (78%) | SU+METF | RSG+SU+METF |
| Baseline | ||
| Age | 64.38 (9.62) | 63.44 (9.35) |
| Black | 13.17% | 9.20% |
| Hispanic | 8.89% | 10.89% |
| Baseline HbA1c | 7.19 (0.73) | 7.46 (0.83) |
| Duration of diabetes > 10 years | 19.14% | 21.93% |
| Comorbidity Score | 4.05 (1.38) | 4.02 (1.66) |
| Endpoint Outcome | ||
| CVD | 2.29% | 1.84% |
| Mortality | 2.58% | 2.91% |
Then the result of repeating Steps 2 and 3 showed that the odds ratio (OR) of CVD was 0.28 for the (SU+MET+RSG) group vs. the (SU+MET) group with a 95% confidence interval (CI) equal to (0.09, 0.83) in the poorer glucose control stratum, while in the better control stratum the OR of CVD was 0.76 with a 95% CI equal to (0.55, 1.06). The above results suggested that if all assumptions hold true, RSG as an add-on to (SU+MET) could be associated with a reduced CVD-related hospitalization among those type 2 diabetics with poorer glycemic control overtime, while RSG was not associated with increased mortality in either glycemic control stratum (results shown in column 2 of Table 3). Similar results were found when the (SU+MET) group was used as the reference group in the Step 1 hybrid GMM analysis (see column 3 of Table 3).
Secondary Analyses
For the Step 1 analysis in this example, we have also considered the GMM approach in [12] to derive principal strata associated with HbA1c based on the likelihood of observed M from both treatment conditions (see column 4 of Table 3). This method resulted in similar HbA1c strata as those identified by the hybrid GMM approach [13]. The necessary and sufficient conditions under which the two GMM approaches lead to the same result remains a topic for further research. For this application example, we believe that assumption (A4) and the robustness of the choice of reference treatment group in the hybrid GMM analyses could be the key.
Interpretation
Using a rigorous causal modeling approach, we found that RSG use in this VAHCS cohort not to be associated with an increased CVD risk as reported in previous studies. This result could be explained by that (i) the study cohort was restricted to those who met the drug tolerability and safety criteria; and (ii) the VAHCS has adopted a more restricted guideline regarding RSG use compared with that used in the other health care systems [32] which appears to be consistent with a recent announcement by the FDA regarding restricting RSG use [33]. The FDA guideline is more restrictive than is the VAHCS guideline. In particular, with the adjustment of covariates, propensity score of treatment group, and glucose strata in our analyses, our result suggested that RSG as an add-on to (MET+SU) could reduce CVD hospitalization among individuals in the poorer glycemic control stratum. Since the RSG effect on HbA1c is not clinically significant in either stratum, its effect on CVD is likely to be through a pathway that is independent of its glucose-lowering effect as suggested in the literature [34]. Regarding the significant beneficial effect of RSG on reduced CVD among those with poorer glycemic control, it could be due to that the poorer glycemic control group tends to be more insulin resistant or obese, who, in theory, respond to RSG better compared to the better glycemic control group [35,36].
4 Simulations
4.1 Primary
To evaluate the performance of our proposed methods for applications similar to our example here, we have conducted simulations under various departures of model assumptions for non-randomized studies. We focused on assumptions (A3)–(A5) since they are not typical in the previously established causal modeling framework. We considered four scenarios, each with simulated data that reflect a different degree of departure from (A3)–(A5) while no violation of (A1) nor (A2). Scenario I assumes no violation of (A3)–(A5); Scenario II assumes violation of (A4); Scenario III assumes violation of the first component of (A3) and (A5); and Scenario IV assumes all violations in Scenarios II and III. To set up the violation of (A4) for Scenarios II and IV, we let the log-odds of Yi = 1 depend on the slope of Mi such that and , where denotes the slope of M for subject i with Si = s and Zi = a. To set up the violation of the first component of (A3) and (A5) for Scenarios III and IV, we let 20% of the control group in stratum 1 have the mean of baseline M that is one unit lower than the counterfactual M at baseline among those in the treatment group (for example, this 20% subset could represent individuals who are motivated under the control condition; see columns 4–5 of Table 4). In terms of the treatment assignment in each stratum, we first derived the distribution of xi based on the baseline comorbidity scores seen in our application example, and then the propensity score for the treatment group of each subject was derived under Si ⊥ Zi|xi (the second component of (A3) holds) for each Scenario such that log(Pr(Zi = 2|xi, Si = 1)/Pr(Zi = 1|xi, Si = 1)) = log(Pr(Zi = 2|xi, Si = 2)/Pr(Zi = 1|xi, Si = 2)) = 0.5 * xi.
We then considered the possibility of departure from Si ⊥ Zi|xi separately since it is the key property of principal strata [9], but not warrant by GMM analyses under CES’s. To assess the impact due to violation of Si ⊥ Zi|xi, we considered situations allowing Pr(Zi = a|Si = s, xi) ≠ Pr(Zi = a|Si = s′, xi) in conjunction with Scenarios I–IV, where Pr(Zi = a|Si = s, xi) ≠ Pr(Zi = a|Si = s′, xi) was constructed by assuming log(Pr(Zi = 2|xi, Si = 1)/Pr(Zi = 1|xi, Si = 1)) = 0.5 * xi and log(Pr(Zi = 2|xi, Si = 2)/Pr(Zi = 1|xi, Si = 2)) = xi.
In our simulated data, we set n = 1000 in each dataset and n = 500 for each stratum. The model parameters that generated M and Y are given in Table 4. These true model parameter values were chosen such that they are comparable to the model estimates in the application example. Once we obtained within each stratum based on the propensity score model for the treatment group, the intermediate and endpoint outcome variables were then generated based on
where s = 1, 2, αs = 0 under Yi(*) ⊥ Mi(*)|Si, xi (Scenarios I and II), and αs = 0.3 under the violation of Yi(*) ⊥ Mi(*)|Si, xi (Scenarios III and IV). Our simulation results were derived based on 500 independent simulated datasets using the estimation procedure as described in Section 2.5. Table 5 presents the simulation results: the top panel was derived based on GMM’s assuming Si ⊥ Zi|xi, and the bottom panel was derived based on GMM without the constraint Si ⊥ Zi|xi. We conclude our simulations below.
Under no violation of model assumptions (i.e., Scenario I in conjunction with Si ⊥ Zi|xi), the biases associated with treatment effect (relative to the standard errors) on the endpoint outcome Y or the trajectory parameters of M are negligible as expected. The coverage associated with treatment effects on Y fall between (0.794,0.888). These results are similar to those when only Si ⊥ Zi|xi is violated – the coverage associated with treatment effects on Y fall between (0.764,0.926). Since the model that generated the simulated data was comparable to the model estimates from the application example, the results under Scenario I imply that under no violation of model assumptions, for studies with cohorts similar to that in our application example, our proposed method is expected to find consistent estimates for principal strata and principal effects with the coverage of true principal effects similar to those shown in column 2 of Table 5.
Under the violation of (A4) (i.e., Scenario II), regardless whether Si ⊥ Zi|xi is violated, the biases associated with treatment effects on the endpoint outcome Y or the trajectory parameters of M seem negligible. Also, the coverage of the treatment effects on Y is slightly inferior to that under Scenario I.
Under the violation of model assumptions (A3) and (A5) (i.e., Scenarios III and IV), there are substantial biases associated with trajectory parameters of M. Compared to Scenarios I and II, although the biases associated with treatment effects on the endpoint outcome Y remain negligible, the coverage of treatment effects on Y is generally reduced. Despite the biases associated with the trajectory parameters of M, the biases associated with treatment effects on the endpoint outcome Y are limited. This could be explained by (i) while Y is correlated with M via its slope conditioned on the stratum, this association is the same for all the control group in stratum 1, regardless whether (A3) and (A5) are violated; and (ii) compared to the rest of the control group in stratum 1, the 20% of the control group in stratum 1 who violate (A3) and (A5) their M′s are more distant from M′s of subjects in stratum 2, and hence the impact on estimating the distribution of Y due to biased estimation of M (or misstratification) is limited. Note that under Scenarios III and IV, the number of principal strata in the fitted GMM is misspecified: the true model assumes K = 3, while the fitted GMM assumes K = 2. Thus these simulation results can also be interpreted as the impacts of misspecification of K on the estimation of trajectory strata and treatment effects on the outcomes.
4.2 Secondary
The simulation results above suggest that our stepwise estimation procedure proposed in Section 2.5 yields robust principal effects regardless the biases associated with estimating the distribution of M under various departure from (A3)–(A5). To further evaluate the robustness of our proposed stepwise estimation procedure for PST analyses, we examined the asymptotic correlations among parameter estimates associated with M (e.g., θ̂s’s) and those associated with Y (e.g., β̂s’s). We expanded our investigation of Scenario II above under each of the following study designs: six repeated measures of M with n = 200 and n = 1000, and two repeated measures of M with n = 200, where model parameters associated with M are the same as those shown in column 2 of Table 4, while the model associated with Y assumes: ; and . It shows that under (II-a)–(II-c) the asymptotic correlations between θ̂s’s and β̂s’s fall in (−0.04,0.05), and their asymptotic 95% confidence intervals, derived either empirically from 500 simulations or based on Fisher’s Z-transformation [37], all contain 0 – these small correlations among model estimates imply the nearly orthogonality between parameter estimates associated with M (θ̂s’s) and those associated with Y (β̂s’s). In contrast, under (II-d), the asymptotic correlations between θ̂s’s and β̂s’s fall in (−0.27,0.33), and the asymptotic 95% confidence intervals of some correlations do not contain 0 (imply non-negligible correlations between parameters of M and parameters of Y). These results suggest that deriving principal strata based on M(*) only (instead of (Yobs, M(*)) jointly) under the GMM framework may have limited impact on the estimation of principal strata even when Y is correlated with M conditioning on S. Based on [38], one potential explanation for this phenomena could be that parameter estimates associated with M are “insensitive” to parameter estimates associated with Y when (i) the Fisher orthogonality holds between parameter estimates associated with Y and parameter estimates associated with M under a bounded association between Y and M (e.g., under (II-a)–(II-c)), or (ii) some “insensitivity” criterion similar to the equation (2) in [39] holds even in the absence of the Fisher orthogonality (e.g., (II-d) when the association between Y and M exceeds a certain threshold).
5 Summary
Longitudinal studies often contain rich data for principal stratification analyses, which yet requires complex modeling. This paper demonstrates that the GMM approach can be effective for identifying principal strata in longitudinal studies under scientifically plausible model assumptions and identifiability constraints. In particular, the GMM technique is integrated with both PST and PSC techniques to identify principal effect using a 3-step estimation procedure in the context of longitudinal CES. This integration is critical to warrant rigorous causal analyses since in the longitudinal CES setting, the treatment assignment often depends on baseline characteristics, and that the treatment effect may vary by the heterogeneity of the intermediate variable(s). The proposed causal model is applied to a longitudinal CES of T2DM.
Properly accounting for confounding has been a major focus in causal modeling research. Below we use two examples to demonstrate its importance in analyses of longitudinal CES. In contrast to the causal model proposed herein, GMM analyses of the application example based on a one-step estimation of the joint likelihood of () without propensity score adjustment (which is not appropriate for this non-randomized CES) found no significant RSG effect on CVD nor on mortality in either stratum (OR for CVD in the better control group was 0.90 with 95% CI = (0.45,1.81); OR for CVD in the poorer control group was 0.28 with 95% CI = (0.05,1.59); OR for mortality in the better control group was 1.31 with 95% CI = (0.73,2.39); OR for CVD in the poorer control group was 0.97 with 95% CI = (0.30,3.14)). This result differed from the 3-step GMM analysis results shown in Table 3. The discrepancy associated with the RSG effect on CVD found in these different analyses suggests the impact of conducting PST analyses ignoring the fact that the study was not randomized. We have also compared our results in Table 3 to a naive logistic regression analysis where covariates and HbA1c values were adjusted for as predictors. The logistic regression analyses showed that RSG was not significantly associated with CVD hospitalization (OR = 0.78, 95% CI = (0.39, 1.31)) nor mortality (OR = 1.19, 95% CI = (0.74, 1.90)). It was expected that the estimated OR’s associated with CVD and mortality derived from the naive logistic regression analyses would be closer to those in the better control stratum (78% of the sample) as shown in Table 3, while the confidence intervals were wider in the naive logistic regression analyses due to combining subjects from different HbA1c strata. The discrepancy in the RSG effects found above suggests the impact of ignoring strata (or a special case of misspecification of the number of strata) and the fact that the study was not randomized.
Note that our results are subject to plausibility of assumptions (A1)–(A5) which are not all verifiable with the data available to us. Our simulations shown in Section 4 suggests that the violation of (A3)–(A5) has a limited impact on the estimation of the treatment effect on the endpoint outcome. Further sensitivity analyses are needed to study the potential and limitation of the proposed method. For example, an approach that integrates the pseudoclass technique [18] and the technique in [39] can be considered for assessing the differential impact on misstratification, and biases in stratum-specific propensity scores and principal effects due to various departure from model assumption (A3). In particular, the violation of (A3) and (A5) can be due to misspecification of the number of strata in PST analyses using GMM. Therefore, it is critical to use more robust statistical procedures (e.g., BIC [42,43] and comprehensive residual diagnostics [18]) to identify the correct number of mixture components in GMM.
Besides assumptions (A1)–(A5), further model constraints or additional data are often needed to identify stratum specific causal effects. A rather challenging situation in PST analyses using GMM (although not seen in our application example described in Section 3) is when two different principal strata under the same treatment condition differs in the mean rate of change in M during the post-treatment follow-up period, but not M at baseline (e.g., two strata with the same baseline but different mean rates of change in M under each treatment condition). In this case, it is possible to identify principal strata and principal effects under additional model constraints. Three identifiability constraints inspired by [7] are described in Section 2.4.
For longitudinal CES’s with a continuous intermediate variable M measured repeatedly and a binary outcome, our proposed method is appropriate for assessing the heterogeneity of principal effects across strata, or whether the treatment effect on the endpoint outcome Y varies by the trajectory stratum of the intermediate variable M. In general, comparing principal effects across strata can be viewed as moderation analyses since it assesses the extent to which the treatment effect on the endpoint outcome varies by the intermediate response to the treatment. In certain situations, comparing these principal effects can lead to mediation analyses [40,41]. For example, if there are two strata where the mean trajectories of M for the control group are the same between the two strata, but the treatment effect on the slope of M differs between the two strata: one stratum with a null treatment effect on the slope of M, and the other with a non-null treatment effect. Suppose that the treatment effect on the endpoint outcome is mediated by the treatment effect on the slope of M. Then the indirect treatment effect (or the treatment effect on Y that is mediated by M) can be assessed by the difference in treatment effects on Y between these two strata, and the natural direct treatment effect on Y can be assessed by the treatment effect in the stratum with null treatment effect on the slope of M. In this type of mediation modeling, (A3) together with Yi(*) ⊥ Si(*)|xi is equivalent to the sequential ignorability assumption in the sense of [38], which is crucial for causal mediation analyses in the GMM framework proposed here.
Finally, while there exist two promising GMM approaches for PST analyses in Step 1 [12,13], it is not yet completely clear how they are connected to one another (e.g., the two approaches yield similar result in our application example as well as that in [13]. We should be able to gain more clarity on this subject by conducting sensitivity analyses to examine how different model assumptions/constraints affect the similarity or departure between the two GMM approaches.
Figure 1.
Q-Q plot of Propensity Scores for Receiving RSG+SU+MET: RSG+SU+MET Group vs. SU+MET Group (open circle: better glucose control stratum solid circle: poorer glucose control stratum)
Acknowledgments
Dr. Wang’s research is supported in part by K25-DK075092, R01-DA031698, and R21-CA161180. Dr. Jo’s research is supported in part by R01-DA031698, R01-MH086043, and R01-MH066319. Dr. Brown ’s research is supported in part by R01-MH040859. The authors thank Prevention Science Methodology Group for helpful comments, and Dr. Rick Downs for providing clinical insights regarding treating type 2 diabetes at Veterans Administration Health Care System.
Contributor Information
Chen-Pin Wang, Email: wangc3@uthscsa.edu, Department of Epidemiology and Biostatistics, University of Texas Health Science Center, San Antonio TX, 78229, USA.
Booil Jo, Email: booil@stanford.edu, Department of Psychiatry and Behavioral Sciences, Stanford University, Stanford CA 94305, USA.
C. Hendricks Brown, Email: hendricks.brown@northwestern.edu, Department of Psychiatry and Behavioral Sciences, Northwestern University, Chicago IL 60611, USA.
References
- 1.Institute of Medicine Committee on Comparative Effectiveness Research. On Initial National Priorities for Comparative Effectiveness Research. National Academy of Sciences Press. 2009 [Google Scholar]
- 2.Rosenbaum PR, Rubin DB. The causal role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- 3.Joffe MM, Colditz GA. Restriction as a method for reducing bias in the estimation of direct effects. Statistics in Medicine. 1998;17(19):2233–2249. doi: 10.1002/(sici)1097-0258(19981015)17:19<2233::aid-sim922>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 4.Achy-Brou AC, Frangakis CE, Griswold M. Estimating treatment effects of longitudinal designs using regression models on propensity scores. Biometrics. 2010;66(3):824–833. doi: 10.1111/j.1541-0420.2009.01334.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang CP, Hazuda H. Better Glycemic Control Is Associated With Maintenance of Lower-Extremity Function Over Time in Mexican American and European American Older Adults With Diabetes. Diabetes Care. 2011;34(2):268–273. doi: 10.2337/dc10-1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rubin DB. On the limitations of comparative effectiveness research. Statistics in Medicine. 2010;29(19):1991–1995. doi: 10.1002/sim.3960. [DOI] [PubMed] [Google Scholar]
- 7.Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91(434):444–455. [Google Scholar]
- 8.Frangakis CE, Rubin DB. Addressing complications of intention-to-treat analysis in the combined presence of all-or-none treatment-noncompliance and subsequent missing out-comes. Biometrika. 1999;86(2):365–379. [Google Scholar]
- 9.Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58(1):21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lin JY, Ten Have TR, Elliott MR. Longitudinal nested compliance class model in the presence of time-varying noncompliance. Journal of the American Statistical Association. 2008;103(482):462–473. [Google Scholar]
- 11.Lin JY, Ten Have TR, Elliott MR. Nested markov compliance class model in the presence of time-varying noncompliance. Biometrics. 2009;65(2):505–513. doi: 10.1111/j.1541-0420.2008.01113.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Muthén BO, Brown HC. Estimating drug effects in the presence of placebo response: Causal inference using growth mixture modeling. Statistics in Medicine. 2009;28(27):3363–3385. doi: 10.1002/sim.3721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jo B, Wang CP, Ialongo NS. Using latent outcome trajectory classes in causal inference. Statistics and Its Interface. 2009;2(4):403–412. doi: 10.4310/sii.2009.v2.n4.a2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Muthén BO, Brown CH, Masyn K, Jo B, Khoo ST, Yang CC, Wang CP, Kellam S, Carlin J, Liao J. General growth mixture modeling for randomized preventive interventions. Biostatistics. 2002;3(4):459–475. doi: 10.1093/biostatistics/3.4.459. [DOI] [PubMed] [Google Scholar]
- 15.Neyman J, Dabrowska DM, Speed TP. On the application of probability theory to agricultural experiments. Essay on principles. Section 9 translated in Statistical Science. 1990;5(4):465–472. [Google Scholar]
- 16.Rubin DB. Bayesian inference for causal effects: The role of randomization. Annals of Statistics. 1978;6(1):34–58. [Google Scholar]
- 17.Bandeen-Roche K, Miglioretti DL, Zeger SL, Rathouz PJ. Latent variable regression for multiple discrete outcomes. Journal of the American Statistical Association. 1997;92(440):1375–1386. [Google Scholar]
- 18.Wang CP, Brown CH, Bandeen-Roche K. Residual diagnostics for growth mixture models: Examining the impact of a preventive intervention on multiple trajectories of aggressive behavior. Journal of the American Statistical Association. 2005;100(471):1054–1076. [Google Scholar]
- 19.The Expert Committee on the Diagnosis and Classification of Diabetes Mellitus. Report of the Expert Committee on the Diagnosis and Classification of Diabetes Mellitus. Diabetes Care. 1997;20(7):1183–1197. doi: 10.2337/diacare.20.7.1183. [DOI] [PubMed] [Google Scholar]
- 20.Dawid AP. Conditional independence in statistical theory (with discussion) Journal of the Royal Statistical Society Series B. 1979;41(1):1–31. [Google Scholar]
- 21.Rubin DB. The design versus the analysis of observational studies for causal effects: Parallels with the design of randomized trials. Statistics in Medicine. 2007;26(1):20–36. doi: 10.1002/sim.2739. [DOI] [PubMed] [Google Scholar]
- 22.Tan MH, Baksi A, Krahulec B, Kubalski P, Stankiewicz A, Urquhart R, Edwards G, Johns D GLAL Study Group. Comparison of pioglitazone and gliclazide in sustaining glycemic control over 2 years in patients with type 2 diabetes. Diabetes Care. 2005;28(3):544–550. doi: 10.2337/diacare.28.3.544. [DOI] [PubMed] [Google Scholar]
- 23.UKPDS Group. UKPDS 33: Intensive blood glucose control with sulphonylureas or insulin compared with conventional treatment and risk of complications in patients with type 2 diabetes. Lancet. 1998;352(9131):837–853. [PubMed] [Google Scholar]
- 24.Akaike H. A new look at the statistical identification model. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
- 25.Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6(2):239–472. [Google Scholar]
- 26.Mclachlan GJ, Krishnan T. The EM algorithm and extensions. New York: Wiley; 1997. [Google Scholar]
- 27.Muthén LK, Muthén BO. Mplus user’s; guide. Los Angeles: Muthén & Muthén; 1998–2011. [Google Scholar]
- 28.Diamond GA, Bax L, Kaul S. Uncertain Effects of Rosiglitazone on the Risk for Myocardial Infarction and Cardiovascular Death. Annals of Internal Medicine. 2007;147(8):578–581. doi: 10.7326/0003-4819-147-8-200710160-00182. [DOI] [PubMed] [Google Scholar]
- 29. http://www.healthquality.va.gov/diabetes/DM2010-FUL-v4e.pdf.
- 30.Schwartz KL, Monsur JC, Bartoces MG, West PA, Neale AV. Correlation of same-visit HbA1c test with laboratory-based measurements: A MetroNet study. BioMed Central Family Practice. 2005;6:28. doi: 10.1186/1471-2296-6-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tseng CL, Brimacombe M, Xie M, Rajan M, Wang H, Kolassa J, Crystal S, Chen TC, Pogach L, Safford MM. Seasonal patterns in monthly hemoglobin A1c values. American Journal of Epidemiology. 2005;161(6):565–574. doi: 10.1093/aje/kwi071. [DOI] [PubMed] [Google Scholar]
- 32. http://www.pbm.va.gov/CriteriaForUse.aspx.
- 33. http://www.fda.gov/Drugs/DrugSafety/ucm255005.htm.
- 34.Stafylas PC, Sarafidis PA, Lasaridis AN. The controversial effects of thiazolidinediones on cardiovascular morbidity and mortality. International Journal of Cardiology. 2009;131(3):298–304. doi: 10.1016/j.ijcard.2008.06.005. [DOI] [PubMed] [Google Scholar]
- 35.Sharma AM, Staels B. Review: Peroxisome proliferator-activated receptor gamma and adipose tissue–understanding obesity-related changes in regulation of lipid and glucose metabolism. Journal of Clinical Endocrinology Metabolism. 2007;92(2):386–395. doi: 10.1210/jc.2006-1268. [DOI] [PubMed] [Google Scholar]
- 36.Lu M, Sarruf DA, Talukdar S, Sharma S, Li P, Bandyopadhyay G, Nalbandian S, Fan W, Gayen JR, Mahata SK, Webster NJ, Schwartz MW, Olefsky JM. Brain PPAR-γ promotes obesity and is required for the insulin-sensitizing effect of thiazolidinediones. Nature Medicine. 2011;17(5):618–622. doi: 10.1038/nm.2332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fisher RA. Frequency distribution of the values of the correlation coefficient in samples of an indefinitely large population. Biometrika. 1915;10(4):507–521. [Google Scholar]
- 38.Jorgenson B, Knudsen SJ. Parameter orthogonality and bias adjustment for estimating functions. Scandinavian Journal of Statistics. 2004;31(1):93–114. [Google Scholar]
- 39.Imai K, Keele L, Yamamoto T. Identification, inference, and sensitivity analysis for causal mediation effects. Statistical Science. 2010;25(1):51–71. [Google Scholar]
- 40.Jo B. Causal inference in randomized experiments with mediational processes. Psychological Methods. 2008;13(4):314–336. doi: 10.1037/a0014207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gallop R, Small DS, Lin J, Elliott MR, Joffe MM, Ten Have TR. Mediation analysis with principal stratification. Statistics in Medicine. 2009;28(7):1108–1130. doi: 10.1002/sim.3533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hancock GR, Samuelsen KM, editors. Advances in Latent Variable Mixture Models. Greenwhich CT: Information Age; 2007. pp. 317–341. [Google Scholar]
- 43.Nylund KL, Asparouhov T, Muthn BO. Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Structural Equation Modeling. 2007;14(4):535–569. [Google Scholar]