Stance width changes how sensory feedback is used for multisegmental balance control

Abstract

A multilink sensorimotor integration model of frontal plane balance control was developed to determine how stance width influences the use of sensory feedback in healthy adults. Data used to estimate model parameters came from seven human participants who stood on a continuously rotating surface with three different stimulus amplitudes, with eyes open and closed, and at four different stance widths. Dependent variables included lower body (LB) and upper body (UB) sway quantified by frequency-response functions. Results showed that stance width had a major influence on how parameters varied across stimulus amplitude and between visual conditions. Active mechanisms dominated LB control. At narrower stances, with increasing stimulus amplitude, subjects used sensory reweighting to shift reliance from proprioceptive cues to vestibular and/or visual cues that oriented the LB more toward upright. When vision was available, subjects reduced reliance on proprioception and increased reliance on vision. At wider stances, LB control did not exhibit sensory reweighting. In the UB system, both active and passive mechanisms contributed and were dependent on stance width. UB control changed across stimulus amplitude most in wide stance (opposite of the pattern found in LB control). The strong influence of stance width on sensory integration and neural feedback control implies that rehabilitative therapies for balance disorders can target different aspects of balance control by using different stance widths. Rehabilitative strategies designed to assess or modify sensory reweighting will be most effective with the use of narrower stances, whereas wider stances present greater challenges to UB control.

humans commonly adjust their stance width as environmental contexts change. Changes in preferred stance width are associated with changes in neurological impairment (Horak et al. 2005), age (McIlroy and Maki 1997; Swanenburg et al. 2010), and reoccurrence of falls (Swanenburg et al. 2010). However, the influence of stance width on sensory feedback control is still poorly understood. Therefore, the current study characterizes how changing stance width influences the way humans use sensory feedback information for upper body (UB) and lower body (LB) balance control.

Neural control of bipedal stance varies across stance width (Bingham et al. 2011) because stance width has a major impact on frontal plane biomechanics. Wider stances permit larger excursions of the body's center of mass (CoM) before reaching the limits of the base of support. Also, changing stance width impacts the physics governing LB motion. For example, a unit of LB torque applied about a hip joint is more effective in accelerating the LB in wide vs. narrow stance (Bingham et al. 2011; Goodworth and Peterka 2012; Scrivens et al. 2008), and interaction torques from the UB and surface are stance width dependent (Goodworth and Peterka 2012). In addition, the influence of LB sway and surface tilt on the pelvis orientation angle varies in magnitude and direction as stance width changes (Day et al. 1993; Goodworth and Peterka 2012). Finally, because changing stance width alters the stretch of muscles and tendons that span hip joints (Day et al. 1993; Scrivens et al. 2008), feedback from proprioception and intrinsic stiffness/damping (due to nonlinear springlike muscle/tendon properties and the influence of tonic muscle activation) may also vary with stance width.

The biomechanical changes described above are likely linked to changes in sway and muscle activity observed in previous studies. Previous studies have shown that increasing stance width is associated with lower spontaneous sway (Day et al. 1993; Goodworth and Peterka 2010), lower muscle activations following a surface translation (Henry et al. 1998; Torres-Oviedo and Ting 2010), lower responses to artificial vestibular stimulation (Day et al. 1997), lower movement responses to centripetal accelerations (Goodworth et al. 2013), and responses that vary in direct proportion to perturbation amplitude (Goodworth and Peterka 2010). However, because changes in neural control are likely to occur concurrently with stance width-related changes in biomechanics, it is challenging to tease apart the individual contributions of neural mechanisms and biomechanics on the basis of experimental observations alone.

To overcome this obstacle, modeling approaches have been developed to account for experimental data from healthy subjects responding to a sudden surface translation that evoked frontal plane sway (Bingham et al. 2011; Scrivens et al. 2008). It was found that a single set of neural feedback control parameters could not accurately describe sway behavior across all stance widths, and thus neural control must vary across stance width. Moreover, wider stances placed greater constraints on the range of feedback control parameters compatible with stability (i.e., stability based on control systems concepts whereby a system returns to a steady-state condition following an impulse perturbation) (Bingham et al. 2011). Model results also indicated that the effectiveness of hip torque in accelerating the LB increased with stance width, and thus less corrective torque generation in proportion to body sway was required to control balance at wider stance widths (Bingham et al. 2011). However, this model was limited in that frontal plane biomechanics were represented as a single-degree-of-freedom mechanical system that assumed that the pelvis and UB moved as a single segment whose orientation relative to the LB was entirely determined by LB geometry. Additionally, this model did not attempt to ascribe the source of orientation information used for feedback control to any particular sensory system. Finally, nearly all previous stance width studies have tested participants on a stationary or translating (as opposed to tilting) surface. In these experimental conditions, all sources of sensory feedback provide congruent orientation information, making it difficult, if not impossible, to tease apart how the contributions of individual sensory systems change across stance width. Thus it is unknown how neural feedback control varies across stance width when a feedback control scheme is required to explain experimentally observed motion of both the UB and LB and, additionally, how sensory feedback from vestibular, visual, and proprioception systems varies across stance width and stimulus amplitude. Dissecting individual sensory system contributions is important because balance is often compromised due to neurological disorders that degrade one system to a greater extent than others.

To address the topic of how sensory feedback contributes to balance control in a multisegment body, a frontal plane modeling study was recently performed (Goodworth and Peterka 2012). The model included separate UB and LB segments with feedback control originating from both non-time-delayed passive feedback sources and time-delayed sensory feedback from visual, vestibular, and proprioceptive sources. The model accounted for experimental data from healthy subjects standing in a narrow stance configuration and responding to continuous surface tilts at different stimulus amplitudes. The model indicated that LB passive feedback was negligible compared with LB active feedback. LB active control was similar to previous single-degree-of-freedom frontal plane studies (Cenciarini and Peterka 2006; Oie et al. 2002). Also, changes in sensory contributions across stimulus amplitude and between eyes open and eyes closed were attributed to a sensory reweighting mechanism.

Sensory reweighting occurs when reliance on one sensory system increases while, at the same time, reliance of another sensory system decreases (Allison et el. 2006; Ernst and Banks 2002; Peterka 2002). Failure to properly make use of sensory reweighting can lead to impaired balance and falls (Nashner et al. 1982; Peterka 2002). A model-based interpretation of LB experimental results by Goodworth and Peterka (2012) showed that, with increasing stimulus amplitude, subjects decreased their reliance on proprioception, encoding body motion relative to the surface, and increased reliance on vestibular and visual information, encoding motion relative to earth vertical and a stationary visual scene, respectively. In contrast, subjects did not vary their use of sensory feedback in the UB control system nearly as much as in the LB system.

Sensory reweighting was identified when there was a monotonic increase in one sensory feedback parameter that was accompanied by a decrease in a different sensory parameter as stimulus amplitude changed or between eyes open and closed. Thus, to determine whether the sensory reweighting mechanism was influenced by stance width, it was necessary to characterize system changes across different surface tilt amplitudes and between eyes open and closed. Modeling is necessary to distinguish stimulus-response changes due to sensory reweighting vs. stimulus-response changes due to increases (or decreases) in overall stiffness. Overall stiffness can change if the contribution from one sensory system changes without reciprocal changes in other systems. Modeling can also help distinguish between torque generated from active mechanisms (i.e., time-delayed feedback of sensory origin) or passive mechanisms (i.e., non-time-delayed feedback from intrinsic mechanical properties), thus lending insight into previous speculations that passive LB stiffness increases with stance width (Day et al. 1993; Scrivens et al. 2008).

Therefore, the current study aims to answer previously unanswered questions: Do sensory contributions to UB and LB control vary across stance width? Does amplitude-dependent sensory reweighting contribute to UB and LB control, and, if so, does it change across all stance widths? Do passive UB and LB contributions change with increasing stance width?

The proposed model in the current study is an extension of existing frontal plane models (Bingham et al. 2011; Cenciarini and Peterka 2006; Goodworth and Peterka 2012; Oie et al. 2002; Scrivens et al. 2008). The model includes stance width-dependent biomechanics (i.e., interaction torques, LB and UB inertia, gravity-related parameters, and pelvis tilt biomechanics) along with passive and active feedback control mechanisms. The inclusion of passive mechanisms helps us to understand whether changing stance width alters the contribution of intrinsic biomechanical stiffness/damping to balance. The inclusion of active mechanisms enables us to quantify changes in feedback from different sensory systems across stance width and to characterize the presence (or absence) of sensory reweighting at each stance width.

METHODS

Experiment Description

Previously acquired experimental data (Goodworth and Peterka 2010) were used in the current study. All subjects gave their informed consent before being tested with a protocol approved by the Institutional Review Board at Oregon Health & Science University. Data are from the seven subjects who exhibited similar control strategies across all test conditions. Average (±SD) body parameters were as follows: mass, 70.2 ± 7.1 kg; height, 172.3 ± 6.3 cm; L4/L5 spinal joint height above surface, 106 ± 4.1 cm; UB CoM height above L4/L5, 17.6 ± 2.6 cm; greater trochanter height above surface, 89.5 ± 5.3 cm; hip joint center height above surface, 91.2 ± 5.6 cm, and distance between hip joint centers, 17.5 ± 1.1 cm.

In each subject, body sway was evoked in the frontal plane through continuous tilts of the surface on which subjects stood. Subjects responded naturally, listening to a short story with headphones, and maintained straight knees. Subjects stood with either eyes open (EO) or eyes closed (EC) at one of four different stance widths. The four stance widths included an intermalleolar distance of 5 cm (narrow stance), 12 cm (parallel stance), 21.5 cm (medium stance), and 32 cm (wide stance). During EO tests, subjects viewed a stationary, complex checkerboard pattern lining a 1.4-m-diameter half-cylinder-shaped screen (Peterka 2002). The surface tilt axis was horizontal and perpendicular to the subject's frontal plane at ankle height centered between the subject's feet. The surface tilt velocity input was based on a pseudorandom ternary sequence (Davies 1970) with a 43.72-s cycle duration that was repeated at least 6 times during each test. The power spectrum of surface tilt velocity had approximately equal amplitude spectral components ranging from 0.023 Hz to about 16.7 Hz, which allowed characterization of the balance control system across a wide bandwidth. The surface tilt waveform was scaled to provide peak-to-peak position amplitudes of 1°, 2°, or 4°.

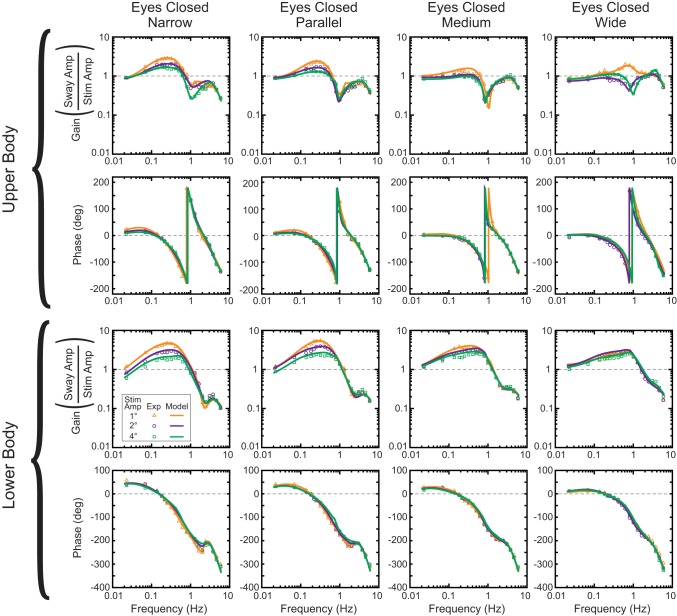
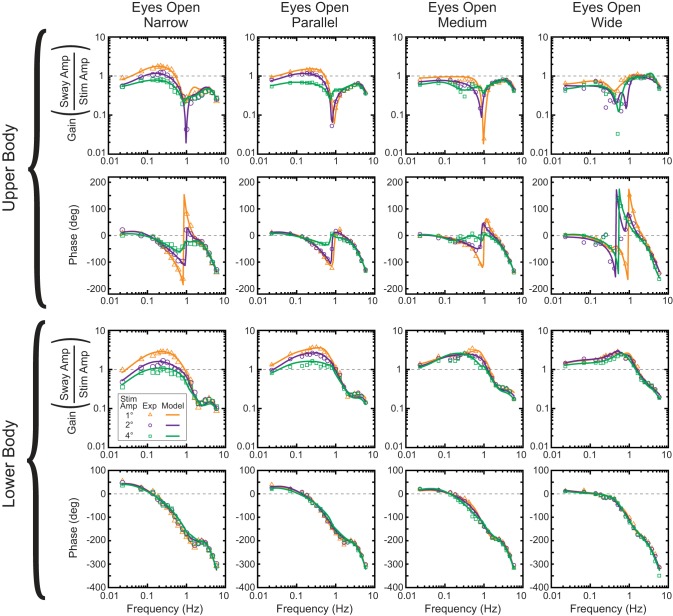
The LB and UB sway angles with respect to earth vertical were measured and used to calculate frequency-response functions (FRFs). Twenty-four FRFs were calculated for each subject from EO and EC tests performed at the three stimulus amplitudes and four stance widths. Across-subject mean FRFs were also calculated for each amplitude and stance width in the EO and EC conditions. Our LB and UB FRFs provided a nonparametric frequency-domain representation of the relation of the sway responses to the surface-tilt stimulus (Bendat and Piersol 2000). The LB and UB FRFs are expressed as a set of gain and phase values that vary with frequency. Each gain value indicates the ratio of the amplitude of LB or UB sway to the surface tilt amplitude at a particular stimulus frequency, and each phase value (expressed in degrees) indicates the relative timing of the LB or UB sway with respect to the surface tilt at a particular frequency. LB FRF phases were “unwrapped” using the Matlab (The MathWorks, Natick, MA) unwrap function, but UB phases were not unwrapped because some EO UB phase data did not unambiguously exhibit continuously increasing phase lag with increasing frequency (Fig. 1 vs. Fig. 2).

Fig. 1.

Model predictions of frequency-response functions (FRFs) in eyes closed (EC) conditions. Symbols represent experimental data, and lines are the model-predicted FRFs. Model FRFs are from the fits to across-subject mean experimental FRFs.

Fig. 2.

Model predictions of FRFs in eyes open (EO) conditions. Symbols represent experimental data, and lines are the model-predicted FRFs. Model FRFs are from the fits to across-subject mean experimental FRFs.

Each individual FRF calculation included the averaging of a larger number of adjacent FRF values at higher frequencies than at lower frequencies. This averaging method produced statistical confidence bounds on gain and phase data that were similar across the full range of frequencies even though the signal-to-noise ratio of sway response data, particularly for LB sway, tended to diminish with increasing frequency (as indicated by lower coherence function values at higher frequencies; see Fig. 6 in Goodworth and Peterka 2010). The similar magnitude of confidence bounds across frequency ensured that the full range of FRF data could be used for estimating model parameters based on wide bandwidth FRF data.

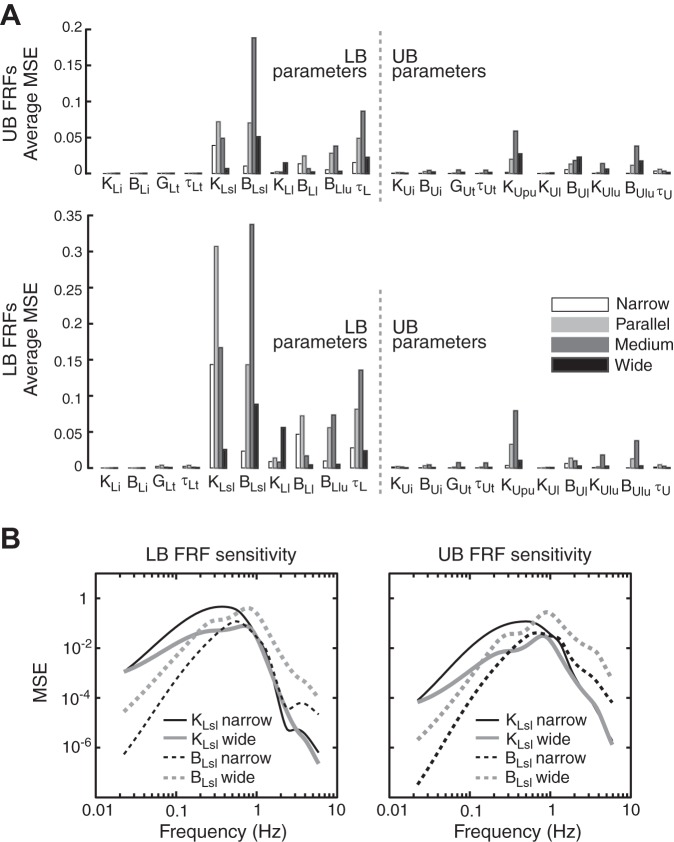
Fig. 6.

Sensitivity analysis characterizing how variations in model parameters influence LB and UB FRFs in the EC condition. A: summary bar plots of sensitivities of FRFs to control parameter variations were obtained by calculating an average mean square error (MSE) value at each stance width when parameters were varied ±5% from their nominal values (see methods). B: the frequency dependence of sensitivities to parameter variation is illustrated for 2 LB-to-surface proprioception feedback parameters, K_Lsl and B_Lsl. MSE vs. frequency plots are based on ±5% parameter variations relative to the nominal parameter value followed by averaging across MSE values from all stimulus amplitudes.

Model Description

The development, rationale, and assumptions behind the current model were described in detail in Goodworth and Peterka (2012), and additional information is given in the Appendix. Briefly, frontal plane body mechanics were modeled as a two-segment, inverted-pendulum structure (i.e., LB and UB segments) with an additional representation of how pelvis orientation angle (θ_P) changed as a function of surface tilt and LB sway angles (see Fig. 1 in Goodworth and Peterka 2012). Representation of the LB as a single segment is possible because the LB, consisting of two legs and a pelvis, is a closed-chain mechanical system with only one degree of freedom in the frontal plane (when knees are straight). For each stance width, equations of motion were linearized about an upright position. Parameters in the LB equation of motion varied with stance width, whereas parameters in the UB equation were essentially constant across stance width.

The input stimulus to the model was the surface tilt angle (θ_S), and model output responses were UB sway (θ_U) and LB sway (θ_L) angles with respect to vertical. LB and UB control were not independent of each other because of interaction torques and because sensory-derived inputs to LB and UB control mechanisms were shown to be influenced by motions of both body segments and by the surface rotation.

UB sway and LB sway was a function of torque generated about the UB and LB joints in response to the surface-tilt stimulus. UB torque (T_U) was the summation of all UB torques generated and applied about a joint between the pelvis and the UB. LB torque (T_L) was the summation of all LB torques generated and was applied about a single equivalent LB ankle joint. The two-segment mechanical model coefficients were scaled so that T_L applied about this equivalent LB ankle joint produced the same motion as if T_L was distributed equally among all four LB joints (i.e., ¼ of T_L applied to each of the 2 ankle joints and 2 hip joints).

The corrective torques T_L and T_U necessary for stability were assumed to be provided by feedback mechanisms. Feedback consisted of active (i.e., muscle activation based on sensory signals encoding kinematics or kinetics of body motion) and passive control mechanisms (i.e., forces arising from intrinsic biomechanical properties of muscle/tendon systems). Most active control mechanisms were assumed to arise from feedback of sensory-derived internal estimates of body segment position and velocity, similar to previous balance models (e.g., Bingham et al. 2011; Cenciarini and Peterka 2006; Kuo 1995; Mergner 2010). The representation of active control mechanisms is also supported by psychophysical experiments that have shown subjects perceive and combine body motion and orientation signals even where there is no direct peripheral sensor (e.g., Mergner et al. 1997) and by neurophysiological experiments that suggest the central nervous system has access to processed peripheral sensory signals such as the motion and orientation of the head (Angelaki et al. 1999; Merfeld and Zupan 2003; Mergner et al. 2009) and limbs (Bosco and Poppele 1993; Bosco et al. 2000; Casabona et al. 2004).

Table 1 defines the various sensory signals assumed to participate in LB and UB control. The active mechanisms generate torque by muscle contractions evoked in relation to signals from sensory systems that encode body kinematics (angles and angular velocities) and muscle force. LB and UB active mechanisms included time delays (τ_L and τ_U, respectively) that represent neural transmission, central processing, and muscle activation delays. Most active mechanisms include stiffness and damping parameters that determine the corrective torque generated in relation to sensory signals encoding various kinematic motion variables (i.e., the value of stiffness and damping parameters determine how much corrective torque is generated in proportion to angular position and angular velocity variables, respectively).

Table 1.

Sensory-derived signals represented as model parameters

Sensory Origin	Definition	Model Parameter
Vestibular (EC) or vision + vestibular (EO) combined with intersegmental proprioception	Encodes θL	KLl
	Encodes θ̇L	BLl
UB-to-LB proprioception (muscle spindles, receptors in joints and ligaments)	Encodes θL − θU	KLlu, KUlu
	Encodes θ̇L − θ̇U	BLlu, BUlu
LB-to-surface proprioception (muscle spindles, receptors in joints and ligaments)	Encodes θS − θL	KLsl
	Encodes θ̇S − θ̇L	BLsl
Vestibular (EC) or vision + vestibular (EO) combined with intersegmental proprioception	Encodes θU	KUu
	Encodes θ̇U	BUu
UB-to-pelvis proprioception (muscle spindles, receptors in joints and ligaments)	Encodes θP − θU	KUpu
	Encodes θ̇P − θ̇U	BUpu
Kinetic proprioception (Golgi tendon organs, load receptors)	Encodes TL	GLt, τLt
Kinetic proprioception (Golgi tendon organs, load receptors)	Encodes TU	GUt, τUt

Sensory signals are assumed to accurately encode physical variables. These sensory signals represent the output of central nervous system processing of information conveyed by primary sensory afferents (Angelaki et al. 1999; Casabona et al. 2004; Mergner et al. 1991, 1997). For kinematic feedback from sensory systems encoding joint motion, K is the proportionality constant between joint angle and corrective torque generation (a “stiffness” parameter) and B is the proportionality constant between joint angular velocity and corrective torque generation (a “damping” parameter). For kinetic feedback from sensory systems encoding torques, G is the proportionality constant between torques applied to joints of the body (T_L or T_U) and corrective torque generation, with the additional assumption that this corrective torque is low-pass filtered (filter time constants τ_Lt and τ_Ut). EC, eyes closed; EO, eyes open; θ_L, lower body (LB) sway angle; θ_U, upper body (UB) sway angle; θ_S, surface tilt angle; θ_P, pelvis orientation angle.

Our convention for labeling model parameters representing kinematic feedback is to use K to represent stiffness parameters and B to represent damping parameters. Each K and B includes a subscript L or U to indicate whether the feedback contributes to torque applied to the LB and UB, respectively. The subscript is further extended by using lowercase letters to indicate the source of the sensory signal. For example, K_Lsl is an LB stiffness parameter (torque generated in proportion to angular position) associated with a proprioceptive signal encoding the angle θ_S − θ_L. The active control mechanisms also include kinetic feedback components that generate corrective torque in relation to sensory signals that encode T_L and T_U, and are configured as positive feedback control loops (Peterka 2003). These sensory-derived torque signals, assumed to be low-pass filtered [first-order low-pass filter Laplace equations are G_Lt/(τ_Lts +1) for the LB and G_Ut/(τ_Uts +1) for the UB], provide feedback control that moves the body segments toward an earth-vertical orientation. Kinetic feedback is assumed to have a similar propagation and processing neural delay as kinematic feedback.

Our convention for parameter symbols that represent passive stiffness (K) and damping (B) mechanisms includes the subscript L or U for LB or UB contributions, respectively, and the subscript i for “intrinsic.” The passive mechanism in the LB generates torque with no time delay in proportion to θ_S − θ_L (proportionality factor defined by the stiffness parameter K_Li) and in proportion to the derivative of θ_S − θ_L (proportionality factor defined by the damping parameter B_Li). This mechanism represents the intrinsic stiffness and damping from muscles, tendons, joints, and ligaments in the LB that tend to orient the LB perpendicular to the surface. In the UB, the passive mechanism generates torque with no time delay in proportion to θ_P − θ_U (stiffness parameter K_Ui) and in proportion to the derivative of θ_P − θ_U (damping parameter B_Ui) and tends to orient the UB perpendicular to the pelvis.

Because the values of model control parameters determine the magnitude of corrective torque generated per unit of LB or UB sway, parameter values were used to infer the relative contribution of one source of feedback compared with another and how sensory contributions vary as a function of stimulus amplitude and stance width.

Estimation of Model Parameters

Model parameters associated with the mechanical model (inertia- and gravity-related proportionality factors on θ_L, θ_U, and θ_S) were determined for each subject on the basis of anthropomorphic measurements and then averaged across subjects. Remaining model parameters representing control mechanisms were estimated from curve fits to the experimental UB and LB FRFs (from both average and individual subject FRFs) by using a constrained nonlinear optimization routine, “fmincon” (Matlab Optimization Toolbox; The MathWorks), that minimized a cost function equal to the sum of the mean squared errors (MSEs) from LB and UB FRFs of the normalized difference between model-predicted FRFs and experimental FRFs (Peterka 2002) at frequencies between 0.023 and 5.9 Hz. After control parameters were obtained, the model was used to predict impulse response functions (IRFs) that were used for comparison with experimental IRFs (Goodworth and Peterka 2010) and aided in verifying the FRF fit results. Model stability was confirmed in each test condition by using Matlab Simulink (The MathWorks) to predict the 25-s time course of LB and UB sway evoked by a 1° surface tilt with a peak velocity of ∼35°/s. The metric for stability was that both UB and LB sway velocity decayed to zero.

Using these optimization methods, we were able to obtain stable models from fits to the across-subject average FRF data from all EC and EO tests and to individual subject FRFs from all EC tests. We were not able to obtain stable models from fits to all individual subjects' EO FRFs, particularly in the medium and wide stance conditions. Therefore, we only report EO results based on fits to across-subject mean FRFs, whereas we report EC results from fits to both individual and mean FRFs.

Selection of Model Parameters

To determine the specific feedback parameters to include in the model, we began with a previously developed model that described LB and UB dynamics in a narrow stance condition (Goodworth and Peterka 2012). This previous narrow stance model included the control parameters in Table 1 with the exception of K_Llu, K_Ulu, B_Upu, G_Ut, and τ_Ut. We found, however, that as stance width increased, this previous model became progressively less able to account for FRF data, and the parameters identified by the optimized model fits to experimental FRFs in wider stance conditions often resulted in an unstable system. Therefore, starting with the parameters included in the previous narrow stance model, we systematically added feedback control parameters that were previously excluded from the narrow stance model until the new model was able to describe the detailed FRF data across all stimulus amplitudes and stance widths. We added parameters using a systematic approach that was identical to the procedure described in Goodworth and Peterka (2012). Specifically, the approach was to use the smallest possible number of parameters to describe the experimental data to increase confidence in the parameter values (Pintelon and Schoukens 2001). Judgments about the quality of the various model fits were based on their MSE. It was found that the inclusion of K_Ulu, G_Ut, and τ_Ut produced a very large improvement in the accuracy of the model as stance width progressed from narrow to wide, but the inclusion of K_Llu and B_Upu gave very little or no improvement. Thus the model used to characterize the contribution of feedback mechanisms in the remainder of the current study included the parameters listed in Table 1 with the exception of K_Llu and B_Upu, which were set to zero.

Parameter Constraints

All control parameters were allowed to vary across stance width and between EO and EC. Most control parameters were also allowed to vary across stimulus amplitude. The exceptions included time delays (τ_L and τ_U) and passive biomechanics (K_Li, B_Li, K_Ui, and B_Ui), which were fixed across stimulus amplitude because experimental IRFs (Goodworth and Peterka 2010) showed no evidence for amplitude-dependent changes in the IRF time courses prior to the onset of corrective contributions from active mechanisms at τ_L and τ_U in the LB and UB, respectively. Also, the torque feedback time constants (τ_Lt and τ_Ut) were fixed across stimulus amplitude because experimental FRFs showed no evidence for an amplitude-dependent influence of the torque feedback mechanism, which affects gain and phase data at the lower frequencies (Fig. 6 in Goodworth and Peterka 2012). These constraints were accomplished by simultaneously fitting across the three stimulus amplitudes separately at each stance width and each visual condition. The above constraints across stimulus amplitude increased confidence in parameter estimation by reducing the model's degrees of freedom and redundancy in parameter contributions to stimulus-dependent changes in experimental results (Pintelon and Schoukens, 2001).

Model-Predicted FRFs

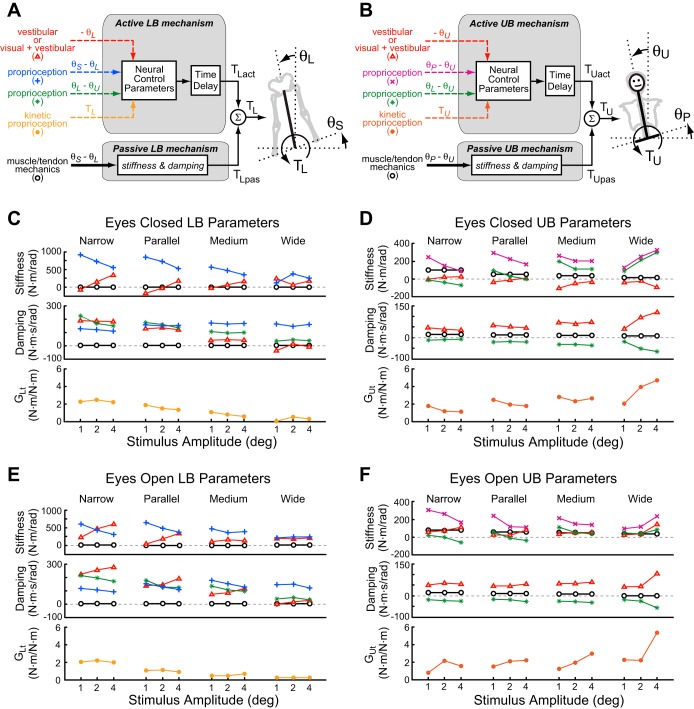
Model-predicted FRFs were obtained by first calculating the Laplace domain expressions of θ_U(s)/θ_S(s) and θ_L(s)/θ_S(s), where s is the Laplace variable. These model-predicted FRFs included the mathematical expressions for both the mechanical system (defined by Eqs. A1–A4 in Goodworth and Peterka 2012 and Eqs. A1 and A2 in the Appendix of the current article) and the hypothesized feedback control mechanisms shown in Fig. 3. The model-predicted LB and UB FRFs were obtained by substituting s = j2πf, where j is √−1 and f is frequency.

Fig. 3.

Block diagrams representing lower body (LB; A) and upper body (UB; B) feedback control mechanisms that generate corrective torques as a function of sensory signals encoding joint motion, segment orientation, or muscle torque (active torque, T_Lact and T_Uact) or as a function of passive mechanics associated with muscle/tendon stretch (passive torque, T_Lpas and T_Upas). In the block diagrams, physical segment kinematic variables are represented with thick solid black lines, sensory signals encoding segment kinematics or torques are represented as dashed lines, and joint torques are thin solid black lines. θ_U is the UB angle, θ_L is the LB angle, θ_P is the pelvis angle, θ_S is the surface angle, T_U is UB torque, and T_L is LB torque. The active mechanisms include a time delay and a set of neural control parameters that specify the transformation from sensory signals to corrective torque. Across all stimulus amplitudes and stance widths, the control parameters, identified from fits to the across-subject mean FRFs, are shown for EC LB control (C), EC UB control (D), EO LB control (E), and EO UB control (F). Plot symbols used in C and E are associated with sensory and mechanical signals defined in the block diagram of the LB control mechanism shown in A, and symbols used in D and F are defined in the block diagram of the UB control mechanism shown in B. Stiffness parameters generate torque in proportion to angular deviations, and damping parameters generate torque in proportion to angular velocity.

Statistics and Sensitivity Analysis

For each model parameter obtained from fits to individual subject FRFs in EC conditions, a separate repeated-measures ANOVA was performed. Statistical model effects included stimulus amplitude, stance width, and interaction effects between stance width and stimulus amplitude with P < 0.05 considered to be statistically significant.

A sensitivity analysis was performed on each of the feedback control parameters (obtained from fits to average FRF data) to characterize the sensitivity of the model-predicted UB and LB sway dynamics to variations in parameter values. Each parameter value was increased or decreased by 5%, and then, for each ±5% adjusted parameter, an UB and LB model-predicted FRF was calculated. The squared-error difference at each frequency point between model-predicted FRFs (calculated from ±5% adjusted parameter values) and model-predicted FRFs (calculated using parameter values from fits to experimental data shown in Fig. 3 and Table 2) was determined for all test conditions. To summarize sensitivity results, we calculated an average MSE value by averaging the squared-error difference for both +5% and −5% parameter variations across frequency points, and then averaging across stimulus amplitudes. Relatively larger average MSE values indicated greater model FRF sensitivity to a particular parameter in comparison to other parameter adjustments that showed smaller average MSE values.

Table 2.

Model parameters for EC and EO conditions from fits to across-subject mean FRFs

			Narrow Stance			Parallel Stance			Medium Stance			Wide Stance
Parameter	Units	EC/EO	1°	2°	4°	1°	2°	4°	1°	2°	4°	1°	2°	4°
KLl	N.m.rad−1	EC	−68	153	356	−181	−29	179	−27	69	167	243	74	171
		EO	231	473	609	40	194	337	103	168	135	200	188	217
KLsl	N.m.rad−1	EC	919	736	554	850	730	527	566	476	356	122	378	254
		EO	614	426	316	651	480	383	469	360	389	220	248	247
KLi*	N.m.rad−1	EC	2.6	2.6	2.6	4.1	4.1	4.1	1.4	1.4	1.4	4.4	4.4	4.4
		EO	8.0	8.0	8.0	2.9	2.9	2.9	0.2	0.2	0.2	9.9	9.9	9.9
BLl	N.m.s.rad−1	EC	188	183	180	128	134	119	41	46	42	−38	12	−9.4
		EO	221	256	278	137	144	193	73	83	115	−1.1	16	25
BLsl	N.m.s.rad−1	EC	128	121	111	157	150	152	169	161	166	162	144	160
		EO	114	107	92	152	126	110	176	150	127	146	147	120
BLlu	N.m.s.rad−1	EC	222	166	150	174	158	133	106	96	97	33	44	39
		EO	211	194	170	176	128	122	134	105	94	39	50	31
BLi*	N.m.s.rad−1	EC	0.1	0.1	0.1	0.2	0.2	0.2	0.1	0.1	0.1	0.1	0.1	0.1
		EO	0.4	0.4	0.4	0.1	0.1	0.1	0	0	0	0.2	0.2	0.2
τL*	ms	EC	117	117	117	114	114	114	113	113	113	104	104	104
		EO	118	118	118	113	113	113	110	110	110	107	107	107
GLt	N.m/N.m	EC	2.2	2.5	2.2	1.9	1.5	1.3	1.0	0.8	0.6	0	0.5	0.3
		EO	2.0	2.2	2.0	1.1	1.1	0.9	0.5	0.5	0.7	0.3	0.3	0.2
τLt*	s	EC	12	12	12	7.4	7.4	7.4	7.1	7.1	7.1	3.5	3.5	3.5
		EO	12	12	12	7.7	7.7	7.7	4.8	4.8	4.8	12	12	12
KUu	N.m.rad−1	EC	−6.4	13	17	−42	−19	4.5	−113	−56	−33	−45	−37	−101
		EO	55	74	112	24	21	79	34	51	49	27	36	142
KUpu	N.m.rad−1	EC	242	142	82	291	218	157	254	196	198	121	247	320
		EO	307	262	164	241	116	108	212	150	138	93	114	234
KUlu	N.m.rad−1	EC	−18	−48	−76	87	23	−10	191	104	105	83	202	292
		EO	17	−1.8	−64	57	−13	−41	109	50	36	47	38	84
KUi*	N.m.rad−1	EC	92	92	92	46	46	46	28	28	28	9	9	9
		EO	77	77	77	57	57	57	45	45	45	37	37	37
BUu	N.m.s.rad−1	EC	46	39	34	57	51	47	73	66	73	42	95	119
		EO	51	59	55	47	45	56	58	58	64	42	45	105
BUlu	N.m.s.rad−1	EC	−11	−8.8	−6.4	−20	−18	−20	−33	−31	−37	−19	−51	−66
		EO	−18	−24	−25	−16	−18	−28	−25	−28	−33	−18	−25	−56
BUi*	N.m.s.rad−1	EC	14	14	14	12	12	12	10	10	10	7.5	7.5	7.5
		EO	14	14	14	11	11	11	7.7	7.7	7.7	5.7	5.7	5.7
τU*	ms	EC	98	98	98	85	85	85	71	71	71	46	46	46
		EO	76	76	76	74	74	74	70	70	70	45	45	45
GUt	N.m/N.m	EC	1.8	1.1	1.1	2.5	1.9	1.8	2.8	2.3	2.6	2.0	3.9	4.7
		EO	0.8	2.1	1.6	1.5	2.1	2.2	1.2	1.9	2.9	2.2	2.2	5.3
τUt*	s	EC	3.3	3.3	3.3	2.6	2.6	2.6	1.0	1.0	1.0	1.9	1.9	1.9
		EO	4.9	4.9	4.9	4.7	4.7	4.7	3.5	3.5	3.5	5.8	5.8	5.8

Values are model parameters for EC and EO conditions from fits to across-subject mean frequency-response functions (FRFs) at 1°, 2°, and 4° peak-to-peak stimulus amplitudes for 4 different stance widths.

^*Parameters that were constrained to have equal values across the 3 peak-to-peak stimulus amplitudes for each stance width. All other parameters were free to vary across stimulus amplitude and stance width.

RESULTS

Model-Predicted FRFs

Model-predicted FRFs were able to account for the detailed features of mean experimental LB and UB FRFs in both EC conditions (Fig. 1) and EO conditions (Fig. 2). For example, for both EC and EO conditions, the narrow stance model accurately described the peaks in LB FRF gains at about 0.3 and 3 Hz, LB and UB phase leads below 0.15 Hz, the peak in LB phase at about 2.5 Hz, UB gain notch at about 1 Hz, and the LB and UB gain reductions with increasing stimulus amplitude below 1 Hz, as well as the amplitude-dependent UB phases in EO conditions between about 0.3 and 2 Hz. Similarly, the wide stance model accounted for the unique frequency-dependent LB and UB FRF curves including the minimal change in LB FRFs across stimulus amplitudes (EC and EO), the smooth decrease in LB phases at frequencies above 1 Hz (compared with the peak present at ∼2.5 Hz in narrow stance), and the variable and amplitude-dependent UB EO phases and EC gains. Model fits based on individual subject data in EC conditions (data not shown) were similarly able to account for these experimental features.

Feedback Control Parameters

Table 2 lists all parameter values for fits to across-subject mean FRFs in EC and EO conditions at the three stimulus amplitudes at each of the four stance widths. These parameters are also plotted in Fig. 3 with the exception of the time delay and torque feedback time constant parameters. Table 3 lists all parameter values for fits to individual subject FRFs in the EC conditions. Figure 4 shows how each parameter (averaged across visual conditions and across stimulus amplitude with parameters values from fits to the mean FRFs) varied across stance width. Table 4 identifies the statistical significance of amplitude, stance width, and the interaction effect between amplitude and stance width on EC parameters.

Table 3.

Model parameters for EC condition from fits to individual subject FRFs

		Narrow Stance			Parallel Stance			Medium Stance			Wide Stance
Parameter	Units	1°	2°	4°	1°	2°	4°	1°	2°	4°	1°	2°	4°
KLl	N.m.rad−1	−174 ± 262	−2.34 ± 262	272 ± 173	−209 ± 262	−76.2 ± 204	93.5 ± 152	−107 ± 107	−71.8 ± 198	40.9 ± 177	191 ± 62.0	43.8 ± 112	102 ± 104
KLsl	N.m.rad−1	1,027 ± 331	931 ± 455	683 ± 355	878 ± 317	782 ± 274	636 ± 310	634 ± 167	625 ± 229	496 ± 253	165 ± 60.3	408 ± 169	330 ± 195
KLi*	N.m.rad−1	3.50 ± 4.27	3.50 ± 4.27	3.50 ± 4.27	3.97 ± 3.13	3.97 ± 3.13	3.97 ± 3.13	27.7 ± 32.9	27.7 ± 32.9	27.7 ± 32.9	32.2 ± 39.6	32.2 ± 39.6	32.2 ± 39.6
BLl	N.m.s.rad−1	203 ± 105	217 ± 116	219 ± 129	111 ± 68.9	128 ± 53.8	129 ± 75.1	46.7 ± 25.4	64.1 ± 48.5	54.5 ± 35.4	−31.6 ± 15.4	7.13 ± 31.1	−0.741 ± 40.3
BLsl	N.m.s.rad−1	118 ± 40.6	112 ± 46.0	97.6 ± 43.0	152 ± 36.3	153 ± 44.2	158 ± 71.6	141 ± 37.3	146 ± 43.0	148 ± 31.0	163 ± 47.4	143 ± 41.3	159 ± 31.4
BLlu	N.m.s.rad−1	204 ± 85.8	153 ± 64.9	142 ± 54.4	148 ± 43.8	151 ± 42.6	134 ± 44.5	70.6 ± 44.2	82.8 ± 39.9	77.6 ± 20.6	40.6 ± 29.5	45.1 ± 19.3	45.3 ± 15.9
BLi*	N.m.s.rad−1	0.17 ± 0.17	0.17 ± 0.17	0.17 ± 0.17	0.15 ± 0.10	0.15 ± 0.10	0.15 ± 0.10	0.51 ± 0.42	0.51 ± 0.42	0.51 ± 0.42	3.05 ± 4.83	3.05 ± 4.83	3.05 ± 4.83
τL*	ms	112 ± 9.4	112 ± 9.4	112 ± 9.4	112 ± 3.1	112 ± 3.1	112 ± 3.1	110 ± 4.1	110 ± 4.1	110 ± 4.1	106 ± 6.0	106 ± 6.0	106 ± 6.0
GLt	N.m/N.m	3.76 ± 4.14	3.18 ± 1.94	2.42 ± 1.40	2.45 ± 1.42	2.53 ± 2.42	2.64 ± 2.59	1.47 ± 0.627	1.39 ± 0.680	1.06 ± 0.455	0.162 ± 0.132	0.700 ± 0.448	0.486 ± 0.299
τLt*	s	14.9 ± 9.81	14.9 ± 9.81	14.9 ± 9.81	12.9 ± 9.83	12.9 ± 9.83	12.9 ± 9.83	8.98 ± 4.26	8.98 ± 4.26	8.98 ± 4.26	5.32 ± 2.21	5.32 ± 2.21	5.32 ± 2.21
KUu	N.m.rad−1	−2.94 ± 68.9	33.0 ± 27.9	−1.42 ± 133	−40.1 ± 37.3	−11.7 ± 54.9	15.0 ± 66.3	−74.4 ± 59.3	−40.2 ± 46.9	−20.4 ± 38.5	−59.1 ± 35.9	−54.7 ± 37.9	−95.5 ± 48.1
KUpu	N.m.rad−1	352 ± 152	281 ± 192	240 ± 210	345 ± 161	322 ± 171	298 ± 251	194 ± 101	241 ± 158	254 ± 127	114 ± 105	191.4 ± 100	277 ± 140
KUlu	N.m.rad−1	54.3 ± 158	4.84 ± 112	42.0 ± 186	113 ± 82.5	75.3 ± 108	29.4 ± 52.7	131 ± 46.1	134 ± 46.1	141 ± 72.4	122 ± 71.4	187 ± 90.4	260 ± 84.1
KUi*	N.m.rad−1	145 ± 102	145 ± 102	145 ± 102	43.6 ± 27.0	43.6 ± 27.0	43.6 ± 27.0	46.3 ± 23.6	46.3 ± 23.6	46.3 ± 23.6	46.6 ± 28.7	46.6 ± 28.7	46.6 ± 28.7
BUu	N.m.s.rad−1	74.0 ± 65.4	52.7 ± 22.8	58.0 ± 34.5	53.7 ± 14.0	55.1 ± 19.1	57.0 ± 29.6	51.2 ± 16.1	63.2 ± 23.9	73.3 ± 25.5	47.6 ± 27.4	78.2 ± 32.4	103 ± 34.5
BUlu	N.m.s.rad−1	−33.4 ± 45.3	−20.6 ± 16.6	−25.0 ± 23.8	−17.6 ± 9.75	−20.5 ± 11.0	−22.1 ± 18.4	−17.3 ± 11.6	−26.0 ± 13.7	−34.3 ± 17.1	−21.6 ± 17.8	−39.0 ± 19.0	−54.1 ± 21.5
BUi*	N.m.s.rad−1	15.2 ± 4.80	15.2 ± 4.80	15.2 ± 4.80	13.5 ± 5.21	13.5 ± 5.21	13.5 ± 5.21	9.98 ± 3.89	9.98 ± 3.89	9.98 ± 3.89	7.35 ± 3.28	7.35 ± 3.28	7.35 ± 3.28
τU*	ms	73 ± 17	73 ± 17	73 ± 17	70 ± 7.7	70 ± 7.7	70 ± 7.7	58 ± 6.5	58 ± 6.5	58 ± 6.5	52 ± 8.9	52 ± 8.9	52 ± 8.9
GUt	N.m/N.m	4.33 ± 3.58	2.68 ± 2.81	1.49 ± 2.00	2.97 ± 2.10	3.21 ± 1.60	3.14 ± 2.33	3.80 ± 2.76	3.94 ± 3.61	4.82 ± 5.23	2.61 ± 1.81	4.23 ± 2.27	4.58 ± 1.43
τUt*	s	9.26 ± 3.87	9.26 ± 3.87	9.26 ± 3.87	10.4 ± 5.67	10.4 ± 5.67	10.4 ± 5.67	6.11 ± 3.97	6.11 ± 3.97	6.11 ± 3.97	2.41 ± 0.89	2.41 ± 0.89	2.41 ± 0.89

Values (means ± SD) are model parameters for the EC condition from fits to individual subject FRFs at 1°, 2°, and 4° peak-to-peak stimulus amplitudes for 4 different stance widths.

^*Parameters that were constrained to have equal values across the 3 peak-to-peak stimulus amplitudes for each stance width. All other parameters were free to vary across stimulus amplitude and stance width.

Fig. 4.

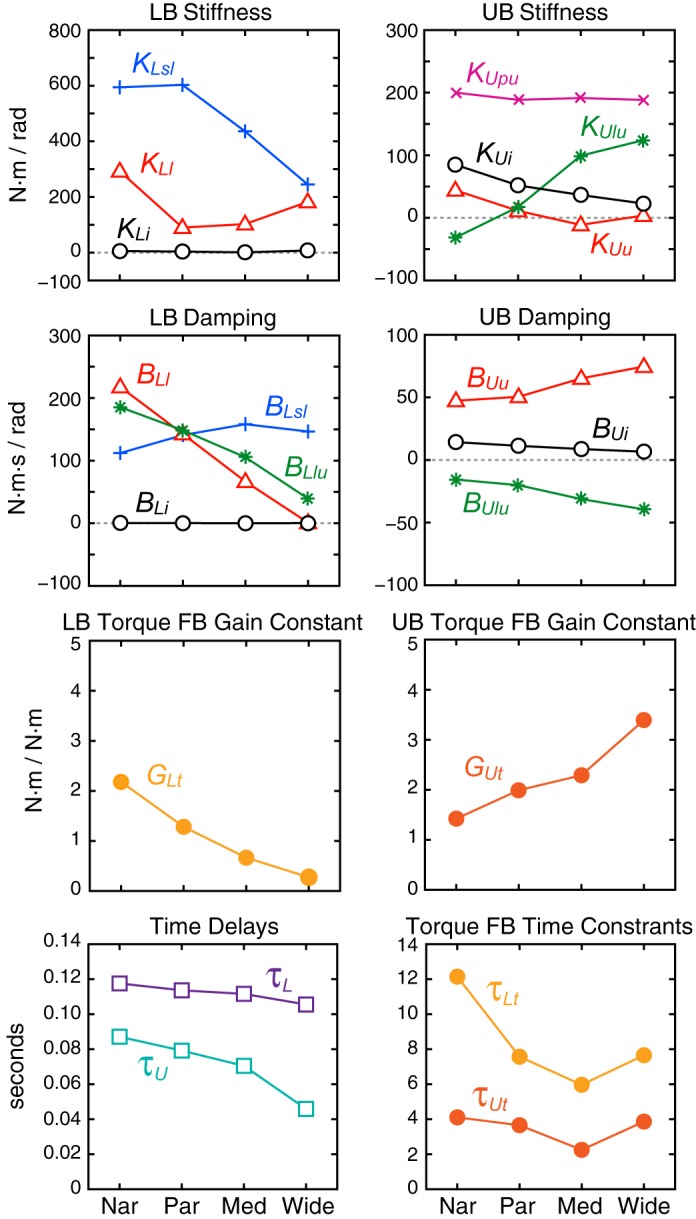
Model feedback (FB) parameters as a function of frontal plane stance width. At each stance width, results shown are the average of parameter values across visual conditions and across stimulus amplitudes. All parameters values are from fits to across-subject mean FRFs. Nar, narrow stance; Par, parallel stance; Med, medium stance; Wide, wide stance. See text and Table 1 for parameter definitions.

Table 4.

Statistical analysis of model parameters in EC condition

	Significance (P < 0.05)
Parameter	Amplitude	Stance Width	Amplitude and stance width interaction
KLl	↑		†
KLsl	↓	↓	†
KLi*		↑
BLl		↓
BLsl		↑
BLlu		↓	†
BLi*		↑
GLt		↓
τLt		↓
τL*		↓
KUu		↓
KUpu		↓	†
KUlu		↑	†
KUi*		↓
BUu	↑	↑	†
BUlu	↓	↓	†
BUi		↓
GUt		↑	†
τUt*		↓
τU*		↓

^*Parameters whose values were constrained to be equal across the 3 stimulus amplitudes in each stance width. These constrained parameters will, by definition, show no statistical effects of amplitude or interaction between amplitude and stance width. ↑Significant upward trend with increasing amplitude or stance width. ↓Significant downward trend with increasing amplitude or stance width. †Significant interaction effect between amplitude and stance width.

EC LB system parameters.

The following discussion about EC parameters is accurate for both fits to mean FRF data and fits to individual subjects' FRF data. In the LB EC control system, parameters representing contributions of the passive mechanism (K_Li and B_Li) were close to zero in all stance widths, indicating that passive mechanics made very little contribution to LB feedback control compared with active mechanisms (Fig. 3C). Nevertheless, both parameters generally increased with increasing stance width (Table 2), and these small increases were statistically significant.

For active LB mechanisms, the largest stiffness parameter contribution to LB active feedback control was from LB-to-surface proprioception (K_Lsl). Torque generated by this feedback tends to orient the LB perpendicular to the surface. The largest contributors to LB system damping were highly dependent on stance width. In narrow stance, the largest damping contributors were vestibular-related (B_Ll), which tends to move the LB upright in space, and UB-to-LB proprioception (B_Llu), which tends to move the LB opposite to the UB (representing a torque-facilitating counter-phase intersegmental motion). Both of these damping parameters showed large and statistically significant decreases with increasing stance width such that, at medium and wide stances, these parameters were considerably smaller in value than the LB-to-surface proprioception damping parameter (B_Lsl). The LB torque generated by the LB-to-surface proprioception damping (B_Lsl), which tends to resist movement of the LB away from alignment perpendicular to the surface, was unique in that it was the only active LB parameter to show an increase with stance width. Most other active LB parameters (K_Lsl, B_Ll, B_Llu, G_Lt, τ_Lt, and τ_dL) showed a significant decrease with increasing stance width, and the vestibular-related parameter (K_Ll) showed no significant change with stance width (Table 4).

In narrow, parallel, and medium stance, there was a monotonic increase in the vestibular-related parameter (K_Ll) and decrease in the LB-to-surface proprioception parameter (K_Lsl) with increasing stimulus amplitude. Correspondingly, stimulus amplitude had a statistically significant effect on both parameters, and there was a significant interaction effect between stance width and stimulus amplitude whereby stimulus amplitude had a larger impact on K_Ll and K_Lsl in narrower compared with wider stance widths. The reciprocal change in these two parameters with increasing amplitude could be considered to represent a sensory reweighting strategy that alters feedback control to adjust for increasing stimulus amplitude by shifting toward increased reliance on vestibular feedback and decreased reliance on surface-orienting proprioceptive feedback. The net effect of this sensory reweighting is to limit the amplitude of body sway evoked by the surface-tilt perturbation while providing sufficient net corrective torque to maintain stability (Peterka 2002). However, no corresponding monotonic amplitude-dependent changes were evident in these two parameters or in other LB parameters in the wide stance condition, indicating that, in wide stance, a sensory reweighting strategy was not used to limit body sway caused by larger surface-tilt perturbations.

EC UB system parameters.

In the UB control system (Fig. 3D), passive stiffness (K_Ui) and damping (B_Ui) made modest contributions compared with active UB control mechanisms in narrow stance. The passive contributions significantly decreased as stance width increased (Table 4).

For active UB mechanisms, the largest stiffness contribution to UB active feedback across all stance widths was from UB-to-pelvis proprioception (K_Upu). Torque generated by this feedback tends to orient the UB perpendicular to the pelvis. The largest UB damping came from the vestibular parameter (B_Uu), which tends to resist movement of the UB away from upright. The negative value of the damping parameter (B_Ulu) produced UB torque that tends to move the body segments in counter-phase motion. All UB parameters were significantly influenced by stance width: K_Ulu, B_Uu, and G_Ut significantly increased with increasing stance width, whereas the remaining UB parameters significantly decreased.

Stimulus amplitude had a significant effect on only two UB parameters: the vestibular parameter B_Uu and the LB-to-UB proprioception parameter B_Ulu. However, this statistical result appeared to be strongly influenced by the amplitude dependency that occurred mainly in the wide stance condition, whereas at other stance widths, these two parameters showed very little change with amplitude (Fig. 3D and Table 3). Similarly, for UB-to-pelvis proprioception (K_Upu), LB-to-UB proprioception (K_Ulu), and torque feedback (G_Ut), the statistical results showing no overall amplitude trend appear to be due to there being an opposite amplitude trend in the wide stance condition compared with the other stance widths. Specifically, both UB-to-pelvis proprioception (K_Upu) and LB-to-UB proprioception (K_Ulu) showed consistent decreases with increasing amplitude at narrow, parallel, and medium stances and showed the opposite amplitude trend at the widest stance. Torque feedback (G_Ut) decreased with amplitude in narrow and parallel stances, showed little change in medium stance, and increased with amplitude in wide stance. These complex interactions between stance width and stimulus amplitude are identified by the significant interaction between amplitude and stance width detected in the statistical analysis (Table 4) for parameters K_Upu, K_Ulu, B_Uu, B_Ulu, and G_Ut.

EO LB system parameters.

The EO LB control system parameters (Fig. 3E) were similar to those in EC LB control. Specifically, the contribution of the passive mechanism was nearly zero, and the patterns of changes in active stiffness parameters across amplitude and stance width were similar to EC results. Similar to EC conditions, there were clear monotonic variations with increasing stimulus amplitude in EO LB stiffness parameters: the visual + vestibular parameter (K_Ll) increased and the surface-to-LB proprioception parameter (K_Lsl) decreased in narrow and parallel stance. As in the EC condition, the variation in these two parameters was reciprocal and thus could be considered to represent a sensory reweighting strategy for adjustment to changes in surface tilt amplitude.

EO UB system parameters.

EO UB parameters (Fig. 3F and Table 2) showed similar patterns of amplitude-dependent and stance width-dependent changes as EC UB parameters. As in EC, the passive stiffness (K_Ui) and damping (B_Ui) made a modest contribution compared with UB active mechanisms. The largest contribution to UB stiffness came from the UB-to-pelvis proprioception parameter (K_Upu), and the largest contribution to damping came from the visual + vestibular parameter (B_Uu). The pattern of parameter variations across stimulus amplitude was highly dependent on stance width. In EO narrow, parallel, and medium stance, there were small monotonic decreases with increasing stimulus amplitude in pelvis-to-UB and LB-to-UB proprioception (K_Upu and K_Ulu, respectively), but in wide stance these parameters increased as stimulus amplitude increased. UB damping parameters showed little or no amplitude-dependent changes except in the wide stance condition, where the visual + vestibular parameter (B_Uu) increased and the LB-to-UB proprioception parameter (B_Ulu) decreased with increasing amplitude.

Parameter variation with stance width.

To more clearly visualize stance width-related changes in parameters, average parameter values from fits to the mean FRFs across EC and EO conditions and across stimulus amplitudes were plotted in Fig. 4. For almost all parameters, the patterns of change across stance width were similar for both EC and EO conditions, and therefore, averaging across visual conditions did not distort the trends seen in EC and EO results. The single exception was the stiffness parameter K_Ll representing the vestibular (EC) or visual + vestibular (EO) contribution to LB control. With EC, K_Ll showed no significant variation with stance width (Table 4 and Fig. 3C), whereas with EO, K_Ll tended to decrease with increasing stance width (Fig. 3E).

For LB control, most kinematic and kinetic sensory feedback parameters showed large decreases with increasing stance width, consistent with less overall LB torque being generated per unit of LB sway angle or angular velocity at wider stance widths. For UB control, most kinematic parameters showed only small changes with stance width, with some parameters increasing and others decreasing in value. The major exception was an increase in the LB-to-UB proprioceptive stiffness parameter (K_Ulu) that increased with stance width. Larger values of this stiffness parameter indicate an increase in the UB torque that moves the UB into alignment with the LB. The UB kinetic torque feedback parameter G_Ut also increased with stance width. UB torque generated by this kinetic feedback pathway mainly influences UB sway at lower frequencies to move the UB toward a vertical orientation.

Parameter changes associated with visual conditions.

Figure 5 shows the difference between sensory feedback parameters from EO vs. EC conditions as a function of stance width. For LB parameters (Fig. 5, left), notable quantitative differences include 1) the vision + vestibular stiffness parameter (K_Ll) was larger in EO, especially in the two narrowest stance widths; 2) the LB-to-surface proprioception stiffness parameter (K_Lsl) was smaller in EO, especially at narrow and parallel stance widths; 3) the visual + vestibular damping parameter (B_Ll) was larger in EO; and 4) the LB-to-surface proprioception parameter (B_Lsl) was slightly smaller in EO. Taken together, LB parameters representing the sense of orientation with respect to vertical (where visual as well as vestibular information could contribute) were larger in EO, whereas parameters representing the proprioceptive sense of LB to surface were lower in EO (especially at the 2 narrowest stance widths). Because the visual + vestibular parameter (K_Ll) values were larger and surface-to-LB proprioception (K_Lsl) values were smaller in EO compared with EC at all corresponding stimulus amplitudes, the corrective torque generated in relation to these parameters will result in a reduced amplitude of tilt-evoked LB sway in EO vs. EC conditions. Qualitatively, the larger visual + vestibular (K_Ll) values in EO vs. EC conditions represent a greater utilization of sensory orientation information signaling LB movement with respect to earth vertical. With EO, both visual and vestibular systems can contribute to an internal estimate of LB deviation from an upright orientation, whereas with EC, only the vestibular system can contribute.

Fig. 5.

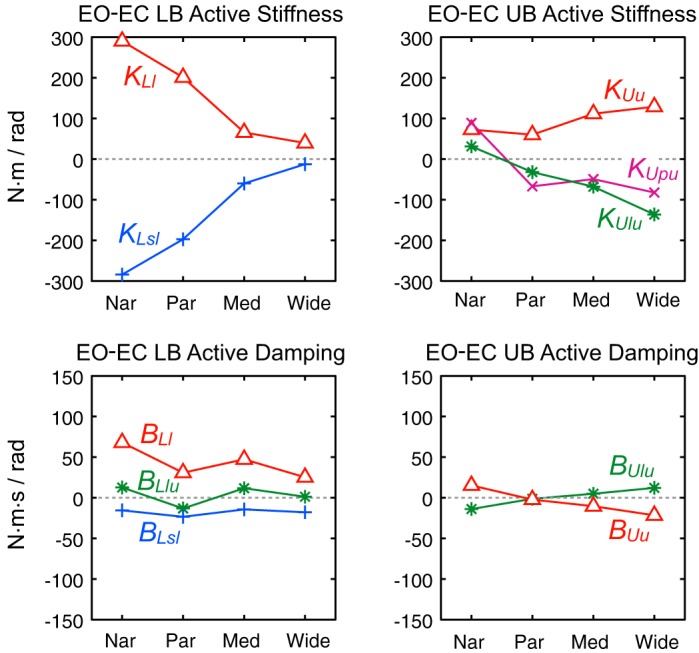
Comparison of EO and EC sensory feedback parameters. EO and EC parameters were averaged across the 3 stimulus amplitudes for each of the 4 stance widths. All results are based on parameters from fits to across-subject mean FRFs. Plots show EO minus EC parameter values for the LB (left) and UB parameters (right). Values greater than zero indicate that parameters were greater in EO compared with EC conditions.

Most UB active parameters showed EO vs. EC differences that varied across stance width (Fig. 5, right). However, one parameter, K_Uu, representing the combined visual + vestibular contribution to UB stiffness, was larger in EO than in EC conditions across all stance widths. Because UB torque generated in proportion to K_Uu moves the UB toward earth vertical, the larger K_Uu values in EO compared with EC are consistent with vision enhancing the ability of the balance control system to maintain upright orientation of the UB during surface-tilt perturbations.

Sensitivity Analysis

Figure 6A summarizes the sensitivity analysis in EC conditions. These EC results were similar to EO results (not shown). This sensitivity analysis reveals that changes in many parameters influenced both UB and LB FRFs. This finding underscores the interdependency of the control of UB and LB segments such that parameter changes in the control of one segment influence sway dynamics in the other segment.

The sensitivity analysis shows that FRFs were more sensitive to changes in LB parameters than in UB parameters. In particular, FRFs were noticeably influenced by changes in six LB feedback parameters (K_Lsl, B_Lsl, K_Ll, B_Ll, B_Llu, and τ_L), whereas FRFs were influenced less by changes in UB feedback parameters (largest changes with K_Upu, B_Ul, and B_Ulu). These results suggest that the nervous system would need to more tightly regulate torque contributions from sensory signals encoding LB motion than from signals encoding UB motion.

The sensitivity analysis also revealed a frequency dependency in the manner in which parameter variations influenced FRFs. Figure 6B shows representative examples of MSE vs. frequency for changes in LB-to-surface proprioception parameters (K_Lsl and B_Lsl). Similar to results shown for K_Lsl, stiffness parameters in general influenced the lower frequencies (<1 Hz) to a greater extent than higher frequencies (>2 Hz). In contrast, the frequency range influenced by damping and time delay parameters was generally higher than for stiffness parameters. Because the experimental data showed amplitude- and vision-dependent changes primarily at lower frequencies (less than ∼1 Hz in the LB and less than ∼1–2 Hz in the UB) with almost no changes at higher frequencies (>2–3 Hz), our sensitivity analysis is consistent with the need for the balance control system to modulate primarily stiffness feedback to achieve the experimentally observed changes in FRFs across stimulus amplitude and between EO and EC conditions.

DISCUSSION

The current study extends the results of two previous studies that used the same set of experimental data (Goodworth and Peterka 2010, 2012). In our 2010 study we characterized frontal plane sway responses to surface-tilt perturbations of various amplitudes at each of four stance widths by using FRFs, IRFs, and measures of sway magnitude. These response characterizations provided detailed descriptive measures of balance control dynamics, but they only allowed for speculative assessments concerning how the balance control system used feedback from sensory systems to achieve the observed behavior. Our 2012 study developed a control system model that was able to account for the detailed FRFs and IRFs from the narrow stance condition and thus provided quantitative estimates of feedback parameters that were attributable to different sensory systems. The current study extends the previous narrow stance model to account for the experimental results from all stimulus amplitudes, stance widths, and visual conditions.

The end product of our current study is a model structure, with associated parameters, that represents a working hypothesis regarding the mechanisms that contribute to the feedback control of frontal plane balance. The model represents the feedback control as a set of pathways associated with motion information encoded by different sensory systems as well as feedback due to passive muscle/tendon mechanics.

The parameter variations that occurred across test conditions revealed how the feedback was reorganized to accommodate the different test conditions. Multiple parameter changes were needed to account for the variations in experimental FRFs across stimulus amplitude (Fig. 3 and Table 4) and stance width (Fig. 4 and Table 4) and between EO and EC conditions (Figs. 3 and 5). The entire set of parameter variations highlights the complexity of the coordinated changes that occur in the balance control system to accommodate changes in biomechanics, external perturbations, and availability of sensory orientation information.

Model Extensions Needed to Account for Wider Stance Data

In developing the previous narrow stance model, we sought to include the fewest number of parameters consistent with the model's ability to account for the detailed features of the narrow stance FRFs (Goodworth and Peterka 2012). We found it unnecessary to include a number of potential sensory feedback parameters because these parameters did not improve the model fits to the experimental FRF data. Specifically, we found it unnecessary to include torque feedback in UB control as well as UB parameters K_Ulu and B_Upu. Also, the LB stiffness parameter K_Llu was not included because it did not improve FRF fits to the narrow stance data.

However, we found that this narrow stance model was unable to account for the FRF data at wider stance widths. Therefore, following the methods we used to identify parameters needed in the narrow stance model, we added additional parameters to the original narrow stance model by systematically identifying and adding only those new parameters that improved the model fits to experimental FRFs at wider stance widths. We found that it was only necessary to add parameters to the UB control system. These included torque feedback parameters (G_Ut and τ_Ut) and an intersegmental proprioceptive stiffness parameter (K_Ulu). Similar to the narrow stance model, the inclusion of K_Llu and B_Upu did not improve model accuracy in the current study.

A concern was how consistent our narrow stance model was when additional parameters were included. A consistent result would be that parameter values identified in our previous narrow stance analysis (with fewer model parameters) would be essentially the same as the corresponding parameter values identified with the new model (with added parameters). Results of the current study for the narrow stance condition confirmed that our model was consistent with the addition of the parameters needed for the wider stance conditions. When the narrow stance FRFs were fit with the model with added parameters, the identified values of the added parameters converged to small values (see G_Ut and K_Ulu in Fig. 3, D and F, and Fig. 4). Additionally, for corresponding parameters in the previous and new models, the parameter values and the changes in these parameters across stimulus amplitudes were essentially identical to the previous results (Figs. 3B and 4B in Goodworth and Peterka 2012). Therefore, these results support our previous finding that position-based feedback of LB-to-UB proprioception and kinetic-based feedback makes only a minor contribution to UB control in narrow stance.

Control System Changes to Accommodate Wider Stance Widths

A major focus was to understand how the balance control system changes to maintain balance control at different stance widths. A common intuition is that “standing is sometimes made easier by adopting a wider stance” (Day et al. 1993) and that wide stance affords greater “ease of control” (Scrivens et al. 2008). Clearly, it is true that wider stance allows for the generation of larger corrective torques to resist large perturbations and for the body CoM to be displaced farther before moving outside of the base of support. However, for a mechanically unstable system controlled by time-delayed feedback, stability (in the control engineering sense) relies on the generation of the proper amount of corrective torque per unit of body motion. Instability can occur if the nervous system generates either too much or too little corrective torque in relation to body sway (Bingham et al. 2011; Peterka and Loughlin 2004).

For the control of frontal plane balance of a mechanical system representing the lower body, Bingham et al. (2011) identified stability criteria for feedback control parameters that were somewhat counterintuitive to the notion that wider stances afford greater “ease of control” if one assumes that “ease of control” implies that a wider range of feedback control parameters are compatible with stable control. Specifically, the Bingham study found that the ranges of stiffness and damping feedback control parameters compatible with stability were actually reduced at wider stance widths. Therefore, compared with narrower stance widths, at wider stance widths there is less room for error in the control mechanisms that set and regulate LB feedback. The magnitude of these feedback parameters was also lower for wider compared with narrower stances. The results of the Bingham study were obtained with the use of a one-degree of freedom body model that assumed that the UB moved with the pelvis. Because of this fairly unrealistic assumption, the possibility exists that different conclusions might be reached if one included separate LB and UB control, and thus included the possibility that LB motion could be influenced by UB motion through the torque interactions between body segments. Additionally, the Bingham model only included time-delayed feedback. One would expect the range of feedback control parameters compatible with stability would be larger if a significant amount of the corrective torque were provided by passive muscle/tendon mechanics that generate torque without time delay.

However, results from our identification of LB feedback control mechanisms are entirely consistent with the analysis of Bingham et al. (2011). First, our modeling results showed that parameters representing the torque contributions of muscle/tendon mechanics (K_Li and B_Li) were very small across all conditions compared with parameters representing active sensory feedback control. Therefore, the Bingham study's assumption that corrective torque is supplied by time-delayed feedback is consistent with our results.

Second, wider stances appear to be associated with lower values of LB feedback parameters such that less LB torque would be generated per unit of LB sway at wider stances compared with narrow stances. In EC conditions, most LB feedback parameters showed quite large decreases with increasing stance width (Table 4 and Fig. 3C), and these decreases were statistically significant. Although statistical results were not available for EO conditions, similar decreases in LB stiffness, damping, and torque feedback parameters were evident at increasing stance widths (Fig. 3E). The results are consistent with previous studies showing reductions in muscle activity with increasing stance width when healthy subjects respond to transient surface perturbations (Henry et al. 1998; Torres-Oviedo and Ting 2010).

In addition, our results suggest that the nervous system tightly regulates the values of active feedback control parameters in the wide stance condition. In wide stance, parameters were essentially the same for both EC and EO, and these parameters did not change in value with changing stimulus amplitudes. This inflexibility to changing amplitude and visual conditions in the wide stance condition (and also to a slightly lesser extent in medium stance) may be due to there being only a very narrow range of LB feedback parameters that are compatible with stability, as indicated by the Bingham study analysis.

Third, having independent UB control did not negate the apparent validity of the Bingham study analysis as it applies to LB control. All UB stiffness, damping, and torque feedback control parameters did change as a function of stance width (Table 4), and some of the largest UB parameter changes across stimulus amplitude occurred in the widest stance position (Fig. 3, D and F). Perhaps the nervous system allows large UB parameter changes with amplitude at wide stance to provide some compensation for the increasing perturbations to the UB (caused by torque interactions between body segments) in conditions where LB control mechanisms are not able to adjust to changing stimulus amplitudes.

Note that although the changes in LB stiffness and damping parameters with stance width indicate that there were neurally mediated changes in the active LB control mechanism, a change in a particular LB parameter does not specify the exact method the nervous system used to achieve the observed change in LB control (see Appendix of Goodworth and Peterka 2012 for a detailed discussion). Specifically, our LB modeling assumed that LB feedback torque was equally distributed between ankle and hip joints. However, the distribution of LB torque can have a large impact on the coupling between LB torque and LB acceleration. For example, in parallel stance (where the LB forms a parallelogram), a given torque applied about an ankle joint or a hip joint would be equally effective in accelerating the LB. However, in stances narrower than parallel, a given torque applied about an ankle joint is more effective in accelerating the LB than if the same torque were applied about a hip joint; and in stance widths greater than parallel, the opposite occurs where a given hip torque is more effective than the same magnitude of ankle torque. This mechanical coupling may explain the quiet stance results by Winter et al. (1996), which indicated that ankle torque dominates tandem stance control, whereas hip torque is more dominate at wider stances. Therefore, the LB stiffness and damping parameter values cannot be interpreted as indicating the absolute value of total LB torque generated because, for example, in wide stance, the same LB motion could be produced with a lower magnitude of total LB torque if all of that torque were applied to the hip joints. Note that parameter values for LB torque feedback are unaffected by the distribution of LB torque. Therefore, the reduction in LB torque feedback (G_Lt) with increasing stance width does unambiguously imply that subjects use LB kinetic cues to a lesser extent with increasing stance width.

Sensory Reweighting

Results from the current study showed some evidence for the contribution of sensory reweighting to frontal plane balance control with changing stimulus amplitude. However, the identified parameter changes with amplitude and stance width revealed a more complex pattern of sensorimotor regulation than has been described in most previous studies that have focused on the motion of the CoM (Cenciarini and Peterka 2006; Kiemel et al. 2006; Peterka 2002). The evidence for this more complex sensorimotor regulation is indicated by several observations of our results compared with previous studies as discussed below.

Previous studies have shown that sway responses to surface or visual tilt stimuli plateau at larger stimulus amplitudes (Goodworth and Peterka 2010; Peterka 2002; Peterka et al. 2011). With this pattern of stimulus-response data, FRFs showed the lowest FRF gains on tests performed with the largest stimulus amplitude (Cenciarini and Peterka 2006; Goodworth and Peterka 2010; Kiemel et al. 2006; Maurer et al. 2006; Mergner et al. 2005; Oie et al. 2002; Peterka 2002; Peterka et al. 2011). These FRF gain reductions with increasing stimulus amplitude have been interpreted as being indicative of a sensory reweighting phenomenon whereby the source of sensory orientation information used for balance control shifts from one sensory system to another. For example, with a surface-tilt stimulus the FRF gains will be high if the test subject is primarily utilizing proprioceptive cues that signal body sway relative to the surface. Alternatively, if the subject is primarily utilizing vestibular or visual cues that provide accurate information about body motion relative to spatial vertical, then the body sway evoked by the surface-tilt stimulus will be low and the FRF gains will be low.

In the current study, evidence for sensory reweighting with changing stimulus amplitude was present in LB active control mechanisms but not in UB control. The primary LB feedback parameter changes consistent with sensory reweighting were the increase in the vestibular or visual + vestibular stiffness parameter K_Ll with increasing stimulus amplitude accompanied by a simultaneous decrease in the proprioception stiffness parameter K_Lsl signaling LB orientation with respect to the surface (most evident in narrow, parallel, and medium stances). There were some apparent amplitude-dependent changes in UB parameters, although the statistical interpretation of amplitude-dependent changes was complicated by a significant interaction of amplitude with stance width (Table 4). Considering the narrower stance width conditions, the UB stiffness parameters encoding pelvis-to-UB (K_Upu) and LB-to-UB proprioception (K_Ulu) decreased with increasing stimulus amplitude in both EC and EO conditions. However, unlike LB control, there was no increase in another UB stiffness parameter to substitute for the decreases in these proprioceptive stiffness parameters (K_Upu and K_Ulu).

Our results imply that the nervous system can independently regulate the contributions of position and velocity feedback to achieve balance control, consistent with other studies in motor control (Hwang et al. 2003). Models used in many previous studies assumed that sensory weights scaled the sensory system contributions to corrective torque generation (Cenciarini and Peterka 2006; Peterka 2002; van der Kooij and Peterka 2011). This assumption effectively meant that the nervous system changes stiffness (position related) and damping (velocity related) contributions to corrective torque in equal proportion. Simpler models using sensory weights were able to account for experimental FRFs characterizing CoM motion up to about 1.5 Hz. However, to account for both LB and UB motion obtained from experiments evoking body motion across a wider bandwidth, we found it necessary to abandon the previous concept of using a single sensory weight factor to scale both the position- and velocity-related contributions. Rather, our model included separate representations of stiffness and damping feedback, and these parameters were allowed to vary independently to account for experimental results. When this was done, results in EC conditions showed that LB sensory reweighting was mostly determined by amplitude-dependent changes in stiffness parameters with essentially no corresponding changes in damping parameters. The sensitivity analysis also showed that changes in stiffness parameters (and LB parameters in general) had the most influence on sway. Together, these results are consistent with the idea that the nervous system modulates parameters that have the largest effect to reach its goal. In EO conditions, results did show corresponding amplitude-dependent changes in both stiffness and damping parameters (K_Ll and B_Ll increasing, and K_Lsl and B_Lsl decreasing with increasing amplitude), although the changes were such that a single weight factor could not account for the observed changes in these pairs of stiffness and damping parameters.

For LB control, subjects used sensory reweighting across stimulus amplitude most at narrow and parallel stance widths. Reweighting diminished with increasing stance width to the point where no LB reweighting occurred in the wide stance condition. In narrower stance conditions, reweighting limits the body sway evoked by larger amplitude surface-tilt perturbations and thus facilitates the functionally important task of keeping the CoM within the base of support. The larger base of support at wider stances diminishes the functional need to limit sway evoked by perturbations and possibly explains the observed absence of reweighting. For example, the CoM would need to tilt about 7° to reach the edge of the base of support in narrow stance and about 15° in wide stance. However, as described in the previous section, the absence of reweighting could also be necessitated by constraints on the range of feedback parameters that are compatible with stable LB control in wide stance.

Sensory reweighting in LB control also influenced UB motion. In EC conditions, especially at narrow and parallel stance widths, UB FRFs showed amplitude-dependent gain reductions without UB FRF phase changes. Previously, this pattern of FRF changes with amplitude has been attributed to changes in balance control parameters consistent with sensory reweighting (Peterka 2002, 2003). However, our results showed that most UB stiffness and damping parameters did not change with amplitude and those that did (mainly K_Upu and weakly K_Ulu) did not change in a manner indicative of sensory reweighting. The major contribution to the UB FRF gain reductions with increasing amplitude was the sensory reweighting changes in LB control. That is, the sensory reweighting in LB control limited the amplitude of LB motion in response to larger amplitude stimuli, and therefore limited that magnitude of intersegmental interaction torques that perturb the UB. Thus the reduction of UB FRF gains at larger stimulus amplitudes was not due to sensory reweighting in UB control, but rather was primarily due to amplitude-dependent changes in LB control.

Sensory reweighting also occurred when subjects were given access to accurate visual orientation cues in EO tests. These vision-related reweighting changes were complex in that they depended on stance width. For LB control in the narrower stance conditions, the visual reweighting was represented by an increase in vestibular + visual parameter (K_Ll) and a corresponding decrease in surface-to-LB proprioception (K_Lsl). These changes account for the reduced FRF gains in EO compared with EC conditions. The visual + vestibular damping parameter B_Ll also increased in EO compared with EC (where B_Ll represented only the vestibular contribution). However, in the wide stance condition, LB control parameters were essentially identical in EO and EC conditions, indicating that access to accurate visual orientation cues had no influence on LB balance control at wide stance. This evidence for lack of a visual contribution to balance at wide stance is consistent with previous observations that the magnitude of frontal plane spontaneous sway was not influenced by vision (Day et al. 1993; Goodworth and Peterka 2010).

Clinical and Research Implications

Our results have both clinical and research design implications. It is common to allow participants to adopt a comfortable stance width in tests of balance function. However, to the extent that comfortable stance width varies between subjects and with age (McIlroy and Maki 1997; Swanenburg et al. 2010) and neurological impairment (Horak et al. 2005), our results indicate that experimenters should expect that balance measures related to the frontal plane sway will be significantly influenced by the neural control properties and biomechanics that vary with stance width.

Our results also imply that therapists should consider providing feedback and exercises that are specific for a particular stance width and balance disorder. For example, because vision had only a minor influence on parameters in wide stance width, patients may be instructed to adopt a wider stance in situations where vision is limited. Similarly, exercises designed to initiate or evaluate sensory reweighting will likely be most effective at narrower stances. In contrast, exercises designed to modify the contribution of sensory feedback to UB control may be more beneficial at wide stances, because the UB control system exhibited large changes across stimulus amplitude in wide stance. Finally, because LB stiffness parameters were generally modulated to a greater extent than damping parameters and postural dynamics were most sensitive to changes in LB stiffness parameters, it may be most beneficial for clinicians to target therapy toward modulation of position-related kinematic feedback for LB control. For example, biofeedback based on body sway position may be more effective than feedback based on sway velocity (Goodworth et al. 2009).

Considerations for Model-Based Interpretation of Frontal Plane Balance

Knee flexion.

To avoid provoking a knee flexion/extension strategy that would greatly increase the complexity of modeling efforts, we purposely limited the magnitude of our surface-tilt stimuli to fairly low values (4° peak-to-peak maximum amplitude). The limited amplitudes we used are behaviorally relevant. Humans normally stand with a predominantly extended posture in both legs, and the legs remain extended while frontal plane balance corrections are made via corrective torques generated in ankle and hip joints (Winter et al. 1996). Furthermore, the use of experimental conditions that minimized subjects' use of knee flexion allowed us to compare our model results with the theoretical predictions developed by Bingham et al. (2011).

However, larger stimulus amplitudes that evoke a flexion/extension strategy are also behaviorally relevant. With larger surface rotations, the overall CoM displacement caused by a mediolateral perturbation is less if the subject flexes the uphill leg (Küng et al. 2009). Without leg flexion, the pelvis orientation is strictly a function of stance width, lower body sway angle, and the tilt angle of the support surface. Leg flexion allows for the mechanical decoupling of the otherwise fixed functional relationship of pelvis orientation to stance width, lower body sway angle, and the surface tilt angle, but then also introduces the need to control the knee flexion angle. One could hypothesize that the decoupling of pelvis orientation would be advantageous for the control of UB orientation. In particular, our results identified a sizable contribution to UB corrective torque from passive mechanisms that tend to orient the UB perpendicular to the pelvis. By using leg flexion, it would be possible to control pelvis orientation such that the pelvis remained oriented in an approximate earth horizontal position independent of lower body sway and surface tilt. In this case, the passive mechanical contributions to upper body torque would help maintain a vertical orientation of the trunk.

Neural coordinate transformations.

We assumed that the nervous system is able to process information from peripheral sensory receptors to obtain accurate internal sensory-derived representations for the various body segment angles (and angular velocities), joint angles (and angular velocities), and torques listed in Table 1. Information from vestibular receptors was assumed to contribute to the sensory signals representing θ_L and θ_U (and their derivatives). We implicitly assumed that peripheral vestibular signals from the semicircular canals and otolith organs are processed centrally via a canal-otolith fusion mechanism (Angelaki et al. 1999; Merfeld and Zupan 2003; Mergner et al. 2009) that provides an accurate, wide-bandwidth representation of head angular velocity in the vertical plane (i.e., compensates for the high-pass filter properties of the semicircular canals) and an estimate of the tilt orientation of the head with respect to gravity. In our model, we further assumed that these vestibular-derived signals of head angular velocity and orientation would be further combined with proprioceptive information, signaling head with respect to trunk and with respect to lower body motion and orientation, to obtain vestibular-derived signals representing θ_L and θ_U. A linear head acceleration signal of otolith origin was not separately represented in our model because our implicit assumption about canal-otolith fusion effectively accounted for the tangential and gravity-related acceleration information encoded by the otoliths during rotational head and body motions.

Model limitations.

The method we used to identify model parameters was limited in that we were unable to identify parameters compatible with stable control when fitting EO FRFs from some individual subjects in wider stance conditions even though stable fits to the across-subject average EO FRFs were obtainable. We do not know with certainty why we were unable to fit EO FRF data from some individuals and not others. Difficulty in fitting FRF data at wider stances could arise from a combination of factors including the narrow range of parameters compatible with stability (Bingham et al. 2011) and the fact that our fit criterion, based on the frequency domain comparisons of model and FRF data, does not guarantee stability. Without augmenting our fit criteria to include some constraint to enforce stability, the methods we used to identify model parameters may be close to an upper limit such that it will not be possible to use these methods to identify parameters in body models that include additional segments (e.g., head and neck segments or multiple spinal segments).

Alternatively, it may be that our model structure is overly simplified or is fundamentally wrong such that no set of parameter values could provide a good fit to the FRF data from some individuals and also be compatible with stability. An example of simplification is that the upper body was represented as a single segment. However, spinal motion is more distributed, and head-on-trunk motion was not represented in our model. Additionally, we only considered that control was provided by passive muscle/tendon properties and by time-delayed feedback. Alternative models might include ones with predictive control or intermittent control with prediction that reduce the sensitivity to time delays in feedback control (Gawthrop et al. 2009, 2011). Indeed, balance control in the wide stance condition may provide a good test case for identifying the necessity of prediction contributing to frontal plane balance control because conventional continuous, time-delayed feedback control affords only marginal stability.

GRANTS

This work was supported by National Institutes of Health Grants R01 AG17960 and R01 DC010779 and a University of Hartford Greenberg Grant.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.D.G. and R.J.P. conception and design of research; A.D.G. and R.J.P. performed experiments; A.D.G., P.M., and R.J.P. analyzed data; A.D.G. and R.J.P. interpreted results of experiments; A.D.G. and R.J.P. prepared figures; A.D.G. and R.J.P. drafted manuscript; A.D.G., P.M., and R.J.P. edited and revised manuscript; A.D.G., P.M., and R.J.P. approved final version of manuscript.

APPENDIX

The model in the current study approximated body mechanics by using a multisegment model. Unlike single-segment mechanics, where motion can be represented with relatively few terms (e.g., Peterka 2003), multisegmental mechanics in the frontal plane are far more complex. A previous publication (Goodworth and Peterka 2012) described the methods we used to derive the linearized equations of motion representing the body mechanics. This Appendix provides an overview of these equations, expressed in the Laplace domain, and describes how equations representing feedback control mechanisms hypothesized in our model were combined with the body mechanics equations to calculate FRFs that characterize the dynamics of LB and UB motion as a function of the surface-tilt stimulus.

The closed-chain mechanics of the LB (2 leg segments and a pelvis segment) and the stance surface were represented as an equivalent single LB segment. The equation of motion for this LB segment is

$$(J_{\text{L}}{s}^2-A_{\text{L}}g)\cdot {\theta }_{\text{L}}(s)+\left(J_{\text{LU}}{s}^2-A_{\text{LU}}g\right)\cdot {\theta }_{\text{U}}(s)+\left(J_{\text{LS}}{s}^2-A_{\text{LS}}g\right)\cdot {\theta }_{\text{S}}(s)=R\cdot {\text{T}}_{\text{L}}(s)$$ (A1)

where s is the Laplace variable, θ_L(s)and θ_U(s) are the Laplace domain representations of the LB and UB segment angles with respect to vertical, respectively, θ_S(s)is the angular tilt of the surface with respect to horizontal, and g is the acceleration due to gravity. The LB corrective torque, T_L(s), is generated by passive and active feedback mechanisms and is assumed to be applied to the LB segment about an equivalent LB ankle joint located at the surface level.

The LB single-segment representation of the closed-chain mechanics accounts for the fact that LB mechanics vary as a function of stance width and also that the effectiveness of T_L in moving the LB depends on whether the actual LB corrective torque was generated at the hip joints or ankle joints. Formulation of this single-segment representation required that the inertial (J) and gravitational parameters (A) in Eq. A1 have different values at different stance widths. More specifically, these parameters varied as a function of the ratio of stance width, S, to hip width, W. The values of the inertial and gravitational parameters in Eq. A1 as a function of S/W are given in Fig. A1D in Goodworth and Peterka (2012) for the mean body mass and segment dimensions of subjects included in this study.

Additionally, the effectiveness of T_L in evoking frontal plane motion is a function of both S/W and the distribution of the total corrective torque (the sum of torques exerted about the 2 ankle joints and the 2 hip joints) between ankle and hip joints. For stance widths wider than parallel stance, hip torque is more effective than ankle torque in accelerating the LB. The opposite is true for stance widths narrower than parallel. The parameter R in Eq. A1 scales the value of T_L to account for the influence of stance width and torque distribution (see Eq. A3 and Fig. A1F in Goodworth and Peterka, 2012).

The equation of motion for the UB segment is

$$J_{\text{UL}}{s}^2\cdot {\theta }_{\text{L}}(s)+\left(J_{\text{U}}{s}^2-A_{\text{U}}g\right)\cdot {\theta }_{\text{U}}(s)={\text{T}}_{\text{U}}(s),$$ (A2)

where T_U(s) is the Laplace domain representation of the UB torque that is generated by both passive and active feedback mechanisms. The parameters in Eq. A2 are independent of stance width and are given in Fig. A1E in Goodworth and Peterka (2012) for the mean body mass and segment dimensions of subjects included in this study.

Passive and active feedback mechanisms (Fig. 3, A and C) contribute to T_L and T_U. The passive contributions are given by

$${\text{T}}_{\text{Lpas}}(s)=K_{\text{Li}}\cdot \left[{\theta }_{\text{S}}(s)-{\theta }_{\text{L}}(s)\right]+B_{\text{Li}}\cdot s\cdot \left[{\theta }_{\text{S}}(s)-{\theta }_{\text{L}}(s)\right]$$ (A3)

and

$${\text{T}}_{\text{Upas}}(s)=K_{\text{Ui}}\cdot \left[{\theta }_{\text{P}}(s)-{\theta }_{\text{U}}(s)\right]+B_{\text{Ui}}\cdot s\cdot \left[{\theta }_{\text{P}}(s)-{\theta }_{\text{U}}(s)\right]$$ (A4)

The pelvis angle θ_P in Eq. A4 is itself a function of θ_S(s) and θ_L(s) (see Eq. A4 in Goodworth and Peterka 2012) such that T_Upas is given by

$${\text{T}}_{\text{Upas}}(s)=K_{\text{Ui}}\cdot \left[{\text{P}}_{\text{R}}{\theta }_{\text{S}}(s)+(1-{\text{P}}_{\text{R}}){\theta }_{\text{L}}(s)-{\theta }_{\text{U}}(s)\right]\dots +B_{\text{Ui}}\cdot s\cdot \left[{\text{P}}_{\text{R}}{\theta }_{\text{S}}(s)+\left(1-{\text{P}}_{\text{R}}\right){\theta }_{\text{L}}(s)-{\theta }_{\text{U}}(s)\right]$$ (A5)

where P_R is a scale factor that characterizes how the pelvis angle changes as a function of the surface angle and LB sway angle. The value of P_R varies with S/W (Fig. A1C in Goodworth and Peterka 2012).

The equations for the active feedback control contributions to T_Lact(s) and T_Uact(s) were formulated similarly to the passive components but were more complex due to there being time delay terms, a greater number of kinematic sensory feedback pathways, and kinetic sensory feedback. The equation for LB torque generated by sensory feedback is given by

$${\text{T}}_{\text{Lact}}(s)=\left\{-\left(K_{\text{Li}}+K_{\text{Lsl}}\right)\cdot {\theta }_{\text{L}}(s)+K_{\text{Lsl}}\cdot {\theta }_{\text{S}}(s)+\left(B_{\text{Llu}}-B_{\text{Li}}-B_{\text{Lsl}}\right)\cdot s\cdot {\theta }_{\text{L}}(s)-B_{\text{Llu}}\cdot s\cdot {\theta }_{\text{U}}(s)+B_{\text{Lsl}}\cdot s\cdot {\theta }_{\text{S}}(s)\dots +\frac{G_{\text{Lt}}}{{\tau }_{\text{Lt}}\cdot s+1}\left[{\text{T}}_{\text{Lact}}(s)+{\text{T}}_{\text{Lpas}}(s)\right]\right\}{e}^{-{\tau }_{L}s}$$ (A6)

and that for the active UB torque is

$${\text{T}}_{\text{Uact}}(s)=\left\{-\left(K_{\text{Ul}}+K_{\text{Upu}}+K_{\text{Ulu}}\right)\cdot {\theta }_{\text{U}}(s)+K_{\text{Ulu}}\cdot {\theta }_{\text{S}}(s)+K_{\text{Upu}}\cdot {\theta }_{\text{P}}(s)-\left(B_{\text{Ul}}+B_{\text{Ulu}}\right)\cdot s\cdot {\theta }_{\text{U}}(s)+B_{\text{Ulu}}\cdot s\cdot {\theta }_{\text{L}}(s)\dots +\frac{G_{\text{Ut}}}{{\tau }_{\text{Ut}}\cdot s+1}\left[{\text{T}}_{\text{Uact}}(s)+{\text{T}}_{\text{Upas}}(s)\right]\right\}{e}^{-{\tau }_{U}s}\mathrm{.}$$ (A7)

Note that the T_Uact Eq. A7 includes the pelvis angle θ_P. As in the calculation for T_Upas, θ_P is a function of θ_L and θ_S and can be replaced by θ_P(s) = P_Rθ_S(s) + (1 − P_R)θ_L(s).

The FRFs describing the dynamic characteristics of LB and UB sway evoked by the surface-tilt stimulus can be determined by using the above set of equations (A1–A3, A5–A7) to calculate the ratios θ_L(s)/θ_S(s) and θ_U(s)/θ_S(s) and then substituting s = j2πf, where j is the imaginary number √−1 and f is the stimulus frequency (in Hz). This substitution results in FRFs expressed as a set of complex (real and imaginary) values as a function of frequency. FRF gain and phase values then can be calculated from the real and imaginary parts of the FRFs at each frequency of interest, such as those corresponding to the experimental data.

We note that it would be possible, but not practical, to solve these equations by hand to obtain closed-form FRF equations for θ_L(s)/θ_S(s) and θ_U(s)/θ_S(s). Therefore, the Matlab Symbolic Math Toolbox was used to obtain the closed-form equations, and these symbolic equations were used in the optimization procedures used to identify the various feedback and time-delay parameter values that best accounted for the experimental FRF data.

Equations describing very simple balance control models that represent the body as a single segment can provide some insight into how balance control is accomplished and into constraints on control parameters (Peterka 2003). However, the closed-form equations for the model in the current study provided us with no particular insights beyond the general appreciation for the complexity of a multisegmental system.