On the localization of complex sounds: temporal encoding based on input-slope coincidence detection of envelopes

Abstract

Behavioral and neural findings demonstrate that animals can locate low-frequency sounds along the azimuth by detecting microsecond interaural time differences (ITDs). Information about ITDs is also available in the amplitude modulations (i.e., envelope) of high-frequency sounds. Since medial superior olivary (MSO) neurons encode low-frequency ITDs, we asked whether they employ a similar mechanism to process envelope ITDs with high-frequency carriers, and the effectiveness of this mechanism compared with the process of low-frequency sound. We developed a novel hybrid in vitro dynamic-clamp approach, which enabled us to mimic synaptic input to brain-slice neurons in response to virtual sound and to create conditions that cannot be achieved naturally but are useful for testing our hypotheses. For each simulated ear, a virtual sound, computer generated, was used as input to a computational auditory-nerve model. Model spike times were converted into synaptic input for MSO neurons, and ITD tuning curves were derived for several virtual-sound conditions: low-frequency pure tones, high-frequency tones modulated with two types of envelope, and speech sequences. Computational models were used to verify the physiological findings and explain the biophysical mechanism underlying the observed ITD coding. Both recordings and simulations indicate that MSO neurons are sensitive to ITDs carried by spectrotemporally complex virtual sounds, including speech tokens. Our findings strongly suggest that MSO neurons can encode ITDs across a broad-frequency spectrum using an input-slope-based coincidence-detection mechanism. Our data also provide an explanation at the cellular level for human localization performance involving high-frequency sound described by previous investigators.

interaural time (itd) and level differences (ILD) are principal acoustic cues for sound localization in the azimuth (review, Grothe et al. 2010). An ITD occurs when a sound source is located at different distances from the two ears, thus generating a disparity in the arrival times. ILDs are created when the head attenuates sound at the contralateral ear. The conventional duplex theory states that ITD is useful at low frequencies where auditory neurons phase-lock to the carrier phase, while ILD is useful at high frequencies (Mills 1972; Rayleigh 1907; Stevens and Newman 1934). However, human listeners can lateralize high-frequency sound with envelope ITDs in the absence of ILDs (Bernstein and Trahiotis 1985, 2002, 2003, 2008; Buell et al. 2008; Rowan and Lutman 2006, 2007; Zhang and Wright 2007).

In mammals, ITD is first encoded by binaural neurons in the medial superior olive (MSO) (reviews, Joris et al. 1998; Palmer and Grothe 2005). The ITD sensitivity of MSO neurons is largely due to the presence of a low-threshold potassium current (I_KLT). Using electrical stimulations, Svirskis et al. (2002) and Jercog et al. (2010) showed that I_KLT makes the cells favorably sensitive to fast-rising slopes of excitatory postsynaptic currents (EPSCs) during coincidence detection, and the sensitivity is affected by inhibition (Jercog et al. 2010; Roberts et al. 2013); slope sensitivity was reviewed in Golding and Oertel (2012).

Scant physiological data are available on the envelope ITD sensitivity of high-frequency MSO neurons (Batra et al. 1997; Guinan et al. 1972; Joris et al. 1998; Spitzer and Semple 1995; Yin and Chan 1990). Behaviorally, the envelope ITD sensitivity of human listeners to sinusoidal amplitude modulation (SAM; Fig. 1A, red) is notably poorer than the ITD sensitivity to unmodulated low-frequency tones (Bernstein and Trahiotis 2002, 2003). An equitable test for envelope ITD sensitivity should employ stimuli that are comparable to low-frequency carriers. From such considerations, emerged the suggestion of a transposed envelope for high-frequency carriers, i.e., a half-wave-rectified low-frequency wave form (Fig. 1A, green), that should lead to auditory nerve (AN) spiking similar to that for pure tones (van de Par and Kohlrausch 1997). Indeed, the ITD sensitivities for transposed and low-frequency pure tones compare well in some parameter regimes (Fig. 1D) (Bernstein and Trahiotis 2002, 2003). Consistent with these findings, recordings in the inferior colliculus (IC) show similar ITD tuning curves with low-frequency pure tones and high-frequency tones modulated with transposed envelopes (Griffin et al. 2005). However, recordings in AN fibers predict that transposed stimuli (for higher than near-threshold intensities) should produce worse ITD sensitivity than pure tones (Dreyer and Delgutte 2006). No physiological recordings under transposed stimuli have been reported in intermediate levels, where a central mechanism must be responsible for extracting ITD sensitivity to envelope from the afferents.

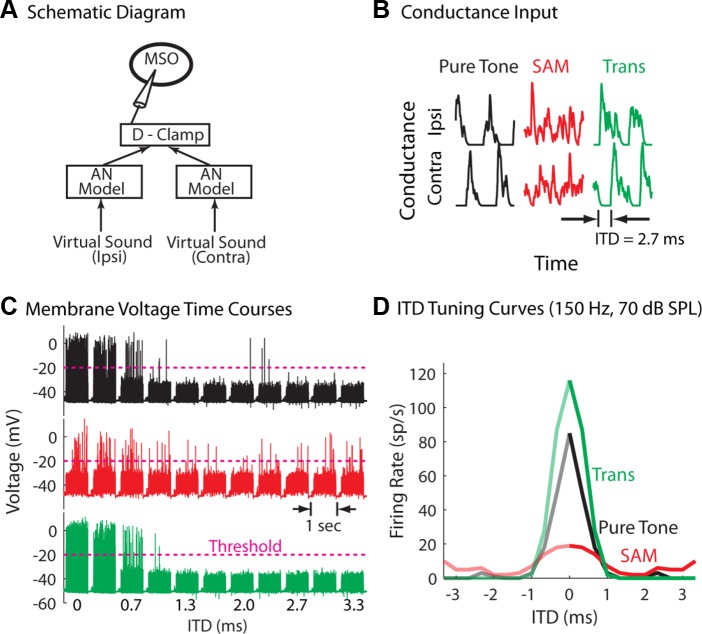
Fig. 1.

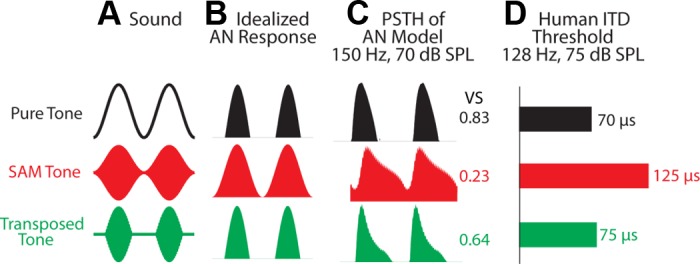
Stimulus types with corresponding physiological/psychophysical responses. A: virtual sound waveforms. The frequency of the pure tone is equal to the modulation frequency, m_f, of the sinusoidal amplitude modulation (SAM) tone and the transposed tone. B: idealized auditory-nerve (AN) responses. C: period histograms of the AN model for tone/m_f = 150 Hz. The numbers are the vector strength (VS) of the AN model response. Note that the peristimulus time histograms (PSTHs) of the AN model to both the pure tone and the transposed tone have fast-rising slopes and intercycle gaps. D: human interaural time difference (ITD) threshold (i.e., the smallest detectable left-ear-leading ITDs) estimated from Bernstein and Trahiotis (2002, their Fig. 3). SPL, sound pressure level.

Our study introduces a novel dynamic-clamp approach to assess in vitro MSO responses to excitatory events elicited by virtual sounds, pure tones and complex sounds. We hypothesize that the intrinsic biophysics of phasic-firing MSO neurons leads to increased ITD-sensitivity for input trains drawn from (AN-like) peristimulus time histograms (PSTHs) that have sharp rising phases and gaps between successive envelope events. We demonstrate with a computational model and experimentally that this sensitivity of MSO neurons to the rising slope of summed EPSCs (referred to as input slope) enables the neurons to encode ITDs carried by transposed envelopes of high-frequency sounds [carrier on-characteristic frequency (CF) AN fibers] as efficiently as they do for low-frequency tones. In addition, we illustrate the potential for MSO neurons to encode ITDs carried by either or low- or high-frequency AN filtered virtual speech sequences.

METHODS

Whole cell recordings.

Gerbils (Meriones unguiculatus) aged postnatal days (P) 15–24 (with a few younger animals, P12 and 13, for selected illustration) were used to obtain whole cell recordings in 150- to 200-μm horizontal brain stem slices. All protocols were reviewed and approved by New York University Institutional Animal Care and Use Committee. The recording pipette (4–7 MΩ) contained a current-clamp solution (in mM): 127.5 potassium-gluconate, 0.6 EGTA, 10 HEPES, 2 MgCl₂, 5 KCL, 2 ATP, 10 phosphocreatinine, and 0.3 GTP (pH 7.2). During recordings, slices were placed in a chamber with artificial cerebrospinal fluid containing (in mM) 125 NaCl, 4 KCl, 1.2 KH₂PO₄, 1.3 MgSO₄, 26 NaHCO₃, 15 glucose, 2.4 CaCl₂, and 0.4 l-ascorbic acid (pH 7.3 when bubbled with 95% O₂ and 5% CO₂) at 32 ± 1°C. The perfusion rate of the oxygenated artificial cerebrospinal fluid in the recording chamber was 2 ml/min.

An Axoclamp2A amplifier, in combination with Labview (National Instruments), was used for stimulus generation, balance of series resistance, and data acquisition. The recorded data were then analyzed with Matlab (MathWorks). The Axoclamp amplifier allowed series-resistance compensation and capacitance neutralization. The sampling rate was 10 kHz.

Virtual sound stimuli.

Basic virtual sound stimuli were similar to those used in a human psychophysics study (Bernstein and Trahiotis 2002), including a low-frequency tone (Fig. 1A, black), a SAM tone (red), and a transposed tone (green). The modulated high-frequency tones had a carrier rate of 5 kHz and a modulation frequency, m_f, equal to the low-frequency tone's frequency (e.g., 150 Hz). The envelope of the SAM was a regular sinusoid, 1 + sin(2π m_f t). The envelope of the transposed-tone was a half-wave rectified sinusoid, |sin(2π m_f t)|₊. The duration of the sound was 1 s. At 70-dB sound pressure level (SPL) and 150 Hz, each AN input fired ∼0.6, 1.2, and 1.0 spikes/cycle for the low-frequency tone, the SAM and the transposed tones, respectively.

One-second speech sequences were also tested to demonstrate, more generally, that the fast-rising envelopes and gaps of more general sounds (like speech) can be used by MSO neurons and models for ITD detection. We used two speech sequences from the HINT data base [HINT: Hearing in Noise Test, see Nilsson et al. (1994)]: the first second of “The boy fell from the window” (SP #2) and “Her shoes were very dirty” (SP #3), and the whole sentence of “Take a look at this” (SP #1). Most neurons were tested only with SP #1.

Statistical analyses.

For statistical analyses, because the data for rates as well as half-widths for 150 Hz as well as for 300 Hz, and between 150 Hz and 300 Hz, were not normally distributed, a Shapiro-Wilcoxon W (goodness-of-fit) test was performed to reveal whether there was a main effect. This was followed by pairwise comparison by a χ² test. Paired comparisons only for significantly different means are shown in results. All statistical tests were performed with a SAS-based JMP software package.

Dynamic-clamp procedure.

An in vitro dynamic-clamp approach is used to study the ITD coding by MSO neurons in response to the virtual sound (Fig. 2A). For each simulated ear, a virtual sound generated in the computer was used as input to a computational AN model (Zilany et al. 2009), whose outputs were spike times of m AN fibers, t_i (i = 1, …, n_m-left or n_m-right); we used on-CF AN fibers for the pure tones and carrier tone on-CF fibers for the modulated sounds. Each spike time, t_i, triggered a brief conductance time course in the form of an α-function, f_α(t) = (t/τ)·e^{1 − t/τ}, with τ = 0.2 ms. We are treating the antero-ventral cochlear nucleus as a simple relay in this study, as done in (Wang et al. 2014). Thus the overall conductance input (G_in) to an MSO neuron is

$$G_{\text{in}}\left(t\right)=G_{\text{syn}}{\displaystyle \sum _t}{f}_{\alpha }\left(t-t_i\right),i=1,\dots ,n_{\text{m-left}},1,\dots ,n_{\text{m-right}}$$ (1)

Synaptic strength, G_syn, was adjusted to yield a large firing-rate range for each stimulus type, as illustrated by Fig. 3. Here we chose a medium spontaneous firing rate for the AN model, because physiological recordings by Dreyer and Delgutte (2006) show that AN fibers with low/medium spontaneous firing rate have better phase locking to the above three stimuli than high spontaneous-rate fibers (their Fig. 6). We chose m = 10 or 15 (see the following subsection, Model simulations, for our rationale for choosing m).

Fig. 2.

An example of measuring ITD sensitivity in vitro to virtual sound. A: schematic diagram of the hybrid approach used to study in vitro neuronal responses to virtual binaural sounds. The AN model (Zilany et al. 2009) generates spike times to virtual binaural sound. The dynamic clamp (D-Clamp) process converts “synaptic” conductance transients triggered by the spikes into synaptic current input (see Eq. 2). B: randomly selected conductance input over two cycles for the low-frequency pure tone, SAM tone, and the transposed tone. Here the conductances are normalized by their peak values for illustration purpose. In this example, the average peak conductances over cycles for the three stimuli were 2.9, 3.0, and 4.1 nS, respectively. C: membrane voltage traces (each 1-s long) for various ITD values, as indicated on the horizontal axis. The dashed lines indicate the threshold for action-potential recognition. When action potentials were not well above the excitatory postsynaptic potentials (EPSPs), the determination of the threshold was verified by inspecting individual action potentials (see text). D: average firing rate derived from C. The firing rates for the negative ITDs are presented as mirror images of the firing rates for the positive ITDs (see text). This medial superior olivary (MSO) neuron recording was obtained from a representative postnatal day 17 (P17) gerbil brain slice.

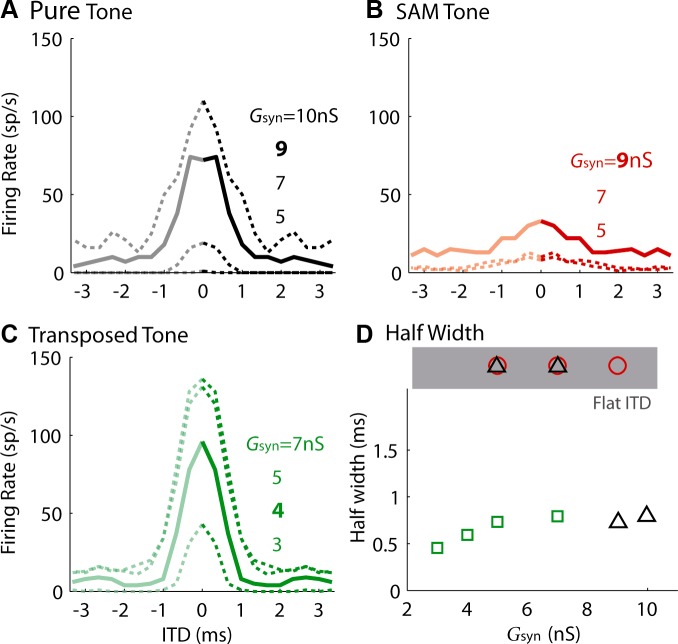
Fig. 3.

Effect of maximum synaptic strength, G_syn (see Eq. 1), on ITD tuning of the pure tone (A), the SAM tone (B), and the transposed tone (C). The solid lines and the corresponding legend in bold were used to represent the neuron's ITD tuning for the population result in Fig. 4. The unitary EPSPs elicited by those chosen values of G_syn were typically 3–4 mV. D: half-width as a function of synaptic strength. Note that the half-width was not computed for ITD tuning curve with a firing-rate range <30 spikes (sp)/s (marked as Flat ITD, shaded area). Tone/m_f = 150 Hz. Sound level = 70-dB SPL.

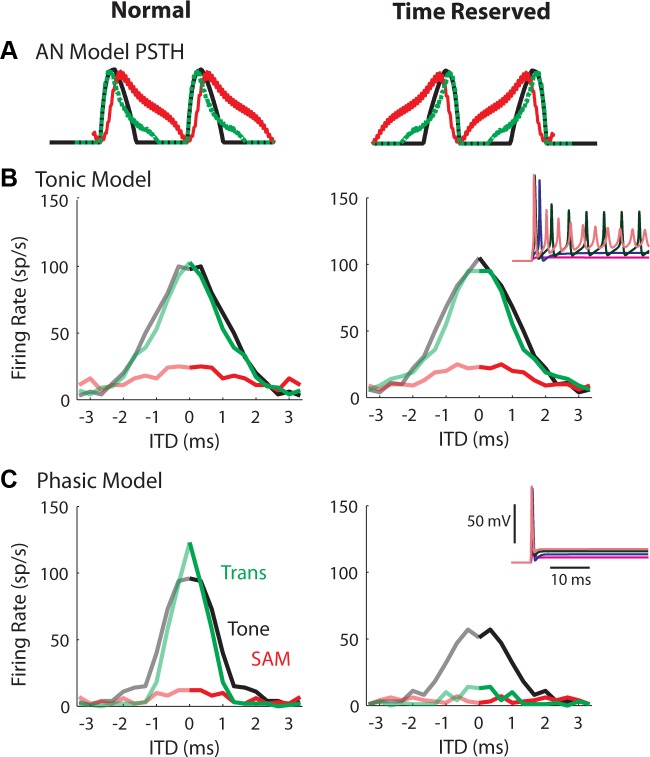
Fig. 6.

ITD tuning curves for sounds obtained from the tonic (B) and the phasic (C) models. Left: original AN input. Right: time-reversed AN input. The inset plots show the membrane responses to a step current input at various amplitudes (2, 5, 10, and 15 nS for the tonic and 10, 25, 50, and 75 nS for the phasic models, respectively). A: the AN input was similar to what MSO neurons received (Fig. 5A), and the synaptic strengths were adjusted based on the rule illustrated in Fig. 3, which generally yielded model firing rates similar to those of the neurons. Tone/m_f = 150 Hz. Sound level = 70-dB SPL. Note that the time reversal protocol reduced the firing rate for the phasic model, but not for the tonic model.

In the dynamic-clamp approach (Prinz et al. 2004), one measures the instantaneous membrane voltage, V_m(t), and then computes the input current:

$$I_{\text{inj}}\left(t\right)=G_{\text{in}}\left(t\right)\cdot \left(V_{\text{m}}-V_{\text{rev}}\right)$$ (2)

where V_rev is the reversal potential of I_inj(t). Since only excitatory inputs were simulated, V_rev = 0 mV (Rothman and Manis 2003). I_inj(t) is then injected into the soma of an MSO neuron.

Model simulations.

Details of the phasic-firing and tonic-firing models can be found in Gai et al. (2009). Briefly, the phasic-firing model was developed as a bushy-cell model (Rothman and Manis 2003) and adapted in various models of MSO (Colburn et al. 2009; Jercog et al. 2010; Wang et al. 2014). It includes a fast sodium current (I_Na), a high-threshold potassium current (I_KHT) and a I_KLT, a hyperpolarization-activated cation current (I_h), and a leak current (I_lk). The current balance equation, neglecting dendritic cable properties (see discussion), is:

$$C_{\text{m}}\frac{\text{d}{V}_{\text{m}}}{\text{d}t}=-I_{\text{Na}}-I_{\text{KHT}}-I_{\text{KLT}}-I_{\text{h}}-I_{\text{lk}}+I_{\text{s}}\left(t\right)$$ (3)

where I_s(t) is the current input. Membrane capacitance, C_m = 12 pF. All of the conductances and channel time constants are multiplied by a factor of 2 and 0.33, respectively, to mimic the recording condition at 32°C.

The tonic model is created by freezing the gating variables, w and z, of I_KLT to the values obtained at the resting potential (Day et al. 2008). The tonic model created in this way has the same resting membrane potential and input resistance as does the phasic model.

For both the physiological recordings and model simulations, the neuron/model received m = 10 or 15 independent AN model inputs for each side (ipsilateral or contralateral). m was chosen to match the values (10 to 24) used in previous modeling studies (Brand et al. 2002; Colburn et al. 2009; Wang et al. 2014). A recent physiological study indicated that MSO neurons may receive fewer independent excitatory inputs (4 to 8 total) than previously estimated (Couchman et al. 2010). To test the effect of the number of inputs, simulations were repeated with fewer AN inputs (m = 3 to 5 at each side) and G_syn was adjusted accordingly. The ITD tuning curve for the low-frequency tone was broadened when m was decreased to 3, but was relatively unchanged for the transposed tone. The tuning curve for the SAM tone continued to show little ITD sensitivity.

RESULTS

Physiological results can explain psychophysical findings.

We used a hybrid approach for delivering a virtual sound input to MSO neurons (Fig. 2A; see methods for details). Figure 2, B–D, shows how ITD tuning was assessed in an exemplar MSO neuron with the dynamic-clamp approach. As shown in Fig. 1A, low-frequency pure tones (f = 150 Hz) or amplitude-modulated high-frequency tones (f = 5,000 Hz, m_f = 150 Hz) were processed by the AN model to generate AN spike times (Fig. 2A). Conductance-based excitatory synaptic currents (Fig. 2B) were then obtained by convolving spike trains from AN fibers (10–15 per ipsilateral or contralateral side) with an alpha function conductance transient (see methods). Although noisy, the synaptic conductance inputs for the low-frequency tone (Fig. 2B, black) and the transposed tone (green) clearly displayed a cluster of responses with an abrupt onset to each tone or modulation cycle, while the input for the SAM carrier contained no clear phase information. Here the actual input time course is plotted; if the input were averaged to generate a period histogram, the SAM-tone response would also show some phase locking (Fig. 1C, red).

The membrane-voltage time courses (Fig. 2C) of an MSO neuron showed fewer spikes, as the time delay (virtual ITD) between the ipsilateral and contralateral conductance input was increased sequentially. In our protocol, the 1-s stimuli were separated by 0.5-s interstimulus intervals. For ease of presentation in the figure, the full interstimulus intervals are represented by short gaps. For each individual neuron, a voltage threshold (pink dashed line) was selected for the identification of action potentials, and voltage transients below this line were considered excitatory postsynaptic potentials. It is known that the height of action potentials at the somata of MSO neurons decreases significantly with the animal's age (Scott et al. 2005). When action potentials were not well above the excitatory postsynaptic potentials, the determination of the threshold was verified by inspecting individual action potentials, i.e., whether there was a change in the slope of the ascending phase and whether the descending phase was steep enough (Kuenzel et al. 2011); otherwise, the data were discarded.

The ITD tuning curves (Fig. 2D) were obtained by computing the firing rates from the voltage traces (Fig. 2C) as a function of ITD. The tuning curves for the low-frequency pure tone (black) and the transposed tone (green) were similar in firing rate and broadness, while the response to the SAM tone was not well tuned (red). Therefore, although the phase locking measured by the vector strength (VS) was lower for the transposed tone than for the low-frequency pure tone (Fig. 1C), the neuron was equally sensitive to the ITDs carried by these two types of stimuli. In this proof-of-concept experiment, the best ITD was always zero, and the firing rates for the negative ITDs are mirror images of the firing rates for the positive ITDs. In principle, we would expect that asymmetry of binaural excitatory input and the presence of inhibition would yield ITD tuning curves similar to those observed in vivo (Brand et al. 2002), at least for the pure tone and transposed tone inputs.

In summary, the sharpness of the ITD tuning curves obtained from this MSO neuron agreed with the human psychophysical result (Fig. 1D), in that the ITD information contained in the low-frequency tone and the envelope of the high-frequency transposed tone was better encoded by the neuronal responses than the ITDs carried by the envelope of the SAM tone.

To quantify the ITD sensitivity, the firing-rate range (defined as the difference of the peak and the minimum firing rates) and half-width (defined as the ITD for which the firing rate was mid-way between the peak and the minimum) were measured for each ITD tuning curve. Note that the ITD tuning curves to virtual sound that were obtained in our preparation depended on the G_syn. Figure 3 shows the effect of G_syn on the ITD tuning for an MSO neuron. In general, both firing rate and half-width increased with G_syn. For the low-frequency pure tone and the high-frequency transposed tone, there were always some values of G_syn that caused a large firing-rate range for an ITD tuning curve (Fig. 3, A and C). In contrast, increasing the G_syn for the SAM tone caused the ITD tuning curve to shift up without increasing the firing-rate range. In other words, the small firing-rate range for the SAM tone observed in the above example (Fig. 2D) was not due to the specific G_syn chosen.

Several values of G_syn were usually tested for each type of stimulus. The G_syn that yielded an ITD tuning curve with its minimum firing rate just above zero (Fig. 3, A–C, thick lines and bold numbers) was chosen as the final value for comparison across stimulus types and across neurons. Due to the limitation of recording time, we were occasionally unable to systematically vary the G_syn. Nevertheless, the general finding that ITD tuning curves to low-frequency tone and transposed tones were similar and showed greater selectivity than those to SAM tones was consistent for 17/18 recorded MSO neurons.

Figure 4 is a scatter plot of the firing-rate range vs. the half-width for the three types of virtual stimuli. Consistent with the results shown in Figs. 2 and 3, the firing-rate range was significantly lower, and the half-width was significantly higher, for the SAM tone (red circles) compared with the other two stimuli (for firing rate, the main effect showed differences: χ² = 38, degrees of freedom = 2, P = 0.0001). Pairwise comparisons were as follows (means ± SE): SAM, 31.1 ± 5.4, n = 18 vs. pure tone, 105.5 ± 4.5, n = 18, χ² = 25, P = 0.0001; SAM, 31.11 ± 5.4, n = 18 vs. transposed tone, 125.6 ± 4.5, n = 18, χ² = 25, P = 0.0001; and for half-width, the main effect showed differences: χ² = 32, degrees of freedom = 2, P = 0.0001. Pairwise comparisons were as follows (means ± SE): SAM, 2 ± 0.13, n = 18 vs. pure tone: 0.83 ± 0.06, n = 18, χ² = 23, P = 0.0001; SAM, 2 ± 0.13, n = 18 vs. transposed tone: 0.8 ± 0.05, n = 18, χ² = 24, P = 0.0001. No statistical difference existed in the firing-rate range or the half-width for the low-frequency tone (black triangles) and transposed tones (green squares). Note the half-width was computed only when the firing-rage range exceeded 30 spikes/s. As shown in the example of Fig. 3B, when the maximum firing rate for the SAM tone was low, the ITD tuning curve was noisy and flat, making it difficult to obtain an accurate measure of half-width. The red circles in the shaded area of Fig. 4 represent all of the responses to the SAM tone that had a flat tuning curve using this criterion.

Fig. 4.

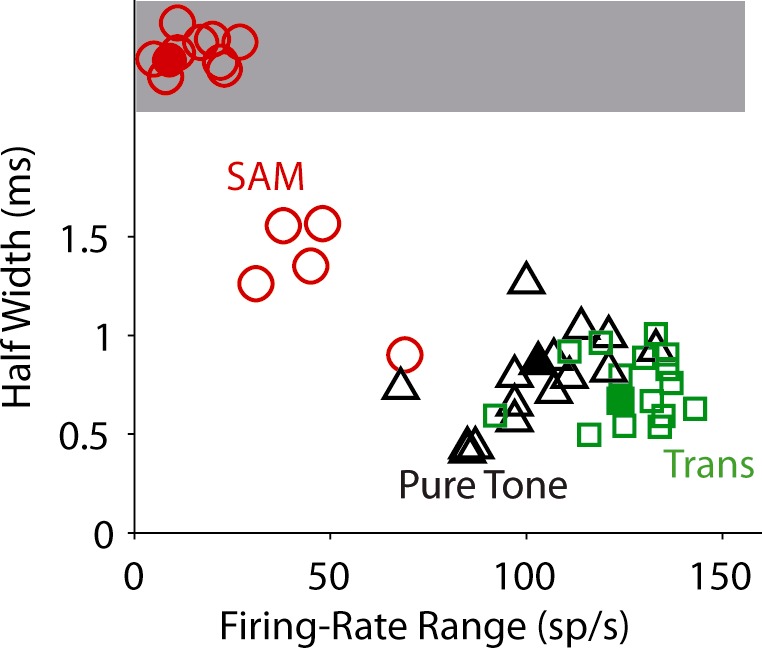
Scatter plots of firing-rate ranges vs. half-widths of the ITD tuning of recorded MSO neurons from animals aged P15 and older (open symbols; n = 14). The phasic-model performance is also plotted for comparison (filled symbols). Symbols in the shaded area correspond to flat ITD curves (firing-rate range < 30 sp/s). Small jitter was added to the data with flat ITD curves to avoid overlapping of the symbols. Tone/m_f = 150 Hz. Sound level = 70-dB SPL.

Here we did not plot the data as a function of age, as we would have for a developmental study, because the age groups were not evenly distributed. We observed slightly broader tuning curves for animals at P12 and 13; nevertheless, the relationship of the tuning curves to the three stimuli remained the same as described above.

The filled symbols in Fig. 4 are for results from simulations with the phasic model (the exact tuning curves are plotted in Fig. 6C, left). Both the firing-rate range and the half-width for the three types of stimuli are within the range of the MSO data. In summary, the ITD tunings of both the MSO data and the phasic model were consistent with the human psychophysical result (Fig. 1D).

Input slope-based coincidence detection underlies the sharp ITD tuning of MSO neurons.

The low-frequency tone (Fig. 2B, black) and the transposed tone (Fig. 2B, green) elicited fast-rising slopes in each stimulus cycle compared with the SAM tone (Fig. 2B, red) for the input to MSO neurons. The input was summed activity across multiple AN fibers on each side. To test the importance of the input slope on creating sharp ITD tuning curves, without changing the input amplitude or the interspike intervals, the AN spike times were reversed in time before generating the conductance input. This resulted in shallower input slopes for all three stimulus types (Fig. 5A, right). Figure 5, B and C, shows how time reversing the AN input affected the ITD tuning of MSO neurons at two different ages. The G_syn was different for each type of stimulus, chosen with the criterion shown in Fig. 3, but was fixed for each stimulus when applying the time reversal. For the neuron from a relatively young animal (P13; resting membrane time constant = 1.5 ms; input resistance = 38 MΩ), the time-reversed input led to a 50% reduction of peak firing rate for the transposed tone (Fig. 5B, green), but had a small effect on the firing rate for the low-frequency tone (Fig. 5B, black). In contrast, time reversal had a dramatic suppressive effect on responses of a slightly older MSO neuron (P16; resting membrane time constant = 0.3 ms; input resistance = 7 MΩ) to all three stimuli (Fig. 5C).

Fig. 5.

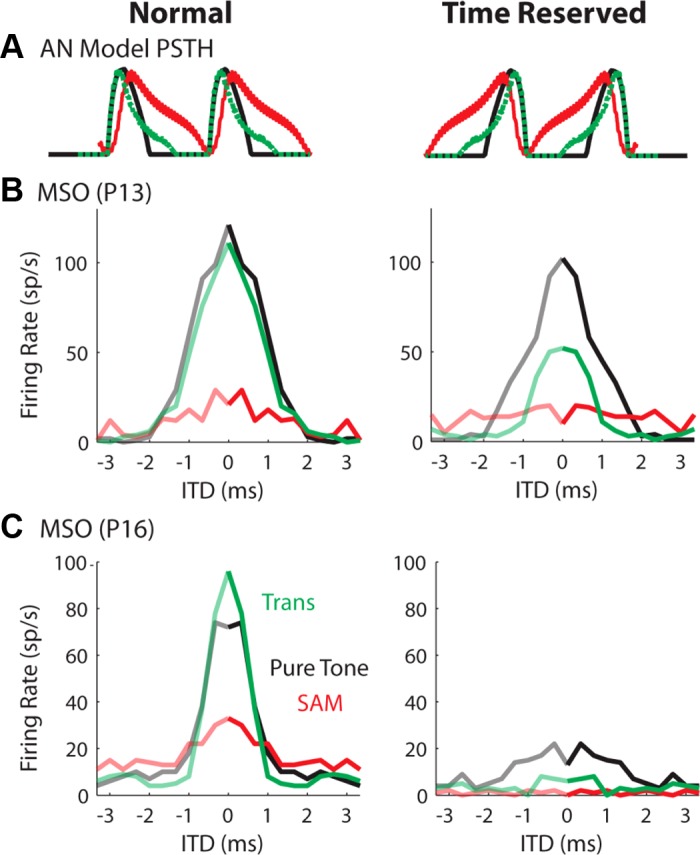
ITD tuning curves to virtual sounds recorded from MSO neurons with original AN input (left) or time-reversed AN input, i.e., AN spike timings reversed (right). A: period histograms of the AN model input realigned for easier comparisons of rising slopes and intercycle gaps. Time reversing the AN input preserves interspike intervals and total inputs per stimulus cycle. B: ITD tuning curves from a P13 gerbil. C: ITD tuning curves from a P16 gerbil. MSO neurons from P16 gerbils are supposed to have more low-threshold potassium conductance than MSO neurons from younger gerbils. Tone/m_f = 150 Hz. Sound level = 70-dB SPL.

The time-reversal result indicates that the input slope threshold of MSO neurons increases with age, which is consistent with an age-dependent increase in the conductance of the I_KLT (G_KLT) (Scott et al. 2005). Although the membrane time constant and input resistance become smaller with more I_KLT, we believe that the neuron's slope sensitivity also results from the nonlinear voltage and time dependence of the KLT channels, not just from the small-membrane time constant. To test this hypothesis, we performed model simulations using the phasic-firing and the tonic-firing models. Figure 6 (insets) shows the model responses to step currents. Both models have the same membrane time constant at the resting membrane potential. We also applied the normal and the time-reversed AN input to the model (Fig. 6). The time reverse decreased the firing rate of the phasic model (Fig. 6C), but had no effect on the firing rate of the tonic model (Fig. 6B).

The firing rate of the phasic model for the low-frequency tone under the same reversal protocol (Fig. 6C, right) was not as low as the MSO neurons (Fig. 5C, right). One possible explanation is that the bushy-cell model has only the I_KLT mechanism, whereas the phasic firing property of mature MSO neurons results from both I_KLT and the low-voltage inactivation of the I_Na (Svirskis et al. 2004). When we enhanced the model's phasic behavior by “left-shifting” the steady-state sodium inactivation function by −10 mV (not shown), the firing rate for the low-frequency tone during time reversal was further decreased compared with Fig. 6C (right).

To test whether sodium inactivation alone might generate substantial slope sensitivity, we considered the tonic model (which does not have nonlinear I_KLT) and we shifted the sodium inactivation by −10 mV. The time reversal had only a minor effect on the firing rate for the low-frequency tone and the transposed tone (not shown). For stimuli with rising phases in such ranges, I_KLT apparently contributes more to the slope sensitivity of MSO neurons during coincidence detection.

To further illustrate the importance of the input slope for the phasic model, we did two more simulations with the models. First, we computed the spike-triggered averages (STAs) of input conductance (Fig. 7) to explore the relationship between the pre- and postsynaptic spikes. Two ITD values, 0 (solid) and 1 ms (dotted), were included in the computation. Both phasic and tonic models received the same conductance input, except that the amplitude of the input was scaled differently (see the caption of Fig. 6). There are clear differences between the STAs of the two models. 1) To initiate a spike, the phasic model required a narrow integration window and a sharper rising slope in its input (Fig. 7, left). When the input became less coincident (i.e., ITD increases from 0 to 1 ms), the model retained its selectivity, and consequently decreased its firing rate (Fig. 6C, left). In contrast, when the input event became broader (i.e., less coincident), the tonic model responded to the broader events with lower amplitude because of more temporal summation (Fig. 7, right). 2) For the SAM stimulus, because it elicited a continuous response that activated the I_KLT, the phasic model required a higher amplitude for the SAM than for the other two sounds (Fig. 7, left). In contrast, the tonic model could fire for a lower amplitude because it responds to temporal summation (Fig. 7, right). 3) Even though the SAM tone caused a shallower rising input most of the time, the phasic model only fired when the input had a rapid rising phase (Fig. 7, left). This is reflected in a similar rising slope in the STA across all three types of stimuli. For the tonic model, the STA had a shallower slope when responding to the SAM than to the other two stimuli, reflecting decreased selectivity to input slope (Fig. 7, right).

Fig. 7.

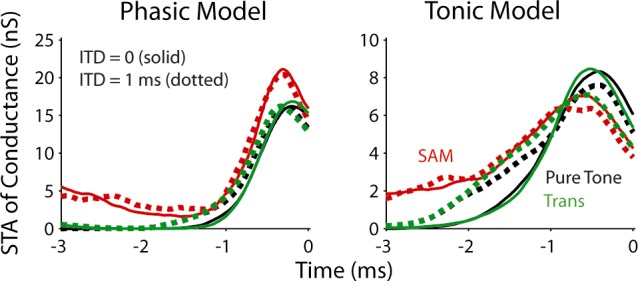
Spike-triggered averages (STAs) of input conductance for the three stimuli obtained with model simulations. Solid lines represent the result for ITD = 0, and dotted lines for ITD = 1 ms. Time 0 was when a spike was marked (i.e., the membrane voltage exceeded −15 mV).

In the second simulation, we replaced the AN spike times, t_i, (i = 1, …, n_m-left or n_m-right), with G_env(t), a time sequence of identical conductance ramps separated by gaps (Fig. 8). The ramp slope (inversely proportional to T_ramp, ramp duration) was varied systematically from one sequence to the next. Each sequence, G_env(t), was delivered as deterministic input to the model as an idealization of an envelope with specified slope for composite EPSGs (Fig. 8). Now the G_in to the model was

$$G_{\text{in}}\left(t\right)={\displaystyle \underset{0}{\overset{\text{t}}{\int }}}{G}_{\text{env}}\left(s\right)f_{\alpha }\left(t-s\right)\text{d}s$$ (4)

In each cycle,

$$G_{\text{env}}\left(t\right)=\{\begin{array}{cc}{A}_{\max }t/T_{\text{ramp}},& 0<t<T_{\text{ramp}}\\ 0,& T_{\text{ramp}}<t<T_{\text{ramp}}+T_{\text{gap}}\end{array}$$ (5)

Samples of the G_env(t) are shown in Fig. 8A. The total duration of the input was 50 ms. T_gap = 3 ms to approximate the gap between individual events for AN responses to the low-frequency tone or the transposed tone at 150 Hz; T_ramp is variable; ramp slope = A_max/T_ramp; ramp area A_max = 0.5 nS/ms and 0.1 nS/ms for the phasic (Fig. 8A, left) and the tonic (right) model, respectively. To prevent the models from firing to monaural input (i.e., no spiking should occur for out-of-phase input), the input amplitude had to be smaller for the tonic model than for the phasic model, because in the tonic case the conductance of the negative-feedback current, I_KLT, is frozen at rest, not voltage-gated. The corresponding conductance input, G_in(t), is shown in Fig. 8B.

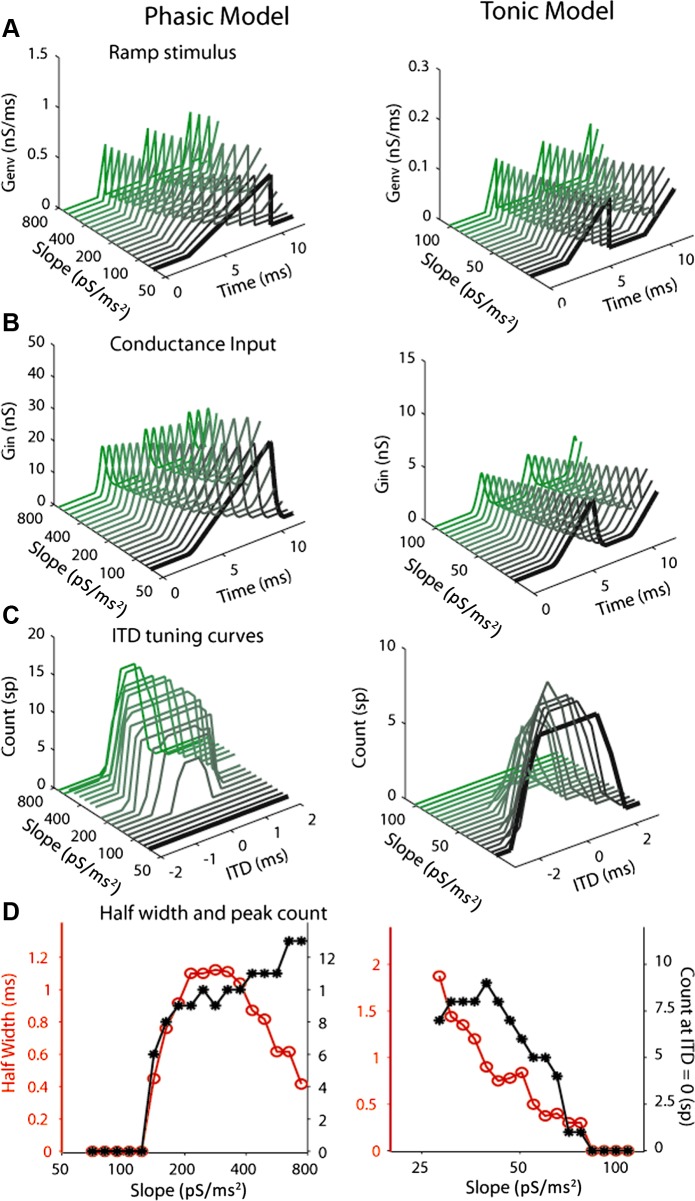
Fig. 8.

Model ITD tuning curves to artificial ramp input with different slopes. A: samples of ramps, G_env(t), used for the phasic and tonic models. The total duration of the stimulus was 50 ms. The gaps between individual ramps were 3 ms. B: maximum area A_max = 0.5 nS/ms and 0.1 nS/ms for the phasic and the tonic model, respectively, and the corresponding conductance input, G_in(t). C: model ITD tuning curves for different ramp slopes. D: half-width (red) and peak spike count (black) derived from the ITD tuning curves as a function of ramp slope.

Figure 8C shows the model ITD tuning curves for different ramp slopes. The half-widths and peak spike counts were derived from the ITD tuning curves as a function of ramp slope (Fig. 8D). The phasic model did not spike until the slope reached a certain value (∼120 pS/dt; C and D, left). Note that this slope threshold persisted even when the overall input amplitude was increased (A_max and T_ramp increased by the same factor) to high values (data not shown). In contrast, the tonic model fired at very shallow slopes (∼28 pS/dt; C and D, right). Although the tonic model showed a lower firing rate with steeper input slopes, this could be overcome by increasing the input amplitude while keeping the slope fixed (data not shown).

ITD tuning curves depend on virtual sound frequency and intensity.

So far, the physiological data and simulations have been based on virtual sounds that are relatively strong, corresponding to about 70-dB SPL, consistent with conditions used in psychophysical studies. The tone and modulation frequencies were initially set at 150 Hz, but the psychophysical data suggest that ITD sensitivity of transposed sound declines at higher frequency. In this study, we also tried higher frequencies and lower sound intensities to examine to what extent our above comparisons for different stimuli hold. Figure 9 illustrates the effect of a higher frequency (300 Hz) on the ITD tuning curves for an MSO neuron in response to the three stimuli at the same sound level. For the 11 neurons that were tested at both frequencies, the firing-rate range for the low-frequency pure tone increased significantly at 300 Hz [mean ± SE: 105.6 ± 4.6 (n = 18) to 219.4 ± 21 (n = 11); χ² = 11.5, P = 0.0007], while the half-widths were generally smaller at 300 Hz than at 150 Hz, but the decrease was not significant [0.85 ± 0.6 (n = 18) vs 0.65 ± 0.4 (n = 11); χ² = 4.3, P = 0.03]. Combining the firing rate and the half-width, we observed sharper ITD tunings at the higher tone frequency.

Fig. 9.

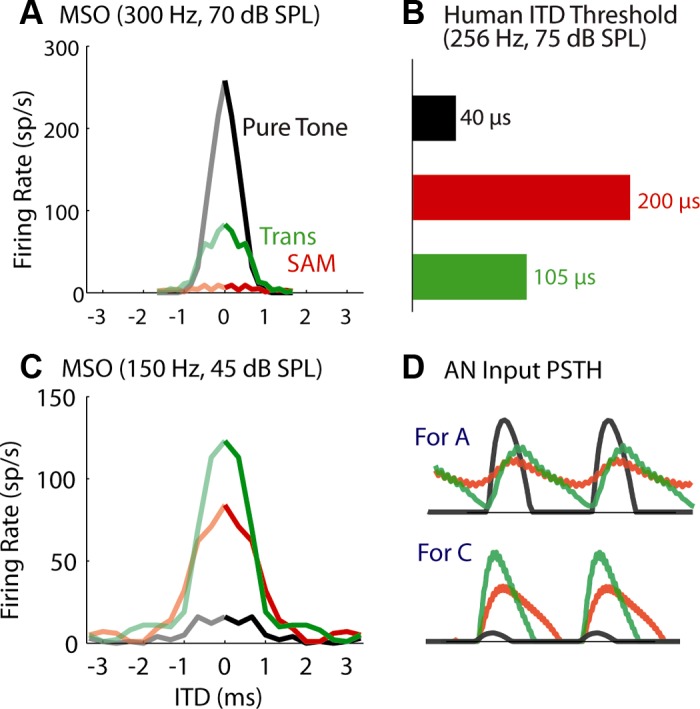
ITD tuning curves of MSO neurons at higher frequency (300 Hz; A), or at lower sound levels (45-dB SPL; C). B: estimated human ITD threshold at higher frequency (256 Hz) from Bernstein and Trahiotis (2002, their Fig. 3). D: the unnormalized period histograms of the monaural AN model input to the neuron for conditions shown in A and C, respectively. Top: when the frequency increased to 300 Hz, the phase locking of AN input degraded for SAM and transposed tones (VS = 0.33 and 0.35, respectively), but not for the low-frequency pure tone (VS = 0.84). The age of the animal was P17 for (A) and P18 for (C).

In contrast, the firing rate for the transposed tone decreased significantly [125.6 ± 4.6 (n = 18) to 76.2 ± 12.6 (n = 11); χ² = 10.5, P = 0.001] when m_f increased (Fig. 9A, green and red), although no significant change was found in the half-width. These trends are consistent with the reduced psychophysical performance (i.e., increased ITD thresholds) observed at higher frequencies (Bernstein and Trahiotis 2002; replotted in Fig. 1D and Fig. 9D, green). The AN period histograms (Fig. 9D, top) indicate poor phase locking to sound envelopes and shallower rising slope at higher m_f. This degradation is a natural result of the attenuation of auditory peripheral filters on frequency sidebands of a SAM or a transposed tone. The psychophysical study by Bernstein and Trahiotis (2002) also showed that, at 64 Hz, the ITD threshold for the low-frequency tone was higher than those for the two amplitude-modulated tones. We did not test such low frequencies because the AN model has a lower frequency limit of 100 Hz.

The psychophysical study (Bernstein and Trahiotis 2002) was performed only at one sound level, 75-dB SPL. At lower sound levels, physiological recordings in AN fibers predict that the difference between the envelope-ITD sensitivities to SAM and transposed tones should be smaller. The ITD tuning curves for the two stimuli obtained at 150 Hz and 45-dB SPL (Fig. 9C) confirmed the prediction. Note that, because we chose medium spontaneous rate for the AN input (see methods for justification), the 45-dB tone was only 5 to 10 dB above threshold for the low-frequency AN fiber (150 Hz), and the firing rate was correspondingly low (Fig. 9D, bottom, black). A larger firing-rate range is expected for MSO neurons that receive AN input with high spontaneous rate.

MSO neurons are sensitive to ITDs carried by virtual speech stimuli.

Speech is naturally rich in frequency and amplitude modulations. It often has abrupt changes and pauses. In addition, the example speech sequence in Fig. 10A shows that the energy bursts normally follow the gaps, making it particularly favorable for the MSO neurons that are sensitive to input slopes. These features of speech, pauses and abrupt changes (say, associated with plosives or certain fricatives in speech), are shared more by the transposed stimuli than by the SAM stimuli. Therefore, we hypothesize that MSO neurons are able to detect the envelope ITD for speech as carried by low-frequency and by high-frequency AN fibers as for pure tones and for transposed tones.

Fig. 10.

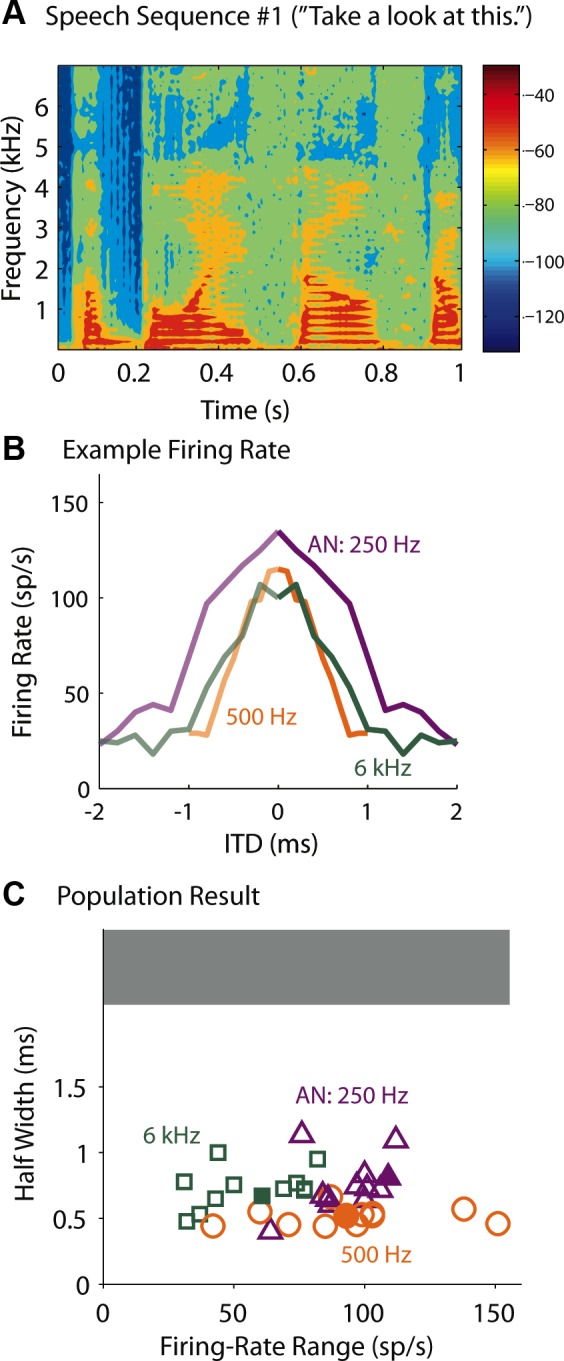
ITD sensitivities to speech. A: spectro-temporal representation of a 1-s speech sequence #1. Color represents energy according to the color bar. B: ITD tuning curves of an MSO neuron to the virtual speech sequence #1. Animal age, P17. C: firing-rate range vs. half-width of the ITD tuning to virtual speech #1, #2, and #3 of recorded MSO neurons from animals aged P15 and older (open symbols; n = 11). Different colors represent different characteristic frequencies of the AN model used to generate the synaptic input to the neurons. The phasic-model performance for speech #1 is also plotted for comparison (filled symbols). Note that ITD information carried by the speech sequences could be encoded for both low- and high-frequency MSO neurons, and none of the neurons showed flat ITD curves (shaded area; firing-rate range <30 sp/s). Sound level = 70-dB SPL. See methods for choice of speech tokens.

We examined the response of MSO neurons (n = 13) to three 1-s-long speech sequences (see methods) that were presented as binaural virtual sounds. Here, the AN model CF varied for each individual neuron. The goal was to compare responses of low- and high-frequency neurons to the same speech sound. Since we did not know the actual CF to which the recorded neurons responded in vivo, each recorded neuron served as a proxy for neurons with different CFs; that is, each recorded neuron was stimulated with AN spike trains corresponding to more than one CF. Figure 10B shows an exemplar neuron, and Fig. 10C (open symbols) shows the population responses. The range of the firing rate (the firing rate was the spike count over the 1-s speech sequence) was comparable for the 250- and 500-Hz CF input, and G_syn was usually chosen to be the same according to the criterion shown in Fig. 3. A higher G_syn was always required for the 6-kHz CF because, for the speech sequences we used, the energy level was lower at high frequencies than at low frequencies (Fig. 10A). For the example shown in Fig. 8A, G_syn = 2, 2, and 2.5 nS for CF = 250, 500, and 6,000 Hz, respectively. Even with larger G_syn, the firing-rate range for the 6-kHz CF input across neurons was significantly lower than those for the other two CF inputs (t-test, P < 0.05, degrees of freedom = 11).

The half-width for the 500-Hz condition was significantly smaller than the half-widths for the other two conditions (Fig. 10C). Simulations with the phasic model showed that the AN with CF = 500 Hz fires more frequently than the AN with the other two CFs to the speech sound we used. As a consequence, for nonzero ITDs (e.g., 0.5 ms), the binaural AN input with CF = 500 Hz activates the I_KLT in the model/neurons more frequently than the AN input with the other CFs, and thereby sharpening the ITD tuning curve.

The filled symbols in Fig. 10C are for results of simulations with the phasic model. Both the firing-rate range and the half-width for the three types of stimuli are within the range of the MSO data. Overall, our result suggests that, for spectro-temporally complex stimuli, the MSO can extract useful information about stimulus azimuthal location from full frequency spectrum.

DISCUSSION

This study was motivated by the behavioral observation that ITD processing is functionally uniform across the frequency spectrum (Rowan and Lutman 2007; Zhang and Wright 2007). While this result appears to challenge the general assumption that ITD information is carried only by low-frequency tones, Bernstein and Trahiotis (2002 and 2003) show that the poor ITD sensitivities to SAM high-frequency tones are due primarily to less precise AN response in each modulation cycle compared with the AN response to low-frequency tones. The use of transposed stimuli provides an unbiased comparison of ITD processing for low- and high-frequency binaural centers. Here, we show that the ITD sensitivity of MSO neurons can account for the behavioral findings, and the extraction of the envelope ITD carried by the transposed stimulus is likely to be resolved at the level of the MSO.

It is important to distinguish the input slope discussed here from the slope referred to in the context of an ITD “slope code” model. The slope code model proposes that the slope, rather than the peak, of the discharge rate carries information about biologically relevant time differences (review: Palmer 2004; Grothe et al. 2010). Our work does not address which portion of the ITD tuning function is used in forming a perception. Rather, we focus on the dynamic feature, slope of a composite EPSC's rising phase (in tones and envelope onsets), and intrinsic cellular biophysics that lead to temporally precise coincidence and ITD detection.

Binaural coincidence detection by MSO neurons is input slope-based.

Phasic neurons in the cochlear nucleus, which provide excitatory inputs to the MSO, are sensitive to the slope of injected current input: these neurons will not respond to a current ramp with slow-rising slope even for large amplitude (McGinley and Oertel 2006). Our laboratory's physiological and modeling studies (Gai et al. 2009, 2010) show that MSO neurons are sensitive to the rising slope of input current in a similar way, even with large background noise.

Although cross-correlation-based models can reproduce certain information-processing properties of MSO neurons (Colburn et al. 1990), in vitro studies using pulsatile or random inputs demonstrate that high-sensitivity coincidence detection by MSO neurons depends on EPSC events with adequately fast-rising slopes (Jercog et al. 2010; Svirskis et al. 2002). Our study generalizes the principle, showing that, even for complex sounds, fast-rising inputs enable MSO to achieve temporally precise coincidence detection. We identified sound features that are likely to elicit the fast-rising slopes in the envelope profile of the summed AN input. Specifically, the sound for effective localization ought to have features that allow the temporal-adaptation mechanism of the AN, which is present in both the AN model and AN physiology, to generate onset-like responses, i.e., gaps between modulation cycles or individual events in natural sound. The input-slope-based coincidence detection was well illustrated by the time-reversal manipulation (Fig. 5), which reversed the AN spike times without affecting the slope of single EPSCs. We believe that this slope-based cellular mechanism underlies MSO neurons' sharp ITD-tuning to the envelope of transposed tones. The PSTHs of the AN fibers to transposed tones have sharp leading edges, even though the envelopes have low-frequency dominated spectra. Our study indicates that binaurally coincident input would not be detected by MSO neurons, unless the composite synaptic input has fast-rising slopes.

Apart from the fast-rising input slope for a transposed tone or speech sound, an accompanying preceding absence of synaptic activity also ensures the excitability of MSO neurons. During the quiescent period, the conductance of the low-threshold potassium channel is reset to its resting value; this reduction of negative feedback allows the neuron to respond to the following activity. In fact, these two features commonly occur together: in the auditory periphery, sound gaps are critical in eliciting the fast-rising slopes in the following events.

Uniform ITD processing by MSO neurons along the tonotopy.

For low-frequency sound, ITD is encoded by phase-locked MSO neurons, but how the envelope ITD of high-frequency sound is encoded physiologically remains unclear. Both MSO and lateral superior olivary (LSO) neurons with high CFs are sensitive to envelope ITDs (Batra et al. 1997; Joris and Yin 1995; Yin and Chan 1990). In contrast to the ITD coding of MSO neurons (i.e., zero or small ITD has the highest firing rate in the tuning curve), LSO neurons have trough-ITD coding (i.e., the best ITD has the lowest firing rate) based on a subtractive mechanism of excitation and inhibition. Using SAM sounds with moderate intensities, these studies show that the ITD tuning of high-CF LSO neurons is comparable or even narrower than the ITD tuning of MSO neurons. However, our study clearly demonstrates that the SAM is not an effective envelope profile for encoding ITDs efficiently; actually, it disadvantages MSO neurons by constantly activating the I_KLT and thus preventing firing, especially at high sound intensities.

So the question remains: whether ITD is encoded solely by the MSO at both low and high frequencies, or by the MSO and the LSO at low and high frequencies, respectively. Since the subtractive mechanism underlying the ITD sensitivity of LSO neurons is based on input amplitude, the trough-to-peak width in its ITD tuning should approximate to one-fourth of the modulation cycle, based on the algorithm illustrated by Joris and Yin (1995; their Fig. 1). This predicts a 1.7-ms trough-to-peak width for an LSO neuron with 150-Hz modulation, broader than the 1.0-ms peak-to-trough width for the MSO neuron (Fig. 2). However, for drawing conclusions about the sharpness of envelope ITD coding, we suggest that future studies apply transposed stimuli when recording from LSO neurons.

For the present study, we assumed that low-frequency MSO neurons do not differ from high-frequency neurons in terms of fundamental cellular properties; rather, it is the afferent input that decides a neuron's CF. Our assumption is consistent with the findings of Scott et al. (2007) that there is little difference along the tonotopic axis of basic properties, including time constant, current thresholds, and spike amplitude of MSO neurons.

Comparisons with previous physiological results.

Responses of the MSO neurons reported here are similar in form to those published for IC neurons (Griffin et al. 2005). In both cases, the ITD tuning curves obtained at 150 Hz or so were comparable for the low-frequency pure tone and the modulated high-frequency tone with transposed envelopes, while the ITD tuning curve to the SAM tone was considerably broader. Thus physiological behaviors of the MSO and the IC are both consistent with the psychophysical study (Bernstein and Trahiotis 2002). When the tone frequency or m_f increases, MSO responses are also consistent with the psychophysical result in that the ITD detection threshold for low-frequency tones improves with increasing frequency, while the threshold for the transposed tone becomes worse (compare Figs. 1D and 8D).

Recordings from AN fibers (Dreyer and Delgutte 2006) predict that transposed stimuli should produce worse ITD sensitivity than pure tones at binaural levels based on the precision of phase locking in the AN. Figure 1C shows the period histograms of the AN model response to the above stimuli, which are quantitatively similar to the physiological data. Although the transposed-tone response has a higher VS (VS = 0.64), indicating a more precise phase locking, than the SAM-tone response (VS = 0.23), it is still lower than the VS for the low-frequency tone (VS = 0.83). It is true that when a neuron performs coincidence detection with an input slope-based (as for the MSO and the phasic model) or amplitude-based mechanism (as for the tonic and cross-correlation models), monaural phase locking to the sound carrier or envelope is essential for ITD coding. However, our results show that the AN's VS does not directly indicate the sharpness of the ITD tuning curve of the MSO. This finding is not surprising, given that VS reflects the timing of the overall response, while the slope-based coincidence detection relies mostly on the rising portion of the input.

Even for amplitude-based coincidence detection, the VS does not predict the sharpness of the tuning curve, as shown by the tonic-firing model's response (Fig. 6B). This is because the neuron and model have a firing threshold, below which the input activity is discarded. The period histograms of the AN responses indicate that the relatively low VS for the transposed tone is mostly caused by its tail (Fig. 1C, green). Therefore, even the tonic model showed similar ITD half-width, although large, to the transposed tone and the low-frequency tone (Fig. 6B).

About idealizations of the models.

We incorporated several idealizations when simulating the conductance-based input for the experimental and computational models. First, we omitted the cochlear-nucleus bushy cells and sent the AN spike times directly to the MSO neuron/model. It is known that bushy cells enhance phase locking to both envelopes and sound carriers (Joris et al. 1994a, 1994b). The enhanced phase locking is likely to generate narrower response clusters in the period histograms (Fig. 1C) and sharper ITD tuning curves for all three stimuli. Nevertheless, the relative differences of leading slopes in the envelopes should persist. Moreover, our conclusions strongly reflect the fact that, for the pure tone and the transposed tone, responses occurred only during one-half of the stimulus cycle, while the SAM tone elicited responses throughout the cycle. Together with the shallower slope of the SAM, the continuous activation of KLT channels reduced the firing of the MSO neurons and their sensitivity to rising depolarization. Therefore, enhanced synchrony would not change our basic conclusion.

We injected the simulated conductance-driven synaptic input current by dynamic clamp into the somata of the MSO neurons. In reality, the MSO neurons are bipolar and receive their inputs through two dendrites. It has been shown that two inputs are likely to generate fewer coincident spikes when they target on the same dendrite, rather than on opposing dendrites (Agmon-Snir et al. 1998). This dendritic feature suppresses monaural coincidence, and thus can sharpen the dynamic range of the ITD tuning curve (peak rate − minimum rate). Nevertheless, we expect that this dendrite-based mechanism that can reduce false positives for fine temporal structure will not have salvaging effects for the poor performance of SAM.

In addition, postsynaptic inhibition was not included in the dynamic clamp or in the computational model. Brand et al. (2002) hypothesize that glycinergic inhibition is responsible for the observed positioning of the ITD-tuning curve's peak outside the physiological range. Here the sharpness of the ITD tuning curves, rather than the best ITD, is key to our conclusions. Therefore, inhibitory input to the MSO was not simulated.

Closing.

Taken together, our study suggests that ITD coding by MSO neurons (assuming that our recorded neurons are representative) is not limited to low-frequency units. High-frequency MSO neurons, by using an input slope-based coincidence-detection mechanism, are sensitive to envelope ITD, perhaps more so than LSO neurons. Our findings imply that, when information about sound location is carried by different waveforms, neurons distributed across the MSO population are sensitive to and can encode with similar precision the locations of both low-frequency sound and modulated high-frequency sound with fast-rising envelopes. Our finding agrees with a psychophysical phenomenon, the Franssen effect, in which two sounds at separate locations, one with an abrupt-onset and the other with a slow-rising envelope, are both perceived as coming from the location of the abrupt-onset sound (Franssen 1960). If the sound with the slow-rising envelope elicits a flat and low-rate ITD tuning curve as the SAM tone does, it is reasonable that the localization is determined solely by the sound with the fast-rising envelope.

Coincidence detection is widely present in the auditory and other sensory systems. For example, the visual system detects coincident activity to extract information about moving objects (e.g., Konig et al. 1996), and the somatosensory systemis capable of using coincidence detection for feature analysis (Roy and Alloway 2001; Rodgers et al. 2006). An input-slope-based coincidence-detection mechanism may exist in other sensory areas if the neurons or networks are phasic, thus providing a selective and sensitive means to encode complex sensory information.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders (NIDCD) Grant 008543 (for J. Rinzel and Y. Gai) and NIDCD Grant 011284 (for D. H. Sanes and V. C. Kotak).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: Y.G., V.C.K., D.H.S., and J.R. conception and design of research; Y.G. performed experiments; Y.G. analyzed data; Y.G., V.C.K., D.H.S., and J.R. interpreted results of experiments; Y.G. prepared figures; Y.G. drafted manuscript; Y.G., V.C.K., D.H.S., and J.R. edited and revised manuscript; Y.G., V.C.K., D.H.S., and J.R. approved final version of manuscript.