Visual Categorization of Natural Movies by Rats

Abstract

Visual categorization of complex, natural stimuli has been studied for some time in human and nonhuman primates. Recent interest in the rodent as a model for visual perception, including higher-level functional specialization, leads to the question of how rodents would perform on a categorization task using natural stimuli. To answer this question, rats were trained in a two-alternative forced choice task to discriminate movies containing rats from movies containing other objects and from scrambled movies (ordinate-level categorization). Subsequently, transfer to novel, previously unseen stimuli was tested, followed by a series of control probes. The results show that the animals are capable of acquiring a decision rule by abstracting common features from natural movies to generalize categorization to new stimuli. Control probes demonstrate that they did not use single low-level features, such as motion energy or (local) luminance. Significant generalization was even present with stationary snapshots from untrained movies. The variability within and between training and test stimuli, the complexity of natural movies, and the control experiments and analyses all suggest that a more high-level rule based on more complex stimulus features than local luminance-based cues was used to classify the novel stimuli. In conclusion, natural stimuli can be used to probe ordinate-level categorization in rats.

Introduction

There is an increasing scientific interest in the visual perception of rodents. Several recent studies have focused upon cortical organization in rodents, elucidating the extent of functional specialization in rodent extrastriate visual areas (Andermann et al., 2011; Marshel et al., 2011). However, the usefulness of this model depends on the visual capabilities of rodents. A number of studies have found behavioral evidence in rats for higher-level visual processing (Zoccolan et al., 2009; Tafazoli et al., 2012; Vermaercke and Op de Beeck, 2012; Alemi-Neissi et al., 2013; Brooks et al., 2013). Although these studies provide evidence for abilities reminiscent of higher-level vision, none of them used very complex naturalistic stimuli. This leaves open the question of how rats would perform in more sophisticated visual tasks in which complex, dynamic stimuli are used for categorization and generalization to new stimuli.

The use of natural stimuli in visual neuroscience has been both defended and criticized. It has been argued that simple artificial stimuli are necessary for uncovering the specific response properties of neurons in each stage of visual processing (Rust and Movshon, 2005). Others have pointed toward evidence suggesting that visual processing cannot be elucidated solely based on experiments with simple stimuli (Kayser et al., 2004; Felsen and Dan, 2005; Einhäuser and König, 2010). For example, humans are more efficient in classifying natural scenes compared with simplistic unnatural stimuli (Li et al., 2002). To find out the extent of the validity of rats as a model in vision research, it is relevant to investigate to what extent experiments with complex stimuli can work.

In monkeys and humans, natural stimuli have been used effectively in highly demanding tasks for superordinate- and ordinate-level categorization (Thorpe et al., 1996; Fabre-Thorpe et al., 1998; Vogels, 1999a; Serre et al., 2007; Greene and Oliva, 2009; Peelen et al., 2009; Walther et al., 2009; Fize et al., 2011). Provided that the stimulus set contains sufficient variation, categorization of natural stimuli requires generalization relying on processing and extraction of category-specific features, invariant to the presence of other information. Therefore, successful performance of an animal on novel category exemplars provides information about the extent of the capabilities of their visual system.

In the present study, rats were trained to discriminate movies containing rats from movies containing other objects and from scrambled movies in a two-alternative forced choice (2AFC) task in a visual water maze (Prusky et al., 2000). After training, the animals were tested for generalization to unseen movies. Several tests were performed, starting with stimuli that could be considered as “typical” exemplars and gradually including more deviant movies, still images, and some controls to exclude the possibility that low-level cues would drive performance. The rats generalized well to new typical movies, and generalization was still significant for slower movies, stationary snapshots, movies with differently colored rats, and movies controlling for local luminance cues. Overall, the findings indicate that the rats were using relatively complex stimulus features to perform the categorization task.

Materials and Methods

Animals

Experiments were conducted with six male FBNF1 rats, aged 25 months at the start of the study. This specific breed was chosen for their relatively high visual acuity of 1.5 cycles per degree (Prusky et al., 2002). One subject was excluded from the data as a result of extreme response bias during training, preventing the rat from reaching above-chance performance in >1200 trials with the first stimulus pair. All rats had previously been used in discrimination experiments, but with unrelated stimuli: sinusoidal gratings of varying orientation and spatial frequency. Animals had ad libitum access to water and food pellets. Housing conditions and experimental procedures were approved by the University of Leuven Animal Ethics Committee.

Stimuli

Pairing of target and distractor stimuli.

Natural movies were selected from our own database of 537 5 s movies created for the purpose of this experiment. They were recorded at 30 Hz (thus including 150 frames) and sized 384 × 384 pixels. For every stimulus, 3 vectors were calculated from the pixel intensities across columns x = 1 … X and rows y = 1 … Y, but per frame t = 1 … T. Note that the monitors presenting the stimuli were gamma corrected to obtain a linear transfer function between pixel intensity values and luminance, so using actual pixel values will not distort the metrics. The first vector contained the average pixel intensities as a function of time t as follows:

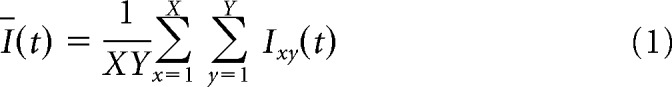The second vector contained the root-mean-squared contrasts as follows:

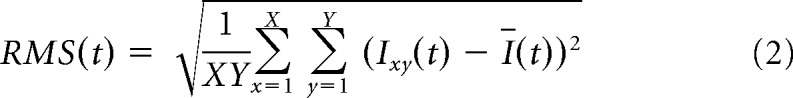The third vector contained the average changes in pixel intensity (this time per frame transition for t = 1 … T − 1) as follows:

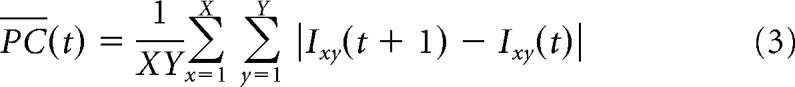Next, we reduced this information by taking the means and SDs across frames/frame transitions t to six features per stimulus: M(Ī), SD(Ī), M(RMS), SD(RMS), M(PC), and SD(PC). Doing this for every stimulus resulted in six feature vectors summarizing our database of 537 stimuli in a relatively low-dimensional space. After taking Z-scores of each of these six feature-vectors (across all 537 movies), each rat movie was paired with a nonrat movie so that the Euclidean distance between them in this standardized space was <1 SD. Without the constraint of 1 SD, the average distance between all possible pairs of movies was 3.24 SDs with a 95% percentile interval of [1.19 6.60].

Training stimulus set.

From these matched stimuli, a general set of five pairs was selected with variability of target and distractor in mind, along with three test sets (see Fig. 1). Note that the previously described method of pairing stimuli with their most similar distractor could result in two rat movies being matched with the same distractor. This was the case for two rat movies in the test sets: one distractor is shared between a target movie of Test Sets 1 and 2 and one between a target movie of Test Sets 1 and 3. There was, however, complete separation of training and test sets. The training set consisted of movie pairs that already included some variability to avoid the possibility of low-level strategies as much as possible, but at the same time enough overlap in content so that it would be possible to pick up some common features. The target movies showed moving rats of the same strain, whereas three of the paired distractors contained a train, one a gloved hand moving in and out of the screen and one a moving stuffed sock. Both stimulus types had varying amounts of camera movement. The degree of variation is illustrated by the fact that the 6D Euclidean distance between the target and distractor movies of the different pairs was relatively large (M = 2.76, calculated from all possible target–distractor combinations excluding the actual pairs), much larger than the distance between target and distractor movies from the same pair (M = 0.65; see Fig. 2A for a plot of the distribution of these distances). Note that the magnitudes of these average distances are still in standardized space, expressed in units of SD across movies. In a later section, we will show that a strategy based upon local luminance cues cannot explain generalization from this training set to test sets containing new stimuli.

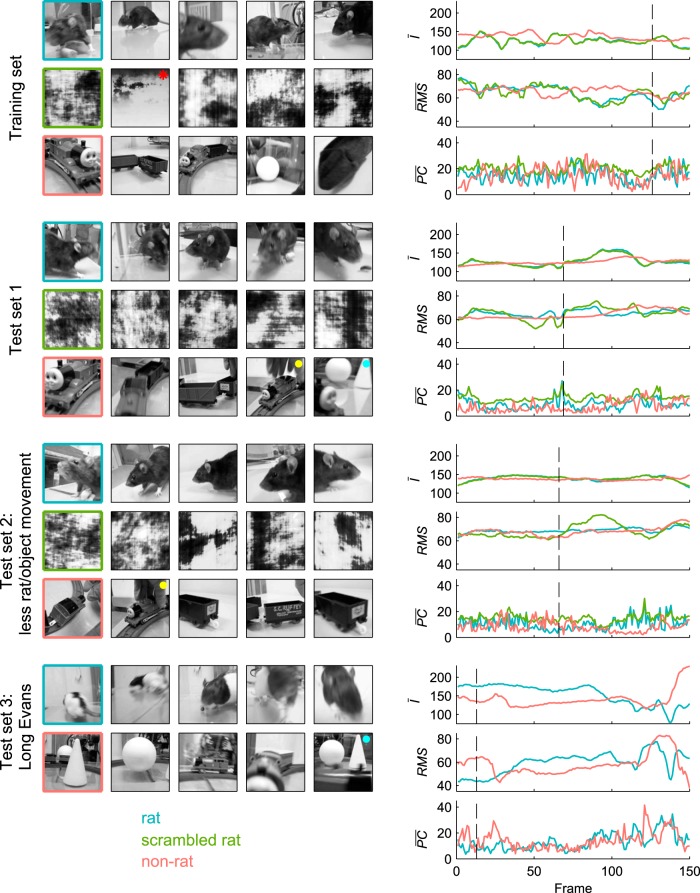
Figure 1.

Stimulus sets. The left side displays three rows of snapshots for each stimulus set, with the first row depicting the five rat movies, the second row the phase scrambled versions of these rat movies, and the third row the natural distractor chosen for each rat movie (for the last stimulus set, the row with scrambled stimuli is omitted because they were not used in the experiments). The snapshots of each target movie and its distractors are taken at the time point at which the frame of the target stimulus (i.e., rat movie) is most similar to the rest of the frames in that movie (i.e., minimal pixel-wise Euclidean distance). The red asterisk indicates the adjusted distractor (see Materials and Methods, Stimuli). Yellow and blue dots indicate the two distractors that were each matched to two rat movies. The right side displays average pixel intensity (Ī), root mean square contrast (RMS), and mean absolute pixel change (PC) as a function of frame number for one target and its distractors of each set (the outline of the chosen movie is colored in the left panel). Dashed lines indicate the location in time of the frame displayed on the left.

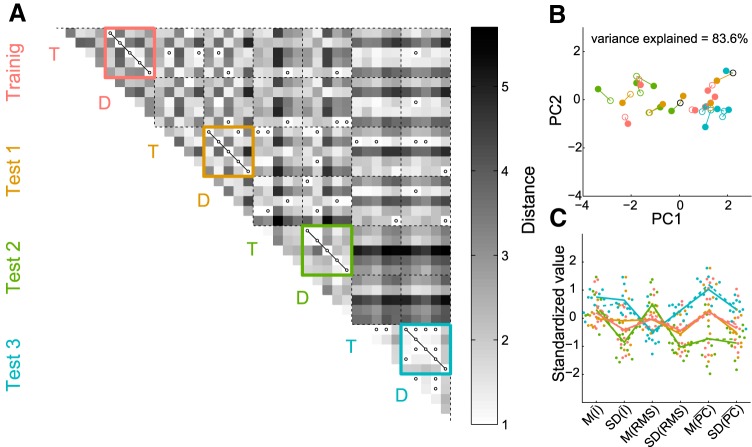
Figure 2.

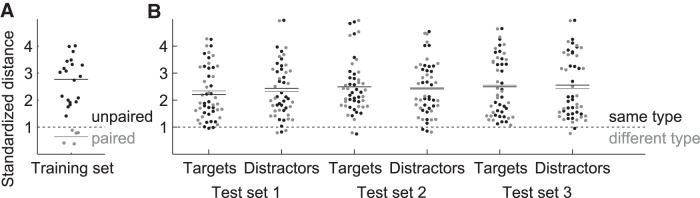
Standardized distances between individual stimuli. A, Bee-swarm plot of the distribution of all pairwise distances between target and distractor movies of the training set for paired (gray) and unpaired (black) target and distractor movies separately. B, Bee-swarm plots for all pairwise distances between either the targets (rat movies) or the distractors (nonrat movies) of a certain test set (e.g., the targets of Test Set 1) and either all training set movies of the same stimulus type (black) or all training set movies of the different stimulus type (gray). For example, for the targets of Test Set 1, all pairwise distances to the rat movies of the training set are shown in black, whereas all pairwise distances to the nonrat movies of the training set are shown in gray.

Test stimulus sets.

Test Set 1, used for generalization purposes, included movie pairs that were very different from the training pairs in terms of low-level properties (Fig. 2B), but were judged to be relatively typical in terms of their high-level content by the experimenters (same strain of rats, similar motion properties, etc.). Test Set 2 included movies in which the rats/objects were more stationary. In quantitative terms, the nonstandardized M(PC) was, on average, 4.22 for the movies of Test Set 2, whereas it was 5.18 and 5.39 for the movies of the training set and Test Set 1, respectively (note that the difference is rather small because there was still camera movement). For the third test set, the target movies included rats of a different strain (Long–Evans), which are white/black spotted rather than uniformly dark. In each test set, all of the natural distractors contained a (moving) train and some of them had objects (a ball, cone) present in them and/or a hand moving one of those objects. Figure 2B shows the distribution of all pairwise distances between either the targets (rat movies) or the distractors (nonrat movies) of a certain test set and either all training set movies of the same stimulus type or all training set movies of the different stimulus type. It is clear that generalization cannot be explained by the six dimensions we used to match targets and distractors, because the distributions of target–target distances and distractor–distractor distances are not systematically lower than the distribution of target–distractor distances. The rat test set movies were not more similar to training set movies of the same type (targets) than to those of the other type (distractors), nor were the nonrat test set movies. Figure 3 illustrates how all of the stimulus sets compare with each other in the standardized 6D stimulus space. Figure 3, A and B, clearly shows that within-pair distances are much smaller than the between-pair variability. Figure 3C shows that, on average, Test Set 1 matches the training set best on all six dimensions. This plot also illustrates that, on average, Test Set 2 not only has the aforementioned smaller change of pixel values M(PC), but also less variability in average pixel intensity SD(Ī), contrast SD(RMS), and change of pixel values SD(PC), all of which is consistent with the more stationary rats/objects.

Figure 3.

Stimulus dissimilarities. A, Distance matrix for all natural movies used in the experiment (in SD units, see Materials and Methods, Stimuli). Colored boxes highlight target (T) and natural distractor (D) combinations per stimulus set. Black circles indicate distances shorter than one (i.e., the criterion for target–distractor match). B, All stimuli in 2D space after principal component analysis on the distance matrix from A. Full markers indicate targets and empty circles indicate distractors (color codes correspond to those in A). Black markers indicate distractors that are shared by two target movies. Variance explained by these first two principal components is 83.6%. C, Parallel coordinates plot showing bee-swarm plots of individual stimuli per dimension and the centroids (averages) of each stimulus set for targets (continuous lines) and distractors (dashed lines) separately in the standardized 6D stimulus space (color codes correspond to those in A).

Scrambled distractors.

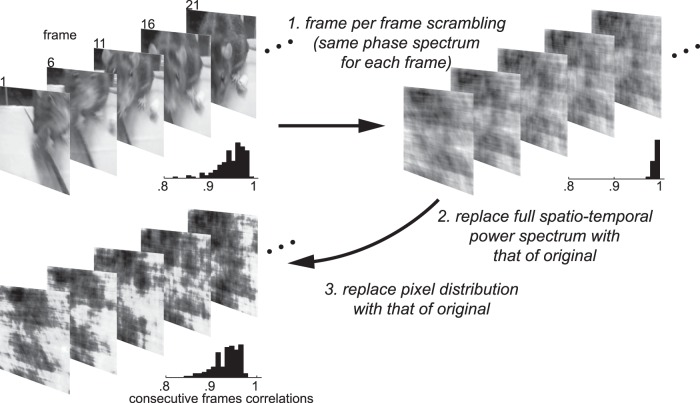
For the training set and first two test sets, additional distractors were created by phase-scrambling the rat movies. On trials using scrambled distractors, a rat movie was only paired with its own scrambled version. The scrambled stimuli were created in three steps, as illustrated in Figure 4. First the spatial amplitude spectrum A(I_t) for each frame I_t in a rat-movie M was estimated by means of a 2D fast Fourier transform (FFT). To each spatial frequency component a random phase angle (drawn from a uniform distribution over the interval [−π, π]) was assigned, resulting in a new phase spectrum ϕ*. A new movie M′ was obtained by performing an inverse 2D FFT on the combination of each frame's amplitude spectrum with the new phase spectrum A(I_t)e^−iϕ*, for t = 1… T. This first step is equivalent to the scrambling method used by Schultz and Pilz (2009). Note that this method uses the same phase spectrum ϕ* for all frames of a particular movie (i.e., for every rat movie, one set of random angles was generated and used), which results in excessive temporal correlation of pixel values in consecutive frames. Therefore, using a 3D FFT, the spatiotemporal phase spectrum of this scrambled result ϕ(M′) and the spatiotemporal amplitude spectrum of the original movie A(M) were taken and combined into a scrambled movie M′′ by performing an inverse 3D FFT on A(M)e^−iϕ(M′). The result of this second step is a movie with consecutive frame correlations comparable to those of the original natural movie (Fig. 4). Finally, to compensate for the expanded range of pixel values (i.e., values outside the range of 0 to 255), in the third step, each scrambled movies' M′′ pixel distribution was replaced by that of the original movie M. The result was a temporally correlated image sequence with identical contrast, luminance, and virtually identical spatiotemporal power spectrum, but not containing any recognizable content. The frame per frame contrast, luminance, and spatial power spectra were highly similar.

Figure 4.

Creation of scrambled stimuli. One example rat movie is represented by five example frames taken in steps of five (the scrambled versions depicted here correspond to these exact frames). For each image sequence, a histogram is inserted showing the distribution of Pearson correlations of pixel values belonging to consecutive frames.

The reason for using the trick in the first step instead of just generating random phase angles for each spatiotemporal frequency component is that the latter would result in a scrambled movie for which each frame is not matched as well with the corresponding frame of the original (a problem that is present in Fraedrich et al., 2010). For example, for the example movie in Figure 4, the mean absolute deviation for frame per frame comparison between the original and 1000 scrambled samples generated using our method is, on average, 2.2 (95% percentile interval [1.5 3.1]) for pixel intensities I, 3.5 (95% percentile interval [3.0 4.0]) for contrast values RMS, 4.9 (95% percentile interval [4.5 5.4]) for changes in pixel intensity PC. The correlation between the spatial amplitude spectra for frequency components lower than one cycle per degree (excluding the zero frequency component) of corresponding frames is, on average, 0.93 (95% percentile interval [.92 0.93]). Conversely, when these statistics are calculated for samples in which scrambling is done by completely randomizing spatiotemporal phase, the values are 16.4 (95% percentile interval [10.7 21.1]) for pixel intensities I, 5.1 (95% percentile interval [3.5 7.0]) for contrast values RMS, 5.9 (95% percentile interval [5.4 6.5]) for changes in pixel intensity PC, and 0.87 (95% percentile interval [.84 0.89]) for the spatial amplitude spectra.

The scrambled version of one rat movie in the training set was adjusted after nine sessions into the training because we suspected that the rat that had started with this particular pair used the luminance difference in the lower part of the screens to achieve above-chance performance suspiciously rapidly. To prevent this from happening, the lower parts of the frames of this one scrambled movie were made brighter by increasing the pixel values according to a linear gradient so that pixel values closer to the bottom of the movie frames were increased more. Specifically, the values of the gradient went from x at the bottom pixel row to zero at the top, where x was chosen so that the average (weighted by a linear gradient ranging from 100% to 0% from bottom to top pixel row) over all frames was equal to that of the original rat movie. Performance of this one animal dropped to chance immediately after this change (data not shown); therefore, for the continuation of the training, this adjusted distractor was used.

Experimental setup and task

Rats were trained to discriminate movies containing a rat versus movies without rat in a 2AFC task in a visual water maze (Prusky et al., 2000). Briefly, the setup consisted of a water-filled V-shaped maze with two arms (Fig. 5). At the end of each arm, a stimulus was shown and a transparent platform was placed just below the water surface in front of the target stimulus. A trial started when a subject was placed in the water at the end opposite to the stimuli and ended when the rat reached the platform. For a quick escape, the animal had to choose the correct arm where the target movie was played. If the rat had entered the wrong arm, it had to swim back to the other arm and sit through a 20 s time interval before being rescued. In the case of an instant correct choice, this interval was 10 s to still ensure some stimulus exposure. Overall, the distribution of time to reach the platform had a mode of 4.7 s (95% percentile interval [3.8 22.5]) for correct trials and a mode of 8.6 s (95% percentile interval [5 27.7]) for incorrect trials. Note that the lower bound of 3.8 s is limited by swimming speed rather than animals waiting before responding, meaning that a mode of 4.7 s would be ∼1 s extra. Between trials, the animals resided under a heat lamp. The water was kept at a temperature of 26–27°C. Stimuli were presented on two 768 × 1024 CRT screens at a width of 24 visual degrees as seen from the divider. Output to the monitors was linearized and the mean luminance was 53 and 52 cd/m² for the left and right screen, respectively. The stimuli were played in an infinite loop alternating between forward and backward play to always ensure a smooth transition. The target was always the stimulus containing a rat. The distractor was either the matched nonrat movie or the scrambled version of the rat movie. Each animal was trained for two sessions per day. Each session included 12 trials performed in an interleaved fashion (all rats were tested on trial n before any rat was tested on trial n + 1). The side of the target stimulus was determined according to a standard sequence of LRLLRLRR (Prusky et al., 2000). Specifically, per rat and per session, a random starting point in this sequence was chosen, with the only restriction that no rat could start with the target movie on the same side for two trials. Whenever the end of the sequence was reached, the procedure would jump to the beginning to fill in the remainder of target locations to get to 12 trials. We opted for adopting these stringent constraints used by Prusky et al. (2000) in an attempt to prevent development of response biases. However, this means that, in theory, a rat could predict the correct response if the target had been presented for two consecutive trials on the same side (i.e., after LL or RR). In addition, overall, the probability that the next target will be on the opposite side is much higher than that it will be on the same side, meaning a strategy in which a rat would switch sides would be relatively successful overall. Finally, because the sequence could not start with a repetition (i.e., LL or RR), the platform location on the second trial of each session could always be predicted from that on the first trial. However, the fact that the number of trials per session were limited and that the interleaved testing of animals resulted in a long intertrial interval of at least a few minutes argue against the hypothesis that a rat can pick up the regularities of this sequence. Indeed, Figure 6A shows that the animals did not use any of these potential shortcuts: percentage correct does not fall to chance when trials are not predictable (e.g., the first), nor does it peak on trials that are predictable (the second trial or a trial following a repetition of the same target side). In addition, performance is well above chance even if the target side in a trial was a repetition of that in the previous one (i.e., a switch strategy would not be successful). Moreover, our previous unsuccessful experiments using the same protocol in tasks that turned out to be too challenging indicated that rats will not pick up any potential shortcut even after substantial training. Whenever a rat would reach a response bias of >80% in one session, an anti-bias procedure was used in the subsequent session: on the first two trials, the target was presented to the side opposite of the bias. If the bias persisted in the following session, the target was presented for 75% of the trials on the side opposite to the bias. For all but one animal, this procedure was sufficient to break any persistent response preference. This rat never learned any stimulus pair and thus could not be included in the experiment. Note that bias correction trials were never used during any of the generalization sessions with two platforms. Only the data to test performance on all target–distractor combinations of the training stimuli include bias correction trials (see Testing phase, below).

Figure 5.

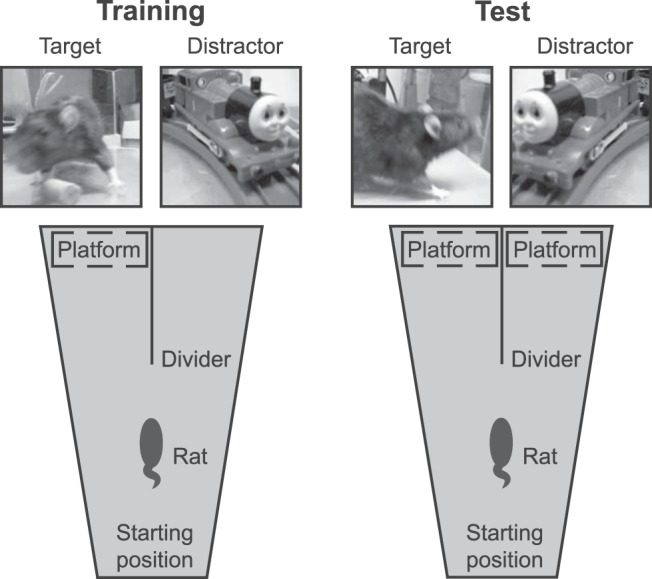
Schematic representation of the 2AFC setup as seen from the top. In each trial, the rat had to find the hidden platform by swimming toward the side showing the target stimulus while ignoring the distractor. During generalization sessions, there was a platform present in front of each screen.

Figure 6.

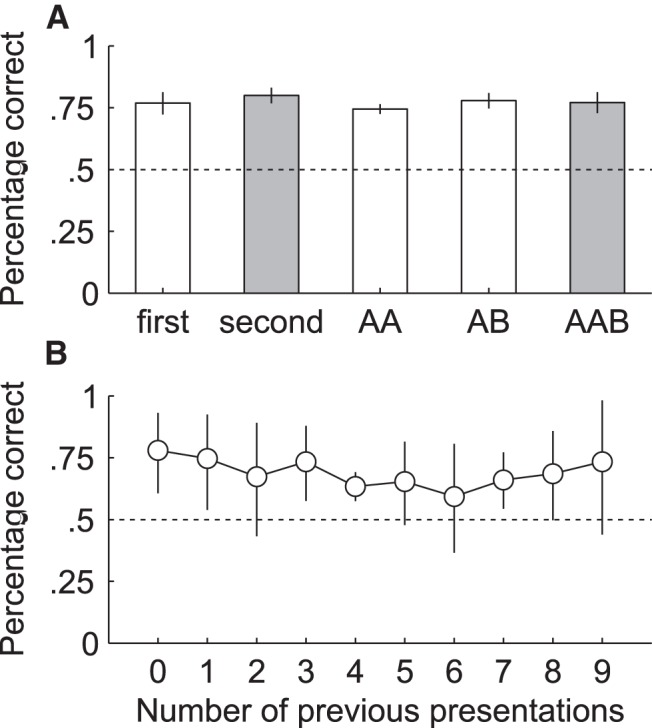
Control analyses to check for potential shortcuts related to the sequence for assigning stimuli to the left or right screen (A) and to check for learning of new pairs during two-platform trials (B). A shows the percentage correct from all sessions in which only one platform was used: for the first trial (first), the second trial (second), trials in which the target was on the same side as on the previous trial (AA), trials in which the target was on the other side as on the previous trial (AB), and trials following two consecutive trials in which the target was on the same side (AAB). The correct response for the cases indicated in gray were perfectly predictable in theory for a subject with full insight in the stimulus sequence, as opposed to all the other data shown here in which the correct response was unpredictable. B, Percentage correct averaged across animals from all trials with new stimulus pairs (and therefore using two platforms) as a function of how many times the animal had seen that pair before. Error bars in both A and B indicate the 95% confidence intervals obtained from a two-sided t test on the arcsine of the square rooted proportions correct per animal (n = 5 per confidence interval).

Training phase.

At the start of training, the subjects were familiarized with the 2AFC task using a white screen as the target versus a black screen as the distractor. This shaping procedure was terminated when all rats had reached a performance of at least 80% correct on three consecutive sessions. The actual experiment consisted of two phases: a training phase and a testing phase. During the former, rats were trained to discriminate the five rat movies of the training set from their distractors (Fig. 1). A rat would start the phase with one target movie and one distractor movie. Whenever performance would reach a criterion of at least 75% correct on four consecutive sessions, the same target movie would be presented with the other type of distractor (the two types being object movies and scrambled movies). Whenever a rat would fail to reach this criterion within a large number of trials (e.g., >300, which would take approximately a month), the decision was made to move to the next pair to advance the training process. This happened a few times because we had chosen some challenging combinations for the training set on purpose to push the animals: both the second training pair containing a movie of a rat relatively far away and high up the screen and the last training pair containing rat-like sock puppet as distractor proved to be difficult. Test Set 1 did not include such challenging combinations. When the criterion was reached again (i.e., after the rat was trained with the two types of distractors for a certain target), a rehearsal intermezzo of the previous combinations started until performance for every pair (assessed on the six last trials per pair) was at least 75% again. Subsequently, the rat moved to a new target movie with the distractor of the same type as that of the latest combination. Except for the first sessions, trials containing a new target or distractor were always mixed with trials containing the most recently learned combination. On every switch to a new movie, the new–old stimulus pair ratio was 1/2 and changed to 2/3 after a full session for which performance on the old pair was 75%. The order in which rats were trained on each target and their distractors was different for every animal. At the end of the training phase, final performance on the training stimuli was assessed by presenting all possible target and distractor combinations (thus no longer only including the original pairings of each target with its two distractors).

Testing phase.

During the subsequent testing phase, generalization to the stimulus pairs of the three test sets was assessed. On these generalization trials, the protocol was changed to limit new learning: both arms contained a platform and the animals were rescued immediately upon reaching it. Therefore, any response was rewarded and, most importantly, there was no negative reinforcement. Figure 6B shows that, on average, the percentage correct on a new stimulus pair did not increase as a function of the amount of times the animal has seen (any of the movies in) that pair. Rather, the figure suggests that if there was any learning at all during the test phase, it had a negative effect on the performance of the animals. Generalization trials were randomly mixed with trials using training movies and only one platform to keep the rats motivated to perform the task well. If a rat acquired a strong response bias during testing with two platforms (i.e., >80% responses in one direction), the data for that particular session were removed from analysis and an anti-bias procedure (see first paragraph of Experimental setup and task, above) was initiated using mixed target–distractor combinations with training stimuli and one platform only. The data obtained during these correction sessions were pooled with the data obtained at the end of the training phase using all possible target and distractor combinations to ensure a sufficiently large number of trials per target × distractor combination. After probing for generalization, specific hypotheses were examined by manipulating the stimuli of Test Set 1 and assessing the effects on performance. It should be noted that not every rat underwent every testing condition because of temporal constraints related to the fact that each animal finished training at a different time (Table 1).

Table 1.

Number of trials used for data analysis per rat and per phase or test condition

Phase	Type	Rat
		1	2	3	4	5
Training		1668	1704	1692	2124	1896
Test training pairs		60	60	60	60	60
Test new combinations		204	180	119	180	240
Test generalization
1: Typical	Natural distractor	48	48	48	48	48
	Scrambled distractor	48	48	48	—	48
	Reduced speed	48	48	48	48	48
	Single frame	48	48	42	24	—
	Changed luminance	48	48	48	—	—
	Single frame, changed luminance	12	48	48	54	—
2: Less rat/object movement	Natural distractor	48	48	48	48	48
	Scrambled distractor	48	48	48	—	48
3: Long–Evans	Natural distractor	48	—	48	—	—

For the generalization data, the numbers of trials are only taken from sessions without response bias (i.e., no more than 80% responses in one direction).

In total, the experiment encompassed 251 behavioral sessions per rat (spread over ∼6.5 months), each containing 12 trials per rat and taking approximately 1 h.

Data analysis

On some occasions, we report the results from a classical one-tailed t test based upon the across-rat variability (n = 5) and using a significance threshold of α = 0.05. These tests are performed on the arcsine of the square root of the proportion correct trials (i.e., y_j^trans = sin⁻¹ $\sqrt{y_j/n_j}$, with y_j correct responses of rat j on n_j trials) to stabilize variance and approximate normality for the transformed proportions (Hogg and Craig, 1995). However, the t tests do not take into account the number of trials on which the performance in each animal is based; in fact, the transformed numbers should not be treated as metric because then we ignore information about the number of trials n_j. The latter issue can be addressed by using a simple binomial test and pooling all trials over animals, but then the unmodeled dependencies can lead to meaningless results. Conversely, logistic regression supersedes transformations for analyzing proportional data (Warton and Hui, 2011). In addition, a hierarchical model is the preferred method to approach dependencies between observations (Lazic, 2010; Aarts et al., 2014), because information on the uncertainty of the estimates on the within-subject level is not discarded, but used in the analysis on the population level.

Given the widespread familiarity with t tests in the neuroscience community, we include t tests for the results on each of the stimulus sets with data from more than three animals and binomial 95% confidence intervals per rat otherwise. However, given the disadvantages of such tests discussed in the preceding paragraph, we also turned to a more comprehensive hierarchical model that allowed us to take into account both the number of subjects and the number of trials per subject. Specifically, a within-subject logistic-binomial model was fit to the data to make inference on animal performances and on comparisons between the different stimulus sets as follows:

In this model the observed number of correct trials y_ij of rat j on stimulus set i is assumed to have a binomial distribution with n_ij denoting the number of trials and p_ij denoting the probability of a correct trial. This probability is estimated by the logistic function f(x) = 1 ÷ (1 + e^−x) (which compresses values between zero and one) of a linear combination of predictors: one for stimulus set (SET, a nominal predictor with 13 levels: five stimulus sets with natural distractors, four with scrambled distractor, and four manipulations of Test Set 1), one for subject (RAT, a nominal predictor with five levels: one for each rat), and one for the interactions between subject and stimulus set (RAT × SET, a nominal predictor covering all interactions between subjects and stimulus sets). The parameters α_i, β_j, and γ_ij (for all i = 1 … 13 and j = 1 … 5) are the estimated deflections from the central tendency μ for each stimulus set, rat, and combination of rat and stimulus set, respectively. These parameters are estimated on the log odds scale (logit(p) = log(p ÷ (1 − p)) for percentage p), meaning that the increase or decrease in percentage correct corresponding to their value is not a constant, but depends on the percentage correct from which the deflection is calculated (for a more detailed discussion of the interpretation of logistic regression coefficients, see Gelman and Hill, 2007). The residuals are assumed to be normally distributed with variance σ_ε². The regression weights for the subject predictor and subject interactions are also assumed to be normally distributed with variances σ_β² and σ_γ², respectively. All three variances, as well as the central tendency and all deflections, are estimated by the data. This model is formally equivalent to the example model of Gelman and Hill (2007). Whereas only the effect of the nominal predictor SET is used for inference, all other parameters are necessary to model the dependencies present in the data (Lazic, 2010).

A slightly modified model was used for inference on different target and distractor combinations: stimulus pair was used as predictor instead of stimulus set, with a variance parameter for its regression weights (α_i ∼ N(0, σ_α²) for i = 1 … 50). This parameter provides shrinkage toward μ on the performance estimates for stimulus pairs (i.e., regularizing the regression), which makes sense because they are estimated from a rather limited number of trials (between 14 and 33, Mdn = 30), whereas there is a large number of parameters (stimulus pair is a nominal predictor with 50 levels).

Estimation was done within the Bayesian framework by approximating the posterior distribution by means of Markov chain Monte Carlo sampling using JAGS (Plummer, 2003; an improved clone of BUGS, one of the most popular statistical modeling packages, Lunn et al., 2009) in R (R Core Team, 2012). JAGS uses Gibbs sampling, which is an algorithm that can draw samples from a joint probability distribution given that all the conditional distributions (i.e., one for each parameter) can be expressed mathematically. The joint posterior distribution was approximated by generating 10,000–20,000 samples (using three chains to check for convergence). The joint posterior distribution quantifies the probability of each parameter value given the data by combining a prior with the likelihood. Noninformative prior distributions were used as to let the data fully speak for themselves and not constrain the estimates in this respect. Specifically, priors for the regression weights were all normally distributed and centered around zero. Large SDs of magnitude 100 were chosen for parameters without hyperprior. Uniform priors ranging from 0 to 100 were chosen for the SDs that were estimated in the model (as in Gelman, 2006). Similar to confidence intervals, a 95% highest-density interval (HDI), containing the 95% most probable parameter values, was used for inference; the mode indicates the single most probable value, which will be called the point estimate from here on. A 95% HDI covers 95% of the posterior probability density (i.e., there is 95% certainty that the underlying population parameter that generated the data falls within the bounds of the interval) and, in addition, there is no value outside the interval that is more probable than the least probable value within the interval (the concept of HDI is explained in further detail in Kruschke, 2011). Values falling outside of the 95% HDI are rejected based on low probability. Essentially, this is a within-subject ANOVA model. However, the logistic-binomial extension makes it appropriate for dichotomous predicted variables. In addition, by including the information about the magnitude of n_ij, one allows for appropriate inference taking into account the (often unbalanced) number of trials over subjects and conditions. In sum, the Bayesian framework permits us to choose the appropriate model for the experiment design and data type.

A different yet very similar model was used to determine whether generalization to new stimuli could be explained by a strategy in which rats use simple cues based on local luminance to achieve above-chance performance as follows:

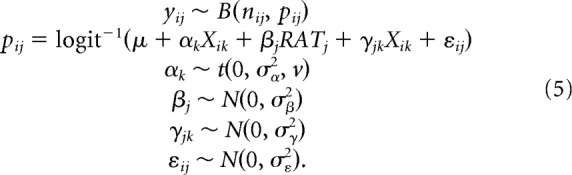This model is the same as the one described above, except that it uses metric predictors X_k. In a first test, X_ik for k = 1 … 36 denote the following predictors for each stimulus pair i: M(Ī) (local mean luminance) and M(PC) (variation in luminance) values of the target and distractor in nine locations of each screen (2 metrics × 9 locations × 2 stimuli equals 36 predictors). Indices i, j, and k denote stimulus pair, rat, and metric predictor, respectively. In a second test, for each stimulus pair i, X_ik for k = 1 … 18 denote the M(Ī) and M(PC) for the distractor subtracted from the same metrics for the target for the corresponding nine locations of the screens. The t distribution on the regression coefficients α_k for our metric predictors provides regularization and avoids overfitting to the data by only allowing strong predictors to have a substantial regression weight (Kruschke, 2011). A uniform prior ranging from 0 to 0.5 was used on the inverse of the degrees of freedom (1 ÷ ν) of the t distribution, allowing it to range from heavy tailed (e.g., ν = 2) to more normal (i.e., ν becomes larger) depending on the data.

Results

Training

Rats were trained to categorize five rat movies versus five object movies and five scrambled movies. The training started with one pair of movies, and gradually other pairs were added. Subjects completed the training phase after a total of 139, 142, 141, 177, and 158 sessions, corresponding to 1668, 1704, 1692, 2124, and 1896 trials (M = 1816.8). Counting a ratio of 40 training sessions per month (2 per working day), this is a training period of 3.5–4.5 months. Table 1 contains the number of trials performed per rat per condition for the training phase and all subsequent test phases.

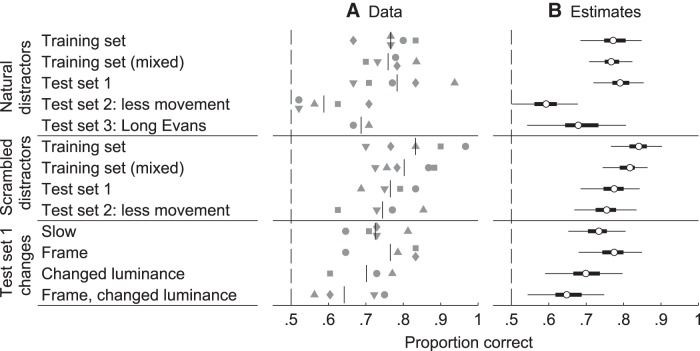
Before the testing phase, six trials per training pair and per animal were conducted to assess performance at the end of training. Performance was significantly different from chance regardless of the distractor type: mean performance was 76.7% correct for the natural distractors (one-tailed t₍₄₎ = 8.76, p = 0.0005, d = 3.92) and 83.3% correct for the scrambled distractors (one-tailed t₍₄₎ = 5.52, p = 0.0026, d = 2.47). Subsequently, all training stimuli were presented in all previously unseen target–distractor combinations. Again, mean performance was higher than chance for both distractors: 75.9% correct for natural distractors (one-tailed t₍₄₎ = 10.2, p = 0.0003, d = 4.54) and 80.3% correct for scrambled distractors (one-tailed t₍₄₎ = 8.24, p = 0.0006, d = 3.69).

For more detailed inference, the model of Equation 4 was fit to the data with a slight modification (see Materials and Methods, Data Analysis). Figure 7 displays the results of this analysis. Although the numbers on top of the heat map in Figure 7A are measured proportions correct per target distractor combination, the colors represent a deflection (α) from the central tendency (i.e., overall performance, μ) for a specific level of the nominal predictor for stimulus pair. Recall that in logistic regression, this deflection is on the log odds scale and an increase or decrease in percentage correct depends on the percentage correct from which the deflection is calculated. Specifically, a certain deflection on the log odds scale is compressed at the ends of the probability scale (or, the difference 55–50% is not of the same magnitude as the difference 95–90%). In using the parameter values α for the color scale, differences in color intensity correspond linearly to differences in performance on an unbound scale. For these data, which have a central tendency of 81.7%, the percentages correct corresponding to different values of α are indicated on the color bar of the heat map. Notice the presence of a pattern where color seems to vary predominantly across columns rather than rows. Because each column shows the data and estimates for a different distractor, this visual inspection already indicates that performance seems to be mostly modulated by the distractor. Target distractor combinations for which the 95% HDI of the regression weight did not include zero are indicated by printing the corresponding measured proportions correct in white bold font to further highlight those combinations for which performance deviates from the overall performance across all stimulus pairs. Recall that the 95% HDI indicates the range of values for which there is 95% certainty that the underlying population parameter that generated the data falls within the bounds of the interval. Values falling outside of the interval are rejected based on low probability. This comparison indicates that performances on several combinations with natural distractor 1 are higher than average, whereas performances on several combinations with natural distractors 2 and 5 and one combination with scrambled distractor 2 are lower than average (although still higher than chance performance, which is 50%). On the two diagonals, the proportions correct for the training pairs are located. Performance for three of these pairs is lower than the criterion of 75% correct that was upheld during training because, for some pairs, we had to continue training without that criterion having been reached. To determine the main effect per movie, we looked at the marginal posterior distributions for effects of targets and distractors separately. Figure 7B shows the estimated proportion correct (i.e., mode of the distribution) and its 95% HDI (indicated by thin error bars) for each target movie independent of the distractor and for each distractor independent of the target. If the estimated proportion correct across all target distractor combinations (indicated by the dashed line) falls outside of the 95% HDI, meaning that this value is highly improbable for this target or distractor, we have strong evidence that this particular movie modulates performance independent of the movie it was paired with. Therefore, we can clearly see that performance is substantially modulated by four natural distractors and one scrambled distractor only.

Figure 7.

Performance on all target–distractor combinations of the training set. A, Heat map of point estimates of the regression weights (α_k) for each different pair. Red indicates performance on this combination is estimated higher than the central tendency over all combinations (μ); blue indicates the reverse (lower than the central tendency, which in most cases is still higher than chance performance). Percentages correct corresponding to regression weights (i.e., 100 ÷ (1 + e^{−(μ+tickvalue)})) are indicated above the color bar. Numbers placed on the heat map are the proportion correct for each combination for all rats pooled together (with marginal proportions at the top and right side). White print indicates that the 95% HDI of the regression weight did not include zero, indicating high certainty (i.e., at least 95%) that performance on this pair was different from the central tendency. B, Summary of the marginal posterior distributions of estimated performances for targets over distractors and vice versa. White dots indicate the mode, thick error bars the 50% HDI, and thin error bars the 95% HDI. The dashed line indicates the central tendency.

Generalization to new movies

Next, performance of the animals was tested on new stimuli. To limit learning effects, each arm of the maze contained a platform during the trials with new stimuli, so there was no negative reinforcement. On Test Set 1, the rats performed significantly higher than chance level. Mean performance was 78.3% correct for natural distractors (one-tailed t₍₄₎ = 4.91, p = 0.0040, d = 2.19) and 76.6% correct for scrambled distractors (one-tailed t₍₃₎ = 7.69, p = 0.0023, d = 3.85). The model of Equation 4 leads to the same conclusions for the natural and scrambled distractors of Test Set 1, because the 95% HDI did not include the chance level of 50% correct (95% HDI [72.0 85.4] and [68.5 84.3] for natural and scrambled distractors respectively; Fig. 8). Overall, we find that the animals were able to generalize to new movies to categorize rat movies from scrambled movies and to categorize rat movies from movies containing another object.

Figure 8.

Performance per stimulus set as estimated by the model (Equation 4). A, Raw performance data (each rat has its own marker), with the vertical lines signifying the mean. B, Summary of posterior distributions, with white dots indicating the mode, thick error bars the 50% HDI, and thin error bars the 95% HDI. This plot indicates for each stimulus set which proportions correct are most probable given the data. Chance level (i.e., 0.5) is rejected when it lies outside of the 95% HDI.

After Test Set 1, a second set was presented using target movies in which the rat was more stationary (as judged qualitatively by the experimenter). For the natural distractors, mean performance was 58.8% correct and estimated different from chance level (95% HDI [50.2 67.8], one-tailed t₍₄₎ = 2.42, p = 0.0366, d = 1.08). Performance of 74.5% correct on the same targets versus scrambled distractors is estimated to be substantially different from chance (95% HDI [66.8 83.5], one-tailed t₍₃₎ = 4.71, p = 0.0091, d = 2.35). With natural distractors, we find that performance on Test Set 2 was estimated lower than performance on Test Set 1 (nonoverlapping 95% HDI). Therefore, either the decreased amount of movement or another factor confounded with it makes generalization more difficult on Test Set 2. One potential confound might be that these movies were less similar to the trained movies (i.e., less typical) in more aspects than just the amount of motion. In a later section, we will present specific manipulations of the motion in the movies of Test Set 1 that are meant to exclude such confounds.

Combining the estimates for the training stimuli with those for Test Set 1 and 2, the proportion correct on stimulus pairs with a natural distractor is estimated lower than that on pairs with a scrambled distractor (95% HDI [−0.64 −0.03] on the log odds scale).

Finally, performance of two rats was assessed for Test Set 3, which contained five target movies of a Long–Evans rat paired with natural distractors. To have a robust estimate in each rat, the rats performed each 48 trials with Test Set 3. Again, posterior distribution indicates performance to be higher than chance (95% HDI [54.2 80.6], binomial 95% confidence intervals for the two animals: [51.6 79.6] and [55.9 83.1]) based on an overall performance of 68.8% correct. Therefore, the fact that the movie includes an animal that is no longer homogeneously dark did not abolish generalization.

Generalization to altered versions of the movies from Test Set 1

Rats were also tested with several manipulations of Test Set 1. In all of these manipulations, the distractors were natural movies.

The first two changes probed how the temporal variation of the movies affect performance to have a more direct test of the effect of motion than provided by Test Set 2. First, we played the movies at 1/4 of their original speed and in a subsequent test only showed one static snapshot. The time point of the snapshot was that for which the frame of the target movie was most similar to all other frames in that movie (i.e., minimal pixel-wise Euclidean distance; Fig. 1). These tests were motivated by the observation of a lower performance on Test Set 2, in which rats were more stationary in the target movies. Mean performance was 72.5% correct for the reduced playback speed and 76.5% correct for the snapshots. Both were estimated to be different from chance (95% HDI [65.3 80.5], one-tailed t₍₄₎ = 7.73, p = 0.0008, d = 3.46 and 95% HDI [68 84.9], one-tailed t₍₃₎ = 5.77, p = 0.0052, d = 2.89, for the speed reduction and static frame, respectively). Comparisons with proportion correct on the unadjusted Test Set 1 do not indicate a decrease in performance (95% HDI [−0.26 0.87] and [−0.51 0.75], on the log odds scale, for the speed reduction and static frame, respectively). Therefore, most likely, the decrease in performance on Test Set 2 had to do with other confounding factors making the movies less typical. The amount of motion does not affect the ability to achieve above-chance performance on Test Set 1 stimuli. The presence of motion is not necessary and rats can differentiate between images containing a rat and other images based upon stationary cues.

Next, we tested whether generalization could be explained by local luminance differences. Indeed, previous studies have shown that, whenever possible, rats tend to use simple cues such as average luminance of the lower part of stimuli in visual discrimination tasks (Minini and Jeffery, 2006; Vermaercke and Op de Beeck, 2012). Figure 9 shows that the average pixel value in the lower half of the target stimuli was consistently higher than that of the lower half of the corresponding natural distractors (note that this was also the case with four out of the five scrambled distractors; data not shown). Therefore, the lower part of target stimuli was made darker, whereas the reverse was done for the distractors. Specifically, pixel values where adjusted according to a linear gradient ranging from x to −x from top to bottom pixel rows for target stimuli and from −x to x for distractors, where x was chosen for each pair so that the difference in average lower half pixel values was just below zero (Fig. 9). In this way, the global luminance was retained. Note that the average lower-half pixel value was calculated across all frames. With full movies, the rats' mean performance was 70.1% correct, which is estimated to be different from chance (95% HDI [59.1 79.7], binomial 95% confidence intervals for each of the three animals: [58.2 84.7], [45.3 74.2], and [62.7 88.0]), and not different from the performance with the original Test Set 1 movies (95% HDI [−0.16 1.12], on the log odds scale). When the same luminance manipulation was applied to the static frame stimuli, mean performance was 64.2% correct, which is also estimated to be different from chance (95% HDI [54.4 74.9], one-tailed t₍₃₎ = 3.43, p = 0.0207, d = 1.72), but in this case it was estimated substantially lower than the performance with the original Test Set 1 movies (95% HDI [0.06 1.13], on the log odds scale). Note that, in this case, there was only one frame, meaning that lower-half pixel intensities were now equal simultaneously at all time. Overall, we still find significant generalization in both tests, showing that animals were not simply picking up a luminance difference in the lower half of the stimuli. Whereas performance on the static pixel intensity adjusted frames did differ from that in Test Set 1 (without this being the case for the pixel-intensity-adjusted movies), the total picture is more complicated because there is no convincing evidence for a difference in performance between the static versus moving adjusted stimuli (95% HDI [−0.5 0.9], on the log odds scale). The lower observed performance can be explained by the fact that rats had been doing more trials with two platforms by then, which might decrease motivation as a result of mistakes being rewarded (see also Fig. 6B). Another possible explanation is that the pixel intensity adjustment is more thorough in the case of one stationary frame, because it is now applied to the level of this individual frame. Most importantly, there is clear above-chance performance for all test sets and for all included stimulus manipulations.

Figure 9.

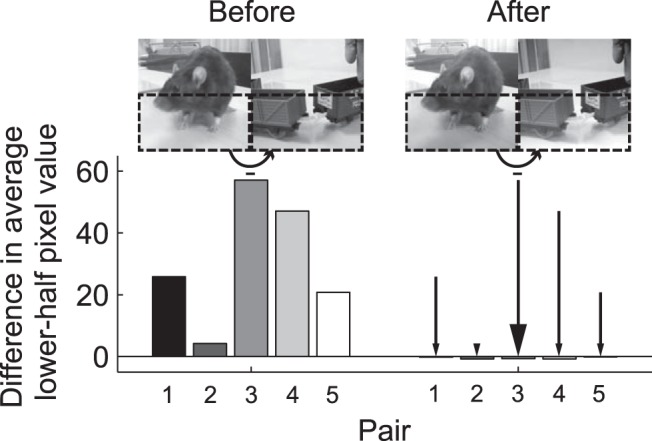
Difference in average lower-half pixel value between target and distractor before and after the adjustment. Bar plots show the average (across width, height, and frames) pixel values in the lower half of the distractor movie subtracted from the same average of the target movie for each of the five pairs of Test Set 1 before (five bars on the left) and after luminance adjustment (five bars on the right). If a bar is not visible, its value is too close to zero. Positive values indicate that the lower part of the target movie is on average (across frames) lighter than the lower part of the distractor movie. Snapshots show the first frame of an example pair (corresponding to the third bar in each set of five, with the target on the left and the distractor on the right).

Do rats use a strategy based on local luminance?

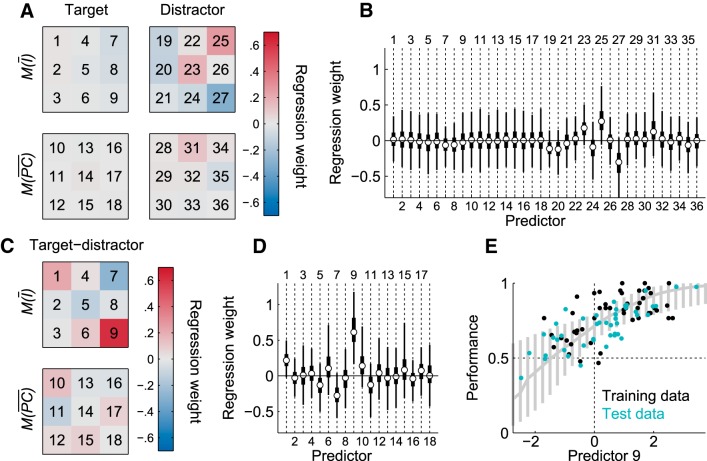
To determine whether rats used a strategy based on local luminance or pixel change, a linear logistic-binomial regression model (see Equation 5) was fit on the rat performance scores with the following predictors: local mean luminance and local mean variation in luminance of the target and distractor in nine locations of each screen. The latter two statistics are the same as M(Ī) and M(PC) (defined in the Materials and Methods), with the exception that they were calculated separately for different locations on the screen: each frame was divided in three by three equally sized (128 × 128 pixels) squares (which together cover the entire frame/screen). Concretely, this means that performance on each stimulus pair is estimated based on 36 metric predictors (2 metrics × 9 locations × 2 stimuli). The model was fit to the performance on all target–distractor combinations of the training stimuli (shown in Fig. 6) to determine whether a strategy that could be learned from these stimuli might allow rats to generalize to the test stimuli. Figure 10A depicts four templates based on the point estimates of the regression weights for the predictors (each of the nine squares of the templates corresponds to one of the nine locations on the stimulus). Note that the highest loading regression weights are for the properties of the distractor, not the target.

Figure 10.

Local luminance cues and performance. A, Templates based on modes of the posterior distributions of the regression weights for the 36 luminance predictors: average pixel values and mean absolute pixel change, each on nine locations of both stimuli (the nine squares in each template correspond to the nine locations on the square stimulus frames). Red indicates average luminance or pixel change in this area correlates positively with performance; blue indicates the reverse. B, Summary of the posterior distributions of the regression weights for each of the 36 predictors, with dots indicating the mode, thick lines the 50% HDI, and thin lines the 95% HDI. C and D are analogs to A and B, but show the results of a model based of the difference in each corresponding local luminance cue on the target and the distractor. Red indicates that a higher difference in average luminance or pixel change in this area for the target versus the distractor correlates positively with performance, while blue indicates the reverse. E, Performance on each target–distractor combination (dot) as a function of the luminance difference in the lower right corner (predictor 9 of the difference template, which is estimated to be different from zero). Only the training data (indicated in black) were used to fit the model. The mode of the posterior distribution and 95% HDIs are indicated in gray as a function of predictor 9. This panel shows that this predictor cannot explain generalization because the model's intercept does not coincide with chance level. At the intercept, where there is no average difference in luminance in the lower right corner of the screens between target and distractor (i.e., predictor 9 is equal to zero), performance is well above chance (as indicated by the data points and the 95% HDI shown in gray).

If rats use one or more of these stimulus properties in their generalization to new stimuli, the regression weights fit to the training data should accurately predict performance in the testing data. For example, if the regression weights represent a real strategy, then we would expect a distractor to be associated with better-than-average performance if it would have a higher-than-average luminance in the top right corner (the most positive regressor in the distractor pixel intensity template in Fig. 10A and/or a lower-than-average luminance in the bottom right corner, the most negative regressor in this template). For all of the predictor regression weights, the 95% HDI included zero (Fig. 10B), so for none of these regression weights was there enough evidence to reject zero. Moreover, the proportion of variance explained by the model (1 − residual variance ÷ total variance) is 0.12 for the training data and 0.01 for the test data (which were not used to fit the model). Therefore, the significant generalization of the rats and the variation in generalization performance among different targets and distractors cannot be explained by a strategy based upon local luminance cues.

Next, the same model was used but with predictors referring to the local difference in luminance between target and distractor (these new predictors correspond to a subtraction of the predictors of the previous model). This new model tests whether a strategy based upon differences between the target and distractor on corresponding local luminance or pixel change values could have allowed for successful generalization. The templates (Fig. 10C) and regression weights (Fig. 10D) indicate that performance on the test set is positively correlated with a difference in luminance (for target minus distractor) on the lower right part of the screen. This difference template model has a proportion of variance explained of 0.12 for the training data and 0.13 for the test data. However, the predicted performance is still 71.5% correct (95% HDI [61.4 80.0]) for the intercept, which is the estimate for when there is no information in the difference template. Indeed, both the model and the training and test data shown in Figure 10E support the conclusion that, whereas performance is modulated by a luminance difference in the lower right corner of the screen, it cannot explain generalization. Rats neither perform at chance when this predictor is zero nor do they prefer the distractor when it is negative. Generalization performance is still ∼70% even when there is no luminance difference.

Discussion

Five out of six subjects were able to complete the training phase. Mixing up the training pairs proved that the acquired decision rule(s) was not bound to these specific target–distractor combinations. In addition, these data with the training movies indicated that the variability in performance for different pairs can mainly be explained by the variability in natural distractors. Subsequently, the animals successfully generalized to a first typical test set, another test set with more stationary rats/objects, and one with a strain of differently colored rats. In general, performance with scrambled distractors was higher than with natural distractors.

Together, the results of the test phase show a successful generalization to a set of novel, unique stimulus pairs. This was the case for pairs with a natural as well as with a scrambled distractor. The latter are more different from the target movies in that they lack naturally occurring feature conjunctions. Even though performance was mainly modulated by the distractor, one cannot conclude that this means the animals used an avoid-distractor strategy. For example, this finding can be explained equally well by the simple fact that the content of the distractor movies was more variable than that of the targets.

Simple behavioral strategies that cannot explain the generalization to novel movies

We investigated several simple strategies that could underlie the main results. For example, rats might have used general differences in motion energy or local luminance. Neither reducing the frame rate nor presenting stationary frames resulted in a substantial reduction of performance. This means that motion cues in the movies were not a critical factor. Likewise, there is no evidence that equalizing the luminance in the lower part of the target corrupted performance on test movies. The latter did affect performance on stationary frames, yet even in this case, it remained well above chance.

Finally, we did a control analysis to determine whether a more complex pattern of local luminance cues could explain generalization. The results show that these cues cannot explain above-chance performance on the test sets. Therefore, we conclude that both simple local luminance and motion energy are insufficient to explain the achieved proportion correct on the test sets, which indicates that generalization relied on a more complex combination of features.

Behavioral strategies that might underlie the generalization to novel movies

Here, we consider three nontrivial and interesting strategies. Although we discuss to what extent they might underlie performance in our experiments, further studies are needed to distinguish between these possibilities.

First, the rats might use contrast templates by comparing the luminance in different screen positions (instead of using the simple luminance cues, which we ruled out). We recently suggested the use of such contrast strategies as an explanation of the behavioral templates in an invariant shape discrimination task (Vermaercke and Op de Beeck, 2012). Such contrast templates can be fairly complex by combining different contrast cues, as has been suggested in the context of face detection by the human and monkey visual system (Gilad et al., 2009; Ohayon et al., 2012). Nevertheless, these templates arise from low spatial frequencies and do not necessarily require orientation selectivity, edge detection, or curvature processing and are effectively used in computational face detection models (Viola and Jones, 2001; Viola et al., 2004).

This property sets the contrast template strategy aside from a second strategy based on shape cues such as edges/lines, corners, and curvature. Hierarchical computational models of object vision based upon the primate literature (Hummel and Biederman, 1992; Cadieu et al., 2007) aim to process the visual input in terms of such shape features that have been shown to drive neurons in inferior temporal cortex in monkeys (Kayaert et al., 2005; Connor et al., 2007). In rats, we currently lack such neurophysiological evidence. Previous studies reporting the use of shape information by rats (Simpson and Gaffan, 1999; Alemi-Neissi et al., 2013) did not make this important distinction and therefore cannot exclude the use of contrast templates.

Third, we cannot exclude the possibility that rats would have a notion of rats as a “semantic” category. However, we believe this possibility is very unlikely, at least when based on visual cues only. First, it takes quite some time to train them to categorize movies containing a congener from nonrat movies. If this category distinction were salient to them, as it is for humans and other primates, we would expect that training with only one pair of movies would allow very good generalization to other pairs. In contrast, training was also relatively slow for later movie pairs. This could be because they tend to use simpler cues first and/or because they do not make this distinction naturally. However, this study cannot draw any conclusions about a possible semantic representation of the category rats relying on one or more other modalities that are more ecologically relevant to rats as a species.

Comparison with categorization of natural stimuli in monkeys

At this point, it is relevant to compare our findings to the two most similar studies in monkeys: Vogels (1999a) and Fabre-Thorpe (1998). Similar to both studies, rats could learn to discriminate successfully natural stimuli belonging to different categories and generalize to novel stimuli. Even though the training period (on average, 151.4 sessions) might seem highly intensive, the average number of training trials (1816.8) is actually relatively low. Vogels (1999a) used probe stimuli to determine whether a single low-level feature led to generalization and concluded that at least feature combinations were required. Similarly, in the present study, a number of probe tests were performed to exclude the simplest low-level strategies. Conversely, Fabre-Thorpe (1998) focused on the speed of categorization during very brief presentations. The setup used in the present study did not allow such a short stimulus presentation, fast response by the rat, or accurate measurement of reaction times. A different setup using still images would be necessary to investigate that aspect of categorization in rats. Finally, the most obvious difference from both Vogels (1999a) and Fabre-Thorpe (1998) is that, in the present study, natural movies were used instead of still natural images. However, presenting snapshots of the movies did not disrupt generalization. Overall, there are interesting commonalities with previous findings in monkeys, but a more systematic comparison requires a study testing both species on the same stimuli in the same task context.

Neural mechanisms

The swimming-based task used here was chosen for its relative ease to train rats and the very low error rate the animals obtained with easy stimuli. This task cannot be combined immediately with experiments involving electrophysiological recordings. Of course, as mentioned in the Introduction, uncovering the visual capabilities of rodents on a behavioral level to evaluate the validity of rodents as a model for vision (Tafazoli et al., 2012) is in itself relevant for the growing group of neuroscientists focusing on these animals. Furthermore, as is the case with other swimming-based tasks used in neuroscience, such as the Morris water maze, techniques such as lesioning, genetic, or pharmacological manipulations and activity mapping with immediate early gene expression can be successfully applied in the context of our task. Finally, an extension with simultaneous neural recordings might use virtual navigation (Harvey et al., 2009) as a paradigm with similar behavioral responses (i.e., “running toward”).

Which neural representations might underlie the categorization performance? In primates, visual features that are encoded in the primary visual cortex (V1) are integrated into higher-level representations in the extrastriate cortex (Orban, 2008). Traditionally, these extrastriate areas are grouped into two anatomically and functionally distinct pathways: a ventral stream providing the computations underlying object recognition and a dorsal stream mediating spatial perception and visually guided actions (Kravitz et al., 2011). Neurons in the ventral stream in monkeys display category specific responses that are tolerant to changes in various image transformations (Vogels, 1999b; Hung et al., 2005). The superordinate distinction between animals and nonanimals has also been related to strong categorical responses in monkey and human ventral regions (Kiani et al., 2007; Kriegeskorte et al., 2008).

Based on the high complexity and variability of the stimuli and on the evidence from the probe tests and the local luminance control analyses presented here, we suggest that a computation based on the integration of features encoded in V1 would be necessary for generalization to novel stimuli. Therefore, as in primates, extrastriate cortical regions might be involved. Previous research has suggested that the rodent visual cortex consists of two streams resembling the dorsal and ventral pathways in primates (Wang et al., 2012). It seems therefore natural to suspect that the putative ventral stream in rodents is involved in learning the categorical distinction between rat and nonrat movies. Indeed, one of these areas has been shown to respond to high spatial frequencies in mice, which might indicate a role in the analysis of structural detail and form (Marshel et al., 2011). However, for now, this proposal remains very speculative given the many differences between rodents and monkeys and the lack of knowledge about rodent extrastriate cortex.

Notes

Supplemental material for this article is available at http://ppw.kuleuven.be/home/english/research/lbp/downloads/ratMovies. This URL directs to a ZIP file containing all movies used in the rat categorization experiment. This material has not been peer reviewed.