Motility efficiency and spatiotemporal synchronization in non-metastatic vs. metastatic breast cancer cells

Abstract

Metastatic breast cancer cells move not only more rapidly and persistently than their non-metastatic variants but in doing so use the mechanical work of the cytoskeleton more efficiently. The efficiency of the cell motions is defined for entire cells (rather than parts of the cell membrane) and is related to the work expended in forming membrane protrusions and retractions. This work, in turn, is estimated by integrating the protruded and retracted areas along the entire cell perimeter and is standardized with respect to the net translocation of the cell. A combination of cross-correlation, Granger causality, and morphodynamic profiling analyses is then used to relate the efficiency to the cell membrane dynamics. In metastatic cells, the protrusions and retractions are highly “synchronized” both in space and in time and these cells move efficiently. In contrast, protrusions and retractions formed by non-metastatic cells are not “synchronized” corresponding to low motility efficiencies. Our work provides a link between the kinematics of cell motions and their energetics. It also suggests that spatiotemporal synchronization might be one of the hallmarks of invasiveness of cancerous cells.

INTRODUCTION

The ability of cells to propel themselves – the so called cell motility^1-3 – is of key importance in the migration of cancerous cells from a primary tumor to places where they can seed distant metastases. Despite decades of research, cancer metastasis remains the major cause of death in cancer patients and an ongoing motivation for research on cell motility⁴. While it is well known that metastatic cells typically move faster and more persistently than their non-metastatic variants^5-7, understanding the physical aspects of cell motility is only in its infancy^8,10, though recently fostered by several cross-discipline initiatives like the NIH’s Physical Sciences Oncology Centers¹¹.

The cell motility cycle generally consists of a number of distinctive processes including cell polarization, membrane extension (i.e., protrusion), formation of cell-substrate adhesions, cytoskeletal contraction, and release of attachments (i.e., retraction), and finally redistribution of adhesion bonds.^3,12,13 To date, cell motility has been characterized mostly in terms of overall cell speed/instantaneous velocity, directional persistence, or motility strategy.¹⁴

Some works also analyzed the efficiency of the process at scales from nano- to microscopic. At the level of individual proteins and their assemblies (~nm to sub-μm), efficiency was considered in the context of actin filaments performing work on and protruding the cell membrane. Polymerization of actin monomers into filaments against a load (due to cell membrane tension) is accompanied by “release” of binding free energy during monomer addition onto the barbed end), which prevents depolymerization. Mogilner and Oster calculated 68% efficiency as the ratio of the work performed by the filament on the cell membrane to the actin binding free energy.¹⁵ When the free energy of hydrolysis of ATP to ADP (occurring soon after actin polymerization) is taken into account, the overall efficiency is lowered to only about 15%.¹⁵

Another measure of efficiency was considered at the μm scales of cell membrane protrusions. This “protrusion efficiency” was defined as the ratio of the distances the cell edge travels in the protruding and retracting states.^16-19 This measure can be interpreted as a success rate of a of a portion of the cell membrane moving outwards — values > 1 indicate net advancement while values < 1 signify net retraction.

However valuable, the above approaches focus only on the local membrane dynamics (at the leading edge of the cell) observed on minute timescales over which there is little or no net cell translocation. As such, these motility measures do not shed much light on the overall efficiency of the whole-cell movement.

A desirable measure of motility efficiency at the scale of an entire cell would be one that compares the actual work done by membrane protrusions/retractions all around the cell perimeter to the minimal work that could be, ideally, expended to achieve the same net cell displacement. Such a measure would be somewhat analogous to the mechanical efficiency used to quantify performance of engines and machines, and would necessarily have to take into account spatial and temporal correlations between protrusions/retractions at different locations. To illustrate, let us first consider two extreme cases. In the first one, drawn schematically in Fig. 1A, the cell “randomly” protrudes and retracts its membrane along the entire perimeter but achieves no or very little net motion of its centroid – even intuitively, we feel that this mode of dynamics is energetically very wasteful as the non-synchronized membrane undulations cost work to form yet do not result in any appreciable cell motility. On the other extreme, one can imagine a situation illustrated in Fig. 1B where all the protruding area “compensates” the retracting area along the direction of motion – in this case, the cell uses all the membrane dynamics most productively to propel itself in intact shape, with no futile protrusions/retractions “to the sides”.

Fig. 1.

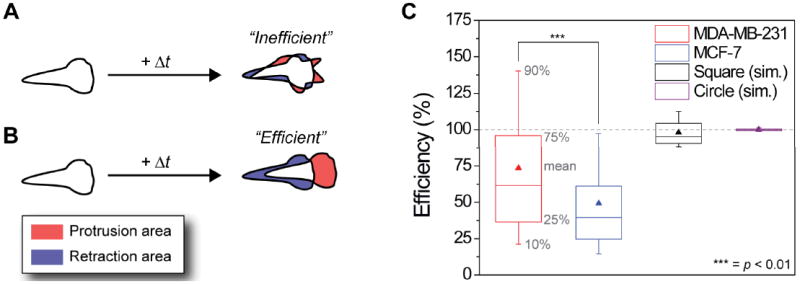
Efficiency η of cancer cell motility. (A) Schematic representation of a cell moving inefficiently, i.e., protrusions (shaded red) and retractions (shaded blue) occur at random locations along the cell boundary and do not lead to a significant net cell displacement. (B) A scheme of a cell that moves efficiently, where protrusions and retraction are oriented along the direction of net cell displacement. (C) Box-and-whisker plot showing the mean (triangle), the 90% percentile (top whisker), the 75% percentile (top box), the 25% percentile (bottom box), and the 10% percentile (lower whisker) of the efficiency of cell motility for each (3 min) time interval for all cells (averaged over 57 cells × 321 time points for each of the cell lines). The mean motility efficiency of metastatic MDA-MB-231 cells (red triangle) is 73.5%, while that of non-metastatic MCF-7 cells is 49%. This difference is statistically significant at the 99% confidence level (p < 0.01). As controls, purely translational (i.e., without any shape changes) motions of various shapes (shown here are a circle and square) were simulated and their efficiencies were found to be very close to 100% (see also ESI^† Section S2). Note: for cancerous cells, some instantaneous efficiencies are above 100%, due to changes in the cell shape translating into large displacement of the centroid but relatively little protrusion and retraction activity (see Fig. S5).

The first objective of the present work is to develop a robust measure of whole-cell motility efficiency – importantly, one whose average over cell trajectories is properly bounded to between 0 and 100%. Using this measure, we then analyze the motions of two types of cells: non-metastatic MCF-7 breast cancer cells,²⁰ and their metastatic MDA-MB-231 counterparts.²¹ We find that the latter move not only more rapidly but with significantly higher whole-cell motility efficiencies. To explain the origin of this difference we analyze the spatial and temporal dynamics along the contours of the two cell types over long time periods (up to 16 hours) using morphodynamic, cross-correlation, and Granger causality analyses. These analyses evidence that metastatic cells orchestrate their protrusion/retraction cycles more effectively than their non-metastatic variants which undulate their membranes in a more chaotic and unproductive fashion. In other words, it is this spatiotemporal synchronization that allows metastatic cells to move more efficiently compared to non-metastatic cells. Our results provide a link between the kinematics (i.e., motility modalities) and the energetics (“motility efficiencies”) of cell migrations.

MATERIALS AND METHODS

Cell culture

MDA-MB-231 and MCF-7 cells (ATCC, www.atcc.org) were cultured in DMEM (Cellgro, cat# 10-017-CV) supplemented with 10% FBS (Fetal Bovine Serum, Atlanta biological, cat# S11150), 0.1% Gentamicin sulfate (Cellgro, cat# 30-005-CR) at 5% CO₂ and at 37°C. Cells were stained using Cell Tracker Orange as described in the accompanying protocol (Invitrogen, cat# C2927) for 30 min, washed with PBS (Cellgro, cat# 21-040-CV), trypsinized, centrifuged and re-suspended in Leibovitz’s L15 medium without phenol red (Life technologies, cat# 21083-027) with 10% FBS. Finally, the cells were allowed to attach to and spread on the substrate for at least 4 hours before imaging

Transfection with fascin-GFP

Cells were transfected with pEGFP-fascin plasmid²² using FuGENE6 (Roche) transfection reagent according to the manufacturer’s instructions.

Imaging

Cells were plated onto glass-bottom dishes (Willco Wells, cat# HBst-5040) coated with 20 μg/mL laminin (Sigma-Aldrich, L2020) for 45 min, incubated in 1% bovine serum albumin (BSA) (Sigma-Aldrich, cat# A7906) for 30 min, and washed with PBS. Imaging was done on a Nikon A1R confocal laser scanning microscope running NIS software, equipped with a Tokai hit stage top incubator (37°C, 5% CO₂), and using a CFI Plan Apo VC 60X Oil objective (0.13 μm/pix).

Protrusion and retraction area analysis

Fluorescence images of motile cells where thresholded using ImageJ 1.44n (http://rsbweb.nih.gov/ij/). The resultant black-and-white, binary images were analyzed using the “analyze particles” module to determine x and y coordinates of the centroid, the total cell area, and the circularity. The images were also analyzed using a house-written script in Processing 1.5.1 (http://processing.org) to determine the area of protrusion and retraction. The efficiency of motility η was calculated from the measured variables as described below and also in Section S2 in the ESI^†.

Morphodynamics

Morphodynamic profiling was performed on non-thresholded fluorescence images using the QUIMP11 plugin for ImageJ 1.44n (http://www2.warwick.ac.uk/fac/sci/systemsbiology/staff/bretschneider/quimp). The resulting output files containing, among others, boundary velocities were analyzed using house-written MATLAB (2010b) scripts to overlay velocities and centroid locations onto DIC (differential interference contrast) images, as shown in movies M3 and M4.

Granger causality

The Granger causality analysis (p < 0.05) was implemented using the available MATLAB toolbox (http://www.sussex.ac.uk/Users/anils/aks_code.htm) and the data passed the covariance stationarity tests using the ADF (Augmented Dickey Fuller) and KPSS (Kwiatkowski, Phillips, Schmidt, Shin) method; see manual of the Granger causality toolbox for more information. The model order, i.e., how many neighboring time intervals are included in Granger causality analysis, was determined using the Akaike Information Criterion and was typically between 5 and 12.

Auto-Correlation and Cross-Correlation

Correlations were calculated by a house-written script using the econometrics toolbox in MATLAB 2010b. All correlations were determined on a per-cell basis. The means and standard deviations (Fig. 3) of the auto-correlation and cross-correlation coefficients (at each lag) were calculated over 57 cells (for each cell line). The significance of the mean correlation values was evaluated by performing the correlation analysis on the same data, which was first randomized using the randperm function in MATLAB 2010b (the resulting mean correlation coefficients are shown as horizontal red lines in Fig. 3).

Fig. 3.

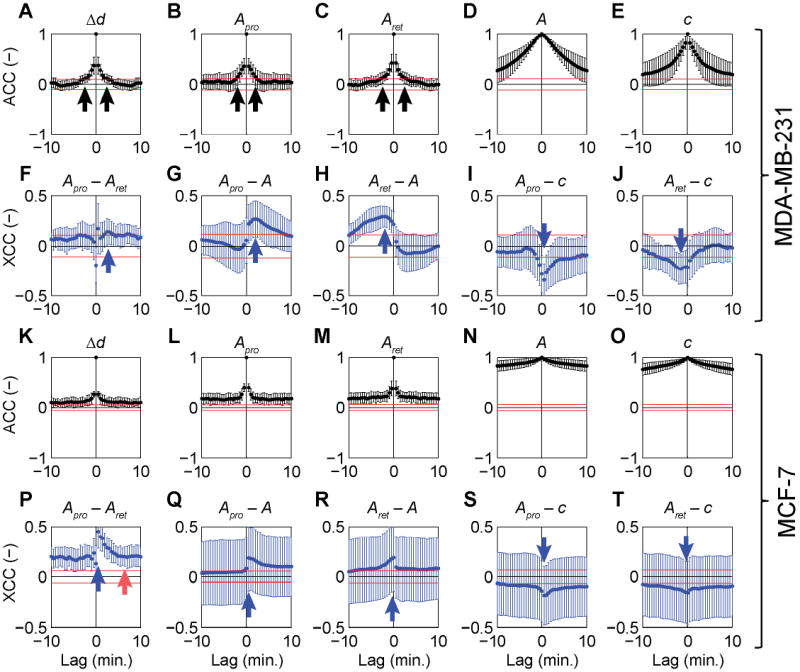
Mean auto-correlations (black) and cross-correlations (blue) with standard deviations (error bars) between distance travelled by the cell centroid at each time interval (Δd), protrusion area (A_pro), retraction area (A_ret), total cell area (A) and cell circularity (c) measured at 30 s intervals for 16 h (i.e., 1920 intervals in total) for 15 cells of each cell type. (A–E) auto correlations for MDA-MB-231 cells. (F–J) Cross correlations for MDA-MB-231. (K–O) Auto correlations for MCF-7. (P–T) Cross correlations for MCF-7. See main text for detailed description. The data in each panel shows the combined correlations over at least 15 different cells, obtained by performing the correlation analysis for each individual cell and calculating the mean and standard deviation for all cells. To determine if the mean correlation coefficient is significant, the 95% confidence bounds for randomized data sets were also calculated (red horizontal lines). To do this, experimental data for each variable (e.g., Δd or A_pro) for each cell, was randomized by changing the order of measured values randomly (randperm function in MATLAB) for each cell and then analyzed using the same method. If the mean correlation coefficient is above the red line (for positive correlation) or below the red line (for negative correlation), it is considered significant.

RESULTS & DISCUSSION

Whole-cell motility efficiency

In order to move, cells use various elements of their cytoskeleton to protrude and retract parts of the plasma membrane. These multifarious processes^1-3,23-29 all use some form of chemical energy to produce mechanical work. The forces exerted by individual cytoskeletal components onto the cell membrane during protrusions are in the pN regime (e.g., actin polymerization against the membrane).¹⁵ Similar pN forces are found in retractions of the cell membrane, following acto-mysosin contractions.^30,31 Since the forces acting during protrusions and retractions are commensurate, the mechanical work – that is, the product of force and distance – performed by a moving cell can be estimated by integrating the membrane displacement along the entire cell boundary. Put differently, to the first approximation, the areas of membrane protrusion and retraction scale with the work performed by the cell.

With these considerations, our measure of whole-cell motility efficiency η is quantified as follows. First, digital micrographs of motile cells are taken and digitized at regular time intervals, Δt = t_i+ ₁ – t_i. The difference in the positions of the cell’s centroid at t_i+ 1 and at t_i defines the effective distance travelled, Δd. New area over which the cell moves during Δt is the protrusion area, A_pro (note: not all of this area must necessarily be in the direction of travel, see Fig. 1A) and the area from which the cell moves away is the retraction area, A_ret. We wish to estimate what fraction of the total area $\mathrm{\Delta }{A}_{\mathit{exp}}=\left|A_{\mathit{pro}}\right|+\left|A_{\mathit{ret}}\right|$ changing during Δt contributes to the actual translocation of the cell and what fraction is used “unproductively” for purposes such as membrane ruffling. This is done by comparing ΔA_exp to the “theoretical area” ΔA_theo (see ESI^†, Section S2), which is the mean area that would be changed (protruded and retracted) if a cell having the same area and circularity moved without shape deformation over the same distance Δd. In other words, an “ideal” 100% efficient cell would protrude and retract ΔA_theo in order to move Δd. Analogously to mechanical efficiency used to describe machine performance³², we define “motility efficiency” as $\eta =\frac{\mathrm{\Delta }{A}_{\mathit{theo}}}{\mathrm{\Delta }{A}_{\exp }}\cdot 100\%$ which takes into account both the translocation of the centroid and the shape change (note: our measure of efficiency should not be interpreted in the strict sense since, depending on the detailed nature of cell deformation, the instantaneous values of η can be either lower or higher than 100%, see ESI^†, Section S2; on the other hand, when averaged over the entire cell trajectory, the values of η are always properly bounded between 0 and 100%).

With these preliminaries, we quantified the motility efficiency of both metastatic MDA-MB-231 and non-metastatic MCF-7 breast cancer cells whose motions on a glass substrate covered with laminin were imaged by confocal microscopy. The cells were stained using a cytoplasmic dye (CellTracker™ Orange, Invitrogen) and imaged at intervals of 30 or 180 seconds for up to 16 hours (keeping the total number of exposures per cell < 2000; for all technical details, see Materials and Methods). At each time interval, the following variables were measured: Δd, A_pro, A_ret, η, as well as total cell area A, cell perimeter length p, and cell circularity c (i.e., 4πA/p², which is 1 for a perfect circle). The areas of protrusion and retraction were determined by thresholding fluorescence images of the cells – this procedure gave binary images of black cells on a white background – and determining if a black pixel appeared (in a protrusion) or disappeared (in a retraction) in each image.

Statistics of these experiments – based on 57 cells for each cell type, 321 time intervals (Δt = 3 min) per cell, and >36,000 data points in total – are summarized in Fig. 1C. The mean efficiency of metastatic MDA-MB-231 cells is 74% ± 54%, (log-normally distributed with Pearson skewness, (mean – mode) / standard deviation = 0.34), whereas MCF-7 cells have a mean efficiency of 49 ± 37% (with Pearson skewness 0.95). These differences are statistically significant at the 99% confidence level as determined by a two sample t-test on log-transformed data of MDA-MB-231 and MCF-7 cells (this comparison is valid because both lognormal distributions of efficiency have comparable variance)³³. These results indicate that a large portion of protrusion and retraction activity in non-metastatic cells is not effectively used to translocate the cells (see Fig. S7A for histograms of efficiency for each time interval and Fig. S7B for the histograms of efficiency averaged over all time intervals per cell). A closer look at the distributions of the recorded variables quantifying cell shapes shows that MDA-MB-231 move more rapidly than MCF-7’s (Fig. S7E, F), protrude and retract larger areas (Fig. S7G, H), and have larger total areas (Fig. S7I, J). Moreover, MDA-MB-231 cells have a lower circularity (see Fig. S7C, D), which is indicative of a higher degree of polarization as compared to MCF-7 cells.³⁴ In addition, the diffusivity of both cell lines was determined by fitting the mean squared displacement (MSD) of the centroid position versus time (Fig. S6). This analysis shows that MCF-7 cells move diffusively, whereas MDA-MB-231 cells display superdiffusion. The latter is clear since the MSD increases with time to the power 1.33 ± 0.02 (note: our efficiency measure is not influenced by the diffusivity of the cell centroid). However, these differences in simple and, in some instances, well-known metrics do not – by themselves – provide any insights why MDA-MB-231 cells move more efficiently (e.g., one could imagine cells making large but uncoordinated protrusions and retractions resulting in a very inefficient net motion). We therefore examined the temporal variations in the measured variables for both cell lines.

A typical set of experimental results is shown in Fig. 2 (see also ESI^† Movies M1 and M2), where the protrusion area, retraction area and total cell area (divided by 10 to fit the same scale) are plotted on the left y-axis and the distance traveled by the cell centroid, on the right y-axis. The representative MDA-MB-231 cell in Fig. 2A displays a fibroblast-like motion³⁵, during which it is tear-shaped most of the time with a clearly-defined leading edge and a “tail”. Notably, large tail retractions (Fig. 2A, blue asterisks) are followed by large protrusions (red asterisks) and coincide with large displacements of the cell centroid. In MCF-7 cells (Fig. 2B), protrusion and retraction areas show only minor fluctuations with sporadically larger “spikes” – at first sight, there retractions and protrusions are not correlated.

Fig. 2.

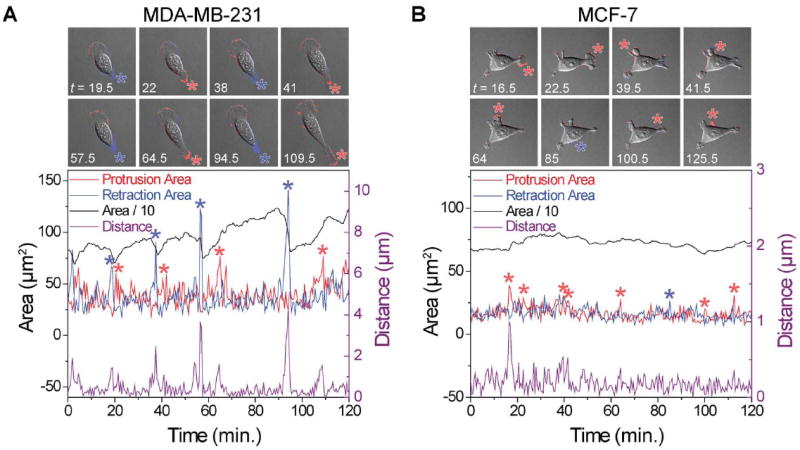
Typical experimental output of retraction–protrusion analysis for a typical single cell imaged at 30 s intervals. (A) A metastatic MDA-MB-231 cell moving persistently toward the top left corner of the images with nearly constant protrusion activity at the leading edge and intermittent large tail retractions (blue asterisks) followed by large tail protrusions (red asterisks). The largest cell centroid displacements (right y-axis) coincide with major retraction and protrusion events (see ESI^† Movie M1). (B) A non-metastatic MCF7 cell, moving first to the right of the image (up to t = 31 min) and then to the left (after t = 31 min). Fluctuations in all variables are notably smaller compared to the MDA-MB-231 cell. No large retractions are observed. The insets above the graphs (each 110 by 110 μm) show the overlay of DIC images and the pixel-based analysis to visualize the protrusion area (red) and retraction area (blue). See also ESI^† Movie M2. For clarity, only 2 hours of data is shown in the graphs.

Temporal correlations

However, more careful analysis of auto-correlations (Fig. 3, black points) and cross-correlations (Fig. 3, blue points), reveals correlated variables in both metastatic MDA-MB-231 and non-metastatic MCF-7 cells. The distance traveled by the cell centroid Δd, the protrusion area A_pro and the retraction area A_ret are all well auto-correlated for lag times τ (where τ = t + nΔt and n is an integer), up to 2 min for MDA-MB-231 cells (Fig. 3A–C, black arrows) and over 10 min for MCF-7 cells (Fig. 3K–M). The time of auto-correlation is significantly greater both for the total cell area A and cell circularity, c – respectively, 25 and 15 min for MDA-MB-231 cells (Fig. 3D, E) and 70 and 75 min for MCF-7 cells (Fig. 3N, O). Colloquially put, these results indicate that protrusions and retractions have relatively “short memory” whereas the total areas and cell circularity have “long memory” (i.e., protrusions/retractions evolve/change on timescales much shorter than those describing evolution of A or c).

Next, we applied cross-correlation analysis to identify leading or lagging indicators between the measured variables (i.e., to determine the temporal sequence in the changes of different variables). The protrusion and retraction areas of MDA-MB-231 cells are anti-correlated at 0 lag with respect to one another, indicating that protrusions and retractions are, to an extent, mutually exclusive. After 30 s, however, the protrusion-retraction correlation increases followed by a second “wave” at 2–4 min (Fig. 3F, indicated by a blue arrow). This means that protrusions precede cell retractions – this, we observe is far from obvious or expected since other cells, for instance, heart fibroblasts, have shown the exactly opposite behavior.³⁶ For MCF-7 cells, protrusions also precede retractions with the cross-correlation being significant from 30 s up to 6 min, at which point the slope of the cross-correlation returns to zero (Fig. 3P, red arrow). We note that the cross-correlation coefficient on the y-axis does not reach zero due to the slow decay of the auto-correlations of both the protrusion and retraction areas (Fig. 3L and M, respectively). For the sake of completeness, we also observe that the circularity of the cell is anti-correlated with the total cell area (not shown) and is therefore also anti-correlated to (preceding) protrusions and to (lagging) retractions (Fig. 3I, J and Fig. 3S, T). Another way of interpreting these trends is that an increase in cell area is associated with a decrease in circularity – that is, with a more elongated cell shape. Moreover, the cross-correlation analyses show that protrusions/retractions are not random events, and that they are correlated with one another. Overall, the temporal correlations in the measured variables are not very different between the two cell types.

Causality analysis

The fact that protrusions precede retractions prompts a question about the causality of this time-ordering: namely, do protrusions cause retractions? To address this question, we analyzed our multivariate time series using the so-called Granger causality method often used in finance^37,38 and neurobiology^39,40. In this approach, a variable X ‘Granger causes’ variable Y if information on the past history of X predicts future values of Y better than would be possible when considering the past values of Y alone. For both cell lines, A_pro and A_ret ‘Granger cause’ A but, at the same time, there is a much weaker Granger cause flowing in the opposite direction (thus pointing to a weak feedback mechanism). This can be seen in Fig. 4A, B, and Fig. 4D, E showing a high Granger causality value for the ‘from A_pro to A’ and ‘from A_ret to A’ fields and a lower value for the ‘from A to A_pro’ and ‘from A to A_ret’ fields. All “causal flows” are summarized in Fig. 4C, F, where the width of the arrows represents the strength of the Granger causality.

Fig. 4.

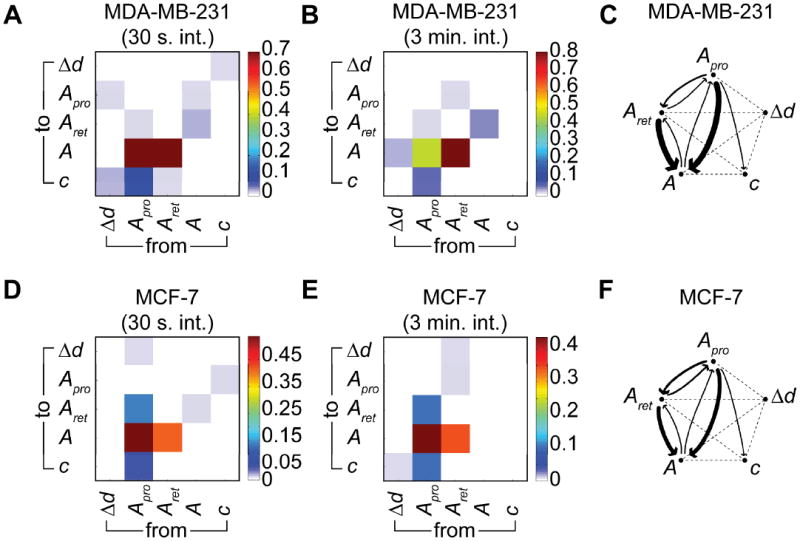
Granger causality analysis (p < 0.05) for the motility characteristics of MDA-MB-231 and MCF-7 cells. (A) Color-coded Granger causality coefficients for 15 MDA-MB-231cells sampled at 30 s intervals for 16 h. (B) The same as panel A but for 57 MDA-MB-231 cells sampled at 3 min intervals for 16 h. (C) Schematic representation of Granger causality flows, where the width of the arrow scales with the Granger causality coefficient. (D) Color-coded Granger causality coefficients for 15 MCF-7 cells sampled at 30 s intervals for 16 h. (E) The same as D but for 57 MCF-7 cells sampled at 3 min intervals for 16 h. (F) Schematic representation of Granger causality flows, where the width of the arrow scales with the Granger causality coefficient.

For both cell lines there is slightly stronger Granger evidence of protrusions causing retractions than the other way around – this agrees with the cross-correlation analysis discussed earlier. At the same time, there is no logical contradiction in the existence of a weaker Granger causality from retractions to protrusions – this weak causality reflects the fact that the network of protein–protein interactions underlying both protrusion and retraction activities is highly interconnected and some of its “hubs” are involved in both processes (e.g., in Fig. S11, ROCK is directly interacting with mDia involved in formation of protrusions, and with myosin IIa involved in actomyosin contractility during cell rear retractions)⁴¹.

Spatiotemporal correlations of protrusions and retractions

The temporal correlation and causality data described in previous sections still do not, by themselves, provide insights into the differences in the motility efficiency of MDA-MB-231 and MCF-7 cells. We therefore investigated not just the temporal correlations but also the spatiotemporal behavior, using morphodynamic profiling^42-44. Briefly, a deformable closed contour, the so-called Kass snake⁴⁵, is tightly fitted around the cell boundary. In this way, virtual markers are positioned along the cell boundary after which the electrostatic contour migration method (ECMM, see ref. 43) is used to monitor the deformation of the Kass snake from time t_i to t_i+₁. The data thus obtained yield local velocities perpendicular to the contour tangent (positive velocities point outwards of the cell and correspond to protrusions; negative velocities point inwards and indicate retractions). Fig. 5A shows a typical result of morphodynamic profiling, where a MDA-MB-231 cell (see Fig. S8 for additional boundary speed maps) is moving persistently using a fibroblast-like motion (same cell as depicted in Fig. 2A) with most of the protrusion/retraction activity at the leading and trailing edges, and with the sides of the cell (L ≈ 0.2 – 0.4 and 0.6 – 0.8) staying quiescent. The leading edge of the cell (L ≈ 0 – 0.2, yellowish “band” in the speed map) exhibits a moderate continuous positive velocity with only minor retractions. In contrast, the cell boundary at the tail (L ≈ 0.4 – 0.6) moves only occasionally, but when it does, it is at a much higher velocity compared to that of the leading edge. A high “negative” velocity (i.e., tail retraction) produces a dark blue horizontal “band” in the boundary speed map, whereas a high positive velocity (i.e., tail protrusion) results in a bright red “band”. The “pairs” of these large tail retractions-protrusions are circled by the dotted ellipses in Fig. 5A. This is in contrast to previous analyses of fibroblasts where large tail retractions lead to increased protrusion activity at the opposite (i.e., leading/front) side of the cell.³⁵ It is also different from the well-known oscillatory protrusion and retraction cycles that occur at the leading edge of motile cells regulated by phosphorylation of RhoA.^46,47 The origin of the cyclical tail retraction-protrusion pairs we observe can be understood based on experiments illustrated in Fig. 6. Therein, when a tail retracts, retraction fibers⁴⁸ are left behind and attached to the substrate (Fig. 6A, B). Shortly thereafter, the tails protrudes “backwards” retracing its previous path, and “cleans” up the deposited fibers (Fig. 6C–E), possibly to facilitate the complete release of the cell’s tail from the substrate (note: the cells were not transfected to visualize the retraction fibers). When MDA-MB-231 cells were transfected with fascin-GFP, the fluorescent signal coincided with these fibers (Fig. 6F). We note that a previous study on B16F1 melanoma cells also showed fascin-rich retraction fibers⁴⁹, though these fibers were emanating from the lamellipodium at the front of the cell, while here we observed fascin-rich fibers mainly at the cell rear. More importantly, no such fibrous structures were observed in MCF-7 cells which also have completely different boundary speed maps (Fig. 5B and Fig. S9) with regions of protrusion/retraction activity at various locations along the cell perimeter (e.g., for the cell in Fig. 5B, at L ≈ 0.1, 0.4 and 0.8). The typical speed of the boundary is about half that compared to the MDA-MB-231 cell. Moreover, the MCF-7 cell does not move persistently, but changes direction on multiple occasions (e.g. at time ≈ 30 and 75 min in Fig. 5B).

Fig. 5.

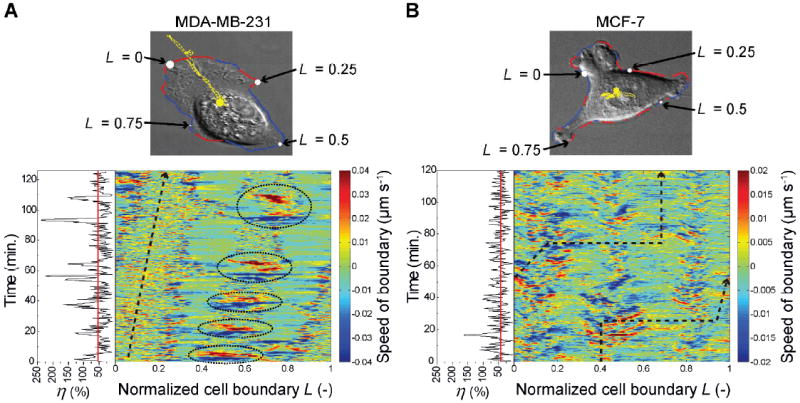
Representative boundary speed maps depicting the (color-coded) speeds along the normalized cell boundary (L) as a function of time. (A) MDA-MB-231 cell (same as in Fig. 2A, see also ESI^† Movie M3). (B) MCF-7 cell (same as in Fig. 2B, see also ESI^† Movie M4). In the images above the maps, coordinate L defines specific location at the cell perimeter and is normalized to between zero and one. The cell contour is colored red in places where the cell protrudes and blue where it retracts. The yellow curves trace the motion of the cells’ centroids. In the maps, the black dashed arrows delineate locations L along the cell boundary intersected by a vector originating at the cell centroid (yellow circle in images) and drawn in the direction of centroid displacement at time t_i (see Fig. S10 for schematic representation). The instantaneous motility efficiencies, η (as defined in the main text, black lines) and the mean efficiencies (red lines) are shown on the left side of the boundary speed maps. For the specific MDA-MB-231 cell, the mean efficiency 53.6% (i.e., lower than average, cf. Fig. 1C); for the MCF-7 cell shown, it is 43.6%.

Fig. 6.

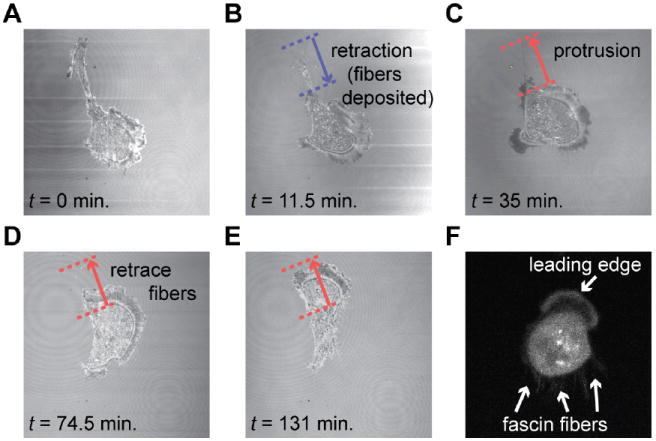
Confocal microscopy in reflection mode of a MDA-MB-231 cell leaving a bundle of fibers on the glass substrate (coated with laminin) after a major tail retraction. (A) The cell retracts its tail along the blue arrow. (B) After retraction of the tail, a “fiber trail” consisting of multiple thin retraction fibers remains on the substrate. (C) Shortly thereafter, the cell retraces its path along the fiber trial. (D–E) The deposited fibers are removed after the cell retraces its previous path and uptakes the fibers. (F) MDA-MB-231 cell transfected with fascin-GFP (confocal microscopy image) showing that the retraction fibers are rich in fascin. See also ESI^† Movie M6.

To complete the analysis, we link the above picture of cell morphodynamics to our discussion of motility efficiency earlier in the text. The side panel in Fig. 5A (black line) reveals that during large boundary protrusions (or retractions) the instantaneous value of η is also high. In addition, the centroid displacements are also largest during these large protrusions and retractions. For MDA-MB-231 cells, these large boundary movements (involving ~20% of the total perimeter length L) lead to a large displacement of the centroid, translating into high instantaneous efficiency values. MCF-7 cells, on the other hand, protrude and retract smaller parts of the cell boundary (< 10% of L for the cell in Fig. 5B) and do so at multiple locations, resulting in small net centroid displacements and in a lower mean efficiency (cf. Fig. 1A). In other words, MDA-MB-231 cells are able to spatiotemporally coordinate significant parts of the cell boundary to perform synchronized large protrusions and retractions. While MCF-7 cells have similar temporal protrusion-retraction activity (as shown using cross-correlation and Granger cause analyses), they lack the ability to spatially localize/synchronize their protrusions and retractions to lead to efficient motility.

Our measure of cell motility efficiency could readily be compared to existing mathematical models that relate cell shape and dynamics to overall motility (see ref. 50 for a recent review of such models). Arguably the simplest mathematical model is that of “spring-and-dashpot”, in which a series of parallel springs and dashpots (accounting for making/breaking of adhesions and cytoskeletal fluid friction) are used to predict cell motility.^13,51 The energy loss due to viscous dissipation⁵² in the dashpots could be calculated, which would allow one to calculate the exact output and input energy of the model, with the ratio of the two providing a measure of motility efficiency. The method to calculate motility efficiencies we have outlined here could in this way be coupled to mathematical models in order to better characterize and quantify cell motility.

CONCLUSIONS

Metastatic breast cancer cells move more efficiently than their non-metastatic variants – this difference reflects better spatiotemporal synchronization of cell boundary retractions and protrusions in metastatic cells. The highest efficiencies are concurrent with large coordinated retraction-protrusion pairs observed mostly at the rear/tail of MDA-MB-231 cells. Although efficiency of motility has been recognized as an important descriptor of various aspects of the motility process^53-55, the present study appears the first one to quantify this measure on the level of entire cells and link it to the dynamics of cell membrane protrusions/retractions. Of course, our results are only the first step towards understanding how the synchronized cell motions emerge from the interactions and intracellular transport²⁹ of the biomolecules underlying cell motility. In this context, a particularly interesting question is the relationship between the spatiotemporal distributions of polarity markers and the synchronized membrane dynamics we observe. Also, to make further generalizations, similar trends should be studied in different types of cells and, ideally, in vivo (though it must be stressed that even the most advanced imaging modalities currently available^56,57 do not offer spatial and/or temporal resolution required for precise single-cell morphodynamic studies in animals or tissue models). In the meantime, the methodology we described provides a new set of theoretical tools with which to quantify cell motility beyond simple velocities and persistence lengths. The main insights our correlation, Granger causality and morphodynamic analyses provide is that spatiotemporal synchronization of large protrusions and retractions greatly increase overall cell motility efficiency – especially for those cells that become invasive.