Markov Transition Model to Dementia with Death as a Competing Event

Abstract

This study evaluates the effect of death as a competing event to the development of dementia in a longitudinal study of the cognitive status of elderly subjects. A multi-state Markov model with three transient states: intact cognition, mild cognitive impairment (M.C.I.) and global impairment (G.I.) and one absorbing state: dementia is used to model the cognitive panel data; transitions among states depend on four covariates age, education, prior state (intact cognition, or M.C.I., or G.I.) and the presence/absence of an apolipoprotein E-4 allele (APOE4). A Weibull model and a Cox proportional hazards (Cox PH) model are used to fit the survival from death based on age at entry and the APOE4 status. A shared random effect correlates this survival time with the transition model. Simulation studies determine the sensitivity of the maximum likelihood estimates to the violations of the Weibull and Cox PH model assumptions. Results are illustrated with an application to the Nun Study, a longitudinal cohort of 672 participants 75+ years of age at baseline and followed longitudinally with up to ten cognitive assessments per nun.

1. INTRODUCTION

In clinical trials and observational studies, it is common that the occurrence of the key event is censored by some competing risk such as disease-related dropout, which could cause non-ignorable missing data. More specifically, in most longitudinal studies on progression to a certain disease when the target population is elderly subjects, death is one of the competing risks. In the Nun study, among the total of 461 subjects – the final analytic sample for parameter estimating, almost half (n=225) died before converting to dementia. Several existing approaches have been developed in joint analysis of the longitudinal measurements and competing risks time-to-event data. Xu and Zeger (2001) proposed a latent variable model to model the relationship between time-to-event data, longitudinal response, and covariates, in which covariates could only affect the longitudinal response through its influence on an assumed latent process. Elashoff et al. (2007) suggested joint modeling of the repeated measures and competing risk failure time data by using latent random variables and common covariates to link the sub-models. However, few involve categorical responses that characterize these data.

Salazar el al. (2007) proposed a suitable approach to the problem by defining a multi-state Markov chain to model the progression of dementia in which death was treated as a competing absorbing state to dementia. A possible alternative is to model the competing risk of death without a dementia as a continuous variable. To this end this manuscript incorporates the Weibull model and Cox proportional hazards (PH) model into Salazar’s Markov model assuming a shared random effect (Albert and Follmann, 2003). Specifically, we introduced a random effect into the model to take into account for the correlation between the survival time and the transition states that is not explained by the model based solely on diagnostic effects in a similar spirit of Xu and Zeger (2001). The closed-form expressions for the conditional marginal likelihood function are derived. The model’s stability to the violation of the assumption on the distributional form of survival is tested in simulation studies.

The manuscript is organized as follows: the model likelihood functions are constructed in Section 2; a simulation study is presented in Section 3; the application to the Nun Study data is presented in Section 4; and a summary of the findings is presented in Section 5.

2. MODEL AND ESTIMATION

2.1 Salazar’s multi-state Markov model

Suppose there are m subjects in the study. For a particular subject, let Y = (Y₁, Y₂, Y₃, …, Y_n) denote the random vector representing the observed cognitive states at n different ordered discrete occasions. Assume the Markov property holds (Bhat and Miller, 2002 or Huzurbazar, 2005), that is, the conditional distribution f(y_k|y₁, …, y_k−1) is identical to the conditional distribution f(y_k|y_k−1) for k = 2, …, n. Then conditioned on Y₁, the joint distribution of the random vector Y can be written as

$$f(y\mid y_1)=f(y_2,y_3,\dots ,y_n\mid y_1)=f(y_2\mid y_1)f(y_3\mid y_2)\dots f(y_n\mid y_{n-1}).$$

Here the subscript y_k refers to the state occupied at kth occasion. In order to simplify the notation, we can use P_yk−1yk = f(y_k|y_k−1) to denote the one step transition probability from state y_k−1 to state y_k. So for instance, if y_k−1 = s and y_k = v then P_sv represents the probability of transition from state s to state v in the kth visits.

In the example to be discussed later – the Nun study data, the status of a participant at each visit was recorded as being one of the states: 1 = intact cognition, 2 = mild cognitive impairments (M.C.I.), 3 = global impairments (G.I.), or 4 = dementia (Tyas et al., 2007). The participants were followed during the study period until death occurred. The conditional distribution of the status of an individual participant at an arbitrary examination given her status at previous examinations was assumed to have the Markov property, i.e., that status at the examination depended on only the most recent previous examination and was independent of status at other previous examinations. Following Salazar et al. (2007), a multi-state Markov chain was used to model transitions from one state to another, in which states 1–3 were considered transient states, whereas state 4 and death (state 5) were absorbing states as shown in Figure 1.

Figure 1.

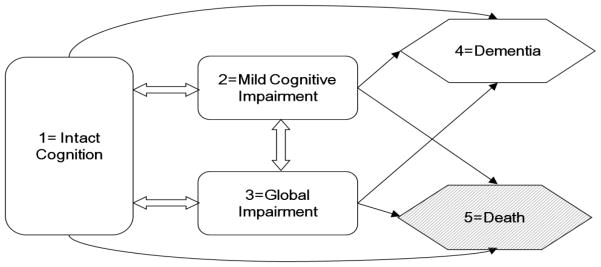
Possible one step transitions between three transient states (1) intact cognition (2) M.C.I. (3) G.I. and two absorbing states (4) dementia (5) death.

Thus the one-step transition probability matrix could be presented in the form of

$$\left[\begin{array}{ccccc}{P}_{11}(\mathit{\Theta }\mid X,\gamma )& P_{12}(\mathit{\Theta }\mid X,\gamma )& P_{13}(\mathit{\Theta }\mid X,\gamma )& P_{14}(\mathit{\Theta }\mid X,\gamma )& P_{15}(\mathit{\Theta }\mid X,\gamma )\\ P_{21}(\mathit{\Theta }\mid X,\gamma )& P_{22}(\mathit{\Theta }\mid X,\gamma )& P_{23}(\mathit{\Theta }\mid X,\gamma )& P_{24}(\mathit{\Theta }\mid X,\gamma )& P_{25}(\mathit{\Theta }\mid X,\gamma )\\ P_{31}(\mathit{\Theta }\mid X,\gamma )& P_{32}(\mathit{\Theta }\mid X,\gamma )& P_{33}(\mathit{\Theta }\mid X,\gamma )& P_{34}(\mathit{\Theta }\mid X,\gamma )& P_{35}(\mathit{\Theta }\mid X,\gamma )\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right].$$

According to Salazar et al. (2007), a multinomial logit parameterization could be applied to link these transition probabilities with the fixed and random effects.

$$log\left(\frac{P_{sv}({\theta }_{sv}\mid X,\gamma )}{P_{s1}({\theta }_{s1}\mid X,\gamma )}\right)={\alpha }_v+X^{\prime }{\beta }_v+{\xi }_v^s+W^{\prime }\gamma ,v=2,3,4,5\mathit{and}s=1,2,3.$$

Here Θ represents the set of all the unknown parameters, α = (α₂, α₃, α₄, α₅) is the vector of intercepts, β_v is the vector of unknown fixed effects for covariates X and ${\xi }_v^s$ is the unknown fixed effects for the prior state s and current state v. Also, γ is the vector of unobserved random effects associated with the subject. The formulation of Salazar’s model in terms of logit functions allows us to find the closed expression for each transition probability as follows

$$P_{sv}(\mathit{\Theta }\mid X,\gamma )=\{\begin{array}{cc}\frac{1}{1+{\sum }_{h=2}^{5}exp({\alpha }_h+X^{\prime }{\beta }_h+{\xi }_h^s+W^{\prime }\gamma )},& v=1\\ \frac{exp({\alpha }_v+X^{\prime }{\beta }_v+{\xi }_v^s+W^{\prime }\gamma )}{1+{\sum }_{h=2}^{5}exp({\alpha }_h+X^{\prime }{\beta }_h+{\xi }_h^s+W^{\prime }\gamma )}& v>1.\end{array}$$

Therefore, based on the conditional distribution of f(y₂, y₃, …, y_n|y₁) the marginal likelihood function for the particular subject is

$$L(\mathit{\Theta }\mid X)={\int }_{\mathit{\Omega }}\prod _{l=2}^n\times \prod _{\begin{array}{l}s=1\dots 3,\\ v=1\dots 5\end{array}}{P}_{sv}{(\mathit{\Theta }\mid X,\gamma )}^{{\delta }_{y_{l-1},s}{\delta }_{y_l,v}}h(\gamma )d\gamma ,$$ (2.1)

with Ω denoting the support for the distribution of the random vector γ. The probability density function for γ is h(·). Here δ_yl−1,s and δ_yl,v are indicator functions valued at 1 if y_l−1 = s and y_l = v, and 0 otherwise. The overall likelihood function can be obtained by evaluating the product of (2.1) across the subjects under study.

2.2 Models with Weibull and Cox Proportional Hazards Survival

In Salazar’s model death is modeled as the competing absorbing state to dementia. A possible alternative approach is to incorporate information on the actual survival times from death of the subjects into the stochastic system. The data of interest involves multinomial responses and the parameterization of a polychotomous logit under a discrete time Markov framework complicating the problem. The hypothesis is that the survival time of those subjects who die without incurring a dementia come from certain parametric or semi-parametric distribution which shares the same random effects used in the Markov transition model. Additionally, these two pieces are conditionally independent given the random effects and their corresponding predictor variables.

In contrast with Salazar’s model, the transition probabilities among cognitive states are modeled with a four-state Markov chain, same transient states but dementia being the only absorbing state. The one-step transition probability matrix now becomes

$$\left[\begin{array}{cccc}{P}_{11}(\mathit{\Theta }\mid X,\gamma )& P_{12}(\mathit{\Theta }\mid X,\gamma )& P_{13}(\mathit{\Theta }\mid X,\gamma )& P_{14}(\mathit{\Theta }\mid X,\gamma )\\ P_{21}(\mathit{\Theta }\mid X,\gamma )& P_{22}(\mathit{\Theta }\mid X,\gamma )& P_{23}(\mathit{\Theta }\mid X,\gamma )& P_{24}(\mathit{\Theta }\mid X,\gamma )\\ P_{31}(\mathit{\Theta }\mid X,\gamma )& P_{32}(\mathit{\Theta }\mid X,\gamma )& P_{33}(\mathit{\Theta }\mid X,\gamma )& P_{34}(\mathit{\Theta }\mid X,\gamma )\\ 0& 0& 0& 1\end{array}\right].$$

Each transition probability P_sv could be postulated in the form of

$$P_{sv}(\mathit{\Theta }\mid X,\gamma )=\{\begin{array}{cc}\frac{1}{1+{\sum }_{h=2}^{4}exp({\alpha }_h+X^{\prime }{\beta }_h+{\xi }_h^s+W^{\prime }\gamma )},& v=1\\ \frac{exp({\alpha }_v+X^{\prime }{\beta }_v+{\xi }_v^s+W^{\prime }\gamma )}{1+{\sum }_{h=2}^{4}exp({\alpha }_h+X^{\prime }{\beta }_h+{\xi }_h^s+W^{\prime }\gamma )},& v>1.\end{array}$$ (2.2)

Assume the survival time (that is, time on study) could be modeled by the parametric Weibull distribution or the semi-parametric Cox PH model. The semi-parametric Cox PH model is used to validate the parametric Weibull model assumption. Therefore, both the parametric and semi-parametric methods are applied to the Nun’s data and the corresponding simulation results and real data analysis results are compared in Section 3 and 4.

When the survival time follows the Weibull distribution, the survival time S ~ Weibull(r, μ), where μ = e^{η₀+Z′η+W′γ}. The probability of a subject failing from the competing risk of death is

$${\pi }_w(S=t\mid \mathit{\Theta },\gamma )={\left[r{e}^{{\eta }_0+Z^{\prime }\eta +W^{\prime }\gamma }{t}^{r-1}exp(-e^{{\eta }_0+Z^{\prime }\eta +W^{\prime }\gamma }{t}^r)\right]}^{\tau }{\left[exp(-e^{{\eta }_0+Z^{\prime }\eta +W^{\prime }\gamma }{t}^r)\right]}^{1-\tau },r>0$$

Here τ is the indicator function valued at 1 if the subject died at time t and 0 otherwise. Θ be the parameter vector associated with both the transition probability and the probability of death. For each subject under study, the conditional marginal likelihood function for the ith subject can be rewritten as

$$L_w(\mathit{\Theta }\mid X,Z)=\int \prod _{l=2}^n\times \prod _{\begin{array}{l}s=1\dots 3,\\ v=1\dots 5\end{array}}{P}_{sv}{(\mathit{\Theta }\mid X,\gamma )}^{{\delta }_{y_{l-1},s}{\delta }_{y_l,v}}\times {\pi }_w(\mathit{\Theta }\mid Z,\gamma )h(\gamma )d\gamma .$$ (2.3)

In the Cox proportional hazards model, we assume the hazard function has the form

$$\lambda (S=t\mid \mathit{\Theta },\gamma )={\lambda }_0(t)exp({\eta }_0+Z^{\prime }\eta +W^{\prime }\gamma ).$$

Here λ₀(t) is the baseline hazard and μ = e^{η₀+Z′η+W′γ} > 0. According to Cox et al. (1984), the contribution to the partial likelihood from the ith subject failing from the competing risk of death is

$${\pi }_c(S=t\mid \mathit{\Theta },\gamma )={\left(\frac{{\mu }_i}{{\sum }_{t_j\ge t_i}{\mu }_j}\right)}^{I_{\{{\tau }_i=1\}}},\mathit{where}\mu =e^{{\eta }_0+Z^{\prime }\eta +W^{\prime }\gamma }.$$

The conditional (on the baseline state) likelihood function for a subject can be rewritten as

$$L_c(\mathit{\Theta }\mid X,Z)=\int {\prod }_{l=2}^n\times {\prod }_{\begin{array}{l}s=1\dots 3,\\ v=1\dots 5\end{array}}{P}_{sv}{(\mathit{\Theta }\mid X,\gamma )}^{{\delta }_{y_{l-1},s}{\delta }_{y_l,v}}\times {\pi }_c(\mathit{\Theta }\mid Z,\gamma )h(\gamma )d\gamma .$$ (2.4)

2.3 Parameter estimation

The parameter estimation is implemented by maximizing the conditional likelihood (Θ|X, Z). In particular, all the calculations are approached by SAS PROC NLMIXED procedure. Assuming that the random effect is distributed as a N(0, σ²) both of the log likelihood functions (in equations 2.3 and 2.4) can be maximized using the Double-Dogleg method combined with the adaptive Gauss-Hermite quadrature method (Raudenbush et al. 2000) to numerically evaluate the integrations and produce the parameter estimates. The likelihood function is not convex in the parameters, therefore convergence of the optimization algorithm is not guaranteed for an arbitrary set of initial values. It is advisable to start with multiple sets of initial values and select the maximizers accordingly. The estimates of the standard errors are computed by Fisher’s information method.

3. SIMULATIONS

The main purpose of the simulation study is to examine the sensitivity of the MLEs of β to the violations of the Weibull model assumption or Cox PH model assumption on the survival time. The goal is to quantify how the distributional form for the survival term affects the model estimates associated with the fixed effects in equation (2.2). The criteria are the bias and the mean squared errors of the MLEs.

Simulations were set to have 1000 iterations, with each containing either 200 or 500 subjects. The corresponding computation time of sample size 200 and 500 by using Intel i5-650 professor (4M Cache, 3.2 GHz) are 13.35 hours and 31.21 hours respectively. Each subject has up to ten follow-up waves starting from a baseline state of intact cognition. Four cases are considered:

1. Total of 200 subjects generated with prior distribution of survival being Weibull

2. Total of 500 subjects generated with prior distribution of survival being Weibull

3. Total of 200 subjects generated with prior distribution of survival being Generalized Weibull

4. Total of 500 subjects generated with prior distribution of survival being Generalized Weibull

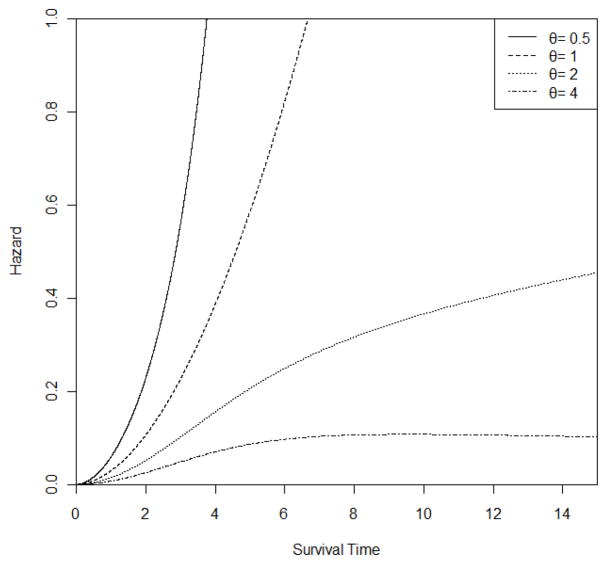
The Generalized Weibull distribution WG(r, μ, θ) has the hazard function, $h(t)=\frac{r\mu }{\theta }{(1+\mu t^r)}^{\frac{1}{\theta }-1}{t}^{r-1}$, where t ≥ 0, r > 0, μ > 0 and θ > 0 (Foucher et al., 2005). If θ is 1, the Weibull formulation is obtained. In the simulation, set r to be a fixed number 2.8593 and log(μ) be a linear function of current age and APOE4 status. The range of μ in the simulation lies between 0.0004 and 0.0103 and the mean value of μ is 0.0013. These choices are motivated by the application discussed in Section 4. Additionally, choose θ = 0.5, 1, 2 and 4 separately. The plots of hazard functions of the Generalized Weibull distribution with r = 2.8593 and μ = 0.0013 were shown on Figure 2. Note that the proportional hazards assumption holds only if θ = 1.

Figure 2.

Hazard Function of a Generalized Weibull Distribution with r = 2.8593 and μ = 0.0013

Thus, two sets of comparisons could be explored: first, the effects of varying the sample size, and second, the effects of violating the original model assumption on the distributional form of survival term with a possible alternative.

In both situations, the transition probabilities were dependent on three covariates: current age (denoted as age), prior state (IC = intact cognition or M.C.I. or G.I. (the reference category)), and the presence/absence of an apolipoprotein E-4 allele (APOE4). The covariates entered in the survival model were age at entry and the APOE4 status of the subject. All the simulations were done using the IML procedure in SAS system. The results are presented in Table 1 and Table 2.

Table 1.

Bias and Mean Squared Error of the model parameters based on the trajectories of 200 subjects when the likelihood for the survival assumes Weibull or Cox Model

			θ=0.5				θ=1				θ=2				θ=4
			Weibull		Cox PH		Weibull		Cox PH		Weibull		Cox PH		Weibull		Cox PH
Risk Factors	State	Para	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e
Markov chain
Age	2	0.101	−0.003	0.001	−0.057	0.004	−0.001	0.001	−0.031	0.002	0.003	0.001	−0.017	0.001	0	0.001	−0.011	0.001
	3	0.181	0.001	0.002	−0.059	0.005	−0.001	0.002	−0.028	0.003	0.002	0.001	−0.015	0.002	−0.003	0.001	−0.01	0.001
	4	0.177	0.067	0.008	0.014	0.004	0.061	0.006	0.031	0.004	0.054	0.005	0.038	0.004	0.051	0.005	0.041	0.003
APOE4	2	0.859	0.015	0.209	−0.102	0.179	−0.015	0.211	−0.082	0.169	−0.002	0.181	−0.064	0.2	−0.027	0.173	−0.025	0.205
	3	1.313	−0.001	0.287	−0.106	0.245	−0.05	0.297	−0.092	0.253	0.01	0.211	−0.044	0.249	−0.036	0.2	−0.044	0.249
	4	1.428	0.121	0.328	−0.031	0.362	−0.06	0.395	−0.042	0.394	0.071	0.319	−0.026	0.369	0.059	0.281	0.009	0.345
Prior states:
IC	2	−1.11	0.028	0.148	−0.001	0.172	0.004	0.16	0.009	0.155	−0.001	0.164	−0.009	0.148	0.003	0.15	0.009	0.119
	3	−3.71	0.003	0.209	−0.016	0.224	0.034	0.181	0.005	0.174	0.011	0.177	−0.025	0.192	−0.013	0.171	0.018	0.165
	4	−5.23	−0.892	6.221	−0.928	5.858	−0.617	4.269	−0.987	5.698	−0.659	4.396	−0.646	4.088	−0.653	4	−0.619	4.109
MCI	2	0.74	−0.026	0.148	0.075	0.168	0.012	0.15	0.067	0.167	0.054	0.161	0.058	0.16	0.05	0.13	0.072	0.134
	3	−2.31	−0.031	0.197	0.05	0.189	0.081	0.174	0.095	0.183	0.061	0.151	0.066	0.165	0.061	0.129	0.089	0.158
	4	−1.93	0.155	0.407	0.174	0.322	0.171	0.28	0.174	0.316	0.193	0.268	0.13	0.236	0.138	0.213	0.177	0.224

Table 2.

Bias and Mean Squared Error of the model parameters based on the trajectories of 500 subjects when the likelihood for the survival assumes Weibull or Cox Model

			θ=0.5				θ=1				θ=2				θ=4
			Weibull		Cox PH		Weibull		Cox PH		Weibull		Cox PH		Weibull		Cox PH
Risk Factors	State	Para	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e	Bias	m.s.e
Markov chain
Age	2	0.101	−0.001	0.000	−0.054	0.003	0.000	0.000	−0.034	0.001	−0.002	0.000	−0.018	0.001	−0.001	0.000	−0.010	0.000
	3	0.181	0.000	0.001	−0.056	0.004	0.000	0.001	−0.036	0.002	−0.001	0.000	−0.020	0.001	0.000	0.000	−0.010	0.001
	4	0.177	0.068	0.006	0.011	0.001	0.057	0.004	0.022	0.002	0.050	0.003	0.032	0.002	0.049	0.003	0.039	0.002
APOE4	2	0.859	−0.020	0.086	−0.140	0.085	−0.067	0.083	−0.084	0.075	−0.026	0.080	−0.074	0.079	−0.038	0.078	−0.046	0.076
	3	1.313	−0.033	0.104	−0.157	0.113	−0.093	0.113	−0.092	0.104	−0.036	0.109	−0.082	0.102	−0.052	0.088	−0.038	0.103
	4	1.428	0.058	0.167	−0.111	0.182	−0.063	0.144	−0.031	0.144	−0.016	0.130	−0.030	0.134	−0.011	0.119	−0.001	0.136
Prior states:
IC	2	−1.110	0.058	0.081	−0.034	0.068	−0.001	0.068	−0.016	0.067	0.050	0.057	−0.011	0.061	0.004	0.056	−0.004	0.054
	3	−3.708	0.063	0.080	−0.027	0.074	0.031	0.087	−0.012	0.076	0.036	0.056	0.005	0.065	−0.002	0.059	−0.014	0.069
	4	−5.226	0.018	0.533	−0.128	1.079	−0.040	0.706	−0.106	0.913	0.011	0.496	−0.032	0.581	0.051	0.460	−0.138	0.724
MCI	2	0.740	0.034	0.078	0.044	0.075	0.008	0.071	0.064	0.067	0.073	0.062	0.055	0.064	0.068	0.061	0.054	0.059
	3	−2.305	0.017	0.074	0.058	0.080	0.040	0.078	0.059	0.066	0.077	0.066	0.077	0.067	0.079	0.055	0.061	0.064
	4	−1.931	0.153	0.149	0.196	0.167	0.130	0.118	0.208	0.132	0.188	0.120	0.164	0.104	0.194	0.100	0.151	0.105

As expected, increasing the sample size improves the estimates in terms of reducing mean square error (MSE). The main savings is in the variance of the estimates since the bias stays almost the same with only one exception, the effect of the transition from intact cognition into dementia. Those biases are reduced considerably when the sample size increased. For example, the bias is −0.892 when sample size is 200 reduced to 0.018 when sample size is 500 for the Weibull model when θ = 0.5. The huge change is due to that the simulation parameter for the transition from intact cognition into dementia is very small, −5.226, which will increase the chance of observing few transitions. However, the chance of observing few transitions will be very rare when the sample size is larger than 300. Similar results were obtained for sample sizes of 300 and 400 (not shown). The results show that as long as the sample size is larger than 300, then the result will have acceptable small MSE and bias.

There is not much difference in term of the bias and MSE when fitting the data assuming a Weibull model or Cox model. The maximum differences between a Weibull model and a Cox model are 1.4289 for MSE and 0.3699(7.08%) for bias.

In all, the results indicate that the maximum likelihood estimates are not sensitive to violations of the assumed Weibull or Cox PH model in the case when the Generalized Weibull Distribution is the true distribution.

4. APPLICATION TO THE NUN STUDY

The Nun Study began enrolment in 1991. The data consists of a cohort of 672 members of the School Sisters of Notre Dame born before 1917 and living in retirement communities in the Midwestern, eastern, and southern United States. The subjects were recruited in phases and received annual cognitive assessments with brain donation at death. Analyses were based on data from ten successive examinations. A total of 211 subjects were excluded from the study due to: only one cognitive assessment (128), presence of dementia at baseline visit (61) or missing APOE4 (22). The final analytic sample consisted of 461 participants, of which 74 survived without dementia, 162 developed dementia and 225 died before converting to dementia. The transitions among the cognitive states are summarized in Table 3.

Table 3.

Number of transitions in the Nun study

Prior Visit	Current Visit
	Intact Cognition	M.C.I.	G.I.	Dementia
Intact Cognition	593	197	54	5
	69.90%	23.20%	6.30%	0.60%
M.C.I.	177	697	136	82
	16.20%	63.80%	12.50%	7.50%
G.I.	16	39	184	75
	5.10%	12.40%	58.60%	23.90%
Dementia	0	0	0	81
	0.00%	0.00%	0.00%	100.00%

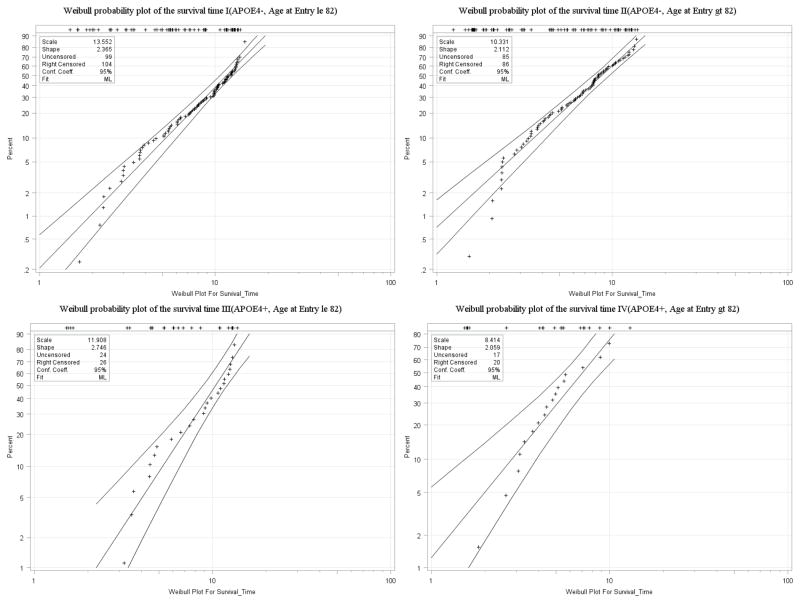
The covariates of interest are age, education level, APOE4 status, and prior state. For simplicity, education was not included in the model simulations; but was considered here since it is a well-known risk factor and found to be significantly associated with dementia in previous studies. The covariates entering in both of the two survival models were age at entry and APOE4 status. As shown in Figure 3 below, subjects were sub-grouped based on their APOE4 status and age at entry, and thus four Weibull probability plots were created as a preliminary look at the model assumption. The estimated cumulative distribution function was computed by Kaplan-Meier estimator in the LIFEREG procedure in SAS. The straight line represents the maximum likelihood fit, with the point wise parametric confidence bands on each side. The plots indicate that the assumed Weibull model fits the data reasonably well although not perfect since skewness arises in the tail of the distribution for some of the groups. Similar results were obtained for Cox PH model, which are not shown.

Figure 3.

Weibull probability plots of the survival time for different cohorts in the Nun study

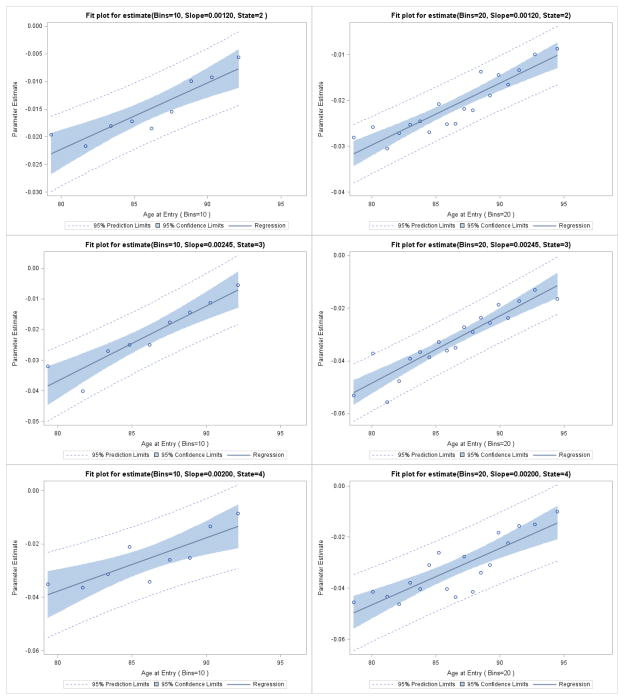
Since current age is the only interval level risk factor, there is interest in determining whether the linearity assumption between the logit of the transition probability and current age is adequate. To this end, we contrasted the linearity assumption against a piece wise constant assumption and test the adequacy of the linearity via the likelihood ratio test. Specifically, split the variable, current age, into 5, 10, 15 and 20 equally spaced bins, and estimate the effect of age for each bin. The resulting regression coefficients were then plotted against the age midpoint of each bin for the cases of 10 and 20 bins given by initial state in Figure 4. For each initial state 2, 3, or 4 the coefficients appear to increase linearly with the age midpoints. The Likelihood Ratio Test for linearity is provided in Table 4 for 5, 10, 15 and 20 bins. Note that none of these tests are significant, supporting the linearity assumption for each state 2, 3, and 4. A similar analysis was conducted to check the linearity of baseline age in the survival component of the likelihood with the same result (which is not shown).

Figure 4.

Assessment of Linearity of Current Age in Transition Matrix using 10 and 20 age bins

Table 4.

Fit Statistics for Linearity Test of Current Age

Bins	−2Log(Likelihood)	LRT	D.F.	P value
5	5598.2	7.3	9	0.61
10	5577.9	27.6	24	0.28
15	5572.4	33.1	39	0.74
20	5554.2	51.3	54	0.58
Linear	5605.5

In Table 5, the first and second column of each model lists the parameters and standard error of parameters obtained by SAS PROC NLIMXED. The third column lists the estimated standard error, which was obtained by using the bootstrap resampling method (Efron, 1981). The two methods of estimating standard errors are almost the same. We found that the standard errors of transition parameter estimates of Weibull model are uniformly smaller than those of Cox PH model. This is likely due to the much larger estimate for the random effect in the Cox model (last line in Table 5).

Table 5.

Maximum likelihood estimates (SE) of Model parameters in the Nun study for two models (base state: 1=Intact Cognition)

		Weibull Model			Cox PH Model
Risk Factors	State	Estimates	s.e	e.s.e.	Estimates	s.e	e.s.e.
Markov chain
Age	2	0.1010*	0.017	0.016	0.1129*	0.020	0.020
	3	0.1813*	0.020	0.019	0.1955*	0.023	0.022
	4	0.1772*	0.024	0.021	0.1873*	0.026	0.027
APOE4	2	0.8585*	0.244	0.307	1.1765*	0.336	0.450
	3	1.3132*	0.274	0.354	1.6383*	0.358	0.492
	4	1.4282*	0.306	0.353	1.7335*	0.383	0.488
Education:
< 16 years	2	1.5658*	0.361	0.345	2.0148*	0.491	0.489
vs. > 16 years	3	1.6105*	0.402	0.421	2.0493*	0.521	0.572
	4	1.4504*	0.446	0.461	1.8779*	0.555	0.620
16 years	2	0.4969*	0.164	0.178	0.7549*	0.246	0.238
vs. > 16 years	3	0.5276*	0.199	0.204	0.7786*	0.270	0.258
	4	0.4032	0.239	0.228	0.6528*	0.300	0.277
Prior states:
Intact Cognition	2	−1.1103*	0.337	0.369	−0.7579*	0.369	0.433
	3	−3.7083*	0.329	0.417	−3.3338*	0.362	0.479
	4	−5.2264*	0.548	1.650	−4.8818*	0.570	1.435
Mild Cognitive Impairment	2	0.7399*	0.328	0.330	0.4734	0.354	0.354
	3	−2.3053*	0.307	0.322	−2.5663*	0.335	0.337
	4	−1.9313*	0.328	0.318	−2.2025*	0.354	0.323
Survival Part:
Age at Entry	-	0.1206*	0.019	0.020	0.0982*	0.014	0.015
APOE4	-	0.4794*	0.231	0.250	0.3937*	0.175	0.185
Sigma	-	1.0026*	0.116	0.134	1.6409*	0.200	0.233

States: 2=Mild cognitive impairment, 3=Global impairment, 4=Dementia;

e.s.e is the estimated standard error from bootstrap resampling method

^*Significant at P < 0.05

Note that in either model, the regression coefficients for all three risk factors are positive and significant at the P < 0.05 level indicating that each factor promotes transitions into each impaired state at the next assessment with only one exception where the p-value for the regression coefficient is only marginally significant (P = 0.09). As noted above, the effect of age is linear. Referring to the Weibull model, the effect of an APOE 4 carrier is to promote transitions into M.C.I, G.I., and dementia as opposed to a transition into the intact cognition with estimated odds ratios (OR) 2.36, 3.72 and 4.17, respectively. Low education (<16 years) versus high education (> 16 years) is associated with even larger ORs of 4.79, 5.01, and 4.26 for similar transitions. More modest ORs are obtained when comparing 16 years of education to > 16 years of education yielding ORs of 1.64, 1.69, 1.50 for similar transitions. The corresponding ORs are 0.33, 0.025 and 0.0054 for prior state intact cognitive and are 2.10, 0.10 and 0.14 for prior state mild cognitive indicating that subjects tend to remain in their prior state. For all three risk factors, the Cox model yields uniformly larger ORs but their statistical significance is about the same due to the increase in the standard error of the regression coefficients. Only baseline age and APOE carrier status predict time to death without dementia.

5. CONCLUSION AND DISCUSSION

Considerable literature has focused on characterizing the relationship between longitudinal response process and time-to-event data. In contrast, relatively little research has been done to accommodate multinomial responses, with even fewer relying on a polychotomous logit parameterization under a discrete-time Markov chain.

As an improvement to Salazar’s multi-state Markov model, this manuscript fits a Weibull distribution and a Cox PH ditribution to model the time to death without a dementia and correlate this with the Markov transition model by incorporating a shared random effect. The simulation study showed model stability in terms of violations of the distributional assumption on survival time. More specifically, the maximum likelihood estimates are not sensitive to violations of the assumed Weibull model or Cox PH model assumption when, in fact, a Generalized Weibull model should be used instead. Also, the semi-parametric model has almost the same effect as the parametric model.

The application to the Nun study data found that Age, APOE 4 carrier status, and low education are significant predictors of a transition to an impaired state as opposed to a transition to cognitively normal because all the coefficients associated with Age and APOE4 are significant and positive. Remaining cognitively intact favors the highly educated (> 16 years education) which also agrees with the results from the previous models. Age and APOE 4 status are also significant predictors for dying without incurring a dementia. Age at entry is “protective” for subjects from the competing risk of death since older subjects are more likely to become demented before death.

Yu et al. (2009) incorporated the missing portion of the likelihood due to baseline demented individuals into the follow-up likelihood by assuming the two share the same random effect. The complete marginal likelihood function for a subject with baseline can be written as

$$L(\mathit{\Theta }\mid X,Z)=\int \prod _{l=2}^n\times \prod _{\begin{array}{l}s=1\dots 3,\\ v=1\dots 5\end{array}}{P}_{sv}{(\mathit{\Theta }\mid X,\gamma )}^{{\delta }_{y_{l-1},s}{\delta }_{y_l,v}}\times {\pi }_{y_1}(\mathit{\Theta }\mid X_B,\gamma )h(\gamma )d\gamma .$$

Here Θ is the set of parameters associated with the baseline response components. The probability of the baseline state π_y1(Θ|X_B, γ) was similarly modeled by using multinomial logistic regression as for the one-step transition probability P_sv(Θ|X, γ) in the follow-up likelihood. It will also be interesting to combine this approach with our model to find a complete likelihood function that accommodates all the three pieces baseline, follow-up, and survival.

Due to the Markov property assumption, the proposed method works well when the follow-up assessments are evenly spaced, but may lead to biased estimators when the visit times are derivation from the predetermined visit times. Therefore, one potential limitation of our proposed methods is its inability to handle the uneven assessments or skipped visits. The general imputation approaches for the missing data can used to deal with skipped visits But those imputation methods are generally very complex. One simple and popular strategy is so called “last observation carry forward (LOCF)”. However, it is not recommended to use since this approach will introduce bias in the result (Molnar et al. 2008). Uneven assessments call for use of more complex models as discussed by Huzurbazar (2005). Another possible drawback of the proposed method is that the computational burden will become heavier in the current model if a complicated form of the random effects is adopted.

The model proposed in this manuscript has some obvious extensions. Only one competing risk event is considered in this manuscript. The extension to allow for multiple competing events is straightforward although the models will become more complex. Another extension of the model may include considering procedures that do not require a proportional hazard assumption. A Generalized Weibull model will be a good choice since the hazard can be U or inverse U shaped.

Further investigation of the related model stability and verification of the model assumptions, such as Markov assumption for the transition component and the proportional hazard assumption on the survival time, are both of interest. Lastly, the application to the Nun Study data presented here emphasizes one step transition probabilities while clinically there is interest in the long run behavior of the process. That is, instead of estimating how a risk factor affects the odds of a transition into any impaired state at the next assessment there is also interest in determining how each risk factor affects the risk of an eventual dementia diagnosis relative to dying without a dementia diagnosis. Results similar to those provided by Yu et al. (2010) are needed for the model discussed here as well.