A NEW METABOLOMICS ANALYSIS TECHNIQUE: STEADY-STATE METABOLIC NETWORK DYNAMICS ANALYSIS

Abstract

With the recent advances in experimental technologies, such as gas chromatography and mass spectrometry, the number of metabolites that can be measured in biofluids of individuals has markedly increased. Given a set of such measurements, a very common task encountered by biologists is to identify the metabolic mechanisms that lead to changes in the concentrations of given metabolites and interpret the metabolic consequences of the observed changes in terms of physiological problems, nutritional deficiencies, or diseases. In this paper, we present the steady-state metabolic network dynamics analysis (SMDA) approach in detail, together with its application in a cystic fibrosis study. We also present a computational performance evaluation of the SMDA tool against a mammalian metabolic network database. The query output space of the SMDA tool is exponentially large in the number of reactions of the network. However, (i) larger numbers of observations exponentially reduce the output size, and (ii) exploratory search and browsing of the query output space is provided to allow users to search for what they are looking for.

1. Introduction

Currently, metabolomics data analysis necessitates a time-consuming, extensive, and manual cross-referencing of metabolic pathways in order to critically evaluate the measurement data. Recently, a novel in silico approach (IOMA) that integrates metabolomics data with a metabolic network model and infers metabolic fluxes is proposed.¹ IOMA (a) requires many pieces of information (e.g. availability of the stoichiometry matrix of the network, dissociation constants, enzyme turnover rates, mass balance constraints, flux capacity constraints), and (b) infers a single network state with all the computed metabolic fluxes. On the other hand, manual analysis of fluxes in small (and usually abstracted) subnetworks is quite common in life science publications. As examples, see Figs. 5 and 1 in Bederman et al. and Gasier et al., respectively.^2,3 Researchers seek alternative activation/inactivation scenarios in small-scale networks, without the need/access to the additional information such as those needed by IOMA. Note that, even for small-size networks, as the size of the network grows, the number of possible flow (flux) scenarios grows exponentially, which makes manual enumeration error prone. This manual process can be automated using computer science and bioinformatics techniques that employ biochemistry rules and constraints, pre-stored in a metabolic network database. Once the results are obtained, users can also visualize and query them, (e.g. “list those alternative flows where one targeted reaction is active, and another targeted reaction is inactive”).

Fig. 5.

A metabolic network M. Circle nodes are metabolites, rectangle nodes are reactions, and edges represent relations between reactions (which consume and/or produce metabolites) and metabolites.

Fig. 1.

SMDA result as a single G_AI graph.

In this paper, we propose a database-enabled and graph-traversal based technique, called steady-state metabolic network dynamics analysis (SMDA) that infers all allowable (flux) states of a network. Given a set of biofluid- (e.g. blood) and tissue-based metabolite concentration measurements at steady state, SMDA answers the query “list alternative steady-state metabolic network activation/ inactivation (i.e. flux) scenarios, given the observed measurements.” That is, SMDA takes as input from the user (i) metabolomics data, and (ii) a metabolic subnetwork, selected from a metabolic network database already made available to users, and produces a set of possible alternative flow scenarios (i.e. activation/ inactivation scenarios) for the metabolic subnetwork. Then SMDA lets users to further visualize and query the alternatives (not discussed in this paper).

SMDA can be viewed as both a constraint- and rule-based approach. It is constraint based^4,6 in that it uses conditions (pre-stored in a database) to locate all “allowable states”⁷ of a subnetwork in a metabolic network model (also pre-stored in a database). And, SMDA is rule-based in that its graph-expansion and merge strategies employ a number of biochemistry rules to capture the underlying metabolic biochemistry as much as possible.

Advantages of SMDA include:

• Ease of use and simplicity. it is designed as a “first-step” and “online” tool for biochemists and wet lab researchers to:

  • ○ evaluate their hypotheses about observed measurements in small-scale networks, and
  • ○ be used as a “knowledge discovery” tool e.g. to be used for “what if” types of questions.

• No flux optimization. SMDA does not require the knowledge of reaction kinetics or any utility/optimization function for flux optimization.

The disadvantages of SMDA include:

• SMDA returns only two flux values for a reaction: 0 (Inactive), and 1 (Active).

• As is the case with other techniques that return “all allowable states”,⁴ SMDA is inherently exponential in its output size. However, the computational performance of SMDA is acceptable for networks with up to 60 reactions (with some paths/pathways abstracted into “abstract reactions”; see Sec. 5 and Ref. 8).

SMDA is implemented and functional as a prototype both as an online tool, called PathCase-SMDA,⁹ which is part of PathCase family of applications,¹⁰ and as an iPad application named “PathCase MAW“.¹¹

1.1. SMDA Overview

Prior Preparation

We assume a fully hierarchical and compartmentalized metabolic network i.e. one with tissues, organelles, etc. already available in a metabolic network database. The steady-state “activation conditions” (or, the ACT condition set) for each reaction and transport process to be active are characterized a priori, saved in a database, and used during query-time analysis. Initially, the status values of all reactions and all metabolite pools in the metabolic network are Unknown.

Query-time Analysis

At query time, the user chooses a smaller metabolic subnetwork (i.e. query network) to query. SMDA takes the observed metabolite set and the selected subnetwork, referred to as “query network,” as input and executes the following steps.

Initialization

(i) For each biofluid-based metabolite observation, identify whether its transport processes are active (by checking, for each transport process, whether all conditions in its ACT set are satisfied). (ii) For each tissue-based metabolite observation, derive its metabolite pool label, which is one of the following: Unavailable, Available, Accumulated, or Severely Accumulated.

Expansion and Merge Metabolic Subnetwork Traversal and Active Inactive Reaction Assessment

Starting with active/inactive transport processes and tissue-based observed metabolites, and continuing with metabolic reactions in tissues of the query network, locate iteratively those reactions with satisfied or unsatisfied ACT condition sets, and mark (i) those reactions whose ACT conditions are completely satisfied as Active, and (ii) those reactions whose ACT conditions contain at least one unsatisfied ACT condition as Inactive. (This process results in multiple expansions). When two disconnected “active/ inactive subnetworks” “touch” each other, merge them to obtain a larger active inactive subnetwork.

The above-summarized query-time analysis creates and iteratively expands multiple possible metabolic flux subgraphs, called Active–Inactive Graphs (G_AI, where, in each G_AI graph, the status of each reaction and the label of each metabolite pool are clearly marked (i.e. no reactions or metabolite pools with “Unknown” status/label exist). The result is a set of G_AI graph sets, where each G_AI graph set specifies one distinct alternative steady-state activation/inactivation scenario for the metabolic network. An alternative output to G_AI graphs is flow-graphs, where a flow-graph is a G_AI graph without metabolite pool labels; flow-graphs are utilized in Sec. 5. We give an example.

Example 1. Assume that the user selects catabolism of cysteine in liver as the metabolic subnetwork to be queried (as shown in Fig. 1), and has three observed metabolite measurements in cytosol: O₂ as 80 mM/L (we assume that O₂ is “estimated” as it is very difficult to measure O₂ in tissue of intact organ), cysteine as 60 μM/L, and SO₃ (3-sulifino-L-Alanine) as 80 μM/L. Assume that the database conditions state that, ^{in liver cytosol}, “O₂ is marked as Available if it is in between [1, 100] mM/L”, “cysteine is marked as Available if it is in between [1, 100] M/L”, and “SO₃ is marked as Available if it is in between [1, 100] μM/L”. Thus, ths SMDA initialization step concludes that O₂, cysteine, and SO₃ are all Available. Also, the execution of the expansion step as summarized above concludes that there is only one flow-graph with only one G_AI graph in the output of the query, as shown by the (actual) SMDA output of Fig. 1.

In summary, given metabolomics observations and a query network, SMDA locates all possible alternative active–inactive network scenarios on the selected subnetwork. This approach provides compact and complete steady-state views of possible metabolism dynamics as independent and alternative snapshots in the form of user-friendly visual steady-state views of the metabolic network. There are four issues. The first issue is prioritizing and ranking different alternatives produced by SMDA. This issue is not discussed in this paper; please see Ref. 8 for a number of ranking mechanisms.

The second issue is related to the space complexity of SMDA: what happens when, for a large subnetwork, there are many alternative G_AI graphs? As a first response to this issue, SMDA switches to the use of flow-graphs, as opposed to G_AI graphs, where a single flow-graph captures multiple G_AI graphs. Second, SMDA allows for an exploratory search of the resulting G_AI graphs. That is, an “interactive query” execution takes place where, as a response to the query, the user is given the total number of “possible results” (i.e. G_AI graphs) and is then prompted to choose and view different G_AI graphs or flow-graphs in the output with respect to participating metabolites and reactions. For example, the user is told, say, that pyruvate dehydrogenase is active in two flow-graphs and inactive in four flow-graphs, and is given the option of viewing only the first two, or the latter four, or all six flow-graphs. We refer to this process as “exploratory search and browsing“ of the SMDA query output search space.

The third issue is related to the time complexity of SMDA. Given a large metabolic network, SMDA output may increase so fast and so large that SMDA may not complete its execution within a reasonable amount of time. When this case occurs, our suggestion to the user is to reduce the network size either by eliminating subnetworks or by “abstracting” a subnetwork (e.g. a pathway of a metabolism) into an “abstract reaction.” From our interactions with wet-lab biochemists, both approaches are quite common and, used extensively in practice to (manually) analyze the behavior of metabolic networks.^2,3

Finally, the fourth issue is about the way SMDA works: as described earlier, SMDA discretizes metabolite observations into four categories, namely, Unavailable, Available, Accumulated, or Severely Accumulated. This discretization can be done by users employing their domain expertise, as is done in Sec. 5, or it can be done automatically on the basis of ranges for each discretization, which are in turn obtained from the HMDB data source.¹² However, in some cases, HMDB classifies multiple levels of “normal” ranges for metabolites, leading to “observation misclassifications” in SMDA. This issue and the SMDA actions taken are discussed in a separate study.¹³

All figures in this paper are obtained from the web-based SMDA application.⁹ The observation set of Example 1 is available on the web site of the browser-based application PathCase-MAW as “Sample Observation 0” and running the SMDA Tool with Sample Observation 0 produces the results of Example 1. Figure 1 and Example 1 are from a manually constructed mammalian network database, available at PathCase-MAW site.¹⁴ All other examples and visualizations in figures of this paper are obtained from the PathCase-RCMN (ReConstructed genome-scale Metabolic Network) application,¹⁵ which is, in turn, built by importing the SBML of reconstructed metabolic network of Trypanosoma cruzi bacteria:¹⁶ The SMDA tool, an evolution of the OMA Tool,¹⁷ is currently being beta-tested in cystic fibrosis metabolomics data analysis.

This paper is organized as follows. Section 2 specifies a complete condition- and rule-based model of the metabolic network behavior. We

• list the assumptions of our model and define the notion of (quasi-) steady-state for the metabolic network,

• introduce the notion of metabolite pool label identifiers,

• employ a three-valued logic to specify metabolite pool label conditions and Activation Condition Sets for reactions as well as transport processes,

• list transport process rules, and, finally,

• specify a number of basic biochemistry-based rules.

Section 3 presents the SMDA algorithm with the three steps, namely, G_AI (flow-) graph initialization, expansion, and merge steps. The SMDA algorithm iteratively constructs a G_AI Generation Hierarchy where, when it terminates, each leaf node of the hierarchy contains one possible activation/inactivation scenario within the query subnetwork. In Sec. 4, we specify three different alternative expansion strategies for the expansion step, namely, Naïve Expansion, Selective Expansion #1, and Selective Expansion #2. Section 5 illustrates the usefulness of SMDA within a cystic fibrosis related metabolomics research context. Section 6 presents a computational performance evaluation of the SMDA tool by using PathCase-MAW mammalian metabolic network database. SMDA can be viewed as a new approach within the category of metabolic network flux analysis techniques such as flux balance analysis,¹⁸ elementary flux modes,¹⁹ and extreme pathways.²⁰ Section 7 compares SMDA with these other techniques. Section 8 briefly concludes and lists future work.

2. Condition-Based Modeling

2.1. Assumptions and terminology

We make the following assumptions about our environment.

• The complete metabolic network is pre-captured and available in a metabolic network database.

• The metabolic network database models tissue-level compartmentalization; that is, it is a multi-tissue and a multi-compartment (e.g. cytosol, mitochondrion, etc.) environment.

• The metabolic network is “sound” in the sense that all metabolites that are not in biofluids are both produced by (i.e. are a product of) at least one reaction and consumed by (i.e. are a substrate of) at least one reaction.

• Initially, we label each unmeasured metabolite pool size with the identifier “Unknown.” During query-time analysis, the labels may change into one of “Unavailable”, “Available”, “Accumulated,” or “Severely accumulated.” The reason for non-quantitative labeling (as opposed to numerical size values) is that this paper does not employ quantitative pool size estimation techniques, as discussed in more detail in Sec. 2.2.

• No a priori knowledge of the size of each metabolite pool is assumed, except for measured metabolites.

• Given a reaction r and a metabolite m as a substrate, co-factor-in, activator (product, co-factor-out, inhibitor) of r, the knowledge of the lowest (highest) metabolite pool size label of m at steady state for m to activate (inhibit) a reaction so that r is “active” (“inactive”) is assumed to be available. This is discussed in more detail in Sec. 2.4.

• The organism (represented by its metabolic network database) is queried when it is at a steady state for a time interval T. Steady state is defined in terms of two properties:

  1. Production-Consumption Rate Equality (PCRE): During the time interval T, the rate of formation of every metabolite m is (almost) equal to its rate of degradation i.e. all metabolite pool sizes (concentrations) remain (almost) constant during the time interval T. Put another way, production rate of each metabolite is equal to its consumption rate.
  2. Metabolite Pool Label Invariability (MPLI): During the time interval T, all metabolite pool labels stay the same. That is, if the label of a metabolite pool is Available, it stays Available during the time interval T.

The PCRE property at steady state is a natural property, referring to the state of constancy or the homeostasis (equilibrium) of the organism. As an example, in the “fed” state of, say, humans, glucose, through glycolysis, is catabolized to acetyl CoA, which is converted to fatty acids or oxidized in the TCA cycle. Although acetyl CoA is available to both metabolic pathways (i.e. fatty acid synthesis and the TCA cycle), it does not accumulate, as the combined consumption rate of acetyl CoA by fatty acid synthesis and the TCA cycle is (almost) the same as its production by glycolysis.

We use the MPLI property in order to capture a snapshot of the metabolism when metabolite pool size labels also stay constant during steady state. Next we define some terminology.

Definition. (Metabolic Network). A metabolic network is a connected graph G(V, E) with a vertex set V of reactions and metabolite pools (a metabolite pool can be a substrate, regulator or product in a reaction), and a directed edge set E such that there is an edge from node u to node v if (i) v is a reaction, and u is a substrate, regulator of v, or (ii) u is a reaction, and v is a product of u.

Definition. (ProductionRate and ConsumptionRate of metabolite pool m): Consider any metabolite pool m, its producer reactions p₁, p₂; . . . ; p_i, and its consumer reactions c₁; c₂; . . . ; c_j. Let pr_m;k denote the production contribution rate of reaction p_k; 1 ≥ k ≥ i, for metabolite m, and cr_m;v denote the consumption contribution rate of reaction c_v; 1 ≥ v ≥ j, for metabolite m during time period T. Then

• P_m = {(p₁, pr_m;1), (p₂, pr_m;2; . . . ; (p_i, pr_m;i)} is the active producer set of m, where each pair (p_i, pr_m;i refers to a producer p_i of m and its contribution rate pr_m;i; and (pr_m;1 + pr_m;2 +...+ pr_m;i+ is the ProductionRate(m) of m; and

• C_m = {(c₁, cr_m1 +, (c₂, cr_m;2), . . . ; (c_j, cr_m,j+g is the active consumer set of m, where (c_j, cr_m,j refers to an activated consumer c_j of m and its consumption rate cr_m,j; and (cr_m,1+ cr_m,2 + + cr_m,j+ is the ConsumptionRate(m) of m.

Below we formally characterize the notion of (quasi-)steady state for the metabolism.

Definition. ((quasi-)steady state for an organism during a time period): Given an organism Org, its metabolites m_l, 1 ≤ l ≤ n, and two constants ε_ml and T, the organism Org is said to be in a steady state during the time period T if

1. ProductionRate (ml)= ConsumptionRate(ml) ±εml for each m_l; 1 ≤ l ≤ n; during the time period T, and

2. Label of each metabolite m_l, 1 ≤ l n, stays the same during the time period T.

2.2. Metabolite pool label identifiers

The purpose of metabolite pool label identifiers is to simplify the ACT (activation condition) set specifications for reactions and transport processes.

Definition. (Metabolite pool label during a time period): Let T_AVAIL (m), T_ACC (m), and T_SAC (m), T_AVAIL(m) < T_SAC(m) < T_SAC (m), be three threshold constants for metabolite m, stored in the database. Given the metabolite pool m, the label of m during the time period T is marked with one of the following five identifiers.

• Unknown (id:-1): if the metabolite pool size for m, denoted by Size m , is unknown during time period T.

• Unavailable (id: 0): Size(m) is less than the threshold T_AVAIL (m) and ProductionRate (m) ε_m during time period T, where ε_m is a small constant.

• Available (id: 1): Size(m) is greater than or equal to the threshold T_AVAIL (m) and less than the threshold T_ACC(m) during time period T.

• Accumulated (id: 2): Size(m) is equal to or above the threshold T_ACC (m) but less than the threshold T_SAC(m) during time period T.

• Severely Accumulated (id: 3): Size(m) is equal to or above the threshold T_SAC(m) in time period T. This label is used for the product inhibition rule BC4 of Sec. 2.5.

Note that there is a need to use different metabolite pool labels of Available and Accumulated because, for some reactions, “availability” of a metabolite m as a substrate (or regulator) may be sufficant for the reaction (i) to be active through substrate availability (provided that there are no other inhibiting mechanisms) or (ii) to experience the regulating effect (i.e. inhibition/activation) of m, in those cases where m is a regulator. However, for activation/regulation, other reactions may require the “accumulation” of m, at least at moderate levels. We give an example.

Example 2. Acetyl CoA is an allosteric activator of the first (also the committed) step in gluconeogenesis, which is catalyzed by pyruvate carboxylase. And, pyruvate carboxylase activation needs acetyl CoA accumulation. In the fed state of organism, acetyl CoA is produced by glycolysis (hence, is Available), but does not accumulate (hence has “Not Accumulated”). Thus, pyruvate carboxylase is not activated, which leads to the inactivation of gluconeogenesis pathway. But, in the fasting state of the organism, acetyl CoA is produced by β-oxidation, and consumed by the TCA cycle and ketone body synthesis. In this case, accumulation of acetyl CoA occurs (slowly but steadily), since its production rate by β-oxidation is higher than its combined consumption rate by the TCA cycle and ketone body synthesis.

2.3. Metabolite label condition characterization

The metabolite label condition C about the label identifier q of a metabolite pool m is denoted as C 〈q, m〉.

Example 3. Ketone body synthesis requires the accumulation of acetyl CoA to use it as a substrate. Then, the required condition can be stated as C〈Accumulated, Acetyl CoA〉 or, equivalently, as C〈2, Acetyl CoA〉 when the identifier of Available is used.

We employ three-valued logic (True, False, Unknown) in evaluating conditions about metabolite pool labels of reactions.

Definition. (Satisfaction of a metabolite label condition): A metabolite label condition C〈q, m〉 is

1. True if m is marked with the identifier q_actual where either (a) 0 < q· id ≤ _actual · id or (b) q · id = q_actual · = 0

2. False is m is marked with the identifier q_actual where either q_actual(q_actual · id ≠ –1 and q_actual · id < q · id = 0 and q_actual ≥),

3. Unknown if m is marked with the identifier q_actual where q_actual · id = –1.

Example 4. The condition C〉Accumulated, Acetyl CoA〉 (or, C 〈2, Acetyl CoA〉) from Example 3 is True when the corresponding pool of acetyl CoA has the label Accumulated (id: 2) or Severely Accumulated (id: 3).

Definition. (Negation of a condition): Negation of a condition C 〈q, m〉 is denoted as C〈q, m〉 is True if m is marked with an identifier q_actual such that either (a) q_actual · id ≠ –1 q_actual · id < q · id, or (b) q · id = 0 and q_actual · > 0.

Example 5. The negation of the condition from Example 3 i.e. C 〈Accumulated Acetyl CoA〉, is true only Acetyl CoA is marked as Available (id: 1) or Unavailable (id: 0) (i.e. no active producer).

Definition. (Conflicting conditions): Two conditions C〈q₁, m〉 and c〈q₂, m〉 which are defined on the same metabolite m are in conflict if there is label identifier for m that would satisfy both C₁ and C₂.

Example 6. C₁〈Available, Acetyl CoA〉 is in conflict with C₂ 〈Accumulated, Acetyl CoAi〉.

Definition. (Condition subsumption): Condition C₁〈q₁, m〉 subsumes another condition C₂〈q₂m〉 if C₂ is satisfied whenever C₁ is satisfied.

Example 7. C₁〈Accumulated, Acetyl CoA〉 subsumes C₂〈Available, Acetyl CoAi〉.

2.4. Trigger values and activation condition sets for reactions, transport processes, or pathways

The label of a reaction r, a transport process T_c1-to-c2 from compartment c₁ to compartment c₂ (not to be confused by time interval T), or an “abstract pathway” can be one of active, inactive, or unknown, as discussed next.

2.4.1. Reaction

We start with the notion of a “metabolite trigger value” for a reaction, which can be either Available or Accumulated.

Definition. (Trigger value for metabolite m for reaction r to be active): Let m be a metabolite involved in a reaction r. For r to be active, metabolite m is said to have a trigger value t_m,r, where t_m,r ∈ {Available, Accumulated}, if

1. m is a substrate, cofactor-in, or an activator of r, and the metabolite pool identifier for m is t_m,r, or

2. m is an inhibitor of r, and the metabolite pool identifier for m is below (the integer id value of) t_m,r.

Each reaction r (or pathway) is associated with a set of participating metabolite pools and their pre-determined trigger values, already available in a database. Each reaction (or a pathway) is associated with a set of “activation conditions” (i.e. ACT set), which are created based on the participating metabolites and their trigger values, as discussed next.

Definition. (Activation condition set of a reaction/pathway): Activation condition set of a reaction (or a pathway) r, denoted as ACT(r), defines the conditions for r to be active, and is constructed as follows.

• ○ For each m in reaction r, where m is a substrate/cofactor-in/activator of r with trigger value t_m,r; C〈t_m,rm〉 ∈ ACT(r), where t_m,r ∈ {1,2} ( 1 and 2 are ids of Available and Accumulated labels, respectively)

• ○ For each m in r, where m is an inhibitor of r with trigger value t_m,r, C〈t_m,r m〉 ACT (r), where t_m,r, ∈ {1}.

• For each m in r, where m is a product/cofactor-out of r, C 〈3, m〉 ∈ ACT r (Product Inhibition rule 4; 3 is the id of Severely Accumulated label).

• If the ratio Tr = Size (m₁)/Size(m₂) of energy metabolite pairs is specified as an activator for r, then C₁(Accumulated, m₁) ∈ ACT (r), and C₂ (Accumulated, m₂ ∈ ACT(r). If Tr is an inhibitor for r, then C₁ (Accumalated, m₁) ∈ ACT (^r), and c₂ (accumulated, m2) ∈ ACT (r).

As mentioned earlier, the activation condition set ACT of each reaction is defined a priori (oddine) before any metabolomics analysis is carried out.

2.4.2. Transport processes

We view each transport process T_c1-to-c2 as having one metabolite transported from compartment c₁ to compartment c₂, subject to the activation condition set ACT for T_c1-to-c2. We give an example.

Example 8. The transport process T_{blood-to-muscle} (glucose) of glucose from blood to muscle may be characterized within the ACT set as {C〈Available, blood.glucose〉, C〈Available, blood.insulinig〉}. That is, for glucose to be transported from blood to muscle, both glucose and insulin must be at least Available. On the other hand, transport process T_{muscle to blood} (glutamine) of glutamine from muscle to blood can be conditioned based on its availability in muscle i.e. ACT(T_{muscle to blood}(gluta-mine)) contains {C〈Available, blood.glutamineig〉}

We have the following transport process rules.

Rule TR1. Let c₁ and c₂ be two compartments, m be an observed metabolite in compartment c₁, and T_c1-to-c2 (m,c₁,c₂ be m's transport process from c₁ to c₂. Assume that pool label of m in c₂ is Unknown. Then if ACT(T_c1-to-c2 is satisfied then T_c1-to-c2 (m) is active otherwise, it is inactive.

Rule TR2. For active transport processes (i.e. the ACT set is satisfied), we assume that the metabolite pool of the product has the same label with the substrate.

Rule TR3. For transport processes, the product inhibition rule (Please see rule BC4 of Sec. 2.5) does not apply.

2.4.3. Steady-state labels for reactions and transport processes

We define the steady-state label of a reaction/transport process as one of Active, Inactive, or Unknown, based on the satisfaction of its associated activation condition set ACT.

Definition. (Active, Inactive, or Unknown reaction/transport process state): Given a reaction/transport process r with an associated activation condition set ACT (r) defined on the participating metabolites, r is said to be Active (i.e. having a non-zero flux) during the steady-state time period if.

1. All conditions in ACT(r) are satisfied; i.e. all conditions that involve sub-strates, cofactors, and products of r are satisfied, and

2. Among the conditions involving regulators of r, those conditions that include regulator(s) with the highest precedence are satisfied.

Reaction/transport process r is Inactive if there is at least one unsatisfied condition in ACT(r). Otherwise, the state of r is Unknown.

Note that, for some reactions there may be multiple activators and inhibitors, in which case, we assume that (a) we have a priori information about the precedence of regulators, and (b) we make use of such precedence information in deciding whether the reaction is active or inactive.

2.5. Biochemistry-based rules

Next, we list a number of basic biochemistry (BC)-based rules that we use in the rest of the paper.

Rule BC1. For each reaction, when multiple regulators with conflicting regulatory effects (activation or inhibition) on an enzyme are in place, the regulator with the strongest effect (highest precedence) on the enzyme is considered, and the other regulators are ignored.

The regulated reactions in a pathway may be classified as rate-limiting and committed steps. Once the committed step takes place, other reactions in the pathway follow this reaction until the end-product is produced, provided that none of the other regulated processes are blocked or inhibited. A committed step of a pathway is usually one of the early irreversible reactions in the pathway. As an example, in glycolysis, the committed step is the same as the rate-limiting step, PFK1.

Rule BC2. If the committed step of a pathway p is blocked (i.e. inactive), then p is Inactive (i.e. all reactions in p are Inactive).

We associate each compartment with particular pools of metabolites as its input and output. We then connect two compartments in the metabolic network if a transport process connects the two.

Rule BC3. Each input and/or output metabolite of a compartment is associated with a transport process (pre-captured and modeled in the database). A transport reaction and an enzymatic metabolic reaction are connected if they share at least one metabolite pool (i.e. as their substrate and/or product).

Due to similarities in the way they bind to enzymes, substrates are in competition with products to bind to their enzymes. As the concentration of products increase, this competition slows down the rate of enzymes binding the substrates. Hence, the reaction rate decreases. Eventually, when the product accumulation reaches to high levels, the corresponding reaction is inhibited dramatically.

Rule BC4. Whenever a non-biofluid metabolite m is marked as “severely accumulated,” all reactions that produce (and, therefore, due to the steady-state assumption) and consume m are Inactive.

The next set of rules follows from the steady-state assumption.

Rule BC5. If all producers (consumers) of a metabolite pool m are inactive then, due to the PCRE property, regardless of the pool label of m, labels all consumers (producers) of m are Inactive.

Rule BC6. If at least one producer (consumer) of a metabolite m is Active, then (i) m is either Available or Accumulated, and (ii) at least one consumer (producer) of m is Active.

Rule BC7. If the metabolite m is Unavailable, then all consumers (and, thus, due to the steady-state assumption) and all producers of m are Inactive.

Rule BC8. Substrate and product labels of a transport process with no conditions are always the same.

Next, using rules BC1-8, we specify the notion of “inconsistent” metabolite pool and reaction label assignments.

Definition. (Inconsistency): For each Rule BC_i; 1≤i≤8, violation of Rule BC_i, in terms of metabolite pool and/or reaction label assignments constitutes an inconsistency in metabolite pool and reaction labels.

For example, as a product of an Active reaction r, the label of metabolite pool m should not be Severely Accumulated, since it violates Rule BC4.

3. Active/Inactive Graph Generation and Expansion

Starting from a given set of observations, we employ iterative backward and forward reasoning with the goal of identifying possible metabolic mechanisms which may have led to the observed changes. We first give some definitions.

Definition. (Reaction participants): Given a reaction r, RP (r) is the set of substrates, products, and regulators of r (i.e. “Reaction Participants” of r).

We refer to a metabolite pool concentration measurement as an observation. Next we define the notion of Active/Inactive graph, which has labeled reactions and labeled reaction participants.

Definition. (Active/Inactive graph G_AI): An active/inactive graph G_AI(R_AI, δ_AI,S_RP, δ_RP, M; O) is a connected subgraph of the metabolic network M with respect to a set O of observations where (i) R_AI consists of a set of reactions or pathways in the subgraph G_AI (R_AI, δ_AI, S_RP, δ_RP; M; O) (ii) each reaction/pathway in R_AI is assigned a label of Active or Inactive through the function δ_AI :R_AI→ {Active, Inactive}, (iii) S_RP is the set of reaction participants (i.e. substrates, products, activators, etc.) of reactions in R_AI, and (iv) each reaction participant of a reaction in S_RP is assigned a label of Unavailable, Available, Accumulated, Severely Accumulated through the function δ_RP :S_RP → {Unavailable, Available, Accumulated, severely Accumulated}.

During the G_AI graph generation process, inconsistencies in G_AI are avoided where inconsistency is as defined in Sec. 2.5.

3.1. Initial G_AI generation

A generated G_AI graph should be valid, as defined below.

Definition. (Valid Active/Inactive graph): A G_AI graph is valid when

1. all metabolite pool/reaction labels in G_AI are consistent

2. for all active reactions r in G_AI, ACT(r) is satisfied, and

3. for all inactive reactions r in G_AI, ACT (r) contains at least one unsatisfied condition.

3.1.1. Converting observations into metabolite pool labels

As discussed in Sec. 1, there are two alternative ways of converting metabolite observations into discretized metabolite pool labels of Available, Unavailable, Accumulated, or Severely Accumulated. In the first way, users can decide on these labels themselves using their domain expertise. In the second way, given a quantitative concentration statement on a metabolite pool m, SMDA compares the value with threshold constants (obtained from HMDB) for the metabolite m, and then marks m with the corresponding label identifier label. SMDA marks m only with one identifier, which is the highest satisfied identifier. However, thresholds obtained from HMDB may be problematic: (1) HMDB may have more than one “normal” level for a metabolite, or (2) there may be no information at all. Please see Cicek et al.¹³ for more details.

When observations on metabolite concentrations are converted into one of Unavailable, Available, Accumulated, or Severely Accumulated, to distinguish between metabolites in different compartments, we use the underscore notation and refer to metabolite m in compartment c as ‘m_c”

Finally, for each observed biofluid metabolite, we investigate iteratively which of the possible G_AI graphs (initially, each contains only one measured biofluid metabolite) is valid. We illustrate the initial G_AI graph construction with an example from the metabolic network of T. cruzi (all network visualizations, except Fig. 1, are from PathCase-RCMN for T. cruzi).

Example 9. Let pi be an observed metabolite in compartment cytosol, denoted as pi_c, and the label of pic_c be Available. Let phosophatetransporter, peroxisome and phosphatetransportl be two such transport processes transporting pi_c from compartment cytosol to compartment glycosome, and from cytosol to compartment mitochondria, respectively (see Fig. 2). By evaluating their ACT sets, we locate whether the two transport processes phosophatetransporter, peroxisome and phosphatetransportl are active (By Rule BC8, at least one must be active). This means that one of the three alternative G_AI graphs involving pi_c is consistent.

Fig. 2.

Illustration of three alternative versions of transport processes.

3.2.G_AIgraph expansion

Each valid G_AI graph is iteratively expanded at each step with a set of reactions and/or transport processes. We start with some definitions.

Definition. (Distance between two metabolite pools): The number of reactions on the shortest path that connect two metabolite pools, regardless of reaction directions, is the distance between two metabolite pools.

Definition. (Border metabolite pool): Given a metabolite pool m and a non-empty active/inactive graph G_AI (R_AI, δ_AI, S_RPδRP, M, O), m is called a border metabolite pool of G_AI if, in the metabolic network M, there is a pair of reactions (r₁, r₂ such that m participates in both r₁ and r₂, and r₁ ∈ R_AI, r₂ ∈ R_AI.

Note that when a G_AI graph contains only a single metabolite pool m, m becomes a border metabolite pool of G_AI. Also, the label of a border metabolite in a G_AI graph is one of Unavailable, Available, Accumulated, or Severely Accumulated, and never Unknown. We denote the border metabolite pool set of G_AI as BMP(G_AI).

The process of extending a given G_AI graph to a new G_AI graph via the addition of new reactions connected to its border metabolite pools is called G_AI graph expansion. The newly added reactions of the G_AI graph are assigned the label values of either Active or Inactive (which are consistent i.e. not in conflict with the existing reaction label assignments in the graph). If there is no such consistent expansion, then the expansion is terminated. Next we characterize the G_AI graph expansion process.

Definition. (G_AIgraph expansion): Let G_AI (R_AI, δ_AI, S_RP, δ_RP, M, O) denote the original G_AI graph to be expanded;

G^exp_AI(R^exp_AI, δ^exp_AI, S^exp_RP, δ^exp_RP; M, O) denote one of the alternative G_AI graph expansions of G_AI (R_AI, δ_AI, S_RP, δ_RP,M,O);

BMP(G_AI+ denote the set of all border metabolite pools of G_AI;

NRS(BMP(G_AI)) denote the set of (“new”) reactions involved with border metabolites and not (yet) in G_AI, i.e. those reactions r, where r has, as a substrate/ product/regulator, a metabolite pool in BMP(G_AI) and r is not in R_AI;

NMP(NRS(BMP(G_AI)) denote the set of (new) metabolite pools p, where p participates, as a substrate, product, or regulator, in a reaction of NRS(BMP(G_AI)) and p is not R_AI. Then the expansion G^exp (R^exp, δ^exp_AI, S^exp_RP, M, O) is characterized as follows.

1. R^exp_AI = R_AI U NRS(BMP(G_AI))

2. S^exp_RP = S_RP U NMP(NRS(BMP(G_AI)))

3. Each r in R^exp_AI is assigned the label of Active or Inactive through the function ^exp_AI: R^exp_AI →{Active, Inactive}

4. Each metabolite in S^exp_RP is assigned one of the labels Unavialable, Avialable, Accumulated, Severely Accumulated through the function δ^exp_RP: S^exp_RP → {Unavialable, Avialable, Accumulated, Severely Accumulated}.

5. δ^exp_AI is consistent with δ_AI.

6. δ^exp_RP is consistent with δ_RP.

End of Definition

Border metabolite pools of G^exp_AIcan be characterized as those metabolite pools which (i) are not in G_AI, and (ii) participate in reactions that are not in G^exp_AI. Clearly, border metabolite pools of G^exp_AI are always within one reaction distance from any border metabolite pool of G_AI.

Note that the G_AI graph expansion process is not unique. Each expansion step of G_AI graph generates a new “alternative” G_AI graph by assigning different labels to new reactions. At each step, the newly formed set of G_AI graphs that are alternatives of each other is called a G_AI-group. Each G_AI graph in the same G_AI-group is non-redundant, meaning each G_AI graph has at least one reaction or metabolite pool assignment differing from the corresponding assignment in any other G_AI graph in the same group.

G_AI graph generation/expansion process is represented as a hierarchy, called the G_AI generation hierarchy, where each node represents a G_AI graph of the metabolism, and each edge from parent to child in the G_AI generation hierarchy represents the expansion of the parent G_AI graph in the next step by additional reactions leading to a new child G_AI graph. Branching in the G_AI generation hierarchy occurs whenever alternative (i.e. OR-connected), but conflicting, graph extension steps are taken, which leads to alternative G_AI graphs. Each such set of alternative graphs forms a G_AI-group.

The G_AI generation hierarchy is a directed acyclic graph, with only one node that does not have any incoming edges, called root, and with any other node containing a G_AI-group. The hierarchy is constructed as follows.

Initialization

Level 0: root is a dummy node at level 0 i.e. it does not contain any information. Root has ∥O∥ immediate children, one for each observation in O.

Level 1: Each immediate child of root is a G_AI-group, with only one G_AI graph containing (i) a single node corresponding to a measured metabolite pool in the set O of observations, and (ii) no reactions.

Expansion-and-merge

Level i: Nodes in each level i I > 1, of the hierarchy are constructed from the G_AI- groups in level (i –1) in two steps, as follows.

Expansion step: let Gr be a G_AI-group node in level (i – 1). each G_AI graph in Gr is expanded following a G_AI graph expansion as specified by the G_AI graph expansion definition. The set of all such expanded graphs of Gr forms a new G_AI- group node at level i in the hierarchy.

Merge step: Let G_AI-groups GrX and GrY be two newly expanded G_AI-groups of the expansion step. Let Gx and Gy be the G_AI graphs of G_AI-groups GrX and GrY, respectively. If Gx and Gy have a non-zero number of common border metabolites with identical border metabolite labels, then GrX and GrY are merged into a single G_AI-group, say, GrZ, in the hierarchy by (i) merging Gx with Gy, and placing the result in GrZ, and (ii) replacing GrX and GrY by GrZ into the hierarchy at level i.

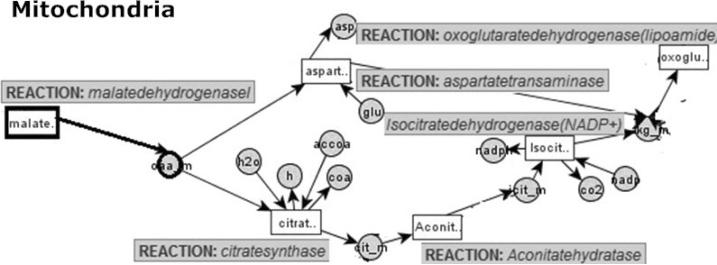
Example 10. Consider a part of a metabolic network M, shown in Fig. 3. Reaction malatedehydrogenasel is already decided as Active, and oaa_m is a border metabolite with a label value other than Unknown. Assume that oaa_m is already assigned the pool label identifier Avialable. The border metabolite oaa_m is involved in two reactions, namely, aspartatetransaminase and citratesynthase, whose label assignments are not yet made.

Fig. 3.

A partial metabolic network M. Circle nodes are metabolites, rectangle nodes are reactions and edges represent relations between reactions (which consume and/or produce metabolites) and metabolites.

Based on the network of Fig. 3 and given the pool label identifier information of Avialable on oaa_m, we would like to generate possible valid G_AI graphs with active/inactive reactions in the metabolic network. At the same time, each valid G_AI graph must preserve the observed Avialable pool label mark for oaa_m.

Next, starting from the border metabolite oaa_m, we generate different possible G_AI graphs. New G_AI graphs are generated by expanding the initial metabolic subgraph with reactions from the larger metabolic network M. Figure 4 shows the original G_AI graph and the next level of the G_AI generation hierarchy. Each of G_AI1, G_AI2, G_AI3, and G_AI4 is distinct and non-redundant. Thus, they form alternatives of each other, called a “G_AI-group.”

Fig. 4.

The first level of the G_AI graph generation hierarchy for the metabolic network in Fig. 3.

End of Example 10

We next discuss the creation of G_AI graphs in more detail. For a given metabolite pool m, R(m) denotes the set of producer and consumer reactions of m in the metabolic network; and r.label represents the current label (i.e. active, inactive, unknown) assignment for reaction r.

Definition. (Label assignment for reactions in the reaction set R (m) of metabolite m): Given a metabolite pool m, SA(R(m, δ_SA;m is a label assignment for reactions in R(m), where each reaction in r(m) is assigned a label of either Active or Inactive, through a function δ_SA,m: R (m) → {Active, Inactive}

Note that the number of possible label assignments for a set of consumer/producer reactions of a given metabolite pool m is exponential in the number of consumers and producers of m.

Remark 3.1: Given a metabolite pool m, let i be the number of consumer reactions of m, and j be the number of producer reactions of m in the metabolic network. Then, the maximum number of possible distinct label assignments for m's producers and consumers is 2^i+j.

Note that one does not need to evaluate each such combination of reaction label assignment as a valid G_AI graph expansion.

Metabolite pool label assignment for metabolite m in G_AI is subject to three requirements:

1. Conditions that involve m are either True or False, but not Unknown, and

2. For each reaction r in G_AI, either all conditions in ACT(r) are True, or ACT (r) contains at least one False condition, and

3. All rules (of Secs. 2.4.2 and 2.5) are satisfied.

To check the satisfaction of all three requirements above, our approach (described in Sec. 3.4 next) is as follows. For initialization, start with observed biofluid metabolites and non-biofluid metabolites as “seed” metabolites; use satisfied conditions of observed biofluid metabolites to locate their transport processes (i) with ACT sets having only satisfied conditions (in which case they are Active transport processes), or (ii) with at least one unsatisfied condition (in which case they are Inactive transport processes). When (i) and (ii) fail for a transport process, then the label of transport process is unknown. Next, after the initialization (of G_AI graphs), repeat the G_AI graph expansion process (as defined above) via the “border metabolites” of G_AI graphs, until there are no more border metabolites involved in active reactions. For more details, see the supplement.⁶

Next, for a given border metabolite m, we define the notion of a “^{valid label assignment} for R(m)” the reaction set (i.e. all producers and consumers) of m.

Definition. (Valid label assignment for reactions in the reaction set of a border metabolite m): Given the graph G_AI (R_AI, δ_AI, S_RP, δ_RP, M, O), a border metabolite pool m in G_AI, the reaction set R(m) of m, let SA(R(m), δ_SA,) be a valid label assignment for in R(m)with respect to G_AI if the following conditions hold.

1. No Label Conflict Among Reactions: For each reaction r where r where r ∈ R (m), δ_sa,m (r) = δ_AI (r) or r ∈ R_AI.

2. Backward Compatibility: The label assignment SA(R(m), δ_SA,m results in a set Q of pool label assignments for the border metabolite m, each resulting in a new expanded G_AI graph. Then, for a G_AI and the metabolite pool assignment q in Q, the following two conditions hold:

   • ○ With m having the label q, all the conditions in the ACT sets of “active” reactions in R_AI υ R(m) are satisfied by the assignment q.
   • ○ With m having the label q, for each “inactive” reaction r in R_AI υ R(m) that involves the border metabolite m in its ACT set, there is at least one unsatisfied condition.

3.3. Merging G_AI graphs

During the G_AI graph expansion, it is possible to have two G_AI graphs in two different G_AI groups to intersect, in which case the two graphs are reconciled into a single G_AI graph (leading to a G_AI graph generation “hierarchy,” rather than a G_AI generation “tree”). If the reconciliation is not possible, then it means that the two G_AI graphs are not consistent, and the metabolic network model characterized by merging the two G_AI graphs is inconsistent. In such a case, this specific merger of the two G_AI graphs is stopped, the inconsistency is noted, and the expansion of the G_AI generation hierarchy is continued for other possibilities.

To expedite the process of expanding the G_AI graphs, we start by assigning labels to observed metabolites and forming single-node G_AI graphs. Initially, each observed metabolite in a biofluid results in a single G_AI-group with a single G_AI graph. We attempt to merge G_AI graphs in different G_AI-groups when they intersect i.e. when two G_AI graphs that are in two distinct G_AI-groups have the same border metabolite(s). We illustrate the process with an example (see Ref. 8 for the full Example 11).

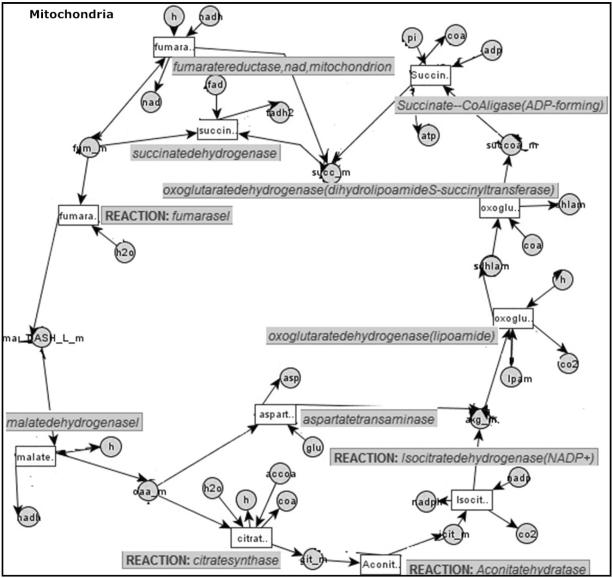
Example 11. Consider the metabolic network M of Fig. 5. Assume C Avialable, akg_mi and C〈Avialable, succoa_m〉 are satisfied from observed measurements, as shown in Fig. 5. Let us say, after multiple expansions, we reach a point where G_AI-Group-1 has G_AI3 with border metabolites {oaa_m, sdhlam_m}; and G_AI-Group-2 has G_AI4 with border metabolites {succ_m, sdhlam_mg, as shown in Fig. 6.

Fig. 6.

The G_AI graphs before merging two G_AI-groups.

Since both groups have the same border metabolites {sdhlam_m}, we merge the two groups of G_AI graphs into one group: Let the newf G_AI graphg to be created by merging G_AI3 and G_AI4 be G_AI6. For each reaction with active or inactive label in G_AI3 and G_AI4, we assign the same label in G_AI6. For border metabolites in G_AI6, we assign each border metabolite a common possible label that both G_AI3 and G_AI4 have as the border metabolite e.g. the label of sdhlam_m becomes Avialable.

3.4. Algorithm sketch

Input to the SMDA algorithm is a set of quantitative metabolite concentration values and a metabolic subnetwork to which the user wants to restrict the analysis. The very first initialization step starts from an observed, possibly a biofluid metabolite, and results in a G_AI graph per observed metabolite, where each such single-node graph is placed in a single G_AI-group. In each expansion step, a G_AI graph is expanded with a producer/consumer reaction set of a “border metabolite” while the validity of reaction label assignments are enforced, as described in Sec. 3.2. Each possible expansion with a different label assignment on the same metabolite pool, or expansions on different metabolite pools, leads to a distinct G_AI graph. Expansion can result in alternative G_AI graphs, all placed into a yet another G_AI-group. This process builds the G_AI generation hierarchy, where nodes are G_AI-groups, and, distinct extensions lead to branching in the hierarchy. At the end, each leaf level node in the hierarchy represents a complete G_AI graph set i.e. one possible activation/inactivation scenario. At any point during the expansion process, if a border metabolite with no valid label assignment is encountered, then the expansion of the G_AI graph is stopped, and it is eliminated as an invalid G_AI graph. The expansion process is performed in a breadth-first manner. In Fig. 7, we present a sketch of the SMDA algorithm. Note that G_AI graphs in different G_AI-groups are AND-alternatives. G_AI graphs in the same G_AI-group are XOR-alternatives.

Fig. 7.

Sketch of the SMDA algorithm.

4. G_AI Graph Expansion Strategies

As explained in detail in Secs. 3.2 and 3.4.2, G_AI graph expansion is the process of generating new G_AI graphs from a given G_AI graph by adding new reactions (with labels), which are attached to the border metabolite pools. The performance of the algorithm is highly dependent on the expansion strategy chosen, as the number of new G_AI graphs generated depends on the strategy used. Intuitively, an expansion strategy that avoids the generation of those G_AI graphs that will be ruled out later will result in better performance and smaller output size. Next we discuss alternative expansion strategies.

Naïve Expansion is the strategy that is presented in Sec. 3.2. The new reactions to be added to new G_AI graphs are selected as those that have a metabolite pool, as a substrate/product/regulator, which is a border metabolite of the G_AI graph being expanded. More formally, given the border metabolite pool set BMP(G_AI, the reactions expanded are NRS(BMP(G_AI)). That is, we expand G_AI graphs with reactions we encounter via border metabolites. This is the most straightforward expansion strategy and generates a more bushy expansion hierarchy as many reactions are covered at a single step.

Selective Expansion #1: Excluding energy metabolites and those with regulatory roles

Energy metabolites such as NAD /NADH and AMP/ADP/ ATP are metabolite pools that play a mostly regulatory energy production/consumption role in many reactions in the metabolic network. Energy metabolite pools are highly connected in the metabolic network and therefore, once one of these metabolite pools is placed in the border metabolite pool set BMP(G_AI), the naïve expansion results in expanding all reactions that energy metabolite pools play a role in. This in general increases the number of alternative G_AI graphs generated, especially in cases where the number of observed metabolite pools is low. The reason is, many reactions in the metabolic network will be expanded and it is very likely that the pools in the set NMP(RS(BMP(G_AI++) will have Unknown labels, thereby forcing the algorithm to generate all possible labeling combinations. To avoid this problem, selective expansion #1 considers only a subset of the border metabolite pools, and excludes from the expansion the set of energy metabolite pools as well as any pool playing a regulatory role in the reaction to be expanded.

Selective Expansion #2: Expansion with partial information

Both Naive and Selective Expansion #1 strategies use the border metabolite pools, and all combinations of the newly encountered pools to assign statuses to reactions. A third approach is to generate all possibilities for the metabolite pools with Unknown status first, as the algorithm needs complete information about metabolite pool labels of all metabolite pools participating in a reaction. However, this might not be the case at all times. There can be a case where the knowledge about the metabolite pool labels of only the border metabolite pools might be sufficant to assign a status to a reaction. As an example, by biochemistry rules BC7 and BC8, the availability/ unavailability of a pool can lead to activation or inactivation of a reaction regardless of the pool statuses of the rest of the metabolite pools.

Considering the above issues leads to the generation of fewer number of G_AI graphs during expansion. Note that there might be multiple metabolite pool label assignments that create multiple scenarios. Moreover, using those inferred metabolite pool labels can enable us to assign status to a reaction, which could not be done using the border metabolite pools only. So it may be the case that, even if we could not assign a status to a reaction with the metabolite pool labels given in the border metabolite pool list, we might be able to do so, given the extra information of assigning a status to another reaction (as illustrated in Ref. 8).

5. Use of SDMA in Cystic Fibrosis Metabolomics Analysis

In this section, we present an example analysis that illustrates the use of SMDA in a real-world setting, involving cystic fibrosis data.²¹ Cystic fibrosis is a lethal disease caused by a mutation on the cystic fibrosis transmembrane receptor (CFTR) gene, which results in lung infection and digestive system disorders. One of the major symptoms is low BMI (body mass index) i.e. unhealthy body weight.²² In order to verify that SMDA produces valid and useful results that can be furthered by manual analysis, we present our approach on experimental data²¹ from a mouse model of cystic fibrosis.

5.1. Data

The mice used in the experiments, referred to as DF508 mice or CF mice, are six weeks old. DF508 mice are homozygous for the F508del mutation on the CFTR gene and are compared against wild-type (WT) control mice. Metabolome data are obtained for each genotype and averaged. The metabolite measurements we use in this test are for the metabolites: D-glucose, palmitate, stearate, palmitoleic acid, oleic acid and triacylglcerol in cytosol of liver and succinate, fumarate, citrate in mitochondrion of liver. Gene expression data reveal that the expression of gene ELOVL, which is responsible for the transcription of the enzyme that elongates palmitate is down by 3-fold and the expression of the gene SCD1 that desaturates palmitate to palmitoleic acid and stearate to oleic acid is down by 22-fold. By carbon labeling, the production of palmitate and stearate from D-glucose is down by twofold as compared against the WT mice.

5.2. Input of the algorithm

Metabolite observation labels

Sometimes, in deciding about the observed metabolite labels, users can use their insight as opposed to using thresholds directly. Following this approach, here we do not classify observations using the thresholds and instead use the statistics that are Avialable in the data to define the metabolite label discretization i.e. Avialable, Accumulated, etc. as follows. We compare the metabolite levels of WT vs. DF508 to decide on the metabolite pool labels for DF508 measurements. For example, if a measurement is decided to be Avialable in WT, and, p-values are significantly high at 0:05(p = 0:05) in DF508 then the DF508 observation is labeled as Accumulated; or if p-values of DF508 measurement are significantly high at (p = 0:01) then the DF508 observation is labeled as Severely Accumulated. The same reasoning applies for being significantly low as well. The DF508 observations mentioned above translate to Avialable for the following metabolites: D-glucose, succi-nate, fumarate, and citrate. And, they translate to Accumulated for metabolites: Palmitate, Stearate, Palmitoleic Acid, Oleic Acid, and Triacylglcerol.

Enzyme availability

Although gene expression data do not have one-to-one correspondence with enzyme levels, due to the significance of the observations, for the reactions mentioned earlier, we input the SCD1 and ELOVL as Unavialable. Rest of the enzymes are marked as Avialable.

Choosing the Metabolic subnetwork to use for SMDA

The metabolic network consists of the following pathways: Abstracted version of glycolysis (single reaction with input D-glucose and output pyruvate), TCA cycle and de novo lipogenesis (DNL). As stand-alone reactions, we input elongation of palmitate, desaturation of palmitate, desaturation of stearate, esterification of palmitate, esterification of stearate, and hydrolysis of acetyl-CoA. As transport reactions we input, pyruvate transport (from cytosol to mitochondrion), citrate transport (from mitochondrion to cytosol), palmitate transport (from blood to cytosol and vice versa), stearate transport (from blood to cytosol and vice versa), oleic acid transport (from blood to cytosol and vice versa), palmitoleic acid transport (from blood to cytosol and vice versa) and triacylglycerol transport (from cytosol to blood).

5.3.Results

The goal of the SMDA analysis is to find alternative activation/inactivation scenarios for the flow of carbon from D-glucose to palmitate and then to the successors of palmitate. We know as the ground truth that the flow from D-glucose to palmitate and then to stearate is negligible (Glycolysis → TCA Cycle → Citrate Transport → DNL). So, given the metabolite and enzyme observations,!we are looking for the cases in our result space where the above-mentioned path is not completely active.

Given (i) the above input, (ii) the assumption that all enzymes are Avialable unless specified otherwise, and (iii) if a pool is not Unavialable then it is being consumed and produced, SMDA returns 144 G_AI graphs. In 96 of them, we observe that the path between D-glucose and palmitate/stearate is Active; therefore, we disregard these conflicting cases. In 48 out of 144 G_AI graph cases, we find that the above-mentioned path is partially Active. That is, although D-glucose is utilized by glycolysis to pyruvate, after getting into the TCA Cycle, the flow does not go into de novo synthesis of fatty acids.

Dwelling upon these cases reveals that there might be two other ways carbon being directed by a pathway other than DNL, which produces palmitate. The first case occurs when citrate is not transported out of mitochondrion, and the TCA cycle is Active either partially or completely. There are 30 such G_AI graph cases. In the second case, citrate is transported out, and DNL starts by converting citrate into acetyl-CoA and oxaloacetate; however, acetyl-CoA is hydrolyzed into acetate, instead of continuing into DNL and producing palmitate. There are 18 such G_AI graph cases.

It has been reported in the literature that CF patients face the “fatty liver” problem.²³ This occurs when the fat synthesized in liver is not transported out to blood and then possibly adipose tissue, but stays there. The literature reports a possible problem with triacylglycerol transport. In the above-mentioned 48 flow-graph cases, we find 24 cases where triacylglycerol transport is inActive, which are ”more likely candidates” for this problem. In these cases, triacylglycerol is being produced, and then hydrolyzed back into fatty acids. In all such 48 G_AI graph cases, we have transport reactions for palmitate, palmitoleic acid, oleic acid, and stearate Active in both ways, which makes sense since we have input their producers as Inactive, and, as the mice have these fatty acids in their diet, those pools enter and exit liver. As an example, we pick the G_AI graph in Fig. 8 as a good candidate to explain the ground truth. This is the snapshot of the result provided by the Java applet through the web-based SMDA tool. In Fig. 8, thick arrows and white rectangles symbolize Active reactions, and gray rectangles with thin arrows symbolize inActive reactions. Dashed lines represent transport reactions. In this case, D-glucose is utilized in the TCA cycle to produce energy, rather than being transported out and converted into fat for storage, which might explain the fact that cystic fibrosis mice have significantly low fat storage. Inactivity of triacylglycerol transport into blood is an extra clue. The ‘availability” of fatty acids in the liver is explained by the diet input and blood exchange.

Fig. 8.

A candidate G_AI graph that explains cystic fibrosis data.

In summary, based on the observations, SMDA was able to capture 48 flow-graph cases that are consistent with the ground truth (i.e. the lack of flux from D-glucose to palmitate). Based on the literature on triacylglycerol transport, we have shrunk our result space down to 24 cases and were able to pick the G_AI graph shown in Fig. 8 as a candidate activation scenario to explain the metabolic activity in the liver of a cystic fibrosis mouse.

6. Computational Performance Evaluation of SMDA

In this section, the computational performance of the SMDA algorithm is empirically evaluated, and different expansion strategies of Sec. 4 are compared with real data.

6.1.Experimental settings

Environment

The experiments are performed on a Dell PowerEdge R710 Server with two Intel^® Xeonr® quad processors and 48 GB main memory, running the Windows Server 2008. The web application server is Microsoft IIS 7. The database server is Microsoft SQL Server 2010. The SMDA web site is implemented with Microsoft ASP.NET; and the client visualization is implemented with Java.

Database

The metabolic network database, constructed from data in the literature and continually expanded, includes mammalian metabolic pathways that are built for PathCase Metabolomics Analysis Workbench, with 22 pathways, 202 metabolites, 375 metabolite pools, and 240 reactions. The thresholds are set up according to the Human Metabolome Database (HMDB).¹²

Observations

Metabolomics observations used in experiments are from cystic fibrosis mice metabolomics profiles, although we took to liberty of using observation subsets in some experiments.

6.2. Experimental results

6.2.1. Relationship between the number of observations and the number of G_AI and flow-graphs

In this experiment, we evaluate the performance of SMDA for different number of user observations. We experiment with three different size subnetworks. For each subnetwork, we change the number of metabolite pool observations and record the number of graphs in the result, as listed in Table 1.

Table 1.

Number of observations versus number of output graphs for small subnetworks.

Subnetwork	# Reactions	# M. Pools	# Observations	#GAI-graphs	#flow-graphs
Pentose Pathway	8	16	1	8,938	846
			2	860	423
			3	588	376
Glycolysis Pathway	14	25	1	152	12
			2	8	8
			3	4	4
Glycolysis + TCA	24	48	2	332,288	160
Cycle pathways			4	166,144	80
			6	128	32

Observation 1

For small subnetworks, a linear increase in the number of observations results in an exponential decrease in the number of G_AI and flow-graphs in the output.

From Table 1, regardless of the size of the subnetwork, the number of G_AI and flow-graphs decreases as we provide more observations as input. Note that, in some cases, increasing the number of observations will not reduce the number of graphs, since there is only one possible label for the input pools in the results. Then the input pool observation is really duplicate information with no reduction on the result size.

In another experiment, for a larger subnetwork, we observe how the algorithm scales. We choose a connected subnetwork with 6 pathways, 48 reactions, and 132 metabolite pools. The number of G_AIand flow-graphs vs. different numbers of observations is shown in Table 2.

Table 2.

Number of observations versus number of graphs for a large network.

# Reactions	# M. Pools	# Observations	# GAI-graphs	# flow-graphs
48	132	17	3,072	40
		23	1,536	20
		31	384	12
		33	192	12
		35	192	12
		37	192	12

From Table 2, we can see that, even in a large subnetwork, we can get reasonably small numbers of G_AIand flow-graphs with increased number of pool observations.

Observation 2

For larger subnetworks, a linear increase in the number of observations results in an exponential decrease in the number of G_AI-graphs and a linear decrease in the number of flow-graphs in the output.

6.2.2. Algorithm time efficiency

The execution time is composed of two parts: expansion time and merge time. For each subnetwork, we execute each of the three expansion strategies. The results show that, in general, increasing the number of observed pool observations decreases the execution time exponentially. This is due to the fact that, with more observed values, expansion time is decreased exponentially by reducing the expansions of many small subnetworks, instead of one large network. However, in some experiments, increasing the number of pool observations has actually increased the execution time, instead of decreasing it. In those cases, we have found that merge time costs are significantly higher than expansion time costs.

Observation 3

A linear increase in the number of metabolite pool observations results in an exponential decrease in the execution time of the algorithm.

Figure 9 shows how the algorithm behaves with “Selective expansion 1” strategy. The results are similar for “Naïve expansion” and “Selective expansion 2” strategies.

Fig. 9.

SMDA time cost for a single network versus the number of observations for Glycolysis and TCA Cycle combined.

6.2.3. Comparing expansion strategies for a large subnetwork

Next we use the connected subnetwork of Table 2 with 6 pathways, 48 reactions, and 132 metabolite pools. Figure 10 shows execution times of different expansion strategies.

Fig. 10.

Expansion strategy times for a subnetwork with six pathways.

Since “Selective Expansion #1” excludes the set of energy metabolite pools during the expansion, it takes less time than other two expansion strategies when the observations are less.

Observation 4

Selective Expansion #1 time costs are invariably much less than the time costs of Nave Expansion and Selective Expansion #2 Strategies.

7. Related Work

Metabolic network analysis techniques are used to study the dynamics of cellular metabolism. They include metabolic control analysis (MCA),²⁴ flux balance analysis (FBA),¹⁸ metabolic flux analysis,²⁵ and metabolic pathway analysis (more specifically, elementary flux mode analysis (EMA)¹⁹ and extreme pathway analysis (EPA)).²⁰ Next we briefly discuss FBA and EMA and briefly compare them with SMDA.

FBA, a widely applied method for the computation of stationary fluxes in large-scale metabolic networks, is based on convex analysis imposing an objective function subject to several constraints, to determine the metabolic flux vector. Critiques of FBA include (i) identification of only one optimal solution, (ii) predicted flux distributions being hypothetical (i.e. depending on the choice of the flux criteria), and (iii) exponential time complexity.

EMA reduces the metabolic network into all possible, unique, non-divisible paths. Each EMA vector specifies a minimal set of enzymes in that if only the enzymes of a given EMA vector is operating, inhibition of any of the enzymes would eliminate the steady-state flux in the system. In comparison, SMDA returns all possible activation/inhibition scenarios, and since the output space is exponential, it then employs exploratory search and browsing.

Comparison of MCA, EMA, and SMDA approaches

Next we briefly list the differences between the MCA (or FBA), EMA, and SMDA approaches: different goals. The four approaches are useful in different contexts, focus on providing different sets of information to users, and have different goals.

1. MCA focuses on “control as a property of the whole system”: One can (i) measure (at quasi-steady state) the effect of single enzyme perturbations on the system, and (ii) calculate the control distribution, relating the system behavior to individual reactions.

2. EMA can be used for tasks such as the recognition of operational modes, determination of all optimal paths, and analysis of network flexibility (structural robustness, redundancy).⁸ Under steady-state conditions, the metabolic fluxes of an organism can be expressed as non-negative, linear, weighted combinations of elementary flux modes¹⁹; however, identifying the weighting factors to determine the fractional contributions of each elementary mode is difficult, if not impossible.^26,27 Visualizations of elementary flux modes within a given KEGG pathway are also Avialable (via YANAsquare).

3. SMDA, working with possibly large metabolic network within a multi-tissue (organ) environment (i.e. not within a cell) and assuming steady-state behavior, returns to users all metabolic action scenarios as well as their visualizations within the metabolic network. Allowing users to quickly concentrate on locating possibly activated paths for a given set of observed metabolite concentration changes. SMDA does not derive (steady-state) flux values of the MCA (FBA) method, and, thus, there are no control-related (i.e. rate limitation) conclusions (of the MCA method).

Different underlying fundamentals

SMDA is rule-based and employs graph traversal and expansion algorithms across the metabolic network. In comparison, MCA and FBA involve solving a set of under-constrained differential equations corresponding to a possibly smaller metabolic network at hand. EMA determines elementary fluxes via a linear combination of “null space basis vectors” of the stoichiometry matrix.²⁸

Ease of use

MCA (or FBA), even with the easiest-to-use GUI-oriented software tools (such as COPASI), requires (i) additional information to be collected and provided by the users including the stoichiometry information, and (ii) setup and usage expertise, for biologists to use them. The EMA tools YANA and YANAsquare do provide user-friendly elementary flux derivations and their visualizations. In comparison, SMDA uses a metabolic pathways database, which already contains the metabolic network, biochemistry-based rules and other information, so that all that a user is to provide is a set of observed metabolite changes and the selected subnetwork.

Modeling-related restrictions/assumptions

As listed earlier, MCA has a number of assumptions (such as requiring a connected network of pathways)²⁹ that are not needed for SMDA. EMA also requires connectivity.

Computational Complexity

Computational complexity of MCA is exponential in the number of reactions involved, forcing users to use various techniques such as compaction, aggregation, and clustering/merging. Computational complexity of EMA is also exponential,³⁰ and various approaches to tackle the high complexity are proposed such as parallel computing,³¹ network decomposition, and “functional conversion of flux cones”. SMDA is also exponential in the number of reactions.

8. Conclusions and Future Work

We have presented a new approach for classifying activation inactivation scenarios, given a set of metabolite observations and a metabolic subnetwork. One future research direction is to incorporate Exploratory Data Mining and Analysis capabilities for the SMDA query output search space.

Biography

Ali Cakmak received his B.Sc. degree in 2003 from the Computer Engineering Department at Bilkent University, Ankara, Turkey, and his Ph.D. degree in 2008 from the Electrical Engineering and Computer Science Department at Case Western Reserve University, Cleveland, Ohio, USA. After completing his Ph.D., he worked as a post-doctoral research associate for a year in the same department. Presently, he works at Oracle USA in Redwood Shores, California. His research interests broadly lie in the fields of bioinformatics, data mining, data management, systems biology, information extraction, query optimization, and digital libraries. His works have been published in prestigious journals and conferences including Bioinformatics, BMC Bioinformatics, BMC Systems Biology, Journal of Bioinformatics and Computational Biology, VLDB Journal, PSB, CSB, ACM BCB, EDBT, and SAC. He has served on the program committees of several conferences, and also as a reviewer for major bioinformatics journals. In 2008, he was nominated by the Case School of Engineering and selected for participation in the American Association for the Advancement of Science Program for Excellence in Science.

Xinjian Qi is a Ph.D. candidate at the Department of Electrical Engineering and Computer Science, Case Western Reserve University, Cleveland, Ohio, USA. He received his Master of Engineering Degree in Communication and Information Systems from the Air Force Engineering University, China, in 1999. Since August 2008, he has been with the Database and Bioinformatics Research Group, Case Western Reserve University, as a research assistant. His research interests include database systems, bioinformatics, systems biology, metabolomics, and biochemical pathways analysis.

A. Ercument Cicek is a Ph.D. candidate in Computer Science at Department of Electrical Engineering and Computer Science, Case Western Reserve University, Cleveland, Ohio, USA. He received his B.Sc and M.Sc degrees in Computer Science and Engineering from Sabanci University, Istanbul, Turkey, in 2007 and 2009, respectively. His research interests include bioinformatics, biological databases, and knowledge discovery.

Ilya Bederman received his Ph.D. in Nutritional Biochemistry from the Department of Nutrition of Case Western Reserve University, Cleveland, Ohio, USA. His postdoctoral work included studying metabolism of adipocytes in mouse models of obesity (Mentor Dr. Previs) and metabolic alterations during muscle atrophy (Dr. Cabrera). Using stable isotopes and mass spec-trometry, he has studied intermediary metabolism in a variety of animal models. He currently works in the Department of Pedi atrics, Case Western Reserve University, as a senior research associate. In collaboration with Dr. Mitchell Drumm, he is studying metabolic alterations in cystic fibrosis, using genetic mouse models of cystic fibrosis.

Leigh Henderson received her B.S. degree in Systems Biology from Case Western Reserve University (CWRU) in 2010. She has been researching the metabolomics of cystic fibrosis since joining the laboratory of Dr. Mitchell Drumm in 2009. She is currently studying genetics as a graduate student at CWRU.

Mitchell Drumm received his Ph.D. in Human Genetics from the University of Michigan in 1990. He joined the faculty in the Departments of Pediatrics and Genetics at Case Western Reserve University as an Assistant Professor in 1992 and is currently Professor of Pediatrics and Genetics at Case Western Reserve University and Vice Chair of Research in the Department of Pediatrics. He is the Director of Basic Research for the Willard Bernbaum Cystic Fibrosis Center at Case Western Reserve University and Rainbow Babies and Children's Hospital in Cleveland, Ohio, USA.

Gultekin Ozsoyoglu is a Professor at the Department of Electrical Engineering and Computer Science, Case Western Reserve University, Cleveland, Ohio, USA. He received his B.S. degree in Electrical Engineering and M.S. degree in Computer Science from the Middle East Technical University, Ankara, Turkey, in 1972 and 1974, respectively, and the Ph.D. degree in Computing Science from the University of Alberta, Edmonton, Alberta, Canada, in 1980. Prof. Ozsoyoglu's current research interests include data bases, bioinformatics, and, recently, web data mining. He has published in all major database and bioinformatics conferences and journals such as ACM Transactions on Database Systems, IEEE Transactions on Knowledge and Data Engineering, IEEE Computer, VLDB Journal, Journal of Computer and System Sciences, Bioinformatics, BMC Bioinformatics, and BMC Systems Biology. He has served in program committees and panels of all major database conferences and many bioinformatics conferences. He was an ACM national lecturer and general or program chair of many conferences and workshops in databases and bioinformatics.