Developing Risk Prediction Models for Kidney Injury and Assessing Incremental Value for Novel Biomarkers

Abstract

The field of nephrology is actively involved in developing biomarkers and improving models for predicting patients’ risks of AKI and CKD and their outcomes. However, some important aspects of evaluating biomarkers and risk models are not widely appreciated, and statistical methods are still evolving. This review describes some of the most important statistical concepts for this area of research and identifies common pitfalls. Particular attention is paid to metrics proposed within the last 5 years for quantifying the incremental predictive value of a new biomarker.

Introduction

There has recently been a surge of interest in biomarkers throughout medicine, including nephrology. Biomarkers for AKI are particularly exciting for their potential to overcome the limitations of serum creatinine and improve risk prediction (1). Risk prediction is most valuable when it enables clinicians to match the appropriate treatment to a patient’s needs or when it allows public health systems to allocate resources effectively. Risk prediction can also be valuable in clinical research settings. For example, a risk prediction model that identifies patients at high risk for an adverse outcome could be used for enrollment in a clinical trial for a preventive therapy.

The broad purpose of this article is to provide guidance for nephrology researchers interested in biomarkers for a binary (dichotomous) outcome, acknowledging that statistical methods in this field continue to evolve. Specific goals are (1) promoting good statistical practice, (2) identifying misconceptions, and (3) describing metrics that quantify the prediction increment. We pay particular attention to recent proposals that rely on the concept of reclassification to evaluate new markers, especially net reclassification improvement (NRI) statistics.

Data Example

We will use clinical and biomarker data from the Translational Research Investigating Biomarker Endpoints in AKI (TRIBE-AKI) study (2) to illustrate the prediction of AKI (a 100% rise in serum creatinine) after cardiac surgery, a common outcome of interest in nephrology. TRIBE-AKI enrolled and followed 1219 adults undergoing cardiac surgery and collected serial urine and plasma specimens in the perioperative period. Biomarkers were measured by personnel blinded to clinical outcomes. For simplicity, we use data from one of the study’s six centers.

Developing a Risk Prediction Model

There are many algorithms for combining predictors into a classifier or risk prediction model. We focus on logistic regression because it is flexible and relatively familiar to clinicians. The logistic model produces a formula for combining predictor variables into a “risk score.” For example, the Society of Thoracic Surgeons (STS) score (3) combines patient data into a risk score for dialysis after cardiac surgery (MI indicates myocardial infarction, and NYHA indicates New York Heart Association):

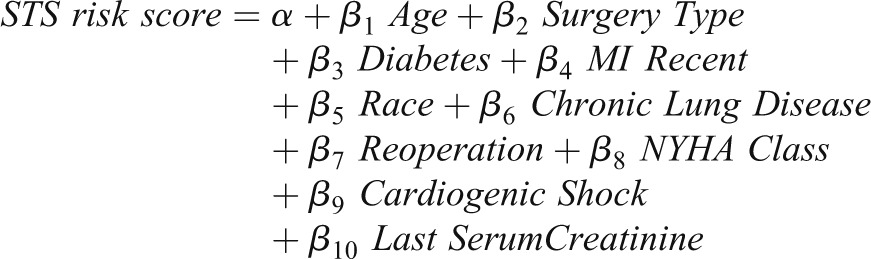Two challenges in developing a risk prediction model are (1) choosing predictors and (2) assessing model performance (discussed below). In classic epidemiologic language, individuals with the outcome are “cases,” and individuals without the outcome are “controls.” Sometimes cases are “events” and controls are “nonevents.” A standardized definition of a case is important. There was no consensus definition of AKI until recently (4,5).

Choosing Predictors: Model Selection

A candidate predictor is any variable that might be used in the risk model. Any variable associated with the outcome is a candidate predictor; the association need not be causal (6). A large literature covers a variety of methods and ad hoc approaches for variable selection. Automated approaches include stepwise methods, but stepwise methods often miss important predictors, especially in small datasets (7), and have other problems (8–10). Ad hoc approaches use prior knowledge of the relationship between variables and outcomes to select predictors. Important considerations in variable selection include the following:

• A candidate predictor should be clearly defined and measureable in a standardized way that can be reproduced in the clinic (6).

• Variables that are challenging to collect in some patients can be problematic (e.g., family history) for future applications of the risk model.

• It is usually disadvantageous to categorize continuous variables (11–14). A U-shaped relationship between a predictor and the outcome may call for sophisticated modeling; categorization is rarely adequate.

• The set of candidate predictors expands when one considers transformations of predictors (e.g., marker M as well as log[M]) and statistical interaction terms (such as M1∙M2).

• Sample size and the number of events limit the number of predictors that should be considered. A rule of thumb is that there should be at least 10 cases for every parameter estimated in the model (15). Even when the development dataset is large, a smaller and simpler model may have practical advantages.

• Categorical variables with more than two categories consume more degrees of freedom than continuous or binary variables. For example, a variable with three categories counts as two variables; a variable with four categories counts as three variables, and so forth.

• The predictiveness of a variable in isolation does not guarantee the variable will improve predictions in a model that includes other variables (6,16).

• The predictiveness of a marker can vary in different settings and will vary for different outcomes. For example, serum troponin levels are accurate predictors of myocardial ischemia in patients with symptoms of chest pain or electrocardiographic changes. However, in broad clinical settings, elevated serum troponin levels are not specific for myocardial ischemia and may instead indicate noncardiac causes (17).

The Importance of Calibration

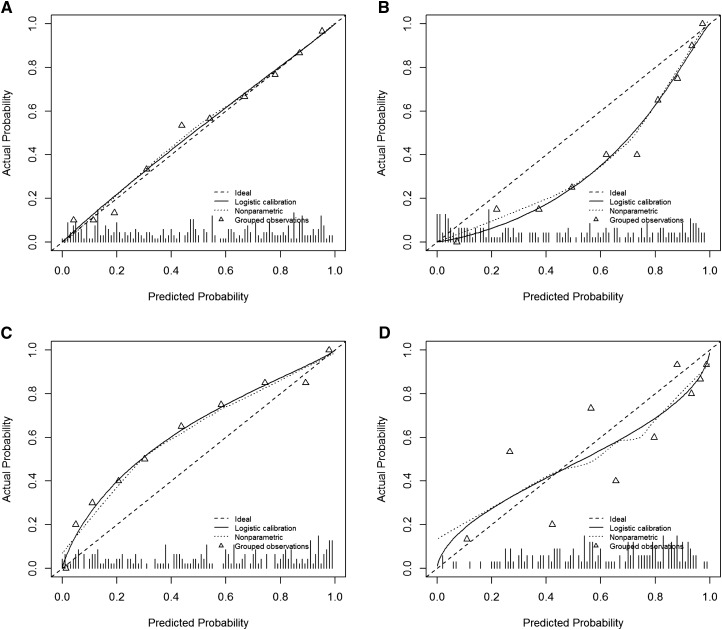
To be valid, a risk prediction model must be well calibrated. Among individuals for whom the model predicts a risk of r%, about r% of such individuals should have the event. Figure 1 shows a well calibrated model and three examples of poor calibration. Good calibration is necessary but not sufficient for good risk prediction. If the prevalence of an outcome is 10%, a perfectly calibrated risk model assigns everyone a 10% risk. The purpose of developing risk-prediction models is to give more refined or “personalized” estimates of individual risks. In many applications, it is most useful when predicted risks are either very low (e.g., <1%) or high (e.g., >20%).

Figure 1.

Calibration plots allow the visual assessment of risk model calibration, a fundamental aspect of model validity. The diagonal line represents the ideal scenario where the actual and predicted probabilities are equal. The triangles are estimates of the actual event rates for groups with similar predicted probabilities. The solid line represents an estimate of the actual event rate for every predicted probability. The hash marks along the horizontal axis show the distribution of predicted probabilities for the dataset. (A) Calibration plot for a well calibrated risk model. Predicted probabilities and observed event rates are nearly identical. (B) Calibration plot for a risk model that tends to overestimate risks. For example, the group of patients with predicted probability of about 0.4 has an event rate<20%. (C) A risk model that tends to underestimate risks. (D) A risk model that is poorly calibrated in a haphazard way, sometimes overestimating risks and sometimes underestimating risks.

Assessing Model Performance

Evaluating the performance of a predictive model is challenging. The practical application of the model is often unknown in the early stages of model development. Another challenge is avoiding optimistic bias in assessing model performance. A model will perform better with the data that developed the model than with new data. Using the development data to assess model performance is sometimes called resubstitution, and we refer to the resulting estimates of model performance as reflecting resubstitution bias. The simplest way to avoid this bias is to evaluate a risk model on independent data. When independent data are not available, one can reserve a subset of a development dataset for evaluating a final model. This is known as “data-splitting” or the “hold-out” strategy. The Supplemental Material describes data-splitting as well as two more sophisticated, computationally intensive methods of avoiding resubstitution bias: cross-validation and bootstrapping.

Measures of Model Performance

A useful tool in biomarker research is the receiver-operating characteristic (ROC) curve. For a continuous marker or a risk score, there are many different thresholds that could be used to delineate patients to be labeled “positive” and “negative.” For every possible threshold, the ROC curve plots the true-positive rate (TPR) against the false-positive rate (FPR). The TPR is also called the sensitivity and the FPR equals 1−the specificity. A useless marker or risk model has an ROC curve on the 45-degree line. The better a marker or risk model can distinguish cases and controls, the higher the ROC curve above the 45-degree line.

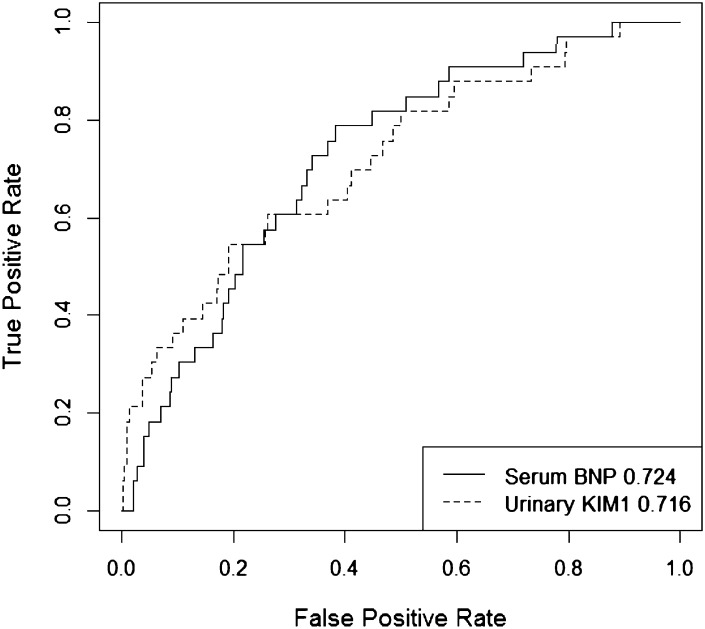
A single-number summary of an ROC curve is the area under the ROC curve (AUC), also called the concordance index. AUC values range from 0.5 (useless marker) to 1 (perfect marker). A single number cannot describe an entire curve, so AUC is necessarily a crude summary. We are often interested in models with small FPRs, and in those instances we care most about the left portion of the ROC curve. Figure 2 shows the ROC curves for two markers. Serum B-type natriuretic peptide has higher AUC than urinary kidney injury molecule-1 (KIM-1), but urinary KIM-1 performs better than serum B-type natriuretic peptide at low FPRs.

Figure 2.

ROC curves show the range of true and false positive rates afforded by a marker or risk model. The figure shows ROC curves for two biomarkers. The numbers in the legend are the AUC values for each marker. Serum BNP has higher AUC than urinary KIM-1, although urinary KIM-1 performs better at low false-positive rates. BNP, B-type natriuretic peptide; KIM-1, kidney injury molecule-1.

Another issue with AUC is its clinical relevance. AUC has the following interpretation: it is the probability that a randomly sampled case has a larger marker value (or risk score) than a randomly sampled control. This interpretation shows why AUC is a measure of model discrimination: how well a model distinguishes cases and controls. However, cases and controls do not present to clinicians in random pairs, so AUC does not directly measure the clinical benefit of using a risk model or marker.

Two other important concepts are positive predictive value and negative predictive value. Positive predictive value is the probability that someone who “tests positive” is actually a case. Negative predictive value is the probability that someone who “tests negative” is actually a control.

All of the measures mentioned above are important, but they do not directly address the practical utility of a risk model. In nephrology, the anticipated use of risk models in the near term is for planning clinical trials. Suppose a trial is planned to evaluate a treatment to prevent AKI following cardiac surgery. Assuming a 5% event rate, a study designed to have 90% power for a treatment that reduces the risk of AKI by 30% must randomly assign 7598 patients (assuming α=0.05). Such a trial would likely be prohibitively expensive. However, suppose a risk model can be used with a threshold that defines a screening rule with a 25% FPR and an 80% TPR. Enrolling only “screen-positive” patients increases the expected event rate from 5% to 14.4%. The sample size required for 90% power is 2418 (holding α=0.05). The tradeoff is that many patients must be screened to identify those eligible for the trial. In our example, we expect to screen 3.6 patients to identify one eligible for the trial.

The Prediction Increment

When a new biomarker is considered, there are often established predictors of the outcome. Occasionally, a new marker is so predictive it can supplant established predictors. However, most candidate markers are modestly predictive, so the central question is whether they can improve prediction beyond existing predictors (2,18–22). The improvement in prediction contributed by a marker is called the incremental value or the prediction increment of the marker. The predictiveness of a marker on its own is called the individual predictive strength.

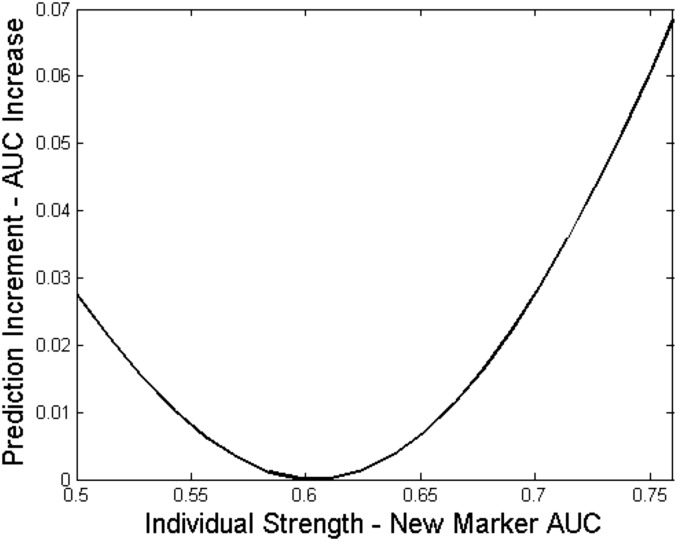
When investigators seek biomarkers with high incremental value, there are two common misconceptions. First, they often assume it is desirable that the new marker has minimal correlation with existing predictors. In reality, a marker that is correlated with existing predictors may improve prediction more than an uncorrelated marker (16). A second misconception leads investigators to screen candidate markers for individual strength, believing that a marker with larger individual strength will have higher incremental value. In fact, a marker’s incremental value is generally not an increasing function of its individual strength (16) (Figure 3).

Figure 3.

The prediction increment of a new marker is not a monotone function of its marginal strength. The baseline risk model is modestly predictive on its own, with area under the receiver-operating characteristic curve (AUC)=0.7. A new marker is added to aid prediction, and it is correlated with the baseline risk. The figure shows that the prediction increment of the new marker can increase or decrease as its individual strength increases. In the figure, the prediction increment is measured by the increase in AUC. However, results are similar for other popular measures of incremental value.

Evaluating the Prediction Increment

There is broad agreement that a new marker should be judged in terms of its incremental value and not its individual predictive strength (23), but there is no consensus on how incremental value should be measured. We review traditional measures and newer proposals. We end by applying all the measures to assess the incremental value of urinary KIM-1.

TPR, FPR, AUC

The previous section describes the TPR and the FPR. For evaluating the prediction increment of a new marker, one can examine how these quantities change with the addition of the new marker (e.g., ΔTPR and ΔFPR). Similarly, for assessing the prediction increment of a new marker Y over established predictors X, a common metric is the change in AUC (ΔAUC). However, the shortcomings of AUC carry over to ΔAUC. The DeLong test should not be used to test the null hypothesis that ΔAUC=0 (24), although this is the method implemented in most statistical software. In fact, P values for ΔAUC are not necessary and should be avoided (see below) (25). These issues have prompted interest in alternative measures of the prediction increment.

Reclassification Percentage

A reclassification table cross-tabulates how patients fall into risk categories under the baseline risk model that uses the established predictors, and the expanded risk model that additionally incorporates the new marker (Table 1). The reclassification rate (RC) (26) is the proportion of patients in the off-diagonal cells of the reclassification table. As a descriptive statistic, a small RC means that the marker will rarely alter treatment. However, a large RC does not imply that the new marker is valuable. The RC does not differentiate between cases reclassified to higher and lower risk categories, the latter representing worse performance of the expanded risk model.

Table 1.

Reclassification table for predicting severe AKI

Baseline Risk Model	Expanded Risk Model: Baseline Model + KIM-1, n (%)
	Cases				Controls
	0%–10%	>10%–≤25%	>25%	Total	0%–10%	>10%–≤25%	>25%	Total
0%–10%	9 (29.0)	0 (0.0)	0 (0.0)	9 (29.0)	364 (83.1)	15 (3.4)	0 (0.0)	379 (86.5)
>10%–≤25%	0 (0.0)	4 (12.9)	4 (12.9)	8 (25.8)	18 (4.1)	25 (5.7)	5 (1.1)	48 (11.0)
>25%	0 (0.0)	2 (6.5)	12 (38.7)	14 (45.2)	1 (0.2)	1 (0.2)	9 (2.1)	11 (2.5)
Total	9 (29.0)	6 (19.4)	16 (51.6)	31 (100)	383 (87.4)	41 (9.4)	14 (3.2)	438 (100)

Risk thresholds at 10% and 25% define low-, medium-, high-risk categories. Baseline risk model is composed of cardiopulmonary bypass time and postoperative serum creatinine. Expanded risk model is composed of baseline risk markers and urine kidney injury molecule-1 (KIM-1). Performance measures were calculated from reclassification table. The reclassification rate (RC) is the proportion of the population in the off-diagonal cells in the reclassification table. About 19.4% of cases and 9.1% of controls are reclassified. Overall, 9.8% of the sample is reclassified, so RC=9.8%. The three-category event net reclassification improvement (NRI_ev) is calculated using only the data on cases, summing the proportions in the upper diagonal and subtracting the proportions in the lower diagonal: (0+0+4)/31−(0+0+2)/31=0.06, so NRI_ev=0.06. The three-category nonevent net reclassification improvement (NRI_ne) is calculated using only the data on controls, summing the proportions in the lower diagonal and subtracting the proportions in the upper diagonal: (18+1+1)/438–(15+0+5)/438=0, so NRI_ne=0. RC, NRI_e, and NRI_ne depend on the number of risk categories and the specific thresholds used to define those categories. The most important information in the table is in the “Total” row and columns, which show how each risk model distributes cases and controls into risk categories. This information is also in Table 3.

Net Reclassification Indices (Categorical)

In 2008, Pencina and colleagues (27) proposed net reclassification improvement (NRI) statistics to improve upon RC. The NRI is the sum of the “event NRI” (NRI_e) and the “nonevent NRI” (NRI_ne). In most NRI papers, a case is usually an “event” and a control is called a “nonevent.” The event NRI is the proportion of cases that move to a higher risk category minus the proportion who move to a lower risk category. Similarly, the nonevent NRI is the proportion of controls who move to a lower risk category minus the proportion who move to a higher risk category. Using the notation of conditional probabilities:

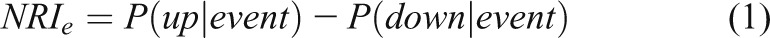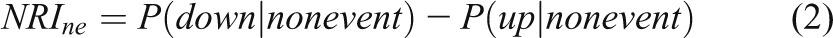Thus, NRI_e (NRI_ne) is the net proportion of events (nonevents) assigned a more appropriate risk category under the new risk model. The word “net” is crucial for correct interpretation. NRI=NRI_e+NRI_ne, but the simple sum of the event and nonevent NRIs leads to an index that is difficult to interpret (28). It is clearer to report NRI_e and NRI_ne separately. Doing so is also more informative, as our example will illustrate.

The categorical NRI can be sensitive to the number of risk categories and the specific thresholds used (29,30). Choosing risk thresholds just to calculate categorical NRIs can be misleading and makes it difficult to compare the performances of models in different publications. For three or more risk categories, NRI statistics are unacceptably simplistic because they simply count reclassification as “up” or “down” (31). When there are two risk categories, this criticism does not apply. However, for two risk categories, NRI statistics are renamed versions of existing measures (31): NRI_e equals change in sensitivity; NRI_ne is equivalent to the change in specificity. The traditional terminology is more descriptive than “event and nonevent two-category NRI statistics.”

NRI (Category-Free)

Examining definitions (1) and (2), “up” can mean any upward movement in predicted risk, and “down” can mean any downward movement. The category-free NRI (NRI^>0) interprets the NRI definitions this way. NRI^>0 is the sum of the category-free event NRI, 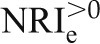, and the category-free nonevent NRI, .

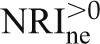While intuitively appealing, NRI^>0 is a coarse summary without clinical relevance. Tiny changes in predicted risks “count” the same as substantial changes that influence treatment decisions.

Hilden and Gerds (32) note that NRI statistics are not based on a proper scoring rule, a mathematical concept that in practical terms means that NRI statistics can make an invalid risk model appear to be better than a valid risk model. Research with real and simulated data have demonstrated this phenomenon (32,33). For example, a useless “noise” variable can tend to yield positive values of NRI, even in independent data (32,33). With NRI statistics, P values offer insufficient protection against false-positive results. In a set of simulated biomarker investigations, NRI P values yielded statistically significant results for useless new biomarkers 63% of the time when P values were computed on the training data and 18%–35% of the time on independent data (34). Collectively, these results indicate that NRI statistics have the potential to mislead investigators into believing a new marker has improved risk prediction when in fact it only adds noise to the risk model.

Integrated Discrimination Improvement

Pencina and colleagues (27) also proposed the integrated discrimination improvement (IDI) index, which is a reformulation of the mean risk difference (MRD). The MRD is the average risk for cases minus the average risk for controls. Roughly, an effective risk model tends to assign higher risks to cases than to controls, so MRD is large. For a measure of the prediction increment, one can consider the improvement in the MRD, denoted ΔMRD, comparing an expanded model to a baseline model. IDI is the same as ΔMRD. “Mean risk difference” is the more descriptive term so we continue with MRD, although IDI is currently more common. MRD is a coarse summary of risk distributions, just as AUC is a crude summary of an ROC curve. Like AUC, MRD is interpretable but not directly clinically relevant. Like NRI, IDI can be viewed as the sum of the event IDI (IDI_e), and nonevent IDI (IDI_ne) (35). The published formula for the SEM of the IDI is incorrect, yielding invalid P values and confidence intervals (36). More research is needed to identify reliable methods for confidence intervals (36,37).

Clinical Utility

Measures such as AUC and MRD summarize model performance without concern for clinical consequences. Suppose predictive model A has much greater specificity but slightly lower sensitivity than predictive model B. If A and B are screening tests for a serious condition for which a false-positive result has minimal consequences, then model B is superior to model A. Yet model A may be favored by some metrics that ignore clinical consequences.

Net benefit (NB) is a measure that incorporates information on clinical consequences, specifically the relative “benefit” of correctly identifying disease and the “cost” of a false-positive result (38).

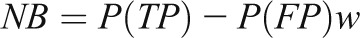where P(TP) is the proportion of the population that is true positive and P(FP) is the proportion that is false positive. The weight w is the benefit of identifying a true-positive result relative to the cost of a false-positive result. For example, if one is willing to accept nine false-positive results to capture a single true-positive, then w=1/9. The weight w is mathematically related to the risk threshold r above which a patient informed of the costs and benefits of treatment prefers treatment to no treatment (w=r/[1−r]). A patient or clinician may be more comfortable specifying r than w, but they are equivalent. A risk model with NB=0.02 has the same NB as a model that identifies 2/100 cases with zero false-positive results.

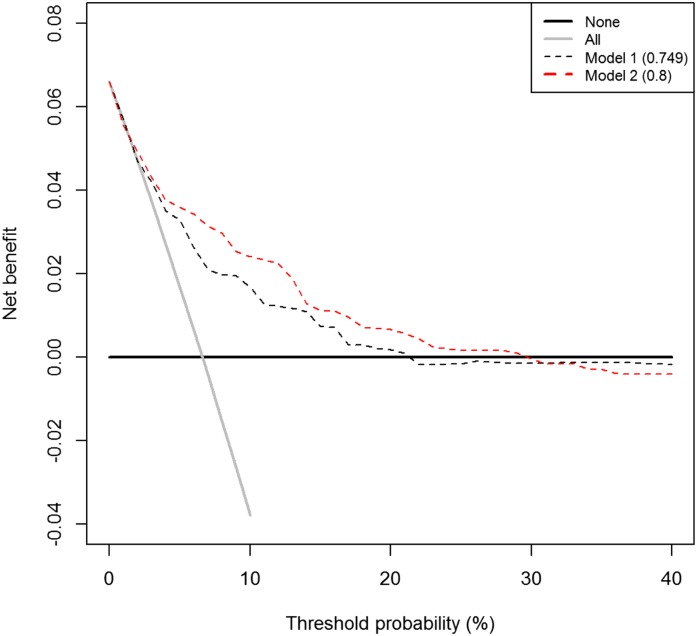
“Decision curves” display NB as a function of the risk threshold r. Decision curves can be useful if there is no consensus on costs/benefits for false- and true-positive results, or if different end users of a risk model weigh the costs and benefits differently. Figure 4 gives an example of a decision curve and its interpretation.

Figure 4.

Decision curves display the relationship between Net Benefit and the risk threshold for treatment. Decision curves apply to situations where a binary decision must be made in light of a patient’s risk for an outcome. For example, on the basis of a patient’s 10-year risk of cardiovascular disease, a clinician must decide whether to prescribe statin treatment. Two default strategies are the “treat all” strategy, represented by the gray line, and the “treat none” strategy, represented by the black line. Decision curves are helpful when investigators have an idea of the appropriate risk threshold for treatment or when different end-users have different thresholds. Decision curves cannot be used to choose a risk threshold. Shown are a decision curve for a model that uses clinical variables to assign risk of the outcome (model 1) and an expanded model that additionally uses a biomarker (model 2). The threshold probability is the minimum risk threshold at which a clinician/patient informed of the costs and benefits of treatment would prefer treatment. Model 2 offers higher net benefit than model 1 for risk thresholds of 5%–30%. Below 3%, models 1 and 2 offer the same net benefit as the “treat all” strategy. Above 30%, the “treat none” strategy offers the highest net benefit. The numbers in the legend are the AUC values for each risk model.

Two-Stage Hypothesis Testing: A Misguided Approach

Researchers sometimes evaluate a new marker in two stages. First, they regress the outcome on the new marker and the established predictors. If the P value for the regression coefficient of the new marker is significant, they perform another statistical test based on a measure of incremental value. For example, they test ΔAUC=0. However, the second statistical test is redundant to the first test, is less powerful, and may not be statistically valid (24). Any hypothesis testing should be limited to the regression coefficient, noting that statistical significance is no guarantee of clinical importance.

Example: The Prediction Increment for Urinary KIM-1

Table 2 gives performance measures for a baseline model and an expanded model adding KIM-1. Whenever possible, we used bootstrapping (Supplemental Material) to correct for resubstitution bias. Table 2 allows readers to consider the information each measure affords. All values are sample estimates of population quantities and appropriately presented with confidence intervals in practice.

Table 2.

Measures of model performance and the prediction increment for kidney injury molecule-1 in the AKI dataset

Measure	Base Model	Expanded Model	KIM-1 Prediction Increment
Cut-point free measures
AUC	0.840a	0.857a	0.017a
MRD	0.215a	0.245a	0.030a,b
IDI			0.037b
IDIe	0.277	0.312	0.035
IDIne	0.051	0.049	0.002
NRI>0	–	–	0.408
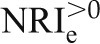
	–	–	0.226
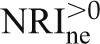
	–	–	0.183
Risk threshold 10%
TPR	0.695a	0.691a	−0.004a,c
FPR	0.136a	0.128a	−0.008a,d
RC	–	–	0.072
NRI	–	–	0.009
NRIe	–	–	0.000c
NRIne	–	–	0.009d
Risk threshold 25%
TPR	0.429a	0.493a	0.064a,c
FPR	0.026a	0.034a	0.008a,d
RC	–	–	0.028
NRI	–	–	0.058
NRIe	–	–	0.065b
NRIne	–	–	−0.007c
Risk thresholds 10% and 25% (delineating low, medium, and high risk)
RC	–	–	0.098
NRI	–	–	0.065
NRIe	–	–	0.065
NRIne	–	–	0.000

Measures of model performance and the prediction increment for kidney injury molecule-1 (KIM-1) in the AKI data set. The base model includes time on cardiopulmonary bypass and serum creatinine, and the expanded model additionally includes urinary KIM-1. For the purposes of illustration, we report all measures discussed in the text, including measures that we do not recommend. AUC, area under the receiver-operating characteristic curve; MRD, mean risk difference; IDI, integrated discrimation improvement; IDI_e, event IDI; IDI_ne, nonevent IDI; NRI^>0, category-free net reclassification improvement; 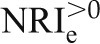, category-free event NRI; 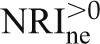, category-free nonevent NRI; TPR, true-positive rate; FPR, false-positive rate; RC, reclassification rate.

^aCorrected for resubstitution bias using a bootstrapping technique (Supplemental Material).

^bΔMRD is the same as IDI. In this example, the numbers are different because the MRD values are corrected for resubstitution bias; there is no corresponding method for IDI statistics.

^cΔTPR is the same as the two-category event NRI. Values in the table differ because ΔTPR is corrected for resubstitution bias; there is no corresponding method for NRI statistics.

^dΔFPR is equivalent to the two-category nonevent NRI. Values in the table differ because ΔFPR is corrected for resubstitution bias; there is no corresponding method for NRI statistics.

Controls are most of the sample, and the nonevent two-category NRI is negative (−0.007) for the 25% risk threshold. The two-category NRI of 0.058 hides this, which is one reason why the overall NRI can mislead.

For purposes of illustration, suppose 10% and 25% are established thresholds delineating low-, medium-, and high-risk categories for AKI. The statistics at the bottom of Table 2 do not help us understand whether KIM-1 aids risk prediction. We prefer Table 3, which shows how each risk model distributes cases and controls into the risk categories. For cases, the expanded risk model performs better, shifting cases to higher-risk categories. However, the expanded model also places more controls in the high-risk category, so the expanded risk model performs worse for controls.

Table 3.

Distribution of cases and controls into risk categories

Variable	Baseline Risk Model (%)		Expanded Risk Model (%)
	Cases	Controls	Cases	Controls
0%–10%	29.0	86.5	29.0	87.4
>10%–≤25%	25.8	11.0	19.4	9.4
>25%	45.2	2.5	51.6	3.2

Both risk models place 29% of cases into the low-risk category, but the expanded risk model places more cases into the highest-risk category. This suggests that the expanded risk model does a better job at identifying cases as high risk. However, the expanded risk model also places more controls into the highest-risk category. Because the controls are most of the population, this could be a serious drawback for the expanded risk model. Note that this table extracts the information from the “Total” row and columns of Table 1.

Summary

Statisticians, epidemiologists, and clinicians currently struggle to reach consensus on best practices for developing risk prediction models and assessing new markers. Table 4 summarizes most of the guidelines discussed in this paper.

Table 4.

Guidelines for evaluation a risk prediction model and the incremental value of a new biomarker

Guidelines for evaluating a risk prediction model
Assess model calibration.
Avoid resubstitution bias with proper use of data-splitting or more sophisticated methods (Supplemental Material).
An unbiased assessment of a model's performance must account for the model selection procedure.
AUC and MRD are informative but coarse summaries of a risk model's ability to discriminate cases and controls, lacking clinically meaningful interpretations.
If there are established and justified risk thresholds, examine TPR and FPR. NB summarizes TPR and FPR into a single number when the relative benefits and costs of true- and false-positive result are quantified.
If there are no established risk thresholds, examine TPR and FPR for a variety of thresholds, or the ROC curve. In addition, examine the decision curve to examine NB over a range of risk thresholds.
Guidelines for assessing the incremental value of a new biomarker
Good performance of a marker on its own does not always imply high incremental value.
Do not exclude a marker as a candidate predictor because it is correlated with other predictors.
Do not use two-stage hypothesis testing. Limit hypothesis tests to testing regression coefficients.
Focus on the performance of the expanded risk model, comparing it with the performance of the baseline risk model.
Category-free NRI statistics can be misleading.
For ≥3 risk categories, categorical NRI statistics should not be used.
For 2 risk categories, NRI statistics are equivalent to changes in TPR and FPR (i.e., changes in sensitivity and specificity). We recommend retaining the traditional terminology.

AUC, area under the receiver-operating characteristic curve; MRD, mean risk difference; TPR, true-positive rate; FPR, false-positive rate; ROC, receiver-operating characteristic; NB, net benefit; NRI, net reclassification index.

Disclosures

None.