A proprioceptive neuromechanical theory of crawling

Abstract

The locomotion of many soft-bodied animals is driven by the propagation of rhythmic waves of contraction and extension along the body. These waves are classically attributed to globally synchronized periodic patterns in the nervous system embodied in a central pattern generator (CPG). However, in many primitive organisms such as earthworms and insect larvae, the evidence for a CPG is weak, or even non-existent. We propose a neuromechanical model for rhythmically coordinated crawling that obviates the need for a CPG, by locally coupling the local neuro-muscular dynamics in the body to the mechanics of the body as it interacts frictionally with the substrate. We analyse our model using a combination of analytical and numerical methods to determine the parameter regimes where coordinated crawling is possible and compare our results with experimental data. Our theory naturally suggests mechanisms for how these movements might arise in developing organisms and how they are maintained in adults, and also suggests a robust design principle for engineered motility in soft systems.

1. Introduction

Crawling is a common strategy for locomotion in soft-bodied animals, such as worms and larvae, that cannot exploit the mechanical advantage provided by rigid limbs. Instead, the absence of a rigid skeleton and the corresponding capability of large body deformations allow these animals to move in challenging environments. Forward locomotion in these organisms is typically achieved by the propagation of peristaltic waves along the animal body, with alternating contraction and relaxation of muscles, either in a prograde or retrograde fashion.

Understanding how coordination between different segments can be achieved in such simple organisms is an old question that has attracted the attention of researchers for nearly a century [1–5], with coordination attributed to a central pattern generator (CPG). In this scenario, the contribution of sensory feedback is limited at best, and often not invoked at all. While the CPG hypothesis does describe crawling in some species such as lampreys and has been exploited in robotics [6], both old and new experimental facts have highlighted the importance of proprioception, sensory feedback, brain–body coupling and substrate interaction in a number of organisms. For example, in various crawling animals, locomotion persists even if the ventral nerve cord has been cut [7], and sensory feedback seems to play a key role [1,8,9]. Indeed, there is a growing realization of the coupling between brain, body and environment in locomotory systems [10]. Theoretical efforts to understand soft-bodied locomotion can be classified into two main streams: (i) purely neural models for periodic locomotory patterns, and (ii) biomechanical models where the internal dynamics is prescribed and locomotion is achieved by exploiting the resulting reaction forces applied by the substrate. For models belonging to the first family, the focus is on a neural network capable of generating periodic activity patterns that may be able to excite the muscle with the correct timing for locomotion, and the interaction with the substrate plays a minor role (see [11] for an example and [6] for a review). In the second family (biomechanical models), the focus has been on coupling neural excitation on the motion of the body interacting with the substrate (see [12,13] as examples). Few approaches integrate these different perspectives, although important exceptions are the recent studies of worm locomotion in Caenorhabditis elegans [14,15].

Here, we consider the interplay between internal and external dynamics via body–substrate mechanics and sensory feedback in soft-bodied locomotion, with the goal of understanding both the generation and the maintenance of coordinated rhythms. Our approach takes the form of a mathematical model for the neuromechanics of crawling that explicitly couples sensory processes to muscular contraction and body–substrate mechanics, and allows us to understand the relative importance of centralized control and local sensory feedback. We start in §2 with a description of a minimalistic model for crawling locomotion, which is then analysed in §3. The role of noise and diffusive neural coupling is discussed in §4. A comparison between our predictions with experimental measurements is reported in §5, where we also discuss our study in the context of the development and evolution of crawling patterns in organisms, along with some lessons for engineered systems.

2. Mathematical model

Any model of crawling must couple the generation of internal forces responsible for locomotion with the mechanics of the interaction of the body with the substrate, along with feedback via a sensory mechanism that couples the neuronal and mechanical systems of the body through the substrate and proprioceptively.

(a). Body–substrate mechanics

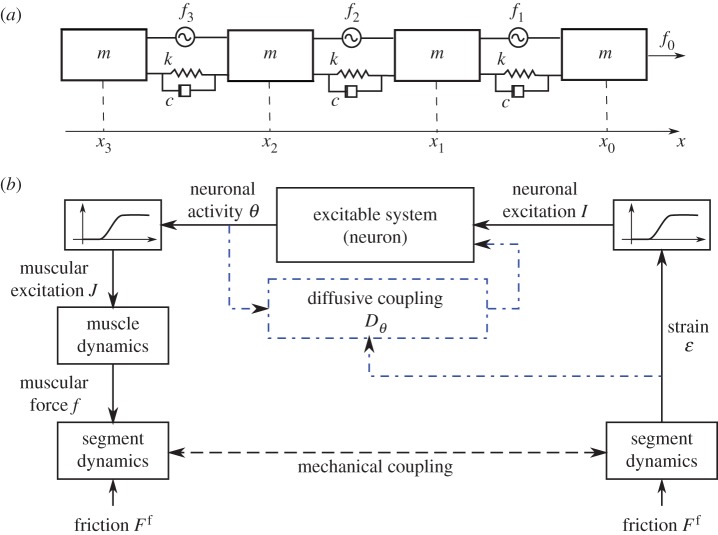
Minimally, the motion of a deformable body interacting with a solid substrate can be described by a linear chain of masses linked by springs with stiffness k and linear damping coefficient c, and actuated by muscles f_i, as shown in figure 1a. We assume that the muscular actuators f_i in the ith segment can apply contractile forces f_i ≥ 0 and that the interaction with the substrate is via asymmetric solid friction 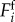, consistent with the fact that most earthworms and larvae have denticles that prevent backward slipping, and they may even actively modulate the friction [12]. Then, the dynamics of the generic ith segment is governed by

2.1

where u_i(t) = x_i(t) − x_i(0) is the displacement and 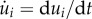. Here, we have neglected the effect of inertia, consistent with observations [12,16]. Within this simplified setting, the activation of the force f_i pulls the ith mass forward, thus inducing an elongation of the following segment that can in turn be sensed by a stretch receptor to trigger the activation of the (i + 1)th muscle. Once properly tuned, such a local feedback loop causes the propagation of a retrograde travelling wave of muscular activity that translates into forward motion of the body (see the electronic supplementary material for details).

Figure 1.

(a) Schematic of a mechanical model for crawling. (b) Local feedback loop responsible for coordination. The body is represented as a chain of masses linked by linear springs with stiffness k and damping c. The muscles are represented by the actuators f and the interaction with the substrate by asymmetric solid friction F^f. The corresponding equation of motion is given by equation (2.2). The feedback loop represented here shows that the motor neuron θ gets activated when the strain ∂_xu reaches a given threshold 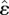and the muscle f contracts when the neuronal activity θ crosses a threshold (see equations (2.4) and (2.5)). The dash-dotted blocks indicate the potential presence of neural coupling (see equation (4.1)). (Online version in colour.)

Despite the conceptual simplicity of such discrete models and their potential for describing the locomotion of maggots, leeches and similar animals [12], the presence of solid friction and external viscosity in equation (2.1) makes a continuum description more suitable when the number of segments is large and several of them may move simultaneously. Then the dynamical equation (2.1) reads

2.2

where ∂_x(·) = ∂(·)/∂x, ∂_t = ∂(·)/∂t, A_c and A_m are, respectively, the body and the muscle cross-sectional area, u(x,t) is the displacement of a cross-section, E the body Young's modulus, μ the body viscosity, f(x, t) the internal stress induced by the muscles and

2.3

the friction force per unit length, where forward motion is resisted by a force F and backward motion by n_fF (n_f > 1).

(b). Proprioceptive neuromechanical interaction

The dynamics of the body must be complemented with a muscular programme to induce forward propulsion, via one of two basic circuit strategies: (i) a global CPG for muscle activation with the correct timing and built-in global synchronization between different CPG subunits [6], and (ii) a local feedback mechanism that couples the segment deformation with the muscle activation locally via stretch receptors [7,15]. We start with a discussion of this latter framework, and eventually treat the general case where one or both types of circuit may be at play.

We assume that the deformation of a segment is sensed by stretch receptors that trigger excitable motor neurons, which in turn lead to muscle contraction. This sensory feedback scheme is represented schematically in figure 1b; when the elongation of a segment crosses a given threshold, a motor neuron is activated and its activity leads to muscular contraction of the segment, thus extending the next segment along the body. The presence of substrate friction automatically implies that the effects of muscular contraction are localized. This then leads to propagating retrograde waves; prograde waves can also be easily achieved by active modulation of the friction (through body deformation, as in earthworms) or by changing the form of the feedback, for example by triggering the neuron in the preceding segment once the contraction exceeds a given threshold or by considering extensile forces (generated by more complex combinations of circumferential and longitudinal muscular arrangements) instead of contractile forces.

For the neural system, we assume that excitable neurons are quiescent when the mechanical strain is below a given threshold and fire when triggered, similar to what is seen in swimming organisms [17]. Minimally, this can be described in terms of a simple integrate and fire model [18]

2.4

where the phase 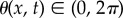is the neuronal activation level, τ_θ is the neuronal relaxation time and we have defined the sigmoidal function Σ as Σ(y; β, γ) = (1 + e^{−β(y−γ)})⁻¹, with β being the sensitivity and γ being the threshold. Then, the second term in equation (2.4) characterizes the sigmoidal response of the stretch receptor with threshold 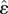, maximum amplitude v_I and sensitivity s_I, and leads to a robust feedback loop because it does not require accurate strain sensors, but only simple strain threshold detectors. We see that when the thresholding function 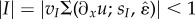, the system has a globally stable equilibrium θ* = sin⁻¹(I), but when |I| > 1 the system has no equilibrium and θ varies dynamically between 0 and 2π. In this approach, neural excitation is purely local and long-range coupling arises only through the body–substrate interaction.

Further, we assume that the generation of the muscular force f follows the minimal first-order dynamical law

2.5

where the second term is the sigmoidal muscular activation with threshold , maximum force F_max and sensitivity s_J induced by the motor neuron, and τ_f is the characteristic muscle relaxation time. The second sigmoid characterizes the periodicity of the phase on the interval .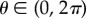

Finally, to trigger excitation, we assume for simplicity that the ∂_xf(0, t) is periodic in order to induce periodic movements of the head. It is important to emphasize that the actual mechanism for producing the first segment excitation is irrelevant for the propagation of muscular activity along the body and any mechanism giving rise to periodic excitation provides the same results as the ones reported in the following sections. For example, similar crawling patterns can be obtained by replacing the periodic head excitation with a bistable system in the head neuron, such as 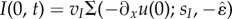, so that a new wave is automatically triggered as soon as the first segment is relaxed. An example of a neural mechanism capable of inducing such periodic excitation is described in [15], where a simple network of excitatory and inhibitory neurons in the head generates a periodic pattern of activity that triggers the muscular wave propagation. In our framework, we limit excitation only to the first segment, at odds with the traditional CPG framework, which assumes that a central nervous system directly controls muscle activity in the whole body, with little or no influence from either body mechanics or the external environment.

To complete the formulation of the model, we also specify the initial conditions u(x, 0) = θ(x, 0) = f(x, 0) = 0 and the boundary conditions ∂_xu(0, t) = ∂_xu(l, t) = 0, consistent with force-free ends.

3. Neuromechanics of proprioceptive crawling

To determine the range of parameters that allow for proprioceptive rhythmic movements and the dynamics associated with the crawling gait, we need to solve the set of equations (2.2), (2.4) and (2.5). Before starting, we scale all times by the viscoelastic relaxation time scale T = μ/E and length scales by the size L of a contraction pulse, obtained from equation (2.2) by balancing the muscular forces with the friction L = (F_max A_m − EA_c)/F.¹ We also normalize the muscle stress and the friction force to rea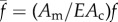d and 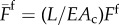. With these choices for the typical length and time scales, we find that the dimensionless maximum muscular force is related to the friction by the equation F_max = F + 1 so that any constraint on F_max also implies a condition on F.

For steady retrograde locomotion, we look for travelling wave solutions of equations (2.2), (2.4) and (2.5) of width ξ_s moving at speed ν, leading to strides of length L_s. Looking for solutions of the form g(x, t) = g(x + νt) for the neuromechanical variables u, θ, f leads to the coupled ordinary differential equations

3.1

3.2

3.3

where the primes indicate differentiation with respect to ξ = x + νt, with boundary conditions u(±∞) = θ(±∞) = f(±∞) = 0 corresponding to the far-field quiescent state. Equations (3.1)–(3.3) can be analytically solved (see the electronic supplementary material for details) and numerically validated by solving the full nonlinear system of partial differential equations (2.2), (2.4) and (2.5) using a finite difference method. In figure 2, we show a retrograde crawling pattern with parameters chosen to mimic earthworm locomotion (refer to [2] and appendix A). The travelling wave velocity v is set by the requirement that a segment stops when the internal stress, which is proportional to ∂_xxu, vanishes (see the electronic supplementary material for details).

Figure 2.

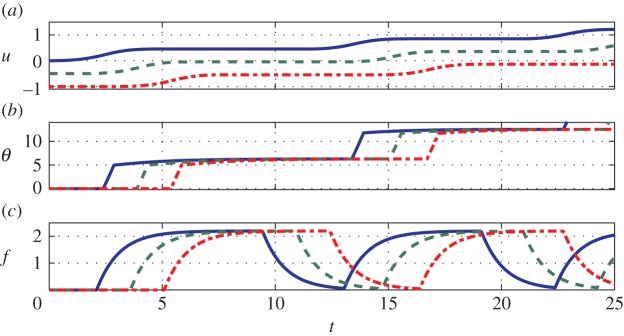
(a) Displacement u, (b) neuronal activity θ and (c) muscular force f obtained by simulating equations (2.2), (2.4) and (2.5) with F = 1.2, n_f = 10, τ_θ = 2, v_I = 21, 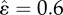, s_I = 10³, τ_f = 1, F_max = 2.2, 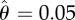and s_J = 10³. We plot only three out of the total number of simulated segments for clarity. See also the electronic supplementary material, movie 2. (Online version in colour.)

Despite the presence of many dimensionless parameters 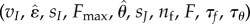, the locomotor performance is significantly affected only by the subset 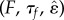(see below), parameters that are easily controllable in common experimental conditions. In fact, the maximum friction force F can be adjusted by changing the substrate (or using cuticular mutants for certain larvae), and sensory feedback that influences both muscular relaxation times and the threshold strain can be regulated genetically [8]. On the other hand, the locomotor pattern is insensitive to the exact values of the neural activation threshold of the sigmoidal sensitivities s_I and s_J. Furthermore, if 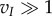and 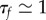, the neuronal parameters τ_θ and v_I are only required to satisfy

3.4

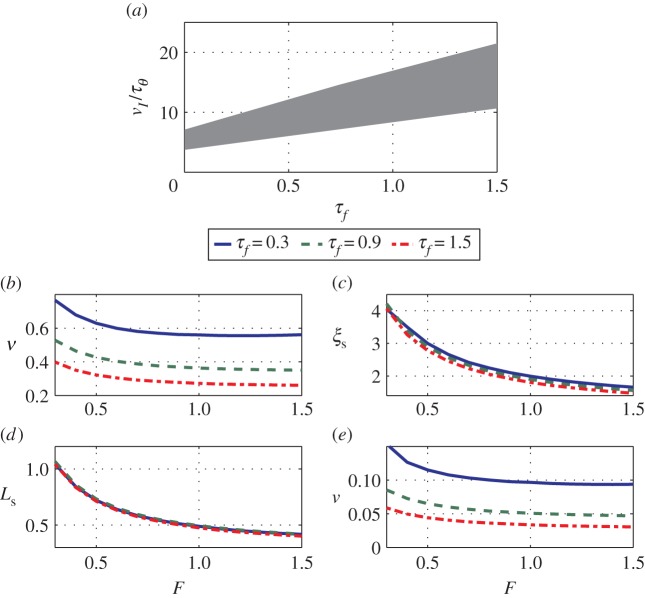
corresponding to the activation 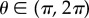when the excitation I = 0, as derived in the electronic supplementary material (equation B21) and shown in figure 3a. Finally, there is a lower bound on τ_θ, and on the solid friction asymmetry coefficient n_f to allow the muscular forces to overcome friction and lead to directional movement (see the electronic supplementary material for details). In figure 3b–e, we show the normalized travelling wave velocity v, pulse width ξ_s, stride length L_s and body centre of mass velocity v as a function of the forward friction F and the muscular relaxation time τ_f. We note that while both the pulse width ξ_s and the stride length L_s depend on the friction force F, they are only weakly dependent on the muscular relaxation time τ_f (see the electronic supplementary material). On the other hand, both the travelling wave velocity v and the body velocity v are monotonically decreasing functions of the relaxation time τ_f, because slower muscular dynamics increases the time required to reach the frictional threshold force, consistent with our detailed analysis (see the electronic supplementary material). Overall, increasing the static friction F (i.e. decreasing the ratio F_max/F) induces a degradation of all of the locomotory performance, as expected.

Figure 3.

(a) The shaded area represents the region in the τ_f – (v_I/τ_θ) plane where coordination is achieved for F = 1.2 (see in equation (3.4)). (b–e) Estimates of (b) (normalized) travelling wave velocity v, (c) pulse width ξ_s, (d) stride length L_s and (e) body centre of mass velocity v for ɛ = 0.6 (typical value for earthworms, as reported in appendix A) and as functions of friction F and muscular relaxation time τ_f. (Online version in colour.)

4. The role of noise and diffusive neural coupling

Compared with a CPG, our proprioceptive neuromechanical model might seem unduly complex. However, this is not true, because much of the difficulty associated with the maintenance of globally synchronized motion is now automatically resolved by coupling the mechanics of the body and substrate with a local neural circuit. Then, coordination during crawling locomotion is based entirely on local neuronal dynamics, muscular contraction and sensory feedback that assigns a crucial role to body–substrate mechanics. This coupled approach naturally leads to locomotor behaviours that are relatively robust to noise in both the internal dynamics and the environment, while suggesting developmental pathways for how coordination arises in biological systems, and design principles for artificial robotic crawling machines.

Our results for the deterministic case treated so far are qualitatively unchanged in the presence of both internal and external sources of noise. For example, additive Gaussian noise on the right-hand side of equations (2.2), (2.4) and (2.5) does not disrupt coordination until the noise amplitude is about 10–20% of the maximum values assumed by, respectively, F^f, I and J (electronic supplementary material, movie 3). Similarly, the addition of neural coupling between segments (i.e. of a term proportional to θ_xx on the right-hand side of equation (2.4)), does not change the qualitative nature of the propagation of waves of muscular contraction along the body (see the electronic supplementary material, movie 4) where equation (2.4) has been replaced with

4.1

with D_θ = 0.01; higher values for D simply correspond to a rescaling of the maximum value of the neural excitation I.

This robustness to the presence of diffusive neural connections might explain some experimental observations associated with the development of rhythmic patterns during the unhatched larval stage in Drosophila melanogaster. Although travelling waves of neural excitation are observed even in the absence of sensory stimulus [19,20], they are easily disrupted, and it is thought that sensory feedback is important to stabilize them. One possible scenario that accounts for this is that larvae start out with diffusive neural connections to trigger the rhythmic pattern during the early stages of development where sensory feedback is very limited or even absent. As development progresses, and a stiff cuticle and an array of stretch receptors are formed, the larva might use this rough template to progressively tune the sensory feedback network to improve the robustness of the rhythmic coordination observed in larvae that have hatched.

5. Discussion

Our proprioceptive neuromechanical framework allows us to explain old and new observations that show that local dynamics coupled with sensory feedback suffice to generate robust rhythmic rectilinear crawling seen in different organisms [7,9], without the need for a globally synchronized CPG. Our model also provides a number of testable predictions for the stride length, stepping time, body velocity and travelling wave speed. For example, using data from experiments on earthworms [2], we find that the available dimensionless parameters are 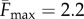, 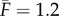and 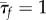(see appendix A). In the absence of available measurements of v_I and τ_θ, we simply ensure that they satisfy the constraints of equation (3.4) for the existence of travelling wave solutions. Then, the solutions of the continuum model (equations (3.1)–(3.3)) yield the predictions 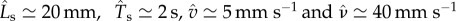in good agreement with measurements on earthworms 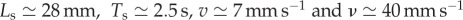[2].

More importantly, all these quantities show the right scaling behaviour with respect to total body mass. In fact, according to the data reported in [2,21], and by assuming that the main source of stress is provided by the internal pressure [21] and that a cylindrical worm deforms under its own weight, the friction force per unit length scales as 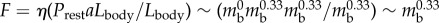, where η is the coefficient of static friction and 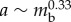is the width of the contact area (see ch. 4 and 5 of [22]). A similar process leads to a scaling relation for the muscular force given by 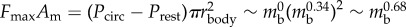. Finally, the intrinsic cuticle and muscle mechanical properties follow the relations 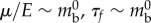. Balancing the muscular force and the friction then leads to the scaling law 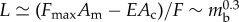. When combined with the reported data [2,21] (see appendix A), this implies that

5.1

that is, the normalized crawling velocity, stride length, stepping time and travelling wave velocity are not affected by the body size, in agreement with the experimental observations [2,21] (see appendix A for details).

A similar scaling argument can be used to predict how body, muscle and neuron properties scale in other organisms, even in the absence of direct measurements for all the quantities involved, suggesting a variety of developmental pathways. For example, the scaling in D. melanogaster is similar to earthworms, whereas in Malus domestica the stride frequency is significantly affected by the body mass and scales as m^0.68, and therefore either the body viscoelastic properties or the muscle properties (or both) should vary during development [23].

Our model thus sharpens biological questions about the relative importance of centralized control and local/distributed sensory feedback for the development and maintenance of coordinated locomotion [19,20]. It also suggests alternative design of bioinspired robotic systems by replacing global coordination and actuation by decentralized modules where most of the control effort is replaced by elementary interactions of the body with the substrate that can trigger switch-like behaviour and thus lead to coordinated locomotion [24].

Appendix A. Comparison with experiments

A comparison of our predictions and experimental data on the locomotory characteristics of earthworms described in [2,21] as a function of body mass m_b is possible using the relevant parameters for our model as reported in table 1, together with typical values that we have used to simulate a 5 g earthworm.

Table 1.

Experimental data about earthworms, as reported in [2,21].

parameter	symbol	value for mb = 5 g	scaling
body mass	mb	5 g	mb
body length	Lbody	176 mm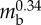
internal pressure at rest	Prest	110 Pa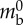
longitudinal contraction pressure	Plong	340 Pa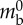
circular contraction pressure	Pcirc	600 Pa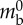
body radius	rbody	4.5 mm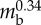
typical strain	ɛtyp	0.6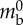
cuticle thickness	tc	50 µm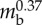
wall Young's modulus	E	10 kPa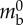
stride length	Ls	28 mm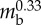
stepping time	Ts	2.5 s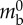
crawling speed	υtyp	7 mm s−1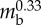
contraction wave velocity	v	40 mm s−1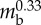

As shown in the main text, all the kinematic quantities show the correct scaling with respect to body mass, and therefore we only need to test whether we are able to correctly predict L_s, υ, ν and T_s for one body size, which we chose to be 5 g, as reported in table 1. The friction per unit length can be estimated as 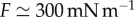by approximating the body with a cylinder that deforms under its own weight, preserving a constant internal pressure, as discussed in the main text. Similarly, an estimate for the muscular force of approximately F_maxA_m = 30 mN is deduced from the difference in internal pressure between contracted and elongated segments, an estimate that is also in agreement with the measurements reported in [25]. Using these estimates, the typical length scale reads 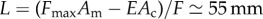, consistent with the observation that in real earthworms about one-third of the body contracts simultaneously. Unfortunately, we do not have direct experimental measurements of the cuticle viscosity μ and of the muscle relaxation time τ_f, although in [26] the step response of a single segment is modelled as a slightly underdamped second-order dynamical system. Approximating this using the overdamped system in our model, we get 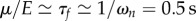, also in agreement with the data reported in [27] and, for larvae, in [28]. By using these estimates in our continuum model (equations (2.2), (2.4) and (2.5), or, equivalently, equations (3.1)–(3.3) in the main text), we obtain the predictions reported in §5.

Funding statement

We thank NSF Robobees project for partial financial support.