Mathematical modeling of the dynamic mechanical behavior of neighboring sarcomeres in actin stress fibers

Abstract

Actin stress fibers (SFs) in live cells consist of series of dynamic individual sarcomeric units. Within a group of consecutive SF sarcomeres, individual sarcomeres can spontaneously shorten or lengthen without changing the overall length of this group, but the underlying mechanism is unclear. We used a computational model to test our hypothesis that this dynamic behavior is inherent to the heterogeneous mechanical properties of the sarcomeres and the cytoplasmic viscosity. Each sarcomere was modeled as a discrete element consisting of an elastic spring, a viscous dashpot and an active contractile unit all connected in parallel, and experiences forces as a result of actin filament elastic stiffness, myosin II contractility, internal viscoelasticity, or cytoplasmic drag. When all four types of forces are considered, the simulated dynamic behavior closely resembles the experimental observations, which include a low-frequency fluctuation in individual sarcomere length and compensatory lengthening and shortening of adjacent sarcomeres. Our results suggest that heterogeneous stiffness and viscoelasticity of actin fibers, heterogeneous myosin II contractility, and the cytoplasmic drag are sufficient to cause spontaneous fluctuations in SF sarcomere length. Our results shed new light to the dynamic behavior of SF and help design experiments to further our understanding of SF dynamics.

INTRODUCTION

Anchorage-dependent cells exist in a state of isometric tension and are constantly subjected to mechanical cues from their environment. External mechanical signals can be sensed through focal adhesions, sites that connect and transmit forces between the actin-myosin cytoskeleton and the extracellular matrix ^1,2. The actin-myosin cytoskeleton is the primary intracellular structure generating cellular contractile force and bearing tension. Cells can also remodel the cytoskeleton in response to mechanical and chemical cues in their surroundings ^3–6. The mechanisms in which actin structures remodel in response to mechanical changes are not fully understood.

Actin stress fibers (SFs) are pre-stressed linear polymers made up of a series of sarcomeric subunits that extend along the axial length of the SF. SF pre-stress originates from myosin-based contractility and the boundary conditions tethering the filaments at one or both ends ^1,2. Similar to muscle sarcomeres, SF sarcomeres are thought to be contractile units and are identified by proteins such as α-actinin and zyxin, which make up their borders akin to the Z-line the muscle sarcomeres ^7–10. Fluorescently labeled α-actinin and zyxin have been used to track sarcomere dynamics in living cells ^11–16 and subsequently have led to better understanding of the dynamic structural changes that occur within SFs. These experiments provide a new opportunity for deeper investigation of SF biomechanics.

Recently we ¹⁷ and others ^15,18 reported fluctuations in SF sarcomere lengths in steady state, resting SFs. In our investigations we used mouse embryonic fibroblasts due to their robust actin cytoskeleton. We found the most changes in length occurred between 1.0 μm shortening and lengthening from the initial sarcomere length ¹⁷. We aim to develop a mathematical model using what is known about the mechanical environment of actin SFs in order to explain the dynamics of SF sarcomeres we observed in the lab. Another goal of this model is to help design experiments needed in the future to more fully define the mechanical determinants behind sarcomere remodeling in actin SFs.

Although actin SFs have many molecular components, we focus on actin and myosin because they are the most abundant proteins in sarcomeres and likely predominate the mechanical properties and behavior of the SF sarcomeres. Nearly 75% of the dry mass of a single sarcomere isolated from Sarcophaga bullata flight muscle is made up of myosin and actin ¹⁹, indicating many of the structural and mechanical changes of sarcomeres may be largely due to those two proteins. Here we use our mathematical model to investigate the role of actin viscoelasticity and contractile forces from myosin as the major players responsible for sarcomere length fluctuations in resting SFs.

The mechanical properties likely vary between adjacent sarcomeres due to molecular heterogeneity that exists along these structures. In terms of actin, many computational models used to describe SF dynamics have assumed that actin stiffness is homogeneous along the length of a SF ^11,20,21. However, there is experimental evidence suggesting SFs have local variations in actin stiffness across the cell ^22,23. The changes in actin stiffness along a single SF may result in stiffness differences amongst neighboring sarcomeres, and therefore regulate the amount of spontaneous lengthening or shortening that occurs. Our model will test the hypothesis that this variability of actin stiffness between individual sarcomeres, which varies over time, may be a major factor driving fluctuations in sarcomere length.

In addition to actin, heterogeneity of myosin-driven contractility may also contribute to the changes in sarcomere length between adjacent SF regions. Myosin II molecules arrange themselves in periodic spacing along the lengths of SFs ¹⁰. Increased myosin contractility has been hypothesized to contribute to shortening of sarcomeres in NIH3T3 mouse fibroblasts ¹⁸, though this hypothesis has not been verified by experimental testing. In laser severing induced SF retraction assays, cells treated with myosin inhibitors (Y27632, ML7, or blebbistatin) failed to retract its actin SFs following laser severing, suggesting that the retraction of pre-stressed SFs requires myosin activity ^1,24. In contrast, SFs within cells treated with calyculin A, which stimulates continual myosin activation, exhibited simultaneous shortening of sarcomeres near focal adhesions and lengthening of sarcomeres in the center regions of the same SFs ¹³. Such regional variation in the sarcomeric response suggests that, in different regions of a single SF, groups of myosin motors may act independently and have different magnitudes of contraction.

Another key factor in the mechanical behavior of SFs suggested by the retraction studies was the presence of cytoplasmic drag forces ^1,25,26. As the SF retracted through the cytoplasm, the sarcomeres near to the severed end shortened faster and by a greater amount than sarcomeres further away. The damping occurring along the length of the retracting SF suggests the presence of an external viscous force. Our model will consider for cytoplasmic drag forces acting on the actin SFs.

In summary, we hypothesized the fluctuations in sarcomere lengths in steady state, resting SFs are driven by the dynamic heterogeneity of stiffness and myosin II contraction along the length of the SF. To test this hypothesis, we designed a mathematical model of an actin SF. The mechanical determinants within our model were actin viscoelasticity, active myosin II contraction, and cytoplasmic drag forces. The model made valid predictions of a retracting SF when simulating a laser severance experiment. When random dynamic fluctuations in stiffness and myosin II contractility were added to generate dynamic heterogeneity, sarcomeres within our model exhibited spontaneous length fluctuations similar to what has been seen in vivo.

MATERIALS AND METHODS

Cell Culture

Mouse embryonic fibroblasts (MEFs) from a zyxin −/− mouse, stably expressing zyxin-green fluorescent protein (GFP), were used for live cell microscopy. MEFs were cultured in Dulbecco’s Modified Eagle Media with 10% fetal bovine serum (Hyclone, Logan, UT), sodium pyruvate, penicillin/streptomycin, and L-glutamine. MEFs were plated on fibronectin-coated glass coverslips (10 μL/mL), and imaged 3–6 days after they were plated. Additional details of these methods have been previously published ^16,17,27.

Imaging and Data Analysis

MEFs were plated in Delta TPG culture dishes (Bioptechs, Butler, PA) and were imaged in Dulbecco’s Modified Eagle Media/F12 media (Invitrogen, Carlsbad, CA) with 10% fetal bovine serum. Live cell imaging was done using a spinning disk confocal (Andor Technology, Belfast, Northern Ireland) on an inverted TI300 microscope (Nikon, Melville, NY). The imaging time interval was 10 seconds during an imaging period of 10 minutes. A 60x 1.4 NA Plan Apochromat lens (Nikon) was used, along with a DV887 1024 x 1024 or DV885 512 x 512 electron-multiplying charge-coupled device cameras (Andor Technology). A more detailed description can be found in Smith et al ¹⁶.

Sarcomeric Model of a Stress Fiber

A SF was modeled using a one-dimensional series of discrete elements for the calculation of baseline, resting fluctuations in SF length. Each discrete element represented a single sarcomere and consisted of a linear elastic spring, a linear viscous dashpot, and an active contractile unit all connected in parallel (Figure 1A), as used in previous SF active contraction models²⁸. The SF was represented as N_sarc elements arranged end-to-end and had N_nodes nodes (N_nodes = N_sarc + 1). The length of each sarcomere was randomly assigned based on the distribution of lengths reported by Chapin et al 2012 ¹⁷. The dynamic model ran from time t = t₀ to t = t_f with a step size in time of t_d. The values of N_sarc, N_nodes, t₀, t_f and t_d are given in Table 1. For each time step, the displacement of each node was calculated by balancing all forces acting on the node from its left (L) and right (R) neighboring sarcomeres (Figure 1B): elastic force (f_spring), myosin contractile force (f_contract), internal viscous force (f_visc,int), external drag force (f_drag), and external load (f_external). For all nodes numbered i = 1 to i = N_nodes from left to right (positive direction points to the right), the force balance for a node i at time t = n was:

$$f_{\mathit{springR}}^n+f_{\mathit{contractR}}^n+f_{\mathit{visc},\mathit{intR}}^n-f_{\mathit{springL}}^n-f_{\mathit{contractL}}^n-f_{\mathit{visc},\mathit{intL}}^n-f_{\mathit{drag}}^n+f_{\mathit{external}}^n={ma}_i^n$$ (Eqn. 1)

Figure 1. Formulation of the mathematical model.

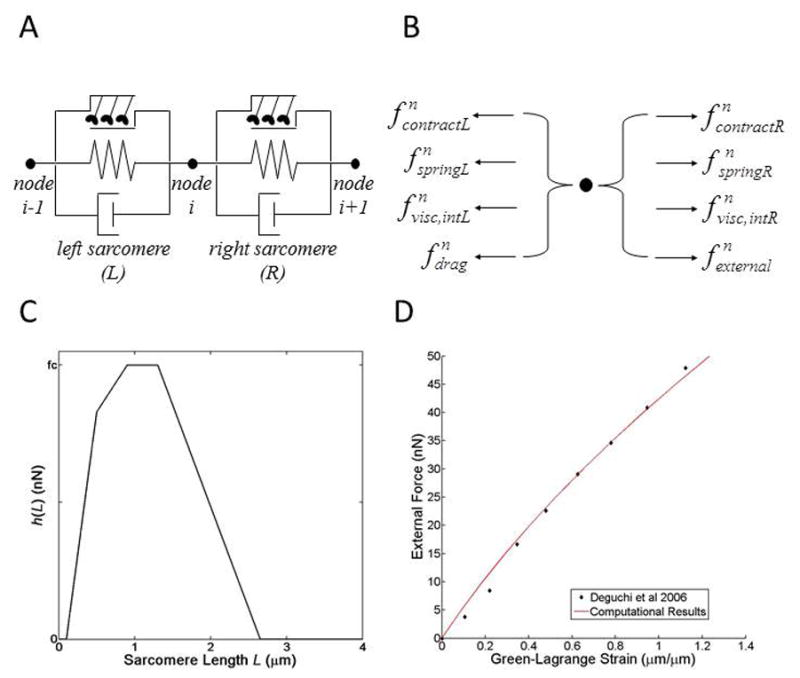
(A) Each stress fiber is depicted as a discrete element consisting of an active contractile unit (top), a linear elastic spring (middle), and a linear viscous dashpot (bottom) connected in parallel. (B) Forces at a node i (shown in panel A) at each time point (t = n). f_spring, = elastic force; f_contract, = contractile force; f_visc,int, = internal viscous force; f_drag, = external drag force; f_external = external load. (C) The simulated sarcomere length-force relationship. h(L) = force function. f_c = maximum f_contract. (D) Applied external force vs. Green-Lagrange strain in the entire stress fiber during uniaxial extension. Simulated data is presented in red, experimental data from Deguchi et al, 2006 ²⁵, is presented in black points.

Table 1.

Parameters used in mathematical model

Parameter*	Description	Value	Notes or Sources
Nsarc	Number of sarcomeres	8	-
Nnodes	Number of nodes	9	Nnodes = Nsarc + 1
Lsarc	Length of sarcomere	1.6 ± 0.063 μm (mean ± standard error)	Randomly generated using a normal distribution [17]
t0	Start time	0 seconds	[17]
tf	End time	600 seconds	[17]
td	Time step	10 seconds	[17]
ksarc	Sarcomere stiffness	33.1 nN/μm	[25]
m	Sarcomere mass	8.25 μg	[19]
γ	Dampening parameter of internal viscoelasticity	0.01 nN-s/μm	Calibration exercise
η	Dampening parameter of cytoplasmic drag	6.5 nN-s/μm	Calibration exercise
fc	Maximal myosin contractile force (i.e., maximal fcontract)	32.7 nN	Calibration exercise
a	Amplitude of fluctuation function, y(t)	0 < a ≤ 1	Randomly generated using a uniform distribution
T	Period of fluctuation function, y(t)	10 ± 10% minutes for myosin. 4 ± 10% minutes for actin.	Randomly generated using a normal distribution
ϕ	Phase shift of fluctuation function, y(t)	− π ≤ ϕ ≤ π	Randomly generated using a uniform distribution

^*: Unless otherwise mentioned in the text, all the parameters remain constant throughout all simulations, with the exception of L_sarc, which is generated from a normal distribution.

In Eqn. 1, the forces acting on node i are grouped on the left, and the inertial term involving the nodal mass (m) and acceleration (a_i) are on the right. L indicates forces acting on the node from the sarcomere to the left, while R indicates forces due to the sarcomere on the right. The mass of a sarcomere was calculated from the mass of dried insect flight muscle ¹⁹ and half the sarcomere mass was projected to each node to determine nodal mass (m).

Any external force applied to the sarcomere was represented with f_external and was considered non-zero only at the far-right node (i.e., i = N_nodes). Biologically, f_external can be thought of as the force applied at a focal adhesion, for example an applied load acting on the interface where a cell attaches to its extracellular matrix environment. f_external can also be thought of as the force applied at the non-focal adhesion end of a SF, for example an applied load by AFM techniques as described in the work of Deguchi et al. ²⁵. Mathematically, this force is only applied to the non-focal adhesion end (i.e., f_external only contributes to the force array at the far right node). Specifically, external force was used to replicate the in vitro uniaxial tensile testing of SFs by Deguchi et al.²⁵ to determine the stiffness parameter of the model. Elastic forces were calculated using Hooke’s Law, and therefore were dependent on the current length of the sarcomere and a linear stiffness (also called spring constant) k such that

$$f_{\mathit{springL}}^n=k_{\mathit{sarcL}}\mathrm{\Delta }{L}_L=k_{\mathit{sarcL}}\left(u_i^n-u_{i-1}^n\right),f_{\mathit{springR}}^n=k_{\mathit{sarcR}}\mathrm{\Delta }{L}_R=k_{\mathit{sarcR}}\left(u_{i+1}^n-u_i^n\right),$$ (Eqn. 2)

where L is the sarcomere length and u_i is the displacement of node i. The stiffness of each sarcomere was set in a way so that the bulk stiffness of the SF, k_B, matched the results from ex vivo tensile testing of SFs dissected from bovine smooth muscle cells ²⁵. Linear regression was performed on force vs. change in SF length data from Deguchi et al to calculate k_B (k_B = 4.14 nN/μm, R² = 0.992). Simulations of uniaxial extension with external loads (f_external) varying from 0 to 50 nN were used to obtain a force-strain plot for our SF model when only considering passive elasticity to compare with ex vivo results from Deguchi et al (Figure 1D).

The dashpot within each discrete element represented the internal viscoelasticity within the molecular structure of the SF sarcomere. The dissipative force from the dashpot component was calculated from the rate of change of length of the sarcomere and a damping parameter γ such that

$$f_{\mathit{visc},\mathit{intL}}^n=\gamma \frac{d}{dt}\mathrm{\Delta }{L}_L=\gamma \left(v_i^n-v_{i-1}^n\right),f_{\mathit{visc},\mathit{intR}}^n=\gamma \frac{d}{dt}\mathrm{\Delta }{L}_R=\gamma \left(v_{i+1}^n-v_i^n\right),$$ (Eqn. 3)

where v_i is the velocity of node i.

We also considered an external viscous force (i.e. drag force) due to drag from the surrounding cytoplasm. The drag force for node i was calculated using the velocity of the node and a damping parameter η such that

$$f_{\mathit{drag}}^n=\eta v_i^n.$$ (Eqn. 4)

Non-muscle myosin II causes active contraction of the sarcomere. The magnitude of active contraction within each sarcomere was calculated using a force function, h(L) such that

$$f_{\mathit{contractL}}^n=h(L_L),f_{\mathit{contractR}}^n=h(L_R),$$ (Eqn. 5)

where the function h(L) depends on the current length of the sarcomere (see “Myosin Contraction Model” below).

A backward difference was used to cast velocity (v) and acceleration (a) into terms involving nodal displacement:

$$v_i^n=\frac{1}{t_d}\left(u_i^n-u_i^{n-1}\right),a_i^n=\frac{1}{t_d}\left(v_i^n-v_i^{n-1}\right)=\frac{1}{{t_d}^2}\left(u_i^n-u_i^{n-1}\right)-\frac{1}{t_d}{v}_i^{n-1}.$$ (Eqn. 6)

After substituting all the force representations (Eqns. 2–5) and numerical derivatives (Eqn. 6) into Eqn. 1, we are left with an equation consisting of nodal displacements at time points n and n−1 as well as various parameters. After arranging all unknowns (nodal displacement at t = n) to the left side of the equation and all knowns (nodal displacement at t = n−1, parameters) to the right side, we obtain the following equation for each node:

$$\begin{array}{l}\left(k_{\mathit{sarcL}}^{\ast }+\frac{1}{t_d}{\gamma }^{\ast }\right)u_{i-1}^n-\left(k_{\mathit{sarcL}}^{\ast }+k_{\mathit{sarcR}}^{\ast }+\frac{2}{t_d}{\gamma }^{\ast }+\frac{1}{t_d}{\eta }^{\ast }+\frac{1}{{t_d}^2}\right)u_i^n+\left(k_{\mathit{sarcR}}^{\ast }+\frac{1}{t_d}{\gamma }^{\ast }\right)u_{i+1}^n=\\ \left(\frac{1}{t_d}{\gamma }^{\ast }\right)u_{i-1}^{n-1}-\left(\frac{2}{t_d}{\gamma }^{\ast }+\frac{1}{t_d}{\eta }^{\ast }+\frac{1}{{t_d}^2}\right)u_i^{n-1}+\left(\frac{1}{t_d}{\gamma }^{\ast }\right)u_{i+1}^{n-1}-\frac{1}{t_d}{v}_i^{n-1}+h^{\ast }(L_L)-h^{\ast }(L_R)-f_{\mathit{external}}^{\ast n}\end{array}$$ (Eqn. 7)

The ()* notation denotes any quantity that has been mass normalized, such that for an arbitrary scalar x,

$$x^{\ast }=\frac{x}{m}.$$ (Eqn. 8)

During each time step, we simultaneously calculate nodal displacement by assembling the force balance equations for each node into a matrix problem,

$$\left[K^n\right]\left\{u^n\right\}=\left\{f^n\right\},$$ (Eqn. 9)

where [Kⁿ] is a square matrix (N_nodes × N_nodes) and contains coefficients from the unknown terms on left-hand side of Eqn. 7, {uⁿ} is a column vector containing the unknown nodal displacements, {u} = {u₁, u₂, u₃, …, u_Nnodes}^T, and {fⁿ} is a N_nodes × 1 column vector containing the known terms found on the right hand side of Eqn. 7. Displacement was constrained at the left end of the SF (u₁ = 0). When constructing the force balance for the far right node (i = N_nodes), all the terms in Eqn. 1 related to the right sarcomere (R) were ignored. In some simulations as specified in the text, an external load f_external was applied to the right end of the SF. In other simulations also as specified in the text, displacement was constrained for the far right node (u_Nnodes = 0).

Solving Eqn. 9 for {uⁿ} by inverting [Kⁿ] gives us nodal displacements and therefore the position of the nodes in the current configuration. We then calculate [Kⁿ⁺¹] and {fⁿ⁺¹} to calculate displacement at the next time point and continue this process until the simulation ends.

Myosin Contraction Model

Non-muscle myosin II drives sarcomeres to contract. This contractile force was represented using an overlap model derived from filament overlap theory describing tension in skeletal muscle fibers ^26,29. For this myosin representation, contractile force depends on the length of the sarcomere as the current length of the sarcomere determines the degree of overlap between interacting myosin and actin filaments. The contraction force function h(L) was a piece-wise function that generated contractile force based on sarcomere length (Figure 1C).

$$f_{\mathit{contract}}^n=h(L^{n-1}).$$ (Eqn. 10)

To simplify formulation of our mathematical model and keep the force function h(L) out of the sparse matrix [K], we made the myosin II contractile force to be dependent on the sarcomere length at the previous time step (t = n−1) as opposed to the current time step (t = n). Error due to this assumption should be negligible as long as the time step t_d stays sufficiently small.

Random Fluctuations in Time

We first investigated whether the fluctuation of sarcomere lengths in resting-state SFs was merely due to the length-force relationship of myosin II and the heterogeneous distribution of sarcomere lengths seen in vivo ¹⁷ However, we observed that sarcomeres within our simulations of resting-state SFs did not exhibit the low-frequency fluctuations as seen in vivo. To add dynamic heterogeneity, we implemented additional time-dependency into certain mechanisms within our math model. These time-dependencies would need to be oscillatory in nature and have a low natural frequency compared to the sampling window in order to replicate the behavior of in vivo sarcomeres. To accomplish this, we created a random fluctuation function, y(t). Fluctuations due to y(t) were designed to be sinusoidal in nature and represent cycles of recruitment/de-recruitment of actin and myosin molecules within each sarcomere. Each sarcomere was assigned a random sinusoidal wave of the form

$$y(t)=asin\left(\frac{2\pi t}{T}+\varphi \right),$$ (Eqn. 11)

where a was the amplitude of the sinusoid and determined the amount of scaling, T was the period of the wave (i.e., the amount of time the wave takes to complete one cycle), and ϕ was the phase shift that determined at which point during its cycle the wave is at when t = 0. The use of a sinusoid function when constructing the random fluctuations ensured that fluctuations were unsteady yet not divergent. For each sarcomere, a, T, and ϕ were assigned random values based on normal distributions.

Each fluctuation function has a randomly generated amplitude, frequency, and phase shift (see Table 1). Each sarcomere was assigned a random sinusoid wave based on Eqn. 11 for actin (y_actin(t)) and myosin (y_myosin(t)). The result was significant heterogeneity amongst the random fluctuations from sarcomere to sarcomere. The actin fluctuation function, y_actin(t), was used to vary the stiffness of the sarcomere, k_sarc, throughout time. The myosin fluctuation function, y_myosin(t), was used to vary the magnitude of myosin contraction, h(L_sarc), over time. To determine if fluctuations in actin and myosin could produce sarcomere length fluctuations, we performed simulations of resting-state SFs with actin fluctuations only, with myosin fluctuations only, and with both actin and myosin fluctuations.

RESULTS

Our research group recently tracked SF sarcomere dynamics over time and quantitatively described how the lengths of neighboring SF sarcomeres fluctuate in a compensatory manner ¹⁷. These results (summarized in Table 1) laid the foundation of formulating a mathematical model presented in this study in order to give us insight of these phenomena and help design future experiments. In addition to these published experimental results ¹⁷, we also performed additional analysis especially for this model. As previously described ¹⁷, SF sarcomere dynamics were tracked using high-resolution fluorescent light microscopy and cells stably expressing zyxin-GFP, a common SF sarcomere border protein. Figure 2 shows scatter plots of all sarcomere length change for each minute of the imaging session. There is no significant difference between any imaging session during the 10-minute imagine period. Additionally, the magnitude of change in sarcomere length is consistent regardless of the starting sarcomere length (data not shown). We have used this and previously published data in our model.

Figure 2. Stress fiber sarcomeres have consistent fluctuations in length.

Solid and outlined gray points indicate the change in sarcomere length compared to the initial sarcomere length, shown for each minute of a 10-minute imaging sequence. The black lines indicate mean and standard error. n = 53 to 58 sarcomeres, per time category.

A mechanical model was constructed and implemented in order to describe the sarcomere length fluctuation data from the experiments ¹⁷. The computational implementation of this model was verified by comparing simulation results to the analytical solution to a single sarcomere formulation of Eqn. 7 with a constant myosin contractile force (data not shown). To calibrate the remaining parameters in our model, we simulated a severed SF and the resulting retraction. Laser severing experiments have been used to understand the mechanical environment of a SF as it retracts through the cytosol ^1,24. Upon severance of the SF, sarcomeres closest to the cut site shorten the most while sarcomeres farthest from the cut site shorten the least (Figure 3A) ¹¹. Our benchmarks were determined from Colombelli et al 2009 ¹¹ who found that SFs retracted an average of 8 μm upon severance. They also found that this shortening was highly nonlinear, and the majority of length change occurred within the first 20 seconds following severance. We optimized the remaining parameters within the model so that results of our severed SF simulation matched with the behavior described by Colombelli et al. 2009 ¹¹. Parameters that varied during the optimization were the myosin contraction magnitude (f_c, see Figure 1C), the internal viscoelasticity damping parameter (γ), and the cytoplasmic drag force damping parameter (η). The values of the parameters determined by the calibration exercise are given in Table 1. Our simulated edge retraction matches the length change and decays with a time constant as reported by Colombelli et al 2009 (Figures 3A–B).

Figure 3. Computational model is validated using experimental results.

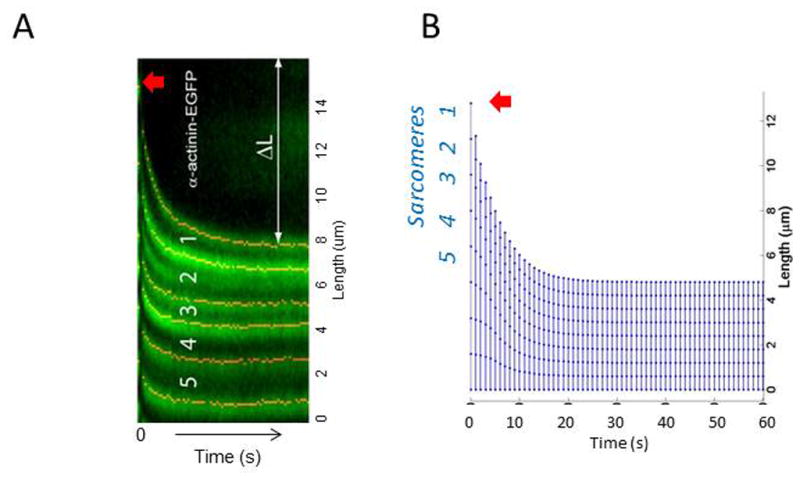
(A) Colombelli et al tracked α-actinin-EGFP in laser cut SFs. Sarcomere 1 is closest to the cut site (red arrow), and 5 is the farthest sarcomere in this particular stress fiber. The change in length of the retracting fiber is shown by ΔL. Image taken from Colombelli et al 2009 Journal of Cell Science (B) Using parameters based on experimental results from our work, and others (e.g., Colombelli et al 2009 in (A)), our simulated results look similar in the way sarcomeres 1–5 retract and shorten.

The parameters in Table 1 were used in the simulations of sarcomeres within resting-state SFs. Parameter values were prescribed by the user, determined from a literature source, or determined during the calibration exercise. Unless otherwise mentioned, all the parameters in Table 1 remained constant throughout all simulations in Figures 4–6 (see below), with the exception of initial sarcomere length which is randomly generated from a normal distribution and varies between each simulation.

Figure 4. Introducing variable actin stiffness.

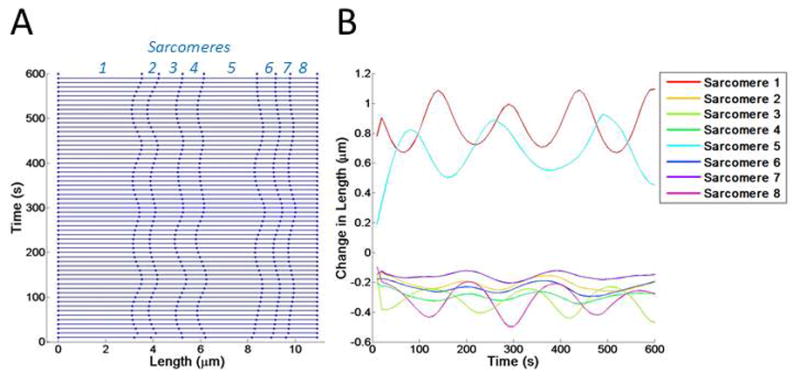
(A) Kymograph showing changes in sarcomere length over time. Sarcomeres 1–8 are indicated. (B) The changes in length of each sarcomere are shown with a colored line, corresponding to the sarcomere number.

Figure 6. Introducing variable actin stiffness and myosin activity.

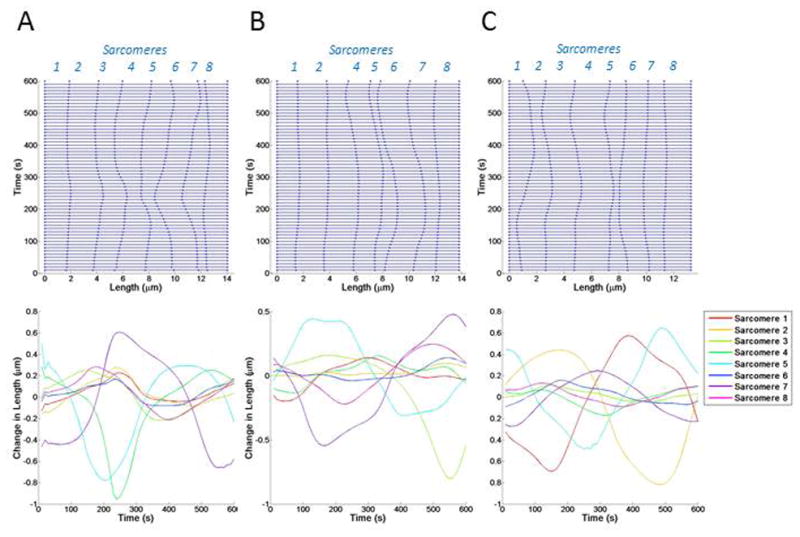
Kymographs showing changes in sarcomere length over time. Sarcomeres 1–8 are indicated in blue italicized font on the right y axis. The changes in length of each sarcomere are shown with colored lines, corresponding to the sarcomere number. Three simulations (A–C) are shown.

Our first simulations considered random fluctuations in sarcomere stiffness only. We implemented heterogeneous stiffness by assigning each sarcomere a random fluctuation function that oscillated the sarcomere stiffness, k_sarc, over time (Figure 4). Assigning each sarcomere a fluctuation function with a randomly generated amplitude, period, and phases resulted in each sarcomere having a different stiffness value at each point in time. In these simulations, each sarcomere’s length simply oscillated around the value determined by the myosin contractile force. Sarcomeres showed periodic lengthening and shortening but did not return to the initial length.

The next round of simulations involved fluctuations in myosin contractility only. In these simulations, actin stiffness was kept uniform and constant while the force applied by myosin varied between sarcomeres and over time. We found that sarcomeres with varying myosin activity produced regular sinusoidal changes in length (Figure 5). The regular sinusoidal nature of these length changes meant that sarcomeres regularly returned to their original length but did not stay at any one length value for long. These results showed no persistence in sarcomere length.

Figure 5. Introducing variable myosin activity.

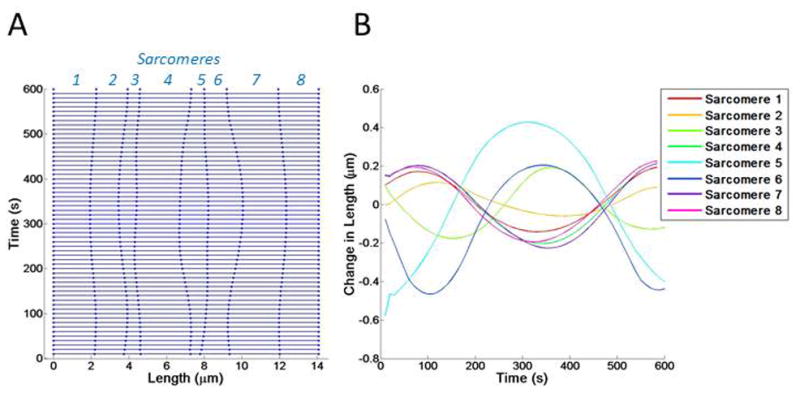
(A) Kymograph showing changes in sarcomere length over time. Sarcomeres 1–8 are indicated in italicized blue font on the right y axis. (B) The changes in length of each sarcomere is shown with a colored line, corresponding to the sarcomere number.

In the last round of simulations, we assigned fluctuations to both actin stiffness and myosin activity (Figure 6). Sarcomeres in these simulations exhibited highly irregular changes in length (up to 1 μm) and persisted at or around this new length before returning to the initial sarcomere length (average of 2.5 minutes). In these simulations, approximately 50% of sarcomeres did not change length by more than 20% over the 10-minute time period. However, 15% of sarcomeres experienced length changes greater than 50% in each simulation. These results suggested that heterogeneous actin stiffness and myosin contractility are sufficient to cause length fluctuations of individual sarcomeres as well as induce large changes in length in neighboring sarcomeres. There is a lag between fluctuations in myosin and sarcomere length, although it is highly irregular and not constant. This lag arises from several factors, the first being viscosity within the system. Dissipation of motion along the stress fiber causes changes in length to lag behind loading. Additionally, the current state of stress and myosin contraction in the neighboring sarcomeres also influences the lag between changes in length and myosin contraction in an individual sarcomere.

Lastly, we performed numerous simulations with different random seeds to predict the length changes in resting-state sarcomeres seen in our past experiments ¹⁷ We collected distributions of length changes and rate of length changes amongst sarcomeres from 7 simulations to compare with data collected from live cells (Figure 7). Each simulation represented a different SF in different cells, similar to the experimental conditions ¹⁷. The distribution of length changes from all the simulations was centered around 0 μm (Figure 7A). Almost all length changes in the distribution were less than 1 μm, and approximately 75% of length changes were less than 0.4 μm. The distribution of rate of length changes was also centered around 0 μm/min, with approximately 90% of the rates less than 0.4 μm/min (Figure 7B). The experimental and simulated data for sarcomere change in length and rate of change in length were very similar by t-test (p = 0.005, though difference between means is biologically insignificant, in Figure 7A; p = 0.63 in Figure 7B).

Figure 7. Statistical comparison between experimental and simulated data.

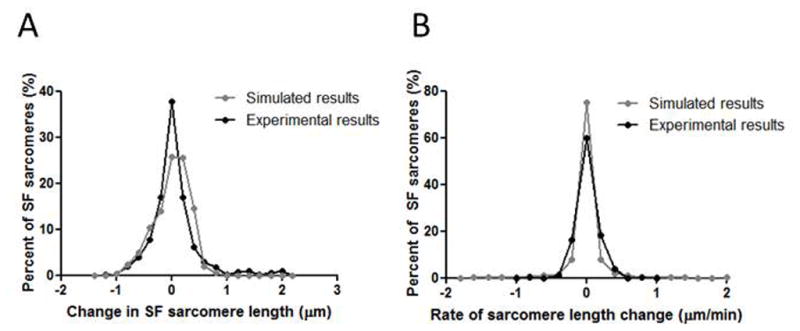
(A) Frequency distribution of changes in sarcomere length in live cells. Black line is experimental data (previously reported in Chapin et al 2012 Biophysical Journal ¹⁷). Gray line is simulated data. (B) Frequency distribution of rates of sarcomere length change in live cells. Black line is experimental data (previously reported in Chapin et al 2012 Biophysical Journal ¹⁷). Gray line is simulated data. The experimental and simulated data were very similar by t-test (p = 0.005 in Figure 7A, p = 0.63 in Figure 7B).

DISCUSSION

In this study, we simulated a biological phenomenon that was discovered by our own experiments and no one has simulated before. Additionally, almost all published stress fiber mathematical models used static mechanical properties, and the present study is the first to consider the role of dynamical mechanical properties in a stress fiber mathematical model. Specifically, in previous experiments we observed changes in SF sarcomere length in quiescent, live cells over time ¹⁷. In this work we present a mathematical model to help shed light into the mechanisms behind this dynamic behavior. Our mathematical model included force contributions from actin stiffness, myosin contraction, internal viscoelasticity, and cytoplasmic drag. There exist cycles of polymerization/de-polymerization or recruitment/de-recruitment of actin and myosin molecules even during resting state ^30–32, and a sinusoidal function is a good mathematical way to add periodicity without instability. We found that by including local fluctuations in actin stiffness and myosin activity between adjacent sarcomeres our mathematical model was able to simulate sarcomeres with “breathing”-like fluctuation behavior that closely resembled our experimental data.

Our findings suggest these factors are sufficient to cause sarcomere length fluctuations. Fluctuating myosin II contractility seems to have the most profound effect, however the best results were obtained when both actin and myosin were allowed to fluctuate. Although the mechanics regulate the behavior of neighboring sarcomeres, we need to consider dynamic changes in the mechanical properties that may result from other processes within the cell such as actin polymerization/de-polymerization and myosin recruitment/de-recruitment. We demonstrated that certain in vivo behaviors of the cytoskeleton could only be simulated when the mechanical determinants of the system were allowed to vary dynamically.

The calibration exercise involving the simulation of a retracting SF (Figure 3) was used to assign values to the myosin contractile force (f_c), the internal viscoelasticity damping parameter (γ), and the cytoplasmic drag damping parameter (η). In the retraction simulation, f_c determined the final retraction distance while γ and η determined the rate of retraction. If γ and η are both set to zero, then the retraction of the SF was purely elastic and the SF instantaneously ‘snapped’ to its retracted state. Increasing the damping parameters caused the retracting end to move slower and increased the decay time of retraction distance vs. time. During this exercise, we found that increasing the cytoplasmic drag damping parameter, η, produced much more realistic results than increasing internal viscoelasticity damping parameter, γ (data not shown). Increasing either parameter resulted in increased motion damping. However in simulations that involved increasing γ only, all sarcomeres within the SF retracted at the same rate. Conversely, increasing η caused sarcomeres near the retraction site to shorten quicker than sarcomeres further away. Many studies involving retraction SFs have seen sarcomeres near the severance site shorten at a higher rate compared to sarcomeres further away, forming a ‘collapsed cap’ ^1,11,33 Our model suggests that cytoplasmic drag force is the main cause of this behavior and plays a significant role in determining the mechanical behavior of SFs. Stachowiak and O’Shaugnessey 2009 made similar observations in that external viscosity due to the cytoplasm was necessary for non-uniform sarcomere shortening and formation of the collapsed cap in SF retraction simulations ³³.

Many mathematical models of actin SFs represent myosin contraction based on A.V. Hill’s model of skeletal muscles ³⁴. The Hill model involves a hyperbolic relationship between contractile force and velocity of isometric sarcomere shortening. Mathematical models of actin SFs using the Hill model have successfully predicted SF retraction in simulations of laser severance ^11,29,35. In this work, we venture away from the classic Hill model and developed our myosin II model based on sliding filament overlap theory. Data suggests a relationship between sarcomere length and contractile force which we adapted for use in our SF model ^28,29. This myosin representation suggests an ‘optimal’ sarcomere length that generates a maximum amount of contraction force (f_c, peak of the curve in Figure 1C). When the sarcomere becomes extended past this length, overlap between actin and myosin decreases and myosin-driven contractility cannot occur as efficiently. Likewise, if sarcomeres shorten past this optimal length, myosin-driven contractility loses effectiveness due to structural hindrance and force decreases. Our SF model was able to accurately simulate a retracting SF using this sliding filament model for myosin II and make predictions similar to other SF models ^11,33. We also were able to extend this formulation to generate realistic fluctuations of sarcomere lengths over time. We found that our model was more sensitive to changes in myosin force f_c and actin stiffness k_sarc than the viscosity parameters (γ and η). Additionally, we found that cytoplasmic drag played a more important role in SF behavior than internal viscoelasticity (i.e., η ≫ γ). Previous SF models using the Hill model for myosin II contraction found that external and internal sources of friction and viscous damping played approximately equal roles. Arguably these differences can simply be attributed to differences in the mathematical formulations between these models. At the very least, our results suggest there may be multiple mathematical formulations that accurately predict actin SF behavior.

We designed our SF model using a force vs. sarcomere length relationship for myosin II as we initially hypothesized that heterogeneity in myosin II contraction along the SF due to non-uniform sarcomere lengths caused the length fluctuations we observed in vivo. However, this formulation of the model was not able to realistically predict these length fluctuations. We were not able to produce realistic length fluctuations until we allowed for both heterogeneity along the SF and dynamic changes in these properties via our random fluctuation functions. Actin polymerization/de-polymerization may contribute to sarcomere length changes, either by producing a ‘pushing’ force that extends or retracts the sarcomere or by changing the stiffness of the sarcomere under myosin contraction. Fluorescently-labeled actin monomers have been shown to incorporate into SFs at sarcomere edges ^36–38, and many proteins involved in actin polymerization localize at sarcomere borders ^16,39, though these factors have not been examined in the context of SF sarcomere length fluctuations. Myosin has been shown to vary between individual sarcomeres in striated muscle fibers ⁴⁰. There have also been reports of different levels of myosin II isoforms and sites of myosin light chain phosphorylation that differ across a SF ^13,41, suggesting levels of myosin-driven contractility may also differ along the length of a single SF. The dynamic changes in molecular motors and the cytoskeleton have been discussed in other publications ⁴² and demonstrate the importance of molecular dynamics when considering SF mechanics. In our model, we represent the molecular dynamics of actin and myosin II using random fluctuations functions. We assume that the fluctuations in actin and myosin activity within SFs are cyclic in our choice of a sine function, but do not claim that the sine functions accurately describes the dynamics and myosin within live cells. Rather, these functions demonstrate that dynamic changes in mechanical properties are necessary to fully describe the mechanical behavior of SFs.

Several improvements could be made to our model in order to further elucidate the mechanism behind sarcomere length fluctuations in live cells. Our model was one-dimensional and assumed uniform properties through the thickness of the SF. Most likely the properties of the SF are heterogeneous throughout the thickness as well as along the length of the fiber, and including this heterogeneity may improve accuracy of our simulations. Additionally, we used a random process to fluctuate the levels of actin and myosin activity within the SFs. However, these processes could be explicitly modeled using molecular dynamics which would provide deterministic mechanisms for changes in actin and myosin over time. This process will be difficult as relationships between molecular concentration of actin and myosin and the mechanical properties of the SF sarcomeres need to be established. Additionally, there may be other molecules that contribute to the mechanical behavior of the SF such as α-actinin ^43,44, zxyin ¹⁶, or titin ^45–47. Our mathematical model set out to represent the overall activity of all these molecules and the consequences for SF mechanics using our fluctuation functions and we made no attempt to explicitly model the contribution of individual molecule types. SF sarcomeres showed greater standard deviation in their length fluctuations when force was applied to the cytoskeleton at the focal adhesion ¹⁸. In the future as the link between SF sarcomere structure and force transmission becomes clearer, our model may be used to describe how forces travel from the extracellular environment into the cell through the cytoskeleton and estimate forces within the cytoskeleton of live cells. Additionally, stress fiber networks in cells are highly branched and interconnected, and these inter-fiber links might manifest themselves as external loads in the model. One way of representing these contributions would be to apply force vectors at interior nodes where the cross-links attach to the stress fiber. However, this would most likely require the model to be re-designed and implemented in 2D or 3D rather than our current 1D formulation. Finally, Colombelli et al. ¹¹ and Burridge et al. ⁴⁸ suggest that myosin activation increases the tension and crosslinking of the stress fiber. It would be interesting to consider the myosin-dependence of stress fiber crosslinking as we introduce more complexity into our model in future studies.

In conclusion, we designed a mathematical model to show that the spontaneous sarcomere length fluctuations in resting, steady-state SFs can be driven by heterogeneous properties between neighboring SFs and dynamic changes in stiffness and contractility over time. Understanding how these factors play a role in SF sarcomere maintenance and repair will lead to a better knowledge of actin SF mechanics in live cells. Hypotheses regarding actin SF dynamics in live cells can be difficult to test experimentally. Computational modeling allows us to test hypotheses despite this lack of experimental options. Such models allow us to test our current understanding of SF dynamics and help us understand the ways in which cells respond to forces in their environment. Additional, our simulations can also help guide future experiments in actin SF mechanics.