Genome-Wide Estimation of Linkage Disequilibrium from Population-Level High-Throughput Sequencing Data

Abstract

Rapidly improving sequencing technologies provide unprecedented opportunities for analyzing genome-wide patterns of polymorphisms. In particular, they have great potential for linkage-disequilibrium analyses on both global and local genetic scales, which will substantially improve our ability to derive evolutionary inferences. However, there are some difficulties with analyzing high-throughput sequencing data, including high error rates associated with base reads and complications from the random sampling of sequenced chromosomes in diploid organisms. To overcome these difficulties, we developed a maximum-likelihood estimator of linkage disequilibrium for use with error-prone sampling data. Computer simulations indicate that the estimator is nearly unbiased with a sampling variance at high coverage asymptotically approaching the value expected when all relevant information is accurately estimated. The estimator does not require phasing of haplotypes and enables the estimation of linkage disequilibrium even when all individual reads cover just single polymorphic sites.

LINKAGE disequilibrium (LD) refers to the nonrandom association of alleles at different loci. Estimating LD and analyzing its pattern are important for several reasons. First, the genealogies of two physically close sites are identical, unless there are recombination events between the sites (Sved 1971; Hudson 1983). Because the amount of LD between sites declines with the number of historical recombination events between them, the former provides insight into the latter, which cannot be observed directly (Hudson 2001; Stumpf and McVean 2003; McVean et al. 2004). Second, studying patterns of LD is important for gene mapping. In association studies, extensive LD facilitates the identification of candidate regions of functional importance (Gabriel et al. 2002; International HapMap Consortium 2003), whereas weaker LD enables finer-scale analyses (Zhu et al. 2000; Tishkoff and Williams 2002). Third, significant improvements in inference of population demographic parameters can be made from analyses of LD patterns. By comparing the LD decay pattern in the same region across different populations, differences in effective population size or recombination rates among populations can be inferred (Frisse et al. 2001; Reich et al. 2001; Conrad et al. 2006). Furthermore, the historical change in effective population size in a population can be inferred by examining the relationship between map distance and degree of LD between sites (Hill 1981; Hayes et al. 2003; Tenesa et al. 2007). Finally, LD is one of the most powerful means for detecting signatures of genetic forces such as gene conversion and natural selection (Hudson et al. 1994; Langley et al. 2000; Frisse et al. 2001; Przeworski and Wall 2001; Sabeti et al. 2002; Eberle et al. 2006; Kim et al. 2007).

Population-level high-throughput sequencing (Mardis 2008; Shendure and Ji 2008) provides unprecedented opportunities for analyzing genome-wide and local patterns of LD. The technologies are rapidly improving (Glenn 2011). In particular, read lengths are becoming longer and are expected to be much longer in the near future, an ideal situation for estimating LD, as longer reads allow increasing possibilities for the direct phasing of double heterozygotes. However, high-throughput sequencing also imposes some disadvantages. The error rates are high, ranging from 0.001 to 0.01 per base read, in commonly used platforms. Furthermore, error rates are known to vary among different runs, even with the same platform. In addition, as the two chromosomes are randomly sequenced in a particular genetic region in diploid organisms, confident inference of the genotypes of individuals with low depths of coverage is difficult.

Several statistical methods have recently been developed for estimating population parameters from high-throughput sequencing data (Hellmann et al. 2008; Johnson and Slatkin 2008, 2009; Jiang et al. 2009; Lynch 2009; Futschik and Schlotterer 2010; Hohenlohe et al. 2010; Kim et al. 2010; Keightley and Halligan 2011). Of these, Johnson and Slatkin (2009) developed a maximum-likelihood (ML) method for estimating recombination rates from high-throughput sequencing data, considering the difficulties explained above. They focused on estimating recombination rates from LD patterns under an assumed evolutionary model. In this study, we propose an ML method for overcoming the difficulties in the estimation of LD itself.

To study genome-wide patterns of LD using high-throughput sequencing data, researchers can attempt to reconstruct phased haplotypes from unphased genotypes and then estimate LD, using software packages such as fastPHASE (Scheet and Stephens 2006), BEAGLE (Browning and Browning 2007), and MaCH (Li et al. 2010). For putative double heterozygotes, these packages infer haplotypes from relative frequencies of putatively unambiguous genotypes, which are themselves called using another software package. Therefore, these software packages do not maximally use the information for LD estimation, in particular on haplotype phase, contained in the sequence-read data (Bansal et al. 2008; Long et al. 2009). Here we present an ML method for estimating LD in population-level analyses directly from the sequence-read data, without any requirements for phasing haplotypes.

To evaluate the performance of the ML method, computer simulations were carried out to generate sequence-read data and the parameters were estimated and compared to the expectations. The effects of read length and depth of coverage on the precision of the LD estimates were also investigated. The results demonstrate that the proposed method improves the potential of the LD analysis with high-throughput sequencing data and also provide guidelines for designing optimal sequencing strategies with a limited research budget.

Methods

Overall procedure for estimating population parameters

Although there are various measures of LD, the basic one is D (Lewontin and Kojima 1960), which measures the deviation of a haplotype frequency from its expected value under the random association of alleles (Hedrick 1987; Slatkin 2008). Other widely used LD measures such as D′ (Lewontin 1964) and r² (Hill and Robertson 1968) can also be calculated when D and the allele frequencies at two polymorphic sites of interest are estimated, although their statistical properties are problematical (Lewontin 1988; Eberle et al. 2006; Song and Song 2007).

The sequence-read data relevant to our analysis are of two types: those covering just single polymorphic sites and those covering both polymorphic sites. For the former, the numbers of the four different nucleotide reads (i.e., A, C, G, and T) in each individual are recorded as a quartet at the observed sites. For the latter, the numbers of the 16 different types of dinucleotide reads (i.e., AA, AC, AG, AT, … , TA, TC, TG, TT) in each individual are recorded.

Our goal is to estimate the allele frequencies at each site, the LD coefficient D between the pair of polymorphic sites, and the error rate per site, by maximizing the likelihood of the observed set of sequence reads in a population sample. The number of alleles segregating at each site is assumed to be at most two, which is empirically known to be true for the majority of single-nucleotide polymorphisms in diploid organisms (Lynch 2007). Random union of gametes (i.e., Hardy–Weinberg equilibrium) is assumed, to infer genotype frequencies from allele frequencies. Because our estimator requires a collection of read data for each individual, each sequence read is assumed to originate from a particular known individual, for example, by tagging reads when sequencing pooled samples. The allele frequencies and error rate at each site are first estimated from the observed set of site-specific sequence reads, using a method analogous to that developed by Lynch (2009). After obtaining this prior information, D is then estimated in a one-dimensional analysis from the entire set of sequence reads (some of which might cover both polymorphic sites of interest). A simple grid search exploring possible values of parameters is used to find the global maximum of the likelihood.

Estimation of allele frequencies at each site

Prior to embarking on a computationally demanding genome-wide survey of LD, it is more efficient to first identify the restricted set of loci at which polymorphisms are likely to exist. In such analyses, the two most abundant nucleotide reads in the population sample are considered to be candidates for alleles at each site. Then, the frequency of the most abundant nucleotide (which is not necessarily the true major allele) and the error rate per site are estimated by maximizing the likelihood of the observed site-specific read data as a function of the allele frequency and the error rate.

In the population sample of site-specific sequence-read data at site α, let A and a denote the first and second most abundant observed nucleotides, respectively. Let us denote the true frequency of the major (the most abundant) allele in the population sample at the site by p and the sequence error rate per site by ε. Denoting the site-specific genotypes AA, Aa, and aa genotypes 1, 2, and 3, respectively, for each individual i, the log-likelihood of the observed set of reads at site α is given by

$$\ln \hspace{0.17em}{L}_i=\ln \left[{\displaystyle \sum _{g=1}^3{\pi }_g{P}_g\left(n_1,n_2,n_3\right)}\right],$$ (1)

where π_g simply denotes the Hardy–Weinberg expected genotype frequencies [π₁ = p², π₂ = 2p(1 − p), π₃ = (1 − p)² at site α], and n₁, n₂, and n₃ are the observed number of reads of candidate nucleotides A (e.g., C), a (e.g., T), and e (other nucleotides, e.g., in this case A and G), respectively. P_g(n₁, n₂, n₃) is the probability of the specific observed set of nucleotide reads given genotype g, which, given a depth of coverage of the individual n = n₁ + n₂ + n₃, is calculated using the formula for the multinomial distribution:

$$P_g\left(n_1,n_2,n_3\right)=\frac{n!}{n_1!n_2!n_3!}{\displaystyle \prod _{j=1}^3{p}_g{\left(j\right)}^{n_j}}.$$ (2)

Here, p_g(j) is a probability of observed nucleotide read j with genotype g. p_g(j) is a function of ε and is given by summing conditional probabilities of observed nucleotide read j given the true nucleotide on the sequenced chromosome chosen from the pair (Table 1). For example, when g = 2 (Aa), the probability of nucleotide read 1 (A) is p₂(1) = (1/2)(1 − ε) + (1/2)(ε/3).

Table 1. Probability p_g(j) of observed nucleotide read j with genotype g as a function of the error rate ε.

	Nucleotide read
Genotype	1 (A)	2 (a)	3 (e)
1 (AA)	1 − ϵ	$\frac{\mathit{ϵ}}{3}$	$\frac{2\mathit{ϵ}}{3}$
2 (Aa)	$\frac{1}{2}\cdot \left(1-\mathit{ϵ}\right)+\frac{1}{2}\cdot \frac{\mathit{ϵ}}{3}$	$\frac{1}{2}\cdot \frac{\mathit{ϵ}}{3}+\frac{1}{2}\cdot \left(1-\mathit{ϵ}\right)$	$\frac{2\mathit{ϵ}}{3}$
3 (aa)	$\frac{\mathit{ϵ}}{3}$	1 − ϵ	$\frac{2\mathit{ϵ}}{3}$

A and a denote candidate alleles (the two most abundant nucleotide reads in the population sample, e.g., C and T) and e denotes other nucleotide reads (e.g., in this case A and G).

The ML estimate of the allele frequency is found by maximizing the log-likelihood of the observed site-specific reads in the entire population sample, which is calculated by summing the log-likelihoods (Equation 1) over N individuals:

$$\ln \hspace{0.17em}L={\displaystyle \sum _{i=1}^N\ln \hspace{0.17em}{L}_i}.$$ (3)

The estimates of the allele frequency and the error rate at the site, $\widehat{p}$ and $\widehat{\mathit{\epsilon }}$, are obtained by maximizing ln L as a function of p and ε. The significance of the polymorphism at the site can be statistically tested by the likelihood-ratio test (Kendall and Stuart 1979). Specifically, the likelihood of the observed data at the site under the hypothesis of polymorphism can be compared to the corresponding likelihood of the data under the hypothesis of monomorphism to examine whether the former is significantly greater than the latter.

Estimation of the linkage disequilibrium coefficient between sites

The linkage disequilibrium coefficient between the sites, D, is estimated only if there is polymorphism at both sites α and β (i.e., $\widehat{p},\widehat{q}$ significantly < 1, where $\widehat{q}$ is the estimate of the major allele frequency at site β). The likelihood of the entire set of sequence reads in the sample as a function of D is maximized to obtain the ML estimate $\widehat{D}$, using the preestimated values of the allele frequencies and error rate in the likelihood function. D is highly dependent on allele frequencies, and its minimum, D_min, and maximum, D_max, given $\widehat{p}$ and $\widehat{q}$, are

$$\begin{array}{c}{D}_{\text{min}}=-\min \left[\widehat{p}\hspace{0.17em}\widehat{q},\left(1-\widehat{p}\right)\left(1-\widehat{q}\right)\right]\\ D_{\text{max}}=\min \left[\widehat{p}\left(1-\widehat{q}\right),\left(1-\widehat{p}\right)\widehat{q}\right]\end{array}$$ (4)

(Lewontin 1988). Thus, the search for $\widehat{D}$ need not exceed these bounds.

In the entire set of sequence reads with respect to the two polymorphic sites of interest, let k, l, and m denote the number of reads covering just site α, just site β, and both sites, respectively. The two-locus genotypes AB/AB (which consist of AB and AB haplotypes), Ab/Ab, aB/aB, ab/ab, AB/Ab, aB/ab, AB/aB, Ab/ab, AB/ab, and Ab/aB are denoted by 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, respectively. Then, the likelihood of the observed set of reads for the individual is calculated with expressions involving the reads covering sites α, β, or both. Analogous to Equation 1, the likelihood for an individual is calculated by multiplying the probability of each particular genotype and that of the observed set of reads given the genotype and then summing the products over all 10 genotypes,

$$\ln \hspace{0.17em}{L}_i=\ln \left[{\displaystyle \sum _{g=1}^{10}{\theta }_g\left\{1-\left(1-P_{g1}\right)I_1\right\}\left\{1-\left(1-P_{g2}\right)I_2\right\}}·\left\{1-\left(1-P_{g3}\right)I_3\right\}\right],$$ (5)

where θ_g now denotes the Hardy–Weinberg expected two-locus genotype frequencies, which are each products (for gametic homozygotes) or twice the products (for gametic heterozygotes) of two of the four gamete frequencies pq + D, p(1 − q) − D, (1 − p)q − D, and (1 − p)(1 − q) + D. P_g1, P_g2, and P_g3 are the probabilities of the observed nucleotide reads covering just site α, just site β, and both sites, respectively. I₁ is an indicator variable equal to one for reads covering just site α and zero otherwise. Thus, {1 − (1 − P_g1)I₁} becomes P_g1 for reads covering just site α and one otherwise. The same applies to sequence reads covering just site β and both sites. As an example, when there is a mixture of reads covering either site α or site β but not both sites, {1 − (1 − P_g1)I₁}{1 − (1 − P_g2)I₂}{1 − (1 − P_g3)I₃} becomes P_g1P_g2.

The probabilities P_g1, P_g2, and P_g3 are calculated as follows. For the observed sequence reads covering just site α,

$$P_{g1}=\frac{k!}{k_1!k_2!k_3!}{\displaystyle \prod _{j=1}^3{p}_g{\left(j\right)}^{k_j}},$$ (6)

where k₁, k₂, and k₃ are the observed numbers of the most abundant, the second most abundant, and other nucleotides given reads covering just site α, respectively, and k is their sum. p_g(j) is a function of ε and is given by summing conditional probabilities of observed nucleotide read j given the true nucleotide on the sequenced chromosome chosen from the pair (Supporting Information, Table S1). Similarly, P_g2 is calculated for the observed sequence reads covering just site β. For the observed sequence reads covering both sites,

$$P_{g3}=\frac{m!}{m_1!m_2!m_3!m_4!m_5!m_6!m_7!m_8!m_9!}{\displaystyle \prod _{j=1}^9{p}_g{\left(j\right)}^{m_j}},$$ (7)

where m₁, m₂, m₃, m₄, m₅, m₆, m₇, m₈, and m₉ are the observed numbers of dinucleotide reads AB, Ab, Ae, aB, ab, ae, eB, eb, and ee, respectively, and m is their sum. p_g(j) is a function of ε and is given by summing conditional probabilities of observed dinucleotide read j given the true nucleotides on a sequenced chromosome chosen from the pair (Table S2). For example, when g = 5 (AB/Ab), the probability of dinucleotide read 1 (AB) is p₅(1) = (1/2)(1 − ε)² + (1/2)(1 − ε)(ε/3). The log-likelihood for the observed sequence reads in the entire population sample, ln L, is calculated by summing the log-likelihoods (Equation 5) over all N individuals, as in Equation 3. The estimate of the LD coefficient, $\widehat{D},$ is obtained by maximizing the likelihood of the observed set of read data as a function of D.

Expectation and sampling variance of the linkage disequilibrium coefficient estimates

When the LD coefficient D is estimated from known genotypes in a sample of N diploid individuals, the expectation of the ML estimate is

$$E\left(\widehat{D}\right)=\frac{2N-1}{2N}D$$ (8)

(Weir 1996), so we need to multiply the ML estimates by (2N)/(2N − 1) to remove bias. When the haplotypes are phased, and coupling and repulsion double heterozygotes can be distinguished, and again assuming no uncertainty in genotypes, the sampling variance of the ML estimate is

$$\mathrm{Var}\left(\widehat{D}\right)=\frac{p\left(1-p\right)q\left(1-q\right)+\left(1-2p\right)\left(1-2q\right)D-D^2}{2N}$$ (9)

(Hill 1974), where p and q are the allele frequencies at the two polymorphic sites of interest. When coupling and repulsion double heterozygotes cannot be distinguished, the sampling variance of the ML estimate is

$$\mathrm{Var}\left(\widehat{D}\right)=\frac{p\left(1-p\right)q\left(1-q\right)}{N-1}+\frac{\left(1-2p\right)\left(1-2q\right)D}{2N}+\frac{D^2}{N\left(N-1\right)}$$ (10)

(Cockerham and Weir 1977; Weir 1979). The mean and sampling variance of the ML estimates using the proposed approach are expected to asymptotically correspond to these values when depths of coverage are high.

In high-throughput sequencing data, depths of coverage vary among sites, individuals, and chromosomes within individuals, and Equations 8–10 need to be modified to account for this additional source of variation. To accomplish this, we express the expectation and sampling variance of the ML estimates as functions of the mean depth of coverage, μ, by considering the “effective” number of sampled chromosomes/individuals with respect to the inferences at two polymorphic sites of interest; these are defined as the numbers of sampled chromosomes and individuals for which there are sequence reads enabling haplotype and two-locus genotype estimation, respectively. Because of the variability of the depth of coverage among individuals and random sampling of sequenced chromosomes, these numbers are smaller than the actual numbers.

Let us assume that the depth of coverage at each site per individual (X) is Poisson distributed such that

$$f\left(X;\mu \right)=\frac{{\left(\mu \right)}^X{e}^{-\mu }}{X!},$$ (11)

where f is the probability mass function of X and μ is the mean coverage. The probability of zero coverage in an individual is e^−μ.

When the read length is much larger than the distance between polymorphic sites of interest and all reads cover both of the sites, LD can be estimated from haplotypes. In this case, the probability that just one of the two chromosomes is sampled from an individual is

$$\mu e^{-\mu }+{\displaystyle \sum _{k=2}^{\mathrm{\infty }}\frac{{\left(\mu \right)}^k{e}^{-\mu }}{k!}{\left(\frac{1}{2}\right)}^{k-1}}=2\left(e^{\mu /2}-1\right)e^{-\mu },$$ (12)

where the first term on the left side of the equation is the probability that there is only one read for the individual. Both chromosomes are sampled at least once with probability $1-e^{-\mu }-2\left(e^{\mu /2}-1\right)e^{-\mu }=1-\left(2e^{\mu /2}-1\right)e^{-\mu }.$ Therefore, the effective number of sampled chromosomes with phased haplotypes is defined as

$$N_{\text{c}}=N\left[2\left(e^{\mu /2}-1\right)e^{-\mu }+2-2\left(2e^{\mu /2}-1\right)e^{-\mu }\right]=2N\left(1-e^{-\left(\mu /2\right)}\right).$$ (13)

Assuming sequence errors are properly accounted for by the ML method, the expectation and sampling variance of the ML estimates can therefore be anticipated by replacing 2N by N_c in Equations 8 and 9 when all reads cover both polymorphic sites.

At the other extreme, when the read length is smaller than the distance between polymorphic sites of interest, all reads cover just single polymorphic sites, and the estimation of LD needs to be made from unphased genotypes. Let ν denote the probability that the total set of read data specific to a polymorphic site is not informative for the inference of the one-locus genotype of an individual, a situation that arises when one or both of the chromosomes are not read at least once. That is,

$$\nu =e^{-\mu }+\mu e^{-\mu }+{\displaystyle \sum _{k=2}^{\mathrm{\infty }}\frac{{\left(\mu \right)}^k{e}^{-\mu }}{k!}{\left(\frac{1}{2}\right)}^{k-1}}=\left(2e^{\frac{\mu }{2}}-1\right)e^{-\mu }.$$ (14)

The site-specific read data are informative for the genotype inference at either of the sites with probability 2ν(1 − ν) and informative for the genotype inferences at both sites with probability (1 − ν)². Therefore, assuming that the information at the two loci is additive with respect to the inferences of two-locus genotypes, the effective number of sampled individuals is

$$N_i=N\left[\frac{1}{2}·2\nu \left(1-\nu \right)+{\left(1-\nu \right)}^2\right]=N\left(1-\nu \right)=N\left[1-\left(2e^{\mu /2}-1\right)e^{-\mu }\right]$$ (15)

and again Equations 8 and 10 can be adjusted by substituting N_i for N.

In many cases, there is a mixture of reads covering just single polymorphic sites and those covering both polymorphic sites. To predict the sampling variance of the ML estimates in such cases, let γ denote the probability that there is at least one read covering both polymorphic sites for an individual. Then, the sampling variance of $\widehat{D}$ as a function of γ is anticipated, using the above results and the conditional variance formula (Ross 2006), as follows:

$$\mathrm{Var}\left(\widehat{D}\right)=E\left[\mathrm{Var}\left(\widehat{D}|\text{haplotype}\hspace{0.17em}\text{phase}\right)\right]+\mathrm{Var}\left(E\left[\widehat{D}|\text{haplotype}\hspace{0.17em}\text{phase}\right]\right)=\gamma ·\frac{p\left(1-p\right)q\left(1-q\right)+\left(1-2p\right)\left(1-2q\right)D-D^2}{N_{\text{c}}}\hspace{0.17em}+\left(1-\gamma \right)·[\frac{p\left(1-p\right)q\left(1-q\right)}{N_i-1}+\frac{\left(1-2p\right)\left(1-2q\right)D}{2N_i}+\frac{D^2}{N_i\left(N_i-1\right)}]+\gamma ·{\left(\frac{N_{\text{c}}-1}{N_{\text{c}}}D\right)}^2+\left(1-\gamma \right)·{\left(\frac{2N_i-1}{2N_i}D\right)}^2-{\left[\gamma ·\frac{N_{\text{c}}-1}{N_{\text{c}}}D+\left(1-\gamma \right)·\frac{2N_i-1}{2N_i}D\right]}^2.$$ (16)

γ is a function of μ and the probability that a read covers both polymorphic sites given it covers one polymorphic site, φ. Letting d and L be the distance between the polymorphic sites of interest (in base pairs) and read length (in base pairs),

$$\begin{array}{c}\phi =\frac{L-d}{L+d},\hspace{1em}\text{when}\hspace{0.17em}d\le L,\\ \hspace{0.17em}=0,\hspace{1em}\hspace{1em}\hspace{1em}\text{when}\hspace{0.17em}d>L.\end{array}$$ (17)

Generation of sequence-read data by computer simulation

Stochastic simulations were carried out to generate sequence-read data at two sites of interest in samples of N diploid individuals. Individual genotypes were assigned with probabilities equal to their frequencies under given population parameters, p (major allele frequency at site α), q (major allele frequency at site β), and D (LD coefficient between the sites), assuming random union of gametes. The depth of coverage at each site per individual was assumed to be Poisson distributed with mean μ. Letting φ be the probability that a read covers both sites given it covers one site, the numbers of reads covering just site α, just site β, and both sites were assumed to be Poisson distributed with parameters μ(1 − φ), μ(1 − φ), and μφ, respectively, so that the number of reads at each site was Poisson distributed with parameter μ, satisfying φ. Then, the probability that there is at least one read covering both sites for an individual is γ = 1 − e^−μφ. Errors were randomly introduced at each site on a read of each individual with probability ε, assuming each error from a true nucleotide has equal probability ε/3.

Comparison of the LD estimation performance by the proposed method with that by an imputation-based method

To compare the performance of the LD estimation by the proposed ML method with that by widely used imputation-based methods, we estimated LD using the imputation-based phasing software package BEAGLE from the sequence reads generated by the computer simulations described above and compared the bias and sampling variance of the LD estimates by the two methods. We mapped the sequence reads to a reference sequence generated by a computer simulation, which consists of 10,000 random nucleotides, using Novoalign (www.novocraft.com). Each of the polymorphic sites was flanked by 22 nucleotides on both sides in a sequence read, which are each uniquely found in the reference sequence, so that every sequence read is mapped to the correct location. We called the genotypes of the individuals at two polymorphic sites of interest, using SAMtools (Li et al. 2009). The missing genotypes and haplotype phase of the individuals were imputed by BEAGLE version 4 (Browning and Browning 2013). LD coefficients were calculated from the VCF file of imputed genotype data, using VCFtools (Danecek et al. 2011).

Results

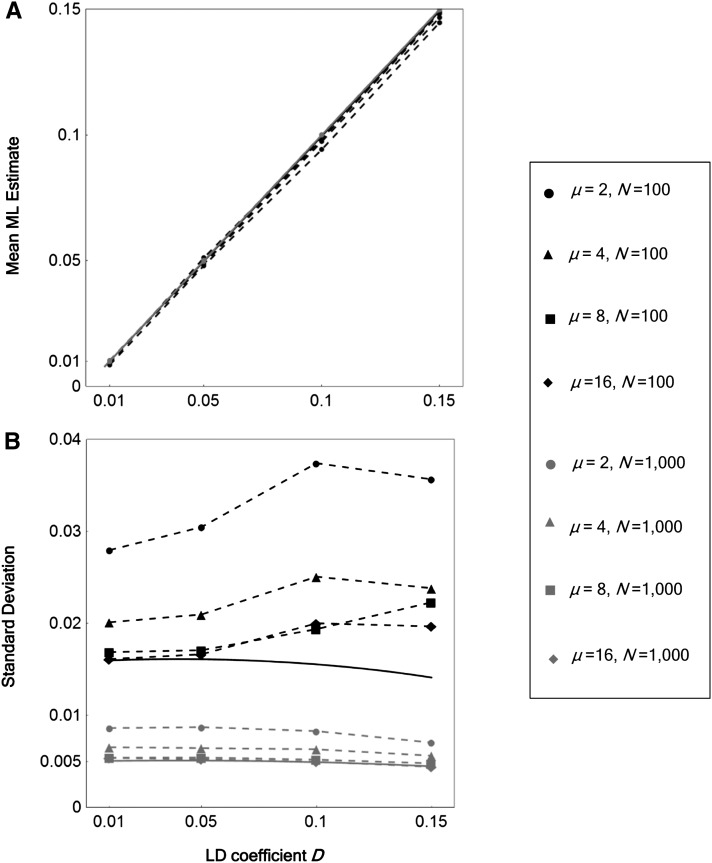
The performance of the LD estimator was evaluated using sequence-read data generated by computer simulations according to the methods described above. A relatively high error rate of 0.01 was assumed, to evaluate the performance in the face of the worst effects of sequence errors expected with widely used sequencing devices (Margulies et al. 2005; Huse et al. 2007). The mean of the LD coefficient estimates, $\widehat{D}$, was nearly unbiased (Figure 1). Furthermore, at high depths of coverage, the sampling variance of the estimates approached the asymptotic value (Equation 9), which is expected when all relevant information is obtained without error. Both the accuracy and the precision of the estimates improved when N (number of sampled individuals) was larger.

Figure 1.

Accuracy and precision of the ML estimates of LD. Sample mean (A) and standard deviation (B) of ML estimates are shown as functions of the LD coefficient D, the number of sampled individuals (sample size) N, and mean depth of coverage μ. Major allele frequency at site α, p = 0.6; major allele frequency at site β, q = 0.7; read length, L = 100; distance between sites of interest, d = 50; and error rate, ε = 0.01. The probability that a read covers both sites given it covers one site, Φ, is 1/3. A total of 1000 simulation replicates were run for each set of parameter values. The asymptotic theoretical sample expectation (given by Equation 8) and standard deviation (given by the square root of Equation 9) of $\widehat{D}$ are plotted by the solid lines (A) and curves (B), respectively.

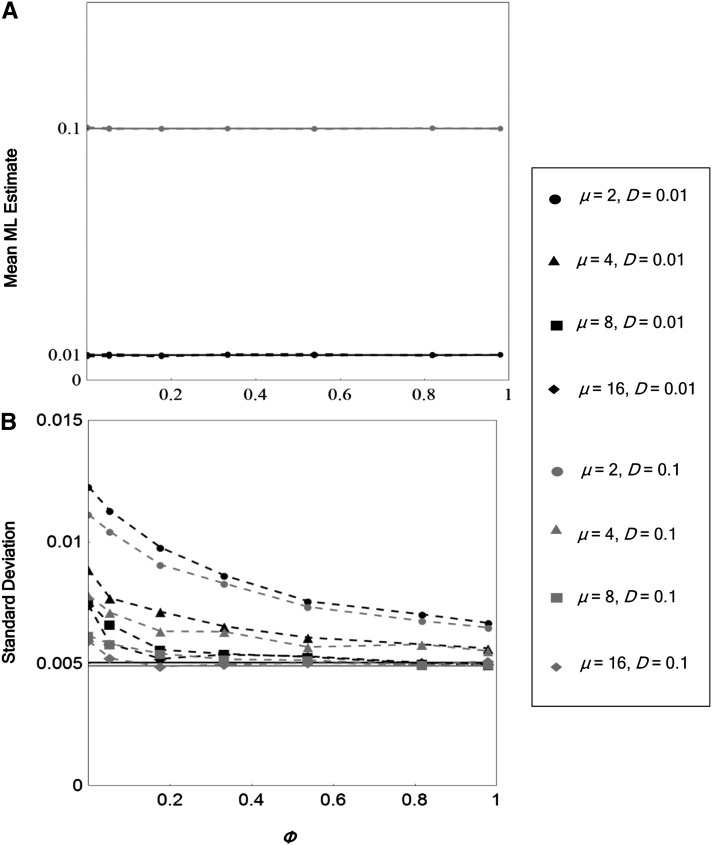
To examine the effect of φ (the fraction of informative reads covering both sites of interest) on the performance of the LD estimator, we varied the distance between the sites of interest, with a fixed read length: L = 100 and d = 1, 10, 30, 50, 70, 90, 100 (Figure 2). The means of the estimates were nearly unbiased regardless of φ, although the sampling variance of the estimates declined with increasing φ. The precision of the estimates greatly improves with initial increases in the depth of coverage, although this improvement diminishes rapidly beyond μ = 4. When φ was lower, the sampling variance was more influenced by the depth of coverage. Even though there are no reads covering both sites when φ is zero, in this case, the mean of the estimates is still nearly unbiased, with the sampling variance of the estimates approaching the asymptotic value (Equation 10) when depths of coverage are high.

Figure 2.

Effect of Φ (the probability that an informative read covers both sites of interest) on the performance of the LD estimator. Sample mean (A) and standard deviation (B) of ML estimates of LD are shown as functions of Φ, LD coefficient D, and mean depth of coverage μ. Sample size N = 1000; major allele frequency at site α, p = 0.6; major allele frequency at site β, q = 0.7; read length, L = 100; and error rate, ε = 0.01. A total of 1000 simulation replicates were run for each set of parameter values. The asymptotic theoretical sample expectation (given by Equation 8) and standard deviation (given by the square root of Equation 9) of $\widehat{D}$ are plotted by the solid lines.

To examine the sensitivity of the LD estimator to allele frequencies, in particular when all reads covered just single polymorphic sites (i.e., φ = 0), we estimated the LD coefficients with various allele frequencies at the two sites of interest (Table 2). A total of 1000 simulation replicates were run to obtain these results, with sample size N = 1000, LD coefficient D = 0.01 or 0.05, and error rate ε = 0.01. Because we defined that the sign of D is positive when major or minor alleles at the two sites are on the same chromosome and negative otherwise, when the allele frequencies are 0.5, the sign of D cannot be defined and therefore the estimates of D are not reported; instead, the mean and sampling standard deviation of the squared estimates of D are reported. Overall, the mean and sampling standard deviation of $\widehat{D}$ estimated from simulated sequence reads agreed well with the theoretical predictions. Furthermore, they were close to the asymptotic theoretical predictions (Equation 8 and square root of Equation 10) when the mean depth of coverage was 16, as then the effective number of sampled individuals is approximately equal to the actual number of individuals in the sample (Equation 15).

Table 2. Sensitivity of the LD estimator to allele frequencies when all sequence reads cover single polymorphic sites.

D	μ	(p, q)	$\widehat{\mathit{D}}$ (mean ± SD)	Theoretical SD $\left(\widehat{\text{D}}\right)$	${\widehat{\mathit{D}}}^2$ (mean ± SD)	Asymptotic theoretical SD $\left(\widehat{\mathit{D}}\right)$
0.01	2	(0.5, 0.5)	NA	0.013	0.0003 ± 0.0004	0.008
0.01	2	(0.6, 0.6)	0.010 ± 0.013	0.012	0.0003 ± 0.0004	0.008
0.01	2	(0.7, 0.7)	0.010 ± 0.011	0.011	0.0002 ± 0.0003	0.007
0.01	2	(0.8, 0.8)	0.010 ± 0.009	0.008	0.0002 ± 0.0002	0.005
0.01	2	(0.9, 0.9)	0.010 ± 0.006	0.005	0.0001 ± 0.0001	0.003
0.01	2	(0.6, 0.9)	0.010 ± 0.008	0.008	0.0002 ± 0.0002	0.005
0.01	16	(0.5, 0.5)	NA	0.008	0.0002 ± 0.0002	0.008
0.01	16	(0.6, 0.6)	0.010 ± 0.008	0.008	0.0002 ± 0.0002	0.008
0.01	16	(0.7, 0.7)	0.010 ± 0.007	0.007	0.0002 ± 0.0002	0.007
0.01	16	(0.8, 0.8)	0.010 ± 0.005	0.005	0.0001 ± 0.0001	0.005
0.01	16	(0.9, 0.9)	0.010 ± 0.003	0.003	0.0001 ± 0.0001	0.003
0.01	16	(0.6, 0.9)	0.010 ± 0.005	0.005	0.0001 ± 0.0001	0.005
0.05	2	(0.5, 0.5)	NA	0.013	0.0027 ± 0.0014	0.008
0.05	2	(0.6, 0.6)	0.051 ± 0.012	0.012	0.0027 ± 0.0013	0.008
0.05	2	(0.7, 0.7)	0.050 ± 0.011	0.011	0.0027 ± 0.0011	0.007
0.05	2	(0.8, 0.8)	0.050 ± 0.009	0.009	0.0026 ± 0.0009	0.006
0.05	2	(0.9, 0.9)	0.050 ± 0.008	0.008	0.0025 ± 0.0007	0.005
0.05	2	(0.6, 0.9)	0.050 ± 0.007	0.008	0.0026 ± 0.0007	0.005
0.05	16	(0.5, 0.5)	NA	0.008	0.0026 ± 0.0007	0.008
0.05	16	(0.6, 0.6)	0.049 ± 0.007	0.008	0.0025 ± 0.0007	0.008
0.05	16	(0.7, 0.7)	0.050 ± 0.007	0.007	0.0025 ± 0.0007	0.007
0.05	16	(0.8, 0.8)	0.050 ± 0.005	0.006	0.0025 ± 0.0005	0.006
0.05	16	(0.9, 0.9)	0.050 ± 0.005	0.005	0.0025 ± 0.0005	0.005
0.05	16	(0.6, 0.9)	0.050 ± 0.004	0.005	0.0025 ± 0.0004	0.005

Sample means and standard deviations of the LD coefficient $\widehat{D}$ and its square ${\widehat{D}}^2$ estimated from simulated sequence data are shown for various major allele frequencies at two polymorphic sites, p and q. The theoretical prediction of the standard deviation (SD) as a function of the mean depth of coverage μ, which is calculated as a square root of the theoretical sampling variance from Equations 10 and 15, is also shown. The theoretical prediction of the asymptotic standard deviation, which is calculated as a square root of the sampling variance given by Equation 10, is the expected level of achievement when individuals are genotyped without errors.

Given that the proposed estimator provides nearly unbiased LD estimates with asymptotically minimal sampling variances, we compared the LD-estimation performance of the proposed estimator to that of a widely used imputation-based method to examine whether the proposed method enables better LD estimates from high-throughput sequencing data than the standard approach of SNP calling followed by genotype imputation. For this purpose, we compared the mean and standard deviation of the LD estimates by the proposed method to those obtained using the widely used imputation-based software package BEAGLE (Browning and Browning 2013) (Table S3 and Table S4). When the major allele frequencies at two sites of interest were intermediate, LD estimates by the proposed estimator were better than those by the imputation-based method in the majority of the examined cases in terms of both accuracy and precision (Table S3). When the major allele frequencies were high, the root mean square deviations (RMSDs) of the LD estimates by the imputation-based method were smaller than those by the proposed estimator in some of the cases (Table S4). However, in those cases, the means of the LD estimates by the imputation-based methods were underestimated. The degree of the underestimation was especially large when major allele frequencies were high and the depth of coverage was low. On the other hand, the means of the LD estimates by the proposed estimator were close to the true values with their standard deviations essentially equal to the RMSD in all of the cases, indicating our method enables essentially unbiased LD estimation from high-throughput sequencing data.

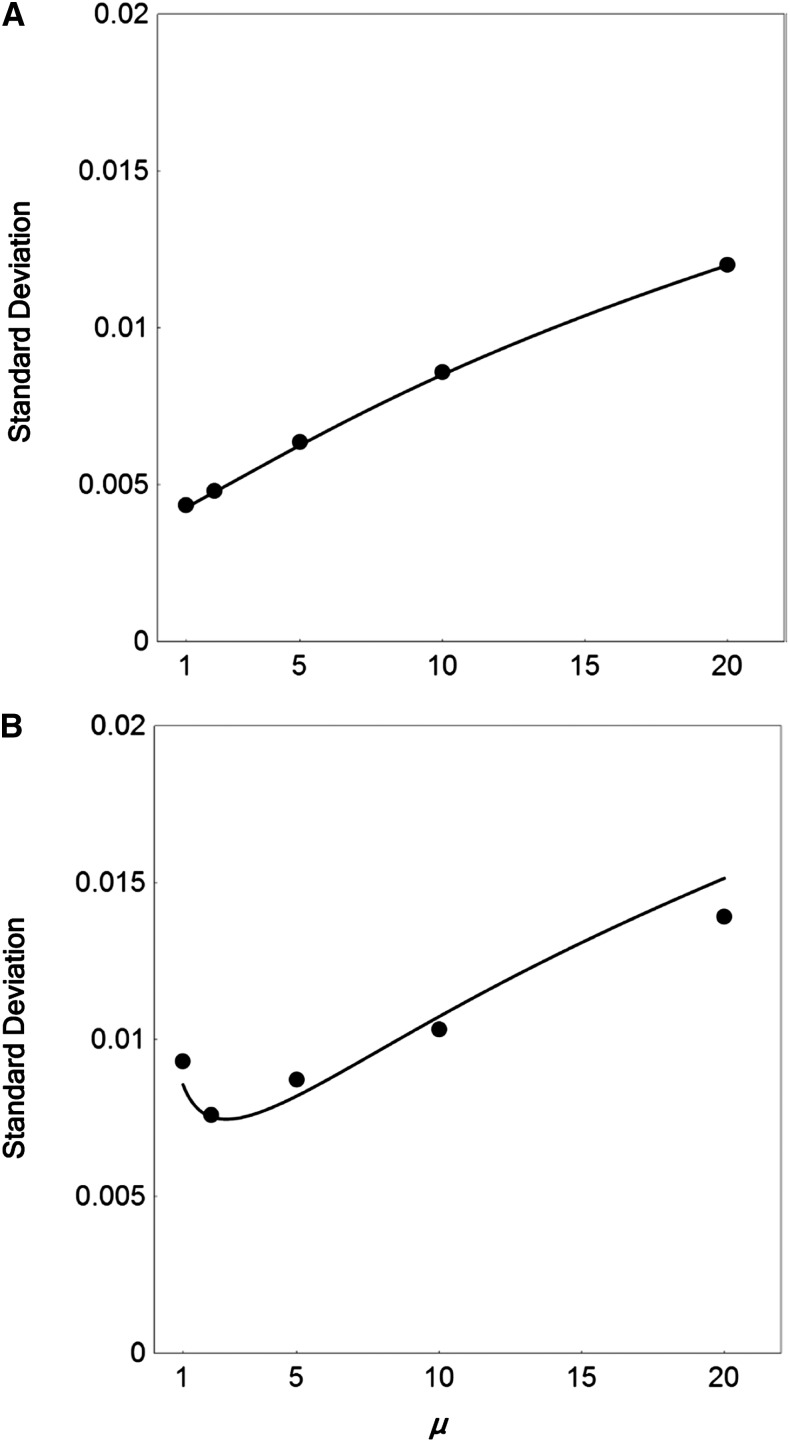
Finally, to find the optimal sequencing strategy for analyzing linkage disequilibrium with a limited research budget, the sampling standard deviation of the estimates of D was examined, fixing the value of the product of the mean depth of coverage (μ) and sample size (N) (Figure 3). When all sequence reads cover both sites of interest (i.e., φ = 1), the minimum sampling variance with a fixed value of μN is achieved at μ = 1 (Figure 3A). When all sequence reads cover just one of the sites of interest (i.e., φ = 0), the minimum sampling variance is at a slightly higher value of μ = 2 (Figure 3B).

Figure 3.

Sampling standard deviation of ML estimates of LD, as a function of the mean depth of coverage μ, estimated from a fixed number of total sequence reads. The product of μ and sample size N was fixed at 1000 such that a twofold increase in μ resulted in a twofold decrease in N. (A) Results when all sequence reads cover both sites of interest; (B) Results when all sequence reads cover just single polymorphic sites. The solid curves show the predicted values of the standard deviation (given by the square root of the theoretical sampling variance) of the estimates of the LD coefficient D from Equations 9 and 13 (A) and Equations 10 and 15 (B). The solid circles show the corresponding values of the standard deviation of $\widehat{D},$ estimated from the simulated sequence read data. The major allele frequencies at two sites of interest p = q = 0.9, D = 0.01, and error rate ε = 0.01. A total of 1000 simulation replicates were run for each set of parameter values.

Discussion

High-throughput sequencing technologies provide unprecedented opportunities for analyzing global as well as local patterns of polymorphisms in various organisms (Pool et al. 2010). In particular, they harbor great potential for haplotype analyses because sequencing occurs on single DNA molecules, allowing for the unambiguous determination of the phases of haplotypes if sequence errors are correctly accounted for. Genome-wide high-throughput sequencing data at the population level are accumulating in various organisms (Cao et al. 2011; Altshuler et al. 2012; Mackay et al. 2012). One of the major discoveries of these projects is the localization of a number of new polymorphic sites harboring alleles with low frequencies. The resultant denser polymorphisms provide excellent opportunities for finer LD analyses essential for understanding the contributions of various evolutionary forces, including mutation, recombination, random genetic drift, and natural selection to genome evolution (Lynch 2007).

Despite the promise, the new technologies have some disadvantages. Unlike conventional Sanger sequencing, high-throughput sequencing rapidly produces massive amounts of sequence data, sacrificing quality for quantity. In particular, high sequence error rates and random sampling of sequenced chromosomes in diploid organisms make estimation of allele frequencies and subsequent population-genomic analyses difficult. Because LD measures in general are dependent on allele frequencies (Lewontin 1988), correctly identifying polymorphic sites and estimating allele frequencies at the sites are especially important for LD analyses.

The proposed LD estimator overcomes problems associated with both sequence errors and the process of random sampling of sequenced chromosomes through their direct incorporation into the likelihood function. Because errors associated with DNA-sequence annotation include not only errors arising at the time of sequencing but also those introduced during sample preparation, it is risky to use externally determined “off-the-shelf” error-rate estimates. The proposed estimator avoids this problem by estimating error contributions from the sequence data themselves.

Unless the depth of coverage is high, just one of the two chromosomes may be sequenced at specific sites in a subset of diploid individuals, and to avoid this error in inference, many studies simply employ an arbitrary minimum coverage cutoff. However, such treatment can discard substantial amounts of informative data; and unless they are statistically accounted for, missing data are likely to introduce bias in population-genetic parameter estimates (Pool et al. 2010). Our results show that ML estimates of LD are nearly unbiased, with sampling variance at high coverages approaching the expectation when haplotype identities are known with certainty. This indicates that the proposed estimator maximally uses all available information. Thus, previously proposed methods of imputation of missing data, which may introduce biases in subsequent analyses (Lin and Huang 2007; Pool et al. 2010; and as shown in our results), are not necessary or often even desirable to obtain unbiased LD estimates. Furthermore, a recent study found that allele frequencies estimated via genotype calling are biased, whereas those estimated directly from mapped sequence reads by ML methods are unbiased, when the depth of coverage is low (Han et al. 2014). Given that carefully made reference panels do not exist for most organisms except for humans and flies, the proposed estimator should be especially useful when applied to high-throughput sequencing data for population-genomic analyses of nonmodel organisms. For example, Khatkar et al. (2010) substantially improved the quality of the bovine genome assembly by estimating pairwise LD between sites with unknown locations and those with known locations. We expect our estimator will play important roles in these kinds of applications, where unbiased estimation of LD is essential for correct inferences.

To exploit the emerging flood of data, an LD estimator specifically designed for the structure of the high-throughput sequencing data is required. Previous LD estimators (Hill 1974; Weir 1979; Feder et al. 2012) do not deal with the confounding effects of sequence errors on LD estimation. Although the most recent LD estimator (Feder et al. 2012) is designed for high-throughput sequencing data, it is limited to analyses of sequence reads containing both polymorphic sites. Our method not only deals with the confounding effects of sequence errors but also enables LD estimation even when all reads cover just single polymorphic sites. A C++ program for data analysis is available upon request, and we are currently implementing the proposed method as part of a software package for population-genomic analyses of high-throughput sequencing data.

When the present LD estimator is applied to huge numbers of sites across the genome, efficient means of application will be required for the analyses. Because LD is relevant only to pairs of polymorphic sites, it is useful to first apply the ML allele-frequency estimator (Lynch 2009) before pursuing the estimation of LD on the restricted set of relevant data. Then, using the ML estimates of allele frequencies and position-specific error rates, the LD coefficients between pairs of polymorphic sites can be rapidly estimated, as this is reduced to a one-dimensional problem. Of course, the simple grid search for finding the ML estimates taken in the allele-frequency estimator and the LD estimator can be replaced by a more efficient algorithm, e.g., the simplex method by Nelder and Mead (1965). Although error rates were assumed to be the same at two sites of interest in this article, this assumption can also be relaxed by rewriting the likelihood function with different error rates at the sites. Obviously, before applying any method to LD analysis, it is important to exclude sites where paralogous sequences are found elsewhere in the genome, for example, by eliminating sites with abnormally high depths of coverage.

Because random union of gametes is assumed in the proposed estimator, it should be applied to a randomly mating population. To study LD in a nonrandomly mating population, the composite linkage disequilibrium measure (Cockerham and Weir 1977; Weir 1979) needs to be estimated from two-locus genotype frequencies. Such an extension can in principle be made by modifying the present likelihood function (Equation 5), although nine parameters must then be estimated.

The present population-level LD estimator and the single-individual disequilibrium estimator developed by Lynch (2008) complement each other. The latter does not assume Hardy–Weinberg equilibrium and estimates global LD patterns as functions of the distribution of heterozygous sites from high-throughput sequencing data in a single individual. The mean of the LD estimates by the proposed population-level estimator is expected to be consistent with the estimates by the single-individual estimator, provided that the population is randomly mating (Lynch 2008). Specifically, the mean of ${\widehat{D}}^2$ is expected to closely correspond to $\widehat{\mathrm{\Delta }}\widehat{\pi }\left(1-\widehat{\pi }\right)/4,$ where $\widehat{\mathrm{\Delta }}$ and $\widehat{\pi }$ are the single-individual genome-wide estimates of LD coefficients and nucleotide diversity, respectively.

Finally, the theoretical results in this investigation can be used to guide the design of optimal strategies for estimating LD from population-level high-throughput sequencing data in the face of a limited budget. In general, regardless of the read length, a mean 2× depth of coverage appears to be the optimal allocation of resources, assuming the cost is proportional to Nμ, the expected total number of sequenced bases per site.

Alternatively, because sequencing costs are decreasing, one may find that the cost for DNA library preparation is more expensive than that for sequencing itself. The optimal strategy in such cases can also be flexibly predicted with the sampling variance formulas. Letting C_l and C_s denote the costs for library preparation per individual and sequencing per genome, respectively, the total cost T is

$$T=C_{\text{l}}N+C_{\text{s}}\left(\mu N\right)=\left(C_{\text{l}}+\mu C_{\text{s}}\right)N.$$ (18)

For example, when C_l = 3C_s, (3 + μ)N = T/C_s. In this case, assuming T = 100,000 and C_s = 20, the minimum sampling variance is predicted to be achieved when μ is somewhere between 2 and 3 (Figure S1), with N then being 833 (with μ = 3) to 1000 (with μ = 2). In some studies, however, the number of available samples may become the limiting factor in designing the optimal study design. Our concepts of effective number of sampled individuals and chromosomes provide insights for designing the optimal strategy in such cases. Equations 13 and 15 show that the effective numbers quickly approach the actual numbers of chromosomes and individuals with higher depths of coverage.

Another complication in real studies is higher variance in depths of coverage than that by the Poisson distribution (Quail et al. 2012). The higher variance in depths of coverage is expected to decrease the effective numbers and therefore increase the optimal depths of coverage. Taken together, if a central goal of a population-genomic survey is the accurate estimation of LD, sequencing as many individuals as possible is the first priority.