How Population Growth Affects Linkage Disequilibrium

Abstract

The “LD curve” relates the linkage disequilibrium (LD) between pairs of nucleotide sites to the distance that separates them along the chromosome. The shape of this curve reflects natural selection, admixture between populations, and the history of population size. This article derives new results about the last of these effects. When a population expands in size, the LD curve grows steeper, and this effect is especially pronounced following a bottleneck in population size. When a population shrinks, the LD curve rises but remains relatively flat. As LD converges toward a new equilibrium, its time path may not be monotonic. Following an episode of growth, for example, it declines to a low value before rising toward the new equilibrium. These changes happen at different rates for different LD statistics. They are especially slow for estimates of ${\sigma }_{\text{d}}^2$, which therefore allow inferences about ancient population history. For the human population of Europe, these results suggest a history of population growth.

LINKAGE disequilibrium (LD) refers to the statistical association between pairs of genetic loci. It is used routinely in localizing disease genes, in detecting natural selection, and in studying population history. In all of these contexts, it is necessary to account for effects of changes in population size.

These effects arise because inhabitants of small populations tend to be close relatives. The genealogical paths that separate them are short, and this reduces the opportunity for recombination. For this reason, LD rises after a fall in population size and falls after a rise.

These effects are understood in a general way and are often studied by computer simulation (Kruglyak 1999; Pritchard and Przeworski 2001). Although this approach has led to important insights, our understanding is still rudimentary. This article uses a deterministic algorithm to explore the effects of growth, of decline, and of temporary reductions (bottlenecks) in population size. It shows that each type of history leaves a distinctive signature in the “LD curve,” which relates the LD between pairs of sites to the distance that separates them along the chromosome.

The paper uses ${\sigma }_{\text{d}}^2$ (defined below) as a measure of LD. This choice is unusual, because ${\sigma }_{\text{d}}^2$ has always been of secondary importance. As we shall see, however, ${\sigma }_{\text{d}}^2$ has dynamical properties that give it deeper time depth than alternative measures of LD. It is readily estimated from data and can be predicted by a deterministic theory, which makes it easy to study the response to changes in population size. This article shows that ${\sigma }_{\text{d}}^2$ is of more than secondary importance. It is useful in its own right as a measure of LD.

Materials and Methods

Software

The various methods were evaluated against simulated data generated by MACS (Chen et al. 2009). Simulation results in Figure 1 are based on my own coalescent program, hetage, written in C. All other analyses were done using ldpsiz, a package of C programs available at github.com/alanrogers/ldpsiz. This package includes several programs: eld, which estimates ${\sigma }_{\text{d}}^2$ and r² from genetic data; preld, which calculates ${\sigma }_{\text{d}}^2$ from the history of population size; and sald, which fits history parameters to an observed LD curve, using the method of simplex-simulated annealing (Press et al. 1992, pp. 451–455), with modifications described by Gao and Han (2012).

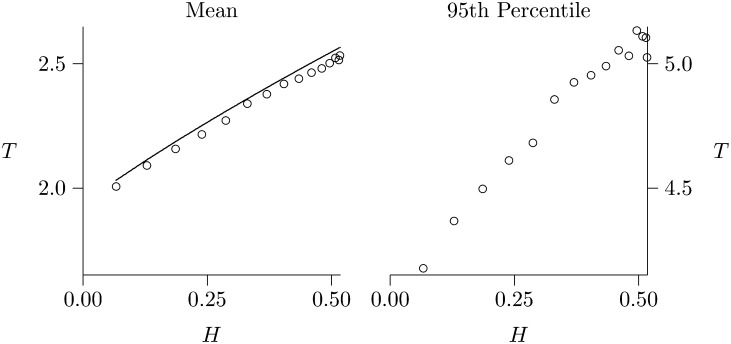
Figure 1.

The depth, T, of gene genealogy given heterozygosity, H. The left and right panels show the mean and the 95th percentile in units of 2N generations. Solid line shows expected values, based on the model of Griffiths and Tavaré (1998, equation 1.5, p. 276). Open circles show results from coalescent simulations. These results assume a sample of 30 diploid individuals and a mutation rate of 0.02 per 2N generations. The slope is greater in the right panel than in the left, indicating that heterozygosity has a stronger effect on the upper tail of the distribution than on the mean.

Measuring LD

Consider a pair of loci (nucleotide sites), A and B. At locus A, alleles A₁ and A₀ have frequencies a and 1 − a. At locus B, alleles B₁ and B₀ have frequencies b and 1 − b. The disequilibrium coefficient, D, is defined such that ab + D is the frequency of gamete type A₁B₁. The sign of D is arbitrary, depending on how one labels the alleles, so the magnitude of LD is often measured by D².

These measures are sensitive to heterozygosity at the two loci, so many authors prefer the squared correlation coefficient (Hill and Robertson 1968),

$$r^2=\frac{D^2}{a\left(1-a\right)b\left(1-b\right)}.$$ (1)

Unfortunately, there is no consensus regarding the expected value of this statistic, even in the simplest case of neutral loci in a randomly mating population of constant size (compare Sved 2009 with Song and Song 2007 and Durrett 2008, p. 98).

Ohta and Kimura (1969, p. 233) proposed a related measure of LD, the “squared standard linkage deviation,” which was also motivated by a desire to minimize the effect of heterozygosity:

$${\sigma }_{\text{d}}^2=\frac{E\left[D^2\right]}{E\left[a\left(1-a\right)b\left(1-b\right)\right]}.$$ (2)

This measure is usually viewed as an approximation to E[r²]. It is most useful in this role when the population size is large and constant and both loci have appreciable heterozygosity (Hudson 1985). In other situations, the two parameters can differ greatly. But even when ${\sigma }_{\text{d}}^2$ fails as an approximation, it is still useful as a measure of LD.

This is not to say that ${\sigma }_{\text{d}}^2$ provides a complete description of variation at a pair of loci. That is a problem with multiple dimensions, which cannot be solved by any scalar-valued measure of LD (Weir 1996, pp. 125–127). Such measures are simplifications and are necessarily incomplete (Schaper et al. 2012). However, as we shall see, ${\sigma }_{\text{d}}^2$ captures enough to provide an interesting window into the history of population size.

Estimation of ${\sigma }_{\text{d}}^2$

One can estimate ${\sigma }_{\text{d}}^2$ from data by replacing the expected values in Equation 2 with averages across the genome. For this purpose, I treat each polymorphic site [single-nucleotide polymorphism (SNP)] as “focal” and compare the focal SNP with each other SNP within some given range. From each comparison, I calculate D² and a(1 − a)b(1 − b). These values are tabulated separately within bins based on the distance in centimorgans between the SNPs. After all comparisons have been tabulated, the estimate $\left({\widehat{\sigma }}_{\text{d}}^2\right)$ is calculated as the sum of D² within a bin divided by the corresponding sum of a(1 − a)b(1 − b).

In this article, I ignore pairs of SNPs separated by >0.3 cM, because there is little LD at these distances in most parts of the human genome.

To estimate uncertainties, I use a moving-blocks bootstrap (Lieu and Singh 1992), with 300 SNPs per block. With diploid data, some genotypes may be unphased. In such cases, I use the EM algorithm to estimate D², as explained in the Appendix.

Deterministic evolution of ${\sigma }_{\text{d}}^2$

Under neutral evolution with constant population size, ${\sigma }_{\text{d}}^2$ converges to an equilibrium value (Ohta and Kimura 1971; McVean 2002). In addition, several authors have introduced recurrence equations, which make it possible to study the transient behavior of ${\sigma }_{\text{d}}^2$ after changes in population size (Weir and Cockerham 1974; Hill 1975; Strobeck and Morgan 1978). The model of Strobeck and Morgan (1978) allows faster calculations but is less numerically stable than that of Hill (1975). I present some results using the former model but focus primarily on the latter. In the Appendix, I summarize Hill’s model and show that it holds not only under the mutational model that he studied, but also under the model of infinite sites (Kimura 1969). It is thus appropriate for use with DNA sequence data.

For bootstrap confidence intervals, I accelerate these calculations by using Equation A2 of the Appendix to approximate a system of ordinary differential equations, which is then solved using standard software.

Sampling bias

Drawing a sample is equivalent to one generation of evolution with a very small population—one whose size equals that of the sample. Because drift introduces LD, there is much more LD in a sample than in the population from which it was drawn.

Hudson (1985, Equation 6) showed that sampling bias in r² equals 1/n, when the sample consists of n gametes. Sampling bias also inflates the value of ${\widehat{\sigma }}_{\text{d}}^2.$ The program preld includes this bias in calculations of the expected value, ${\sigma }_{\text{d}}^2.$ These calculations use the model of Hill (1975) or Strobeck and Morgan (1978) to project the state vector forward one generation, with the population size set equal to the sample size.

Fitting population history to an observed LD curve

The program eld (a part of ldpsiz) estimates the LD curve from genetic data. A second program, sald, can then be used to search for the population history parameters that minimize the sum of squared differences between observed and predicted LD curves. This minimization problem searches a complex surface, with many local minima. To search for the global minimum, sald uses the method of simplex-simulated annealing. For each data set, sald starts 10 simulated annealing jobs on parallel threads. Typically, several of these converge to the same global minimum. sald returns the best of the 10 solutions as fitted parameters.

Results

${\widehat{\sigma }}_{\text{d}}^2$ is average r², weighted by heterozygosities

Equation 2 is equivalent to

$${\sigma }_{\text{d}}^2=\frac{E\left[H_A{H}_B{r}^2\right]}{E\left[H_A{H}_B\right]},$$ (3)

where H_A = 2a(1 − a) is the expected heterozygosity at locus A and H_B is that at locus B. This implies that ${\sigma }_{\text{d}}^2$ is the expectation of r² weighted by the product of the two heterozygosities.

This weighting also carries over to the estimate, ${\widehat{\sigma }}_{\text{d}}^2,$ which is obtained by replacing expectations with averages. Such estimates will be insensitive to loci with low heterozygosity and, for this reason, also insensitive to sequencing error. They should be useful with low-coverage sequence data.

Loci with high heterozygosity have deep gene trees

Weighting by heterozygosity exaggerates the influence of unusually deep gene trees. At some given nucleotide position, let T represent the age of the last common ancestor of the sample. I call this the “depth” of the gene tree for that nucleotide position. Griffiths and Tavaré (1998, Equation 1.5, p. 276) derive the conditionally expected depth, E[T | x, n], given that x copies of the derived allele were observed in a sample of haploid size n. Given the heterozygosity, we can solve for x, but we cannot tell the derived from the ancestral allele. It may be present in x copies or in n − x. At mutation–drift equilibrium, however, these alternatives have probabilities proportional to 1/x and 1/(n − x) (Fu 1995, equation 1). Using these values as weights, I average E[T | x, n] and E[T | n − x, n] to calculate expected tree depth given heterozygosity. The results are shown as a solid line in Figure 1. As Figure 1 shows, tree depth increases with heterozygosity. Simulated values—shown as open circles—agree closely with the theory.

Simulated values also allow us to examine the upper tail of the distribution, as seen in Figure 1, right. The 95th percentile of tree depth increases with heterozygosity even more steeply than does the mean. Thus, heterozygosity has an exaggerated effect on the upper tail of the distribution.

Geneticists often study loci selected for their high heterozygosity (Lewontin 1967; Rogers and Jorde 1996; Clark et al. 2005). A sample of loci selected in this fashion will have gene trees that are unusually deep, especially in the upper tail of the distribution.

Because ${\sigma }_{\text{d}}^2$ is weighted by heterozygosity, it exaggerates the influence of these deep gene trees. For this reason, it should be sensitive to earlier portions of a population’s history. Following a change in population size, it should converge more slowly to the new equilibrium.

Effect of population growth

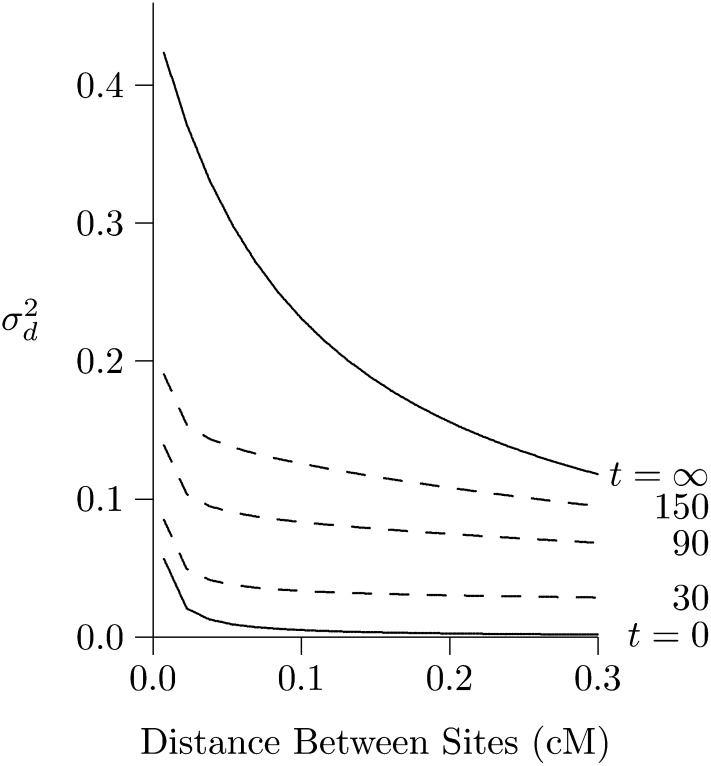
LD will decline following an expansion of population size, because genetic drift is weaker in large populations and produces less LD. This process is illustrated in Figure 2, which shows the effect of an expansion from size 2N = 10³ to 2N = 10⁵. The LD curve of the initial population (labeled t = 0) represents an equilibrium between mutation, drift, and recombination. After the expansion, the LD curve will eventually converge to a new equilibrium, which is labeled t = ∞. This new equilibrium, however, is reached only gradually.

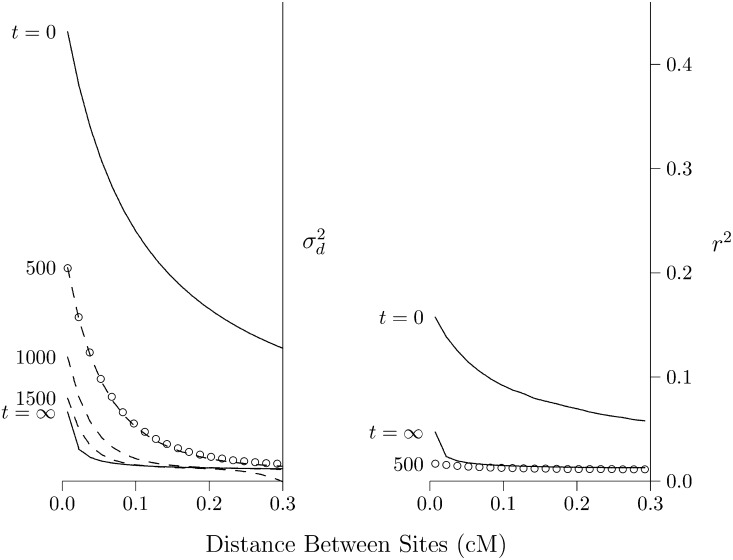
Figure 2.

Effect of population expansion on the LD curve. The population grew suddenly at time t = 0 from 2N = 10³ to 10⁵. Left panel: LD is measured by ${\sigma }_{\text{d}}^2.$ Solid lines show the predicted values at the initial equilibrium (t = 0) and at the eventual equilibrium (t = ∞). Dashed lines show a series of transient states that occur at various values of t, the number of generations since the expansion. These lines are all calculated using the method of Hill (1975). Open circles show values simulated using MACS for t = 500. Right panel: LD is measured by r², and points and lines are based on computer simulation. Calculations assume that u = 1.48 × 10⁻⁸ per site per generation, and the haploid sample size is 100.

LD is measured by ${\sigma }_{\text{d}}^2$ in Figure 2, left, and by r² in Figure 2, right. The dashed lines were calculated using the method of Hill (1975), and the open circles were estimated from data simulated using MACS (Chen et al. 2009). Note that ${\sigma }_{\text{d}}^2$ is still far from equilibrium at generation 500 and does not approach equilibrium until about generation 1500.

The situation is very different in Figure 2, right, where LD is measured by r². By generation 500, r² is close to equilibrium. At the left edge of the graph, it is slightly below the equilibrium. We return to this point later, but for the moment, note simply that r² converges much faster than ${\sigma }_{\text{d}}^2.$ For this reason, the two measures are useful for studying different timescales. We learn from r² about the recent past and from ${\sigma }_{\text{d}}^2$ about more ancient events. Presumably, this difference arises because ${\sigma }_{\text{d}}^2$ is weighted toward loci with high heterozygosity. As shown in Figure 1, this weighting makes it more sensitive to the distant past.

Returning to Figure 2, left, note that the right portion of the curve converges faster than the left. This is because the postexpansion population is large, and genetic drift is weak. The dynamics are therefore dominated by recombination, which is stronger on the right side of the graph. The result is that midway through the process—say at generation 500—the LD curve declines very steeply. Thus, a steeply declining LD curve is the signature of recent population growth (Kruglyak 1999; Pritchard and Przeworski 2001).

The method of Hayes et al. (2003)

Figure 2 suggests that ${\sigma }_{\text{d}}^2$ is likely to be of greater use than r² in inferring the ancient history of population size. Yet the latter statistic is often used instead (Hayes et al. 2003; McEvoy et al. 2011; Tenesa et al. 2007), using a method that is based on the formula E[r²] ≈ ρ, where

$$\rho =\frac{1}{1+4Nc}.$$ (4)

Here, N is diploid population size, and c is the recombination rate (Sved 1971; Sved and Feldman 1973). Although this formula has been criticized (Littler 1973, p. 272; McVean 2002, pp. 987–988; McVean 2007, p. 923; Durrett 2008, p. 98), it is widely used.

Hayes et al. (2003) study a generalization of r² and argue from simulations that the expectation of this statistic is ≈ρ. Furthermore, this approximation even works for populations that have increased in size at a constant linear rate, provided that one interprets N as the population size that obtained 1/2c generations in the past. By inverting Equation 4, they are able to estimate N over a wide range of values of c, which correspond under their model to different points in the past.

Tenesa et al. (2007) work directly with r², but estimate the history of population size in the same way. They also employ a modified predictor,

$$\stackrel{\sim }{\rho }=\frac{1}{2+4Nc},$$ (5)

which in their view accounts better for the effect of mutation. This method is also used by McEvoy et al. (2011). There are two difficulties with this formula. First, Tenesa et al. (2007, p. 521) derive it from a formula of Hill (1975, p. 124), which refers not to E[r²] but to ${\sigma }_{\text{d}}^2.$ Thus, it approximates E[r²] only to the extent that ${\sigma }_{\text{d}}^2$ does. In addition, it uses a fairly crude standard of approximation, taking 10 as ≈11.

The arguments justifying both of these methods assume that population size has increased linearly. Of course, no population can increase linearly forever, so the period of linear increase must end at some point in the past. Furthermore, the method’s results are often interpreted in terms of nonlinear growth trajectories, such as bottlenecks (Hayes et al. 2003, pp. 639–670; Tenesa et al. 2007, p. 525; McEvoy et al. 2011, p. 822). Let us consider how the method behaves in this broader context.

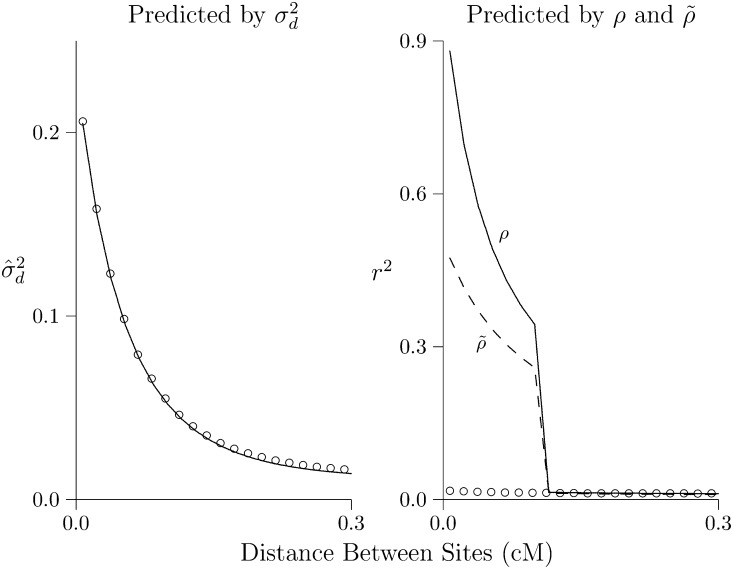
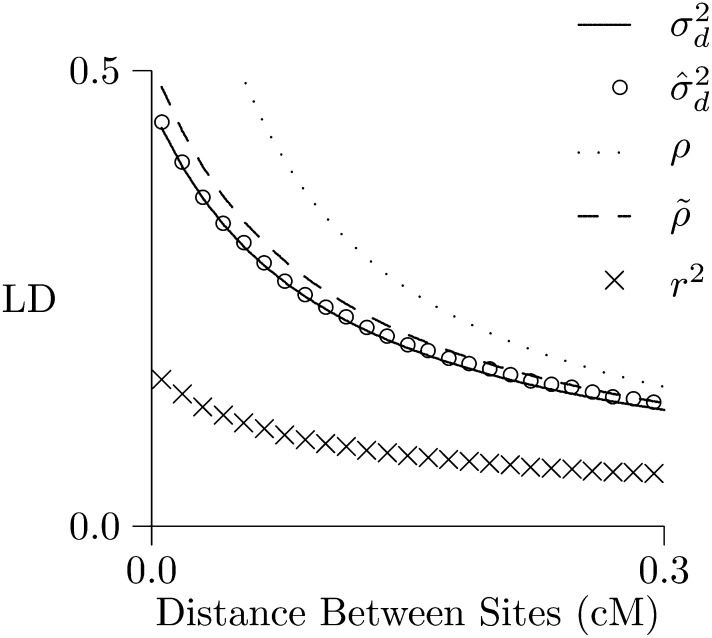
Figure 3 considers a population that expands suddenly in size and is observed 500 generations later. In both panels of Figure 3, the solid lines show predicted LD. In Figure 3, left, LD is measured by ${\widehat{\sigma }}_{\text{d}}^2$ and predicted by ${\sigma }_{\text{d}}^2$ (Hill 1975). In Figure 3, right, it is measured by r² and predicted by ρ and $\stackrel{\sim }{\rho }.$ The open circles show values simulated using MACS (Chen et al. 2009). In the context of this population history, ${\sigma }_{\text{d}}^2$ provides excellent predictions of ${\widehat{\sigma }}_{\text{d}}^2,$ but neither ρ nor $\stackrel{\sim }{\rho }$ predicts r².

Figure 3.

Predicted and simulated LD. Each panel shows the same population 500 generations after expansion from 2N = 10³ to 10⁵. Lines show values predicted by ${\sigma }_{\text{d}}^2$ [left panel (Hill 1975)] and by ρ (right panel, solid line) and $\stackrel{\sim }{\rho }$ (right panel, dashed line). Open circles show results estimated from simulations. Calculations assume that u = 1.48 × 10⁻⁸ per site per generation, and the haploid sample size is 100. Simulations involve 10⁹ bp DNA.

Presumably, this reflects the nonlinearity of the growth trajectory assumed in Figure 3. We expect better accuracy in Figure 4, which evaluates ρ and $\stackrel{\sim }{\rho }$ against a history involving 300 generations of linear population growth, approximated as a series of 20 steps. The period of linear growth corresponds to the region to the right of the dashed line in Figure 4, right. At least in this region, predicted and simulated values should match. Yet as before, ${\sigma }_{\text{d}}^2$ predicts well, but ρ and $\stackrel{\sim }{\rho }$ do not.

Figure 4.

Linkage disequilibrium (${\widehat{\sigma }}_{\text{d}}^2$ or r²) after an episode of linear growth. The population begins at mutation-drift equilibrium with 2N = 10³ and then grows linearly to 2N = 10⁶ over a period of 300 generations. Linear growth is approximated by 20 epochs of 15 generations, within each of which 2N is constant. In the right panel, the region to the right of the vertical line corresponds to the period of linear growth, according to the model of Hayes et al. (2003). All calculations assume that u = 1.48 × 10⁻⁸ and c = 10⁻⁸ per nucleotide. Simulations involve 10⁹ bp of DNA, which are sequenced in a sample of 100 homologous chromosomes.

Finally, Figure 5 evaluates ρ, $\stackrel{\sim }{\rho },$ and ${\sigma }_{\text{d}}^2$ against a history of constant population size. In this case, we get an accurate prediction of ${\widehat{\sigma }}_{\text{d}}^2$ from ${\sigma }_{\text{d}}^2$ and a fairly accurate prediction from $\stackrel{\sim }{\rho }.$ This makes sense, because (as mentioned above) $\stackrel{\sim }{\rho }$ is an approximation to the equilibrium formula for ${\sigma }_{\text{d}}^2.$ On the other hand, neither ρ nor $\stackrel{\sim }{\rho }$ provides a useful prediction of r².

Figure 5.

LD curve under constant population size. Simulated values of r² and ${\widehat{\sigma }}_{\text{d}}^2$ were generated using MACS (Chen et al. 2009). ${\sigma }_{\text{d}}^2$ was calculated using the method of Hill (1975), ρ was calculated from Equation 4, and $\stackrel{\sim }{\rho }$ from Equation 5. All calculations assume that 2N = 1000, u = 1.48 × 10⁻⁸, and c = 10⁻⁸ per nucleotide. Simulations involve 10⁹ bp of DNA, which are sequenced in a sample of 100 homologous chromosomes.

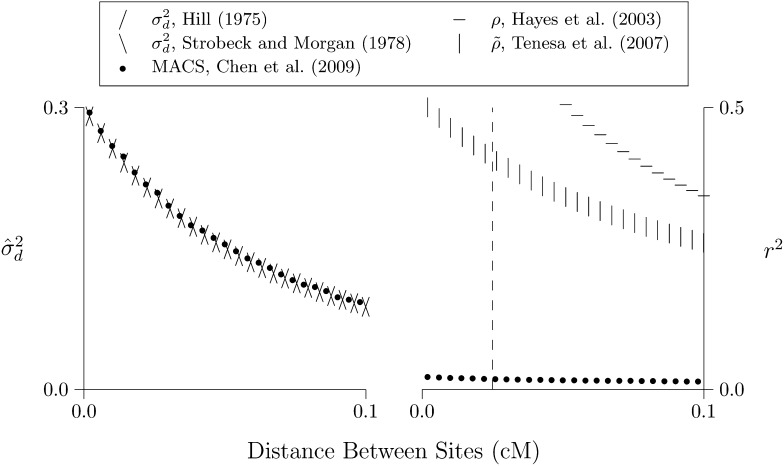
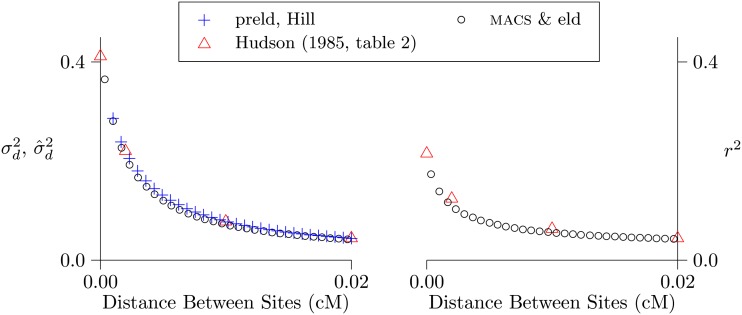
In these analyses, the observed and predicted values of r² are distressingly far apart. Perhaps this discrepancy reflects an error in the simulation software (MACS) or in my own code for estimating r² from simulated data. To find out, I used this software to replicate the published results of Hudson (1985). The results, shown in Figure 6, are reassuring. Given the same parameter values, the code used here produces results indistinguishable from those of Hudson.

Figure 6.

Replication of results of Hudson (1985, table 2). The left panel compares methods for calculating ${\sigma }_{\text{d}}^2$; the right panel compares methods for calculating r². The programs MACS, eld, and preld are described in Materials and Methods. Parameter values: θ = 0.1, 2N = 50,000, n = 50. MACS simulated chromosomes 2 Mb in length. Following Hudson, I correct ${\widehat{\sigma }}_{\text{d}}^2$ but not r² for sampling bias.

It seems fair, therefore, to conclude that the problem lies in the predictors, ρ and $\stackrel{\sim }{\rho },$ neither of which is useful in the cases studied here. It seems unlikely that they will be useful as a basis for inference in real populations.

Effect of population collapse

A collapse in population size produces an effect on the LD curve very different from that of population growth. This is shown in Figure 7, which illustrates two important points. First, the whole process is over very quickly. Even with ${\sigma }_{\text{d}}^2,$ we cannot look very far into the past. Second, the transient curves (the dashed lines) are quite flat. As time passes, the initial curve (labeled t = 0) is elevated without much change in shape. Presumably, this is because the effect of drift is dominant in a small population, so differences in recombination rate do not matter much. The result is that the LD curve becomes high but flat after a collapse in population size.

Figure 7.

Effect of population collapse on the LD curve. At time t = 0, this population collapsed in size from 2N = 10⁵ to 10³. Calculations use the method of Hill (1975), with u = 1.48 × 10⁻⁸. No correction for sampling bias was needed, as these calculations are not compared with simulations.

This pattern is superficially similar to that generated by gene conversion, which reduces LD between closely linked sites (Ardlie et al. 2001). It seems unlikely, however, that these effects will be confused. The effect of gene conversion is probably minor for sites separated by >1 kb (Frisse et al. 2001, p. 838; Chen et al. 2007, p. 764), whereas that of a population collapse extends much farther.

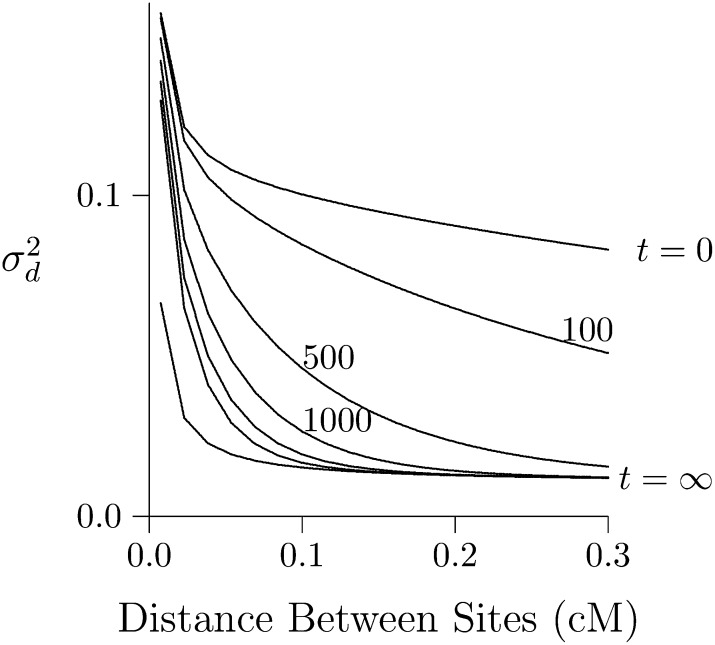
Effect of a bottleneck

Figure 8 shows the effect of a 100-generation bottleneck in population size. Population size was 2N = 10³ during the bottleneck but 10⁵ before and after. The bottleneck ended at time 0, and we observe it in various subsequent generations. In the graph, the curve labeled t = 0 is at the end of the bottleneck and exhibits an LD curve that is high but flat, for reasons just discussed. As time passes, the right portion of the curve (the portion with high rates of recombination) falls much faster than the left, so that by generation 1000, the curve is almost L shaped. This is the signature of a bottleneck in population size.

Figure 8.

Effect of a 100-generation bottleneck in population size. The curves show ${\sigma }_{\text{d}}^2$ at various points after recovery from a 100-generation bottleneck, during which the population had size 2N = 10³. Before and after the bottleneck, its size was 10⁵. Other details are as in Figure 7.

Note the dramatic difference between Figure 2 and Figure 8—between expansion from equilibrium and from a bottleneck. Both curves are declining toward the same equilibrium, but the left portion of the curve declines much more slowly after a bottleneck than after expansion from equilibrium. This can only reflect the state of the population just before the increase in size. The initial population of Figure 2 had been small much longer than that of Figure 8. Consequently, it had less heterozygosity. As we see in the next section, this accelerates the rate of decline in LD between closely linked sites.

It is sometimes suggested that bottlenecks inflate long-range LD, just the opposite of the pattern seen above (Slatkin 2008, pp. 481–482; Tenaillon et al. 2008). This discrepancy, however, evaporates on close inspection. When Tenaillon et al. (2008, figure 6) discuss “long-range” LD, they are referring to pairs of nucleotide sites separated by ∼0.01 cM. In my own analysis, such pairs would be called “tightly linked” and would fall at the left edge of the LD curve. In this region of Figure 8, LD is indeed elevated, in agreement with Tenaillon et al. (2008). In another study, Thornton and Andolfatto (2006, p. 1611) report elevated LD following a bottleneck. But as they do not discuss the shape of the curve, there is no conflict between their results and mine.

The time paths of individual points on the LD curve

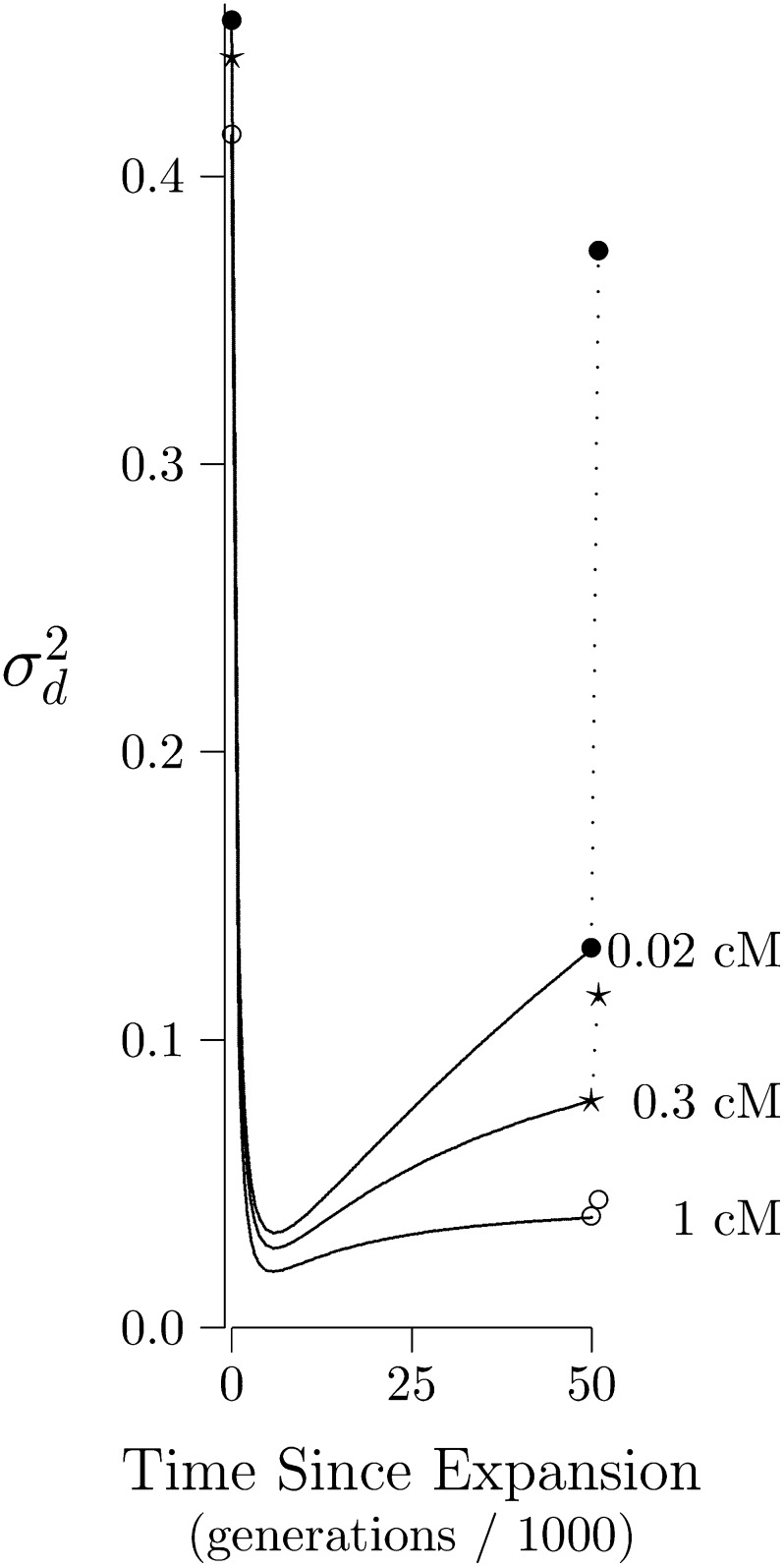
Figure 9 shows the time path of ${\sigma }_{\text{d}}^2$ after an expansion in population size. Because the new population is larger, the new equilibrium will have less LD. But ${\sigma }_{\text{d}}^2$ does not decline monotonically toward this new equilibrium. Instead, it falls rapidly to a smaller value before climbing back slowly toward to the new equilibrium.

Figure 9.

The time path of ${\sigma }_{\text{d}}^2$ after a population expansion. The initial population was small (2N = 10³) and at mutation–drift equilibrium. At time 0 it expands suddenly to a much larger size (2N = 10⁵). Each curve shows the time path of ${\sigma }_{\text{d}}^2$ for a different rate of recombination, measured in centimorgans. There is a curve for tight linkage (•, 0.02 cM), one for somewhat weaker linkage (⋆, 0.3 cM), and one for linkage that it weaker still (°, 1 cM). Dotted lines connect the final value of each curve to its ultimate equilibrium, which would be reached if the population stayed large forever.

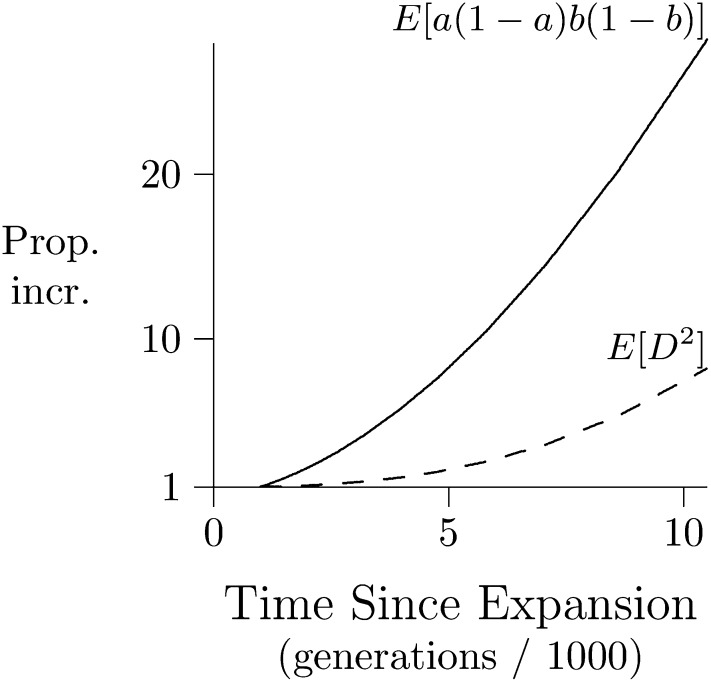
The initial decline in ${\sigma }_{\text{d}}^2$ does not result from any decline in its numerator, E[D²]. Indeed, Figure 10 shows that the numerator actually grows. The decline in ${\sigma }_{\text{d}}^2$ happens because growth in its numerator is outstripped by that in its denominator, E[a(1 − a)b(1 − b)], which increases under the influence of mutation. The proportional increase is large, because our initial population was small and therefore had little heterozygosity. For this reason, the denominator was initially so small that increments caused by mutation had a large proportional effect.

Figure 10.

The time path of the numerator and denominator of ${\sigma }_{\text{d}}^2$ following a population expansion. Dashed line shows numerator of ${\sigma }_{\text{d}}^2$, relative to its value in generation 1000. Solid line shows the denominator in the same way. Loci are separated by 0.02 cM. Population history is as in Figure 9.

Two factors account for the postexpansion growth in the numerator, E[D²], of ${\sigma }_{\text{d}}^2.$ First, D is proportional to heterozygosity (Kaplan and Weir 1992, p. 334), which increases in response to mutation. Ordinarily, the positive effect on D² would be offset by the negative effect of recombination. But in the early generations following our expansion, this negative effect is very weak. This is because the initial population had low heterozygosity. Few recombinant gametes are produced in such a population, because such gametes are produced only by double heterozygotes.

The nonmonotone time path in Figure 9 refers to ${\sigma }_{\text{d}}^2,$ but it seems plausible that r² might obey similar dynamics. This may explain why, in Figure 2, right, the left end of the curve for t = 500 is below the equilibrium.

This also explains why the left portion of the LD curve declines faster after expansion from equilibrium than after a bottleneck. The left portion of the curve refers to tightly linked sites, with weak recombination. In the postexpansion population, genetic drift is also weak because the population is large. Because recombination and drift are both weak, mutation dominates the dynamics. The proportional effect of mutation is large when heterozygosity is low. In the case of expansion from equilibrium, the population has been small a long time, so heterozygosity is low, the proportional effect of mutation is large, and ${\sigma }_{\text{d}}^2$ declines rapidly. Heterozygosity is not so low at the end of a bottleneck, because the population has been small only briefly. Consequently, the proportional effect of mutation is smaller, and ${\sigma }_{\text{d}}^2$ declines more slowly.

LD in the human population of Europe

The methods discussed above generate predictions about LD from assumptions about the history of population size. It is also possible, by fitting predicted to observed curves, to work in the other direction—from data to inferences about population history. This is a problem in statistical inference, and methods for this purpose will be described elsewhere.

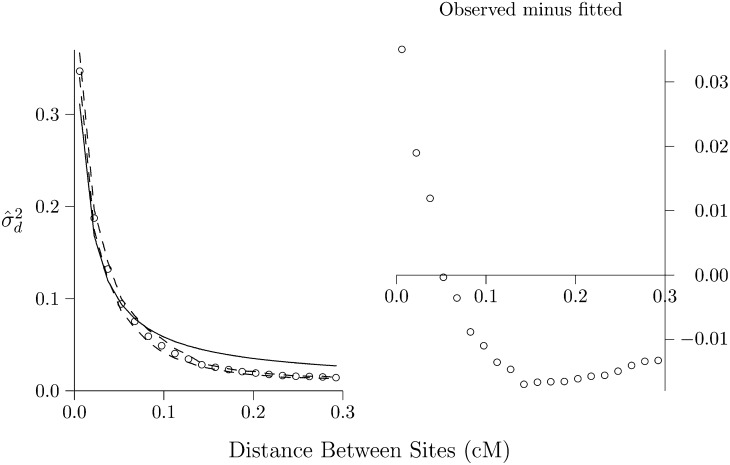
The present methods, however, are useful in exploratory data analysis, as shown in Figure 11. The open circles show ${\widehat{\sigma }}_{\text{d}}^2,$ as estimated from chromosome 1 in European data (1000 Genomes Project Consortium 2012). These are surrounded by dashed lines, which indicate a 95% confidence region generated by moving-blocks bootstrap. These show that chromosome 1 provides accurate estimates of ${\sigma }_{\text{d}}^2.$ Hill (1981) expressed skepticism about the possibility of estimating population size from data on LD. At that time only limited data were available, and it was not possible to estimate LD statistics with great accuracy. This inaccuracy bled into estimates of population size. The narrow confidence region in Figure 11 shows that things have changed.

Figure 11.

LD curve for chromosome 1 in Europe. In the left panel, open circles show the estimated values of ${\sigma }_{\text{d}}^2,$ and dashed lines show a 95% bootstrap confidence region, generated by moving-blocks bootstrap. Solid line shows the equilibrium curve that minimizes squared errors between observed and expected values. In the right panel, differences between observed and fitted values are shown. All analyses are based on a sample of 120 chromosomes. Source: CEU data set from the 1000-Genomes project (1000 Genomes Project Consortium 2012). Genetic map data, downloaded from the 1000-Genomes website, were estimated from phased haplotypes in HapMap Release 22 (NCBI 36) (HapMap 2007).

The solid line in Figure 11 shows the equilibrium curve that fits these data best—the one that minimizes squared errors between observed and predicted values of ${\widehat{\sigma }}_{\text{d}}^2.$ This is the curve for a population of constant size, 2N = 8621. In Figure 11, right, we see the differences between observed and fitted values. Because these differences are positive on the left but negative on the right, it is clear that the observed LD curve declines more steeply than any equilibrium curve. As we have seen, this suggests a history of population expansion in Europe, in agreement with many other analyses of European data.

Discussion

${\sigma }_d^2$ has never been valued for its own sake. It is seen instead as an approximation to the quantity of real interest—the expected value of r². Yet it is often a poor approximation, even in populations of constant size (Maruyama 1982; Hudson 1985, pp. 616–617). It is even worse when population size varies.

Following a change in population size, the mean of r² converges toward its new equilibrium far faster than does ${\sigma }_{\text{d}}^2.$ Presumably, this is because ${\sigma }_{\text{d}}^2$ is sensitive to loci with high heterozygosity, and the gene trees of such loci are deep. Whatever the cause, this difference in rates of convergence has two effects. First, it makes ${\sigma }_{\text{d}}^2$ useless as an approximation to r² in populations that have varied in size. On the other hand, it also means that ${\sigma }_{\text{d}}^2$ itself provides a deep record of demographic history.

To take advantage of this extended record, one must estimate ${\sigma }_{\text{d}}^2$ directly from data. This is easy to do, by using averages in place of the expectations in Equation 2. With genome-scale data, such estimates are quite accurate. This provides a measure of LD that is unique in that one can easily calculate expected LD from the history of population size. With other measures, such inferences would require extensive computer simulations.

Following a population expansion, drift is weak and the dynamics of LD are dominated by recombination. The LD curve begins to decline, and this decline is fastest in the right-hand portion of the curve, where recombination rates are highest. Consequently, the curve will be unusually steep for hundreds of generations following a population expansion.

Following a population collapse, drift becomes strong and dominates the dynamics. It pushes LD upward rapidly and relatively uniformly throughout the curve. Thus, the LD curve becomes high and flat. This pattern has been reported for several human populations, including high-latitude foragers (Kaessmann et al. 2002) and Ashkenazi Jews (Shifman and Darvasi 2001). Yet as Pritchard and Przeworski (2001, p. 7) observe, it has been difficult to explain:

We have several examples in which large regions exhibit more LD than would be expected under either a model of constant population size or a model with rapid population growth. Yet, at the same time studies of polymorphism at a small scale reveal less LD than would be expected. These observations at different scales are hard to accommodate in a single explanation since factors that increase long-distance LD will tend to have an even larger effect on closely linked sites.

As we have seen, this pattern arises naturally from a recent reduction in population size.

A bottleneck in population size begins with an episode of population collapse. At the end of the bottleneck, the LD curve is therefore high but flat. As population size rises at the end of the bottleneck, genetic drift becomes weak and recombination grows in importance. The right portion of the LD curve falls faster than the left, so the curve becomes steeper.

In the left portion of the curve, recombination is weak. Genetic drift is also weak, because of the increase in population size. This allows mutation to play an important role, and its effect distinguishes the two forms of expansion: from equilibrium and from a bottleneck. In the former case, the preexpansion population had little heterozygosity, so each mutational increment has a large proportional effect on the denominator of ${\sigma }_{\text{d}}^2.$ After a bottleneck, the opposite is true, so the left portion of the LD curve declines more slowly. The curve becomes even steeper after a bottleneck than after an expansion from equilibrium.

In summary, (1) when recombination is strong relative to drift, LD declines and the curve becomes steeper; (2) when drift is strong relative to recombination, LD rises but the curve stays flat; and (3) where drift and recombination are both weak, the rate of decline in LD decreases with heterogyzosity.

In the human population of Europe, the LD curve is steep, suggesting a history of population expansion. This might reflect the spread of modern humans into Europe, the spread of farmers during the Neolithic, or the spread of Indo-European speakers.

Appendix

Hill’s model of LD evolution

Hill (1975) incorporates mutation, using the model of infinite alleles. However, most modern work involves either DNA sequence data or SNPs. In these data, alleles are nucleotide states: A, T, G, or C. Nearly all loci have just two alleles, so it is not appropriate to assume an infinity of alleles. Yet as we shall see, Hill’s (1975) results also apply to a more appropriate mutational model—that of “infinite sites” (Kimura 1969), which assumes that mutation never strikes the same site twice.

Hill begins with a vector of moments:

$$y_{hi,jk}=\left(\begin{array}{l}E\left[a_h{a}_i{b}_j{b}_k\right]\hfill \\ E[a_h{b}_j{D}_{ik}+a_h{b}_k{D}_{ij}+a_i{b}_j{D}_{hk}+a_i{b}_k{D}_{hj}]\hfill \\ E\left[D_{hj}{D}_{ik}+D_{hk}{D}_{ij}\right]\hfill \end{array}\right).$$

Here a_i and b_j are the frequencies of allele A_i at locus A and allele B_j at locus B. The disequilibrium coefficients, D_ij, are defined such that a_ib_j + D_ij is the frequency of gamete type A_iB_j. The dynamics of these moments are approximately linear, after dropping terms in u², 1/N², and u/N, where u is the mutation rate and N the diploid population size. Thus, Hill (1975, equation 1) shows that

$$y_{hi,jk}\left(t+1\right)\approx \mathbf{DRM}{y}_{hi,jk}\left(t\right),$$

where D, R, and M are matrices describing the linear effects of drift, recombination, and mutation. So far, the model describes only the changes in frequency of existing alleles. Thus it applies not only to Hill’s model of infinite alleles, but also to the model of infinite sites.

To incorporate mutation, Hill defines a new vector,

$$x={\displaystyle \sum _{h\ne i}{\displaystyle \sum _{j\ne k}{y}_{hi,jk}}},$$ (A1)

where the sums run across all pairs of alleles at each locus. The dynamics of this new vector include an additive contribution, Δx_mut, which represents the effect of mutation to new alleles:

$$x\left(t+1\right)\approx \mathbf{DRM}x\left(t\right)+\Delta x_{\text{mut}}\left(t\right).$$ (A2)

This equation can be iterated across many generations, and it is easy to incorporate changes in population size. At the end of this process, ${\sigma }_{\text{d}}^2$ is calculated as x₃/2x₁ (Hill 1975, p. 124).

The first term on the right side of Equation A1 applies equally to both mutational models. Some reinterpretation is required, however, to relate the second term to the model of infinite sites. In this new context, Δx_mut becomes the contribution of mutations at other sites in the genome, rather than that from new alleles at the same pair of sites. The mutational increments are, however, identical in the two models.

To see that this is so, let us take a close look at the mutational contributions to x, the vector defined above in Equation A1. Under the model of infinite sites, mutation never strikes the same site twice, so each polymorphic site has exactly two alleles. In this biallelic context, we can simplify Hill’s vector of moments as

$$h=\left(\begin{array}{c}E\left[a\left(1-a\right)b\left(1-b\right)\right]\\ E\left[\left(1-2a\right)\left(1-2b\right)D\right]\\ E\left[D^2\right]\end{array}\right).$$ (A3)

Here, a and b are the frequencies of alleles A₁ and B₁, and D is the coefficient of linkage disequilibrium. It is defined such that ab + D is the frequency of gamete type A₁B₁. When each locus is biallelic, Hill’s multiallelic moments reduce to x₁ = 4h₁, x₂ = 4h₂, and x₃ = 8h₃ (Hill 1975, p. 123).

The mutational increments, Δx_mut and Δh_mut, both depend on the heterozygosity, H = E[2a(1 − a)]. The dynamics of heterozygosity under infinite sites are the same as those under infinite alleles (Hill 1975, p. 120):

$$H_{t+1}\approx 2u+\left(1-\frac{1}{2N}-2u\right)H_t.$$

The h_i are nonzero only if both loci are polymorphic. On the other hand, our model assumes that mutation affects only monomorphic sites. This implies that mutational increments to h occur only at pairs of sites in which one site is polymorphic and the other monomorphic. Table A1 summarizes the case in which A is initially polymorphic, and a mutation strikes an initially monomorphic locus, B.

Table A1. Effect of a single mutation at B, assuming that A is initially polymorphic.

	Gamete frequencies
Case	A1B1	A1B0	A0B1	A0B0	D
General	w	x	y	z	wz − xy
Before mutation	0	a	0	1 − a	0
A1-linked mutation	1/2N	a − 1/2N	0	1 − a	(1 − a)/2N
A0-linked mutation	0	a	1/2N	1 − a − 1/2N	− a/2N

Consider first the increment to h₁ = E[a(1 − a)b(1 − b)]. Before mutation, h₁ = 0 because b = 0. After mutation, b = 1/2N, so h₁ becomes E[a(1 − a)(1/2N − 1/4N²)] ≈ H/4N. This accounts for only half the effect of mutation, because there are also pairs at which A is monomorphic and B polymorphic. The expected effect of a single mutation is thus ∼H/2N. The expected number of such mutations per generation is 2Nu. In aggregate, therefore, the increment from mutation is Δ_muth₁ ≈ uH.

To derive the mutational increment to h₂ = E[(1 − 2a)(1 − 2b)D], we assume as before that A is polymorphic but B is not. Because D is zero when either site is monomorphic, h₂ = 0 before mutation. After mutation, there are two cases to consider. With probability a, the mutation falls on an A₁-bearing gamete, and h₂ becomes (1 − 2a)(1 − 2/2N)(1 − a)/2N, as shown in Table A1. On the other hand, with probability 1 − a the mutation falls on an A₀-bearing gamete, and h₂ becomes −(1 − 2a)(1 − 2/2N)a/2N. In expectation, the new value of h₂ is 0. This result is conditional on a mutation at locus B, but an identical argument applies for mutation at locus A. Thus, Δ_muth₂ = 0.

The third moment is h₃ = E[D²]. Because B is initially monomorphic, D₂ = 0 before the mutation. When a mutation occurs at B, it strikes an A₁-bearing gamete with probability a and an A₀-bearing gamete with probability 1 − a. The resulting values of D are shown in Table A1. Squaring these and weighting by a and 1 − a gives

$$E[a\left\{\frac{{\left(1-a\right)}^2}{4N^2}\right\}+\left(1-a\right)\left\{\frac{a^2}{4N^2}\right\}]=\frac{H}{8N^2}.$$

This is the effect on D² of a single mutation at B. There are 2Nu such mutations per generation, so the expected increment from mutation at locus B is 2Nu × H/8N² = uH/4N. Finally, multiply by 2 to account for cases in which A is initially monomorphic and B polymorphic. This gives Δ_muth₃ = uH/2N ≈ 0, ignoring terms of order u/N.

In summary,

$${\mathrm{\Delta }}_{\text{mut}}h\approx \left[uH,0,0\right],$$ (A4)

in agreement with Hill (1975, p. 121). This shows that the mutational increment is the same under the models of infinite sites and infinite alleles. Because of this equivalence, Hill’s results apply equally to both models of mutation.

Estimating Linkage Disequilibrium with Partially Phased Diploid Data

In 1000-genotypes data, not all genotypes are phased. At different loci, the unphased genotypes may correspond to different individuals. Thus, we need a method that can deal with unphased genotypes scattered throughout the data matrix.

The symbols j, k, l, and m represent alleles and will always equal either 0 or 1. I write phased two-locus genotypes in form $\begin{array}{c}jk\\ lm\end{array},$ which says that a diploid individual has genotype jk at locus A and genotype lm at locus B. This represents the union of gametes $\begin{array}{c}j\\ l\end{array}$ and $\begin{array}{c}k\\ m\end{array}.$ This genotype is unordered, in that we cannot distinguish the maternal gamete from the paternal one. Consequently, there is no distinction between $\begin{array}{c}jk\\ lm\end{array}$ and $\begin{array}{c}kj\\ ml\end{array}.$ When I write genotypes in this form, I imply that linkage phase is known. In other words, genotypes $\begin{array}{c}jk\\ lm\end{array}$ and $\begin{array}{c}jk\\ ml\end{array}$ are not equivalent.

Consider a tiny two-locus data set, consisting of three diploid individuals:

$$G_1,G_1,G_3=\begin{array}{c}{j}_1{k}_1\\ l_1{m}_1\end{array},\begin{array}{c}{j}_2{k}_2\\ l_2{m}_2\end{array},\begin{array}{c}{j}_3{k}_3\\ l_3{m}_3\end{array}.$$

On the right, each row corresponds to a locus and each column to a gamete. To estimate linkage disequilibrium (D), we would need to calculate $S={\displaystyle {\sum }_{i=1}^6{x}_i{y}_i},$ where x_i is the ith value in the upper row and y_i is the corresponding value in the lower one. This sum can be written as

$$\begin{array}{c}S=s_1+s_2+s_3=\left(j_1{l}_1+k_1{m}_1\right)+\left(j_2{l}_2+k_2{m}_2\right)+\left(j_3{l}_3+k_3{m}_3\right).\end{array}$$

Here, s_i = j_il_i + k_im_i is the contribution of the ith diploid genotype. This calculation requires phased data, and it is the only step where such data are required in estimating D. To cope with unphased data, we need a method to estimate s_i.

Consider the function $s\left(\begin{array}{c}jk\\ lm\end{array}\right)=jl+km.$ If at least one genotype is homozygous, then phasing does not matter. For example, $s\left(\begin{array}{c}jk\\ ll\end{array}\right)=s\left(\begin{array}{c}kj\\ ll\end{array}\right).$ We can calculate s regardless of phasing. The only genotypes that need concern us are those in which both loci are heterozygous.

As mentioned above, all genic values (j, k, l, and m) are either 0 or 1. Double heterozygotes will look like either $\begin{array}{c}01\\ 01\end{array}$ or $\begin{array}{c}01\\ 10\end{array}.$ (I ignore the equivalent representations $\begin{array}{c}10\\ 10\end{array}$ and $\begin{array}{c}10\\ 01\end{array},$ because genotypes are unordered.) With unphased data, we cannot distinguish between these two cases. Yet they imply different values: $s\left(\begin{array}{c}01\\ 01\end{array}\right)=1$ but $s\left(\begin{array}{c}01\\ 10\end{array}\right)=0.$ For double heterozygotes, I replace s with its expected value, which equals the probability, w, that the genotype is of form $\begin{array}{c}01\\ 01\end{array}$ rather than $\begin{array}{c}01\\ 10\end{array}.$

To calculate this probability, I begin with standard results for the frequencies of the four gamete types, as shown in Table A2. Following Rogers and Huff (2009), I ignore recombination in the most recent generation. Under random mating, these gametes form at random to produce two-locus genotypes. The frequency of genotype $\begin{array}{c}01\\ 01\end{array}$ among double heterozygotes is thus

$$w=\frac{2p_0{p}_3}{2p_0{p}_3+2p_1{p}_2}=\frac{D+Z}{D+2Z},$$ (A5)

where

$$Z=\alpha -\beta D+D^2,$$

$$\alpha =a\left(1-a\right)b\left(1-b\right),$$

and

$$\beta =a+b-2ab.$$

These results can be used to estimate D using the EM algorithm (Dempster et al. 1977). Let K represent the number of unphased double heterozygotes. Each of these is of type $\begin{array}{c}01\\ 01\end{array}$ with probability w and of type $\begin{array}{c}01\\ 10\end{array}$ with probability 1 − w. The expected log likelihood is

$$E\hspace{0.17em}\ln \hspace{0.17em}L={\displaystyle \sum _{i=0}^3{n}_i\hspace{0.17em}\ln \hspace{0.17em}{p}_i}+K[w\left(\ln \hspace{0.17em}{p}_0+\ln \hspace{0.17em}{p}_3\right)+\left(1-w\right)\left(\ln \hspace{0.17em}{p}_1+\ln \hspace{0.17em}{p}_2\right)]=\left(n_0+Kw\right)\ln \hspace{0.17em}{p}_0+\left(n_1+K\left(1-w\right)\right)\ln \hspace{0.17em}{p}_1+\left(n_2+K\left(1-w\right)\right)\ln \hspace{0.17em}{p}_2+\left(n_3+Kw\right)\ln \hspace{0.17em}{p}_3.$$

Note that E ln L depends on p₀, p₁, p₂, and p₃, which are themselves functions of D. The maximum-likelihood estimate of D is the value that maximizes E ln L.

Table A2. Gamete types and frequencies.

Gamete	Sample count	Population frequency
$\begin{array}{c}0\\ 0\end{array}$	n0	p0 = (1 − a)(1 − b) + D
$\begin{array}{c}0\\ 1\end{array}$	n1	p1 = (1 − a)b − D
$\begin{array}{c}1\\ 0\end{array}$	n2	p2 = a(1 − b) − D
$\begin{array}{c}1\\ 1\end{array}$	n3	P3 = ab + D

n_i is the number of copies of gamete i in the sample, excluding unphased double heterozygotes. p_i is the frequency of that gamete type within the population. a is the frequency of allele 1 at locus A, b is the frequency of allele 1 at locus B, and D is the conventional coefficient of linkage disequilibrium.

This is a unidimensional maximization problem, because D is the only unknown. D cannot fall outside the range $\left[\underset{¯}{D},\overline{D}\right],$ where $\underset{¯}{D}$ is the maximum of −a(1 − b) and −b(1 − a), and $\overline{D}$ is the minimum of a(1 − b) and b(1 − a) (Lewontin 1964, p. 55). The initial value of D is set assuming that w = 1/2. In each iteration, if d²E ln L/dD² < 0, then the algorithm tries a Newton step (Hamming 1973, p. 68). If the result is within $\left[\underset{¯}{D},\overline{D}\right],$ then the Newton step is accepted. Otherwise, the algorithm uses a modified version of the bisect algorithm (Hamming 1973, p. 62) to move in the uphill direction, as indicated by the sign of dE ln L/dD.

The modification to bisect allows the algorithm to make large steps when it seems likely that the optimum is at a boundary. For example, if dE ln L/dD > 0 at the current value of D, then motion is to the right, toward $\overline{D}.$ Before deciding how far to move, the algorithm checks the sign of the derivative at $\overline{D}.$ If both derivatives are positive, then the algorithm takes a big step, moving 80% of the distance from D to $\overline{D}.$ But if the two derivatives have opposite sign, then the algorithm takes a small step, moving only 50% of the way to $\overline{D}.$ When dE ln L/dD < 0, the algorithm is similar, except that motion is to the left, toward $\underset{¯}{D}.$