Abstract
Computational analyses have been used to study the biomechanical microenvironment of the chondrocyte that cannot be assessed by in vitro experimental studies; yet all computational studies thus far have focused on the effect of zonal location (superficial, middle, and deep) on the mechanical microenvironment of chondrocytes. The aim of this paper was to study the effect of both zonal and radial locations on the biomechanical microenvironment of chondrocytes in inhomogeneous cartilage under unconfined stress relaxation. A biphasic multiscale approach was employed and nine chondrocytes in different locations were studied. Hyperelastic biphasic theory and depth-dependent aggregate modulus and permeability of articular cartilage were included in the models. It was found that both zonal and radial locations affected the biomechanical stresses and strains of the chondrocytes. Chondrocytes in the mid-radial location had increased volume during the early stage of the loading process. Maximum principal shear stress at the interface between the chondrocyte and the extracellular matrix (ECM) increased with depth, yet that at the ECM-pericellular matrix (PCM) interface had an inverse trend. Fluid pressure decreased with depth, while the fluid pressure difference between the top and bottom boundaries of the microscale model increased with depth. Regardless of location, fluid was exchanged between the chondrocyte, PCM, and ECM. These findings suggested that even under simple compressive loading conditions, the biomechanical microenvironment of the chondrocytes, PCM and ECM were spatially dependent. The current study provides new insight on chondrocyte biomechanics.
Keywords: Chondrocyte, Cartilage, Biphasic, Multiscale, Cell Mechanics
1 Introduction
Articular cartilage is an avascular hydrated connective tissue serving as a low-friction, load-bearing material in diarthrodial joints, and has complex mechanical properties such as depth-dependent inhomogeneity (Schinagl et al., 1997; Wang et al., 2001) and tension-compression nonlinearity (Huang et al., 2005). Chondrocytes are the only cells found in articular cartilage. They are responsible for the production and maintenance of the extracellular matrix (ECM), such as type II collagen and proteoglycan (PG) (Mow et al., 2005). Previous studies have demonstrated that mechanical stimuli modulate the biosynthetic response of chondrocytes (Grodzinsky et al., 2000; Guilak et al., 1994; Sah et al., 1989; Torzilli et al., 1997): static compression significantly inhibits synthesis of proteoglycans and proteins, whereas dynamic compression can stimulate matrix production, the latter strongly depending on the frequency and magnitude of the stimulus. The biosynthetic response of chondrocytes to mechanical stimuli is also dependent on their spatial location within the ECM (Goldring, 2012; Grodzinsky et al., 2000). Chondrocytes in the middle zone synthesize greater amounts of aggrecan than those in the superficial and deep zones, and the synthesis has been correlated with the spatial profile of interstitial fluid flow and matrix deformation (Buschmann et al., 1999; Quinn et al., 1998; Wong et al., 1997). Chondrocytes in the superficial, middle and deep zones have significantly different morphologies, mechanical properties and gene expressions (Choi et al., 2007; Darling et al., 2006; Flannery et al., 1999).
In vitro experimental studies of articular cartilage, while providing fundamental information on ECM biomechanics, are unable to quantify a number of important chondrocyte biomechanical behavior within the articular cartilage, such as local fluid pressure and flow and solid stresses in the PCM. In this regard, several studies used computational models to investigate the biomechanical microenvironment of chondrocytes (Alexopoulos et al., 2005; Baer et al., 2003; Guilak and Mow, 2000; Halloran et al., 2012; Han et al., 2007; Han et al., 2010; Julkunen et al., 2009; Kim et al., 2008; Korhonen and Herzog, 2008; Korhonen et al., 2006; Sibole and Erdemir, 2012; Wu and Herzog, 2000; Wu et al., 1999). A similar multiscale framework was used in all these computational studies, where a macroscale model (in mm) was used for a specific biomechanical test, such as confined or unconfined compression, to determine the solid displacements and fluid pressures at the chondrocyte’s location. These were then used as boundary conditions for the chondrocyte microscale model (in μm) to determine biomechanical behavior in and around chondrocytes. All previous computational studies investigated chondrocytes located at different zones (superficial, middle, and deep) of the cartilage (macroscale model) and found that zonal location effected the mechanical deformation of the chondrocytes. Specifically, superficial zone chondrocytes deformed over 3 times more than chondrocytes in the deep zone (Julkunen et al., 2009; Korhonen and Herzog, 2008; Wu and Herzog, 2000; Wu and Herzog, 2006). However, the effect of radial position of a chondrocyte in an inhomogeneous ECM has not been studied. This analysis is particularly relevant for understanding chondrocyte mechanobiology within articular cartilage subjected to unconfined compression. The aim of this paper was to model the microenvironment of chondrocytes at different spatial locations in articular cartilage during unconfined stress relaxation. We hypothesized that during mechanical loading of the ECM, the biomechanical microenvironment of the chondrocytes within the ECM is significantly affected by the zonal and radial locations of the chondrocytes.
2 Methods
Finite deformation biphasic theory
The hyperelastic biphasic theory proposed by Holmes and Mow (Holmes and Mow, 1990) was used in the present study. The governing equations are
| (1) |
| (2) |
where p is the fluid pressure, I the identity tensor, the solid phase velocity, k the permeability, and the effective stress of the solid matrix defined as
| (3) |
where J is the volume ratio defined as J= det(F), F the Jacobian determinant of the deformation gradient, and (Bonet and Wood, 1997) the Green-Lagrangian strain tensor. The strain energy density function is defined by (Holmes and Mow, 1990)
| (4) |
where I1, I2, and I3 are the invariants of the right Cauchy-Green deformation tensor, C, defined as C=FTF, the dimensionless nonlinear stiffening coefficient β=α1+2α2, and α0, α1, and α2 positive material parameters. α0, α1, and α2 are related to β, aggregate modulus, HA, and Poisson’s ratio, ν, by
| (5) |
The deformation-dependent permeability (Lai and Mow, 1980) is defined by,
| (6) |
where k0 is the initial permeability and m a material parameter.
Biphasic multiscale finite element simulations
The hyperelastic biphasic theory was implemented in COMSOL Multiphysics (Burlington, MA). Solid mechanics in the Structural Mechanics Module and Darcy’s Law in the Earth Science Module were used (Guo et al., 2013; Guo et al., 2012; Guo and Spilker, 2011; Guo and Spilker, 2012). User defined strain energy density function in COMSOL was used to input the strain energy density function (Eq. 4) (Guo et al., 2014).
The local mechanical environments around the chondrocytes in the microscale model (Fig. 1 right side) were assumed to be axisymmetric as the ECM fluid pressure and solid stress/strain gradients around the cells were less than 1% in most regions of the cartilage (Figure S1 Supplementary Material). In the biphasic multiscale approach, an axisymmetric macroscale model (Fig. 1 left side) representing articular cartilage in unconfined compression was first analyzed to determine the solid displacement and fluid pressure at each node of the finite element model. The width and thickness of the articular cartilage were 2.5 mm and 1.5 mm, respectively. Quad meshes with a size of 10×10 μm were used. A ramp displacement of 0.075 mm (5% axial compression) was linearly applied in 100s on the top surface of the articular cartilage and thereafter held as constant. The top boundary of the cartilage was free to slide in the radial direction, and a roller boundary condition was applied to the bottom boundary. A free draining boundary condition was applied to the peripheral (vertical) boundary of the cartilage. The model was solved to 3000 s at which time an equilibrium condition was achieved. Thereafter the solid displacement and fluid pressure at the chondrocyte locations within the ECM were extracted (Fig. 1, middle). Finally using these solid displacements and fluid pressures as boundary conditions for the microscale model, the microenvironmental distributions for the stresses and strains in and around the chondrocytes were determined. In the axisymmetric microscale model, a chondrocyte with a diameter of 10 μm was surrounded by the PCM with diameter of 15 μm, both of which were embedded into the ECM with width of 20 μm and height of 40 μm. The boundary condition transformations were defined by the following.
Fig. 1.

A schematic of the biphasic multiscale finite element method used in the present study. Articular cartilage morphology showing the locations of chondrocytes in the superficial, middle and deep zones of the ECM (left), and the chondrocyte in its PCM (right). The articular cartilage in unconfined compression served as the macroscale model (left). The macroscale model was meshed using quad elements with size of 10×10 μm (middle) to capture the local mechanical environment of the microscale model (right). The solid displacement and fluid pressure on the four boundaries of the 40 μm square at the chondrocyte locations within the macroscale model were transformed and input as boundary conditions into the microscale model for each cell (Eq. 7–12). The numbers in the parenthesis are spatial numbers of the element nodes for boundary conditions transformation.
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
For the solid displacement boundary conditions in the microscale model, the bottom boundary ( z̃ = 0μm ) was modeled as a roller, top boundary (z̃ = 40μm ) was compressed with mean relative axial displacement between the top and bottom boundary of the 40 μm square in the macroscale model, and the peripheral boundary (r̃ = 20μm ) was applied with mean relative radial displacement between two vertical boundaries of the 40 μm square. For the fluid pressure boundary conditions in the microscale model, the mean fluid pressure at the top and bottom boundaries of the 40 μm square in the macroscale model were applied to the top and bottom boundaries of the microscale model, respectively. Because of the axisymmetric assumption used for the microscale model, the mean fluid pressure at the two vertical boundaries of the 40 μm square was applied to the peripheral boundary of the microscale model.
Chondrocytes at nine different locations of the ECM were studied. The spatial location in (r, z) coordinates (in mm) for chondrocytes 1–9 were (0, 1.44), (1.25, 1.44), (2.4, 1.44), (0, 1.05), (1.25, 1.05), (2.4, 1.05), (0, 0.15), (1.25, 0.15) and (2.4, 0.15), respectively.
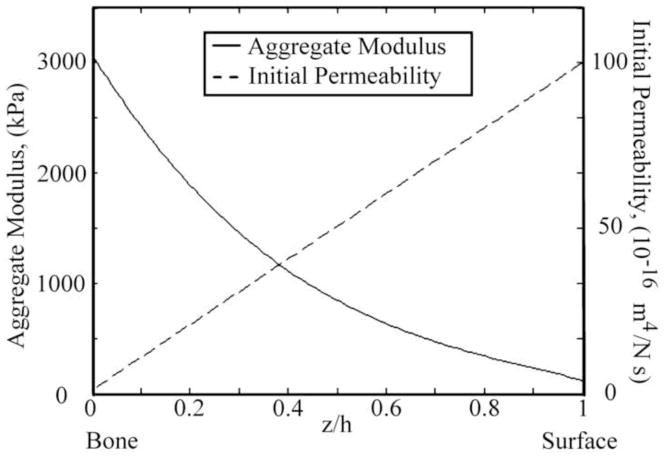
The nonlinear depth-dependent aggregate modulus of the articular cartilage was obtained from published experimental measurements (Chen et al., 2001; Schinagl et al., 1997; Wang et al., 2001) (Fig. 2). At present no experimental measurements are available for the depth-dependency of the initial permeability k0. However, it is generally accepted that the ECM in the superficial zone is more permeable compared to the middle and deep zones. In the present study, the initial permeability k0 was assumed to decrease linearly from 1×10−14 m4/Ns at the articular surface to 1×10−16 m4/Ns at the cartilage-bone interface (Fig. 2). In the microscale model, the aggregate modulus and initial permeability of the ECM was calculated based on the zonal location of the ECM. Material properties of the chondrocyte and PCM were obtained from pervious experimental measurements (Table 1). Since β and m of the chondrocyte and PCM have not been measured, they were assumed to have the same values as those of the articular cartilage.
Fig. 2.
Depth-dependent aggregate modulus (Chen et al., 2001; Schinagl et al., 1997; Wang et al., 2001) and initial permeability of the articular cartilage used in the present study. The initial permeability k0 was assumed to decrease linearly from 1×10−14 m4/Ns at the articular surface to 1×10−16 m4/Ns at the cartilage-bone interface.
Table 1.
Material properties of the biphasic multiscale models
| Aggregate modulus (kPa) | Poisson’s ratio | β | Initial Permeability (m4/Ns) | m | ||
|---|---|---|---|---|---|---|
| superficial | middle/deep | |||||
| Chondrocyte | 0.42 (1) | 0.24 (1) | 0.38 (2) | 0.35 | 5×10−15 (3) | 2.2 |
| PCM | 40 (4, 5) | 0.04 (5) | 0.35 | 4.19×10−17(5) | 2.2 | |
| ECM/Cartilage | see Fig. 2 | 0.1 (6) | 0.35 (6) | see Fig. 2 | 2.2 (6) | |
Trickey et al., 2006;
3 Results
Volume deformation
In general, the deformation of the chondrocytes and their PCM decreased with depth (Fig. 3). The radial location of chondrocytes affected the deformation during the loading process but not at equilibrium. During the ramp loading phase, the effect of the radial location on the deformation was the greatest in the superficial zone: chondrocyte 2 and its PCM had the largest axial and radial deformation. In the middle zone, the three chondrocytes and their PCM had similar axial deformations at the end of the ramp loading phase (t=100s) while chondrocyte 5 and its PCM had the largest radial deformation. In the deep zone at t=100s, the deformations were very small and almost identical for the three chondrocytes.
Fig. 3.
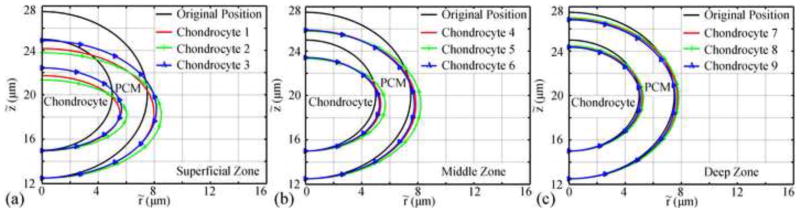
Deformation of the chondrocytes and PCM at t=100s (end of the ramp displacement or peak ramp) in different zones.
The volume ratio in the microscale models decreased with depth (Fig. 4a). At equilibrium, chondrocyte volumes decreased by about 30% in the superficial zone, 10% in the middle zone, and 2% in deep zone. In the same zone, at t=100s, microscale models in the mid-radial location had the largest volume changes. Volume at top and bottom regions of the PCM and adjacent ECM linearly increased in the first 100s, and then gradually decreased (Fig. 4c, blue and red lines). The volume ratios in the other regions of the PCM and adjacent ECM were zone dependent (Fig. 4c, green and magenta lines): in the superficial and middle zone and microscale model 9 of the deep zone, the volumes decreased until equilibrium was achieved; in microscale models 7 and 8 of the deep zone, the volume linearly increased in the first 180s and then slowly decreased. The volume of chondrocytes 1, 4, 6 and 9 (Fig. 4c, black line) decreased until equilibrium was achieved, while the volumes of the other chondrocytes increased in the first tp seconds and decreased thereafter (tp equaled to 30, 30, 100, 180 and 160 s for chondrocyte 2, 3, 5, 7 and 8, respectively).
Fig. 4.
(a) Distribution of the volume ratio at t=100s (peak ramp) in three representative cases. The microscale models had different sizes due to the deformation difference. (b) Five locations were chosen to study the change of the local volume ratio as a function of time. The interface points were 0.5 μm away from the edge to avoid the discontinuous behaviors at the interface. (c) Changes of the local volume ratio with time at different locations in three representative microscale models.
Solid Stresses and Strains
The distributions of stresses and strains in the microscale models (Fig. 5) were similar at each location, but the magnitudes varied with zonal and radial location of the chondrocytes. Low stresses and high strains were found in all chondrocytes. Discontinuities or jumps in the stresses and strains were found at the chondrocyte-PCM and PCM-ECM interfaces, with larger jumps at the PCM-ECM interface.
Fig. 5.
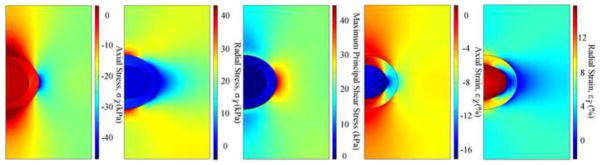
Distributions of stresses and strains in the microscale model of chondrocyte 5 at t=100s (peak ramp). Results for other chondrocytes are similar except for the magnitudes.
Axial and radial stresses
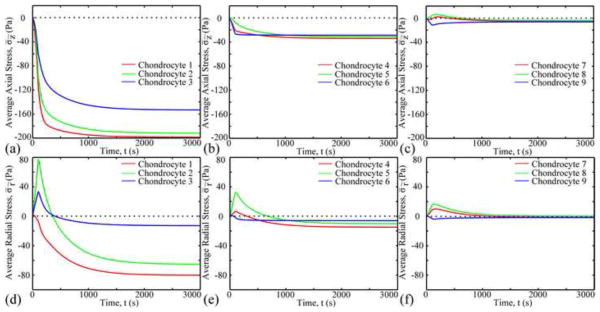
At t=100s, high axial stresses were found in the ECM adjacent to the radial apex of the PCM, and low axial stresses were found in the ECM adjacent to the two vertical apexes of the PCM (Fig. 5). Average axial stresses in the ECM and PCM were over two orders of magnitude and 30 times larger than that in chondrocytes, respectively. The average axial stress in chondrocytes changed with time and zonal and radial location (Fig. 6). Axial stresses in chondrocytes 7 and 8 of the deep zone switched between tension and compression, while only compressive axial stresses occurred in other chondrocytes.
Fig. 6.
Change in average axial (a–c) and radial (d–f) stresses in different chondrocytes as a function of time.
At t=100s, distributions of the radial stress were opposite to those of the axial stress (Fig. 5). Radial stress decreased with depth. Average radial stress in chondrocytes 1, 6 and 9 decreased until equilibrium was achieved, while other chondrocytes increased in the first 100s and then decreased until equilibrium was achieved. At equilibrium, average radial stresses of chondrocyte 2 and 3 were over 4 times larger than those of the other chondrocytes.
Shear stress
High maximum principal shear stress was found around the PCM. The peak shear stress was in the ECM adjacent to the radial apex of the PCM (Fig. 5). For a specific microscale model, the maximum principal shear stress at the chondrocyte-PCM and PCM-ECM interfaces similarly varied as a function of time but had different magnitudes (Fig. 7). The maximum principal shear stress at the chondrocyte-PCM interface decreased with depth, yet that at the PCM-ECM interface had an inverse trend. In the same zone, chondrocytes in the mid-radial location were subjected to the largest maximum principal shear stress for t<200s. However, at equilibrium, the microscale models in the same zone were subjected to similar maximum principal shear stress at the interfaces.
Fig. 7.
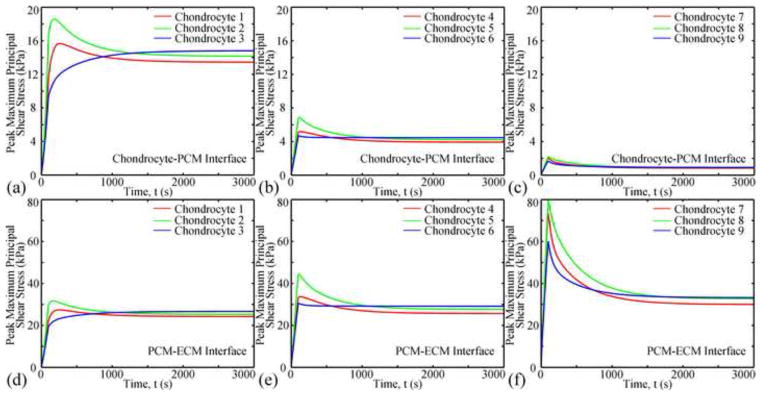
Changes of the peak maximum principal shear stress with time at the chondrocyte-PCM (ac) and PCM-ECM interfaces (d–f).
Axial and radial strains
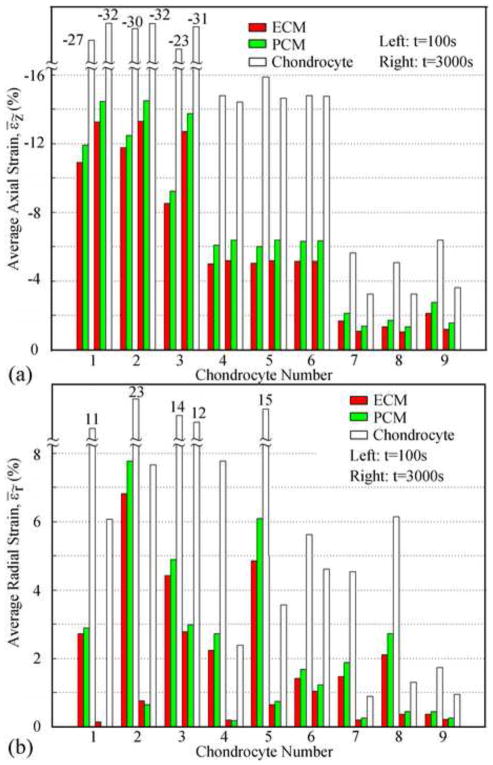
Relatively uniform axial strains were found in all chondrocytes (Fig. 5) and decreased with depth (Fig. 8a). In the superficial zone the average compressive axial strains in the ECM, PCM, and chondrocyte increased after the peak ramp (i.e. end of the ramp displacement), did not significantly change in the middle zone, and decreased in the deep zone. At t=100s, average axial strain in the chondrocytes was 3.0±0.4 times those in the ECM, and 2.5±0.2 times those in the PCM. At equilibrium (t=3000s), the strain amplifications were 2.8±0.3 and 2.3±0.1, respectively.
Fig. 8.
Average axial strain (a) and radial strain (b) in ECM, PCM, and chondrocyte in different locations. Sets of data on the left are at t=100s and those on the right are at t=3000s.
All chondrocytes were subjected to relatively uniform radial strains (Fig. 5) which decreased after peak ramp until equilibrium was achieved (Fig. 8b). In the same zone, chondrocytes in the mid-radial location were subjected to the largest radial strains at t=100s, while at equilibrium, the radial strains increased from the center to the periphery. Similar strain amplifications to that of the axial strain were observed for the radial strains. At t=100s, average radial strains in the chondrocytes were 3.6±0.6 times those in the ECM, and 3±0.6 times those in the PCM. At equilibrium, the strain amplifications were over 11 times for chondrocytes 1, 2 and 4, while for the rest of the chondrocytes the average radial strains was 4.5±0.6 times those in the ECM and 3.9±0.6 times those in the PCM.
Fluid pressure and velocity
Two fluid flux patterns with different flux directions were observed (Fig. 9). Interstitial fluid flowed around and through the chondrocytes. Average fluid velocities within the PCM and chondrocyte (0.5–5 nm/s) were 10–40 times smaller than those in the ECM. In the superficial zone, the fluid pressure at the top boundary of the microscale model was always larger than that at the bottom boundary (Fig. 10). However in the middle and deep zones, fluid pressure between the top and bottom boundaries varied between positive and negative values. Fluid pressure decreased with depth and reached equilibrium faster in the superficial zone than in the middle and deep zones (400s vs1200s), while the pressure difference increased with depth.
Fig. 9.
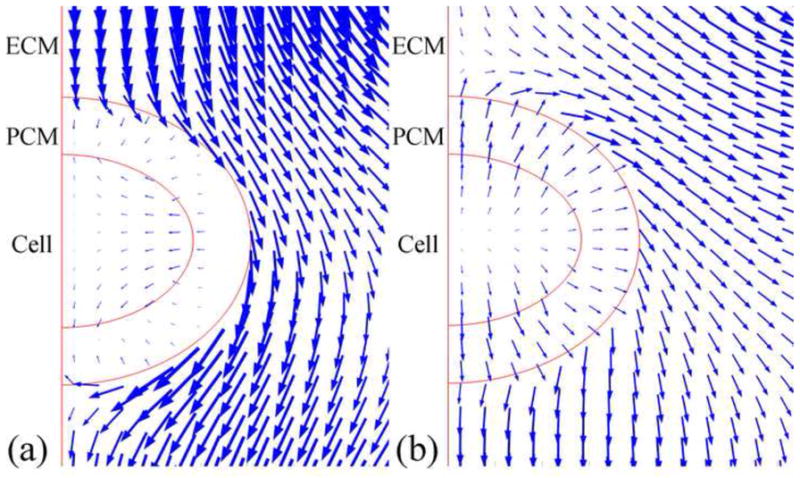
Two fluid flow patterns were observed in the microscale models. Only part of the model around the chondrocyte is shown.
Fig. 10.
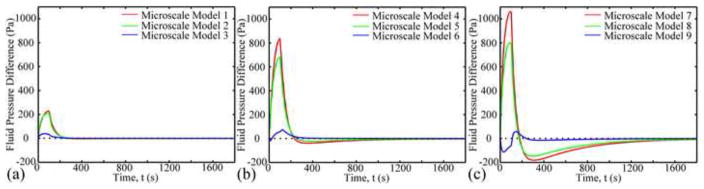
Fluid pressure difference between top and bottom boundaries of the microscale models (top - bottom).
4 Discussion
Using biphasic multiscale finite element analyses, the mechanical microenvironment of chondrocytes in different zonal and radial locations were investigated. It was found that both zonal and radial locations had a significant influence on the solid stresses and strains and fluid pressure in the ECM, PCM, and chondrocytes. Chondrocyte volume deformations and strains were zone dependent (Fig. 3 and 4), decreasing from the superficial zone (~30%) to the deep zone (~2%). This finding is consistent with previous experimental (Choi et al., 2007; Guilak, 1995; Thambyah and Broom, 2013; Wong et al., 1997) and computational studies (Alexopoulos et al., 2005; Han et al., 2007; Julkunen et al., 2009; Korhonen and Herzog, 2008; Wu and Herzog, 2006). The present study also found that the top and bottom regions of the PCM and adjacent ECM had increased volume during the early loading phase (Fig. 4 and 5). This was probably due to the fact that the chondrocyte is two orders of magnitude softer than the PCM and ECM, so that the PCM and ECM would be subjected to little resistance from the chondrocyte when compressed. Increased volume of the PCM and ECM could make the material more permeable and increase the fluid transport between the ECM and chondrocyte. Chondrocytes 5, 7, and 8 had larger volume increases during the loading phase than chondrocyte 2 and 3 (7% vs 2%, respectively). It was also found that the time to reach the peak volume increased with depth (30s vs 180s), suggesting that the mechanobiological response of the chondrocytes in the middle and deep zones may be delayed. The volume increases and decreases of the chondrocyte were a result of competition between tensile or compressive stresses in the radial and axial direction: tensile stress increased the volume and compressive stress decreased the volume (Fig. 6). This result indicates that although the ECM was in compression, some chondrocytes could have increased volume due to the local microenvironment.
Consistent with previous computational studies (Alexopoulos et al., 2005; Guilak and Mow, 2000; Kim et al., 2008), the present study observed jumps in the stress and strain at the chondrocyte-PCM and PCM-ECM interfaces (Fig. 5). This is typical of bi-material interfaces. The jump at the PCM-ECM interface was larger than that at the chondrocyte-PCM interface, suggesting that the PCM serves as a cushion to protect the chondrocyte from the ECM deformation. Since the cartilage in this model was subjected to compressive loads, chondrocytes might be expected to be also under compression; whereas an interesting finding of the current study was that chondrocytes 7 and 8 in the deep zone were subjected to compressive and tensile axial stresses, with the tensile stress being smaller than the compressive stress (Fig. 6). Zonal and radial locations had strong influences on the chondrocyte microenvironment, therefore, both competed with each other and resulted in a mixed effect, for example, average radial stresses in chondrocytes 1, 6 and 9 always decreased, while stresses on chondrocytes in other locations increased in the first 100s and then decreased. Future studies combing finite element and statistical analyses (Leatherman et al., 2014) may reveal further details of this mixed effect.
Maximum principal shear stresses around the chondrocytes were also zone dependent (Fig. 7). Peak shear stress at the PCM-ECM interface increased with depth, while at the chondrocyte-PCM interface they decreased. This finding is probably due to the moduli difference at the interface, which increased with depth at the PCM-ECM interface and was relatively uniform at the chondrocyte-PCM interface (Darling et al., 2006; Guilak et al., 2005; McLeod et al., 2013; Schinagl et al., 1997; Wang et al., 2001).
Strain amplification was observed in the current study (Fig. 8), which is consistent with previous computational (Alexopoulos et al., 2005; Baer et al., 2003; Han et al., 2007; Julkunen et al., 2009; Kim et al., 2008; Korhonen and Herzog, 2008; Wu and Herzog, 2006) and experimental studies (Chahine et al., 2007; Choi et al., 2007; Upton et al., 2008). The magnitude of the strain amplification was about 3, which was within the range of 2–7 reported in previous studies of static loading (Alexopoulos et al., 2005; Chahine et al., 2007). During dynamic loading the strain amplification can be as high as 20 (Kim et al., 2008). Future studies using the current biphasic multiscale approach will be needed to understand dynamic microenvironment of the chondrocyte. The current study also found that radial location affected the axial strain in the microscale models during the ramp loading phase, but not at equilibrium. Another unique finding was that the average axial strain in the ECM, PCM, and chondrocyte increased after the peak ramp in the superficial zone, but did not significantly change in the middle zone, and decreased in the deep zone. Whether or not this finding could correspond to differences in biosynthetic activity of zonal chondrocytes remains unknown.
Due to the low permeability of the PCM, fluid flowed around and through the chondrocyte and PCM (Fig. 9), and intracellular fluid flux was very small (~0.5–5 nm/s), which is consistent with a previous theoretical study (Ateshian et al., 2007). Fluid pressure was found to decrease with depth, while the fluid pressure difference between the top and bottom boundaries of the microscale model increased with depth (Fig. 10). Previous studies had found that fluid shear stress alters chondrocyte metabolism (Smith et al., 2004). Fluid shear stress can be estimated by (Hou et al., 1989), where ω∞ is the fluid velocity, μf the viscosity of the fluid, and k the permeability. The maximum value of the average fluid velocity in the ECM was 170 nm/s. Using the apparent permeability of cartilage (5×10−15 m4/Ns) and viscosity of water (1 mPa*s), the peak fluid shear stress was 0.76 Pa. Since the peak maximum principal shear stress caused by the solid deformation was over 1 kPa, the fluid shear stress was negligible during the static loading condition studied herein. However during dynamic loading, the effect of fluid shear stress might be greater due to larger transient fluid flows.
One limitation of the current study was modeling chondrocytes as spherical in all zones. While this assumption is consistent with most previous computational studies, clearly the shape of the chondrocytes is zone dependent. Several computational studies of chondrocytes in the axisymmetric axis of the macroscale model reported that chondrocyte geometry affected the local deformation behavior in and around the chondrocyte (Baer et al., 2003; Chahine et al., 2007). In the future, it would be of interest to study the effect of chondrocyte shape on their mechanical behavior in different zonal and radial locations. Another limitation was the 2D axisymmetric assumption for the microscale model of chondrocyte close to the edge of the cartilage. Even though relative differences of the solid displacements and fluid pressure in the axial direction between the element node value and the mean value were less than 1%, relative differences of fluid pressure in the radial direction could be as high as 10% (Figure S1 Supplementary Material), which might affect the fluid phase results.
In summary, the mechanical microenvironment of chondrocytes in different zonal and radial locations was studied using biphasic multiscale finite element models. Both locations were shown to have a strong influence on the mechanical microenvironment of the chondrocytes. The current study provides new insights in understanding chondrocyte biomechanics: radial location of chondrocytes affected the deformation during the loading process but not at equilibrium; chondrocytes in the mid-radial location had increased volume during the loading process; jumps of stress and strain at the PCM-ECM interface was larger than those at the chondrocyte-PCM interface; shear stress at the PCM-ECM interface increased with depth, yet those at the chondrocyte-PCM interface had an inverse trend; fluid pressure decreased with depth, while the fluid pressure difference between the top and bottom boundaries of the microscale model increased with depth; and, during static loading condition, fluid shear stress was negligible compared to the solid shear stress. This information will be helpful in the study of chondrocyte mechanobiology when cartilage is subjected to static loading both in vitro and in vivo.
Supplementary Material
Acknowledgments
Research reported in this publication was supported in part by the National Institute of Arthritis and Musculoskeletal and Skin Diseases, part of the National Institutes of Health, under Award Number AR057343. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Conflict of interest
None
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexopoulos LG, Setton LA, Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomaterialia. 2005;1:317–325. doi: 10.1016/j.actbio.2005.02.001. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Costa KD, Hung CT. A theoretical analysis of water transport through chondrocytes. Biomechanics and Modeling in Mechanobiology. 2007;6:91–101. doi: 10.1007/s10237-006-0039-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baer AE, Laursen TA, Guilak F, Setton LA. The micromechanical environment of intervertebral disc cells determined by a finite deformation, anisotropic, and biphasic finite element model. Journal of Biomechanical Engineering. 2003;125:1–11. doi: 10.1115/1.1532790. [DOI] [PubMed] [Google Scholar]
- Bonet J, Wood RD. Nonlinear continuum mechanics for finite element analysis. Cambridge University Press; Cambridge, UK: 1997. [Google Scholar]
- Buschmann MD, Kim YJ, Wong M, Frank E, Hunziker EB, Grodzinsky AJ. Stimulation of Aggrecan Synthesis in Cartilage Explants by Cyclic Loading Is Localized to Regions of High Interstitial Fluid Flow. Archives of Biochemistry and Biophysics. 1999;366:1–7. doi: 10.1006/abbi.1999.1197. [DOI] [PubMed] [Google Scholar]
- Chahine NO, Hung CT, Ateshian GA. In situ measurements of chondrocyte deformation under transient loading. Journal of European Cells and Materials. 2007;13:100–111. doi: 10.22203/ecm.v013a11. [DOI] [PubMed] [Google Scholar]
- Chen A, Bae W, Schinagl R, Sah R. Depth and strain dependent mechanical and electromechanical properties of full thickness bovine articular cartilage in confined compression. Journal of Biomechanics. 2001;34:1–12. doi: 10.1016/s0021-9290(00)00170-6. [DOI] [PubMed] [Google Scholar]
- Choi JB, Youn I, Cao L, Leddy HA, Gilchrist CL, Setton LA, Guilak F. Zonal changes in the three dimensional morphology of the chondron under compression: the relationship among cellular, pericellular, and extracellular deformation in articular cartilage. Journal of Biomechanics. 2007;40:2596–2603. doi: 10.1016/j.jbiomech.2007.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darling E, Zauscher S, Guilak F. Viscoelastic properties of zonal articular chondrocytes measured by atomic force microscopy. Osteoarthritis and Cartilage. 2006;14:571–579. doi: 10.1016/j.joca.2005.12.003. [DOI] [PubMed] [Google Scholar]
- Flannery CR, Hughes CE, Schumacher BL, Tudor D, Aydelotte MB, Kuettner KE, Caterson B. Articular cartilage superficial zone protein (SZP) is homologous to megakaryocyte stimulating factor precursor and is a multifunctional proteoglycan with potential growth promoting, cytoprotective, and lubricating properties in cartilage metabolism. Biochemical and Biophysical Research Communications. 1999;254:535–541. doi: 10.1006/bbrc.1998.0104. [DOI] [PubMed] [Google Scholar]
- Goldring MB. Chondrogenesis, chondrocyte differentiation, and articular cartilage metabolism in health and osteoarthritis. Therapeutic Advances in Musculoskeletal Disease. 2012;4:269–285. doi: 10.1177/1759720X12448454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grodzinsky AJ, Levenston ME, Jin M, Frank EH. Cartilage tissue remodeling in response to mechanical forces. Annual Review of Biomedical Engineering. 2000;2:691–713. doi: 10.1146/annurev.bioeng.2.1.691. [DOI] [PubMed] [Google Scholar]
- Guilak F. Compression induced changes in the shape and volume of the chondrocyte nucleus. Journal of Biomechanics. 1995;28:1529–1541. doi: 10.1016/0021-9290(95)00100-x. [DOI] [PubMed] [Google Scholar]
- Guilak F, Alexopoulos L, Haider M, Ting Beall HP, Setton L. Zonal uniformity in mechanical properties of the chondrocyte pericellular matrix: micropipette aspiration of canine chondrons isolated by cartilage homogenization. Annals of Biomedical Engineering. 2005;33:1312–1318. doi: 10.1007/s10439-005-4479-7. [DOI] [PubMed] [Google Scholar]
- Guilak F, Meyer BC, Ratcliffe A, Mow VC. The effects of matrix compression on proteoglycan metabolism in articular cartilage explants. Osteoarthritis and Cartilage. 1994;2:91–101. doi: 10.1016/s1063-4584(05)80059-7. [DOI] [PubMed] [Google Scholar]
- Guilak F, Mow VC. The mechanical environment of the chondrocyte: a biphasic finite element model of cell–matrix interactions in articular cartilage. Journal of Biomechanics. 2000;33:1663–1673. [PubMed] [Google Scholar]
- Guo H, Maher SA, Spilker RL. Biphasic finite element contact analysis of the knee joint using an augmented Lagrangian method. Medical Engineering and Physics. 2013;35:1313–1320. doi: 10.1016/j.medengphy.2013.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo H, Nickel JC, Iwasaki LR, Spilker RL. An augmented Lagrangian method for sliding contact of soft tissue. Journal of Biomechanical Engineering. 2012;134:084503. doi: 10.1115/1.4007177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo H, Shah M, Spilker RL. A finite element implementation for biphasic contact of hydrated porous media under finite deformation and sliding. Proc Inst Mech Eng H J Eng Med. 2014;228:225–236. doi: 10.1177/0954411914522782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo H, Spilker RL. Biphasic finite element modeling of hydrated soft tissue contact using an augmented Lagrangian Method. Journal of Biomechanical Engineering. 2011;133:111001. doi: 10.1115/1.4005378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo H, Spilker RL. An augmented Lagrangian finite element formulation for 3D contact of biphasic tissues. Computer Methods in Biomechanics and Biomedical Engineering. 2012 doi: 10.1080/10255842.2012.739166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halloran J, Sibole S, Van Donkelaar C, Van Turnhout M, Oomens C, Weiss J, Guilak F, Erdemir A. Multiscale mechanics of articular cartilage: potentials and challenges of coupling musculoskeletal, joint, and microscale computational models. Annals of Biomedical Engineering. 2012;40:2456–2474. doi: 10.1007/s10439-012-0598-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han SK, Federico S, Grillo A, Giaquinta G, Herzog W. The mechanical behaviour of chondrocytes predicted with a micro structural model of articular cartilage. Biomechanics and Modeling in Mechanobiology. 2007;6:139–150. doi: 10.1007/s10237-006-0016-3. [DOI] [PubMed] [Google Scholar]
- Han SK, Federico S, Herzog W. A depth dependent model of the pericellular microenvironment of chondrocytes in articular cartilage. Computer Methods in Biomechanics and Biomedical Engineering. 2010;14:657–664. doi: 10.1080/10255842.2010.493512. [DOI] [PubMed] [Google Scholar]
- Holmes MH, Mow VC. The nonlinear characteristics of soft gels and hydrated connective tissues in ultrafiltration. Journal of Biomechanics. 1990;23:1145–1156. doi: 10.1016/0021-9290(90)90007-p. [DOI] [PubMed] [Google Scholar]
- Hou J, Holmes M, Lai W, Mow V. Boundary conditions at the cartilage synovial fluid interface for joint lubrication and theoretical verifications. Journal of Biomechanical Engineering. 1989;111:78. doi: 10.1115/1.3168343. [DOI] [PubMed] [Google Scholar]
- Huang CY, Stankiewicz A, Ateshian GA, Mow VC. Anisotropy, inhomogeneity, and tension compression nonlinearity of human glenohumeral cartilage in finite deformation. Journal of Biomechanics. 2005;38:799–809. doi: 10.1016/j.jbiomech.2004.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julkunen P, Wilson W, Jurvelin JS, Korhonen RK. Composition of the pericellular matrix modulates the deformation behaviour of chondrocytes in articular cartilage under static loading. Medical and Biological Engineering and Computing. 2009;47:1281–1290. doi: 10.1007/s11517-009-0547-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim E, Guilak F, Haider MA. The dynamic mechanical environment of the chondrocyte: a biphasic finite element model of cell matrix interactions under cyclic compressive loading. Journal of Biomechanical Engineering. 2008;130:061009. doi: 10.1115/1.2978991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korhonen RK, Herzog W. Depth dependent analysis of the role of collagen fibrils, fixed charges and fluid in the pericellular matrix of articular cartilage on chondrocyte mechanics. Journal of Biomechanics. 2008;41:480–485. doi: 10.1016/j.jbiomech.2007.09.002. [DOI] [PubMed] [Google Scholar]
- Korhonen RK, Julkunen P, Rieppo J, Lappalainen R, Konttinen YT, Jurvelin JS. Collagen network of articular cartilage modulates fluid flow and mechanical stresses in chondrocyte. Biomechanics and Modeling in Mechanobiology. 2006;5:150–159. doi: 10.1007/s10237-006-0021-6. [DOI] [PubMed] [Google Scholar]
- Lai WM, Mow VC. Drag induced compression of articular cartilage during a permeation experiment. Biorheology. 1980;17:111–123. doi: 10.3233/bir-1980-171-213. [DOI] [PubMed] [Google Scholar]
- Leatherman ER, Guo H, Gilbert S, Hutchinson I, Maher SA, Santer TJ. Using a statistically calibrated biphasic finite element model of the human knee joint to identify robust designs for a meniscal substitute. Journal of Biomechanical Engineering. 2014 doi: 10.1115/1.4027510. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLeod MA, Wilusz RE, Guilak F. Depth dependent anisotropy of the micromechanical properties of the extracellular and pericellular matrices of articular cartilage evaluated via atomic force microscopy. Journal of Biomechanics. 2013;46:586–592. doi: 10.1016/j.jbiomech.2012.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mow VC, Gu WY, Chen FH. Structure and function of articular cartilage and meniscus. In: Mow VC, Huiskes R, editors. Basic Orthopaedic Biomechanics and Mechano biology. Lippincott Williams & Wilkins; Philadelphia: 2005. pp. 181–258. [Google Scholar]
- Quinn TM, Grodzinsky AJ, Buschmann MD, Kim YJ, Hunziker EB. Mechanical compression alters proteoglycan deposition and matrix deformation around individual cells in cartilage explants. Journal of Cell Science. 1998;111:573–583. doi: 10.1242/jcs.111.5.573. [DOI] [PubMed] [Google Scholar]
- Sah RLY, Kim YJ, Doong JYH, Grodzinsky AJ, Plass AH, Sandy JD. Biosynthetic response of cartilage explants to dynamic compression. Journal of Orthopaedic Research. 1989;7:619–636. doi: 10.1002/jor.1100070502. [DOI] [PubMed] [Google Scholar]
- Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth dependent confined compression modulus of full thickness bovine articular cartilage. Journal of Orthopaedic Research. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
- Sibole SC, Erdemir A. Chondrocyte Deformations as a Function of Tibiofemoral Joint Loading Predicted by a Generalized High Throughput Pipeline of Multi Scale Simulations. PLoS ONE. 2012;7:e37538. doi: 10.1371/journal.pone.0037538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith RL, Carter DR, Schurman DJ. Pressure and shear differentially alter human articular chondrocyte metabolism: a review. Clinical Orthopaedics and Related Research. 2004;427:S89–S95. [PubMed] [Google Scholar]
- Thambyah A, Broom ND. Further insight into the depth dependent microstructural response of cartilage to compression using a channel indentation technique. Computational and Mathematical Methods in Medicine. 2013 doi: 10.1155/2013/358192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torzilli PA, Grigiene R, Huang C, Friedman SM, Doty SB, Boskey AL, Lust G. Characterization of cartilage metabolic response to static and dynamic stress using a mechanical explant test system. Journal of Biomechanics. 1997;30:1–9. doi: 10.1016/s0021-9290(96)00117-0. [DOI] [PubMed] [Google Scholar]
- Upton ML, Gilchrist CL, Guilak F, Setton LA. Transfer of macroscale tissue strain to microscale cell regions in the deformed meniscus. Biophysical Journal. 2008;95:2116–2124. doi: 10.1529/biophysj.107.126938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang CC, Hung CT, Mow VC. An analysis of the effects of depth dependent aggregate modulus on articular cartilage stress relaxation behavior in compression. Journal of Biomechanics. 2001;34:75–84. doi: 10.1016/s0021-9290(00)00137-8. [DOI] [PubMed] [Google Scholar]
- Wong M, Wuethrich P, Buschmann MD, Eggli P, Hunziker E. Chondrocyte biosynthesis correlates with local tissue strain in statically compressed adult articular cartilage. Journal of Orthopaedic Research. 1997;15:189–196. doi: 10.1002/jor.1100150206. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W. Finite element simulation of location and time dependent mechanical behavior of chondrocytes in unconfined compression tests. Annals of Biomedical Engineering. 2000;28:318–330. doi: 10.1114/1.271. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W. Analysis of the mechanical behavior of chondrocytes in unconfined compression tests for cyclic loading. Journal of Biomechanics. 2006;39:603–616. doi: 10.1016/j.jbiomech.2005.01.007. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W, Epstein M. Modelling of location and time dependent deformation of chondrocytes during cartilage loading. Journal of Biomechanics. 1999;32:563–572. doi: 10.1016/s0021-9290(99)00034-2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.