Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Aug 22.
Published in final edited form as: J Biomech. 2014 Jun 9;47(11):2801–2806. doi: 10.1016/j.jbiomech.2014.05.026

Comparison of Intervertebral Disc Displacements Measured Under Applied Loading with MRI at 3.0T and 9.4T

Deva D Chan 1, Paull C Gossett 1, Kent D Butz 2, Eric A Nauman 1,2, Corey P Neu 1,*
PMCID: PMC4125489  NIHMSID: NIHMS603836  PMID: 24968943

Abstract

The purpose of this study was to compare displacement behavior of cyclically loaded cadaveric human intervertebral discs as measured noninvasively on a clinical 3.0T and a research 9.4T MRI system. Intervertebral discs were cyclically compressed at physiologically relevant levels with the same MRI-compatible loading device in the clinical and research systems. Displacement-encoded imaging was synchronized to cyclic loading to measure displacements under applied loading with MRI (dualMRI). Displacements from the two systems were compared individually using linear regression and, across all specimens, using Bland-Altman analysis. In-plane displacement patterns measured at 3.0T and 9.4T were qualitatively comparable and well correlated. Bland-Altman analyses showed that over 90% of displacement values within the intervertebral disc regions of interest lay within the limits of agreement. Measurement of displacement using dualMRI using a 3.0T clinical system is comparable to that of a 9.4T research system. Additional refinements of software, technique implementation, and image processing have potential to improve agreement between different MRI systems. Despite differences in MRI systems in this initial implementation, this work demonstrates that dualMRI can be reliably implemented at multiple magnetic field strengths, permitting translation of dualMRI for a variety of applications in the study of tissue and biomaterial biomechanics.

Keywords: displacement-encoded imaging, high-field MRI, clinical MRI, biomechanics, elastography

INTRODUCTION

The mechanical behavior is closely linked to tissue form and function, particularly in tissues whose primary physiological role is the support of load. As a noninvasive imaging modality, magnetic resonance imaging (MRI) has the capability of measuring not only the morphology but also the biomechanics of tissues in their native mechanical environment (Glaser et al., 2006; Neu and Walton, 2008; Zhong et al., 2010). Noninvasive measurement of displacements under applied loading with MRI (dualMRI) can be implemented on both clinical and high-field research MRI systems (Chan and Neu, 2012; Chan and Neu, 2013). dualMRI involves the synchronization of cyclic loading, which is applied by an MRI-compatible loading device, with displacement-encoded MRI. Numerous factors influence the MRI-based measurement of displacements in biomaterials and tissues, including the magnitude and frequency of cyclic loading, the geometry and configuration of the physical environment, and inherent material properties of the tissue, which is often viscoelastic and heterogeneous (Neu and Walton, 2008; Chan et al., 2009; Chan et al., 2011).

Conversely, the MRI acquisition technique and parameters, the software and hardware limitations on different MRI systems, and the signal and contrast of the image could also affect the measurement of displacements. The precision of the displacement-encoded MRI sequences used with dualMRI is already known to depend on the signal-to-noise ratio and also on the strength of the encoding gradient (Chan and Neu, 2012). Knowledge of how displacements measured on a clinical MRI system compare to those measured on a higher field research system would be of vital importance to the translation of dualMRI applications to clinical use. Therefore, the goal of this study was to compare displacements measured in a cyclically loaded intervertebral disc by dualMRI on a high-field (9.4 Tesla (T)) research MRI system to those measured on a 3.0T clinical system under the same loads.

METHODS

Fresh-frozen human cadaveric lumbar spines (n = 3) were obtained from an organ and tissue donation center (Unyts, Buffalo, NY) and thawed on ice prior to dissection. Motion segments consisting of the 4th and 5th lumbar vertebral bodies and the intervertebral disc were isolated and then potted with a fiberglass resin to be secured in a custom MRI-compatible cyclic loading device. The device permitted cyclic axial compression of the disc at 445 N in the superior-to-inferior direction. Load was applied for 1.5 seconds and then fully released to permit tissue recovery, every 3 seconds, during the preconditioning period and when synchronized with imaging as described below. The discs were wrapped in PBS-soaked gauze to prevent desiccation of the disc during experiments.

Displacements were measured within the human intervertebral discs by dualMRI on a 9.4T Bruker Biospec (Bruker Medical GMBH, Ettlington, Germany). The discs were cyclically loaded, and, for each disc, dualMRI did not commence until a steady state load-displacement response was achieved. dualMRI data was acquired with displacement encoding with stimulated echoes (DENSE) and a true fast imaging under steady-state precession (TrueFISP) sequence. Key acquisition parameters were as follows: echo time (TE) = 1.6 ms, field of view (FOV) = 64 mm × 64 mm, spatial resolution = 234 μm × 234 μm, and slice thickness = 2 mm. Displacements were encoded at 0.32 rad/mm. After imaging, discs were frozen at −20°C and later thawed at 4°C for the 3.0T experiments.

On the other hand, displacements were measured on a 3.0T clinical MRI system (General Electric Signa HDx, Waukesha, WI) using displacement encoding with a single-shot fast spin echo (SSFSE) acquisition. Load parameters were identical to those described previously, and SSFSE acquisition parameters were TE = 62 ms, FOV = 180 mm × 180 mm, spatial resolution = 703 μm × 703 μm, slice thickness = 3 mm, and displacements were encoded at 0.14 rad/mm. Raw displacements from either system were not smoothed prior to the following data analyses; however, because smoothing improves the precision of the displacement measurement (Chan et al., 2012), the variance in raw displacement measurements represent a conservative comparison between the two systems.

Regions of interest (ROIs) were manually selected for each specimen and each MRI system. The selection of the ROI on the lower resolution images (3.0T data) was performed independently of the ROI selection in data from the 9.4T system. Imaged volumes from the 9.4T and 3.0T experiments were manually registered to the same specimen-based coordinate system to permit comparison. The size of the higher resolution 9.4T image was expanded to replicate the same FOV as the 3.0T data and then resized with bicubic interpolation to reduce the spatial resolution, generating an image with the same size (256 × 256 pixels) as the 3.0T image. The same image expansion and interpolation was performed for the displacement maps and ROIs for each specimen. Only points that lay within both the 3.0T intervertebral disc ROI and the reshaped 9.4T ROI were chosen for analysis to eliminate differences resulting from the manual ROI selection and the interpolation process. Displacements in the x (transverse to loading) and y (aligned with loading) directions were compared with a linear regression within each specimen. A Bland-Altman analysis was also performed, with the limits of agreement defined as the bias (i.e., average difference) ± 1.96 × the standard deviation of the differences (Bland and Altman, 1986).

RESULTS

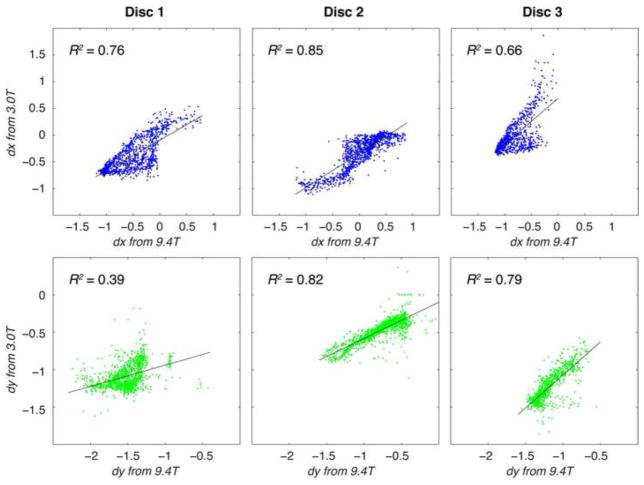
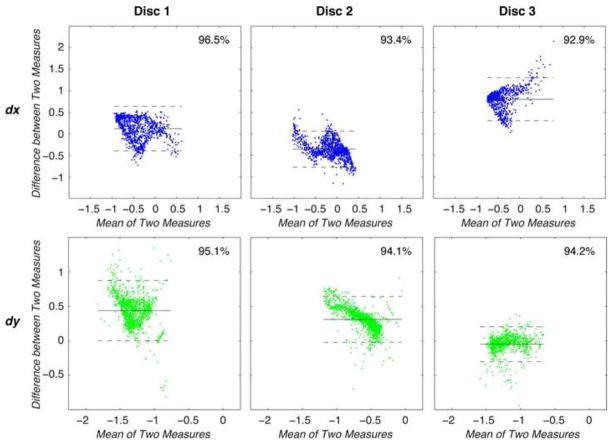
The signal-to-noise ratios of the disc regions of interest in the displacement-encoded images were comparable at 11.13 ± 4.61 and 11.15±2.50 on the 9.4T and 3.0T systems, respectively. Displacements in x and y (dx and dy) measured at 9.4T qualitatively showed similar patterns to those measured at 3.0T (Figure 1). Linear regressions between dx on the 9.4T and dx on the 3.0T showed agreement ranging R2 = 0.66–0.85, and a similar analysis between the 9.4T and 3.0T dy values resulted in R2 = 0.39–0.82 (Figure 2). The standard deviation of differences in displacements ranged from 0.21 to 0.26 mm in x and from 0.13 to 0.22 mm in y in individual discs, with limits of agreement defined as 1.96 times that standard deviation (Table 1). The combined disc analysis resulted in a standard deviation of 0.52 mm for dx and 0.27 mm for dy. Bland-Altman analyses within each specimen showed that a majority (i.e. a range from 92.9% to 96.5%) of displacement values were within the limits of agreement (Figure 3). After grouping all specimens, Bland-Altman analysis showed that 93.4% and 94.1% of dx and dy values agreed (Figure 4). However, the mean differences between dx and dy values of the 3.0T and the 9.4T measurements across all specimens were 0.12 and 0.26 mm, respectively, which were comparable or less than the image pixel dimensions acquired at 9.4T.

Figure 1. Displacements measured on research (9.4T) and clinical (3.0T) MRI systems under applied loading.

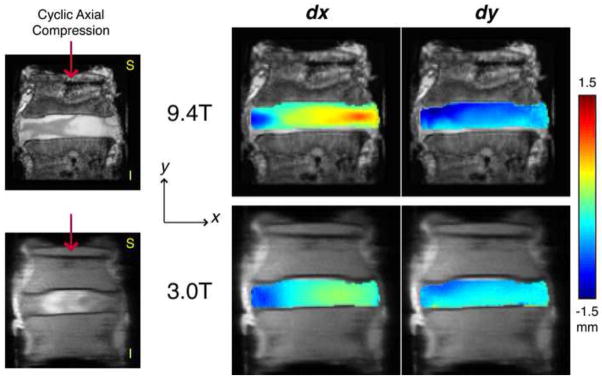
Figure 1

Open in a new tab

Cyclic compression was applied using an MRI-compatible apparatus along the superior-to-inferior axis of cadaveric human intervertebral discs. In-plane displacements were measured in the coronal plane through the widest part of the intervertebral disc in the direction of loading (y) and the direction transverse to loading (x). The high spatial resolution of the 9.4T images, shown here before adjustments were made to match the spatial resolution of the 3.0T acquisition, permits a better representation of the spatial variations in displacements within the disc, as well as a broader range of displacement values.

Figure 2. Linear regression comparisons of displacements measured at 9.4 and 3.0 T in individual discs.

Figure 2

Open in a new tab

Displacements in x and y were measured during axial compression and compared for each overlapping point in regions of interest for each of three disc specimens. In order to encompass all sources of variability in the systems, displacements were not smoothed prior to this comparison. Correlation coefficients (R2) varied from 0.39 to 0.85. Despite numerous sources of differences between the MRI systems (e.g. voxel size) and set up (e.g. specimen positioning), agreement in the correlation coefficient data was observed, with additional analysis presented in Figure 3.

Table 1.

Mean difference and limits of agreement (as defined as 1.96 times the standard deviation) of displacements in the loading (y) and transverse (x) directions were calculated based on a Bland-Altman analysis of the individual specimens and the combined data.

Displacement direction Lower limit of agreement [mm] Mean difference [mm] Upper limit of agreement [mm]
Disc 1 x −0.40 0.12 0.64
y 0.00 0.44 0.88
Disc 2 x −0.77 −0.36 0.06
y −0.02 0.31 0.64
Disc 3 x 0.31 0.80 1.30
y −0.30 −0.05 0.20
Combined Data x −0.90 0.12 1.13
y −0.26 0.26 0.78
Open in a new tab

Figure 3. Bland-Altman analyses were performed to compare displacements measured at 9.4T and 3.0 T in individual discs.

Figure 3

Open in a new tab

For each point, the mean of and the difference between displacements in x and y were plotted to visualize the agreement between the two systems. Between 92.9% and 96.5% of the points of interest fall within the limits of agreement, as listed in Table 1.

Figure 4. Bland-Altman analysis was performed to compare displacements measured in all discs.

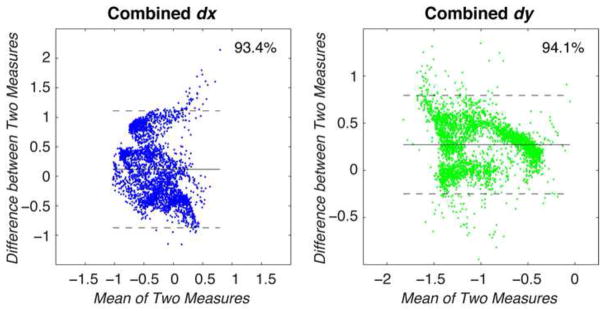
Figure 4

Open in a new tab

Taking the values for all points of interest across all the discs, the mean and difference between x and y displacements were calculated and compared. Values for dx and dy showed that 93.4% and 94.1% of displacement values lay within the limits of agreement, with standard deviations of 0.52 and 0.27 mm, respectively.

DISCUSSION

This study demonstrates similar displacements measured at two different field strengths using dualMRI in the intervertebral disc. Previous studies of intervertebral disc mechanics have used various MRI techniques to compute internal strains via digital image correlation (Gilchrist et al., 2004; O’Connell et al., 2007), tissue stiffness via MR elastography (Cortes et al., 2013), and material properties via correlations to quantitative MRI biomarkers (Antoniou et al., 2013). These and similar MRI-related techniques have also been applied to a variety of other biomechanically relevant soft tissue systems (Herberhold et al., 1999; Hardy et al., 2005; Subburaj et al., 2012).

As expected, displacements within the intervertebral discs reflected both the material properties and the specific loading environment. Qualitative comparison of the displacement fields shows that the bulging of the disc, as evidenced by the dx fields, was consistent under the same cyclic axial compression. The dy fields also showed a greater displacement on one side of the disc than the other, in response to axial compression. However, the displacements measured at 3.0T appeared more diffuse, possibly because of the lower initial spatial resolution at that field.

In comparing the displacement fields measured at 3.0 and 9.4 T, differences in dx and dy can be attributable to the use of two inherently different hardware and software systems, biological variations, and other factors, all of which are discussed further below. The linear correlation analysis shows a varying degree of correspondence between displacements at 3.0 and 9.4 T (R2 = 0.39 to 0.85, Figure 2). Although this analysis is based on a paired design, it is important to note that a number of factors that can affect differences in displacements may not be linear. These include spatial inhomogeneities of the main and gradient magnetic fields, biological variability both between discs and within the same disc after time and handling, and differences in the mechanical systems. Although a multi-factored analysis of variance could also be performed to test several of these factors, that experimental design is challenging in part due to the limited lifespan of biological specimen during repeated testing and the cost-prohibitive imaging time required on MRI systems.

Despite the range of coefficients of variation in the linear analysis, the 3.0T data showed good agreement with the displacements measured at 9.4T under a Bland-Altman analysis (Figure 3), a method that quantifies the agreement between two different measurement techniques without assumptions of linear correlation (Bland and Altman, 1986). The measurement of the difference between displacement values at each point also permitted displacements across all specimens to be compared between 3.0T and 9.4T with a pooled Bland-Altman analysis (Figure 4), which takes into account the differences between field strengths in all the specimens. Therefore, the variability in difference values inherent to biological variability (between different discs) and repeatability of the mechanics (within the same disc) are also included in the limits of agreement of the pooled analysis, in addition to differences inherent to the imaging itself.

Interestingly, the Bland-Altman analysis showed that the mean difference between the two systems in both dx and dy were non-zero. Because the pulse sequence on both systems and the image processing balance the encoding and un-encoding actions, in theory there should be no difference in displacement values due to the imaging systems. However, in practice, MRI systems have their unique technical limitations, so displacement measurements on the two systems can be biased by inhomogeneities in the magnetic field, imperfect gradient timings, and other hardware limitations that affect the generation and measurement of signal phase. To remedy this within each system, a separate no-load calibration scan can be performed with the specimen prior to any loading to aid in removing any sample-specific and location-dependent bias during image processing. However, this essentially doubles the total scan time, leaving a no-load calibration scan of a non-moving imaging phantom as a faster, but possibly less effective, method of reducing system-specific biases.

Because the method of filtering can have an effect on the precision of the displacement measurements (Chan et al., 2012), only the raw displacements, before any smoothing, were examined in this study. We have previously shown that displacement precision also depends on the SNR (Neu et al., 2005; Chan et al., 2012), and image parameters permitted a similar SNR between both systems for this study. Increases in SNR on both systems would presumably improve the correlations and agreement measures. While it would be ideal to vary only the strength of the main magnetic field, there were also differences in the strength of the encoding gradient, the acquisition sequence used to measure displacement-encoded data, and the spatial resolution due to the software and hardware limitations of the two systems in this study. For example, the selection of the imaging slice was based on visualizing landmarks, and the resulting images do not depict identical disc morphologies, especially considering that imaging parameters limit the 3.0T system to 3-mm thick, and 18-mm wide slices. Nonetheless, in the typical circumstances that these displacement data would be used, displacement fields would be smoothed within the regions of interest (Chan et al., 2012) prior to calculations of strain. Although the smoothing parameters would be chosen based on spatial resolution as well as the geometry of the region of interest, the difference between equivalent displacement-encoded images from two different systems would be expected to be no worse than the raw displacement (i.e. without smoothing) condition.

Another consideration in this study, as mentioned above, is the difference in the loading environment between the 9.4T and 3.0T systems. Indeed, the design of a loading apparatus is specific to the desired mechanism, in this case axial compression, as well as constrained by the interface with the imaging hardware. On the 9.4T system, the loading device is supported by a manual gantry and secured to the MRI system with positioning screws. On the 3.0T system, designed primarily for patient use, the loading apparatus was placed on the automatic gantry with supports underneath to hold its position. However, there was no physical attachment of the loading apparatus to the clinical MRI system, so slight variations in the alignment and orientation of the apparatus, which includes the specimen, to the coordinate system of the magnet are also possible. In addition, there may be variations due to the replacement of the potted disc in the loading apparatus for the 3.0T study after it was removed for storage following the 9.4T experiments. An extra freeze-thaw cycle, which was a logistical necessity between experiments, could also have affected the mechanical properties of the disc itself, since freezing is known to affect characterization of cartilage mechanics (Willett et al., 2005). The transport and storage of the discs between testing could also have affected the hydration state of the discs, which would in turn alter their mechanical behavior under compression, though care was taken to minimize hydration state changes through the use of PBS-soaked gauze that completed wrapped the exposed areas of the discs.

Further studies could eliminate the potential for mechanical differences that occur with time, degradation, and storage by using non-biological (e.g. silicone gel) materials. However, few non-biological materials share the viscoelastic and heterogeneous behavior of biomaterials and tissues, potentially limiting the usefulness of such a comparison between systems.

In conclusion, despite inherent differences in 9.4T and 3.0T MRI systems, displacements measured at the two magnetic field strengths correspond qualitatively and quantitatively, according to Bland-Altman analysis. Further research should focus on using a non-biologic material for comparisons and endeavor to reproduce as many of the same hardware, software, and imaging parameters as possible on the compared systems. Additionally, it is important to note that for every new loading apparatus design, differing software implementation, or MRI system, an analysis of internal consistency should be performed to assess displacement bias and precision, in addition to comparisons with previously validated systems. Nonetheless, the results of this study indicate promise that displacements and strains measured on a clinical 3.0T MRI system can be used to characterize mechanical behavior with dualMRI. Translation of dualMRI from research to clinical systems could permit the visualization of the biomechanical response to various loading states, including shear and torsion, in intervertebral discs and other soft orthopaedic tissues.

Acknowledgments

Funding for this study was provided by NSF CMMI 1100554, NIH R25 EB013029-02, NIH S10 RR019920-01, NIH R01 AR063712, NIH R21 AR064178, and Indiana CTSI Core Pilot Funding. Study sponsors were not involved in the design of the study, the collection, analysis and interpretation of data, the writing of the manuscript, nor the decision to publish. The authors thank Aaditya Chandramouli for assistance with specimen preparation and also Limin Li, Gregory Tamer, and Thomas Talavage for their technical expertise on MRI systems.

Footnotes

CONFLICT OF INTEREST STATEMENT

The authors have no financial or personal conflicts of interest to declare.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Antoniou J, Epure LM, Michalek AJ, Grant MP, Iatridis JC, Mwale F. Analysis of quantitative magnetic resonance imaging and biomechanical parameters on human discs with different grades of degeneration. J Magn Reson Imaging. 2013 doi: 10.1002/jmri.24120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–10. [PubMed] [Google Scholar]
  3. Chan DD, Khan SN, Ye XJ, Curtiss SB, Gupta MC, Klineberg EO, Neu CP. Mechanical Deformation and Glycosaminoglycan Content Changes in a Rabbit Annular Puncture Disc Degeneration Model. Spine. 2011;36(18):1438–1445. doi: 10.1097/BRS.0b013e3181f8be52. [DOI] [PubMed] [Google Scholar]
  4. Chan DD, Neu CP. Transient and Microscale Deformations and Strains Measured under Exogenous Loading by Noninvasive Magnetic Resonance. PLoS One. 2012;7(3):e33463. doi: 10.1371/journal.pone.0033463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chan DD, Neu CP. Intervertebral disc internal deformation measured by displacements under applied loading with MRI at 3T. Magn Reson Med. 2013 doi: 10.1002/mrm.24757. [DOI] [PubMed] [Google Scholar]
  6. Chan DD, Neu CP, Hull ML. In situ deformation of cartilage in cyclically loaded tibiofemoral joints by displacement-encoded MRI. Osteoarthritis Cartilage. 2009;17(11):1461–8. doi: 10.1016/j.joca.2009.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chan DD, Toribio D, Neu CP. Displacement smoothing for the precise MRI-based measurement of strain in soft biological tissues. Comput Methods Biomech Biomed Engin. 2012 doi: 10.1080/10255842.2011.641178. [DOI] [PubMed] [Google Scholar]
  8. Cortes DH, Magland JF, Wright AC, Elliott DM. The shear modulus of the nucleus pulposus measured using magnetic resonance elastography: A potential biomarker for intervertebral disc degeneration. Magn Reson Med. 2013 doi: 10.1002/mrm.24895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gilchrist CL, Xia JQ, Setton LA, Hsu EW. High-resolution determination of soft tissue deformations using MRI and first-order texture correlation. IEEE Trans Med Imaging. 2004;23(5):546–53. doi: 10.1109/tmi.2004.825616. [DOI] [PubMed] [Google Scholar]
  10. Glaser KJ, Felmlee JP, Manduca A, Kannan Mariappan Y, Ehman RL. Stiffness-weighted magnetic resonance imaging. Magn Reson Med. 2006;55(1):59–67. doi: 10.1002/mrm.20748. [DOI] [PubMed] [Google Scholar]
  11. Hardy PA, Ridler AC, Chiarot CB, Plewes DB, Henkelman RM. Imaging articular cartilage under compression--cartilage elastography. Magn Reson Med. 2005;53(5):1065–73. doi: 10.1002/mrm.20439. [DOI] [PubMed] [Google Scholar]
  12. Herberhold C, Faber S, Stammberger T, Steinlechner M, Putz R, Englmeier KH, Reiser M, Eckstein F. In situ measurement of articular cartilage deformation in intact femoropatellar joints under static loading. J Biomech. 1999;32(12):1287–95. doi: 10.1016/s0021-9290(99)00130-x. [DOI] [PubMed] [Google Scholar]
  13. Neu CP, Hull ML, Walton JH. Error optimization of a three-dimensional magnetic resonance imaging tagging-based cartilage deformation technique. Magn Reson Med. 2005;54(5):1290–4. doi: 10.1002/mrm.20669. [DOI] [PubMed] [Google Scholar]
  14. Neu CP, Walton JH. Displacement encoding for the measurement of cartilage deformation. Magn Reson Med. 2008;59(1):149–155. doi: 10.1002/mrm.21464. [DOI] [PubMed] [Google Scholar]
  15. O’Connell GD, Johannessen W, Vresilovic EJ, Elliott DM. Human internal disc strains in axial compression measured noninvasively using magnetic resonance imaging. Spine. 2007;32(25):2860–8. doi: 10.1097/BRS.0b013e31815b75fb. [DOI] [PubMed] [Google Scholar]
  16. Subburaj K, Souza RB, Stehling C, Wyman BT, Le Graverand-Gastineau MP, Link TM, Li X, Majumdar S. Association of MR relaxation and cartilage deformation in knee osteoarthritis. J Orthop Res. 2012;30(6):919–26. doi: 10.1002/jor.22031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Willett TL, Whiteside R, Wild PM, Wyss UP, Anastassiades T. Artefacts in the mechanical characterization of porcine articular cartilage due to freezing. Proc Inst Mech Eng [H] 2005;219(1):23–9. doi: 10.1243/095441105X9200. [DOI] [PubMed] [Google Scholar]
  18. Zhong X, Spottiswoode BS, Meyer CH, Kramer CM, Epstein FH. Imaging three-dimensional myocardial mechanics using navigator-gated volumetric spiral cine DENSE MRI. Magn Reson Med. 2010;64(4):1089–97. doi: 10.1002/mrm.22503. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES