Interstitial adenosine concentration during norepinephrine infusion in isolated guinea pig hearts

Abstract

This study determined the effect of norepinephrine (NE) on cardiac interstitial fluid adenosine concentration ([ADO]_isf). Isolated guinea pig hearts were perfused with a Krebs-Henseleit buffer solution. Radiolabeled albumin, sucrose, and adenosine were injected under control conditions and after 3 and 20 min of NE infusion to obtain multiple indicator dilution curves that were used to determine capillary transport parameters for adenosine. These parameters together with venous adenosine concentrations were used in a mathematical model to calculate [ADO]_isf. Capillary transport parameters were not changed significantly by NE infusion. Because of uncertainty regarding two model parameters, two sets of [ADO]_isf values were calculated. One set used best-fit values obtained from indicator dilution curves, and a second set used parameters chosen to provide the highest [ADO]_isf values consistent with indicator dilution curves. Venous adenosine concentrations were 1.9 ± 0.4 nM under control conditions and 243 ± 110 and 45 ± 25 nM after 3 and 20 min of NE infusion, respectively. Calculated [ADO]_isf was 2.6–9.4, 591–1,288, and 166–324 nM, respectively, under these same conditions. We conclude that NE infusion greatly increases [ADO]_isf, and adenosine is responsible for most of the vasodilation at 3 min. The subsequent fall in venous concentration is due to a fall in [ADO]_isf rather than to decreased capillary permeability. Vascular resistance remained low while [ADO]_isf fell, which suggests that additional vasodilators are important during maintained NE infusion.

CONSIDERABLE EXPERIMENTAL EVIDENCE indicates that cardiac adenosine formation and release are elevated in many conditions involving increased myocardial metabolism or decreases in the oxygen supply-to-demand ratio (17, 26). It has proved more difficult to determine whether interstitial fluid adenosine concentration ([ADO]_isf) increases enough to account for the observed vasodilation. Experimental approaches to this problem have included the administration of adenosine receptor antagonists or adenosine deaminase, as well as techniques to estimate [ADO]_isf.

Several reports have demonstrated that metabolic hyperemia in the heart induced by catecholamine infusion is unaffected by doses of adenosine antagonists that attenuate vasodilation in response to exogenous adenosine (2, 10, 15, 19). However, the recent demonstration that methylxanthines increase cardiac adenosine release makes these results difficult to interpret (10, 19). It is possible that [ADO]_isf is elevated enough by methylxanthines to overcome the receptor blockade. Adenosine deaminase experiments have provided evidence both for and against the adenosine hypothesis (2,24). A drawback to this approach is that even without exogenous adenosine deaminase, the capacity for cellular uptake and metabolism of interstitial adenosine is quite high. This makes negative results with adenosine deaminase difficult to interpret.

Negative results with either adenosine antagonists or adenosine deaminase do not necessarily rule out adenosine as a mediator of vasodilation. It is always possible that when adenosine is blocked or reduced, a different vasodilator is released in sufficient quantity to yield nearly the same flow. A method for estimating [ADO]_isf, if reliable, increases the investigator's power to interpret the observations. If [ADO]_isf is elevated enough to account for the vasodilation, then adenosine must play a major role. Several approaches to estimating [ADO]_isf have been used, including pericardial suffusates, epicar-dial wells, epicardial transudate, and intracellular accumulation of S-adenosylhomocysteine (6, 7, 17, 22, 28). These techniques rely on an assumption of equilibrium between adenosine concentration in epicardial fluid and interstitium or between cytosol and interstitium. We have developed a different technique that calculates [ADO]_isf from the arterial and venous concentrations together with capillary transport parameters for adenosine (30). This paper reports our estimates of [ADO]_isf during norepinephrine (NE) infusion in the isolated guinea pig heart.

METHODS

We used an isolated nonworking guinea pig heart preparation described previously (30). The perfusate was a Krebs-Henseleit solution containing 8 mM glucose and 2 mM pyruvate, heated to 37°C bubbled with 95% O₂-5% CO₂, and not recirculated. Perfusion pressure was held constant at 60 cmH₂O (46 mmHg). Coronary flow was measured continuously with an in-line electromagnetic flow probe. Hearts were paced at 300 beats/min. The pulmonary artery was cannulated for the collection of coronary venous effluent, and the left ventricle was vented. To prevent the development of a high capillary filtration coefficient, bovine serum albumin was infused to achieve an arterial concentration of 0.1% (18). Arterial and venous PO₂ were measured using a Corning blood gas analyzer. Venous effluent adenosine concentration was measured by high-performance liquid chromatography (HPLC), using methods previously described (30). Adenosine in the arterial perfusate was below detectable limits.

All hearts were allowed a 45-min equilibration period before experimental interventions. Under control conditions we measured flow and arterial and venous PO₂, and took a sample of venous effluent for measurement of adenosine concentration. We then injected radioactive tracers for the measurement of adenosine capillary transport parameters (see below). Approximately 10 min after this injection, we began an infusion of NE (0.1 ml/min) to achieve a steady-state arterial concentration of ~2 × 10⁻⁷ M. A previous study demonstrated that venous adenosine concentration ([ADO]_v) increases phasically in this situation, with an early peak followed by a decline to a steady state (9). Preliminary experiments indicated that peak adenosine concentration was reached after 3 min of NE infusion with this protocol. Accordingly, we performed a second radioactive tracer injection at the 3-min point and a third tracer injection in the steady state after 20 min of continuous NE infusion. Because collection of indicator dilution outflow samples took ~30 s and because the endogenous [ADO]_v may have been changing during that interval at the 3-min point, we collected venous samples immediately before and after the dilution curve and pooled or averaged these values for the endogenous concentration at 3 min. The 3- and 3.5min [ADO]_v values were measured separately in three hearts for the indicator dilution experiments and in six hearts for the adenosine and dipyridamole infusion series (see below).

To calculate [ADO]_isf we need measurements of arterial and venous adenosine concentrations, perfusate flow, distribution of flow, and the capillary transport parameters for adenosine. The observed albumin outflow curve results from delay and dispersion in large vessels and flow heterogeneity. We used the distribution of flow and the observed albumin curve to calculate a large vessel transport function, h_LV(t), which accounts for delay and dispersion (30). Then h_LV(t) is used as the input function for sucrose and adenosine tracers. Distribution of flow was measured in three hearts with 15-μm radioactive microspheres labeled with ¹⁴¹Ce, ⁵¹Cr, and ⁸⁵Sr. Aliquots of 25–50 μI (~16,000–100,000 spheres) were injected into the perfusion line just proximal to the aorta. Micro-spheres were injected under control conditions and after 3 min and 20 min of NE infusion. Hearts (including atria) were sectioned into 39 transmural pieces for analysis of the distribution of flow. Heterogeneity of flow was analyzed according to King et al. (16) and expressed as the relative dispersion or the standard deviation divided by the mean flow. These methods have been described elsewhere in more detail (11). In our calculations of [ADO]_isf, we used the actual distribution of flow in the three hearts where it was available. In two hearts where such data were not available, we used the average of the relative dispersions in the microsphere hearts to calculate a Gaussian flow distribution.

The capillary transport parameters for adenosine were measured using the multiple indicator dilution technique in five hearts (30). A 25-μl bolus containing ¹²⁵I-labeled albumin (intravascular tracer, 0.2 μCi), [¹⁴C]sucrose (extracellular tracer, 0.5 μCi), and [³H]adenosine (2 μCi) was injected intra-arterially. The injections did not produce vasodilation. During the subsequent 30 s we collected 20 samples of venous effluent. The collecting tubes contained 200 μl of solution consisting of 3 μM 9-(erythro-3-hydroxynonyl)adenine (EHNA; adenosine deaminase inhibitor), 32 μM dipyridamole (adenosine transport inhibitor), and ~4 μM unlabeled adenosine (to aid in HPLC peak identification). In each experiment, indicator injections were made under control conditions, after 3 min of NE infusion, and after 20 min of NE infusion. Venous samples were first counted for ¹²⁵I-albumin in a gamma counter and were subsequently analyzed for [¹⁴C]sucrose and [³H]adenosine by HPLC(30). The sucrose and adenosine fractions were collected, and aliquots were counted in a liquid scintillation counter. The arterial injectate was analyzed identically, and tracer concentrations in the venous effluent were expressed as percent of injected dose per milliliter of effluent. Recovery of injected albumin and sucrose was >90%.

Contribution of endothelium to adensoine release

To assess the contribution of endothelial cells to adenosine in the venous effluent, we used an identical preparation (n = 3) in which the adenine nucleotide pool of the coronary endothelial cells was selectively labeled with ³H. [³H]adenosine (10⁻⁸ M, sp act 40 Ci/mmol) was infused for 30 min, followed by a 30-min washout period. This procedure has been shown to result in the selective uptake of [³H]adenosine by the coronary endothelium, as opposed to myocytes (3, 8, 23). After the washout period, venous samples were collected during drug infusions and were analyzed for adenosine by HPLC. The effect of various agents on the specific activity of adenosine in the venous effluent gives qualitative information on the source of venous adenosine (3, 8). These hearts received an infusion of dipyridamole (10⁻⁵ M) for 20 min, followed by a 20-min washout period, and then an infusion of NE at 2 × 10⁻⁷ M for 20 min. We measured the specific activity of adenosine in venous samples taken just before NE infusion and after 3 and 20 min of infusion. As a means of normalizing these results, relative specific activity was calculated as the ratio of specific activity in the venous effluent to the specific activity in the arterial perfusate during labeling.

Adenosine and dipyridamole infusion

To test the hypothesis that adenosine vasodilation is maximal after 20 min of NE infusion, either adenosine (n = 4) or dipyridamole (n = 4) was infused after 20 min of NE infusion in identical preparations. NE infusion continued as before. Adenosine was infused at an arterial concentration of 1 or 10 μM, and dipyridamole was infused at 10 μM. Infusion rates were 0.1 ml/min.

Calculation of [ADO]_isf

We have developed a model relating [ADO]_isf to [ADO]_v (30). The model assumes that the myocytes are the source of venous adenosine and accounts for uptake of adenosine by myocytes and endothelial cells. To calculate [ADO]_isf, we must know the transport parameters for adenosine movement into and between endothelial cells and its rate of metabolism within endothelial cells (Fig. 1). These parameters [permeability-surface area product of interendothelial gaps, endothelial cell luminal surface, and endothelial cell abluminal surface, respectively (PS_g, PS_ecl, PS_eca), and clearance rate constant for endothelial cells (G_ec) are estimated from the indicator dilution data. The parameters of the model are optimized to give the best prediction of the indicator dilution data, using the National Simulation Resource computer at the University of Washington. With the use of these parameters, the arterial and venous concentrations, and flow, it is possible to calculate [ADO]_isf under steady-state conditions as a function of distance along the capillary. We calculate the average [ADO]_isf by integrating over the length of the capillary and dividing by capillary length (30).

FIG. 1.

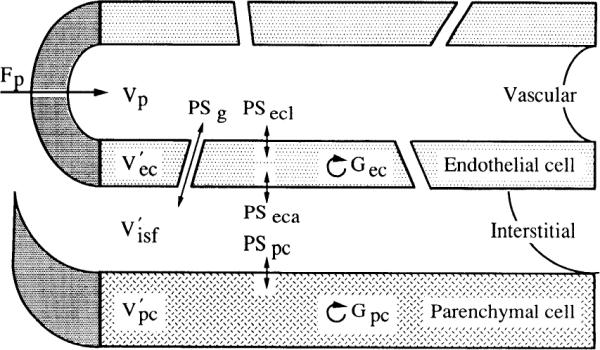
Diagram of capillary-tissue unit showing parameters used to characterize adenonsine transport and metabolism. F, mean flow of solute-containing fluid (ml · min⁻¹ · g⁻¹); G, clearance rate constant for intracellular sequestration and/or consumption (ml· min⁻¹ ·g⁻¹); PS, permeability-surface area product (ml· min⁻ · g⁻¹); V, volume; V′, volume of tracer distribution (ml/g). Subscripts: ec, endothelial cell; eta, endothelial cell abluminal surface; ccl, endothelial cell luminal surface; g, interendothelial gaps; isf, interstitial fluid; p, perfusate; pc, parenchymal cell.

Capillary transport parameter optimization was done using the MMID4 program at the National Simulation Resource Facility. In brief, parameter optimization proceeds by first using the observed albumin curve, flow, the distribution of flow, and an assumed capillary volume [perfusate volume (V_p) = 0.04 ml/g] to calculate a large vessel transport function representing delay and dispersion of injected tracer in arteries and veins. This function and the distribution of flow predict what the outflow curves for sucrose and adenosine would look like if all of the PS and G values in Fig. 1 were set to zero. Next, the sucrose curve is fitted by allowing PS_g and interstitial fluid volume (${\mathrm{V}}_{\mathrm{isf}}^{\prime }$) to vary. ${\mathrm{V}}_{\mathrm{isf}}^{\prime }$ was allowed to assume values between 0.1 and 0.4 ml/g. The resulting best-fit values of these parameters are then fixed while fitting the adenosine data, except that PS_g for adenosine is set equal to PS_g for sucrose × 1.128 (the expected effect on the free diffusion coefficient, the ratio of the square roots of the molecular weights of sucrose and adenosine). The remaining parameters, PS_ecl, PS_eca, permeability-surface area produce for parenchymal cells (PS_pc), G_ec and clearance rate constant for parenchymal cells (G_pc), are then adjusted to fit the adenosine data. Parameters were optimized two at a time in an iterative fashion by use of sensitivity functions (4). These sensitivity functions indicate that PS_eca, PS_pc, and G_pc have very little influence on the indicator dilution curves over the time period in which our samples were collected and will be poorly estimated. Fortunately, these parameters have little influence on the calculation of [ADO]_isf. Because values of G_pc or G_ec >40 ml·min⁻¹·g⁻¹ mean that essentially all of the adenosine taken up is metabolized, we imposed the constraint that G_ec and G_pc must be >40 ml·min⁻¹·g⁻¹. For the calculation of [ADO]_isf, the most important parameters obtained from the optimization are PS_g, PS_ecl, and G_ec. Other parameters exert little influence (30). Further details of parameter determination from indicator dilution curves can be found in Ref. 4.

Statistics

In the indicator dilution series, comparisons were made between the values and parameters obtained during the three different physiological states using analysis of variance followed by Tukey's test. Because of large variabilities in [ADO]_v and calculated [ADO]_isf, these comparisons were done after logarithmic transformation of the data. The effects of adenosine and dipyridamole on coronary flow and oxygen consumption were assessed using the paired t test.

RESULTS

The hemodynamic results of NE infusion are presented in Table 1. In the steady state, flow was doubled and myocardial O₂ consumption ($\mathrm{M}\stackrel{.}{\mathrm{V}}{\mathrm{o}}_2$) was more than doubled. There was a slight but insignificant increase in flow between 3 and 20 min of NE infusion. As previously reported (9), despite the nearly steady-state hemodynamics during this time, [ADO]_v declined after reaching an initial peak. [ADO]_v fell more than fivefold between 3 and 20 min, whereas the decrease in [ADO]_isf was roughly threefold. [ADO]_v values in samples taken at 3 and 3.5 min were not significantly different (152 ± 28 and 142 ± 24 nM, respectively; n = 9). The 3-min values in Table 1 are the average concentrations from the five indicator dilution experiments. Heterogeneity of flow (relative dispersion, RD) is also reported in Table 1. Although there appears to be a trend toward lower RD during NE infusion, this occurred in only one of the three hearts in which heterogeneity was measured. Regional flows ranged from 0.3 to 2.5 times the mean flow.

TABLE 1.

Hemodynamics and capillary transport parameters

	Control	NE (3 min)	NE (20 min)
Flow	4.6±0.2	8.2±0.4*	9.2±0.4*
Flow RD	0.37±0.11	0.28±0.02	0.29±0.03
$\mathrm{M}\stackrel{.}{\mathrm{V}}{\mathrm{o}}_2$	60±3	NA	149±11*
PS g	2.6±0.9	2.9±0.3	2.7±0.3
PS ecl	6.2±0.7	4.9±0.6*	6.3±0.6
Gec	11.6±1.9	15.3±5.9	17.9±5.8
PS eca	39.9±0.1	30.5±5.1	20.4±6.2
[ADO]v	1.9±0.4	243±110*	45±25*†
[ADO]isf	2.6±0.5	591±295*	166±105*†

Values are means ± SE from 5 hearts. NE, norepinephrine; flow (ml · min¹ · g¹); RD, relative dispersion of flow (SD/mean); MV̇o₂, myocardial O₂ consumption (μl · min⁻¹ · g⁻¹); [ADO]_V, venous adenosine concentration (nM); [ADO]_isf, calculated interstitial fluid adenosine concentration (nM); NA, not measured. PS products and G_ec are as defined in Fig. 1 ((ml · min⁻¹ · g⁻¹).

^*P < 0.05 compared with control value

^†P < 0.05 compared with NE 3-min value.

The indicator dilution curves from one experiment are shown in Fig. 2. These follow patterns similar to those seen in a previous study (30). Because the volume of distribution for sucrose is greater than that for albumin, its outflow curve has a lower peak and a greater dispersion. Recovery of injected counts is essentially complete for albumin and sucrose but is considerably lower for adenosine due to cellular uptake and metabolism. The curves during NE infusion have similar shapes but different time courses due to the higher flows. The capillary transport parameters for adenosine obtained from these curves are presented in Table 1. The high values of PS_ecl, PS_eca, and G_ec are consistent with avid endothelial uptake and metabolism of adenosine. Nevertheless, the values of PS_g indicate that adenosine diffusion between the interstitial fluid and plasma compartments will take place. Especially noteworthy in Table 1 is the finding that the capillary transport parameters during NE infusion are nearly the same at 3 and 20 min, except for a slight drop in PS_ecl at 3 min. This slight drop in PS_ecl is probably due to competition between tracer adenosine and the high concentration of endogenous adenosine for the luminal carrier.

FIG. 2.

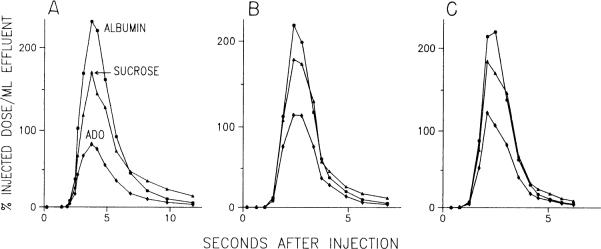
Representative indicator dilution curves before (A), early (B; 3 min), and late (C; min) during norepinephrine (NE) infusion. During both NE curves, tracer appearance is more rapid, and extractions of sucrose and adenosine are lower due to higher flow. PS products calculated from these curves appear in Table 1. ADO, adenosine.

The calculated [ADO]_isf values are also presented in Table 1. NE infusion produces a huge increase in this concentration at 3 min, but the concentration declines substantially by 20 min. It therefore appears that the phasic [ADO]_v during NE infusion is due to a phasic interstitial fluid concentration. At 20 min, [ADO]_isf remains significantly higher than the control level.

Because our indicator dilution curves are of relatively short duration, they do not allow good estimates of the parameters PS_eca and G_ec. Accordingly, we have calculated alternativevalues of [ADO]_isf, using the assumptions that PS_eca is equal to PS_ecl and that G_ec is 1,000 ml·min⁻¹·g⁻¹. This G_ec is an arbitrarily high value meant to simulate a virtually infinite endothelial adenosine metabolism, as suggested by cultured coronary endothelium at low adenosine concentrations (23). PS_g was reduced to 76% of the control value for this calculation to simulate the effect of adenosine uptake within interendothelial clefts (see DISCUSSION). The results of this calculation are a resting [ADO]_isf of 9.4 ± 2.0 nM, 1,288 ± 506 nM after 3 min, and 324 ± 174 nM after 20 min of NE infusion. These higher values place a useful upper limit on our estimates of [ADO]_isf.

The relative specific activities of venous adenosine in the endothelial cell-labeling experiments are shown in Fig. 3. NE infusion caused an immediate drop in relative specific activity, which was maintained for the duration of NE infusion.

FIG. 3.

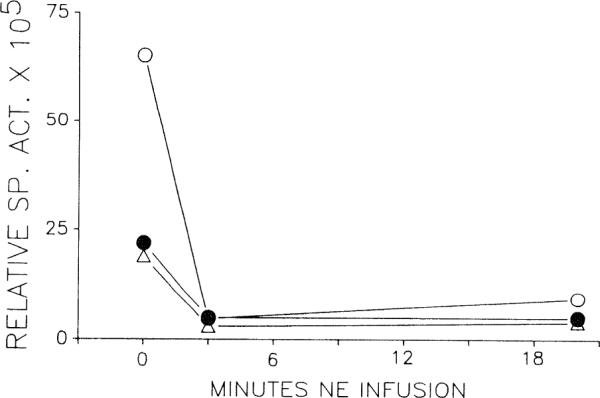
Relative specific activity of venous adenosine after selective endothelial labeling with [³H]adenosine (n = 3). Time zero represents resting conditions. Specific activity falls and remains low during NE infusion. Each symbol represents one heart.

Infusion of either adenosine or dipyridamole after 20 min of NE infusion produced additional vasodilation. Because adenosine at either 1 or 10 μM produced equivalent dilations, the results have been pooled. Adenosine increased flow from 7.3 ± 0.3 to 9.6 ± 0.4 ml·min⁻¹·g⁻¹ (P < 0.05), whereas $\mathrm{M}\stackrel{.}{\mathrm{V}}{\mathrm{o}}_2$ was unchanged (125 ± 5 vs. 128 ± 6 μl·min⁻¹·g⁻¹). Dipyridamole (10 μM) increased flow from 9.5 ± 0.5 to 10.3 ± 0.5 ml·min⁻¹·g⁻¹ (P < 0.05) at oxygen consumptions of 140 ± 8 and 138 ± 6 μl·min⁻¹·g⁻¹, respectively.

DISCUSSION

The major conclusion of this study is that [ADO]_isf in the isolated guinea pig heart increases greatly during NE infusion. The increase is phasic, and this accounts for the phasic adenosine concentrations seen in the venous effluent (9).

Two other possibilities could explain phasic adenosine release. First, the early release and the steady-state release rates could represent two different compartments (such as endothelial cells and myocytes). Second, the interstitial fluid concentration could be constant, but changes in capillary transport of adenosine could result in a phasic venous concentration. Selective endothelial cell-labeling experiments demonstrated that endothelial cells contribute almost none of the venous adenosine during NE infusion. Indicator dilution data demonstrated that the capillary transport parameters for adenosine were essentially unchanged during the period when [ADO]_v declined precipitously. We therefore conclude that phasic adenosine release during NE infusion is the result of a phasic release from myocytes.

Our calculated values of [ADO]_isf are dependent on the assumptions of the model and on our ability to determine the parameters of adenosine capillary transport from indicator dilution curves. The steady-state assumption requires that adenosine concentrations are not changing. Under control conditions and after 20 min of NE infusion this assumption is justified (9). [ADO]_v also did not change during the indicator dilution sample collection period at 3 min. Because we did not measure the detailed time course of [ADO]_v in these experiments, however, we may have missed the peak in some cases, resulting in an underestimate of peak [ADO]_isf.

Our model calculates [ADO]_isf based on [ADO]_v and knowledge of the endothelial barrier to transcapillary adenosine flux. Thus adenosine released into or formed within the interstitial space from any source is consistent with our model. Most adenosine seems to be formed within the cardiomyocytes (3, 7, 8, 20, 24). Production of adenosine from extracellular AMP undoubtedly occurs (14) but does not affect our calculations as long as such adenosine formation occurs in the interstitium rather than in the capillary lumen.

Other critical determinants of calculated [ADO]_isf are the capillary transport parameters for adenosine estimated from the indicator dilution curves. The most important parameters for the calculation are PS_g and PS_ecl, which can be estimated with a high degree of accuracy due to the sensitivity of the indicator dilution curves to these parameters (4, 30). The parameters for endothelial cell adenosine consumption (G_ec) and uptake by the abluminal EC surface (PS_eca) have some influence on the calculation of [ADO]_isf but are not uniquely determined by our indicator dilution curves. We have dealt with this uncertainty by calculating alternative [ADO]_isf values with PS_eca set equal to PS_ecl and with a very high value for G_ec consistent with cultured endothelial cell studies and with epicardial transudate studies (22, 23). The resulting values are somewhat higher and serve as the upper limit for our estimates of [ADO]_isf.

Experiments with cultured coronary endothelial cells have suggested that adenosine does not cross the endothelial barrier at physiological concentrations (23). Our indicator dilution results disagree with this interpretation. Although the endothelium takes up and metabolizes a large fraction of the adenosine presented on either side, the observation that PS_g is not zero means that at least some adenosine will get across. When the endothelial adenine nucleotide pool is selectively labeled, the specific activity of venous adenosine decreases sharply during NE infusion and other interventions (3, 8). Most of the adenosine therefore comes from nonendothelial sources and must pass either between or through endothelial cells to reach the capillary lumen. Coronary endothelial cell cultures and the isolated heart apparently differ in their permeability to adenosine.

Our estimates of PS_g might be in error if sucrose is not an appropriate substitute for adenosine after correction for differences in molecular size. For example, adenosine could be subject to endothelial uptake within interendothelial clefts, whereas sucrose is not. If substantial uptake occurs within the clefts, we could overestimate PS_g and underestimate [ADO]_isf. We have analyzed the possible magnitude of this phenomenon in the APPENDIX. If we assume that the nucleoside transporter density is the same within the clefts as it is on the luminal surface, then the fraction of adenosine molecules passing through the clefts depends on pore geometry and, more specifically, on the surface area-to-volume ratio in the clefts. Thus wider clefts allow more adenosine through than do narrow, more numerous, clefts. As detailed in the APPENDIX, clefts of 150 Å width allow the passage of 82% of the adenosine, whereas a cleft width of 100 Å allows the passage of 76%. However, these calculations assume the most favorable possible conditions for uptake within pores, with the concentration in the endothelial cell (C_ec) equal to the concentration in the perfusate (C_p) = 0. Our calculations of C_ec suggest that it is intermediate between C_p and the concentration in the interstitial fluid (C_isf), even assuming that no adenosine is formed within endothelial cells. If we use the average of C_isf and C_p as an estimate of internal cleft adenosine concentration, there is essentially zero gradient for uptake within the clefts both at rest and during NE infusion. A gradient for uptake within clefts can only occur if we are wrong in our estimate of G_ec, making C_ec much lower. Accordingly, when we made our alternative [ADO]_isf calculations with G_ec = 1,000 ml·min⁻¹·g⁻¹ and PS_ecl = PS_eca, we multiplied PS_g for adenosine by 0.76 (the fraction traversing a 100-Å cleft) to reflect potential uptake within clefts.

Examination of the [ADO]_isf values in individual hearts (data not shown) reveals that although the time course is similar in every experiment, the magnitude of [ADO]_isf is highly variable in different hearts. Because the capillary transport parameters for adenosine do not show similar variability but the [ADO]_v does, this suggests that the variability is due to differences in adenosine release from the myocytes during NE infusion. We have observed a similar large variability in adenosine release during NE infusion in other studies (9, 10). It is difficult to reconcile such variable adenosine concentrations with the more uniform hemodynamic responses to NE.

Other laboratories have estimated [ADO]_isf in isolated guinea pig hearts from the adenosine concentration in epicardial transudate or from fluid collected on porous epicardial disks. These results are compiled in Table 2 and are compared with our results. It is apparent that the basal [ADO]_isf values in this study and in our previous study (30) are lower than those using other techniques. Part of this can probably be attributed to our lower [ADO]_v. Lower [ADO]_isf and [ADO]_v probably reflect a lower basal adenosine release from myocytes. This may be due to different flow rates or to the presence of pyruvate in our perfusate. However, when comparing the ratio of interstitial to venous concentrations, our basal ratio of two to three is also lower than most other estimates. Our relatively low flow contributes to this lower interstitial-to-venous ratio, which once again makes direct comparison difficult. In an attempt to factor out the interstudy differences in flow and venous concentration, we have calculated a predicted [ADO]_isf from the flows and venous concentrations in the other studies, using our capillary transport parameters from Table 1. After these adjustments, our resting estimates remain lower than other techniques. Our resting [ADO]_isf estimates might be reconciled with transudate measurements if adenosine transporters are concentrated within interendothelial clefts or if our estimate of G_ec is too low. Alternatively, transudate and disk concentrations may overestimate resting [ADO]_isf. In vitro adenosine dose-response studies suggest that [ADO]_isf values of 150–280 nM (as estimated by transudate and disks) should be within the vasoactive range (21, 25, 29). Because adenosine antagonists or adenosine deaminase infusion have virtually no effect on resting vascular resistance (10, 24), this argues in favor of a lower resting [ADO]_isf.

TABLE 2.

Estimates of [ADO]_isf in isolated guinea pig hearts

Method	Conditions	[ADO]v, nM	[ADO]isf, nM	ISF/Venous Ratio	Predicted [ADO]isf, nM	Reference
Transudate	Rest	30	180	6	73	6
Transudate	Rest	37	191	>5	113	22
	Dipyridamole	90	785	9	623
SAH	Rest	9	80	9	13	7
Epicardial disk	Rest	4	280	70	6	28
	Dipyridamole	27	1,190	44	69
Epicardial disk	Rest	17	154	9	35	13
	Norepinephrine	461	496	1	1,071
Capillary transport	Rest	4	5–12	1.5–4		30
	Dipyridamole*	44	191	4
Capillary transport	Rest	2	3–7	1.5–3.5		This Study
	Norepinephrine†	45	166–324	4–7

Predicted [ADO]_isf was calculated from the cited study's flow and [ADO]_v using our average capillary transport parameters from Table 1. ISF, interstitial fluid; SAII, accumulation of S-adenosylhomocysteine. During dipyridamole it was assumed that endothelial adenosine uptake is blocked (PS_ecl = PS_eca = 0).

^*Constant pressure conditions.

^†Values after 20-min NE infusion.

During dipyridamole infusion, our results essentially agree with the transudate technique (22) but not with the epicardial disk method (28). We would have predicted a higher [ADO]_isf than the epicardial disk study during NE infusion (13). All techniques agree on the directional changes in [ADO]_isf with these interventions, but the actual concentrations are highly dependent on the method.

Is increased [ADO]_isf responsible for the coronary vasodilation observed during NE infusion? This question is difficult to answer because the concentration-response curve to interstitial adenosine is unknown. There is an endothelial-dependent component to adenosine vasodilation, which means that intracoronary adenosine infusions cannot be used to estimate its interstitial potency (12, 23). Rat cremaster surface vessels have a mean effective concentration (EC₅₀) of 0.1 μM for adenosine in the superfusate (21). The EC₅₀ in dog coronary artery strips (25) or rings (29) has been reported as 0.2 and 0.55 μM, respectively. Dipyridamole infusion might also be used to estimate the sensitivity to interstitial adenosine, since dipyridamole apparently produces coronary vasodilation by increasing adenosine concentration (i.e., the dilation is blocked by aminophylline) (1). We have estimated the [ADO]_isf during near maximal vasodilation with dipyridamole in the guinea pig heart to be 0.19 μM (30). In summary, the available techniques suggest that adenosine is a powerful vasodilator at interstitial fluid concentrations near 0.2 μM. Both the peak [ADO]_isf and the lower steady-state [ADO]_isf that we have calculated during NE infusion should therefore produce substantial vasodilation.

If adenosine is responsible for both peak and steady-state vasodilation despite its decline in concentration, this implies that both peak and steady-state concentrations are supramaximal on the interstitial fluid adenosine concentration-response curve. The adenosine and dipyridamole infusion experiments after 20 min of NE infusion refute this possibility, since both produced additional vasodilation. We are led to the conclusion that at least one other vasodilator in addition to adenosine must be present after 20 min. Between 3 and 20 min, vascular resistance is essentially constant but is always short of maximal vasodilation. This implies that the concentration of this additional vasodilator increases as [ADO]_isf declines. Adenine nucleotides are released from isolated guinea pig hearts together with adenosine during isoproterenol infusion and are potent vasodilators (5). However, nucleotide release declines even faster than adenosine release, indicating that nucleotides are not the missing steady-state vasodilator.

In conclusion, our results indicate that the [ADO]_isf during NE infusion in the nonworking isolated guinea pig heart reaches an early peak of ~1 μM. Adenosine accounts for most of the vasodilation at that time if resistance vessels are as sensitive to interstitial adenosine as in vitro experiments suggest. [ADO]_isf falls considerably during continued NE infusion, implying that at least one additional vasodilator is necessary to maintain steady-state reductions in vascular resistance. It remains to be determined whether these findings apply in preparations more physiological than the isolated heart.

APPENDIX

Consideration of the influence of adenosine uptake during passage through interdothelial clefts on the ratio C_isf/C_p and on flux through the cleft

If the interendothelial cleft walls were equipped with adenosine transporters at densities (number of transporters per unit surface area) near those on the luminal surface, then adenosine uptake within the cleft would reduce the amount of intravascular tracer adenosine that reaches the interstitium from the plasma. This would mean that a higher fraction of adenosine would be trapped in endothelial cells and less in myocytes than would occur if adenosine uptake occurred only at the luminal and abluminal free surfaces. It would also imply that the calculated values from venous outflow samples would be underestimated if cleft absorption were not accounted for.

Conceptually, consideration of the intracleft surfaces is a simple extension of models that account for transport across both luminal and abluminal surfaces. In modeling analyses (4, 30) the uptake at the luminal surface, PS_ecl, is inferred by the difference from a nonabsorbed reference marker confined to remain extracellular. Given that this is done correctly, then the amount taken up by endothelial cells is the sum of that taken up on three surfaces: luminal, cleft, and abluminal. This then poses the question of whether our previous analyses, ignoring the possibility of uptake within the cleft, accounted for the observed endothelial trapping by overestimating the uptake at the abluminal surface, PS_eca, relative to the competing routes of loss from the interstitial fluid via uptake by parenchymal cell, PS_pc, and return flux to the plasma, PS_g. If so, then the high estimates of PS_eca might be lowered.

The corollary of cleft uptake is therefore that the ratios of [ADO]_isf/[ADO]_p (adenosine concentration in the perfusate) must be raised compared with our previous estimates. This would bring our estimates closer to those obtained by collecting interstitial transudates.

The estimation of uptake by the cleft walls requires a lot of assumptions but is worth attempting, since there is no way to make a direct measurement. Let us first estimate the surface area of the sides of the clefts (S_cleft) and secondarily guess the transporter capacity of the cleft walls (P′). One starts with the anatomy and checks the result against the estimate of the conductance along the cleft from capillary to interstitial fluid, PS_g, for the extracellular solute, sucrose, which is not absorbed.

The interendothelial clefts, diagrammed in Fig. 4 (right), extend without limit throughout the vascular system, and so we estimate the length per gram of myocardial tissue (L_cleft).

FIG. 4.

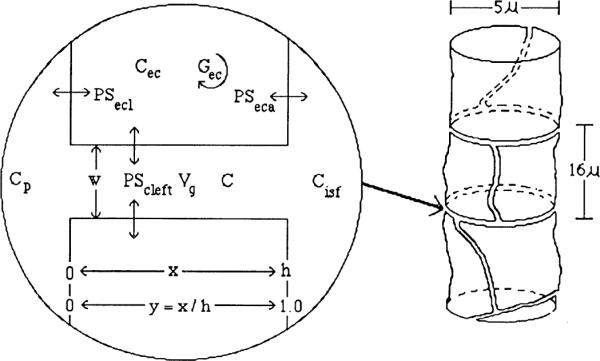
Left: diagram of interendothelial cleft with uptake on sides. Right: diagram of endothelial cells tiling a capillary. Dimensions are appropriate for the heart. C, concentration; h, depth of cleft; w, width of cleft; x, distance along unit; y, fraction of distance from plasma to interstitial fluid.

The total cleft length, L_cleft, is calculated from the pattern of tiling of endothelial cells within a small cylinder. We do this in two ways, which turn out to give similar results. The first is to calculate the lengths of perimeters around endothelial cells that tile the capillary surface area (S_c,; 500 cm²/g) as if it were in a plane

$$\begin{array}{cc}\hfill L_{\mathrm{cleft}}& =S_{\mathrm{c}}\frac{\text{cell circumference}∕2}{\text{cell area}}\hfill \\ \hfill & =S_{\mathrm{c}}\pi r_{\mathrm{ec}}∕\pi r_{\mathrm{ec}}^2\hfill \\ \hfill & =S_{\mathrm{c}}∕r_{\mathrm{ec}}\hfill \\ \hfill & =500∕(8\times {10}^{-4})\hfill \\ \hfill & =6\times {10}^5\mathrm{cm}∕\mathrm{g}\hfill \end{array}$$

where r_ec is the radius of endpthelial cells.

The second approach is to consider endothelial cells to tile a small cylinder. Electron-microscopic observations show that one cell wraps itself around a segment of the capillary. In cross sections one sees one junction more often than two. From Fig. 4 (right), one can see that there is one circumferential and one axial edge per endothelial cell. These two edges sum to approximately two times the axial length for roughly square-shaped cells. Then, with r_c as the capillary radius

$$\begin{array}{cc}\hfill L& =2\times \text{capillary lengths}(\mathrm{cm}∕\mathrm{g})\hfill \\ \hfill & =2S_{\mathrm{c}}∕2\pi r_{\mathrm{c}}\hfill \\ \hfill & =500∕\pi (2.5\times {10}^{-4})\hfill \\ \hfill & =6\times {10}^5\mathrm{cm}∕\mathrm{g}\hfill \end{array}$$

These are similar results. Each side of the cleft has a surface area of L_clefth, where h is the depth of the cleft from the capillary lumen to the interstitium, so the total cleft surface is

$$\begin{array}{cc}\hfill S_{\mathrm{cleft}}& =2L_{\mathrm{cleft}}h\hfill \\ \hfill & =2(6\times {10}^5)(0.7\times {10}^4){\mathrm{cm}}^2∕\mathrm{g}\hfill \\ \hfill & =84{\mathrm{cm}}^2∕\mathrm{g}\hfill \end{array}$$

This is ~16% of S_c, and the uptake by endothelial cells might be of this order.

Now we do a check. Is this S_cleft compatible with observed capillary PS_g, values for unabsorbed solutes? Data available for sucrose in guinea pig hearts (30) range from group means of 1.67–2.47 ml·g⁻¹· min⁻¹. If we take a middle estimate of 2 ml· g¹· min¹, can this be explained? Given that the permeability axially through the cleft, without absorption at the walls, is P = D/h (where D is the axial diffusion coefficient), S_g = L_cleft × width, and cleft width = 15 nm, then the predicted PS_g, = D × L_cleft × width/h = (0.5 × 10⁻⁵ × l/2)(6 × 10⁵)(15 × 10⁻⁷)/(0.7 × 10⁻⁴) cm³ ·g⁻¹ ·s⁻¹ = 1.9 ml ·g⁻¹ ·min⁻¹. [This assumes that the intracleft diffusion coefficient is one-half of the free diffusion coefficient in water. The value for diffusion through myocardial sheets is 23% (27), but pores themselves are probably less tortuous than tissue.] The answer is satisfactorily close to observed values.

To return to the question of uptake in the cleft, one can develop an expression to account for its influence on the concentration profile within the cleft from plasma to interstitial fluid. The calculation is for diffusion and exchange along a planar cleft (or cylindrical pore) with equivalent transmembrane conductance PS_cleft as in Fig. 4. The equations are

$${\mathrm{V}}_{\mathrm{g}}=\frac{\partial \mathrm{C}(x,t)}{\partial t}=P\prime S_{\mathrm{cleft}}[\mathrm{C}(x,t)-{\mathrm{C}}_{\mathrm{ec}}\left(t\right)]+\frac{{\mathrm{V}}_{\mathrm{g}}D}{L}\frac{{\partial }^2\mathrm{C}(x,t)}{\partial x^2}$$ (A1)

where V_g is the volume of the interendothelial gap and x is the distance along the gap, and where C(0, t) = C_p, and C(h, t) = C_isf are held constant at the ends of the cleft, and

$$\begin{array}{cc}\hfill {\mathrm{V}}_{\mathrm{ec}}\frac{\partial {\mathrm{C}}_{\mathrm{ec}}\left(t\right)}{\partial t}=P{S}_{\mathrm{ecl}}({\mathrm{C}}_{\mathrm{p}}-{\mathrm{C}}_{\mathrm{ec}})+P{S}_{\mathrm{eca}}({\mathrm{C}}_{\mathrm{isf}}-{\mathrm{C}}_{\mathrm{ec}})+& P\prime S_{\mathrm{cleft}}[\mathrm{C}(x,t)-{\mathrm{C}}_{\mathrm{ec}}]-G_{\mathrm{ec}}{\mathrm{C}}_{\mathrm{ec}}\hfill \\ \hfill & {\mathrm{C}}_{\mathrm{p}}\equiv {\mathrm{C}}_{\mathrm{p}}(t=0)\hfill \\ \hfill & {\mathrm{C}}_{\mathrm{isf}}={\mathrm{C}}_{\mathrm{isf}}(t=0)\hfill \end{array}$$ (A2)

assuming oceans relative to both pathway and endothelial cells, where V_ec, is the volume of the endothelial cell.

When G_ec → ∞, then C_cc ≡ 0, and there it becomes obvious that C_p and C_isf cannot be constant or even transiently regarded as constant when P_ecl and P_eca are similar to P′.

Nevertheless, when this fundamental issue is ignored to arrive at an approximate solution, Eq. A2 can be omitted and Eq. A1 becomes

$$\frac{\partial \mathrm{C}(x,t)}{\partial t}=-\frac{P\prime S_{\mathrm{cleft}}[\mathrm{C}(x,t)-{\mathrm{C}}_{\mathrm{ec}}]}{{\mathrm{V}}_{\mathrm{g}}}+\frac{D{\partial }^2\mathrm{C}(x,t)}{\partial x^2}$$

In steady state, when ∂C/∂t has gone to 0, then at each x we have

$$0=-\frac{P\prime S_{\mathrm{cleft}}[\mathrm{C}\left(x\right)-{\mathrm{C}}_{\mathrm{ec}}]}{{\mathrm{V}}_{\mathrm{g}}D}+\frac{{\partial }^2\mathrm{C}}{\partial x^2}$$

P′S_cleft the units of milliliters per minute, V_g has the units of milliliters per gram, and D has the units of centimeters squared per second. We assign β² = P′S_clert/(60V_gD) cm⁻ for convenience in calculation.

Translating, we get β² = P′ × cleft surface-to-volume ratio/D. We assume for a test that the density of transporters is the same inside the cleft as on the luminal surface and so take P′ = PS_ecl/S_ecl = (6 ml · g⁻¹ · min⁻¹)/(500 cm²/g) or P′ = 2.0 × 10⁻⁴ cm/s. The cleft surface-to-volume ratio, accounting for trans- port at both walls, is 2/cleft width; if width = 15 nm, then S_cleft/v_g, = 1.3 × 10⁶ cm¹. We then take D to be about one-half of the diffusion coefficient in water or 0.3 × 10⁻⁵ cm²/s. Then β² = (2.0 × 10⁻⁴)(1.3 × 10⁶)/(0.3 × 10⁻⁵) = 9 − 10⁷ cm⁻² and β =9.500 cm⁻¹. Quadrupling the cleft wall permeability dobles β The ratio of uptake along the walls to diffusion along the cleft is governed by the dimensionless group βh. At low βh, axial diffusion dominates; at high βh, uptake dominates.

With the boundary conditions C(0) = C_p and C(h) = C_isf and using y = z/h to define the position as a fraction of the cleft depth, we obtain the solution

$$\mathrm{C}\left(y\right)={\mathrm{C}}_{\mathrm{ec}}+\frac{({\mathrm{C}}_{\mathrm{isf}}-{\mathrm{C}}_{\mathrm{ec}})\sin h\left(\beta hy\right)+({\mathrm{C}}_{\mathrm{ec}}-{\mathrm{C}}_{\mathrm{p}})\sin h\left[\beta h(y-1)\right]}{\sin h\left(\beta h\right)}$$

Some resultant profiles for arbitrarily chosen fixed valus of C_p, C_isf, and C_ec are shown in Fig. 5. With h = 0.7 μm, then βh = 9,500 × 0.7 × 10⁻⁴ = 0.66. The low value suggests that if P′ is indeed similar to the luminal surface permeability, then uptake along the cleft is inconsequential because the profiles of C(y) for βh = 0.66 are almost straight. Both panels in Fig. 5 show a lOO-fold range of β. For maximum effect, we assume in both that C_ec is low (bottom) or zero (top).

FIG. 5.

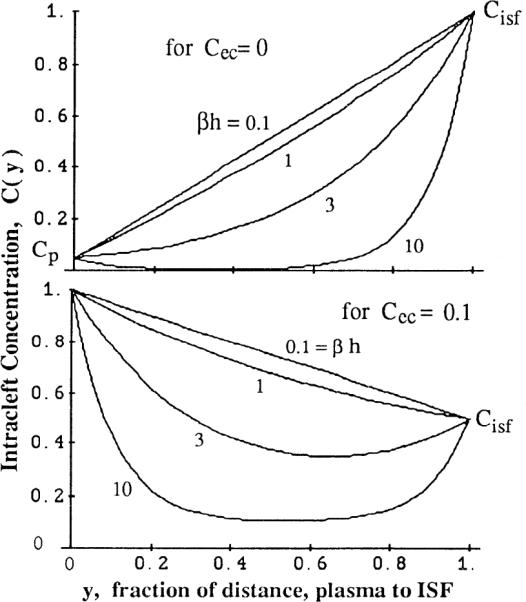
Concentration profiles along cleft of lenght h between plasma (at y = x/h = 0) and interstitium (at y = 1). Fractional uptake is governed by dimensionless parameter βh, ratio of lateral permeation to axial diffusivity in cleft {where β = [PS_cleft/(60V_cleftD)]^1/2}. Expected values for βh are <1. Top: fixed concentrations are C_p = 0.05, C_ec = 0, and C_isf = 1 μM. Bottom: C_p = 1, C_ec = 0.1, C_isf = 0.5 μM. With βh ≥ 3, there is net influx into cleft from both ends.

With constant cross-sectional area and diffusion coefficient, the diffusional flux through any cross section along the cleft is proportional to the concentration gradient, dC/dx, at that point. The fraction of adenosine entering the cleft from the capillary at x = 0 that passes through the other end of the cleft at x = h is equal to the ratio of dC(h)/dx to dC(O)/dx. Maximum adenosine uptake within the cleft occurs when C_ec = 0. In the case where C_isf = 0 also

$$\frac{\mathrm{dC}\left(h\right)}{\mathrm{d}x}∕\frac{\mathrm{dC}\left(0\right)}{\mathrm{d}x}=\frac{2}{e^{+\beta h}+e^{-\beta h}}$$

With βh = 0.66, the fraction passing through is 0.82. The relationship over a wide range is shown in Fig. 6.

FIG. 6.

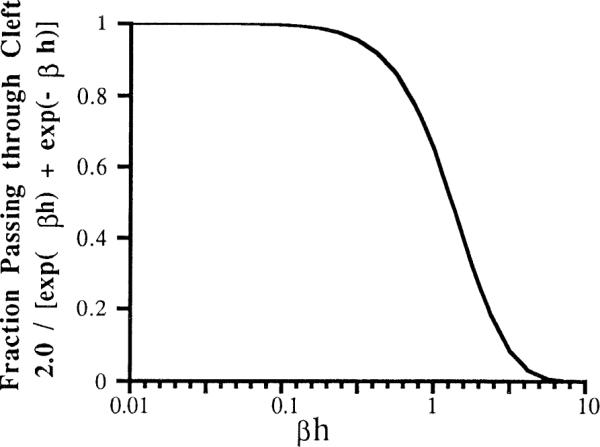
Fraction of tracer passing through cleft as function of product of β, permeability-to-diffusivity ratio, and cleft length h. Expected values for βh are <0.2–0.7.

This approximate calculation, therefore, leads to the same conclusion as does the consideration of the surface areas for permeation, namely that the effect of cleft wall permeation is for a few percent reduction in adenosine passing between the interstitial fluid and capillary and a few percent increase in endothelial uptake.