Prior probability and feature predictability interactively bias perceptual decisions

Abstract

Anticipating a forthcoming sensory experience facilitates perception for expected stimuli but also hinders perception for less likely alternatives. Recent neuroimaging studies suggest that expectation biases arise from feature-level predictions that enhance early sensory representations and facilitate evidence accumulation for contextually probable stimuli while suppressing alternatives. Reasonably then, the extent to which prior knowledge biases subsequent sensory processing should depend on the precision of expectations at the feature level as well as the degree to which expected features match those of an observed stimulus. In the present study we investigated how these two sources of uncertainty modulated pre- and post-stimulus bias mechanisms in the drift-diffusion model during a probabilistic face/house discrimination task. We tested several plausible models of choice bias, concluding that predictive cues led to a bias in both the starting-point and rate of evidence accumulation favoring the more probable stimulus category. We further tested the hypotheses that prior bias in the starting-point was conditional on the feature-level uncertainty of category expectations and that dynamic bias in the drift-rate was modulated by the match between expected and observed stimulus features. Starting-point estimates suggested that subjects formed a constant prior bias in favor of the face category, which exhibits less feature-level variability, that was strengthened or weakened by trial-wise predictive cues. Furthermore, we found that the gain on face/house evidence was increased for stimuli with less ambiguous features and that this relationship was enhanced by valid category expectations. These findings offer new evidence that bridges psychological models of decision-making with recent predictive coding theories of perception.

Introduction

Through past experience we are able to improve our internal model of the world and, consequently, our ability to anticipate, perceive, and interact with relevant stimuli in our environment. Indeed, there is a growing body of evidence to suggest that the brain proactively facilitates perception by constructing feature-level models or templates of expected stimuli (Clark, 2013; Summerfield & Egner, 2009). Neural correlates of predictive stimulus templates have been observed in visual (Jiang, Summerfield, & Egner, 2013; Kok, Failing, & de Lange, 2014; Summerfield, Egner, Greene, et al., 2006; White, Mumford, & Poldrack, 2012), auditory (Chennu et al., 2013), somatosensory (Carlsson, Petrovic, Skare, Petersson, & Ingvar, 2000), and olfactory (Zelano, Mohanty, & Gottfried, 2011) cortex, highlighting feature prediction as a fundamental property of perception. It follows that feature-level predictions are compared with incoming sensory signals to determine a match between the expected and observed inputs. Thus, the extent to which expectations influence perception should depend, not only on the prior probability of a stimulus, but also the predictability of its content as well as the overlap in expected and observed features. For example, general expectations of encountering an animal are less informative about the forthcoming sensory experience than say, expecting to be greeted at the door by a familiar family pet. In the latter case, the set of predictable sensory features is constrained in comparison with the limited predictability afforded by anticipating any animal at all. However, it is presently unclear how feature-level uncertainty influences the underlying dynamics of perceptual expectation and decision-making.

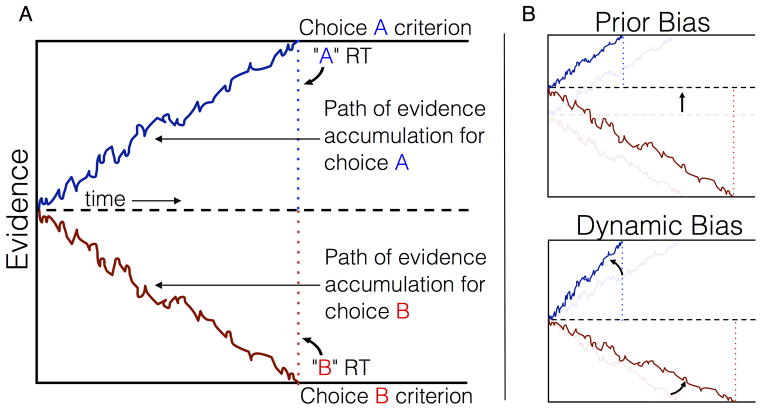
Behaviorally, prior expectations bias the speed and accuracy of perception. When incoming sensory information is consistent with prior knowledge, stimuli are recognized more swiftly and with greater precision, whereas performance suffers when prior beliefs are contradicted by observed evidence (Carpenter & Williams, 1995; Król & El-Deredy, 2011a, 2011b; Puri & Wojciulik, 2008). Formal theories of perceptual decision-making, such as the drift-diffusion model, are centered around the assumption that recognition judgments are produced by sequentially sampling and accumulating noisy evidence to a decision criterion (Gold & Shadlen, 2007; Ratcliff, 1978). When no prior information is available, the distance to the decision criterion is the same for alternative choices and the rate of evidence accumulation is determined solely by the strength of the observed signal (Figure 1A). However, access to advance knowledge such as the prior probability of alternative outcomes, may be leveraged to bias performance in favor of one choice over the other. One strategy is to preemptively increase the baseline evidence for the expected choice, reducing the amount of evidence that must be sampled to reach the corresponding criterion (Fig. 1B, top) (Edwards, 1965; Leite & Ratcliff, 2011; Link & Heath, 1975; Mulder, Wagenmakers, Ratcliff, Boekel, & Forstmann, 2012). Alternatively, prior knowledge may be used to dynamically weight incoming evidence, accelerating evidence accumulation for the more probable outcome (Fig. 1B, bottom) (Cravo, Rohenkohl, Wyart, & Nobre, 2013; Diederich & Busemeyer, 2006). Traditionally, baseline and rate hypotheses have been framed as alternative explanations of decision bias. However, converging behavioral and neurophysiological evidence now suggests that expectations may recruit both mechanisms (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Diederich & Busemeyer, 2006; Hanks, Mazurek, Kiani, Hopp, & Shadlen, 2011; van Ravenzwaaij, Mulder, Tuerlinckx, & Wagenmakers, 2012).

Figure 1. Schematic of Drift-Diffusion Model.

(A) The unbiased diffusion model shows two decisions for equal strength “A” (blue) and “B” (red) stimuli. Blue and red dotted lines mark the reaction time for each choice, equal for “A” and “B” decisions in this scenario. (B) Bias mechanisms. Prior Bias Model (PBM), the starting-point is shifted toward more probable boundary, decreasing criterion for expected choice (“A”) and increasing criterion for the alternative (“B”). Dynamic Bias Model (DBM), prior probability increases the slope of accumulation for the expected choice (“A”) and decreases slope for the alternative (“B”).

While diffusion models have provided valuable insights into the dynamics of perceptual judgment, they are agnostic about the exact sources of expectation bias and the stage of information processing at which prior knowledge is integrated with sensory evidence. Recent progress has come from tracking neural activity as human and animal subjects anticipate and categorize noisy perceptual stimuli. These studies have found compelling evidence that expectations bias sensory representations both prior to and during evidence accumulation via recurrent communication between early feature-selection and higher-order cognitive processing domains. For instance, human neuroimaging studies have detected anticipatory signals or “baseline shifts” in sensory regions that are selective for expected stimuli (Esterman & Yantis, 2010; Kok et al., 2014; Shulman et al., 1999) as well as enhanced contrast between early target and distractor representations (Jiang, Summerfield, & Egner, 2013; Kok et al., 2012). Hierarchical models of perception, such as predictive coding, propose that these early sensory modulations represent a feature-level template of the expected stimulus, generated by top-down inputs from higher-order regions that encode more abstract predictions (i.e., category probability). The predictive template is updated to reflect each sample of evidence until uncertainty is sufficiently minimized and a decision can be made. In the event of a match, top-down gain is amplified to accelerate evidence accumulation and speed the decision, whereas mismatches are associated with greater reliance on bottom-up information and slower decision times, suggesting sensory gain is lowered to allow more evidence to be sampled (Summerfield & Koechlin, 2008).

Indeed, the neural correlates of perceptual expectations (discussed above) during pre- and post-stimulus epochs bear a striking resemblance to the prior and dynamic bias mechanisms proposed by sequential sampling models. More importantly though, these findings imply that the influence of prior knowledge is conditional on the precision at which abstract (i.e., categorical) expectations are mapped onto incoming evidence at the feature level. Thus, the effect of prior knowledge on the mechanisms of decision bias should reflect two critical bits of information – uncertainty in the features of the expected category as well as the categorical ambiguity of the observed features. Moreover, each of these sources of uncertainty is intuitively mapped to a distinct stage of the decision process, with uncertainty in the expected features influencing pre-sensory evidence and stimulus ambiguity affecting post-sensory evidence accumulation. The latter has been confirmed in a recent study showing that the representational distance between a stimulus and a discriminant category boundary in feature space could be used to predict RT, and furthermore, that this relationship could be explained by adjusting the drift-rate in a sequential sampling model (Carlson, Ritchie, Kriegeskorte, Durvasula, & Ma, 2013). Compared to stimuli with more ambiguous features, located closer to the category boundary, stimuli represented further away were categorized more rapidly due to a higher drift-rate on decision evidence (i.e., faster rate of evidence accumulation). However, it remains unclear how prior knowledge influences this relationship and how uncertainties in predicted and observed stimulus features interact during perceptual decision-making (see Bland & Schaefer, 2012 for review).

We investigated these questions by fitting alternative diffusion models to behavioral data obtained in a probabilistic face/house discrimination task. Faces and houses were strategically chosen for several reasons. These categories have been relied upon extensively and continue to be used in behavioral and neuroimaging studies of perceptual decision-making. Thus, it is of general interest how basic properties of these stimuli may come to bear on the decision process and how subtle differences between face and house categories might affect experimental outcomes. More importantly, however, faces and houses naturally differ in the predictability of their exemplars. Faces exemplify a highly homogeneous category, all constructed of the same basic features with a similar spatial layout. Conversely, houses have greater feature-level and spatial variability, making them less predictable stimuli. Thus, we predicted that face expectations, which are more precise at the feature-level, would produce a greater change in the starting point of decision evidence compared to house expectations, which involve greater uncertainty at the feature level. Additionally, we quantified the feature-level ambiguity of individual stimuli, allowing us to further explore the interaction between prior and present evidence on decision mechanisms. Specifically, we predicted that less “ambiguous” stimuli (see Methods) would be associated with accelerated rates of evidence accumulation (Carlson et al., 2013) and that this relationship would be strongest when the stimulus matched the expected category.

Methods

Subjects

Subjects included 25 native English speakers. All subjects reported normal or corrected-to-normal vision. Two subjects were eliminated from further analysis for having chance-level performance. The remaining 23 subjects (16 female) ranged in age from 21 to 27 years (mean age = 23.09). Informed consent was obtained from all subjects in a manner approved by the Institutional Review Board of the University of Pittsburgh. Subjects were compensated at a rate of $10 per hour for their participation.

Stimuli

Stimuli included 42 neutral-expression face and 43 house grayscale images (85 total), originally measuring 512×512 pixels. Face images were taken from the MacBrain Face Stimulus Set (courtesy of the MacArthur Foundation Research Network on Early Experience and Brain Development, Boston, MA). All house stimuli were generated from locally taken pictures of houses in Pittsburgh, PA. All images were cropped so that only the face or house was left over a white background. Face and house stimuli were then normalized, noise-degraded, and converted into movies using the following procedure. All images were individually transformed into a two-dimensional, forward discrete Fourier transform (DFT) via a Fast Fourier Transform algorithm using Matlab (2010a, The Mathworks Inc., Natick, MA). The DFT for each image was then converted into separate phase-angle and amplitude matrices. The amplitude matrix was averaged across all images within a category to normalize the contrast, luminance, and brightness of each image in that set. In order to introduce a controlled level of noise into each image, each individual phase matrix was filtered with a white Gaussian noise (AWGN) filter, convolving the signal in the original phase matrix with a specified level of noise to achieve a desired signal-to-noise ratio (SNR) in the filtered matrix. An inverse FFT was then applied to the combined average within-category amplitude matrix and image-specific noise-convolved phase matrix.

This procedure produced a single still frame of the original image embedded in a quantifiable level of randomly distributed noise. By repeating this procedure for each image and concatenating each randomly degraded copy in a sequence, we were able to produce a dynamic display of noise over the signal (face, house) in the original image. Visually, this created the appearance of television static over a stationary object. The image processing procedure was repeated a total of 90 times per stimulus. All 90 still frames, each containing a unique spatial distribution of noise, were concatenated at 15 frames per second to produce a movie running 6 seconds in length.

Our goal was to identify a common SNR that increased the difficulty of the discrimination sufficiently in order to encourage subjects to utilize the cues on both face and house trials. One approach would be to normalize stimuli between categories based on subject-wise psychophysical assessments, allowing stimuli from different categories to be equated perceptually. However, psychophysically matching face and house stimuli could diminish hypothesized category-specific effects of interest in the current study. A pilot study was conducted in which subjects made face and house discriminations for stimuli degraded at various noise levels in order to determine an appropriately challenging noise level. Based on this study, we chose to include an equal number of 68% and 69% degraded stimuli in each set, yielding an average noise-level of 68.5% for face and house stimuli. The decision to include two noise levels was motivated by the following factors: (1) collapsing across 68% and 69% noise levels produced an error-rate for both categories that would allow for estimation of error RT distributions in the diffusion model; (2) including multiple noise-levels in each set served to decrease within-category sensory reliability which has been shown to promote the use of prior information during perceptual decision-making (Hanks et al., 2011). All reported analyses were performed with noise levels collapsed into a single condition.

Behavioral Task

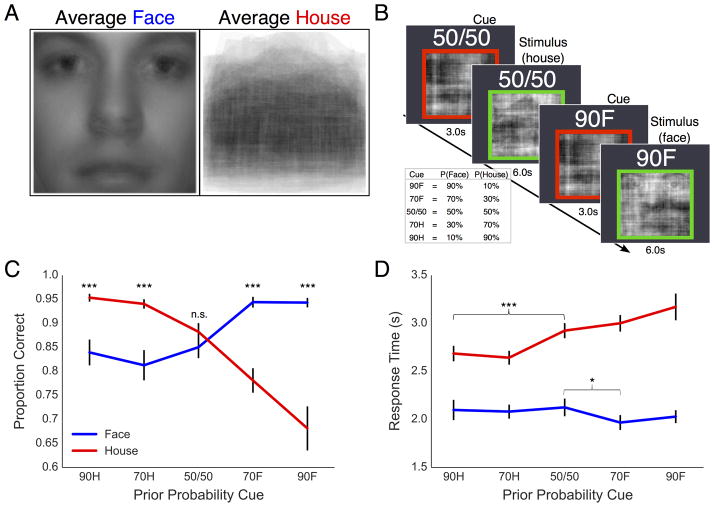
Subjects discriminated between noise-degraded face and house stimuli. Each discrimination trial was preceded by a cue informing the participant of the probability that the upcoming stimulus would be a face or house (Fig. 2B). The cue phase consisted of a screen-centered movie of full noise (~100% noise) surrounded by a red border. Above the border a number-letter combination was displayed informing subjects of the prior probability of each category. Subjects were explicitly informed of the cue prior to beginning the study and received an explanation of how the cue should be interpreted. For example, a 90F cue indicated a 90% probability of seeing a face and a 10% probability of seeing a house on the upcoming trial. The complete list of cues included a 90% and 70% prior for each category as well as a 50/50 cue indicating a neutral prior (i.e. 90F, 70F, 50/50, 70H, 90H; see Fig. 2B). After 3.0 seconds, the border turned green to indicate that a trial had begun and an image was present within the static. Subjects were given 6.0 seconds to respond and indicated their choice by pressing one of two buttons. Prior to beginning the main experiment, subjects were given a chance to practice the task for a maximum of 15 minutes or until they were comfortable with the paradigm. In the main experiment, subjects completed a total of 500 trials, split across five blocks of 100 trials each. Each of the five probabilistic cues was included 100 times, pseudorandomly distributed across the 500 trials for each participant. Cues were reliable predictors of the probability of seeing each category on the upcoming trial (e.g. the 90F cue was followed by a face 90% of the time and a house only 10% of the time). Stimulus presentation and data collection were programmed in the PsychoPy software package (Peirce, 2007).

Figure 2. Average face and house stimuli, task design, and behavioral data.

(A) Average of all original face and house images used to generate noise-degraded movie stimuli. (B) Behavioral task and probabilistic cues (table) with corresponding face and house prior probabilities. Two cue-stimulus trials are shown. (C) Mean accuracy for face (blue) and house (red) stimuli. (D) Mean RT in seconds correct face (blue) and house (red) choices. Error bars are the standard error. n.s.=not significant, *p<.05; **p<.01; ***p<.001.

Comparing Faces and Houses in Feature Space

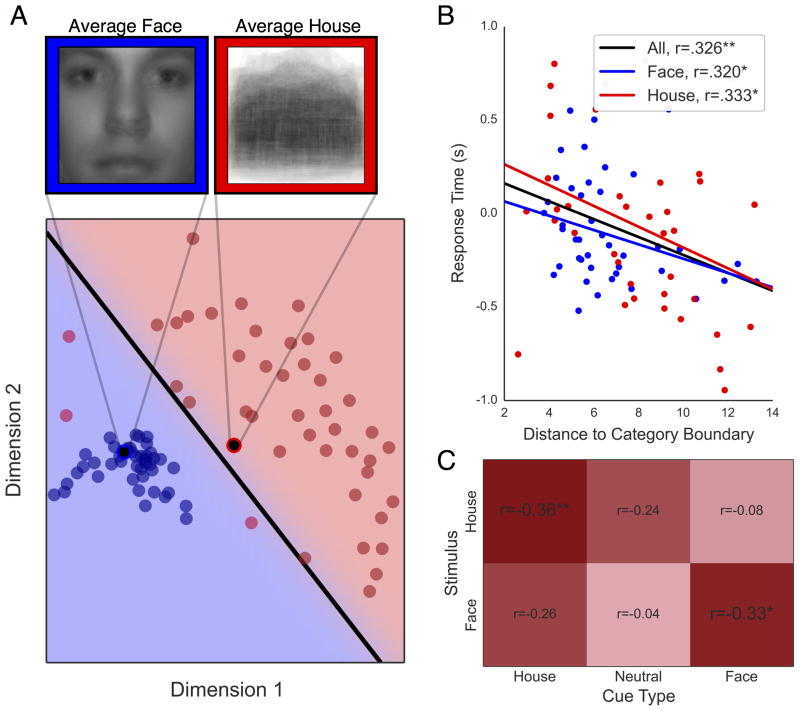
In order to visual the shared feature-level information within face and house categories, all face and house images were averaged together to produce a single “template” stimulus for each category (Figure 2A). Next, in order to visualize the feature variability within face and house categories, all stimuli were submitted to a similarity analysis and projected into a low-dimensional feature space using the Image Similarity Toolbox in Matlab (Seibert, Leeds, & Tarr, 2012). The similarity between each pair of images was derived by overlaying the images and summing the squared difference of their pixel values. Classical Multi-Dimensional Scaling (MDS) analysis (Seber, 2009) was then performed on the similarity matrix to visualize face and house stimuli in a two-dimensional coordinate plane. Plotting each stimulus exemplar according to its MDS coordinates provided a useful visual representation of the feature variability within each category as well as the difference in feature-reliability between categories (Figure 3A).

Figure 3. Multidimensional scaling (MDS) and correlation of face/house representational distance with response time.

(A) face (blue dots) and house (red dots) stimuli projected into two-dimensional feature-space based on classic MDS. Average face and house stimuli are plotted as black circles surrounded by a blue and red ring, respectively. Category boundary estimated by linear discriminant analysis is shown as a black line separating face and house stimuli. The LDA boundary correctly classified 100% of face stimuli and 93% of house stimuli. (B) Mean RT plotted as a function of the representational distance of individual face (blue) and house (red) stimuli. Correlation lines are shown for all stimuli (black), face (blue), and house (red) stimuli. (C) Heatmap and correlation coefficients for representational distance and RT for face (bottom row) and house (top row) stimuli across cue type (columns). *p<.05; **p<.01; ***p<.001

Subsequently, a linear discriminant analysis (LDA) was performed using the Scikit-Learn package in Python (Pedregosa et al., 2011) to find the optimal linear boundary separating face and house stimuli in the MDS coordinate plane. The linear boundary may be conceptualized as a decision boundary between face and house categories, similar to the decision criterion in classic signal detection theory. The Euclidean distance from each exemplar stimulus to the category boundary, hereafter referred to as the representational distance, thus provides an index of its discriminability from the opposing category.

Previous studies have shown that representational distance is a reliable predictor of decision speed, where stimuli further from the category boundary are associated with faster response times (Carlson et al., 2013). We first sought to replicate this finding using a similar procedure to that found in Carlson et al. (2013), calculating the Spearman’s rank order correlation between the distance to category boundary and the mean RT for each stimulus exemplar. Note that in Carlson et al. (2013), feature reduction was performed on functional magnetic resonance imaging (fMRI) data indexing the neural response to individual stimulus exemplars in primary visual and inferotemporal cortex. However, in the present study, feature-reduction is performed on the stimuli themselves.

All exemplar RTs were normalized to eliminate subject-level differences. Correlations were first calculated for face and house stimuli collapsing across cue-type to determine a main effect of representational distance on RT. Subsequently, the mean exemplar RTs were split by cue-type, collapsing 70 and 90% predictive cues into a single variable for face and house categories to ensure adequate trial counts per condition. This allowed us to investigate how the cued expectation of a face or house modulated the relationship between representational distance and RT. Finally, representational distance was included as a regressor in diffusion model fits to evaluate how drift-rate was affected by the interaction between probabilistic cues and categorical ambiguity (see below).

Hierarchical Drift-Diffusion Model

In the full Ratcliff Drift-Diffusion Model (Ratcliff & McKoon, 2008) (hereafter, the diffusion model), evidence is stochastically accumulated in a single decision-variable (DV) from a predetermined starting-point z, located at some point between two decision boundaries, separated by a distance a. As evidence is sampled, the DV drifts toward the boundary supported by the signal at an average rate of v, called the drift-rate, with a variance η, reflecting the intratrial noise in the system. Additionally, the model parameterizes non-decision time t_er to account for non-decision related sensory and motor processing, as well as intertrial variability in drift-rate s_v, starting-point s_z, and non-decision time s_t parameter. Evidence accumulation is terminated once the DV reaches one of the two criterion boundaries, initiating the corresponding choice and marking the response time (RT). Traditionally, the effects of prior knowledge have been modeled as a bias in the baseline or starting-point, referred to here as the prior bias model (PBM; Figure 1B, top), or alternatively, as a bias in the rate of evidence accumulation, referred to here as the dynamic bias model (DBM; Figure 1B, bottom). In a recent study, predictive cues led subjects to bias both of these mechanisms, shifting the starting-point closer to the more probable boundary and increasing the drift-rate for that category (van Ravenzwaaij et al., 2012). We refer to this model as the multi-stage model (MSM).

Diffusion models were fit to choice and RT data using HDDM (Wiecki, Sofer, & Frank, 2013), an open source python package for hierarchical Bayesian estimation of drift-diffusion model parameters. Here, the term hierarchical means that group- and individual subject-level parameters are estimated simultaneously, such that group-level parameters form the prior distributions from which individual subject estimates are sampled. A recent study comparing HDDM with alternative estimation approaches showed that hierarchical fitting requires fewer observations (i.e., experimental trials) to recover parameters and is less susceptible to outlier subjects than traditional methods (Wiecki et al., 2013). More details regarding hierarchical Bayesian models and model fitting procedures can be found in the supplementary materials.

All model parameters were estimated using three Markov Chain Monte-Carlo (MCMC) chains of 5K samples each with 1K burn-in samples to allow the chain to stabilize. The three chains were used to calculate the Gelman-Rubin convergence statistic for all model parameters. For all model parameters, this statistic was close to 1 (+/− 0.01), suggesting that 5K samples was sufficient for MCMC chains to converge. Models were response coded with face responses terminating at the upper decision boundary and house responses at the bottom. This allowed for meaningful interpretation of bias in the starting-point parameter, where a shift upward or downward from ½a corresponded to a face or house bias, respectively. Separate drift-rates were estimated for face and house stimuli such that a positive drift produced a face response and negative drift produced a house response.

We compared four hypothetical models of choice bias differentiated by which parameter or set of parameters was free to vary across probabilistic face/house cues. All models contained single group-level estimates of the intertrial variability in the drift-rate, starting-point, and non-decision time. Additionally, all models included a single estimate for boundary separation and non-decision time at the subject level, parameterized by their respective group-level means and standard deviations. For each subject in the hierarchical PBM, separate starting-points were estimated for each of the five cues. In the DBM, separate face and house drift-rates were estimated for each of the five cues. We fit two versions of this model to the data: the DBM, in which starting-point was fixed at ½a, and the DBM+, in which the starting-point was estimated from the data. Finally, the MSM can be viewed as a combination of the PBM and DBM. Separate starting-points, face drift-rates, and house drift-rates were estimated for each of the five cues. A summary of the parameters included in each model and their dependencies is given in Table 1.

Table 1. Description of diffusion model parameters and parameter dependencies.

Parameter dependencies (•, –, S, C) for all group- and subject-level parameters (rows) are listed for each of the four hierarchical models (columns). •, free parameter with no dependencies; –, fixed parameter; S, parameter dependency on stimulus category (e.g. group and subject level parameters estimated separately for face and house stimuli); C, parameter dependency on cue type (e.g. group and subject level parameters estimated for all five cue types).

Parameters		Models
Group	Subject	PBM	DBM	DBM+	MSM
μa, σa	ai	•	•	•	•
μv, σv	vi	S	S, C	S, C	S, C
μt, σt	teri	•	•	•	•
μz, σz	zi	C	–	•	C
sv		•	•	•	•
st		•	•	•	•
sz		•	•	•	•

To ensure that model selection was not biased by the coding conventions described above, we refit each of the four models using an alternative coding scheme in which biases in starting-point and/or drift-rate were estimated relative the value in the neutral condition (see supplementary materials for more information). These models fit the data following the same rank order as the models explained above, confirming that model selection was not biased by the coding conventions described above. The remainder of the article refers to the models explained above, as the alternative coding convention was not well suited for assessing category specific effects of interest on bias parameters (see supplementary materials for more detailed explanation).

Finally, the best-fitting model was re-fit to the data including representational distance as a regressor on the drift-rate parameter for each stimulus category for each cue type, collapsed into face, house, and neutral cues (see Wiecki et al., 2013 for details). Specifically, the model assumed that the effect of cue type on face and house drift-rates was also dependent on the trial-wise representational distance or feature-level “ambiguity” of the observed stimulus. Note that this model was not included in the model comparison and selection process but was fit post-hoc to determine an interaction between representational distance and cue-type on drift-rate using the framework of the best-fitting model.

Model Comparison and Hypothesis Testing

Several methods, both quantitative and qualitative, were used to contrast alternative diffusion models. Because comparisons involved models of varying complexity, we used Deviance Information Criterion (DIC) to evaluate model performance. The DIC is a measure of model deviance (i.e. lack-of-fit) that is further penalized by the effective number of parameters used to fit the model to the data (Spiegelhalter, Best, Carlin, & Linde, 1998); thus, models with lower DIC values are favored. Conventionally, a difference of 10 or greater between model DIC scores is interpreted as significant and the model with the lower score is declared the best-fit model (Burnham & Anderson, 2002; Zhang & Rowe, 2014). DIC was chosen for model comparison as it is more appropriate for comparing hierarchical models than other more commonly used criterion measures such as Akaike information criterion (AIC) or Bayesian information criterion (BIC) (Spiegelhalter et al., 1998). Because diffusion models were fit hierarchically rather than individually for each subject, a single DIC value is calculated for each model which reflects the overall fit to the data at the subject and group levels.

Another aim was to assess how well alternative models qualitatively fit the data. To explore this, simulations were run using parameters estimated in each model to generate theoretical data sets for comparison with the empirical data. For qualitative comparisons, we refit each model to single-subject data in order to generate subject-level parameters that were not influenced by the group-level trends, as is the case in the hierarchical model. For each of the four models (i.e., the PBM, DBM, DBM+, and MSM), each individual subject’s parameters were used to simulate 100 theoretical datasets, each including the same trial counts per condition as individual experimental datasets. For each of the 100 simulated datasets, subject-wise mean RT (correct only) and accuracy were calculated for each cue-stimulus condition and averaged for comparison with the corresponding empirical estimates.

For the best-fit model, we performed follow-up contrasts to test whether the hypothesized bias parameters systematically and reliably changed across probabilistic cues. Contrasts were performed by subtracting the posterior estimated in the neutral condition (i.e., 50/50 cue) from the posterior in each predictive cue condition (i.e., 90H, 70H, 70F, and 90F cues) for each bias parameter in the model (i.e., μ_vH, μ_vF, μ_z). This yielded a probability density over the difference of means for the two conditions. For each posterior difference, we estimated the 95% credible interval for the distribution and also the probability mass on each side of the zero value for testing one-tailed hypotheses. For instance, the one-tailed hypothesis that a parameter value is expressly increased from condition A to condition B with a probability of at least 95% may be tested by estimating the probability mass to the right of zero for the posterior difference μ_B−μ_A. The hypothesis is supported if the positive probability mass meets the significance criterion and is rejected otherwise.

Behavioral Data Analysis

Fast response outliers were removed from the data for each subject using the exponentially weighted moving average (EWMA) algorithm packaged in D-MAT, an open source Matlab toolbox for fitting diffusion models (Vandekerckhove & Tuerlinckx, 2007). In total, 1.56% of trials were eliminated based on subject-specific EWMA estimates. Mean RT (correct trials only) and accuracy measures were analyzed separately using a 2 (stimulus: face, house) × 5 (cue: 90H, 70H, 50/50, 70F, 90F) repeated-measures ANOVA model. Finally, a one-way repeated measures ANOVA was run within face and house categories separately to test the simple effect of probabilistic cues on RT and accuracy. All analyses revealed that the data significantly violated the sphericity assumption. Thus, Greenhouse-Geisser corrected results are reported for both measures. All pairwise comparisons reported are corrected for multiple comparisons using a Sidak HDR correction.

Results

Behavioral Results

Patterns of accuracy (Figure 2C) and RT (Figure 2D) confirmed that subjects biased performance in favor of the cue-predicted category. We observed a significant main effect of stimulus on RT, F(1, 22)=191.53, p<.001, but not choice accuracy, F(1, 22)=2.44, p=.13. There was a significant main effect of cue on RT, F(4, 58.03)=8.08, p<.001, and accuracy, F(4, 72.1)=10.14, p<.001. Importantly, analyses revealed a significant interactive effect of stimulus category and cue on RT, F(2.18, 47.95)=9.66, p<.001, as well as accuracy, F(1.53, 33.61)=31.96, p<.001, indicating that responses on face and house trials were differentially modulated by the cue predictions. Consistent with our predictions, post-hoc contrasts revealed significantly higher accuracy for the more probable stimulus category on trials following a non-neutral probabilistic cue (Fig. 2C; all p<.001) but no reliable difference between categories in the neutral condition, t(22)=1.18, p=.25. Conversely, analysis of RT revealed that face responses were reliably faster than house responses regardless of the preceding cue (Fig. 2D; all p<.001).

To further explore how probabilistic cueing affected face/house decisions we examined the effect of predictive cues on choice accuracy within each category separately. Accuracy increased with prior probability for both face, F(4, 30.85)=14.53, p<.001, and house, F(4,30.85)=32.84, p<.001, stimuli. However, pairwise comparisons revealed that while valid predictive cues increased choice accuracy similarly for face and house stimuli, invalid face but not house cues had diminishing effects on the accuracy for the opposing category. This finding suggests that house predictions had a weaker effect on the final decision outcome than face predictions, supporting our hypothesis that the salience of prior information is proportional to the feature-level predictability of the stimulus.

Within-category analysis of the cue effect on RT (see Fig. 2D) revealed that marginally and highly predictive cues reliably increased the speed of house responses (both p<.001). Face RT was comparatively less sensitive to cueing, showing a significant advantage in the 70F but not 90F cue condition relative to neutral. In contrast with accuracy, RT was not reliably affected by invalid cues in either face or house categories relative to the neutral cue condition (all p>.05).

Representational Distance and Response Time

Another goal was to assess how representational distance of individual stimuli affected decision performance. Specifically, we examined the relationship between RT and the distance from the face/house category boundary for individual exemplars (see Methods). Figure 3B shows a significant linear decrease in RT for face and house stimuli with increasing distance from the category boundary. In other words, stimuli with less ambiguous features are categorized more rapidly. Critically, when exemplar RTs were split by cue type, the negative correlation between representational distance and RT only remained significant for trials in which the cue was a valid predictor of the stimulus category (Figure 3C). Indeed, this outcome is consistent with the notion that the rate at which feature-level evidence is integrated towards a decision depends on the match between expected and observed evidence.

Diffusion Model Comparison

We next tested whether face/house expectations lead to (1) a prior bias in the starting-point (i.e., PBM), (2) a dynamic bias in the rate of evidence accumulation with the starting-point fixed at the unbiased position (i.e., DBM), (3) a dynamic bias in the rate of evidence accumulation with a free starting-point parameter (i.e., DBM+), or (4) a bias in both the starting-point and accumulation rate (i.e., MSM). Based on estimated DIC values for each model (see Table 2), the MSM provided the best account of face and house biases across probabilistic cues. Because the DIC score for the MSM lower than all other models’ by at least 10 (Burnham & Anderson, 2002), this suggests the MSM provided a sufficiently better fit to the data than competing models to justify its greater complexity.

Table 2. Penalized model fit statistics for competing diffusion models.

PBM: starting-point estimated across probabilistic cues. DBM: both face and house drift-rate parameters estimated across probabilistic cues. DBM+: both face and house drift-rate parameters estimated across probabilistic cues with free starting-point parameter. MSM: starting-point and face and house drift-rate parameters estimated across probabilistic cues. D̄, the expected deviance score for each model that measures lack of fit between the model and the data. pD, the effective number of parameters used to fit the model. DIC, deviance information criterion summarizes each model as a combination of its (lack of) fit to the data and its complexity, DIC = D̄ + pD. Thus, the model with the lowest DIC score is favored over alternatives.

Model	D̄	pD	DIC
PBM	35459.62	151.65	35611.28
DBM	35863.31	210.68	36073.99
DBM+	35358.03	219.15	35577.18
MSM	35295.95	257.01	35552.96

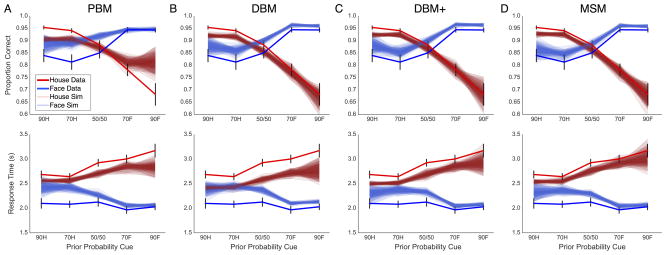
In addition to ranking models by their estimated DIC scores, we evaluated the performance of each model by how well it recovered empirical accuracy (Figure 4, top row) and RT means across conditions (Figure 4, bottom row). Simulations from the PBM (Fig. 4A) displayed reasonable fits to observed RT means but failed to capture basic experimental effects on choice accuracy. In contrast, simulations from the DBM (Fig. 4B) provided close fits to accuracy means but were less successful at recovering RT means, falling outside two standard errors of the empirical mean in all but a few conditions. Simulations from the DBM+ (Fig. 4C) and MSM (Fig. 4D) provided similarly adequate fits to both RT and accuracy means. Ultimately, however, the MSM simulations produced closer fits to the data, falling within two standard errors of the observed mean accuracy in all but one condition and mean RT in all but two conditions. In sum, the MSM provided the best fit to observed data, in both complexity-penalized DIC rankings and qualitative model comparisons.

Figure 4. Qualitative comparisons between empirical behavioral measures and model-simulated predictions.

For each hierarchical model, (A) PBM, (B) DBM, (C) DBM+, and (D) MSM, the model-predicted average accuracy (top) and RT (bottom) for face (transparent blue) and house (transparent red) stimuli are overlaid against empirical averages (solid lines).

Face/House Bias Parameters in the MSM

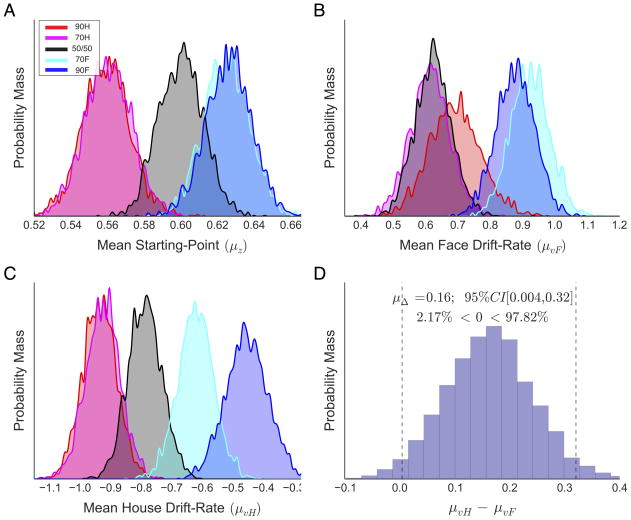
Next, we examined how probabilistic cues affected bias parameters for face and house stimuli. Mean parameter estimates for all four hierarchical models may be found in Table 3; however, the following sections focus exclusively on parameter estimates from the best-fit model, or MSM. Posterior probability distributions of starting-point (Figure 5A), face drift-rate (Figure 5B), and house drift-rate (Figure 5C) estimates revealed systematic effects across probabilistic cues. As expected, face and house predictive cues shifted the starting-point closer to the more probable choice boundary compared to the neutral condition, higher for faces and lower for houses (Fig. 5A). However, although starting-point estimates displayed the expected pattern across face and house cues, the absolute estimates fell closer to the face than the house boundary in all cue conditions (all z_cue > ½a). On valid cue trials, face (Fig. 5B; 70F: light blue, 90F: blue) and house (Fig. 5C; 70H: light red, 90H: red) drift-rates were accelerated relative to neutral. However, invalid cues had distinct effects on face and house drift-rates. House drift-rates on trials following a face cue (Fig. 5C; 70F: light blue, 90F: blue) were shifted closer to zero from the neutral cue distribution, suggesting face cues suppressed the rate of house evidence accumulation (Fig. 5C; 70F: light blue, 90F: blue). In contrast, face drift-rates on trials following a house cue (Fig. 5B; 70H: light red, 90H: red) showed substantial overlap with the neutral cue estimates, suggesting that house cues did not suppress the rate of face evidence accumulation.

Table 3. Mean posterior parameter estimates for competing diffusion models.

Posterior means computed for each parameter (columns) in all four diffusion models (rows). Parameters included in all models are boundary separation (a), non-decision time (ter), inter-trial variability in the drift-rate (sv), starting-point (sz), and non-decision time (st). Single face (v_F) and house (v_H) drift-rate estimates are given for the PBM. A single starting-point (z) is given for the DBM and DBM+ models, fixed by experimenters in the DBM and estimated from the data in the DBM+. For models including a bias in the starting-point (i.e., PBM, MSM), starting-points are given for each of the predictive cues (z_90H, z_70H, z_70F, z_90F) and the neutral cue (z_n). For models including a bias in the drift-rate (i.e., DBM, DBM+, MSM), drift-rates are given for each of the predictive cues (v_90H, v_70H, v_70F, v_90F) and the neutral cue (v_n), split into separate rows for face (F) and house (H) stimuli. Blank cells (--) are due to differences in each model’s designated bias parameter(s).

Model	a	ter	sv	sz	st	vF	vH	z	z90H	z70H	zN	z70F	z90F		v90H	v70H	vN	v70F	v90F
PBM	3.21	.85	.18	.03	.91	.75	−.80	--	.52	.52	.59	.67	.67		--	--	--	--	--
DBM	3.37	.69	.26	.03	.73	--	--	.50	--	--	--	--	--	F	.81	.73	.83	1.19	1.15
														H	−.81	−.80	−.61	−.43	−.27
DBM+	3.37	.75	.28	.03	.79	--	--	.59	--	--	--	--	--	F	.63	.56	.65	1.01	.97
														H	−1.0	−.99	−.78	−.58	−.42
MSM	3.30	.79	.23	.03	.83	--	--	--	.56	.56	.60	.62	.63	F	.69	.61	.62	.92	.87
														H	−.93	−.92	−.78	−.62	−.45

Figure 5. Mean starting-point and drift-rate posterior distributions from MSM across prior probability cues.

Distributions show the posterior probability of mean (A) starting-point, (B) face drift-rate, and (C) house drift-rate in each probabilistic cue condition. (D) Contrast of posterior face and house drift-rate estimates in the neutral cue (i.e., 50/50) condition, showing a significantly higher house than face drift-rate (vertical dotted lines show the 95% credible interval of the difference).

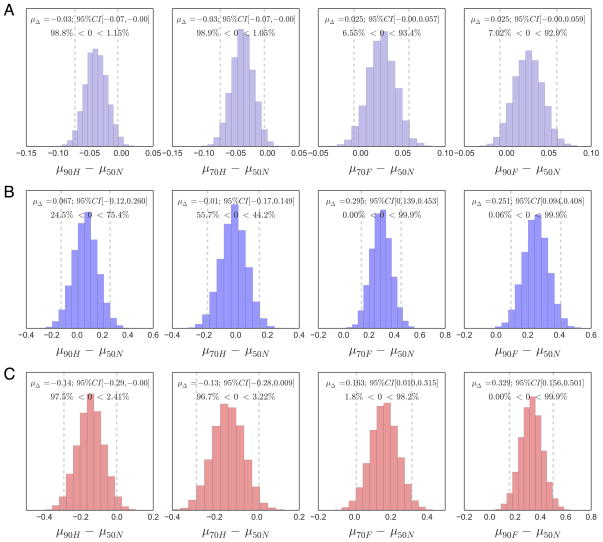
To evaluate the significance of these effects, we performed statistical contrasts comparing posterior estimates in each predictive cue condition with the corresponding parameter’s estimate in the neutral cue condition (see Model Comparison and Hypothesis Testing in Methods). Figure 6 shows the contrast distributions with in-figure inferential statistics for each comparison. Starting-point estimates in the 90H (Fig. 6A, left) and 70H (Fig. 6A, middle-left) cue conditions were significantly closer to the house boundary (i.e., lower) than in the neutral cue condition. Neither 90F (Fig. 6A, right) or 70F (Fig. 6A, middle-right) starting-points were significantly closer to the face boundary than in the neutral cue condition, however, both were significantly higher than starting-points in the house cue conditions as well as when compared to the unbiased starting-point in the model (z=½a). As noted above, face drift-rates were significantly faster following face predictive cues (Fig. 6B, right panels) and were unaffected by house predictive cues (Fig. 6B, left panels) relative to the neutral cue condition. Also reinforcing our interpretations above, house drift-rates were significantly faster following house predictive cues (Fig 6C, left panels) and slower following face predictive cues (Fig. 6C, right panels) compared to neutral. Interestingly, between-category comparisons of drift-rate across cues indicated that the drift-rate for house stimuli was significantly higher than that for faces in the neutral condition (see Figure 5D). We propose an explanation for this unexpected outcome in the discussion.

Figure 6. Posterior contrasts of MSM bias parameters between probabilistic and neutral cue conditions.

Distributions are the difference between posterior estimates in each probabilistic cue condition with the corresponding posterior estimates in the neutral cue (i.e. 50/50) condition for (A) starting-point, (B) face drift-rate, and (C) house drift-rate. In-figure text contains the mean and 95% credible interval (visualized as dotted lines) for each contrast distribution in addition to the proportion of the distribution that falls to the left and right of the zero value. Significant contrasts are marked by distributions in which 95% or more of the probability mass falls to one side of zero.

Drift-Rate Bias Determined by Match Between Expected/Observed Features

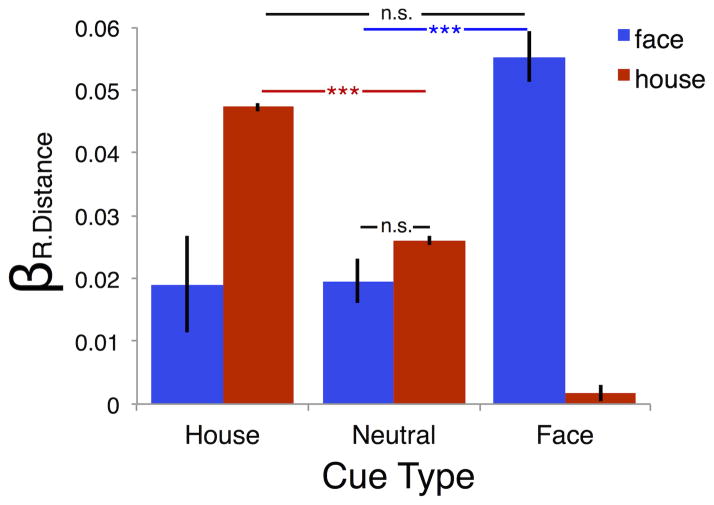
Finally, we investigated the interaction between prior knowledge and representational distance on the drift-rate for face and house stimuli. This was achieved by refitting a version of the MSM to the data in which representational distance was included as a regressor on the face and house drift-rates in each cue condition (collapsed into face cue, neutral cue, and house cue types). Figure 7 shows the absolute beta weights for representational distance on face and house drift-rates for each of the three cue types. 2 (stimulus: face, house) × 3 (cue type: house, neutral, face) repeated-measures ANOVA was performed to evaluate the reliability of mean differences in the effect of representational distance on the drift-rate parameter. We observed a significant interaction between stimulus and cue-type F(1.37, 30.10)=96.53, p<.0001, suggesting that the effect of representational distance on face and house drift-rates was conditional on the validity of prior expectations. Pairwise comparisons revealed that, relative to the neutral condition, valid cues significantly increased the positive effect of distance on the drift-rate for both face, t(22)=10.30, p<.001, and house, t(22)=20.20, p<.001. The mean difference observed between categories was not significant in the neutral cue condition or when the cue was a valid predictor of the stimulus category (both p>.05), suggesting that representational distance affected face and house drift-rates similarly across cue types.

Figure 7. Effect of stimulus representational distance on drift-rate.

A second version of the MSM was fit to the data including representational distance as a regressor on the drift-rate parameter. The regression coefficient for representational distance on face (blue) and house (red) trials is shown for each of the cue types (on the x-axis). In this version of the MSM, cues were collapsed into three types: face cue, neutral cue, and house cue. Error bars are the standard error. n.s.=not significant, *p<.05; **p<.01; ***p<.001

Discussion

Recent neuroimaging studies have found that prior expectations about a future sensory experience are projected into sensory space as feature-level stimulus templates. Further evidence suggests that these templates are updated dynamically according to the match between the predicted and observed sensory inputs (Rahnev, Lau, & de Lange, 2011; Summerfield & Koechlin, 2008). Here, we sought to bridge these findings with the widely held belief that perceptual decisions are produced by sequentially sampling evidence to a decision threshold, modeled as a bounded drift-diffusion process. First, we showed that cued expectations of face and house stimuli led to a prior bias in the starting-point as well as a dynamic bias in the drift-rate. Next, we confirmed our hypothesis that face expectations, which are more reliable than house expectations at feature-level, would have a more salient affect on pre-sensory evidence in the starting-point. Finally, we showed that RTs were faster for less ambiguous stimuli in the context of valid expectations and that this relationship could be explained by an interaction between stimulus ambiguity and expectation validity on the drift-rate of face/house evidence. These findings complement recently proposed predictive coding theories, suggesting that the effects of expectation on perception depend on the precision at which abstract prior knowledge is translated into feature-space and mapped onto observed evidence.

Multi-Stage Model of Decision Bias

Previous studies, both behavioral and neurophysiological, have produced mixed findings regarding the mechanism(s) by which prior expectations bias decision outcomes. For instance, there is evidence that prior expectations decrease the distance to threshold for the more likely choice (Edwards, 1965), for instance, by priming relevant feature-selective sensory neurons (Kok et al., 2014; Shulman et al., 1999). However, conflicting reports have suggested that top-down signals serve to increase the rate of evidence accumulation for a particular choice (Diederich & Busemeyer, 2006), for instance, by improving the quality of signal read-out from competing pools of sensory neurons (Cravo et al., 2013). Not until more recently has it been considered that expectations might influence these mechanisms in conjunction (Hanks et al., 2011; Leite & Ratcliff, 2011; van Ravenzwaaij et al., 2012). The results of the diffusion model analysis in the current study support this hypothesis, showing that subjects incorporated probabilistic face/house cues by modulating both the starting-point and rate of evidence accumulation. We termed this the multi-stage model (MSM) to denote that a change in the starting-point implies a prior bias during pre-stimulus processing, whereas a bias in the drift-rate implies a dynamic bias in the treatment of post-stimulus sensory evidence.

We are not the first to report an effect of prediction on both prior and dynamic bias mechanisms. Earlier studies have found that predictive knowledge (i.e. prior probability) biases both mechanisms, but only when there is additional uncertainty in the quality of sensory information across trials (Hanks et al., 2011; Leite & Ratcliff, 2011). However, this claim is challenged by a recent study showing that human subjects incorporate prior knowledge in both mechanisms across fixed and variable difficulty trials (van Ravenzwaaij et al., 2012). Nevertheless, this may explain why both starting-point and drift-rate biases were necessary to explain expectation effects in the current study, as sensory evidence was more reliable in the face than the house category. Although, we cannot rule out the possibility that subjects would have invoked the same strategy on a similar cued prediction task with perceptually matched alternatives (see van Ravenzwaaij et al., 2012). Additional research will be required to understand the conditions under which prior knowledge is integrated during pre- versus post-sensory epochs of the decision process.

Category-Specific Effects of Expectation

Category-specific effects of expectation emerged at several levels of analysis, including standard analyses of choice speed and accuracy as well as in fits to the diffusion model. For instance, valid predictive cues increased accuracy equivalently for faces and houses, whereas invalid cues impaired choice accuracy on house but not face trials. This is equivalent to saying face cues simultaneously increased the face hits (i.e., see face, report “face”) and face false-alarms (see house, report “face”) whereas house cues only increased house hits. Computational models have shown that a concurrent increase in hit and false-alarm rates in the context of probabilistic expectations implies an increase in the baseline activity of feature-selective sensory units (Nobre, Summerfield, Wyart, & Christina, 2012). Indeed, this explanation is in line with diffusion-model analyses in the current study. Specifically, face expectations materialized as an explicit increase in the baseline level of face evidence whereas house expectations only served to reduce the magnitude of prior face bias. In other words, house cues moved the starting-point closer to but never below the neutral position.

Assuming the starting-point reflects the strength of a prediction template, one interpretation of this implicit prior face bias is that subjects performed the task using face detection strategy. That is, rather than accumulating the difference between face and house evidence, the decision was made by comparing each sample of evidence with a face template and accumulated as “face” or “not face”. Indeed, previous studies involving face/house decisions have come to similar conclusions, noting that category-specific effects in behavioral and fMRI data could be explained if subjects used such a strategy (Summerfield, Egner, Mangels, & Hirsch, 2006). A face detection strategy is an appealing interpretation of the lack of prior house bias in the present study as this may further explain the counterintuitive finding that the drift-rate was larger for houses than faces when the cue contained no predictive information (e.g., 50/50 cue). In this scenario, house drift is driven by two “not-face” signals in the stimulus, one from the house image and the other from the noise introduced by the stimulus degradation procedure. Thus, contrasting the sum of house and noise signals with a face template would lead to an accelerated drift toward the house, or “not-face”, boundary.

However, that subjects exclusively used a face-detection strategy to perform the task does not fully agree with other findings in the present study. For instance, we found that representational distance accelerated the drift-rate on decision evidence and that this effect was strongest on valid cue trials for both face and house categories. In accordance with hierarchical models of perception (i.e. predictive coding), our interpretation of this effect assumes that the increase in drift gain is specifically due to the match between an already formed prediction template and the features in the observed stimulus. According to this view, a prior house template would need to be present in order for valid house cues to actively facilitate the distance-mediated increase in drift-rate.

One possibility is that the observed patterns in the starting-point are a reflection of concurrent top-down modulation in face and house-selective regions or local competition between regions. For instance, both the implicit face bias and trial-wise cue dependencies in the starting point could be produced by simultaneously priming feature-selection for faces and houses in proportion to their respective feature-level reliability, scaled by their prior probability. Moreover, a local competition between face and house representations fits with the combined observations that face but not house cues shifted the starting-point closer to the more probable boundary and subsequently suppressed the rate of evidence accumulation for the alternative choice. However, in the drift-diffusion model, starting-point and drift-rate parameters represent the difference in evidence for alternative choices prior to and during evidence accumulation, respectively. Thus, it is unclear from the present study how sources of face and house evidence were individually modulated by predictive cues. Indeed, similar questions have arisen in previous studies regarding the mechanisms of top-down control, the precision by which higher-order regions target evolving sensory representations (de Gardelle, Waszczuk, Egner, & Summerfield, 2013; Kok et al., 2012; Kveraga, Ghuman, & Bar, 2007), and the local interactions between competing populations of sensory neurons during decision-making (Alink, Schwiedrzik, Kohler, Singer, & Muckli, 2010; Desimone, 1998; Kastner & Ungerleider, 2001). We believe that future investigations of these phenomena will provide a much-needed clarity to the ongoing study of perception and decision-making.

Merging Theories of Mind and Brain

One of the current challenges in cognitive neuroscience is to develop formal theories that apply to multiple scales of observation, from single-unit neural activity to its consequences at the behavioral level. The diffusion model is somewhat unique in this respect. Originally developed as a cognitive process model, it has since been successfully used to explain patterns of neural integration in frontal and parietal cortex. For instance, single neurons in the lateral intraparietal area (LIP) and frontal eye fields (FEF) of the macaque have been shown to accumulate evidence about motion direction (Gold & Shadlen, 2007). These neurons accelerate their firing at a rate proportional to the motion coherence in a random dot stimulus until reaching a set threshold at decision time and returning to baseline. Additionally, human neuroimaging studies have localized patterns of evidence accumulation in the dorsolateral prefrontal cortex (dlPFC) (Heekeren, Marrett, Bandettini, & Ungerleider, 2004; Philiastides, Auksztulewicz, Heekeren, & Blankenburg, 2011; Ploran et al., 2007; Ploran, Tremel, Nelson, & Wheeler, 2011). However, due in part to the generality and simple assumptions of the diffusion model, it has proven more challenging to characterize the neural implementation of other proposed decision mechanisms, such as those that mediate decision bias. Thus, it remains contentious as to whether a direct mapping exists between bias parameters in the diffusion model and the neural mechanisms of expectation (see Simen, 2012 for discussion).

In contrast with the phenomenological nature of sequential sampling models, cortical feedback theories such as predictive coding make more precise predictions about the neural implementation of perceptual expectations (Friston, 2005; Spratling, 2008). Predictive coding posits that expectations are generated hierarchically in a top-down manner, becoming less abstract at lower levels of representation. Incoming sensory information is evaluated against the lowest-level stimulus template, producing a feedforward prediction error signal that is used to update beliefs about the cause of sensation until error is sufficiently explained away. It is currently not well understood how diffusion model parameters map onto the mechanisms proposed by predictive coding, or even if these two frameworks are compatible with one another (See Hesselmann, Sadaghiani, Friston, & Kleinschmidt, 2010).

While the current study does not conclusively answer this question, the results of our diffusion model analysis appear consistent with many assumptions of predictive coding. For instance, predictive coding assumes that prior knowledge affects sensory representations both prior to and during stimulation, in agreement with our finding that modulation in both the starting-point and drift-rate were required to explain cued expectation biases. Additionally, cued expectations differentially affected decision dynamics for face and house stimuli, suggesting that expectation bias occurred at the level of stimulus representation, as opposed to domain-general evidence accumulation. Specifically, face but not house expectations manifested as overt increases in the baseline evidence for that category. This finding, in particular, lends itself to a predictive coding interpretation because of the relative predictability of face and house stimuli and the central role precision plays in predictive coding. That is, more precise (i.e., face) predictions should have greater influence on pre-stimulus sensory representations (i.e., strong priming of target-selective neurons and/or inhibition of distractor neurons), consistent with observed biases in the starting-point parameter. Finally, we found compelling evidence that prior expectations conditionally enhanced the effect of representational distance on response speed by increasing the gain on evidence accumulation when the stimulus matched the expected category.

Conclusions

In conclusion, we showed that expectations bias decisions by modulating both the prior baseline and dynamic rate of evidence accumulation. Moreover, we found that predictive information exerted a greater bias in the baseline evidence for the more reliably predictable (i.e. face) category and that the rate of evidence accumulation was specifically modulated by the match between expected and observed sensory features. This study contributes to a growing body of literature on the dynamics of prediction and perceptual decision-making, demonstrating that the extent to which expectations bias perception hinges on the ability to transform abstract prior knowledge into precise feature-level predictions.