Poisson’s Ratio and Young’s Modulus of Lipid Bilayers in Different Phases

Abstract

A general computational method is introduced to estimate the Poisson’s ratio for membranes with small thickness. In this method, the Poisson’s ratio is calculated by utilizing a rescaling of inter-particle distances in one lateral direction under periodic boundary conditions. As an example for the coarse grained lipid model introduced by Lenz and Schmid, we calculate the Poisson’s ratio in the gel, fluid, and interdigitated phases. Having the Poisson’s ratio, enable us to obtain the Young’s modulus for the membranes in different phases. The approach may be applied to other membranes such as graphene and tethered membranes in order to predict the temperature dependence of its Poisson’s ratio and Young’s modulus.

Introduction

Elastic properties play an important role in a number of membrane processes, as for example, membrane fusion (Chernomordik and Kozlov, 2008) and modulations of membrane channel activities (Schmidt and MacKinnon, 2008; Sansom and Biggin, 2010; Mashaghi et al., 2013b). In cells, the outer membranes are supported by the underlying actin networks. The mechanical stress is then dominated by the associated actin cytoskeleton at length scales larger than the mesh size of the actin network (30–300 nm) (Morone et al., 2006). On small length scales, however, the contribution of the lipid bilayer will dominates. As such, efforts have been made to study the mechanical properties of bilayer patches with dimensions close to the mesh size of the actin cytoskeleton (Claesson et al., 2011).

When considering a membrane as a two-dimensional body, i.e., neglecting its thickness, its mechanical properties in the absence of anisotropies can be characterized by two elastic constants according to continuum elasticity theory. In common practice of material characterization, these parameters are typically the Young’s modulus and the Poisson’s ratio. Estimates for the Young’s modulus of membranes have been provided by experiments (Tierney et al., 2005; Popescu et al., 2006). However, the measuring of the Poisson’s ratio is not straightforward, due to the small thickness of membranes in the nanometer range (Mitchell et al., 2003; Martins et al., 2009). From the theoretical aspect, mechanical properties of lipid membranes are commonly investigated based on the Helfrich Hamiltonian. The main physical quantity obtained from such studies is the bending rigidity. The Young’s modulus and Poisson’s ratio are interrelated by formula that incorporate the bending rigidity, but neither Young’s modulus nor Poisson’s ratio have been determined separately so far.

Simulations and theoretical models have been used to provide important information on elastic (Goetz and Lipowsky, 1998; Lindahl and Edholm, 2001; Ayton et al., 2002) and viscous properties of lipid bilayers (Jeon and Voth, 2005). Investigating the mechanical properties of thin films is not limited to biomembranes and represents an active area of research in materials science. Efforts have been put into predicting the Poisson’s ratio of films made of various materials by means of computer simulations. For instance Galvao et al. has employed molecular dynamics simulations using reactive empirical bond-order potentials to investigate the mechanical properties of graphene nanoribbons (Martins and Galvao, 2010). Baughman et al. proposed a model to estimate the Poisson’s ratio of fiber networks and successfully applied it to carbon nanotube sheets (buckypaper) (Hall et al., 2008).

In this work, we introduce a method for determining the Poisson’s ratio ν in simulations and apply it to the coarse grained lipid membrane model, which was introduced by Lenz and Schmid (2005). This method is general and applicable to any other surfaces. After determining the bending rigidity k_c from the power spectrum of membrane height fluctuations, we are able to calculate the Young’s modulus E.

Materials and Methods

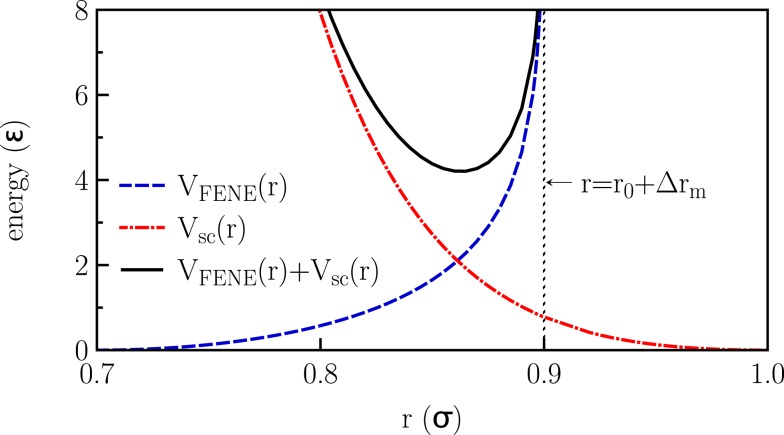
Monte Carlo simulations of lipid bilayers with periodic boundary conditions in lateral directions were carried out for the coarse grained model introduced by Lenz and Schmid (2005). In this model, single-tail amphiphiles are considered, which are represented by six tail beads and one slightly larger head bead (with a size ratio of 1–1.1). Beads belonging to one molecule are connected via finitely extensible non-linear elastic (FENE) springs (Grest and Kremer, 1986) with a bond stretching potential Figure 1:

$$V_{\text{FENE}}\left(r\right)=-\frac{{\mathrm{\upsilon }}_{\text{FENE}}}{2}{\left(\mathrm{\Delta }{r}_m\right)}^2\log \left[1-{\left(\frac{r-r_0}{\mathrm{\Delta }{r}_m}\right)}^2\right]$$ (1)

Figure 1.

Interactions applied in the model.

Here r is the distance between adjacent beads, ν_FENE characterizes the strength of the spring, r₀ is the optimal bond length (no stretching), and Δr_m is the maximal stretching distance. The stiffness of the tails is taken into account by a harmonic bond-angle potential

$$V_{\text{ba}}\left({\mathrm{\theta }}_{ijk}\right)={\mathrm{\upsilon }}_{\text{ba}}\left(1-\cos {\mathrm{\theta }}_{ijk}\right)$$ (2)

where θ_ijk is the bond-angle associated with three adjacent beads. Both the non-bonded beads belonging to the same molecule and the beads belonging to different molecules interact via a soft-core potential:

$$\begin{array}{ll}\hfill V_{\text{sc}}\left(r\right)& =\left[V_{\text{LJ}}\left(r\right)-V_{\text{LJ}}\left(r_{\text{c}}\right)\right]\mathrm{\theta }\left(r_{\text{c}}-r\right)\end{array}$$ (3a)

$$\begin{array}{ll}\hfill V_{\text{LJ}}\left(r\right)& =\mathrm{ϵ}\left[{\left(\frac{{\mathrm{\sigma }}_{\text{LJ}}}{r}\right)}^{12}-2{\left(\frac{{\mathrm{\sigma }}_{\text{LJ}}}{r}\right)}^6\right]\end{array}$$ (3b)

where θ_(.) is the Heaviside step function. The solvent molecules are represented by a phantom model of beads that interact with the lipid beads via V _SC(r) (with same parameters as the head beads) but do not interact with themselves. All model parameters have been chosen according to the referenced model (Lenz and Schmid, 2005) and are summarized in Table 1.

Table 1.

Interaction potentials of the referenced model and corresponding parameters.

Interaction type	Potential	Parameters
Tail–tail	Vsc	ϵ = 1, σLJ = 1, rc = 2σLJ
Head–tail		ϵ = 1, σLJ = 1.05, rc = 1σLJ
Solvent–tail		ϵ = 1, σLJ = 1.1, rc = 1σLJ
Head–head
Solvent–head
Solvent–solvent	None
Bond length	V FENE	νFENE = 100, r0 = 0.7, Δrm = 0.2
Bond angle	V ba	νba = 4.7

r is the distance of the connecting vector of two particles and θ is the angle between every three adjacent beads. The SI values are calculated using σ_LJ ~ 6Å and ϵ ~ 3.6.10⁻²¹J (Neder et al., 2010).

Lipid bilayers exhibit a rich spectrum of structures and phase transitions (Nagle and Tristram-Nagle, 2000; Illya et al., 2005; Seto et al., 2008; Thakkar et al., 2011). The fluid state at high temperatures is characterized by a disordered arrangement of the lipid tails and a comparatively high lipid mobility. Upon cooling, this fluid state undergoes a phase transition to a gel state, where the lipid molecules are more ordered and have a lower mobility. Other possible phases are the interdigitated phase, in which lipid tails from opposing monolayers interpenetrate.

By scanning the phase diagram of the referenced model (Lenz, 2007), firstly we equilibrated lipid bilayers for about two millions Monte Carlo (MC) steps to produce different phases for the aim of this work, see Figure 2. In the reduced units, ϵ/k_B for the temperature T and $\mathrm{ϵ}/{\mathrm{\sigma }}_{\text{LJ}}^3$ for the pressure P, the corresponding thermodynamic variables are: P = 2 and T = 1.08 for the gel phase, P = 1 and T = 1.3 for the fluid phase, P = 0.5 and T = 1.16 for the interdigitated phase. The characteristic parameters for different phases including the average chain length $\overline{l}$, thickness of the bilayer d, area per lipid A, and chain order parameter S_z are summarized in Table 2.

Figure 2.

Snapshots of the simulated lipid membrane in the (A) gel, (B) fluid, and (C) interdigitated phase. Lipid’s head beads and tail bead are shown in red and green, respectively.

Table 2.

Characteristic parameters of lipid bilayers.

Phase	$\overline{l}\left({\mathrm{\sigma }}_{\text{LJ}}\right)$	d (σLJ)	$A\left({\mathrm{\sigma }}_{\text{LJ}}^2\right)$	Sz
Fluid	3.3	5.48	1.68	0.42
Gel	3.8	7.64	0.96	0.72
Interdigitated	4	4.8	1.8	0.98

$\overline{l}$ denotes the average chain length, d thickness of the bilayer, A area per lipid, and S_z chain order parameter.

Simulations were performed under constant temperature and pressure condition (NPT ensemble) for lipid bilayers with different sizes. To investigate the power spectrum of the surfaces height fluctuations, we simulated a bilayer whose upper and lower leaflets consist of 64 × 64 lipid molecules. About 17000–72000 beads were chosen for the solvent model (precise number depends on simulated phase). For performing the analysis of the Poisson’s ratio, we equilibrated rectangular bilayers consist of 12 × 24 lipid molecules per leaflet to three different phases.

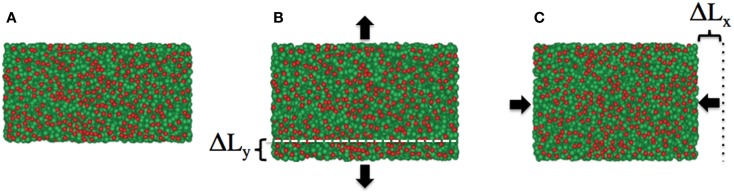
To determine both E and ν, we need to determine one of these elastic constants separately. Utilizing the periodic boundary conditions, we introduce a method to compute the Poisson’s ratio for the surface (Abedpour et al., 2010). The Poisson’s ratio is the negative ratio of the transverse strain changes divided by the axial strain changes in a body when it is stretched or compressed along the axial direction under the tension below the proportional limit. For the infinitesimal diagonal strains, the Poisson’s ratio can be replaced by the ratio of the relative length changes as ν_ij = −ΔL_i/η_jL_i, where η_j ≡ ΔL_j/L_j is defined as the fraction of the axial length change. Here i ≠ j and i = x, y, and z. In the method, we present here the length between neighboring lipids is rescaled by a factor of (1 + η) in axial direction, let say y-direction, and the subsequent change of the simulation box size in perpendicular directions, in this case x- and z-direction, are monitored. While keeping the rescaled box length (1 + η) L_y constant, for fixing the pressure in the simulations, the box dimensions are now allowed to fluctuate in only the x- and z-directions. When the initial mean lengths in x and z-direction were L_x and L_z, new mean values of L_x + ΔL_x and L_z + ΔL_z are reached after rescaling, by re-equilibrating the system for a few number of MC steps, see Figure 3.

Figure 3.

Snapshots of the lipid membrane in fluid phase as (A) initial configuration, (B) after increasing the bilayer size in y-direction by a factor of (1 + η), and (C) the relaxed bilayer fixing the membrane size in y-direction and variable x-direction. As a consequence of positive Poisson’s ratio for the bilayer in this phase, the membrane size in x-direction is reduced and equilibrated after a few number of MC steps. Lipid’s head beads and tail bead are shown in red and green, respectively.

During the simulation, to accelerate the thermalization procedure after extending the box along the axial direction, we slightly increased the temperature in the system, which results in producing the more mobility for the particles. For the fluid phase, we set the initial temperature to T = 1.3 and then changed it to T = 1.4 for about extra 400 steps and then switched back to the original value. Similarly, for the gel and interdigitated phases, the initial temperatures were T = 1.08 and T = 1.16 and were switched to T = 1.2 and T = 1.3, respectively.

A common analysis of the elastic properties of a membrane relies on the Helfrich Hamiltonian (Helfrich, 1973), which describes the cost of elastic free enthalpy associated with fluctuations of the membrane height (deviations from flat surface). When parameterizing the membrane in Cartesian coordinates (x,y) →(x,y,h(x,y)) (Monge gauge), the Helfrich Hamiltonian is, for small fluctuations, given by

$$H=\int \text{d}x\text{d}y\left[\frac{k_{\text{c}}}{2}{\left({\nabla }^{2}h\right)}^2+\frac{\mathrm{\sigma }}{2}{\left(\nabla h\right)}^2\right]$$ (4)

where k_c is the bending rigidity and σ is the surface tension. Equation (4) is applied when the membrane is considered as a body with zero thickness. A generalized elastic theory for membranes with finite thicknesses was suggested by Brannigan and Brown (2006) and applied to the Lenz–Schmid model recently (West et al., 2009; Neder et al., 2010).

To determine h(x, y) from the simulations, we discretized the (x, y)-plane into a regular grid with spacing 2σ_LJ, determined in each cell (i, j) the mean z-coordinates z₊(i, j) and z₋(i, j) of the head beads in the upper and lower leaflet, respectively, and calculated the height h(i, j) − [z₊(i, j) + z₋(i, j)]/2 (the average $\overline{h}$ was subtracted subsequently). For a membrane of lateral size L × L, Eq. (4) predicts:

$$⟨{\left|ĥ\left(q\right)\right|}^2⟩=\frac{{\text{k}}_{\text{B}}\text{T}{\text{L}}^2}{k_{\text{c}}{q}^4+\mathrm{\sigma }{q}^2}$$ (5)

for the power spectrum of the fluctuations, where ĥ(q) is the Fourier transform of h(x, y) at wave vector q, q = |q|, and <… > denotes an equilibrium average. In the numerics, ĥ(q) is calculated from a discrete Fourier transform of h(i, j). It is clear that Eq. (5) can hold true only for a q-range 2π/L ≪ q ≪ 2π/σ_LJ, where neither the finite system size nor the (atomistic) bead size affects the fluctuations. The corresponding q-range for system sizes amenable within reasonable computing time is unfortunately not large, but fits of < |ĥ(q)|² > ∕k_BTL² as function of q² in a range 0.5 ≤ q² ≤ 1 yield a good agreement with Eq. (5) for our sizes.

Results and Discussions

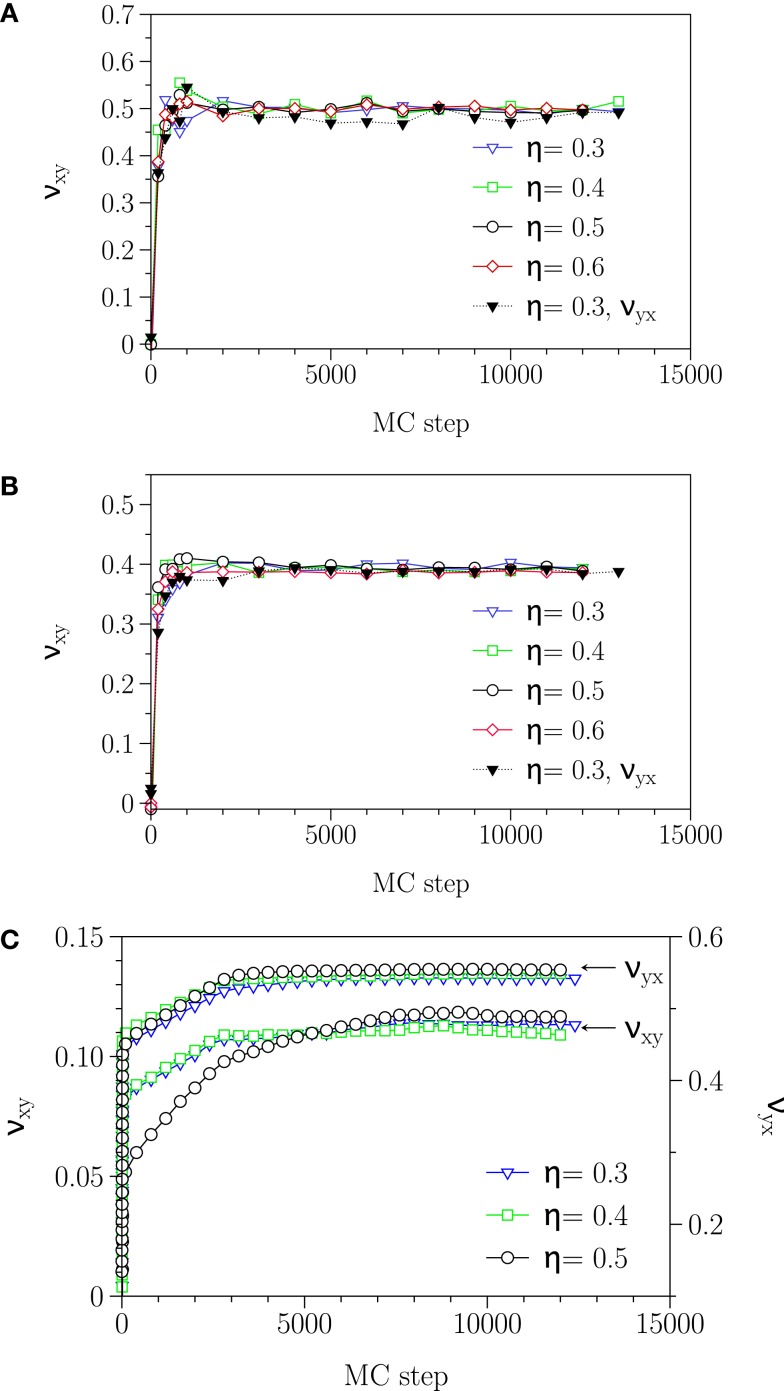
In Table 3, the obtained Poisson’s ratios ν_yx, ν_zx, and ν_xy as well as ν_zy for different phases are summarized. As demonstrated in Figure 4, the Poisson’s ratio obtained in this way is independent of the rescaling factor η as long as η is neither too large, which leads to destroy the membrane structure nor too small, which dose not produce enough free space for particles to move. According to the Table 3 and Figure 4, fluid and interdigitated phases have the same measured Poisson’s ratio for both x and y-directions. It means that these two phases are isotropic in the plane of bilayer. However, this is not the case any more for the gel phase. The measurements show that, a bilayer in the gel phase behaves as an anisotropic material, which has two distinguishably different values for the two different directions in the plane of the bilayer.

Table 3.

Elastic constants obtained from simulations of lipid membranes in different phases.

Phase	kc(ϵ)	νxy	νzy	νyx	νzx	E(ϵ/σ3)
Gel	10.56	0.11	0.44	0.54	0.04	–
Fluid	5.2	0.50	0.25	0.50	0.26	0.28
Interdigitated	7.6	0.40	0.12	0.39	0.13	0.67

Figure 4.

Relaxation of −ΔL_i/η_jL_i in (A) fluid, (B) interdigitated, and (C) gel phase. The plateau value reached after about 5000 MC steps, independent of the value of η, yields the Poisson’s ratio ν. In the gel phase, Poisson’s ratio has different values for ν_xy and ν_yx and this phase acting as an anisotropic surface.

Conversely, when the bilayer was extended in the perpendicular direction to the tilt plane, lipids reorganize themselves in such a way that the bilayer laterally shrank. For the present work, lipids bond lengths in the z-direction (perpendicular to the bilayer plane) have not been rescaled. The reason is that, to observe the Poisson’s effect, the length between the beads should be rescaled by a factor, which produces enough space for particles to rearrange. However, in the z-direction, this increase should occur between the bonded beads inside a lipid, which causes a bond breaking. The reported values for ν_zx and ν_zy are the resulted relative length changes in the bilayer mean length due to the lateral extension of bilayers in x- and y-direction, respectively.

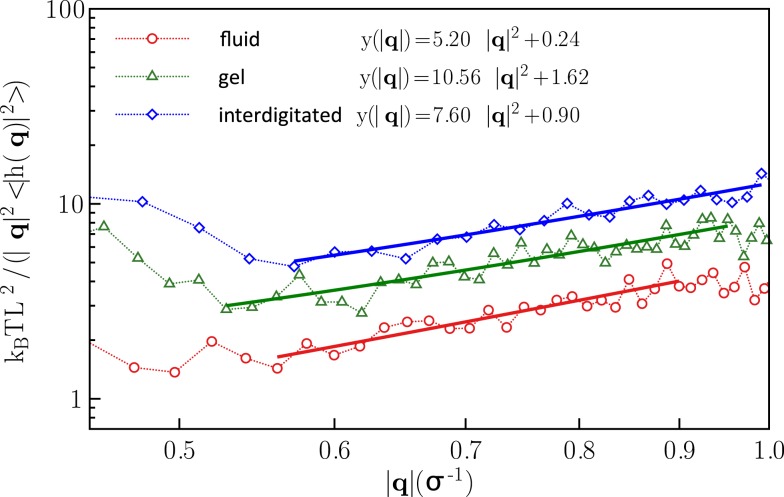
The values obtained for the bending rigidity k_c are 5.2ϵ for the fluid phase, and 7.6ϵ for the interdigitated phase. For the gel and fluid phases, the results agree with the previous computational reports (West, 2008; West et al., 2009) and experimental findings (Falcioni et al., 1997; Liu and Zhang, 2009). The spectral density for the interdigitated phase was calculated according to the same method. We report here bending rigidity for interdigitated phase. Figure 5 illustrates the fluctuation spectra of the height for three studied phases and fits to the Eq. (5).

Figure 5.

Fluctuation spectra for the fluid, gel, and interdigitated phases and fits to the Eq. (5).

Within two-dimensional elasticity theory, the bending rigidity k_c is related to the Poisson’s ratio ν and the Young’s modulus E according to (Landau et al., 1986)

$$k_{\text{c}}=\frac{E{d}^3}{12\left(1-{\mathrm{\nu }}^2\right)}$$ (6)

where d is the mean membrane thickness, for which we obtain, 5.48σ_LJ, and 4.86σ_LJ for the fluid, and interdigitated phases, respectively. Substituting the founded values for the Poisson’s ratios and the bending rigidities for bilayers in two isotropic phases into Eq. (6), one can obtain the according Young’s moduli. The Young’s moduli calculated in this way are 0.28 and 0.67 in units of ϵ/σ³ for the fluid and interdigitated states, respectively. Obviously, the observed anisotropicity in the gel phase dose not allow to use the above theorem for the bilayer in this phase.

The approach presented in this article could be applied to membranes with more complex lipid compositions, given that the experimentally verified interaction models exist for those lipids. The approach could also be combined with more accurate simulation of bilayers. Full atomistic simulations and in particular ab initio simulations, could in principle provide more accurate descriptions of the system but comes with a huge computational burden (Mashaghi et al., 2012, 2013a).

Conclusion

We have performed Monte Carlo simulations of the coarse grained lipid bilayer model to gain insight into the mechanical properties of planar lipid membranes. By using a rescaling method, we could determine the Poisson’s ratio ν for different phases, in addition to the bending rigidity determined from an analysis of the membrane height fluctuations based on the Helfrich Hamiltonian. This allows us to calculate also the Young’s modulus E for different phases. The approach is accurate, easy to implement and may be applied to other membranes such as graphene (Abedpour et al., 2010), in order to predict the temperature dependence of its Poisson’s ratio and Young’s modulus. Other interesting systems to study are crystalline metallic nanowires where elastic modulus controls their structural performance and functional behavior such as their resonance frequency under oscillatory load typically applied during actuation and sensing (Chen et al., 2006; McDowell et al., 2008).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.