Abstract
Motor neuron activity is coordinated by premotor networks into a functional motor pattern by complex patterns of synaptic drive. These patterns combine both the temporal pattern of spikes of the premotor network and the profiles of synaptic strengths (i.e., conductances). Given the complexity of premotor networks in vertebrates, it has been difficult to ascertain the relative contributions of temporal patterns and synaptic strength profiles to the motor patterns observed in these animals. Here, we use the leech (Hirudo sp.) heartbeat central pattern generator (CPG), in which we can measure both the temporal pattern and the synaptic strength profiles of the entire premotor network and the motor outflow in individual animals. In this system, a series of motor neurons all receive input from the same premotor interneurons of the CPG but must be coordinated differentially to produce a functional pattern. These properties allow a theoretical and experimental dissection of the rules that govern how temporal patterns and synaptic strength profiles are combined in motor neurons so that functional motor patterns emerge, including an analysis of the impact of animal-to-animal variation in input to such variation in output. In the leech, segmental heart motor neurons are coordinated alternately in a synchronous and peristaltic pattern. We show that synchronous motor patterns result from a nearly synchronous premotor temporal pattern produced by the leech heartbeat CPG. For peristaltic motor patterns, the staggered premotor temporal pattern determines the phase range over which segmental motor neurons can fire while synaptic strength profiles define the intersegmental motor phase progression realized.
Introduction
To produce rhythmic movements such as walking, nervous systems must produce rhythmic activation of the motor neurons that underlie these movements. Typically, these rhythmic patterns are generated by central pattern generators (CPGs) (Marder and Calabrese, 1996), rhythmically active networks of neurons capable of producing the pattern in the absence of sensory feedback. While considerable attention has been given to and insight gained into how proper intersegmental coordination is achieved within a CPG (Borgmann et al., 2009; Smarandache et al., 2009; Puhl and Mesce, 2010; Fuchs et al., 2011), we know considerably less about how synaptic drive from a CPG coordinates motor neurons. The rhythmic synaptic drive to motor neurons (either excitatory or inhibitory) provided by a CPG is produced by the temporal pattern of spikes in premotor interneurons (i.e., the temporal pattern) combined with the patterns of strengths in the synaptic connections (i.e., the synaptic strength profiles) of the premotor interneurons onto motor neurons.
The time-varying synaptic conductances in motor neurons of the hindlimb locomotor network (Endo and Kiehn, 2008) and turtle scratch (Berg et al., 2007) have been decomposed into their excitatory and inhibitory components to understand how the premotor networks that generate the synaptic conductances are organized. Because of the complexities of the hindlimb locomotor and turtle scratch networks, however, it has proved difficult to determine the relative contribution of the temporal pattern and synaptic strength profiles to functional motor output. Indeed, in only a few vertebrate preparations (Biró et al., 2008; Soffe et al., 2009; Gabriel et al., 2011) have candidate premotor interneurons been identified so that a temporal pattern can be matched with synaptic strength profiles.
Invertebrate preparations, with their simple and accessible nervous systems, provide several useful models for the analysis of motor neuron coordination (Marder and Bucher, 2007; Goaillard et al., 2009; Buschges et al., 2011; Johnson et al., 2011). We used the leech heartbeat CPG to assess the relative contributions of temporal pattern and synaptic strength profiles in the functional coordination of motor neurons. This system would seem ideal for this analysis because, in addition to its small number of neurons, it provides a series of motor neurons all receiving input from the same premotor interneurons of the CPG but that must be coordinated differentially to produce a functional pattern (see Fig. 1). These properties allow a theoretical and experimental dissection of the rules that govern how temporal patterns and synaptic strength profiles are combined in motor neurons so that functional motor patterns emerge. Moreover, we have acquired a database of premotor temporal patterns and synaptic strength profiles with associated motor output patterns from individual animals that, despite considerable animal-to-animal variability at all three levels maintained functional output (Norris et al., 2011). While such variation has been well documented in other systems (Marder and Goaillard, 2006; Schulz et al., 2007; Tobin et al., 2009), the relationship between variation in input to variation in output, which we address here, is only now beginning to be explored (Goaillard et al., 2009; Marder, 2011; Marder and Taylor, 2011).
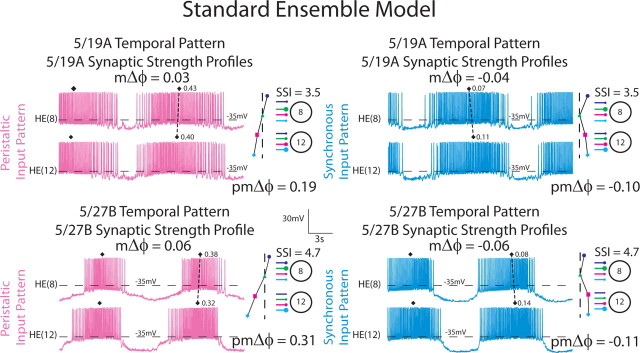
Figure 1.
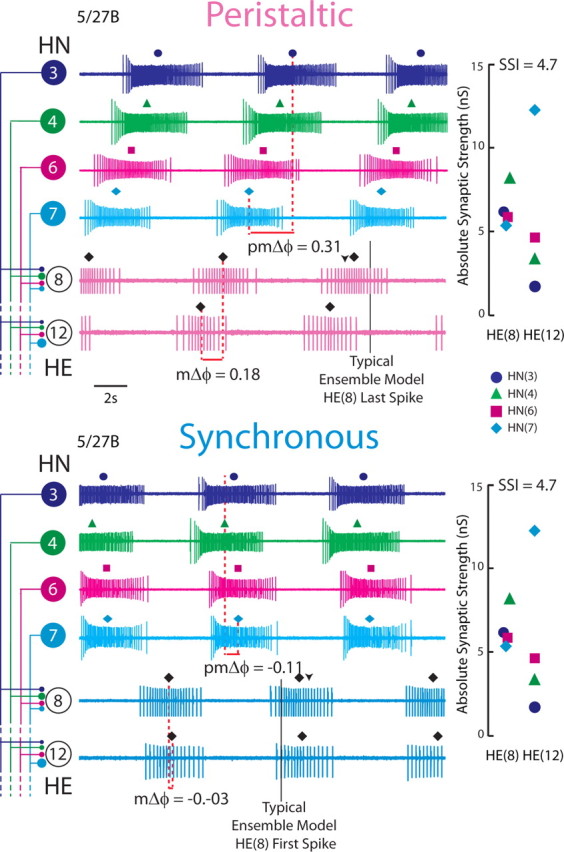
Simultaneous ipsilateral extracellular recordings from the HN(3), HN(4), HN(6), and HN(7) premotor interneurons and from the ipsilateral HE(8) and HE(12) motor neurons for the 5/27B preparation in both synchronous and peristaltic coordination modes. The absolute synaptic strength profiles for the HE(8) and HE(12) motor neurons in this preparation, measured immediately after the record illustrated was taken, is shown to the right, while on the left the iconic circuit diagram labels the extracellular traces. The large circles represent cell bodies of the heart (HN) interneurons and heart (HE) motor neurons, and the small filled circles, inhibitory synaptic connections. The connections are sized in proportion to their relative strengths as embodied in the synaptic strength profiles on the right. The middle spike is indicated above each HN or HE burst. On the peristaltic traces, the downward arrowhead indicates the middle spike of the HE(8) ensemble model motor neurons, while the vertical line indicates the typical point where the HE(8) model motor neurons tend to stop firing (as measured in phase). On the synchronous traces, the downward arrowhead indicates the middle spike of the HE(8) ensemble model motor neurons, while the vertical line indicates the typical point where the HE(8) model motor neurons tend to start firing (as measured in phase). The premotor phase progression (pmΔϕ) and the motor phase progression (mΔϕ) are defined in Materials and Methods. The data in this figure were kindly provided by Dr. Brian J. Norris (California State University, San Marcos, CA) from experiments described by Norris et al. (2011). The color/symbol schemes describing each premotor heart interneuron is repeated in Figures 2A2, 3, 6, and 9 (see key).
Materials and Methods
Animals and solutions.
Leeches (Hirudo sp.) were purchased from a commercial supplier (Leeches USA) and maintained in artificial pond water at 15°C. Animals were anesthetized in ice, and then dissected in chilled saline. Individual ganglia from midbody segments 8 and 12 were dissected and pinned out, ventral surface up, in 35 mm Petri dishes lined with Sylgard (184; Dow Corning). The ventral sheath of the ganglion was removed with fine scalpels in all experiments. We superfused the preparation with leech saline containing the following (in mm): 115 NaCl, 4 KCl, 1.8 glucose, 10 HEPES buffer, and 1.8 CaCl2, adjusted to a pH of 7.4 using NaOH, at 1–2 ml/min in a bath volume of 0.5–1 ml. All experiments were performed at room temperature. Heart motor neurons were identified based on soma location on the ventral aspect of the ganglion, soma size, and by their characteristic activity of rhythmic bouts of firing interrupted by barrages of IPSPs. In all experiments in this study, 10−4 m bicuculline methiodide was added to the leech saline after cell identification to block inhibitory synaptic input to heart motor neurons (Schmidt and Calabrese, 1992).
Intracellular recording techniques.
For intracellular voltage recordings from heart motor neurons, we used sharp microelectrodes (∼25–40 MΩ filled with 2 m KAc and 20 mm KCl) made from borosilicate glass (1.0 mm outer diameter; 0.75 mm inner diameter; A-M Systems). Intracellular recordings and current injections were made using an Axoclamp 2A amplifier (Molecular Devices) in discontinuous current-clamp mode using a sampling rate of 2.5–3.0 kHz. To ensure electrode settling, the electrode potential was monitored with an oscilloscope.
In all experiments, both heart motor neurons in a given ganglion were impaled and recorded simultaneously. After penetration, the input resistance of both cells was measured using −0.3 nA pulses. We did not proceed with experiments unless the input resistance of both motor neurons was >30 MΩ, and the difference in input resistance between the two heart motor neurons was <15%. Upon termination of the experiment, the microelectrode was withdrawn from the cell and the electrode potential was recorded. Only experiments in which the electrode potential was within ±5 mV of ground were accepted in this study. Thus, holding potential was normally accurate within ±5 mV.
Data acquisition.
Data were digitized (5 kHz sampling rate) using a digitizing board (Digi-Data 1200 Series Interface; Molecular Devices) and acquired using pCLAMP 9.2 (Molecular Devices) on a personal computer (Dell).
Data analysis.
Electrophysiological and model data were analyzed off-line using a combination of pCLAMP 9.2 (Molecular Devices) and custom scripts written in MATLAB (Mathworks) and Spike2 (CED Systems). First, the raw voltage recordings were high-pass filtered (cutoff frequency, ∼1 Hz). These data were then used for spike detection. Spike detection was performed using methods reported previously (Norris et al., 2006).
After detection, spikes were grouped into bursts as follows: after an interburst interval of 500 ms, the next spike detected was considered the first spike in that burst. Each subsequent spike was included in that burst until the interspike interval >500 ms (i.e., the interburst interval) was encountered. A minimum of four spikes were required to qualify as a burst.
We define period as the interval between successive middle spikes of the peristaltic HN(4) interneuron [THN(4)]. We then computed the phase of the heart motor neurons with respect to the synaptic input pattern that they received. We define phase as the difference in time for a spike of interest of a heart motor neuron (or interneuron) and the time of the middle spike of the phase reference, the peristaltic HN(4) interneuron THN(4). This difference is then normalized to the cycle period of the phase reference, given by the following:
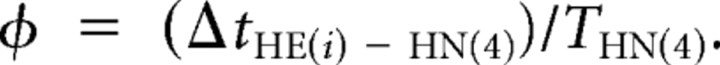 |
We calculated the average middle (m) spike phase, burst period (T), and duty cycle (D) for each heart motor neuron. In the text and figures, the generic term phase and symbol ϕ are applied to the middle spike phase as defined above. In figures, we indicate the middle spike phase of a heart motor neuron (model or living) within each burst by a filled diamond above that burst. All phase values are expressed modulo one. Duty cycle is defined as the difference between the average last spike phase and the average first spike phase as follows:
 |
Because the duty cycle is the difference of two averages, a SD is not reported.
Standard heart motor neuron ensemble model.
We used a previously developed model of the ensemble of heart motor neurons (García et al., 2008). Briefly, the motor neurons in this model were single-compartment, conductance-based models whose membrane potential (Vm) is given by the following current-balance equation:
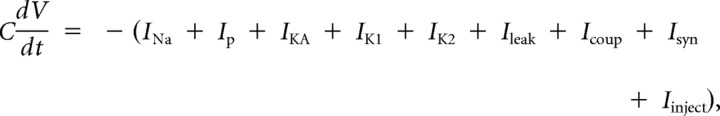 |
where t is time, C is the total membrane capacitance, Ileak is the leak current, Icoup is the current due to electrical coupling between the heart motor neurons in a given segment, ISyn is the sum of the inhibitory synaptic currents arising from each of the premotor inputs, and Iinject is any injected current. The model motor neurons contained five voltage-gated currents: (1) a fast Na+ current (INa), (2) a persistent Na+ current (IP), (3) a fast transient K+ current (IKA), (4) an inactivating delayed rectifier K+ current (IK1), and (5) a non-inactivating delayed rectifier K+ current (IK2). The Hodgkin–Huxley equations (Hodgkin and Huxley, 1952) describing these voltage-gated currents were the same as those used in a model of an oscillator heart interneuron (Hill et al., 2001). Each motor neuron was modeled as an isopotential cylinder whose length and diameter were both 60 μm with a specific membrane resistance of 1.1 Ωm2 and a specific membrane capacitance of 0.05 Fm−2. With these parameters, the input resistance of a model motor neuron was 97 MΩ. The maximal conductances of the individual ionic currents as well as electrical coupling were set empirically so that the activity of the model motor neurons mimicked those observed during intracellular recordings of heart motor neurons in the absence of synaptic input (García et al., 2008). The heart motor neuron ensemble model was implemented in GENESIS (General Neural Simulator System), with each model motor neuron receiving its segment-appropriate inhibitory synaptic input (see below). The model used the Euler integration method with a time step of 0.0001 s. We recorded and saved the computed synaptic conductance waveforms arising from each premotor input as described below as well as their sum [gSyn(t)] (see Fig. 2B2) in each motor neuron for subsequent use in the dynamic clamp (see below).
Figure 2.
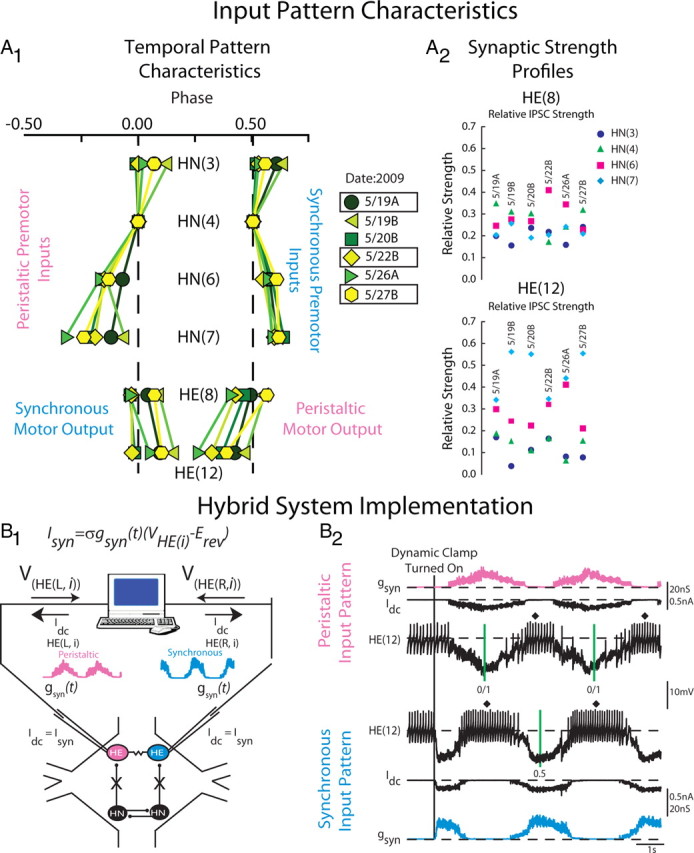
Heart motor neuron ensemble model input pattern characteristics and hybrid system implementation. A1, Simplified bilateral phase diagram illustrating the temporal pattern of the four premotor heart interneurons and the HE(8) and HE(12) motor neurons measured in six experimental preparations denoted by the date in 2009 on which the experiments occurred. The letter next to the date denotes the preparation number for that date (A, first; B, second). The line connecting the same colored symbols show the intersegmental phase relationships between the premotor HN interneurons for both the peristaltic and synchronous coordination modes. Motor output is shown opposite its matched premotor input pattern because motor output is out of phase with its premotor input. The color/symbol scheme describing the temporal patterns of the premotor heart interneurons in the different preparations is repeated in Figures 4 and 7 (see key). Preparations 5/19A, 5/22B, and 5/27B were used both in modeling studies as well as in hybrid system experiments (boxes). A2, Synaptic strength profiles of the HE(8) (top) and HE(12) (bottom) heart motor neurons showing the strength of each premotor heart interneuron input, derived from each of the six preparations whose temporal patterns are illustrated in A1. The color code is the same as in Figure 1 (see key). The data for A1 and A2 are adapted from Norris et al. (2011). B1, Hybrid system setup. We recorded simultaneously from a pair of heart (HE) motor neurons [VHE(L,i) and VHE(R,i)] in a given segment, and pharmacologically isolated the motor neurons from their premotor heart (HN) interneuron inputs. The dynamic clamp computes and injects, in real time, the artificial equivalent (Idc) of the appropriate synaptic current (ISyn), into the heart motor neurons according to the equation indicated (see Materials and Methods). One motor neuron received a model derived peristaltic time-varying synaptic conductance waveform [gSyn(t)] (pink) and the other motor neuron the synchronous equivalent (light blue). See Materials and Methods for details. B2, Exemplar dynamic-clamp experiment and determination of phase in the hybrid system experiments. At the beginning of the voltage recording, the heart motor neurons were firing tonically; gSyn is 0 nS. The vertical line shows when the dynamic-clamp synapse was activated. The dynamic clamp injects a time-varying current (Idc) proportional to the synaptic conductance gSyn. In subsequent figures, Idc is omitted and only gSyn is shown. The vertical green lines on the peristaltic trace represent the middle spike of our phase reference, the peristaltic HN(4) interneuron. The interval between the two green lines is the cycle period of the phase reference. The vertical green line on the synchronous trace represent the middle spike of the synchronous HN(4) interneuron. In subsequent figures, the middle spike of heart motor neuron bursts are indicated by a filled diamond, and the average phase for an experiment is indicated next to it. The green vertical lines are omitted in subsequent figures.
Derivation of synaptic input patterns used in model simulations.
The model motor neurons received an inhibitory synaptic input pattern that consisted of both a temporal pattern and segment specific synaptic strength profile. Both input components were determined from six physiological experiments of the type performed by Norris et al. (2011). The time series of spikes in all the premotor heart (HN) interneurons is termed their temporal pattern and was taken from simultaneous extracellular recordings of the ipsilateral HN(3), HN(4), HN(6), and HN(7) premotor interneurons in both the peristaltic and synchronous coordination modes (see Fig. 1). For each preparation, the peristaltic and synchronous input patterns were aligned to each other to create a bilateral input pattern—left synchronous–right peristaltic—by assigning a phase of 0.0 to the middle spike of the first peristaltic HN(4) premotor interneuron burst [therefore, the peristaltic HN(4) premotor interneuron is our absolute phase reference] and a phase of 0.51 to the middle spike of the first burst of the synchronous HN(4) premotor interneuron. These phase values match the average phase difference between the two HN(4) interneurons as measured in the living system (Norris et al., 2006). Each segmental pair of model motor neurons received the same temporal pattern (one peristaltic, the other synchronous) offset by an intersegmental conduction delay of 20 ms per segment. Thus, the model heart motor neurons in segment 12 receives the same temporal pattern as the model heart motor neuron in segment 8, offset by 80 ms. Because the spike timings used in our temporal patterns come from living preparations, the temporal patterns are not precisely regular, and therefore the average phases presented for model simulations display a variance.
The distributions of segment-specific synaptic conductances elicited by each premotor heart interneuron in a postsynaptic heart motor neuron (synaptic strength profile) were also derived from the six preparations in which the temporal patterns were measured as in the study by Norris et al. (2011) (see Figs. 1, 2A2). In that study, they recorded from each of the premotor heart interneurons, as described above, and then voltage clamped the HE(8) followed by the HE(12) motor neurons. They recorded spontaneous IPSCs in the heart motor neurons arising from activity in the premotor interneurons for multiple bursts in each coordination mode. From these recordings, they generated spike-triggered averages of the IPSCs for each presynaptic heart interneuron. They selected the peak of the spike-triggered average as their measure of an individual premotor heart interneurons synaptic input. These IPSCs were converted to conductances using a reversal potential of −62 mV (Angstadt and Calabrese, 1991). The set of four maximal conductances (gSynHN(i)) is unique to each segmental motor neuron pair; thus, each motor neuron pair has a unique synaptic strength profile. Each model motor neuron pair received their segment-specific synaptic strength profile. In the model, each premotor heart interneuron spike elicited a unitary synaptic conductance that followed a double exponential function scaled by the synaptic weight for that input in that motor neuron (gSynHN(i)). The model computes gSyn(t) from the sum of the inhibitory synaptic conductances (gSynHN(i)) associated with each of the four individual presynaptic inputs, HN(i). The amplitude of each IPSC implemented in the motor neurons was modulated throughout each premotor interneuron burst to conform to observed short-term synaptic plasticity (Norris et al., 2007b; García et al., 2008). The heart motor neuron ensemble model with standard cellular parameters (García et al., 2008) is referred to here as the standard ensemble model. In this study, we varied the input patterns introduced to the ensemble model motor neurons; the cellular parameters of the model motor neurons, including electrical coupling, were held constant.
Heart motor neuron ensemble model simulations.
The temporal patterns and synaptic strength profiles used as inputs to the standard ensemble model were taken from six preparations (see Fig. 2A1,A2) from the study by Norris et al. (2011) as described above. In figures and text, these preparations will be identified by the date in 2009 on which the experiments were performed and will be referred to collectively as our physiological data set. The activity phases and motor phase progressions measured in these preparations constituted target phases and/or motor phase progressions that were used to compare our model simulations to the physiological data set. In one series of simulations (here referred to as “home” simulations), the temporal pattern was paired with its own synaptic strength profiles. In another series of simulations (here referred to as “mixed” simulations), a given temporal pattern was paired with the five other synaptic strength profiles. The six preparations chosen were similar in period (range, 8.8–9.3 s) but varied both in their temporal patterns and their synaptic strength profiles.
To quantitatively compare the six temporal patterns and assess their relative contributions to intersegmental motor phase, we computed the premotor phase progression for each input pattern in each coordination mode. The premotor phase progression (either peristaltic or synchronous) is defined as the difference in phase between the last firing premotor interneuron and the first firing premotor interneuron and was positive if the HN(4) fired late in the sequence (peristaltic) or negative if it fired early in the sequence (synchronous) (see Fig. 1). For example, the 5/19A temporal pattern had a premotor peristaltic phase progression of 0.19, while the 5/27B temporal pattern had a premotor peristaltic phase progression of 0.31 (see Figs. 1, 2).
To quantitatively compare the synaptic strength profiles from the six preparations and to assess their contribution to intersegmental motor phase, we computed a synaptic strength index (SSI). The synaptic strength index is defined as the sum of two ratios as follows:
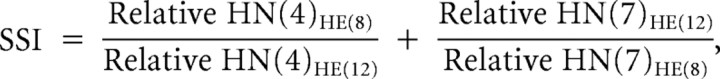 |
where Relative HN(i)HE(j) is the relative synaptic strength of premotor HN interneuron i in the heart (HE) motor neuron in segment j. The SSI assesses the summed disparity in the strength of the two key premotor HN(4) and HN(7) inputs in the HE(8) compared with the HE(12) motor neurons. The HN(4) input is typically the strongest in the HE(8) and is rather weak in the HE(12) motor neuron, while the HN(7) input is typically the strongest in the HE(12) motor neuron and is rather weak in the HE(8) motor neuron (Norris et al., 2011) so the SSI for a given preparation typically has a value >3. The 5/22B preparation is atypical because the HN(4) input is relatively weak in the HE(8) motor neuron and the HN(7) input is not much stronger than the HN(4) input in the HE(12) motor neuron, leading to an SSI of 2.4 (see Fig. 2A2).
To compare simulation outputs among themselves, we computed the motor phase progression for each input pattern in each coordination mode. The motor phase progression (either peristaltic or synchronous) is defined as the difference in phase between the HE(12) motor neuron and the HE(8) motor neuron; negative motor phase progressions indicate that the HE(8) motor neuron leads the HE(12) motor neuron and vice versa (see Fig. 1). We also computed the motor phase progressions of the same six preparation from which we derived the input patterns for use as model target values.
In some model simulations (and in follow-up hybrid system experiments), we inverted the 5/27B synaptic strength profiles to test the effect of the disparity in strength of the HN(4) and HN(7) interneurons in the HE(8) and HE(12) motor neurons on the motor phase progression between these two motor neurons. Based on the average synaptic strength profiles presented by Norris et al. (2007a, 2011), the strongest input, on average, to the HE(8) motor neuron arises from the HN(4) interneuron, while the strongest input, on average, to the HE(12) motor neuron arises from the HN(7) interneuron. In our inverted synaptic strength profiles, we made the HN(4) interneuron input the weakest in segment 8 and made the HN(7) input the strongest, while in segment 12 we made the input from the HN(7) interneuron the weakest and the input from the HN(4) interneuron the strongest. In the HE(8) motor neuron, we inverted the 5/27B synaptic strength profile by exchanging the synaptic conductance value of the HN(4) interneuron with that of the HN(7) interneuron and by exchanging the synaptic conductances of the HN(3) and HN(6) interneurons. In the HE(12) motor neuron, we inverted the 5/27B synaptic strength profile in the following manner: (1) we made the HN(7) interneuron the weakest relative input by setting its synaptic conductance to that of the weakest input, the HN(3) interneuron; (2) we made the HN(4) interneuron input the strongest relative input by setting its conductance to that of the HN(7) interneuron; (3) we set the synaptic conductance of the HN(3) interneuron to that of the HN(6) interneuron; and (4) we set the HN(6) synaptic conductance to that of the HN(4) interneuron. These changes in assignment of the synaptic strengths produced an SSI with a value <1, and we assessed how this artificially low SSI affected both synchronous and peristaltic motor phase progressions in model and hybrid system experiments.
Hybrid system design and implementation.
We used the dynamic clamp (Sharp et al., 1993; Sorensen et al., 2004) to produce a virtual version of the HN–HE synapse. The dynamic clamp both computes and injects, in real time (time step, 0.0001 s), a model of the synaptic current (ISyn) based on the intracellularly recorded membrane potential (Vm), a time-varying conductance [gSyn(t)], and a reversal potential (ESyn), implemented according to Ohm's law. Because we are linking a synapse model with heart motor neurons in the living system, we refer to these preparations as hybrid systems. The dynamic-clamp synapse was implemented according to the following equation:
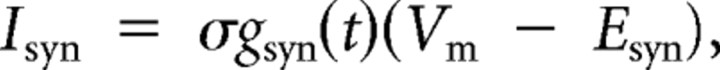 |
where ISyn is the synaptic current, gSyn(t) is the time-varying synaptic conductance waveform representing the sum of all the individual synaptic inputs to a model motor neuron, σ is a parameter used to scale gSyn(t), Vm is the membrane potential of the motor neuron, and ESyn is the synaptic reversal potential (Angstadt and Calabrese, 1991). To generate the synaptic conductance waveforms introduced in our hybrid system experiments, we extracted gSyn(t) from ensemble model simulations (see above). For simplicity, we label gSyn(t) as gSyn in figures and text (see Fig. 2B2). The synaptic conductance waveforms used in our hybrid system experiments were the same as in the ensemble model, except they were scaled by σ. The scaling factor allowed us to increase the overall synaptic conductance while preserving the relative synaptic strength of the individual premotor synaptic conductances.
All dynamic-clamp calculations were performed using a real-time dedicated processing board (DS1104; dSPACE). We activated the dynamic-clamp synapse only when motor neurons were spiking tonically and had no discernible IPSPs in the voltage recording (see Fig. 2B1,B2). We introduced the following synaptic conductance waveforms in the HE(8) and HE(12) motor neurons: (1) the 5/19A temporal pattern paired with its synaptic strength profiles, (2) the 5/27B temporal pattern paired with its synaptic strength profiles, (3) the 5/27B temporal pattern paired with the 5/22 synaptic strength profiles, and (4) the 5/27B temporal pattern paired with the inverted version of the 5/27B synaptic strength profiles (described above). In each experiment, we introduced 11 cycles of inhibitory synaptic conductance, yielding 10 bursts of activity.
Statistics.
Data were compiled and analyzed using Microsoft Excel (2010; Microsoft), SigmaPlot 11 (Systat Software), Minitab (version 14; Minitab), or MATLAB (Mathworks). We generated an average phase and duty cycle for each preparation, and the average (±SD; n = 6) across animals or simulations was used for all statistical analyses. We considered a model phase to approximate a target phase if the model was within 0.03 phase units of a given target phase. The 0.03 designation corresponds to one-half of the SD of phases for the physiological data set, and allowed us to provide some modest variability for a target phase when considering mixed-model simulations. For model simulations we analyzed motor phase progressions using a two-way (Temporal Pattern by Synaptic Strength Profiles) ANOVA. In the hybrid system experiments, we analyzed all phases using a one-way repeated-measures ANOVA. Our a priori comparisons of interest were between the 5/19A home simulation synaptic conductance waveform (i.e., temporal pattern matched with its synaptic strength profiles), the 5/27B home simulation synaptic conductance waveform, and the 5/27B temporal pattern paired with the 5/22 synaptic strength profiles, synaptic conductance waveform. Therefore, we used pairwise t tests as follow-ups to the ANOVA. Statistical significance was set at p < 0.05 for all statistical tests.
Results
Background to our models
The leech heartbeat system has been described in detail (Kristan et al., 2005; Norris et al., 2006, 2007a,b), so we briefly summarize here. Blood flow in the medicinal leech is driven by the rhythmic constriction of a bilateral pair of heart tubes, with one heart tube constricting with a rear-to-front pattern (i.e., peristaltic), while the other heart tube constricts nearly synchronously along most of its length (i.e., synchronous). The heart tubes receive excitatory input from an ipsilateral member of a pair of HE motor neurons, located in midbody segments 3–18 of the 21 midbody segmental ganglia (Maranto and Calabrese, 1984). The firing pattern of the heart motor neurons (i.e., the fictive motor pattern) is bilaterally asymmetric, with motor neurons on one side firing with a rear-to-front progression, while those on the other side fire nearly synchronously (Fig. 1) with appropriate side-to-side coordination of these two firing patterns (Wenning et al., 2004a,b). The spontaneous tonic activity of heart motor neurons in segments 7 through 14 is sculpted into bursts (Schmidt and Calabrese, 1992) by rhythmic inhibitory input arising from the ipsilateral member of each of four pairs of heart [HN(3), HN(4), HN(6), and HN(7)] interneurons within the heartbeat CPG (Norris et al., 2007a,b, 2011). The firing pattern of the premotor interneurons is also bilaterally asymmetric like that of the heart motor neurons (Fig. 1) and with appropriate side-to-side coordination. The asymmetry in firing patterns is not permanent, however; there are regular side-to-side switches in the peristaltic and synchronous patterns in the heart interneurons that underlie the changes in both the fictive motor pattern and the rhythmic constriction patterns of the heart tubes. We have previously measured quantitatively both the firing pattern (the temporal pattern) (Norris et al., 2006) of the premotor inputs and the pattern of synaptic strength of each of the premotor interneurons onto the heart motor neurons [the synaptic strength profiles (Norris et al., 2007b, 2011)]. Here, we focused on two pairs of heart motor neurons (i.e., in midbody segments 8 and 12) that receive the identical complement (4) of premotor synaptic inputs, and thus receive the identical temporal pattern of input during rhythmic activity in each of the two coordination modes but with different relative synaptic strengths (synaptic strength profile), and that express motor phase progressions large enough to capture the peristaltic and synchronous motor patterns (Fig. 1). On average, across animals, these two motor neurons have very different synaptic strength profiles (Norris et al., 2007b, 2011). We have also quantified animal-to-animal variability at all levels of the system: premotor phase progressions, synaptic strength profiles, and motor phase progressions (Norris et al., 2011) (Fig. 2A1,A2). Despite the considerable variability in these components of the system, all preparations had discernible peristaltic and synchronous patterns of activity. We concluded that each animal arrives at a unique combination of temporal pattern and synaptic strength profiles (within limits) such that functional peristaltic and synchronous patterns were always expressed.
Standard ensemble model simulations: segmental motor phase
We began our investigation into the relative contributions of premotor temporal patterns and synaptic strength profiles to motor neuron coordination, and the relationship between variation in input to variation in output by performing simulations with our previously developed model of the ensemble of heart motor neurons (García et al., 2008). We selected 6 preparations (from a total of 12), identified by the date on which the experiment took place in 2009, in which the temporal pattern, synaptic strength profiles, and motor output had all been measured in the living system (Fig. 2A1,A2) (Norris et al., 2011). These six preparations represent our physiological data set for this work; the phase of the HE(8) and HE(12) motor neurons as well as the motor phase progressions [the difference in phase between the HE(12) motor neuron and the HE(8) motor neuron (mΔϕ)] of these preparations represent target phases or motor phase progressions to which we compared our model output (Tables 1–3). The preparations selected were similar in period in the peristaltic and synchronous modes and showed modest variability across preparations (range of periods, 8.6–9.3 s). These preparations, however, displayed considerable variability in the premotor phase progression (pmΔϕ) of their temporal patterns (Fig. 2A1), their synaptic strength profiles (Fig. 2A2), which varied in their relative synaptic strengths and in their order of synaptic strengths, and finally in their motor phase progression (mΔϕ) (Fig. 2A1).
Table 1.
Peristaltic and synchronous HE(8) phase
| Synaptic strength profiles | ||||||||
|---|---|---|---|---|---|---|---|---|
| Synchronous HE(8) phase | ||||||||
| SSI | 5/19A | 5/19B | 5/20B | 5/22B | 5/26A | 5/27B | Target | |
| 3.5 | 4.4 | 5.6 | 2.4 | 5.5 | 4.7 | |||
| Temporal pattern | ||||||||
| 5/19A | 0.07 | 0.09 | 0.09 | 0.13 | 0.11 | 0.10 | 0.04 | |
| 5/19B | 0.09 | 0.10 | 0.09 | 0.14 | 0.13 | 0.12 | 0.09 | |
| 5/20B | 0.07 | 0.06 | 0.07 | 0.08 | 0.07 | 0.06 | 0.96 | |
| 5/22B | 0.07 | 0.08 | 0.07 | 0.11 | 0.10 | 0.09 | 0.97 | |
| 5/26A | 0.05 | 0.05 | 0.05 | 0.07 | 0.07 | 0.05 | 0.96 | |
| 5/27B | 0.06 | 0.08 | 0.07 | 0.10 | 0.10 | 0.08 | 0.07 | |
| Peristaltic HE(8) phase |
||||||||
|---|---|---|---|---|---|---|---|---|
| SSI | 5/19A | 5/19B | 5/20B | 5/22B | 5/26A | 5/27B | Target | |
| 3.5 | 4.4 | 5.6 | 2.4 | 5.5 | 4.7 | |||
| Temporal pattern | ||||||||
| 5/19A | 0.43 | 0.41 | 0.43 | 0.39 | 0.39 | 0.41 | 0.49 | |
| 5/19B | 0.43 | 0.41 | 0.44 | 0.46 | 0.40 | 0.46 | 0.56 | |
| 5/20B | 0.39 | 0.37 | 0.39 | 0.37 | 0.37 | 0.39 | 0.47 | |
| 5/22B | 0.38 | 0.35 | 0.38 | 0.36 | 0.34 | 0.37 | 0.43 | |
| 5/26A | 0.33 | 0.33 | 0.35 | 0.32 | 0.31 | 0.33 | 0.41 | |
| 5/27B | 0.39 | 0.34 | 0.39 | 0.38 | 0.35 | 0.38 | 0.57 | |
Bold values indicate home simulations.
Table 2.
Peristaltic and synchronous HE(12) phase
| Synaptic strength profiles |
||||||||
|---|---|---|---|---|---|---|---|---|
| Synchronous HE(12) phase | ||||||||
| SSI | 5/19A | 5/19B | 5/20B | 5/22B | 5/26A | 5/27B | Target | |
| 3.5 | 4.4 | 5.6 | 2.4 | 5.5 | 4.7 | |||
| Temporal pattern | ||||||||
| 5/19A | 0.11 | 0.14 | 0.13 | 0.13 | 0.13 | 0.14 | 0.10 | |
| 5/19B | 0.12 | 0.13 | 0.13 | 0.15 | 0.13 | 0.15 | 0.16 | |
| 5/20B | 0.09 | 0.13 | 0.12 | 0.10 | 0.15 | 0.13 | 0.98 | |
| 5/22B | 0.11 | 0.13 | 0.13 | 0.12 | 0.13 | 0.14 | 0.97 | |
| 5/26A | 0.08 | 0.10 | 0.10 | 0.09 | 0.10 | 0.11 | 0.06 | |
| 5/27B | 0.11 | 0.13 | 0.12 | 0.12 | 0.13 | 0.14 | 0.10 | |
| Peristaltic HE(12) phase |
||||||||
|---|---|---|---|---|---|---|---|---|
| SSI | 5/19A | 5/19B | 5/20B | 5/22B | 5/26A | 5/27B | Target | |
| 3.5 | 4.4 | 5.6 | 2.4 | 5.5 | 4.7 | |||
| Temporal pattern | ||||||||
| 5/19A | 0.40 | 0.35 | 0.37 | 0.38 | 0.36 | 0.37 | 0.43 | |
| 5/19B | 0.41 | 0.37 | 0.40 | 0.41 | 0.36 | 0.41 | 0.48 | |
| 5/20B | 0.36 | 0.32 | 0.32 | 0.37 | 0.32 | 0.35 | 0.37 | |
| 5/22B | 0.33 | 0.30 | 0.30 | 0.34 | 0.29 | 0.32 | 0.32 | |
| 5/26A | 0.30 | 0.25 | 0.27 | 0.30 | 0.23 | 0.27 | 0.26 | |
| 5/27B | 0.33 | 0.30 | 0.29 | 0.35 | 0.28 | 0.32 | 0.39 | |
Bold values indicate home simulations.
Table 3.
Peristaltic and synchronous HE(8)—HE(12) motor phase progression (mΔφ)
| Synaptic strength profiles |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Synchronous HE(8)–HE(12) motor phase progression (mΔφ) | |||||||||
| SSI pmΔφ | 5/19A | 5/19B | 5/20B | 5/22B | 5/26A | 5/27B | Average mΔφ | Target | |
| 3.5 | 4.4 | 5.6 | 2.4 | 5.5 | 4.7 | ||||
| Temporal pattern | |||||||||
| 5/19A | −0.10 | −0.04 | −0.04 | −0.04 | −0.01 | −0.02 | −0.05 | −0.04 | −0.06 |
| 5/19B | −0.11 | −0.03 | −0.03 | −0.04 | −0.01 | 0.00 | −0.03 | −0.04 | −0.07 |
| 5/20B | −0.13 | −0.02 | −0.07 | −0.05 | −0.02 | −0.08 | −0.07 | −0.02 | −0.02 |
| 5/22B | −0.09 | −0.04 | −0.05 | −0.06 | −0.01 | −0.03 | −0.05 | −0.03 | −0.00 |
| 5/26A | −0.08 | −0.03 | −0.05 | −0.05 | −0.01 | −0.02 | −0.05 | −0.05 | −0.09 |
| 5/27B | −0.11 | −0.04 | −0.05 | −0.06 | −0.01 | −0.03 | −0.06 | −0.04 | −0.03 |
| Average mΔφ | −0.01 | −0.03 | −0.05 | −0.03 | −0.05 | −0.05 | |||
| Peristaltic HE(8)–HE(12) motor phase progression (mΔφ) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| SSI pmΔφ | 5/19A | 5/19B | 5/20B | 5/22B | 5/26A | 5/27B | Average mΔφ | Target | |
| 3.5 | 4.4 | 5.6 | 2.4 | 5.5 | 4.7 | ||||
| Temporal pattern | |||||||||
| 5/19A | 0.19 | 0.03 | 0.06 | 0.06 | 0.01 | 0.03 | 0.04 | 0.04 | 0.07 |
| 5/19B | 0.19 | 0.02 | 0.04 | 0.04 | 0.05 | 0.04 | 0.05 | 0.04 | 0.08 |
| 5/20B | 0.21 | 0.04 | 0.05 | 0.07 | 0.01 | 0.05 | 0.04 | 0.04 | 0.10 |
| 5/22B | 0.19 | 0.04 | 0.05 | 0.08 | 0.02 | 0.05 | 0.05 | 0.05 | 0.11 |
| 5/26A | 0.34 | 0.03 | 0.08 | 0.09 | 0.01 | 0.08 | 0.05 | 0.06 | 0.15 |
| 5/27B | 0.31 | 0.06 | 0.05 | 0.10 | 0.03 | 0.07 | 0.06 | 0.06 | 0.18 |
| Average mΔφ | 0.04 | 0.06 | 0.07 | 0.02 | 0.05 | 0.05 | |||
Bold values indicate home simulations.
To quantify the variation in the premotor input patterns across preparations, we computed the premotor phase progression (pmΔϕ) of the input as the difference in phase between the last firing premotor interneuron and the first firing premotor interneuron for each preparation in each coordination mode (peristaltic and synchronous). These preparations varied between a synchronous premotor phase progression of −0.08 and −0.13 (front premotor interneurons leading) [mean, −0.24; coefficient of variation (CV), 0.17] and between a peristaltic premotor phase progression of 0.19 and 0.34 (middle premotor interneurons leading) (mean, 0.24; CV, 0.29) (Table 3). The absolute value of the average, the range, and the CV of the peristaltic premotor phase progression were all considerably larger than those of the synchronous premotor phase progression as they are in the larger sample of 12 preparations described by Norris et al. (2011).
In the synaptic strength profiles of the HE(8) and HE(12) motor neurons, there are clear trends but also considerable animal-to-animal variability (Norris et al., 2007b, 2011). These trends can be described as intersegmental gradients in synaptic strength of the four premotor inputs across the motor neurons, and they appear to be important in establishing intersegmental phase differences in the peristaltic coordination mode (Norris et al., 2011). All ipsilateral motor neurons, HE(7)–HE(14), receive the same peristaltic temporal input pattern and can fire in a phase progression only if they have different synaptic strength profiles. To quantify this type of variation and its effect on the intersegmental synaptic gradients and then assess its relationship to the motor phase progression, we computed the SSI (see Materials and Methods) for each of the six preparations in our sample. The sample preparations varied between 2.4 and 5.6 (mean, 4.4 ± 1.2 SD) by this measure (Tables 1–3). We considered the three preparations straddling the mean (i.e., falling between 3.5 and 4.7) as comparable with the others having either low or high SSI values.
We ran simulations in which a temporal pattern was matched with (1) its own synaptic strength profiles (i.e., home simulations) or (2) the other five synaptic strength profiles (i.e., mixed simulations). In the case of the home simulations, our target phase (or motor phase progression) was the physiological counterpart of the home simulation (e.g., we compared the 5/27B home simulation to the 5/27B physiological preparation); in the mixed simulations, our target phase (or motor phase progression) was the phase observed for a given physiological temporal pattern (for example, a simulation in which the 5/27B temporal pattern was matched with the 5/22B synaptic strength profiles phase was compared with the phase or motor phase progression observed in the 5/27B physiological preparation). To facilitate simulation comparisons, in which data are presented in Tables 1–3, temporal patterns are listed on the row; therefore, comparisons to the appropriate target phase or motor phase progression are made by reading across a row. In all simulations, the cellular properties of the model motor neurons were held constant at their standard values (García et al., 2008).
In our previous modeling study (García et al., 2008), we paired a specific temporal pattern (i.e., a temporal pattern from one preparation) with a synaptic strength profile based on the average synaptic strength profiles measured in the living system (Norris et al., 2007b). We then compared model output to our averaged motor neuron phase data (Norris et al., 2007a). We found that HE(8) model motor neurons were phase delayed when compared with the living system in the synchronous mode and phase advanced when compared with the living system in the peristaltic mode. It was possible, therefore, that the discrepancy in phase between the model and living system was due, in part, to our failure to account for the animal-to-animal variability in temporal patterns, synaptic strength profiles, and output phase recently reported in the living system (Norris et al., 2011). Here, we addressed this possibility directly by using multiple input patterns and then comparing ensemble model output to a target phase (as defined above). Table 1 shows the phasing observed in the HE(8) model motor neuron in both modes with each of the six home simulations shown on the diagonal, while the mixed simulations are shown on the off-diagonal.
In the synchronous mode home simulations (Table 1, diagonals), HE(8) model motor neuron phases were delayed when compared with their target phases (average delay, 0.05), just as in our previous modeling work (García et al., 2008). In those physiological preparations in which phase was delayed sufficiently (at least 0.03 phase units; 5/19A, 5/19B, and 5/27B) when compared with the average phase of the physiological data set (0.02), home simulation phases approximated (within 0.03 phase units) (see Materials and Methods) their target phases. In those physiological preparations in which the HE(8) model motor neuron was phase advanced when compared with the average phase of the physiological data set (5/20B, 5/22B, and 5/26A), home simulation phases were delayed when compared with their target phases.
In the synchronous mode mixed simulations, changing the synaptic strength profile matched with a given temporal pattern resulted in both phase advances and delays when compared with the home simulations (Table 1, rows). In mixed simulations, the target phase was the living system phase observed for the temporal pattern on each row (as described above). In most cases, the correspondence between the model and target phase was either unaffected, or the model phase deviated further from its target phase upon changing the synaptic strength profile.
In the peristaltic mode home simulations (Table 1, diagonals), HE(8) model motor neurons were phase advanced when compared with their target phases (average advance, 0.11), just as in our previous modeling work (García et al., 2008). In no case did a home simulation approximate the target phase. When considering the peristaltic mode mixed simulations, changing the synaptic strength profile matched with a given temporal pattern also resulted in both phase advances and delays when compared with the home simulations (Table 1, rows), but no combination of temporal patterns and synaptic strength profiles provided a phase delay large enough to cause the model phase to approximate a given temporal patterns target phase.
As described above for the HE(8) model motor neurons, we compared the phase observed in the home simulations of the HE(12) model motor neuron to their target phases (Table 2). In our previous modeling efforts (García et al., 2008), we found that HE(12) model motor neurons like the HE(8) model motor neurons were phase delayed when compared with the living system in the synchronous mode, but, unlike the HE(8) model motor neurons, HE(12) model motor neurons were similar to the living system in the peristaltic mode.
In the synchronous mode home simulations (Table 2, diagonals), HE(12) model motor neuron phases were delayed in five of six home simulations when compared with their target phases (average delay, 0.07), just as in our previous modeling work (García et al., 2008). In most cases, the correspondence between the model and target phase was either unaffected or the model phase deviated further from its target phase upon changing the synaptic strength profile.
In the peristaltic mode home simulations (Table 2, diagonals), HE(12) model motor neurons were phase advanced in five of six home simulations when compared with their target phases (average advance, 0.05) and phase delayed in one home simulation. Three of six home simulations, however, produced a phase that approximated (within 0.03 phase units) their target phases (the 5/19A, 5/22B, and 5/26A home simulations) with the 5/22B home simulation producing only a slight phase delay compared with its target phase. The approximation in peristaltic phase between HE(12) model home simulations and their target phases was not observed in the HE(8) model motor neurons. Changing the synaptic strength profile associated with a temporal pattern had mixed effects on the ability of the model to approximate the target phase with no synaptic strength profile providing a uniform improvement.
Our modeling results suggest that the discrepancies in firing phase observed between the HE(8) model motor neurons and the living systems are not simply due to animal-to-animal variability in the input pattern or the target phase. Only when a physiological preparation generated an HE(8) motor neuron phase that was delayed substantially from the average of the physiological data set did a model phase approximate a target phase. In the peristaltic mode, in both home and mixed simulations, the HE(8) model was phase advanced compared with a target phase.
To resolve the difference in phasing between the HE(8) model motor neurons and the heart motor neurons in the living system, the model motor neurons need to be modified in some way. In the peristaltic mode, part of the required modification to the model motor neurons appears to be the addition of intrinsic properties that allow them to sustain firing at the beginning of premotor inhibitory synaptic input, like the living motor neurons. Figure 1 shows an extracellular recording from ipsilateral HE(8) and HE(12) motor neurons along with simultaneous ipsilateral extracellular recordings from the HN(3), HN(4), HN(6), and HN(7) premotor interneurons in the peristaltic mode in the 5/27B preparation; the synaptic strength profiles measured (immediately subsequent to the extracellular record shown) in this preparation is shown to the right. Note the sizable synaptic conductance provided to the HE(8) motor neuron by the HN(6) and HN(7) interneurons. Although the synaptic inputs of the HN(6) and HN(7) interneurons reduced the firing frequency of the HE(8) motor neuron, it was not until the HN(4) interneuron began to fire that the HE(8) motor neuron stopped firing. The vertical line on the extracellular trace shows where the HE(8) model motor neuron stopped firing in response to the same synaptic input pattern. The ability of living heart motor neurons to sustain their bursts as premotor inhibitory input begins promotes a phase delay compared with the model motor neurons. In the synchronous mode, although the model motor neurons can approximate the target phase (Tables 1, 2), the range of phases where this occurs appears to be restricted to preparations in which we observed HE(8) phases delayed substantially from the average of the physiological data set; therefore, the model motor neurons will need to be modified in such a way as to promote a phase advance by initiating their burst firing as premotor inhibitory input wanes (Fig. 1), as suggested previously (Wright and Calabrese, 2011).
In HE(12) model motor neurons receiving the peristaltic input pattern, unlike in the HE(8) model motor neurons, several temporal patterns can, with their own synaptic strength profiles, produce output similar to that measured in the physiological data set (i.e., the target phase). In three of six home simulations (5/19A, 5/22B, and 5/26A), model phase approximated its target phase, with the 5/22B simulation being phase delayed compared with its target. In the other three home simulations, the HE(12) model motor neuron was phase advanced compared with the target phase. These results suggest that, with the standard set of intrinsic properties, the distribution of phases assumed by the HE(12) model motor neurons in the peristaltic mode with the input patterns used has some overlap with the distribution of HE(12) motor neuron phases observed in the living system. This overlap accounts for the ability of the models to approximate the target phase in the living system. However, in those home simulations in which model phase was advanced compared with the target phase (such as the 5/27B preparation illustrated in Fig. 1), some capacity of the model motor neurons to fire as inhibition begins will no doubt be required to approximate the target phase, as suggested above for the HE(8) motor neurons (Fig. 1). In HE(12) model motor neurons receiving the synchronous input pattern, as in the HE(8) model motor neurons, only when a physiological preparation generated an HE(12) motor neuron phase that was delayed substantially from the average of the physiological data set did a model phase approximate the target phase. Thus, the model HE(12) motor neurons, like the model HE(8) motor neurons, will need to be modified in such a way as to promote a phase advance by initiating their burst firing as premotor inhibitory input wanes (Fig. 1).
Standard ensemble model simulations: intersegmental motor phase progression
In our study of animal-to-animal variability in the leech heartbeat CPG (Norris et al., 2011), we observed that, despite the variability in both temporal patterns and synaptic strength profiles, discernible peristaltic and synchronous motor phase progressions were observed in every animal, although the sizes of the motor phase progressions were variable. In that study, we proposed that each animal arrives at its own combination of temporal pattern and synaptic strength profiles to generate their stereotyped albeit individual motor patterns. Although our model motor neurons did not always hit the target segmental phase, we investigated whether our ensemble model would at least produce appropriate peristaltic and synchronous motor phase progressions between the HE(8) and HE(12) model motor neurons for both modes and how premotor phase progression and synaptic strength profiles affected the motor phase progression. For this analysis, we computed the motor phase progressions (mΔϕ) across the same home and mixed simulations as above.
To illustrate our procedure, Figure 3 shows the output from model simulations in which the input patterns were derived from the 5/19A and 5/27B preparations. Iconic representations of the premotor temporal patterns and synaptic strength profiles are shown to the right of the voltage traces. The synaptic strength profiles were fairly close as measured by the SSI (i.e., 5/19A: SSI = 3.5; 5/27B: SSI = 4.7) (see Materials and Methods), although the total synaptic conductance was larger in the 5/27B preparation (note the difference in duty cycle). The synchronous premotor phase progressions were similar (5/19A: pmΔϕ = −0.10; 5/27B: pmΔϕ = −0.11), whereas the peristaltic premotor phase progressions were different between the two input patterns (5/19A: pmΔϕ = 0.19; 5/27B: pmΔϕ = 0.31). When receiving the 5/19A home input pattern, the peristaltic motor phase progression (mΔϕ) was 0.02, while the synchronous motor phase progression (mΔϕ) was −0.04 [the HE(8) leads the HE(12) model motor neuron in phase]; when receiving the 5/27B home input pattern, the peristaltic motor phase progression (mΔϕ) was 0.06, while the synchronous motor phase progression was (mΔϕ) −0.06 (Fig. 3, Table 3). These results indicate that the ensemble model produces appropriate peristaltic and synchronous motor phase progressions when using these two input patterns.
Figure 3.
Our ensemble model home simulations are illustrated with simultaneous bilateral voltage traces from the HE(8) and HE(12) model motor neurons receiving the 5/19A input pattern (top two panels) and the 5/27B input pattern (bottom two panels). The dashed line connecting filled diamonds shows the intersegmental motor phase progressions, peristaltic (pink) and synchronous (light blue), between the two motor neurons. An iconic representation of the temporal pattern, peristaltic and synchronous, and synaptic strength profiles with SSIs measured in the living system in those preparations is shown to the right of the corresponding voltage traces. The vertical dashed lines are aligned to the HN(4) interneuron middle spike phase, facilitating a comparison of the temporal patterns (i.e., the premotor phase progression) of the premotor interneurons measured in these preparations. The large circles represent cell bodies of the HE(8) and HE(12) motor neurons. The sizes of the filled circles show the relative synaptic strengths of the premotor HN interneurons onto the heart motor neurons measured in the living system in those preparations. The color code is the same as in Figure 1.
Relative contributions of temporal patterns and synaptic strength profiles to synchronous motor phase progressions: ensemble model simulations
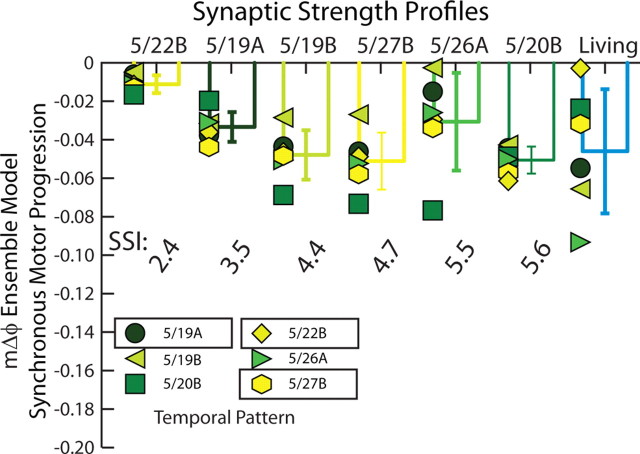
Table 3 and Figure 4 summarize the synchronous motor phase progression for all 36 (6 home, 30 mixed) simulations. In Figure 4, each symbol/shade of green represents a simulation in which a temporal pattern (identified by date) was matched with the synaptic strength profiles listed on the horizontal axis. The bars show the means and SDs of the motor phase progressions across the temporal patterns. The synaptic strength profiles were ordered by increasing value of the SSI. The synchronous motor phase progressions observed in the living system are shown on the right side for comparison. The range of these motor phase progressions represents the biological range for the experiments used as inputs to the standard ensemble model. As can be seen, all combinations of temporal patterns and synaptic strength profiles yield synchronous motor phase progressions that fall within the range of the physiological data set, suggesting that, although the segmental phase of both the HE(8) and HE(12) model motor neurons tend to be phase delayed with respect to their target phase (Tables 1, 2), the model generates synchronous motor phase progressions across temporal patterns and synaptic strength profiles as observed in the living system (Norris et al., 2011). Our simulations predict that, in the synchronous mode, multiple combinations of temporal patterns, regardless of premotor phase progression and synaptic strength profiles, including profiles with low values of the SSI (i.e., ones in which the order of relative synaptic strengths does not conform to trends), can produce a functional synchronous motor phase progression.
Figure 4.
Synchronous motor phase progressions for the ensemble model when the six temporal patterns were matched with each of the six synaptic strength profiles. Each symbol (color code: Fig. 2A1) is the synchronous motor phase progression between the HE(8) and HE(12) model motor neurons when the temporal pattern (indicated by the appropriate symbol) is matched with the synaptic strength profiles indicated on the horizontal axis. The synchronous motor phase progression measured in the living system for each of the six experimental preparations in the physiological data set is also shown. The bars indicate the mean motor phase progression for given synaptic strength profiles across temporal patterns ± SD. Synaptic strength profiles are listed in order of increasing SSI.
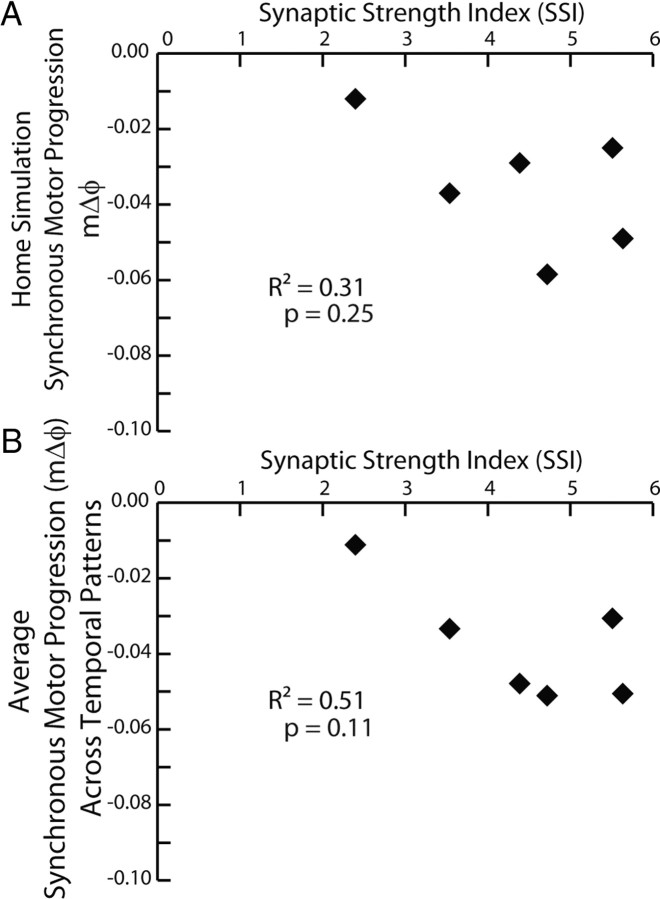
We analyzed this data set by performing a two-way (Temporal Pattern by Synaptic Strength Profile) ANOVA, which showed a significant effect of both the temporal pattern (F = 4.04; df = 5; p < 0.01) and the synaptic strength profiles (F = 11.44; df = 5; p < 0.01). For the temporal pattern, subsequent post hoc testing (Tukey's p < 0.05) showed that the 5/19B temporal pattern (pmΔϕ = −0.11) yielded an average motor phase progression (average mΔϕ = −0.02), which was significantly smaller than that (average mΔϕ = −0.05) of the 5/20B temporal pattern (pmΔϕ = −0.13) with no other pairwise differences. For the synaptic strength profiles, subsequent post hoc testing (Tukey's p < 0.05) showed that the 5/22B synaptic strength profiles (SSI = 2.4 and the smallest in this data set) yielded an average motor phase progression (average mΔϕ = −0.01) that was significantly smaller than that for all other synaptic strength profiles except that (average mΔϕ = −0.03) of the 5/26A synaptic strength profiles (SSI = 5.51), and the 5/26A synaptic strength profiles (SSI = 5.51) yielded a significantly smaller average motor phase progression (average mΔϕ = −0.03) than that (average mΔϕ = −0.05) of the 5/27B synaptic strength profiles (SSI = 4.7), with no other pairwise differences. Because there was an effect of the synaptic strength profiles in this analysis, we correlated the motor phase progression (both that for the home simulation and that for the average across temporal patterns) with the SSI of the synaptic strength profiles. Neither of these correlations was significant (Fig. 5).
Figure 5.
A, B, Correlation of the synchronous motor phase progression versus SSI (see Materials and Methods) for both the ensemble model home simulations (A) and from the average synchronous motor phase progression for the given synaptic strength profiles across temporal patterns from the mix-and-match simulations (B).
Relative contributions of temporal patterns and synaptic strength profiles to synchronous motor phase progressions: hybrid system experiments
Because the model motor neurons contained a minimal set of intrinsic electrical properties (García et al., 2008), we wanted to test our modeling prediction that, in the synchronous mode, multiple temporal patterns and synaptic strength profiles can generate a synchronous motor phase progression in living heart motor neurons (i.e., in the presence of their actual intrinsic properties). We extracted the synaptic conductance waveforms generated from three of the model simulations (and a special pattern described below) and used them as inputs in dynamic-clamp experiments (Fig. 6A). We used the HE(8) and HE(12) peristaltic and synchronous synaptic conductance waveforms from the following ensemble model simulations: (1) the 5/19A home simulation (pmΔϕ = −0.10, SSI = 3.5) (A1), (2) the 5/27B home simulation (pmΔϕ = −0.11, SSI = 4.7) (A2), (3) the 5/27B temporal pattern (pmΔϕ = −0.11) matched with the 5/22B synaptic strength profiles that have a very low SSI (SSI = 2.4) (i.e., in these profiles the order of the relative synaptic strengths does not conform to the trends) (A3); and we added a fourth pattern (4) the 5/27B temporal pattern (pmΔϕ = −0.11) matched with an inverted 5/27B synaptic strength profiles (SSI = 0.9) (A4; described below). Each of these waveforms was introduced to the same bilateral pair of motor neurons (i.e., one received the synchronous and the other received the peristaltic waveform) in a given experiment (n = 6). We then calculated the phase of the motor neurons for each synchronous waveform and computed the synchronous motor phase progression. The same experiments were used for a corresponding analysis of the peristaltic waveforms (see below). In agreement with our modeling results, there was no difference in the average synchronous motor phase progression between input waveforms derived from the 5/19A home simulation, the 5/27B home simulation, and the 5/27B temporal pattern matched with the 5/22B synaptic strength profiles (Fig. 6B; one-way repeated-measures ANOVA, p > 0.05).
Figure 6.
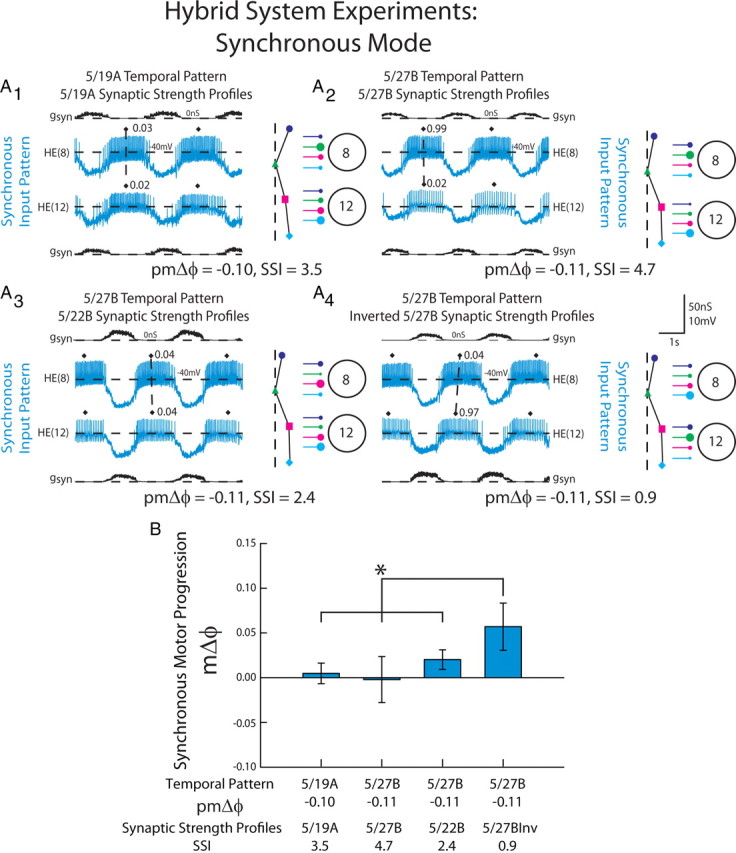
The response of HE(8) and HE(12) motor neurons receiving dynamic clamp-mediated synchronous synaptic conductance waveforms extracted from ensemble model simulations. A, Intracellular recordings and synaptic conductances (gSyn) of the HE(8) and HE(12) motor neurons receiving the synchronous 5/19A temporal and synaptic strength profiles (A1), 5/27B temporal pattern and synaptic strength profiles (A2), the 5/27B temporal pattern matched with the 5/22B synaptic strength profiles (A3), and the inverted 5/27B synaptic strength profiles (A4) are shown. An iconic representation of the temporal pattern (left panel) and the synaptic strength profiles (right panel) are shown to the right of the voltage trace (color code: Fig. 1). The vertical dashed lines are aligned to the HN(4) interneuron middle spike phase, facilitating a comparison of the temporal patterns of the premotor interneurons measured in these preparations. The large circles represent cell bodies of the HE(8) and HE(12) motor neurons. The sizes of the filled circles show the relative synaptic strengths of the premotor HN interneurons onto the heart motor neurons measured in the living system on those days. B, Average (±SD; n = 6) synchronous motor phase progression of the heart motor neurons from experiments described in A. The brackets represent the statistical comparison of the 5/27B temporal pattern matched with the 5/27B inverted synaptic strength profiles to the other input waveforms. The asterisk and brackets indicate a significant difference in motor phase progression between the 5/27B temporal pattern matched with the conductance waveform of the 5/27B inverted synaptic strength profiles and the other input patterns (one-way repeated-measures ANOVA, p < 0.05).
To test the contribution of the synaptic strength profiles to the synchronous motor phase progression, we inverted the synaptic strength profiles for the 5/27B input pattern by exchanging the synaptic conductance arising from the HN(4) interneuron measured in the HE(8) motor neuron (the strongest input of that segment) with the synaptic conductance arising from the HN(7) interneuron in the HE(8) motor neuron (the weakest input of that segment). We also exchanged the synaptic conductances associated with the HN(6) and HN(3) interneurons in this segment. This manipulation made the relatively weak HN(7) interneuron input the strongest in the HE(8) model motor neuron, while making the strong HN(4) interneuron input the weakest. In the HE(12) model motor neuron, we inverted the synaptic strength profile of that segment by making the strong HN(7) interneuron input in that segment the weakest and made the weaker HN(4) input the strongest (see Materials and Methods). These inverted synaptic strength profiles (SSI = 0.9) were then matched with the 5/27B temporal pattern. When this conductance waveform was introduced to the HE(8) and HE(12) model motor neurons, a large, positive motor phase progression (mΔϕ = 0.06) was produced that was significantly different from the other combinations of temporal patterns and synaptic strength profiles (Fig. 6B; one-way repeated measures ANOVA, p < 0.05). This positive phase progression, produced with a synchronous temporal pattern, is outside the normal range of synchronous phase progressions observed in the living system (Fig. 4) and similar to what is normally observed in the peristaltic mode in the living system, and was confirmed in a corresponding ensemble model simulation (data not shown).
These results suggest that, in the living system, multiple combinations of temporal patterns and synaptic strength profiles can generate a functional synchronous motor phase progression. We attribute this to the fact that the premotor inputs arise nearly synchronously; therefore, synaptic strength profiles may vary in their order from the trends with a consequent small SSI and still produce a functional synchronous motor phase progression. However, although the range of synaptic strength profiles observed in the living system do not strongly alter synchronous motor phase progression in the living system, there are synaptic strength profiles (albeit artificial ones) that can overwhelm the synchronous premotor temporal pattern and result in a nonfunctional motor phase progression.
Relative contributions of temporal patterns and synaptic strength profiles to peristaltic motor phase progressions: ensemble model simulations
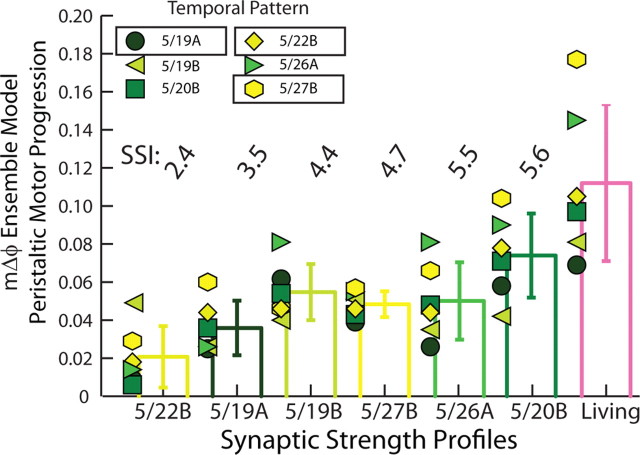
Table 3 and Figure 7 summarize the peristaltic motor phase progressions across all model simulations (6 home; 30 mixed). Data in Figure 7 are organized as in Figure 4. Across synaptic strength profiles, the 5/19A temporal pattern generated, on average, very small peristaltic motor phase progressions (average mΔϕ = 0.04) across synaptic strength profiles. The 5/27B temporal pattern generated, on average, the largest peristaltic motor phase progressions (average mΔϕ = 0.06) across synaptic strength profiles. The synaptic strength profiles are fairly close (5/19A SSI = 3.5; 5/27B SSI = 4.7) and the order of their relative synaptic strengths match the trends; their premotor phase progressions, however, were different: pmΔϕ = 0.19 for 5/19A versus pmΔϕ = 0.31 for the 5/27B preparation. Across the 36 simulations performed, there was no significant effect of temporal pattern as assessed by two-way ANOVA (F = 2.54; df = 5; p = 0.06), so we did not perform post hoc test to distinguish these two temporal patterns.
Figure 7.
Peristaltic motor phase progression in the ensemble model when the six temporal patterns were matched with each of the six synaptic strength profiles. Each symbol (color code: Fig. 2A1) is the peristaltic motor phase progression between the HE(8) and HE(12) model motor neurons when the temporal pattern (indicated by the appropriate symbol) is matched with the given synaptic strength profiles indicated on the horizontal axis. The peristaltic motor phase progression measured in the living system for each of the six experimental preparations in the physiological data set is also shown. The bars indicate the mean motor phase progression for the given synaptic strength profiles across temporal patterns ± SD. Synaptic strength profiles are listed in order of increasing SSI.
Across temporal patterns, the 5/22B synaptic strength profiles generated, on average, the smallest peristaltic motor phase progression (average mΔϕ = 0.02), whereas the 5/20B synaptic strength profiles generated, on average, the largest peristaltic motor phase progression (average mΔϕ = 0.07). The premotor phase progressions of these two preparations were similar: pmΔϕ = 0.21 for 5/20B versus pmΔϕ = 0.19 for 5/22B; the synaptic strength profiles, however, were different: the 5/20B profiles showed an order of relative synaptic strengths that matched the trends and consequently SSI = 5.6, the largest in this data set, whereas the 5/22B profiles showed an order of relative synaptic strengths that did not match the trends and consequently SSI = 2.4, the smallest in this data set. Across the 36 simulations performed, there was a highly significant effect of synaptic strength profiles as assessed by two-way ANOVA (F = 8.93; df = 5; p < 0.01). Subsequent post hoc testing (Tukey's p < 0.05) showed that the 5/22B synaptic strength profiles (SSI = 2.4) yielded an average motor phase progression (average mΔϕ = 0.02), which was significantly smaller than that for all other synaptic strength profiles except that (average mΔϕ = 0.04) of the 5/19A synaptic strength profiles (SSI = 3.5 and the second smallest in this data set), and the 5/19A synaptic strength profiles (SSI = 3.5) also yielded a significantly smaller average motor phase progression (average mΔϕ = 0.04) than that (average mΔϕ = 0.07) of the 5/20B synaptic strength profiles (SSI = 5.6 and the largest in this data set), with no other pairwise differences.
In our previous work (Norris et al., 2011), we showed that there were very few significant correlations between the relative synaptic strength of an individual premotor input and HE(8) or HE(12) heart motor neuron phase in the living system. We attributed this lack of correlation to the fact that animal-to-animal variability in the relative strength of each premotor input and in the temporal pattern of the inputs masked relatively straightforward correlations such as those observed in the stomatogastric nervous system (Goaillard et al., 2009). Indeed, in follow-up simulations in which we fixed the temporal pattern and synaptic strength of three of the premotor interneuron inputs and varied the fourth across the range of synaptic strengths observed in the 12 fully characterized living preparations (Norris et al., 2011), strong and significant correlations were observed. In our six home simulations, we also did not find correlations between any one input and the phase of an individual motor neuron or the peristaltic motor phase progression, suggesting that, as in the living system, the animal-to-animal variability in temporal patterns and synaptic strength of the four inputs obscures simple correlations in the ensemble model.
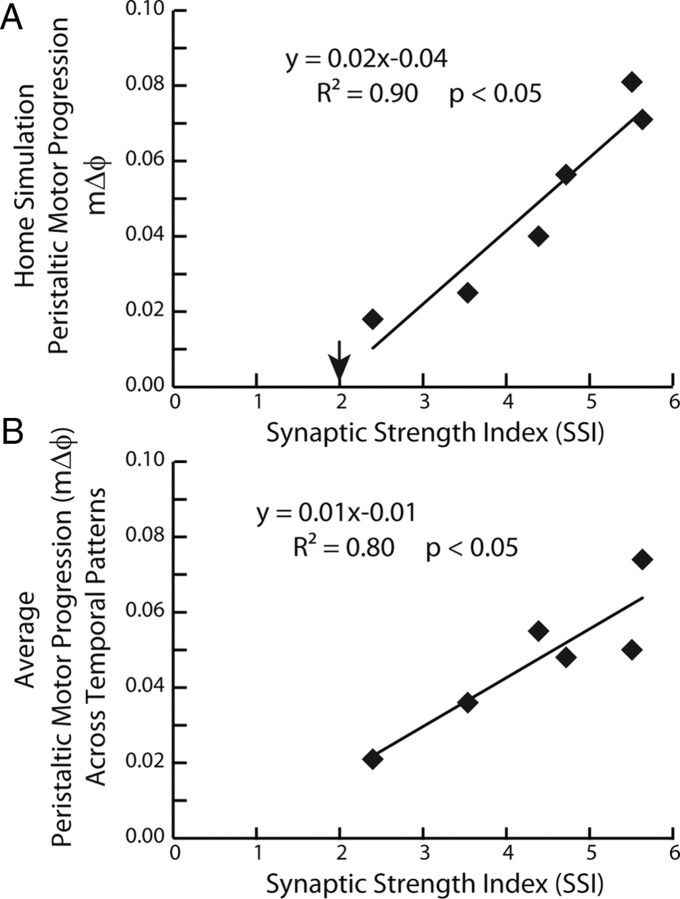
Because there was a strong effect of the synaptic strength profiles in our analysis of the 36 peristaltic simulations, we correlated the motor phase progression [both that for the home simulation (Fig. 8A) and the average motor phase progression across temporal patterns (Fig. 8B)] with the SSI of the synaptic strength profiles. The SSI is a metric that captures the hypothesized effectiveness of the synaptic strength profiles in segments 8 and 12 in promoting a large peristaltic motor phase progression (see Materials and Methods). In both cases, a significant amount of variability in the peristaltic motor phase progression was explained by its regression on the SSI (home simulations: R2 = 0.90, F = 15.73, df = 1, p < 0.05; average across temporal patterns: R2 = 0.80, F = 37.57, df = 1, p < 0.05). These results suggest that, in the model, the stronger the HN(4) interneuron input in the HE(8) motor neuron and, simultaneously, the HN(7) interneuron input in the HE(12) motor neuron, the larger the peristaltic motor phase progression will be. However, when the SSI was correlated to the six preparations in the physiological data set, no correlation was found (R2 = 0.12; p > 0.05). We attribute this lack of correlation to animal-to-animal variability, including variability in the intrinsic electrical properties of the HE motor neurons.
Figure 8.
A, B, Correlation and regression line for the peristaltic motor phase progression versus the SSI for both the ensemble model home simulations (A) and from the average peristaltic motor phase progression for the given synaptic strength profiles across temporal patterns from the mix-and-match simulations (B). The downward arrow in A indicates the SSI value at which the peristaltic motor phase progression changes sign and the motor phase progression no longer resembles a true peristaltic progression between the HE(8) and the HE(12) motor neurons. Because the correlations were significant, regression lines were also computed: equations are shown.
These results predict that synaptic strength profiles with large SSIs (i.e., those that conform to trend in the order of relative synaptic strengths) will generate larger peristaltic motor phase progressions than synaptic strength profiles with small SSI (i.e., those that do not conform to trend) when matched with the same premotor phase progression. They also suggest that input patterns with larger peristaltic premotor phase progressions generate larger peristaltic motor phase progressions than input patterns with smaller premotor phase progressions when matched with comparable synaptic strength profiles (SSIs).
Relative contributions of temporal patterns and synaptic strength profiles to peristaltic motor phase progressions: hybrid system experiments
Again, we used the dynamic clamp to test the prediction of our modeling experiments. Specifically, we tested the hypotheses that synaptic strength profiles with larger SSIs (thus showing an order of relative synaptic strengths that match the trends) and larger premotor phase progressions generate larger peristaltic motor phase progressions in the heart motor neurons in the living system. For this analysis, we used the data for the peristaltic synaptic conductance waveforms introduced into the motor neurons in the experiments of Figures 6A1–A4 and 9. Although considered separately, the data for Figures 6 and 9 are thus derived from the same experiments. Our comparisons of interest were those highlighted in the modeling results above: (1) between the 5/19A home (pmΔϕ = 0.19; SSI = 3.5) and 5/27B home (pmΔϕ = 0.31; SSI = 4.7) waveforms and (2) between the 5/27B home (pmΔϕ = 0.31; SSI = 4.7) waveform and the 5/27B temporal pattern (pmΔϕ = 0.31) matched with the 5/22B synaptic strength profiles, which do not conform to trend in the order of relative synaptic strengths and have consequently SSI = 2.4, the lowest in this data set.
Figure 9.
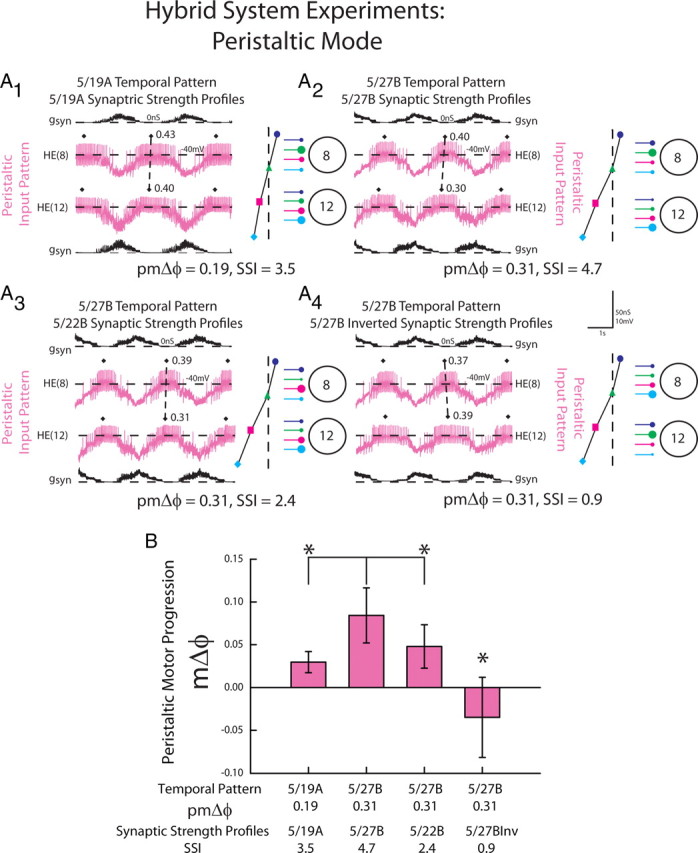
The response of HE(8) and HE(12) motor neurons receiving dynamic clamp-mediated peristaltic synaptic conductance waveforms extracted from ensemble model simulations. A, Intracellular recordings and synaptic conductances (gSyn) of the HE(8) and HE(12) motor neurons receiving the peristaltic 5/19A temporal and synaptic strength profiles (A1), 5/27B temporal pattern and synaptic strength profiles (A2), the 5/27B temporal pattern matched with the 5/22B synaptic strength profiles (A3), and the 5/27B inverted synaptic strength profiles (A4) are shown. An iconic representation of the temporal pattern (left panel) and the synaptic strength profiles (right panel) are shown to the right of the voltage trace (color code: Fig. 1). Organization and symbols as described in the legend of Figure 6. B, Average (±SD; n = 6) peristaltic motor phase progression of the heart motor neurons from experiments described in A. The asterisks and brackets indicate significant differences in the peristaltic motor phase progression between the 5/27B home simulation and both the 5/19A home simulation and 5/27B temporal pattern matched with the 5/22B synaptic strength profiles (paired t test, p < 0.05).
There was a significant difference in the peristaltic motor phase progression across all the input waveforms (Fig. 9B; one-way repeated measures ANOVA). In follow-up comparisons, the 5/27B home waveform generated a larger peristaltic motor phase progression than the 5/19A home waveform (paired t test, p < 0.05). Because the synaptic strength profiles (SSIs) for these two preparations were comparable and the order of relative synaptic strengths conforms to trend in both, we treated this as a test of the prediction that a larger premotor phase progression generates a large motor phase progression.
The peristaltic motor phase progression generated by the 5/27B home waveform (pmΔϕ = 0.31; SSI = 4.7) was significantly greater than that generated by the mixed waveform consisting of the 5/27B temporal pattern (pmΔϕ = 0.31) matched with the 5/22B synaptic strength profiles (SSI = 2.4) (paired t test, p < 0.05). Because both synaptic strength profiles were matched with the same temporal pattern, we treated this as a test of the hypothesis that synaptic strength profiles with large SSIs (i.e., those that conform to trend in the order of relative synaptic strength) generate larger motor phase progressions than synaptic strength profiles with low SSIs (i.e., those that do not conform to trend in the order of relative synaptic strength).
We also assessed how inverted synaptic strength profiles would affect the peristaltic motor phase progression. When the conductance waveform derived from the 5/27B temporal pattern (pmΔϕ = 0.31) with inverted synaptic strength profiles (SSI = 0.9) (Fig. 9A4) was introduced to the HE(8) and HE(12) motor neurons, it generated a negative phase progression (−0.03) that was significantly different from the other combinations of temporal patterns and synaptic strength profiles (Fig. 9B; one-way repeated-measures ANOVA, p < 0.05). The same negative motor phase progression was confirmed in a corresponding simulation in the ensemble model (data not shown). Despite the fact that the temporal pattern had a positive premotor phase progression, this conductance waveform with inverted synaptic profiles produced a negative motor phase progression, similar to that observed in the synchronous mode in the living system. This result suggests that, in addition to significantly affecting the motor phase progression observed in the peristaltic mode, synaptic strength profiles not conforming to trend and thus with a low SSI (albeit an artificial one) can overwhelm a temporal pattern with a large peristaltic premotor phase progression and result in a nonfunctional motor phase progression.
Synaptic strength index as predictor of peristaltic motor phase progression in motor neuron ensemble simulations
In addition to predicting how large a peristaltic motor phase progression can be, the SSI can also estimate how far synaptic strength profiles may deviate from the trends across animals before they overwhelm the potential peristaltic motor phase progression provided by the temporal pattern and produces a negative peristaltic motor phase progression, as in the dynamic-clamp experiments of Figure 9. In the home simulations, the x-intercept (Fig. 8A, downward arrow) represents the SSI where the peristaltic motor phase progression reverses sign. This value is 2.0 in the home simulations and is compatible with synaptic strength profiles in which the HN(4) and HN(7) interneuron inputs are equal in strength in both the HE(8) and HE(12) motor neurons. In the physiological data set, the 5/22B preparation had the smallest SSI (2.4), while the 5/20B preparation had the largest SSI (5.6), thus explaining their ability to affect the peristaltic motor phase progression realized by any temporal pattern with which they were matched. The SSI for the 5/27B inverted synaptic strength profiles, however, was 0.9, thus the negative peristaltic motor phase progression in our modeling and hybrid system experiments. Together, these results suggest that, for a given temporal pattern, higher SSI values will result in larger peristaltic motor phase progressions than smaller SSI values.
We caution here that the SSI is an ad hoc measure applicable only to the two motor neurons that we chose—the HE(8) and the HE(12) motor neurons. The mechanism of coordination that we explored is based on a series of intersegmental gradients of synaptic strengths of the various heart interneuron inputs to the HE(7)–HE(14) motor neurons as manifested in our averaged physiological data across animals (Norris et al., 2007a, 2011). We focused on the middle of section of these gradients when we chose the HE(8) and HE(12) motor neurons for study. After analyzing these gradients in this region, we tried to capture their ability to produce the peristaltic motor phase progression in a measure and thus constructed the current SSI. Other SSIs could be constructed that focus on different regions of the synaptic gradients of the premotor heart interneurons or indeed for other systems that depend on similar synaptic gradients for coordination of motor neurons. If we had considered, for example, the HE(7) and HE(11) motor neurons instead, we would have constructed a different SSI, because the HN(7) input in the HE(7) is usually 0 and the HN(3) input tends to be the largest.
Discussion
The goal of the present study was to determine the relative contributions of the temporal pattern and synaptic strength profiles of premotor inputs to coordination of phase differences among motor neurons during rhythmic activity. We investigated motor neurons that receive the same complements of premotor synaptic inputs—and thus the same temporal input pattern—but differ in the relative strengths of those inputs (synaptic strength profile) (Fig. 1). We made use of natural variation among individuals in the temporal pattern, the synaptic strength profiles, and indeed in the motor phase progression to aid in this investigation. We also investigated the consequences of this natural variation in input for motor output. The coordination that we studied here seems analogous to intersegmental coordination of motor neurons in other rhythmic behaviors such as undulatory swimming in leeches or lampreys (Mullins et al., 2011) or swimmeret beating in crayfish (Smarandache et al., 2009), but it differs from those well studied systems, where segmentally repeated motor neurons that are active in a phase progression receive segment-specific premotor inputs and thus different temporal input patterns. The mechanism of coordination of these heart motor neurons is thus fundamentally simpler but remains of general importance because we can dissect and thus study separately the roles of temporal pattern and synaptic strength profiles.
In the synchronous mode, our modeling and hybrid system data indicate that many different combinations of temporal patterns and synaptic strength profiles can interact to produce a functional synchronous motor pattern. It was only when we used artificially inverted synaptic strength profiles that we observed dramatic departures from the synchronous motor phase progression. We attribute the ability of multiple combinations of temporal patterns and synaptic strength profiles to produce synchronous motor phase progressions to the near-synchronous premotor temporal patterns that the nervous system produces, so that, within limits, differences in variability of synaptic strength profiles matter little (Fig. 2B).
In the peristaltic mode, our modeling data suggest that temporal patterns with a large premotor phase progression (large pmΔϕ) promote larger motor phase progressions (Fig. 7, Table 3). In our dynamic-clamp experiments, the 5/27B temporal pattern (pmΔϕ = 0.31) produced, on average, larger peristaltic motor phase progressions than the 5/19A temporal pattern (pmΔϕ = 0.19) (Fig. 9), supporting this suggestion. The effect of the synaptic strength profiles on peristaltic motor phase progression can be illustrated by reference to Figure 1 taken from the 5/27B preparation (SSI = 4.7). In the HE(8) motor neuron, having the HN(4) interneuron provide the strongest synaptic input with the HN(7) interneuron the weakest (thus promoting a large SSI), allows the HE(8) motor neuron (Fig. 1) to fire through the weaker inhibition from the HN(7) interneuron (note that this is the first input that both motor neurons receive in the peristaltic mode). Then, as the HN(4) interneuron begins to fire, its strong input adding to the HN(7) and HN(6) inputs silences the HE(8) motor neuron. In the HE(12) motor neuron, having the HN(7) interneuron provide the strongest synaptic input, with the HN(4) interneuron being very weak (Fig. 2A) allows the HN(7) interneuron, being the first input, to terminate the burst of the HE(12) motor neuron, promoting a phase advance with respect to the HE(8) motor neuron, and thus promoting a larger peristaltic motor phase progression.
In essence, there are intersegmental gradients of synaptic strength of the four different premotor inputs as these inputs progress from the HE(8) to the HE(12) motor neurons. These intersegmental gradients are tuned to produce a peristaltic motor phase progression and are strongly manifested in the average physiological data across preparations collected in the study by Norris et al. (2011). The SSI, by simultaneously considering the difference in strength between the HN(4) and HN(7) inputs in the HE(8) and the HE(12) motor neurons, captures the tuning of these gradients that promotes the largest peristaltic motor phase progression possible given a particular temporal input pattern (Figs. 7–9). The 5/26A (Fig. 2A2) synaptic strength profiles (SSI = 5.5) provide an interesting case. Although this preparation bucks trend in that the HN(6), not the HN(4), is the strongest input in the HE(8) motor neuron, the HN(4) input is yet weaker in the HE(12) motor neuron leading to a ratio HN(4) in HE(8)/HN(4) in HE(12) = 3.3, and although the preparation again bucks the trend in that the HN(7) is a relatively strong input—similar to the HN(4) input—in the HE(8) motor neuron, the HN(7) input is so overwhelmingly strong in the HE(12) motor neuron that the ratio HN(7) in HE(12)/HN(7) in HE(8) = 2.2. Thus, this preparation has developed effective synaptic gradients, albeit somewhat unusual in structure, as demonstrated in our modeling studies (Figs. 7, 8) and as demonstrated by the large motor phase progression that it produced in the living system (0.15) (Table 3). Reversing the synaptic gradients, as we did when we used inverted synaptic profiles in the dynamic-clamp experiments of Figure 9 (but also Fig. 6), caused the SSI to fall below 1 and the motor phase progression also to reverse.
Our results further indicate that the heartbeat CPG can reliably produce peristaltic motor patterns by generating the largest premotor phase progression possible. The premotor phase progression between the HN(7) and HN(3) interneurons establishes the maximum amount of motor phase progression (phase range) available to the motor neurons that these premotor interneurons exclusively innervate [i.e., the HE(7) to HE(14) motor neurons]. The synaptic strength profiles set up intersegmental gradients, which for the HE(8) to HE(12) motor neurons is embodied in the SSI, that determines where in this range any heart motor neuron does fire and thus determines the motor phase progression that is realized. Our correlational analysis of Figure 8 suggests that, in the limit that the SSI approaches infinity, the phase difference between the HE(8) and the HE(12) motor neuron will approach the phase difference between the HN(4) and the HN(7) interneurons.
General relevance
The general principle that emerges from our work is that even when motor neurons share the same complement of synaptic inputs, they can fire differentially (e.g., in a phase progression) if there are gradients of synaptic strength of these inputs across the motor neuron population and the premotor inputs fire at different times. Moreover, these gradients do not interfere when synchronous activity is required across the motor neuron population so long as the premotor inputs fire in near synchrony.
Taking the crayfish swimmeret system as an example (Smarandache et al., 2009) can illustrate how insights derived here may be applied to other systems. In that system, four segmental oscillators are interconnected by coordinating neurons that decrease their synaptic strength with distance between the oscillators. This pattern would seem to lead to simple gradients, but due to the large phase difference (0.25) between each oscillator, inputs of different strength arrive at different phases of the cycle of each oscillator, and the phase response curve of each oscillator to synaptic input shows the typical bilobed shape (Mulloney and Hall, 2007). Thus, control of intersegmental phase between oscillators has some similarities to peristaltic coordination of HE(8)–HE(12) heart motor neurons with the added complexity that each oscillator receives a different complement of inputs. Dynamic-clamp experiments of the type we performed may help to elucidate the mechanisms of coordination in this system. Indeed, such analysis may also prove useful in vertebrate spinal motor neurons, if different input patterns can be decomposed into temporal and synaptic strength components (Endo and Kiehn, 2008).
An important aspect of our analysis is the use of data from individual animals rather than average data and the construction of multiple models based on these individual data. This approach has received significant attention of late (for an enlightening review, see Marder, 2011). Our experience with this approach is mixed. On the one hand, we were able to better isolate the effects of temporal pattern and synaptic strength profiles by considering data from individuals. On the other hand, our individualized models suffer from the same deficiencies as our previous model using averaged synaptic strength data (García et al., 2008). Despite the extensive level of detail incorporated into the synaptic drive in our models and regardless of whether individual or averaged data were used for describing the input or specifying the motor output, we have not achieved accurate phasing, particularly in the peristaltic coordination mode. Completely specifying synaptic drive and motor output has clearly not been sufficient and yet more parameters must be measured simultaneously—in this case, most likely the addition of motor neuron intrinsic properties (i.e., our use of a simplified motor neuron model must come into question). The leech heartbeat system has made the specification of input and output, while difficult, at least feasible, but determining motor neuron intrinsic properties in voltage clamp will be another matter. Every system is likely to come up against such walls; perhaps optimization and/or database techniques (Prinz, 2010) using models can help surmount such walls (Hendrickson et al., 2011).
Footnotes
This work was supported by a Ruth L. Kirschstein National Research Service Award, funded by National Institute of Neurological Disorders and Stroke Grant NS-8472431, National Science Foundation Integrative Graduate Education and Research Traineeship Program Grant DGE-0333411, and American Psychological Association/Diversity Program in Neuroscience Predoctoral Fellowship 5 T06 MH-1882, funded by the National Institute of Mental Health (T.M.W.), and by National Institute of Neurological Disorders and Stroke Grant NS-24072 (R.L.C.). We thank A. Wenning for careful reading of this manuscript and help with preparation of figures, and B. J. Norris for sharing his data with us.
References
- Angstadt JD, Calabrese RL. Calcium currents and graded synaptic transmission between heart interneurons of the leech. J Neurosci. 1991;11:746–759. doi: 10.1523/JNEUROSCI.11-03-00746.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg RW, Alaburda A, Hounsgaard J. Balanced inhibition and excitation drive spike activity in spinal half-centers. Science. 2007;315:390–393. doi: 10.1126/science.1134960. [DOI] [PubMed] [Google Scholar]
- Biró Z, Hill RH, Grillner S. The activity of spinal commissural interneurons during fictive locomotion in the lamprey. J Neurophysiol. 2008;100:716–722. doi: 10.1152/jn.90206.2008. [DOI] [PubMed] [Google Scholar]
- Borgmann A, Hooper SL, Büschges A. Sensory feedback induced by front-leg stepping entrains the activity of central pattern generators in caudal segments of the stick insect walking system. J Neurosci. 2009;29:2972–2983. doi: 10.1523/JNEUROSCI.3155-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Büschges A, Scholz H, El Manira A. New moves in motor control. Curr Biol. 2011;21:R513–R524. doi: 10.1016/j.cub.2011.05.029. [DOI] [PubMed] [Google Scholar]
- Endo T, Kiehn O. Asymmetric operation of the locomotor central pattern generator in the neonatal mouse spinal cord. J Neurophysiol. 2008;100:3043–3054. doi: 10.1152/jn.90729.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs E, Holmes P, Kiemel T, Ayali A. Intersegmental coordination of cockroach locomotion: adaptive control of centrally coupled pattern generator circuits. Front Neural Circuits. 2011;4:125. doi: 10.3389/fncir.2010.00125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel JP, Ausborn J, Ampatzis K, Mahmood R, Eklöf-Ljunggren E, El Manira A. Principles governing recruitment of motoneurons during swimming in zebrafish. Nat Neurosci. 2011;14:93–99. doi: 10.1038/nn.2704. [DOI] [PubMed] [Google Scholar]
- García PS, Wright TM, Cunningham IR, Calabrese RL. Using a model to assess the role of the spatiotemporal pattern of inhibitory input and intrasegmental electrical coupling in the intersegmental and side-to-side coordination of motor neurons by the leech heartbeat central pattern generator. J Neurophysiol. 2008;100:1354–1371. doi: 10.1152/jn.90579.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Schulz DJ, Marder E. Functional consequences of animal-to-animal variation in circuit parameters. Nat Neurosci. 2009;12:1424–1430. doi: 10.1038/nn.2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrickson EB, Edgerton JR, Jaeger D. The use of automated parameter searches to improve ion channel kinetics for neural modeling. J Comput Neurosci. 2011 doi: 10.1007/s10827-010-0312-x. [DOI] [PubMed] [Google Scholar]
- Hill AA, Lu J, Masino MA, Olsen OH, Calabrese RL. A model of a segmental oscillator in the leech heartbeat neuronal network. J Comput Neurosci. 2001;10:281–302. doi: 10.1023/a:1011216131638. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson BR, Brown JM, Kvarta MD, Lu JY, Schneider LR, Nadim F, Harris-Warrick RM. Differential modulation of synaptic strength and timing regulate synaptic efficacy in a motor network. J Neurophysiol. 2011;105:293–304. doi: 10.1152/jn.00809.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristan WB, Jr, Calabrese RL, Friesen WO. Neuronal control of leech behavior. Prog Neurobiol. 2005;76:279–327. doi: 10.1016/j.pneurobio.2005.09.004. [DOI] [PubMed] [Google Scholar]
- Maranto AR, Calabrese RL. Neural control of the hearts in the leech, Hirudo medicinalis. 1. Anatomy, electrical coupling, and innervation of the hearts. J Comp Physiol. 1984;154:367–380. [Google Scholar]
- Marder E. Quantification of Behavior Sackler Colloquium: variability, compensation, and modulation in neurons and circuits. Proc Natl Acad Sci U S A. 2011;108(Suppl 3):15542–15548. doi: 10.1073/pnas.1010674108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- Marder E, Goaillard JM. Variability, compensation and homeostasis in neuron and network function. Nat Rev Neurosci. 2006;7:563–574. doi: 10.1038/nrn1949. [DOI] [PubMed] [Google Scholar]
- Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci. 2011;14:133–138. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullins OJ, Hackett JT, Buchanan JT, Friesen WO. Neuronal control of swimming behavior: comparison of vertebrate and invertebrate model systems. Prog Neurobiol. 2011;93:244–269. doi: 10.1016/j.pneurobio.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulloney B, Hall WM. Local and intersegmental interactions of coordinating neurons and local circuits in the swimmeret system. J Neurophysiol. 2007;98:405–413. doi: 10.1152/jn.00345.2007. [DOI] [PubMed] [Google Scholar]
- Norris BJ, Weaver AL, Morris LG, Wenning A, García PA, Calabrese RL. A central pattern generator producing alternative outputs: temporal pattern of premotor activity. J Neurophysiol. 2006;96:309–326. doi: 10.1152/jn.00011.2006. [DOI] [PubMed] [Google Scholar]
- Norris BJ, Weaver AL, Wenning A, García PS, Calabrese RL. A central pattern generator producing alternative outputs: phase relations of leech heart motor neurons with respect to premotor synaptic input. J Neurophysiol. 2007a;98:2983–2991. doi: 10.1152/jn.00407.2007. [DOI] [PubMed] [Google Scholar]
- Norris BJ, Weaver AL, Wenning A, García PS, Calabrese RL. A central pattern generator producing alternative outputs: pattern, strength, and dynamics of premotor synaptic input to leech heart motor neurons. J Neurophysiol. 2007b;98:2992–3005. doi: 10.1152/jn.00877.2007. [DOI] [PubMed] [Google Scholar]
- Norris BJ, Wenning A, Wright TM, Calabrese RL. Constancy and variability in the output of a central pattern generator. J Neurosci. 2011;31:4663–4674. doi: 10.1523/JNEUROSCI.5072-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA. Computational approaches to neuronal network analysis. Philos Trans R Soc Lond B Biol Sci. 2010;365:2397–2405. doi: 10.1098/rstb.2010.0029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puhl JG, Mesce KA. Keeping it together: mechanisms of intersegmental coordination for a flexible locomotor behavior. J Neurosci. 2010;30:2373–2383. doi: 10.1523/JNEUROSCI.5765-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt J, Calabrese RL. Evidence that acetylcholine is an inhibitory transmitter of heart interneurons in the leech. J Exp Biol. 1992;171:329–347. doi: 10.1242/jeb.171.1.329. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, Marder EE. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc Natl Acad Sci U S A. 2007;104:13187–13191. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp AA, O'Neil MB, Abbott LF, Marder E. The dynamic clamp: artificial conductances in biological neurons. Trends Neurosci. 1993;16:389–394. doi: 10.1016/0166-2236(93)90004-6. [DOI] [PubMed] [Google Scholar]
- Smarandache C, Hall WM, Mulloney B. Coordination of rhythmic motor activity by gradients of synaptic strength in a neural circuit that couples modular neural oscillators. J Neurosci. 2009;29:9351–9360. doi: 10.1523/JNEUROSCI.1744-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soffe SR, Roberts A, Li WC. Defining the excitatory neurons that drive the locomotor rhythm in a simple vertebrate: insights into the origin of reticulospinal control. J Physiol. 2009;587:4829–4844. doi: 10.1113/jphysiol.2009.175208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorensen M, DeWeerth S, Cymbalyuk G, Calabrese RL. Using a hybrid neural system to reveal regulation of neuronal network activity by an intrinsic current. J Neurosci. 2004;24:5427–5438. doi: 10.1523/JNEUROSCI.4449-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobin AE, Cruz-Bermúdez ND, Marder E, Schulz DJ. Correlations in ion channel mRNA in rhythmically active neurons. PLoS One. 2009;4:e6742. doi: 10.1371/journal.pone.0006742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenning A, Cymbalyuk GS, Calabrese RL. Heartbeat control in leeches. I. Constriction pattern and neural modulation of blood pressure in intact animals. J Neurophysiol. 2004a;91:382–396. doi: 10.1152/jn.00526.2003. [DOI] [PubMed] [Google Scholar]
- Wenning A, Hill AA, Calabrese RL. Heartbeat control in leeches. II. Fictive motor pattern. J Neurophysiol. 2004b;91:397–409. doi: 10.1152/jn.00528.2003. [DOI] [PubMed] [Google Scholar]
- Wright TM, Jr, Calabrese RL. Contribution of motoneuron intrinsic properties to fictive motor pattern generation. J Neurophysiol. 2011;106:538–553. doi: 10.1152/jn.00101.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]