Automated Gastric Slow Wave Cycle Partitioning and Visualization for High-resolution Activation Time Maps

Abstract

High-resolution (HR) multi-electrode mapping has become an important technique for evaluating gastrointestinal (GI) slow wave (SW) behaviors. However, the application and uptake of HR mapping has been constrained by the complex and laborious task of analyzing the large volumes of retrieved data. Recently, a rapid and reliable method for automatically identifying activation times (ATs) of SWs was presented, offering substantial efficiency gains. To extend the automated data-processing pipeline, novel automated methods are needed for partitioning identified ATs into their propagation cycles, and for visualizing the HR spatiotemporal maps. A novel cycle partitioning algorithm (termed REGROUPS) is presented. REGROUPS employs an iterative REgion GROwing procedure and incorporates a Polynomial-surface-estimate Stabilization step, after initiation by an automated seed selection process. Automated activation map visualization was achieved via an isochronal contour mapping algorithm, augmented by a heuristic 2-step scheme. All automated methods were collectively validated in a series of experimental test cases of normal and abnormal SW propagation, including instances of patchy data quality. The automated pipeline performance was highly comparable to manual analysis, and outperformed a previously proposed partitioning approach. These methods will substantially improve the efficiency of GI HR mapping research.

Introduction

Gastric motility is initiated and coordinated by electrical activity termed slow waves (SWs). SWs are generated and propagated by the interstitial cells of Cajal (ICCs), and conducted passively to the adjacent smooth muscle cells, causing depolarization and inducing contractions when co-regulatory conditions are met, as occurs after a meal.²³ In an intact network, the frequencies of ICCs synchronize to the single fastest frequency in the syncytium, in a process known as entrainment.²³ In the human stomach, SWs therefore arise from a pacemaker area which has the highest intrinsic frequency, located near the greater curvature of the mid to upper corpus, and then propagate toward the antrum at a frequency of ≈3 cycles per minute (cpm).¹⁷ Abnormal SW activity has been associated with gastric motility disorders, such as gastroparesis,¹⁹ functional dyspepsia,¹⁶ and gastro-esophageal reflux disease.³ In gastroparesis, ICC loss may be an underlying or contributing cause.⁹

The recent advent of high-resolution (HR) electrical mapping has been an important advance for evaluating gastric SW behaviors.^14,15 HR mapping involves the placement of spatially dense arrays of many electrodes (typically >100, spaced at 2–10 mm), and recording simultaneously from all sites, in order to provide a detailed understanding of SW propagation across the target organ. These recordings can be used to generate activation time (AT) maps that provide a spatiotemporal quantification of the spread of electrical activity, and therefore significantly more detail than was revealed with past sparse electrode approaches.^5,14,18 For example, recent HR studies of the normal canine, porcine, and human stomachs have revealed significant new information regarding the origin and propagation dynamics of slow wave activity.^7,15,17 HR mapping has also been applied to investigate the mechanisms of gastric dysrhythmia, revealing complex focal and reentrant activities similar to behaviors seen in cardiac fibrillation,¹⁴ and to better define the effects of gastric pacing on SW activity.¹⁸ The clinical significance of these findings now awaits to be determined.

Although it is a relatively new technique in gastroenterology, HR mapping has been widely used for many years in cardiology where it has led to routine tools for the management of dysrhythmias.^10,24 A large number of methods now enable the efficient analysis of cardiac mapping data.^{1, 21, 22} In the GI field, however, the application of HR mapping has been constrained by the poor efficiency of data processing and analysis. In a 256 channel 10 minute gastric recording, there may be ≈30 SW cycles, comprising >7500 individual events, to individually assess, mark, map, and characterize. Until recently, this task has mostly been performed manually, presenting a laborious and time-consuming assignment.

To improve the efficiency of GI HR mapping, an effective algorithm for automating the identification of SW ATs was recently developed and validated, termed the “falling-edge variable threshold” (FEVT) method.⁸ Identification of ATs is the first critical step for analyzing HR mapping data, because they are required to generate the spatiotemporal AT (isochronal) maps, as well as to calculate SW frequencies, velocities, and amplitudes. The FEVT method detects ATs at a sensitivity and positive predictive value (PPV) of >90%, offering >100× time savings compared to manual identification.⁸ However, the analysis of GI HR mapping remains laborious, because robust automated methods are still required for clustering the marked ATs into their individual propagation cycles—which must be performed before the AT maps are generated.

This study, therefore, had two aims: (1) to introduce and validate an improved method for partitioning of SW wavefronts; and (2) to introduce and validate automated methods for generating accurate spatiotemporal AT maps using the partitioning result. The successful automation of these combined processing steps would greatly improve the efficiency of GI HR mapping research, therefore, enabling its increased application.

Methods

Experimental Methods, Signal Acquisition, and Filtering

Data for this study were acquired from recent in vivo porcine gastric HR mapping studies.⁷ Details of the ethical approval, and surgical, anesthetic, and recording methods are also described in Egbuji et al.⁷ Briefly, HR gastric mapping was performed using up to six tessellated flexible printed circuit board (PCB) arrays (4 × 8 electrode configuration; inter-electrode distance 7.62 mm)⁵ covering a large area (up to 93 cm²) of gastric tissue. Unipolar recordings were acquired at 512 Hz using the ActiveTwo System (BioSemi, Amsterdam). Signals were preprocessed by applying a second-order digital Butterworth bandpass filter of 0.017–1 Hz (1–60 cpm) in order to minimize baseline wander and high frequency noise.

Flexible PCBs achieve a modestly inferior signal to noise ratio (SNR) compared to the resin-embedded platforms used for GI HR mapping in some studies,^5,15 but are most suitable for human use.^5,17 Therefore, the performance of the FEVT method is somewhat lower when applied to PCB recordings (PPV ≈87%, sensitivity ≈90%),⁸ providing a more rigorous testing scenario for the novel methods described herein.

Selection of Test Case Data

Four data sets (120 s duration) from four porcine subjects were selected for algorithm validation because these segments represented a range of scenarios encountered during porcine HR mapping,⁷ including normal and abnormal propagation. Normally, gastric SWs propagate aborally as a transverse band of activation.⁷ However, periodic abnormal SW behaviors are observed during porcine HR gastric mapping,⁷ such as retrograde propagation, ectopic, and competing pacemakers. Robust analysis methods must correctly identify normal propagation patterns, as well as a range of abnormal ones. For emphasis on potential clinical applicability, three out of four test cases involve abnormal propagation patterns, as described below:

1. Normal corpus propagation: During normal propagation, consecutive wavefronts are often simultaneously detected by a large mapping array.^15,17 A robust cycle partitioning algorithm must correctly determine which ATs belong to the distinct cycles, otherwise AT maps will be highly distorted and misleading. The first test case was from a corpus recordings on the greater curvature (Fig. 3a), featuring simultaneous, consecutive propagating wavefronts.

2. Retrograde propagation: One test case involves retrograde propagation recorded in the upper corpus/distal fundus (Fig. 4a). Robust analysis methods must correctly identify propagation patterns spreading in a direction opposite to that of normal.

3. Ectopic Pacemaker: One test case includes an ectopic pacemaker recorded in the upper corpus/distal fundus (Fig. 5a). Robust analysis methods must correctly identify propagation patterns which enter the recording field at a position that may change between consecutive cycles.

4. Competing Pacemakers/Colliding Wavefronts: One test case includes competing pacemakers; the location of one of these varies over consecutive cycles (Fig. 6b). In general, two respective wavefronts (one from each pacemaker) collide in the central field of the recording array. Subsequently, the wavefronts merge, and continue propagating aborally. Robust analysis methods must correctly identify such relatively complex propagation patterns, including the number and position of pacemakers contributing to an independent cycle. This recording is also taken from the upper corpus/distal fundus (Fig. 6a).

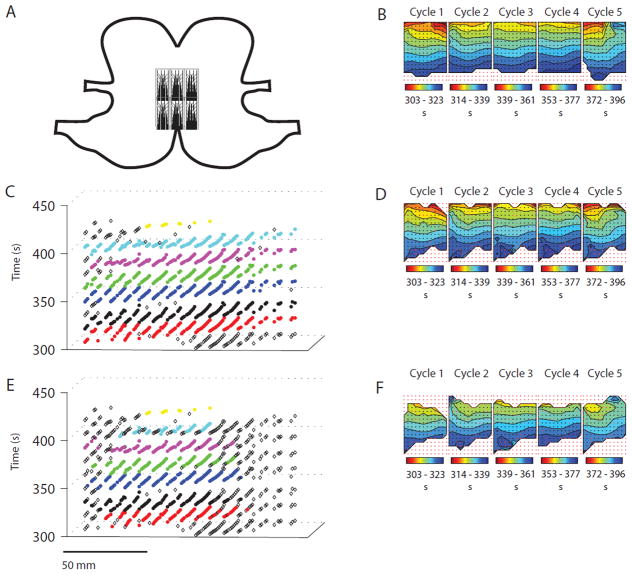
Figure 3.

Cycle partitioning results for Experiment 1: Normal aboral SW propagation. The electrode array is placed on the greater curvature of the lower/distal corpus (a). The REGROUPS AT maps (d) compare well with the corresponding manually generated maps (b), with slight exception in cycle 5 near the top-right array, where the SIV scheme interpolated ATs. The WM algorithm consistently failed to appropriately cluster the active proximal region near the top of the array (e), leading to reduced spatial coverage in the AT maps (f)

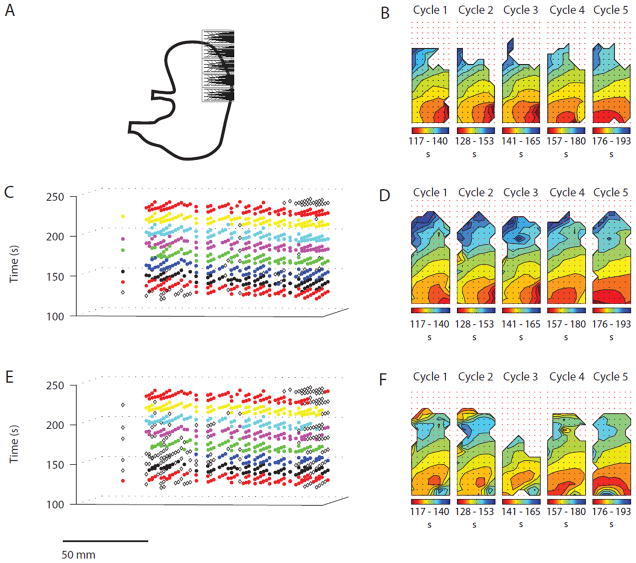
Figure 4.

Cycle partitioning results for Experiment 2: Patchy data quality and ectopic pacemaker. The REGROUPS-derived AT maps (d) show a similar, but slightly larger, extent in spatial coverage relative to the manual maps (b). The WM result (e and f) was comparable in terms of spatial coverage to the manual AT maps for most cycles (1, 2, 4, and 5). WM clustering for cycle 3 terminated prematurely leading to reduced coverage. Isochrones for most cycles (1, 2, 3, and 5) are drawn inaccurately in the proximal and distal regions due to misclustering

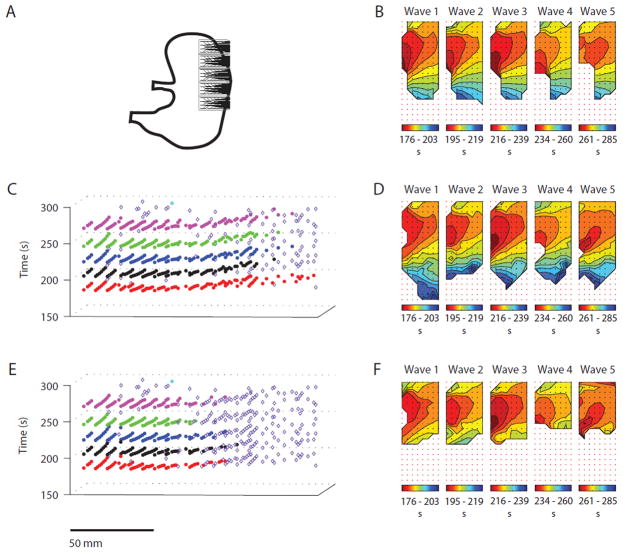
Figure 5.

Cycle partitioning results for Experiment 3: Patchy data quality and ectopic pacemaker. AT maps for all methods indicate the SW propagates radially outward from the pacemaker site. The REGROUPS AT maps (d) exhibit a spatial extent of the SW similar to that indicated in the manual AT maps (b), while WM clustering terminated prematurely (e), substantially reducing the coverage (f)

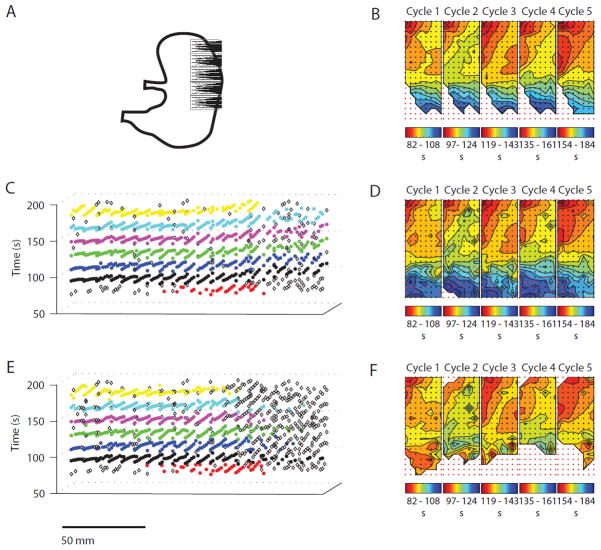
Figure 6.

Cycle partitioning results for Experiment 4: Competing pacemakers/colliding wavefronts. The manual (b) and REGROUPS (d) maps demonstrate highly similar isochrone orientations, with greater spatial coverage in the latter. WM maps (f) also generally show colliding wavefronts. However, map accuracy is reduced due to misclustering (most prominent in cycle 1, bottom and cycle 5, bottom-right), and early termination (d) (most prominent in cycles 3–5)

Importantly, three of these test cases also had patchy data quality, which results from suboptimal or obstructed electrode contact, or due to interfering signals (e.g., respiration artifacts). A robust cycle partitioning algorithm should properly cluster ATs across patchy data gaps, otherwise it may terminate early, generating incomplete and/or faulty AT maps.

Previous Work Motivating the REGROUPS Algorithm

A “wave mapping” (WM) method was previously introduced and applied to partition independent wavefronts in the rat myometrium.¹² Briefly, this method implemented an iterative procedure whereby the AT of a seed electrode T_seed was compared to the ATs at (up to) eight adjacent electrode sites T_k, where ‘k’ indexes the adjacent electrodes. If the difference in ATs between the seed and kth adjacent electrode was small enough, |T_seed – T_k| ≤ Δt_max, then T_k was grouped with T_seed, and T_k (eventually) became the new seed. All ATs that are grouped in this manner were considered to represent ATs from the same cycle. The value of Δt_max was an invariant, chosen by the user prior to commencing the clustering algorithm.

Crucially, the WM approach employed only a single reference AT from the seed electrode to which another AT on an adjacent electrode is compared. Therefore, the accuracy of the WM algorithm was sensitive to the initial state as well as outliers in the marked ATs, making the routine prone to inaccurate results. This lack of robustness may be less problematic when using exclusively manually marked ATs, because outliers can be manually screened, but this is very time-consuming. Moreover, we have found that the WM method is inadequate when applied to a typical FEVT automarked data, because the results typically include a small fraction of false-positives (FPs), where signal noise or artifacts (e.g., respiration) mimicked true events.⁸ We have also found that the WM method is inadequate when applied to data sets with patchy quality: It terminates prematurely, due the lack of information regarding the SW velocity.

We investigated adapting existing cardiac field mapping algorithms for GI data. Rogers et al.^21,22 presented a cardiac wave front isolation method specifically designed to counter the premature wavefront termination problem arising in noisy or sparse data sets. Their algorithm also used an iterative “flood-fill” scheme, and incorporated a spatiotemporal filtering step to join or disconnect multiple wavefronts utilizing an unconnected digraph framework. “Undersized sibling” wavefronts were (potentially) merged according to a set of rules regarding their size and contact times, and assumed valid ventricular propagation patterns. The final set of isolated wavefronts was found to be strongly dependent on the merging threshold parameter.²¹ While this method is well suited for identifying complex cardiac wavefront propagation, we sought to develop a method that avoids as many a priori assumptions as possible regarding valid propagation patterns, and that is relatively insensitive to algorithm parameter values. In addition, because the mechanisms of wavefront propagation are physiologically distinct in the stomach (entrainment) and the heart (a reaction-diffusion phenomenon²⁵), a new wavefront isolation method suited to gastric SW propagation dynamics was sought.

As an alternative approach to existing cardiac or GI wave mapping methods, we developed a data-driven approach with two principles in mind: that it should properly partition (1) FEVT automarked ATs and (2) effectively handle more complex data sets, described above.

Our novel method, “Region Growing Using Polynomial-surface-estimate Stabilization” (REGROUPS), is based on the observation that a propagating gastric wavefront is spatiotemporally smooth—i.e., well described by a second-order polynomial surface.⁶ The REGROUPS method incorporates a continuously updating spatiotemporal filter by updating the coefficients defining the polynomial surface whenever another AT is added to the group of points representing the wavefront. The idea that a second-order surface is suitable for representing the principle features of a propagating gastric wavefront was informed by previous cardiac and GI velocity-field mapping studies.^1,6 Recently, this approach has been applied to graphically present SW velocity fields in several studies.^7,17,18

Description of the REGROUPS Algorithm

The REGROUPS algorithm (Fig. 1) works by clustering (x, y, t) points representing ATs into groups that represent independent SW cycles. Here, (x, y) denotes the position of an electrode site (relative to an arbitrary reference) when the array is laid flat, and t denotes an AT marked at that site. During the experiment, the flexible electrode array is curved to conform 3D geometry of the stomach, but the interelectrode spacing is maintained because the array does not stretch.

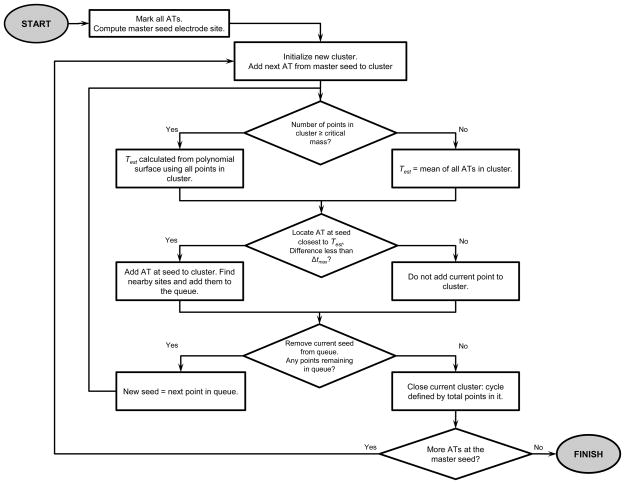
Figure 1.

REGROUPS algorithm flow chart. Each iteration initializes a new cluster starting at the master seed. The algorithm contains two critical decision points: (1) determining the method for estimating the activation time (T_est), and (2) whether the estimated AT at an adjacent site is close enough to the marked (actual) AT. One cluster of (x, y, t) points represents one partitioned cycle. See text for full description of algorithm

REGROUPS employs an iterative “flood fill” or “region growing” procedure similar to that described in Lammers et al.¹² and Rogers et al.²² It is initialized by creating a master list of all marked ATs, and judiciously selecting the master seed electrode site in automated fashion (see “Automated Master Seed Selection” section). Each iteration begins by assigning the next consecutive AT marked at the master seed to the newly initialized cluster, and establishing a queue containing the (x, y) positions of nearby sites. A “nearby” site is defined as falling within a distance $\sqrt{2}{d}_{min}$ of the seed electrode, where d_min denotes the minimum distance between the seed and the closest site containing (at least) one AT. The factor of $\sqrt{2}$ essentially defines a circular search radius (for a square lattice array) to include sites located diagonal to the seed. It is important to note that d_min is not necessarily equal to the inter-electrode spacing (although it often will be), which enables the algorithm to successfully “jump” across areas of patchy data quality.

The first queue entry (electrode site) becomes the current seed, and all ATs at that site, AT(x, y, j) (where j = 1,…, J indexes the marked ATs) are tested for membership. A point (x, y, t) in AT(x, y, j) is assigned membership to the cluster (or not) based on comparison to an estimated AT, T_est. The AT which minimizes the estimate error is assigned membership to the cluster, if the difference is small enough: min_j|AT(x, y, j) – T_est| ≤ Δt_max. Once assigned, membership is never revoked. A point can be assigned membership to (at most) one cluster. Upon assignment, that (x, y, t) point is removed from master list of ATs so that it is never tested again. If the tested point is clustered, its nearby sites are added to the back of the queue, if they are not already in it. If the tested point is not clustered, it may be tested again for membership only after a new cluster has initialized (a new activation time surface is calculated) at the next iteration. Regardless, the current seed is removed from the queue, and the next queue element becomes the current seed. Thus, the region in (x, y, t) space representing an independent cycle grows, terminating when the queue of nearby sites becomes empty. At this stage, the cluster contains all ATs from one SW cycle. The same process is repeated anew to identify another independent cycle, starting back at the master seed. Each iteration produces a cluster of (x, y, t) points, which represent the dynamics of an independent SW cycle. Points which are not assigned membership to any cluster are termed “orphans.”

A critical new step introduced here is to implement a second-order polynomial surface, T(x, y), to act as a continuously updating spatiotemporal filter, where:

$$T(x,y)=p_1{x}^2+p_2{y}^2+p_{3}xy+p_{4}x+p_{5}y+p_6$$ (1)

Using only the (x, y, t) points already in cluster, the vector of coefficients that defines the surface, p = [p₁, p₂, p₃, p₄, p₅, p₆], is computed using a previously described least-squares-fitting procedure¹:

$$\mathbf{p}={({\mathbf{A}}^T\mathbf{A})}^{-1}{\mathbf{A}}^T\mathbf{t}$$ (2)

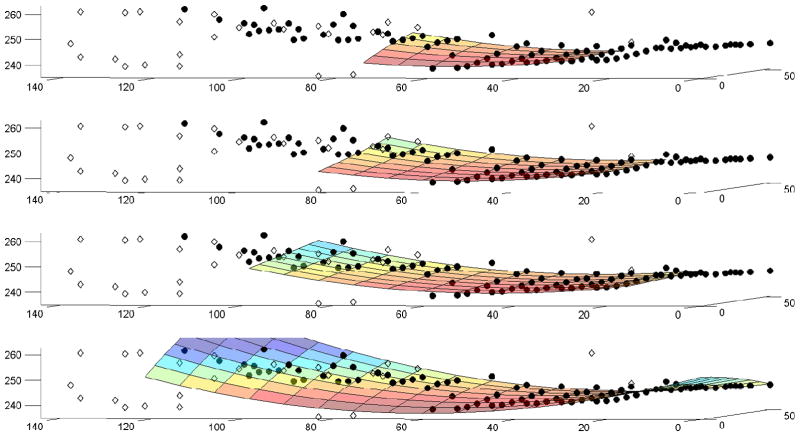
where A is a matrix whose rows are created using the (x, y) electrode positions of points already in the cluster: [x², y², xy, x, y, 1]; and t is a column vector containing the corresponding ATs marked at those electrode sites. Having solved for the vector of coefficients p that defines the polynomial surface in Eq. (1), an estimate of the AT at a nearby site (x_n, y_n) can be obtained by simply extending the surface into that region: T_est = T(x_n, y_n). As illustrated in Fig. 2, the coefficients describing the surface, p, are automatically updated every time another point is added to the cluster. Therefore, the data set at hand determines the form of the polynomial surface, making it substantially more robust and more widely applicable for distinguishing independent cycles in a variety of SW behaviors. It is important to note that at least six points are required to obtain a fully determined system of equations. However, we generally grow the cluster to a “critical mass” of N_crit ≈ 12 points before implementing the second-order surface estimation. Prior to using the polynomial surface estimate, T_est is computed as the mean of the ATs of the points already assigned membership in the cluster.

Figure 2.

The second-order surface T(x, y) updating according to the points already in the cluster. Filled circles represent points which, at the end of clustering, are clustered into the cycle; unfilled diamonds represent points that were rejected during clustering (orphans). The subpanels (top to bottom) show the second-order surface when clustering is approximately 1/4, 1/2, 3/4, and fully complete. Time is represented on the vertical axis (units of s). The (x, y) coordinates represent the electrode site positions (units of mm)

Automated Master Seed Selection

The outcome of clustering/region growing techniques is dependent on the selection of the master seed, particularly when the data quality is patchy (sparse). We automated this selection such that the master seed is chosen to be at an electrode position (x, y)_master which is typically embedded in a region providing the maximal density of information about the propagating wavefront. This approach grows the cluster outward from the region where the spatial density of data is highest, helping to insure that the subset of points initially assigned to the cluster is statistically cohesive, limiting the likelihood of outliers being assigned membership to the nascent cluster. Automated seed selection is a three-step process:

1. For each electrode site, tally N(x, y), the total number of ATs detected at an electrode site location (x, y).

2. Compute the center of mass (CM) (x_CM, y_CM) using the entries of N(x, y):

   $$x_{CM}=\frac{{\sum }_{i}N(x_i,y_i)x_i}{{\sum }_{i}N(x_i,y_i)}$$

   where the sum is taken over all electrode sites, indexed by i. The y-coordinate y_CM is similarly computed.

3. Check if (x_CM, y_CM) corresponds to the coordinates of an electrode with marked ATs. If yes, then the master seed is selected to be the CM. If not, move the master seed to the closest electrode site meeting this condition. In practice, the master seed is usually selected to be at the CM.

Automated Spatial Interpolation and Visualization (SIV) of AT Maps

Pseudo-colored AT (isochrone contour) maps were automatically generated for each cycle identified by REGROUPS. To achieve this, each electrode site’s AT is represented by a colored pixel according to the set of clustered ATs representing one cycle. An electrode site with no AT marked in that cluster is temporarily left blank (white). The FEVT method yields a small fraction of false negatives (missed event detection), depending on the SNR,⁸ and the algorithm should rationally discern which sites are likely blank due to patchy data quality vs. electrode sites that are positioned over quiescent tissue. AT maps should be interpolated for the former, but not the latter.

In our experience, it is atypical to find a small quiescent region of tissue surrounded by active tissue, hence the guiding principle informing the visualization algorithm was that blank electrode sites surrounded by several active (non-blank) sites should be interpolated into the AT map. We therefore developed a 2-stage spatial interpolation and visualization (SIV) scheme that conservatively interpolates AT maps using information from neighboring active sites, according to the following rules (Suppl. Fig. 1A):

1. If a blank site is bordered by ≥3 directly adjacent (including diagonal) active sites, the AT is linearly interpolated from adjacent active sites’ ATs, and correspondingly pseudo-colored (termed an “interpolated site”).

2. If the total number of active plus interpolated sites (from stage 1) bordering a still-blank site is ≥4, then interpolate the still-blank site.

Using this 2-stage scheme, as opposed to a recursive one, prevents a run-away interpolation process from inappropriately filling in blank sites across the entire array. The choice of the parameter values used in the SIV scheme is discussed in “Discussion” section.

Finally, the pixelated AT maps are converted into a smooth, filled contour representation with isochronal lines spaced at 2 s intervals (Suppl. Fig 1B). Two reasons for performing the conversion are: (1) to aid easy visual interpretation—investigators commonly remark that smooth contours are easier to visually process²⁰; and (2) to adhere to the tradition of presenting AT maps as smooth contours.^13,17 No information is lost or gained during the conversion (see Suppl. Fig. 1B). The smooth contour style is used in Figs. 3, 4, 5, and 6 to show the cycles of SW propagation.

Methods of Validation and Comparison

Control and experimental arms were developed to compare completely automated vs. completely manual results, starting from raw data and ending with AT maps. This approach therefore sought to validate the FEVT-REGROUPS-SIV pipeline as a complete package, rather than any of these in isolation, to demonstrate the real-world practicability of the complete system.

Experimental Arm

Activation times were identified via the FEVT method (refer to Erickson et al.⁸ for full details). The REGROUPS and SIV algorithms were applied to each FEVT auto-marked data set to identify the first five consecutive SW cycles. In addition, a modified version of the previous WM method was also applied to each data set for comparison. For a fair comparison, we improved the original version of WM to relax the restriction on testing ATs only at adjacent electrode sites, allowing it to jump over areas of patchy data quality, in the same manner as REGROUPS. The SIV scheme was applied to the result of both the REGROUPS and WM methods to generate isochronal AT maps to directly investigate the effect of the polynomial surface estimation step.

Control Arm

Activation times were manually assessed and marked by a fully blinded investigator. ATs were manually marked at the apparent point of steepest negative slope using Smoothmap v3.05.¹¹ The resulting ATs were then manually partitioned to identify the first five consecutive SW cycles, with resultant isochronal maps being generated in MATLAB. The manually generated maps were considered to be the gold standard for comparison.

Quantitative Comparison

The automated results were quantitatively compared to the manually derived results in terms of AT mapping (1) area of coverage, and (2) isochronal timing accuracy, as follows:

1. Spatial Coverage: The spatial coverage true positive rate (TPR), false-positive rate (FPR), and false-negative rate (FNR) were calculated. The TPR is defined as the number of electrodes sites in common to both manual and automated maps, as a fraction of the total number of sites filled on the automated maps. The FPR rate accounts for the sites which were filled in the automated, but not the manual AT map. The FNR accounts for the sites which were filled in the manual, but not the automated, AT map. These rates were used to compute the sensitivity (Sens.), the positive predictive value (PPV), and the area ratio of coverage (A_roc) performance metrics, as follows:

   $$\text{Sens}.=\frac{\text{TPR}}{\text{TPR}+\text{FNR}}\text{PPV}=\frac{\text{TPR}}{\text{TPR}+\text{FPR}}{\mathrm{A}}_{\text{roc}}=\text{Sens}.\times \text{PPV}$$

   An ideal algorithm achieves a value of 1 for all metrics (range 0–1). Incomplete spatial coverage in the AT maps decreases Sens., whereas inappropriate filling of sites which should be left blank decreases PPV. Tuning an algorithm for increased sensitivity tends to reduce specificity (PPV), and vice-versa. Hence, the A_roc metric gives the single best overall performance measure.

2. Isochronal Timing Accuracy: The coefficients of the second-order polynomial surfaces (i.e., the vector p in Eq. (2)) effectively characterize the spatiotemporal dynamics (velocity) of each SW cycle. To compare the automated vs. manual isochronal timing accuracy, the “coefficient correlation score” (CCS) was computed as the normalized dot product of the first five coefficients, p_1–5 = [p₁,…,p₅], for the surfaces describing a cycle partitioned via the automated and manual methods:

   $$\text{CCS}=\frac{{\mathbf{p}}_{1-5}^{\text{auto}}·{\mathbf{p}}_{1-5}^{\text{manual}}}{\Vert {\mathbf{p}}_{1-5}^{\text{auto}}\Vert \Vert {\mathbf{p}}_{1-5}^{\text{manual}}\Vert }$$ (3)

   The “dc offset” coefficient (p₆) was ignored because it only reflects the bias for manual analysis to consistently mark ATs about 100 ms earlier than the point of true steepest derivative.⁸ The CCS value falls within a range of −1 to 1, with a score of 1 representing perfect agreement between automated and manual methods. Small excursions below a value of 1 (i.e., CCS ≈0.90) typically resulted when all points were clustered properly into SW cycles, but the extent of spatial coverage differed slightly (e.g., Fig. 5d; see Fig. 7 Exp. 3 cycles 1–3). In this case, the interpretation of SW activity represented in the automated AT map is not altered. A larger excursion (i.e., CCS ≤0.80) resulted when (at least) one region of points was misclustered (e.g., Fig. 6f, see Fig. 7 Exp. 4 cycle 1; and Fig. 4f, see Fig. 7 Exp. 2 cycles 1, 2, and 5), which may alter the interpretation of SW activity based on the AT maps. It should be noted that the surface fitting can be very sensitive to cases with erroneously clustered points and/or reduced spatial coverage, in which case the CCS value can be as low as ≈−1 (e.g., Fig. 3f, cycle 5; and Fig. 4f, cycle 2).

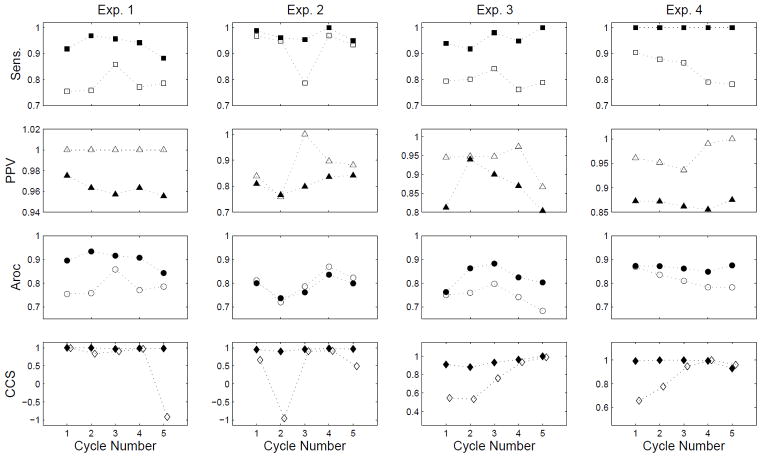
Figure 7.

Quantitative comparison of AT map spatial coverage and isochronal timing accuracy of the REGROUPS and WM methods to manual outcomes. Data points show Sens., PPV, A_roc, and CCS, computed for Δt_max = 5 s (see text for description of these quantities). Outcomes for each of four experimental test case are represented in columns. Filled and unfilled markers indicate the result for the REGROUPS and WM algorithms, respectively. Each series of five points in Experiments (“Exp.”) 1–4 corresponds to each of five partitioned SW cycles shown in Figs. 3, 4, 5, and 6, respectively. The REGROUPS method was observed to achieve more accurate overall spatial coverage (A_roc) and more consistent timing accuracy (CCS) than the WM method across almost all partitioned cycles

Results

Experimental Data Set Results

Activation time mapping outcomes for the manual (control) vs. the FEVT-REGROUPS-SIV and FEVT-WM-SIV methods are presented in Figs. 3, 4, 5, and 6. (For brevity, these acronyms are hereafter shortened to REGROUPS and WM.) All results in Figs. 3, 4, 5, and 6 are presented in the same configuration. Panel a depicts the position of the HR electrode array on the porcine stomach. Panels c and e show the (x, y, t) representation of the cycle partitioning result obtained using the REGROUPS, and WM methods, respectively. Cluster membership is indicated with a distinct color for each cycle. Open diamonds represent marked ATs that were not assigned to any cluster (orphans); they do not contribute to the drawing of AT maps. Panels b, d, and f show the isochronal contour AT maps for the five analyzed manual, REGROUPS and WM cycles, respectively. The slow wave propagates from red to blue. Each solid line (isochrone) demarcates a 2 s time interval. The maps in d and f correspond to the first five full SW events shown in c and e, respectively. All automated results shown in these figures were obtained using a value of Δt_max = 5 s (see “Robustness of REGROUPS Method” section).

In general, Figs. 3, 4, 5, and 6 demonstrate cycle-to-cycle stability obtained with the REGROUPS method, and qualitatively good comparisons between the manual and REGROUPS maps. Slight differences between the automated and manually generated propagation patterns were not judged to significantly alter the interpretations derived from them. Qualitative outcomes for each result are discussed in further detail below, followed by quantitative comparisons.

1. Normal aboral propagation (Fig. 3): The manual and both automated methods generated AT maps showing normal aboral SW propagation. The REGROUPS results (Fig. 3d) showed strong similarity to the manual results (Fig. 3b), with comparable isochronal intervals and orientations, comparable map coverage, and a high consistency between cycles. The WM results (Fig. 3f) demonstrated the same general propagation pattern, with exception of cycle 5, which, lacking information in the proximal field (upper-left corner of the array), less clearly delineates an aboral pattern. The spatial coverage compared less well: WM was primarily limited by incomplete partitioning of the ATs from the proximal field, resulting in more orphans in the proximal region (Fig. 3e) compared to the REGROUPS (Fig. 3c), and therefore reduced AT map coverage.

2. Retrograde Propagation (Fig. 4): The manual and REGROUPS AT maps depict retrograde activity propagating into the fundus. A medial shift in the entry of the wavefront progresses from cycles 1 to 5. The manual maps (Fig. 4b) and REGROUPS maps (Fig. 4d) were highly comparable in terms of isochronal intervals and orientations. Interestingly, however, the REGROUPS consistently demonstrated slightly greater spatial coverage than the manual maps, extending proximally with a physiologically consistent activation pattern, potentially because FEVT may sometimes yield a higher AT detection sensitivity compared to manual marking.⁸ The WM AT maps (Fig. 4f) also illustrate retrograde activity. However, the entry point and propagation direction of the wavefront are confounded due to misclustering of points at the distal edge (bottom-right) of the electrode array for four cycles (1, 2, 4, and 5), and also at the proximal edge for three cycles (1, 2, and 4). The quality of spatial coverage was consistent, though somewhat greater, compared with the manual AT maps, except for cycle 3—a consequence of premature termination of the WM algorithm due to patchy data quality.

3. Ectopic Pacemaker (Fig. 5): All maps demonstrate abnormal propagation from an ectopic pacemaker site near the medial (lesser curvature) porcine fundus. The REGROUPS result (Fig. 5d) showed strong similarity to the manual result (Fig. 5b), with comparable isochronal intervals and orientations. A number of orphans are evident in the distal field (Fig. 5c, right), which may be due to patchy data quality. Importantly, the blinded manual marker also viewed these data as too inconsistent to reliably map, hence spatial coverage of both REGROUPS and manual outcomes was ultimately consistent. A substantially greater proportion of orphans is shown in the WM clustering result (Fig. 5e), because of consistent inappropriate early termination of the algorithm, leading to substantially reduced AT map coverage (Fig. 5f). This outcome is likely due to the relatively high velocity noted near the boundary containing the majority of orphans.

4. Competing Pacemakers/Colliding Wavefronts (Fig. 6): The manual (Fig. 6b) and REGROUPS (Fig. 6d) AT maps demonstrate a high degree of similarity for all cycles. Cycles 1–3 show two wavefronts entering the array from competing pacemakers situated at upper-left and middle-right. These wavefronts collide, then merge into a single wavefront which continues to propagate aborally (bottom of array). The collision boundary generally extends from middle-left to upper-right. Cycle 4 shows this pattern to a lesser extent—the pacemaker at middle-right is less prominent. The manual and REGROUPS maps for cycle 4 also suggest a further ectopic source initiating activity at middle-left, which is more prominent in cycle 5. In a few instances, REGROUPS misclustered a small number of points in isolated fashion (e.g., panel d, cycle 4, sites colored green in an otherwise yellow region at mid- to upper-right), but the effect on interpreting SW activity from these maps is negligible. For all cycles, REGROUPS maps indicated the correct number and location of multiple pacemakers. However, the REGROUPS spatial coverage consistently extends beyond that of the manual maps, likely because FEVT may detect more ATs than manual marking when the SNR is reduced.⁸ In this particular instance, the electrode array at the edge of the field (a five flexible PCB patch) had relatively poor contact, reducing the SNR of the signals, thus rendering the extent of SW propagation in this region ambiguous by manual assessment.

The WM maps (Fig. 6f) also generally demonstrate the same colliding wavefront pattern. However, discrepancies with the manual maps are noted at the bottom of the array, where points are misclustered (most noticeably in cycles 1 and 5), and more orphans exist (cycles 2–5). This result is attributed to poor AT estimation—due to using no velocity information— near the bottom of the collision boundary, where ATs are sparsely marked (Fig. 6e). WM maps, therefore, may erroneously suggest that a third pacemaker exists in the distal field for cycles 1 and 5, and that the colliding wavefronts do not continue to propagate in the aboral direction after merging for cycles 2–5.

Quantitative Analysis: Performance Metrics

Figure 7 shows the performance metrics of the REGROUPS and WM methods compared to the manual outcomes for each of five partitioned cycles in each test case. All results shown are for Δt_max = 5 s, which corresponds to the best overall performance attained by WM averaged across all experiments, in terms of the trade off between spatial coverage and timing accuracy (see Fig. 8 and “Discussion” section). REGROUPS was still found to be superior overall, achieving a higher sensitivity than WM (+13.7%), with a lower PPV (−5.4%). As indicated by the A_roc metric in Fig. 7, the spatial array coverage of REGROUPS was consistently superior (+5.7%) to that of WM. (Results quoted are the median difference, since comparison of outcomes varied widely on a per-cycle basis.) In addition, REGROUPS achieved a higher CCS than WM (+11.6%). Importantly, the CCS metric in Fig. 7 indicates that REGROUPS consistently yielded AT maps very similar to the manually generated result, with CCS ≥ 0.88 for all cycles. By contrast, WM was substantially less consistent, with CCS ≤ 0.66 for 7 of 20 cycles.

Figure 8.

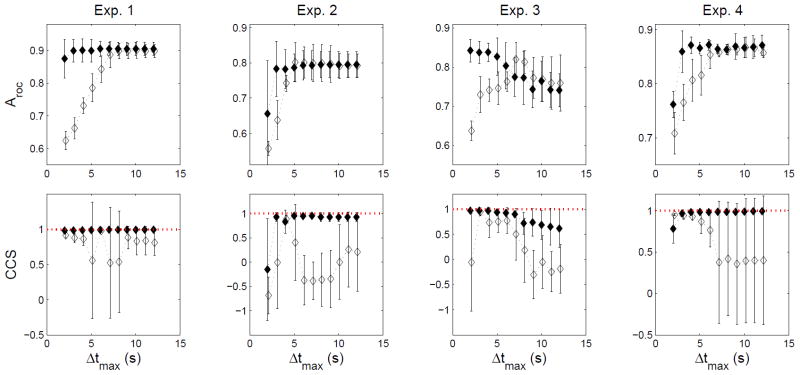
Dependence of spatial array coverage performance metric (A_roc) and isochronal contour accuracy (CCS) on the parameter Δt_max. REGROUPS (solid markers) and WM (unfilled markers) methods are compared to manual outcomes. Each data point with error bars represents the mean ± SD of the performance metric computed across five partitioned cycles for a particular value of Δt_max = 2–12 s, in increments of 1 s. In the bottom row, the dotted red line marks the ideal CCS value of 1. In general, the REGROUPS outcome was observed to be relatively insensitive to Δt_max. By contrast, the WM outcome was observed to be sensitive to this parameter, often unable to achieve both satisfactory array coverage while maintaining accurate isochronal timing accuracy

Taken together, these findings indicate that the REGROUPS polynomial surface stabilization step served to significantly increase the quantity and quality of information contained in the AT maps.

Robustness of REGROUPS Method

The REGROUPS methods make use of two user-selectable parameters: Δt_max and N_crit. The WM method makes use of only the first of these. In order to assess the robustness of these automated methods, we further evaluated their outcomes over a range of Δt_max = 2—12 s, which corresponded to about 1/10—1/2 of a cycle period. Figure 8 shows that the REGROUPS method was observed to be robust to the value of Δt_max, whereas the WM method was not. For each value of Δt_max, the mean and standard deviation of the A_roc and CCS metrics were computed across all five partitioned cycles. The WM outcome depended on the parameter value. The spatial coverage generally increased in a linear fashion for smaller values (≤5 s) of Δt_max, while the isochronal timing accuracy varied significantly depending on Δt_max, generally peaking around Δt_max = 5 s, and failing to attain peak CCS performance for larger values (Fig. 8). By contrast, the REGROUPS performance metrics were found to be highly satisfactory (typically A_roc ≥ 0.8; CCS ≥ 0.9) and essentially invariant when Δt_max ≥ 3 s. One exception was noted in Experiment 3, where A_roc and CCS modestly declined with increasing Δt_max. We attributed this result to larger Δt_max values allowing for inappropriate clustering of some of the FEVT FPs in the distal field (bottom of the array).

The parameter N_crit, which controls when the polynomial surface stabilization is switched on, was also varied. Having examined the automated outcomes for a range of N_crit = 6–36 points (≈5–30% of the total number of electrode sites), we observed that the REGROUPS outcome is essentially invariant to the value of this parameter above, so long as N_crit ≥ 12 points (data not shown). If the critical mass is too small, then the surface was overfit to a small core of points, yielding a poor description of the propagation pattern across the entire electrode array. On the other hand, if the critical mass was too large, then the technique fails to utilize information about the velocity at the wavefront boundary, which is critical for the success of our algorithm.

In summary, REGROUPS was found to be robust to the selection of parameter values over a relatively large range. It is capable of producing accurate AT maps with proper spatial coverage, without the end-user having fine-tune parameter values on a per-experiment basis.

Discussion

This study has presented and validated methods for a major need in the GI high-resolution mapping community—accurate and reliable automated partitioning and visualization of SW ATs into independent propagating wavefront cycles. Importantly, the REGROUPS and SIV methods were demonstrated to perform robustly across a broad range of real-world experimental scenarios, including mapping of normal activity, mapping over regions with quiescent tissue, and mapping retrograde as well as ectopic pacemaker activity. Highly satisfactory performance was obtained across consecutive cycles, even when the spatiotemporal dynamics of the propagation pattern changed one cycle to the next.

The continuously updating second-order polynomial surface estimation step was shown to result in superior robustness of the REGROUPS algorithm, and helped solve the problem of patchy data quality. Continuously updating (a model of) the local velocity yielded good estimates for ATs at both immediately adjacent and more distant electrode sites. Crucially, utilizing a second-order polynomial surface as a spatiotemporal filter made this estimation process insensitive to outliers, helping overcome the problem inherent with noisy and sparse data. Indeed, the result of the fourth test case shows that, for instances when REGROUPS may miscluster a few isolated points, incorporating information from a relatively large number of ATs in the polynomial surface protects against “run-away” misclustering. In practice, this will be highly beneficial, as it is not uncommon for recorded HR data to be somewhat patchy and/or attain a relatively low SNR for some electrode sites, especially when employing the flexible PCB electrodes in the human operating room, when there is often insufficient time to repeat placements of the arrays when contact is not ideal on the first attempt.

Using a low-order model is attractive because it avoids overfitting issues inherent to higher-order models, and it is computationally efficient. In the instances when results obtained using a second-order surface were less than ideal, we investigated whether employing a similar third-order model would be beneficial. However, the third-order outcomes were almost always observed to be worse than those obtained using the second-order surface. The problem with utilizing higher-order surfaces appears to be that the estimated velocity is too large near a boundary of the growing cluster, thus yielding an inaccurate estimate for ATs at nearby sites.

The REGROUPS outcome was found to be robust to the value for Δt_max, within reasonable bounds. Its value should be made generous enough to allow for small (≈10%) AT estimation error, but also generally not exceed more than about 1/2 of a cycle period (<10 s for 3 cpm SWs), so as to adequately filter outliers. If REGROUPS incorrectly regarded a point as an outlier, the SIV scheme often rectified the fault by properly interpolating that site into the AT map. Similarly, an FEVT false-positive mark was often filtered out by REGROUPS. Thus, the FEVT and REGROUPS/SIV methods work synergistically: the new data analysis and visualization pipeline presented here provides a cohesive framework for overcoming the cycle partitioning problems inherent with noisy and sparse data.

By contrast, the WM outcome was observed to be highly sensitive to Δt_max, performing best with this parameter set between 4 and 5 s, but often yielding less than satisfactory results. The fragility is easily understood: the WM method does not incorporate information about the propagating wavefront contained in the spatially varying velocity. Therefore, Δt_max must be set to a relatively large value to properly cluster in regions with a high velocity. Doing so, however, allows outliers (principally FEVT-marked FPs) to enter the cluster. The alternative is to keep Δt_max small to keep outliers out of the cluster, but then points that should have been included in the cluster are too often excluded. The newly introduced polynomial surface estimation step integrated into the REGROUPS algorithm solves this problem.

A potential shortcoming of the REGROUPS algorithm is the method of seed selection. If the spatial density of ATs is bimodal, with ATs marked commonly at either edge of the electrode array, but only sparsely in the middle, then the seed will actually be chosen at a position at which minimal information exists. We have not encountered this situation physiologically. If necessary, future alternative methods would be to choose the seed electrode where N(x, y) is a maximum, or to choose multiple seeds, one for each local maximum in a (smoothed version of) N(x, y).

A potential shortcoming with the SIV scheme is that it may fail to recognize the boundary between active and quiescent regions, causing it to over-zealously interpolate part of a true quiescent zone into an AT map. The values for 3 and 4 adjacent neighbors for SIV stages 1 and 2, respectively, were tuned based on our trial-and-error comparisons with manually generated AT maps. However, increasing these parameter values may lead to incomplete interpolation because only 4–6 active sites typically border the interior of a blank region to be filled in (e.g., see Suppl Fig. 1A, middle of array). This issue could be ameliorated by disallowing interpolation across such a boundary in the direction a suspected quiescent region.

Finally, while we have found the performance of the REGROUPS-SIV method to be robust against variations in several parameters, it is always well advised to consider adjusting these values accordingly to analyze a particular data set, if less than optimal performance is initially achieved.

To date, all published HR maps of SW dysrhythmias have been from animal models with stomachs exhibiting normal or organized abnormal behaviors.^14,18 In the future, during the course of studying the mechanisms of dysrhythmic activities in the human stomach, it may be found that the presented algorithms must be reviewed in light of new clinical evidence. If dysrhythmic activities prove to be highly disorganized (i.e., SW propagation is not smooth), as was recently shown in a study of HR mapping in the canine antrum,¹⁵ then cycle partitioning may prove to be too complex a task for REGROUPS. In this case, alternative visualization approaches may need to be considered—e.g., animated or “activation pattern decomposition” maps of FEVT-detected events.²⁰

The automated mapping pipeline presented here offers major efficiency gains, and we anticipate that it will be widely applied in future GI HR mapping work. Indeed, the FEVT-REGROUPS-SIV combination is already providing reliable analyses for intra-operative human studies of gastric slow wave propagation, in our limited early experience to date. Although the clinical application of HR mapping is limited by its invasiveness, some clinical opportunities to apply it do exist, for example in gastroparesis patients undergoing routine surgeries. In the future, it would be highly desirable to perform a comparative experiment, whereby HR serosal and multichannel cutaneous electrogastrographic (EGG) recordings are made simultaneously. Doing so would help clarify the relation between these two measurement modalities, and allow for comparison of clinically relevant information contained within them.^2,4 We expect that the detailed information about SW propagation gained with HR mapping will help further elucidate the underlying causes and symptoms of normal vs. dysrhythmic gastric function, thus suggesting diagnostic strategies.