Short and long-term energy intake patterns and their implications for human body weight regulation

Abstract

Adults consume millions of kilocalories over the course of a few years, but the typical weight gain amounts to only a few thousand kilocalories of stored energy. Furthermore, food intake is highly variable from day to day and yet body weight is remarkably stable. These facts have been used as evidence to support the hypothesis that human body weight is regulated by active control of food intake operating on both short and long time scales. Here, we demonstrate that active control of human food intake on short time scales is not required for body weight stability and that the current evidence for long term control of food intake is equivocal. To provide more data on this issue, we emphasize the urgent need for developing new methods for accurately measuring energy intake changes over long time scales. We propose that repeated body weight measurements can be used along with mathematical modeling to calculate long-term changes in energy intake and thereby quantify adherence to a diet intervention and provide dynamic feedback to individuals that seek to control their body weight.

1. Introduction

Humans consume food episodically in the form of meals and snacks. In contrast, a continuous supply of energy is required to maintain life and perform physical work. Therefore, even weight-stable humans are practically always in a state of energy imbalance. When we discuss human body weight regulation as a problem of energy balance [1], there is an implicit assumption of time averaging. What is the relevant time scale over which energy is balanced in weight stable people? This basic question has been neglected despite its fundamental role in understanding human body weight regulation.

Here, we explore the question of how short and long-term patterns of energy intake affect body weight using mathematical modeling of human metabolism. We demonstrate the relevant time scale of human energy balance is many months and that body weight is remarkably stable despite large random daily fluctuations in food intake. However, relatively small persistent changes in energy intake can have a substantial effect on body weight over long time scales, although not as large as was previously believed. We show how the sensitivity of body weight to long-term changes in energy intake can be harnessed to provide accurate estimates of changes in free-living energy intake using repeated body weight measurements. Furthermore, such methods allow for monitoring adherence to a lifestyle intervention and the possibility of dynamic model-based feedback control of body weight.

2. Short-term energy intake fluctuations have little effect on body weight

In his classic 1927 metabolism textbook, Eugene Dubois states that “there is no stranger phenomenon than the maintenance of a constant body weight under marked variation in bodily activity and food consumption" [2]. For example, free-living energy intake is known to vary from day to day by 20–30% while body weight fluctuates relatively little [3].

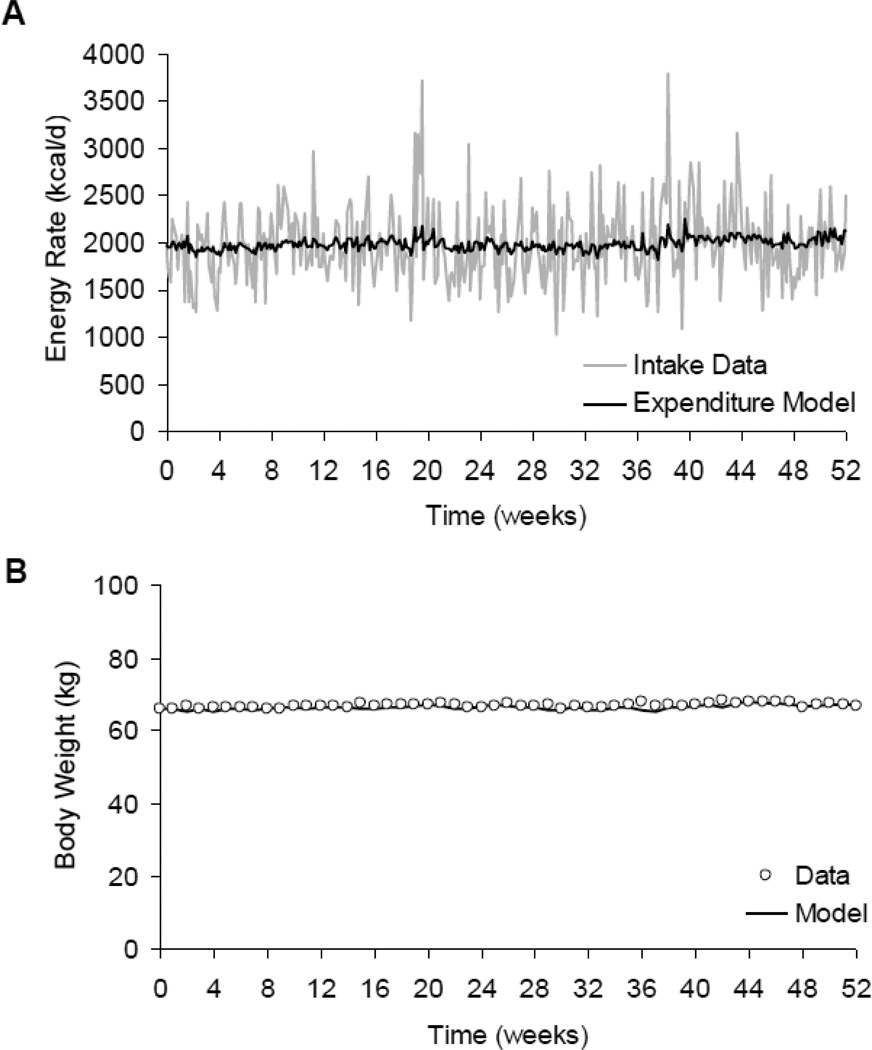
Mathematical models of human energy balance and body weight dynamics have demonstrated that small body weight fluctuations are expected even with relatively large random day-to-day variations of energy intake [4–7]. For example, the gray curve in Figure 1A illustrates the large fluctuations in energy intake of a subject who participated in the Beltsville one year dietary intake study [8]. The black curve in Figure 1A illustrates the estimated energy expenditure in this subject using a computational model of human macronutrient metabolism and body composition dynamics [9]. Despite repeated daily energy imbalances amounting to several hundred kilocalories, Figure 1B shows that the measured and simulated body weight fluctuations were small.

Figure 1.

Large daily fluctuations of energy intake and energy balance lead to little variation of body weight. (A) Daily energy intake data and computer simulated energy expenditure of a participant in the Beltsville one year dietary intake study [8]. (B) Weekly body weight data and computational model simulations illustrating the relative stability of body weight.

In the Appendix, we use a simplified mathematical model of human body weight dynamics to show that the standard deviation of the body weight fluctuations is a decreasing function of a parameter ε representing how energy expenditure varies with body weight. Greater body weight fluctuations are expected when the energy expenditure versus body weight curve is shallower. We previously estimated that the average adult has ε ≈ 22 kcal/kg/d [10] and we show in the Appendix that weight variations on the order of 1 kg correspond to random, uncorrelated, daily energy intake variations on the order of 630 kcal/day. Even for a conceivably low value of ε = 10 kcal/kg/d for an extremely sedentary person, day-to-day food intake variations of ~400 kcal/d are required to result in body weight fluctuations of 1 kg. Therefore, body weight is remarkably stable in the face of random, uncorrelated fluctuations in energy intake.

The reason why body weight fluctuations are small in comparison to variations in energy intake and physical activity is that the slope of the relationship between energy expenditure and body weight causes human weight change to operate on a very slow characteristic time scale. Therefore, the day-to-day fluctuations in food intake are effectively averaged over a long time. By the law of large numbers, the expected standard deviation in the body weight is reduced by a factor proportional to the square root of the averaging time in comparison to the standard deviation of the energy intake. Note that if the energy intake time course exhibits significant autocorrelations, the fluctuations of body weight will become more prominent.

3. Is human energy balance actively regulated through control of food intake?

Weight stability despite large food intake fluctuations might be misinterpreted to imply the existence of a highly sensitive feedback control system whereby each day’s food intake is adjusted to compensate for previous energy imbalances. However, mathematical models demonstrate that active control of food intake is not necessary to explain the stability of body weight in the face of large, uncorrelated, day-to-day energy intake fluctuations. Rather, the long term average energy intake will be stable if fluctuations are uncorrelated such that intake on one day is not significantly influenced by the intake on the day before. In other words, body weight regulation does not require active control of food intake operating on a short time scale.

Another argument for active control of food intake emphasizes the long-term stability of body weight in comparison to the cumulative energy consumed and was articulated by eminent obesity researcher Jeffery Friedman: “The average human consumes one million or more calories per year, yet weight changes very little in most people. These facts lead to the conclusion that energy balance is regulated with a precision of greater than 99.5%” [11]. This example compares the energy content of typical yearly weight gain (about 0.5 kg or 4000 kcal) with the cumulative energy consumed in a year (about 1 million kcal). Unfortunately, this calculation ignores the dynamic adaptations of energy expenditure as body weight is gained that act to counter a persistent increment in energy intake [12]. As has been previously demonstrated [13], without properly accounting for energy expenditure changes, very small persistent increases in energy intake have been erroneously calculated to generate unrealistically huge weight gains over extended time periods. Since such enormous weight gain clearly does not typically occur, this may be mistaken as evidence in support of active control of human energy intake.

When correctly accounting for energy expenditure adaptations, what is the expected long-term weight gain for a persistent change in energy intake? For a person maintaining their average body weight, the long-term mean energy intake equals the long-term mean energy expenditure which is proportional to the body weight. Hence, long-term changes in body weight are related to persistent changes in energy intake by the relation ΔI = εΔW and the new equilibrium weight takes several years to be achieved [12]. Hence, to maintain weight within 1 kg over several years requires that the long-term average energy intake must be accurate to within about ε = 22 kcal/day.

Active control of food intake may be required to limit the long-term drift in energy intake – especially in the face of a dramatic change in the food environment. Is there evidence for such active control of long-term food intake in humans? A decades-long natural experiment provides equivocal evidence. Since the 1970s, U.S. per capita food availability increased by roughly 750 kcal per day whereas average adult increased their energy intake by only about 250 kcal/d over this time period [10]. In other words, the dramatic increase in availability and marketing of highly palatable, convenient, inexpensive, and energy-dense foods may have been actively resisted since only about one third of the increased food available was actually eaten. Thus, these data might be interpreted as evidence that there is active control of human food intake. However, it is unclear exactly how much of an increase in average energy intake would have been expected if there was no active control.

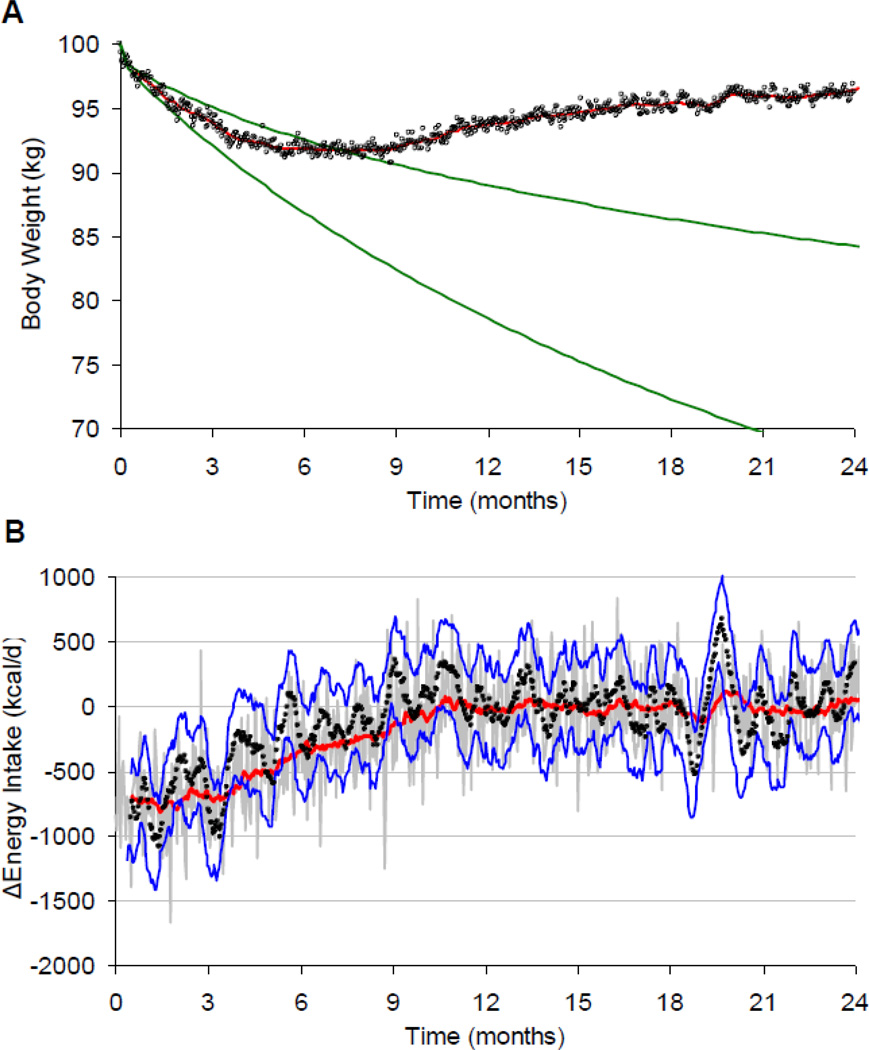
Following periods of experimental overfeeding in humans, ad libitum energy intake generally returns to baseline without an appreciable undershoot as might be expected if food intake were actively controlled [14–17]. However, a substantial degree of hyperphagia was observed following the prolonged period semi-starvation in the Minnesota experiment [18] which may indicate that food intake is actively controlled. Another example that may provide support for the long-term active control of human food intake is that energy intake has been estimated to return to baseline shortly after instituting a diet intervention resulting in weight loss [9, 12] as illustrated in the computational model simulations depicted in Figure 2 where a 100 kg individual was prescribed a reduced calorie diet of 750 kcal/d that was predicted to lead to weight loss falling within the green curves over the subsequent 2 years. This example shown in Figure 2A simulates the ubiquitous weight loss plateau that typically occurs after 6–8 months and the subsequent slow weight regain [19]. Figure 2B illustrates the corresponding energy intake changes (gray curve) and indicates that the weight loss plateau occurred as a result of waning adherence to the prescribed caloric restriction. The red curve in Figure 2B is the 28 day moving average energy intake change showing that at the time of maximum weight loss after 8 months, this simulated individual had an average caloric restriction of only about 250 kcal/d and the average caloric restriction was nil by 10 months. This response might be interpreted as the result of active control of long-term food intake despite intentional caloric restriction. However, it is also possible that food intake is driven primarily by habits that are not subject to active homeostatic control. More data on the long-term response of food intake to environmental perturbations and weight loss interventions are clearly needed. Unfortunately, the largest impediment to collecting such data is the difficulty obtaining accurate and precise measurements of human food intake over extended time periods [20].

Figure 2.

Simulated weight loss plateau and regain as a result of loss of diet adherence. (A) A prescribed 750 kcal/d reduction in baseline energy intake was predicted to result in a body weight trajectory falling within the green curves. However, weight loss typically plateaus after 6–8 months and is often followed by slow regain. (B) The gray curve shows the simulated daily energy intake changes underlying the body weight trajectory. The red curve is the 28 day moving average and the filled black circles and blue curves are the estimated average energy intake and its 95% confidence interval calculated using only the body weight data.

4. Measuring energy intake changes over long time scales

Self-reported measurements of human energy intake (e.g., 24 hour recall, food frequency questionnaire, and diet records) are notoriously inaccurate [21, 22]. New technologies are currently being developed to improve the accuracy of food intake measurements. For example, much progress has been achieved developing remote food photography [23, 24] as well as devices that count bites [25] or measure chewing and swallowing [26]. However, these technologies remain somewhat burdensome for subjects to maintain over the long time periods that are required to investigate the role of energy intake changes in human body weight regulation. An alternative method involves repeated measurements of energy expenditure using the doubly labeled water method along with repeated body composition assessments to measure changes in body energy stores [27]. While this method is theoretically sound and provides accurate measurements of human energy intake over extended time periods, it is prohibitively expensive and involves specialized training and equipment.

It has recently been proposed that validated mathematical models of human body weight dynamics can be used to estimate energy intake changes using repeated body weight measurements [9, 28, 29]. These simple and inexpensive methods for measuring energy intake changes exploit the fact that long-term body weight change is a sensitive predictor of small persistent changes in energy intake. For example, using only the body weight data from Figure 2A, the data points in Figure 2B are the calculated average change in energy intake and the blue curves represent the 95% confidence interval [28]. Thus, repeated measurements of body weight can be translated into the average change in energy intake over extended time periods. Concurrent measurement of physical activity changes (e.g., using accelerometery and/or heart rate monitoring) can also be incorporated in the mathematical model to account for the separate contributions of diet and exercise on body weight change.

5. Adherence monitoring and model-based feedback control of body weight

Given the typically large day to day energy intake fluctuations and the difficulty with accurately self-tracking energy intake, how would an individual know that they are adhering to a target level of caloric restriction during a weight loss program? As illustrated in Figure 2B, repeated body weight measurements can be used to inexpensively estimate average changes in energy intake in near real-time that can be compared to the prescribed diet to monitor diet adherence. In this example, loss of adherence to the prescribed 750 kcal/d diet restriction could have been recognized well before the weight loss plateau.

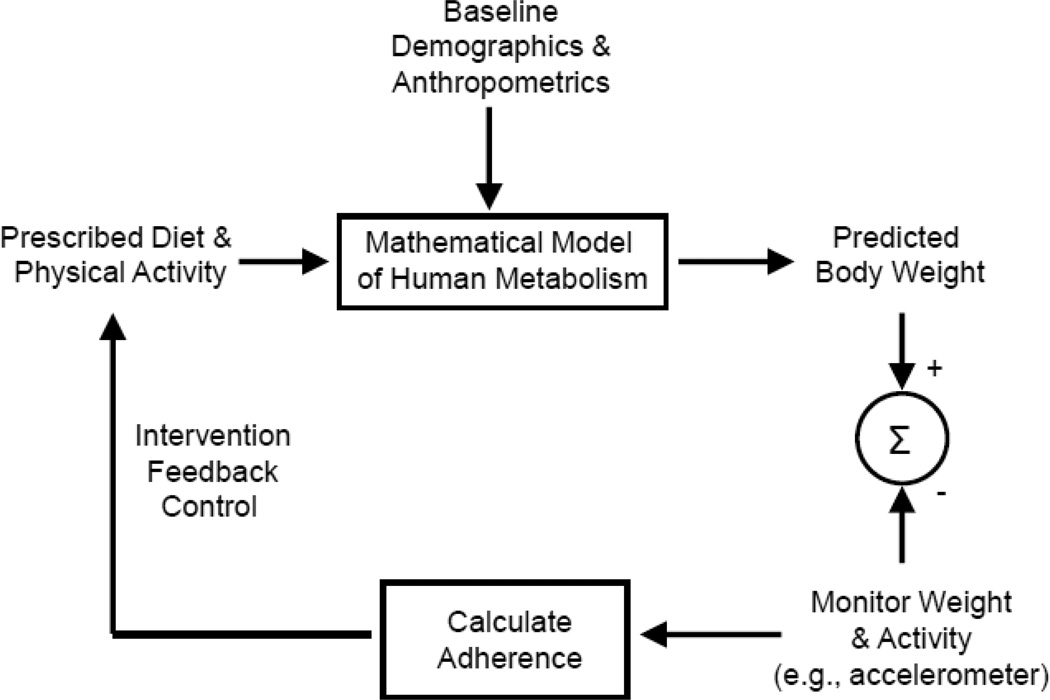
Figure 3 illustrates a schematic of how adherence monitoring using repeated body weight measurements might be used to adjust the weight loss intervention parameters via model-based feedback control to achieve a desired weight loss target [30]. At the outset of the intervention, a personalized mathematical model is generated based on baseline demographics and anthropometrics as well as any direct physiological measurements such as resting energy expenditure, body composition, and physical activity level. Such a personalized mathematical model can be used to calculate the diet and physical activity changes required to achieve and maintain a specified weight loss target [12]. After the weight management intervention is specified and initiated, monitoring body weight (and possibly physical activity) for several weeks can be used to calculate actual change in diet and physical activity. This information can be used to update the mathematical model parameters and generate a prediction of the future body weight trajectory given the calculated level of adherence to the prescribed intervention. The body weight goal can then be modified and/or the intervention parameters can be adjusted to achieve the weight goal. Thus, repeated body weight measurements along with mathematical model simulations results in an iterative adjustment of the body weight goal and prescribed intervention [30].

Figure 3.

Schematic of a method for personalized model-based feedback control of body weight. Using individual anthropometric and demographic data, a personalized mathematical model of metabolism is created to plan a lifestyle intervention to achieve a goal body weight in a specified time frame. By monitoring body weight and physical activity repeatedly, adherence to the intervention can be calculated and used iteratively to provide quantitative feedback regarding revised body weight predictions or changes in the prescribed intervention required to achieve the body weight goal.

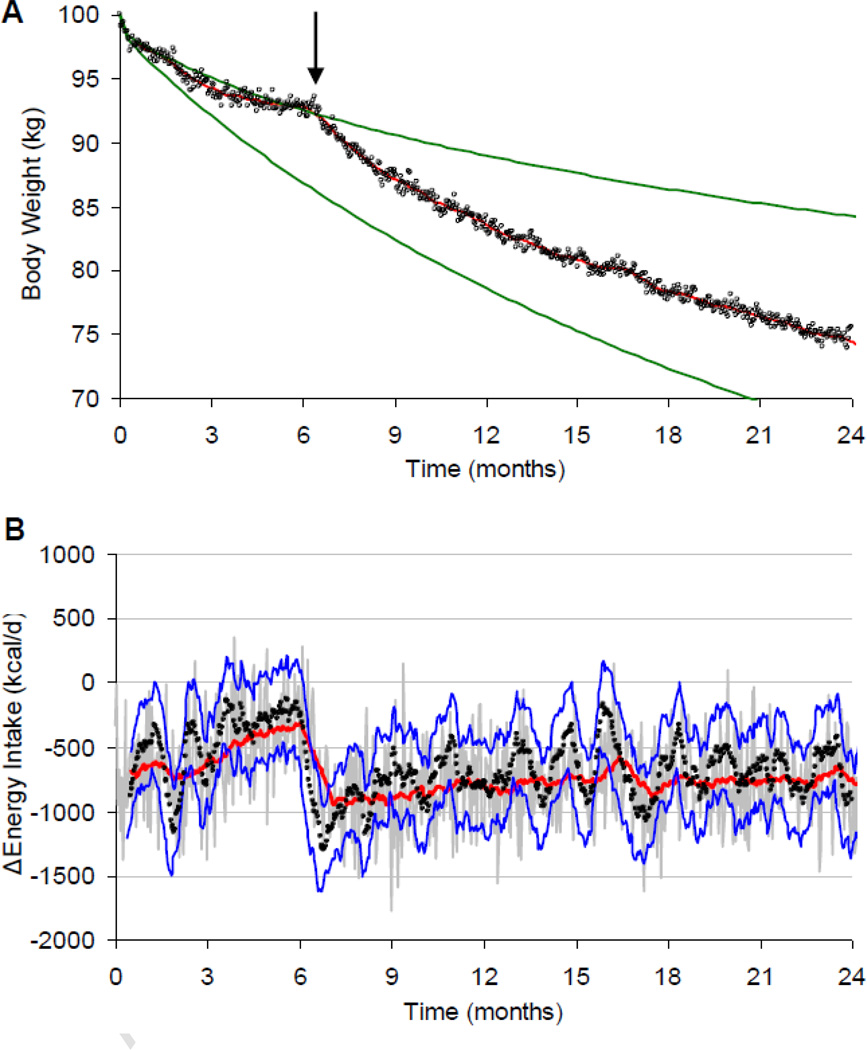
Figure 4 illustrates a hypothetical example where such a model-based feedback control intervention was initiated in the simulated individual shown in Figure 2 beginning at 6 months (arrow). Practical implementation of such a model-based feedback control methodology in real patients could be facilitated using mHealth technologies that allow for frequent remote monitoring of body weight and physical activity along with electronic delivery of feedback messages describing adherence metrics and adjustments to the prescribed intervention. Future research is required to investigate the optimal timing of feedback messages and goal adjustments as well as the overall effectiveness of such a model-based feedback control method of weight management.

Figure 4.

Hypothetical implementation of model-based feedback control of body weight. (A) After weight loss plateaued at 6 months, the control method was implemented to provide feedback on the loss of diet adherence and the revised diet prescription required to achieve the weight loss goal. (B) Continued monitoring of body weight allows for sustained monitoring of adherence to the prescribed intervention.

6. Conclusions

Mathematical modeling of human metabolism and body weight dynamics suggests that the large day to day variations in energy intake are irrelevant for body weight regulation. Rather, persistent changes in energy intake can lead to substantial weight changes over long time scales. Long-term weight gain resulting from a persistent increase in energy intake is not as large as previously supposed and body weight eventually plateaus due to increased energy expenditure and the reestablishment of long term energy balance. Nevertheless, relatively small persistent changes in energy intake will lead to an appreciable increase in the steady state body weight.

More data are required to better understand whether human food intake is under active control or is primarily habitual and follows the changing environment. Unfortunately, it is extraordinarily difficult to directly measure human food intake over extended time periods with accuracy and precision. New devices and technologies are being developed to address these issues [23–26]. Mathematical modeling currently provides the most inexpensive and simplest way to translate repeated measures of body weight into accurate estimates of energy intake changes [28]. These methods will be useful for calculating how energy intake responds following experimental perturbations as well as naturally over the course of time. Furthermore, these new methods have practical implications for weight management interventions since they can be used to monitor adherence to a prescribed lifestyle intervention and provide quantitative dynamic feedback on how to achieve weight goals [30].

Highlights.

• Body weight is relatively stable despite large daily variations in food intake

• Over years, millions of kilocalories are consumed but only thousands are stored

• Mathematical models show that body weight regulation may not require precise control of day-to-day food intake

• We describe promising new methods to monitor diet adherence and control body weight

Appendix

The Energy Balance Equation

We begin our analysis with the energy balance equation where the rate of change in stored body energy is given by the difference between the metabolizable energy intake rate I and the energy expenditure rate. We previously developed and validated a mathematical model of human energy expenditure that included resting metabolic rate, thermic effect of feeding, tissue deposition and turnover costs, and adaptive changes of energy expenditure with over and underfeeding [10, 31, 32]. Using our model of energy expenditure, we demonstrated that the energy balance equation is [10]:

$$\left[\frac{{\eta }_F+{\rho }_F+\alpha {\eta }_L+\alpha {\rho }_L}{(1-\beta )(1+\alpha )}\right]\frac{dW}{dt}=I-\frac{1}{(1-\beta )}[\frac{{\gamma }_F+\alpha {\gamma }_L}{(1+\alpha )}+\delta ]W-b$$

where W is the body weight, I is the energy intake rate, γ_L and γ_F are the regression coefficients relating resting metabolic rate versus lean mass (L) and fat mass (F), respectively [33]. Physical activity energy expenditure is proportional to body weight for most activities [34] and δ represents the level of physical activity. The parameter β accounts for thermic effect of feeding as well as adaptation of energy expenditure during a diet perturbation, η_F and η_L account for the biochemical cost of tissue turnover and deposition [35] assuming that the change of L is primarily accounted for by body protein and its associated water [36]. The parameter α represents the relationship between changes of lean and fat mass: α ≡ dL/dF [37] and b is a constant that defines the steady state body weight.

Assuming that α is approximately constant for modest weight changes [38], we simplify the above equation by introducing parameters ρ and ε to rewrite the above equation as:

$$\rho \frac{dW}{dt}=I-\epsilon W-b$$ (1)

For the average sedentary adult in the US, we have previously estimated that ρ = 9100 kcal/kg and ε = 22 kcal/kg/day [10] and b ~ 600 kcal/d. This simple linear differential equation has an exponential as its solution and the time constant τ = ρ/ε defines the characteristic time scale of weight change. For typical values of the parameters, τ ~ 410 days indicating that body weight changes are very slow.

Fluctuations of Body Weight with Variable Energy Intake

Our goal is to calculate the standard deviation of the body weight as a function of the standard deviation of the food intake. Consider the energy intake rate in equation (1) to be stochastic and written in the form: I = Ī ξ, where Ī is a mean intake rate and ξ is a normally distributed fluctuation with zero mean and standard deviation ${\sigma }_I/\sqrt{dt}$. The convention of stochastic calculus is to scale the standard deviation of the fluctuation by the square root of the time step $\sqrt{dt}$ so σ_I has units of kcal/(square root day). This scaling does not affect the result. Using standard methods of stochastic calculus, the standard deviation of the body weight is given by:

$${\sigma }_w=\frac{o_1}{\sqrt{2\epsilon \rho }}=\frac{{\sigma }_1}{\epsilon \sqrt{2\tau }}$$

Thus for the US population the standard deviation around the average weight is given by the standard deviation of the food intake suppressed by a factor of $\epsilon \sqrt{2t}$ which is equal to 630. In other words, daily variations on the order of 630 kcal/day lead to weight variations on the order of 1 kg. We can also express these quantities in terms of coefficients of variation. The coefficient of variation for weight is related to that of intake by the relation:

$$\frac{{\sigma }_W}{\overline{W}}=\left(\frac{1}{\epsilon \sqrt{2\tau }}\right)\frac{{\sigma }_I}{\overline{W}}=\frac{1}{\sqrt{2\tau }}\left(\frac{\overline{I}}{\overline{I}-b}\right)\frac{{\sigma }_I}{\overline{I}}$$

where we use the formula Ī = εW̄ + b for a person in energy balance. Hence the coefficient of variation in body weight is reduced by a factor of ~20 for the average person with respect to the coefficient of variation of the food intake.

Fluctuations of Body Weight for Variable Physical Activity

If physical activity also fluctuates, equation (1) becomes:

$$\rho \frac{dW}{dt}=I-(\epsilon +a)W-b$$

where a is a normal random variable with zero mean and standard deviation ${\sigma }_a/\sqrt{dt}$. If we assume that there is some correlation c between the intake and activity fluctuations then we can write the full stochastic differential equation as:

$$\rho \frac{dW}{dt}=I-b-\epsilon W+\sqrt{{\sigma }_I^2-2c{\sigma }_I{\sigma }_a+{\sigma }_a{W}^2\zeta }$$

where ζ is a stochastic white noise source. The standard deviation of the body weight can then be calculated to yield:

$${\sigma }_w=\sqrt{(\frac{{\sigma }_I^2}{2\epsilon \rho }+\frac{{\sigma }_a^2{(I-b)}^2}{2{\epsilon }^3{\rho }^3}-\frac{c{\sigma }_I{\sigma }_a(I-b)}{2{\epsilon }^2{\rho }^2})/(1-\frac{{\sigma }_a^2}{2{\epsilon }^3{\rho }^2})}$$

Hence, increased negative correlations between activity and energy intake will increase body weight fluctuations whereas positive correlations will decrease fluctuations. This is expected because energy intake and physical activity have opposing effects on energy balance.

The third moment of the body weight distribution is:

$$\frac{1}{(1-\frac{{\sigma }_a^2}{\epsilon })(1-\frac{{\sigma }_a^2}{2\epsilon })}\lfloor \frac{I^3{\sigma }_a^4}{{\epsilon }^5}+\frac{I{\sigma }_I^2{\sigma }_a^2}{{\epsilon }^3}-\frac{c{\sigma }_I^3{\sigma }_a}{{\epsilon }^2}+\frac{2c^2{\sigma }_I^2{\sigma }_a^2}{{\epsilon }^3}-\frac{3I^{2}c{\sigma }_I{\sigma }_a^3}{{\epsilon }^4}\rfloor$$

Hence, there is positive skewness if physical activity fluctuations are present. However, the extent of the fluctuations can be reduced or possibly reversed if the correlations are negative between physical activity and intake.