Abstract
Purpose
Resent research has suggested that loaded multi-joint movements could reveal a linear force-velocity (F-V) relationship. The aim of the present study was to evaluate the F-V relationship both across different types of vertical jumps and across different F and V variables.
Methods
Ten healthy subjects performed maximum various vertical jumps that were either loaded or unloaded by constant external forces of up to 30% of their body weight. Both the maximum and averaged F and V data were recorded.
Results
The observed F-V relationships proved to be strong (median correlation coefficients ranged .78-.93) and quasi-linear. Their F- and V-intercepts and the calculated maximum power (P) were highly reliable (.85<ICC<.98), while their concurrent validity of with respect to their directly measured values was on average moderate-to-large. The obtained F-V relationships also revealed that (1) the assessment of maximum F and P could be somewhat more reliable and valid than the assessment of maximum V, (2) natural countermovement jumps should be employed rather than the jumps performed from a fixed squat position, while (3) both maximum and averaged F and V variables could be used despite revealing markedly different regression parameters.
Conclusions
The data generally reveal a reliable, valid, strong and quasi-linear F-V relationship across variety of vertical jumps and the recorded F and V variables. Therefore, we conclude that the loaded vertical jumps could be developed into a routine method for testing the force, velocity, and power generating capacity of leg extensors.
Keywords: muscle, power, strength, reliability, validity, linear regression
Introduction
Mechanical properties of muscles have been in research focus due to their importance for understanding both the design and function of human musculo-skeletal system, as well as the effectiveness of various athletic training and rehabilitation interventions aimed to improve physical abilities in various populations [see (Cormie et al. 2011; Frost et al. 2010) for review]. Specifically regarding the high performance and ballistic movements (e.g., jumping, sprinting, and throwing), the research has been particularly focused on the ability of the muscular system to exert a high external force (F) at a high movement velocity (V) and, consequently, to maximize the muscle power output (P).
A non-linear (i.e., approximately hyperbolic) force-velocity (F-V) relationship of both in vitro muscles and isolated muscle groups has been known since the seminal studies of Fenn and Marsh (Fenn and Marsh 1935) and A. V. Hill (Hill 1938). The corresponding power-velocity (P-V) relationship also typically reveals a complex shape with the maximum P observed when muscles act against a moderate external resistance (i.e., F) and, consequently, at intermediate V. The complexity of F-V and P-V relationships severely limited not only the accuracy of their assessment from various functional movements, but also their application in both designing the athletic training and rehabilitation interventions, and various modeling and optimization procedures. However, a number of studies have suggested that a better fit of F-V relationship of various maximum performance multi-joint movements could be a liner one, at least within moderate ranges of F (typically manipulated by varying external loads) and corresponding V. Such results have been obtained from maximum effort squats and vertical jumps [(Vandewalle et al. 1987; Rahmani et al. 2001; Sheppard et al. 2008); see also further text for details], cycling (Driss et al. 2002; Driss and Vandewalle 2013; Nikolaidis 2012), simultaneous leg extensions against various dynamometers and sledge devices (Yamauchi et al. 2009; Samozino et al. 2012, 2014), running (Jaskolska et al. 1999; Morin et al. 2010), or arms and upper body movements (Hintzy et al. 2003; Nikolaidis 2012). Note that F here corresponds to externally measured force, while V is the velocity of the moved center of mass (i.e., body mass and/or external mass). Recent research suggests that the quasi-linear F-V relationship observed from the multi-joint movements could originate from segmental dynamics (Bobbert 2012), rather than from various neural mechanisms (Yamauchi and Ishii 2007).
According to the research cited above, F-V relationship could be obtained from maximum performance multi-joint tasks performed under varying loading conditions that yield a range of recorded F and V. Therefore, the data should be modeled by a linear regression
| (eq.1) |
where F0 is the F-intercept corresponding to the maximum isometric F, and a is the slope that corresponds to F0/V0, (where V0 is V-intercept corresponding to maximum V at zero F). As a result, the P-V relationship calculated from eq. 1 should be of a parabolic shape
| (eq. 2) |
revealing the maximum power output
| (eq. 3) |
Specifically, Pmax is exerted at one half of the maximum velocity (V0/2) achieved when acting against one-half of the maximum external load (F0/2) that muscles can overcome in the tested maximum performance movement (Vandewalle et al. 1987; Samozino et al. 2008; Samozino et al. 2012). The simplicity of the F-V relationship described above could be of apparent importance for both future theoretical research and various practical applications. For example, the relationship could be effectively used in movement modeling and optimization, such as regarding the optimality of the F-V profile to provide the maximum performance jumps (Samozino et al. 2012; Samozino et al. 2013), or for exploring the mechanisms responsible for bilateral deficit (Samozino et al. 2014). Loaded vertical jumps and other multi-joint maximum performance tasks could also provide linear F-V relationships that could enable a comprehensive assessment of the muscular F, V, and P, generating capacity in various populations, as well as the assessment of the effectiveness of various athletic training and rehabilitation interventions (Yamauchi et al. 2009; Nikolaidis 2012; Cormie et al. 2011; Driss and Vandewalle 2013).
Despite the potential importance of the discussed linear F-V model applicable to various multi-joint movements, a number of important problems still remain unresolved. First, we still do not know the reliability of the obtained parameters of the F-V relationship and, consequently, of Pmax. Second, note that the tested functional movements, such as vertical jumps, do not allow for a wide range of loading such as the isokinetically tested simultaneous knee and hip extensions (Yamauchi et al. 2010), and squats (Limonta and Sacchi 2010). As a consequence, the observed parameters such as F0 and V0, as well as the calculated Pmax (see eqs. 1 & 3), are the outcomes of a remote extrapolation of the data observed within relatively narrow F and V ranges. Therefore, the validity of F0, V0, and Pmax for the assessment of functional properties of the tested muscles still remains unknown, while the statements such as that the F-V relationship of leg extensors “can be accurately determined” and utilized for calculation of the optimal balance of F0 and V0 (Samozino et al. 2012) apparently need further support. Furthermore, note that the most of the studies of the F-V relationship have been performed on loaded vertical jumps and other leg extension tests. However, those studies have included various types of vertical jumps comprising of both those performed with [i.e., countermovement jumps; (Limonta and Sacchi 2010; Sheppard et al. 2008)] and without preceding countermovement [squat jumps; (Cormie et al. 2010; Samozino et al. 2012)]. Note also that the arm swing alters both the performance and power output of countermovement jumps (Walsh et al. 2007; Suzovic et al. 2013). However, we still do not know which types of vertical jumps and other simultaneous leg extension tasks could provide the most reliable and valid F-V relationships. The same applies to the type of variables used since both the maximum (Yamauchi et al. 2009; Cormie et al. 2010; Nuzzo et al. 2008; Vandewalle et al. 1987; Sheppard et al. 2008) and average (Rahmani et al. 2001; Samozino et al. 2012) F and V data over a selected movement phase have been used for the assessment of F-V relationships.
The main aim of the present study is to address the unresolved issues regarding the F-V relationship of leg muscles. In order to extend the range of recorded dependent variables, we applied a wide range of external loads that both loaded and unloaded maximum vertical jumps. To provide a more robust set of data, we also tested various types of vertical jumps and recorded both the maximum and averaged values of F and V. Our first aim was to evaluate the pattern, strength and reliability of the F-V relationship of leg extensors. Our second aim was to compare those outcomes both across the different types of vertical jumps and different types of F and V variables. Our third aim was to evaluate the concurrent validity of F0 and Pmax observed from the linear F-V relationships with the directly measured muscle strength and power output. The findings were expected to contribute to our understanding of the mechanical properties and function of the leg extensor muscles, as well as to enable further development and refinement of the methods for routine testing of muscle strength, velocity, and power capacity.
Methods
Participants
We conducted a sample size estimate based on F and V data reported in previous studies (Pazin et al. 2013; Markovic and Jaric 2007b). Based on Cohen's guidelines (Cohen 1988) with an alpha level .05 and power .8, sample sizes 3–12 appeared to be necessary to detect the differences among F, V, and P, observed from the vertical jumps performed under the external loads that ranged between -30% and +30% of body weight (BW). We conservatively recruited 10 healthy and physically active male participants (age 23.4 ± 3.0; body weight 77.3 ± 8.0 kg; body height 182.6 ± 4.2 cm; data shown as mean ± SD). Their body mass index was 23.1 ± 2.5 cm/kg2, while the percent fat was 9.7 ± 2.5 %. Participants' daily physical activity was assessed by a standard IPAQ questionnaire (Taylor-Piliae et al. 2006), where 5 of the participants reported moderate and 5 high levels of physical activity. None of the participants reported any medical problems or recent injuries. They were informed regarding the potential risks associated with the applied testing protocol. All participants gave written informed consent to the experiments, which was in accordance with the Declaration of Helsinki and approved by IRB.
The pulley device and loading conditions
For the purpose of this study, we employed a pulley device that simulates either an increase or decrease in BW (see Figure 1 for illustration). In short, two long rubber bands (resting length 13.5 m, coefficient of elasticity 21 N/m) were extensively stretched to provide the pulling force acting either vertically upward (negative load) or downward (positive load) up to 30 % of the subject's body weight (BW). The bands were attached at the lateral sides of a belt that was fixed approximately at the subject's waist and stretched over a system of low-friction and low-inertia plastic wheels. Therefore, the loading method allowed for unconstrained vertical jumps, while the relative change in their stretched length over the course of the tested jumps was only up 4%, yielding a similar maximum change in the loading force [for detailed description see (Pazin et al. 2011; Leontijevic et al. 2012)].
Figure 1.

Top panel illustrates the loading device providing approximately constant forces pulling downward (positive loading) and upward (negative loading). The middle and lower panels show the time series of the ground-reaction force and velocity of the center of mass obtained from a representative subject under three selected loading conditions of SJ and CMJa. Time series are aligned either with respect to jump initiation (SJ) or the instant of transition from the eccentric to concentric jump phase (CMJa).
The participants were performing jumps on a force plate (AMTI, BP600400; USA) while the pulley system exerted either loading or unloading forces that corresponded to 10%, 20%, 30% of their BW. Since the applied loading mimicked the alteration of the BW, we will refer to the loading magnitudes as 0.7 BW, 0.8 BW, 0.9 BW, 1.0 BW, 1.1 BW, 1.2 BW, and 1.3 BW (1.0 BW corresponding to no load applied). The force platform placed beneath the subjects' feet allowed for an accurate adjustment of the applied loading force.
Experimental protocol
Each participant completed 4 sessions separated by a rest period of 5-7 days. Each session was preceded by a standard warm-up procedure (5 min cycling and 5 min of callisthenic and dynamic stretching). The first testing session included anthropometric measurements, followed by MVC testing, and familiarization with the loaded jumps. The second session included 1RM squat testing, followed by another familiarization with the loaded jumps. The third and fourth session served for the data collection. The participants completed 42 jumps per session (7 loading magnitudes × 3 jump types × 2 trials) that were randomized regarding both the jump type and the loading magnitude. The second trials of the third and fourth session were taken for the calculation of reliability, while the later one served for all remaining analyses.
Experimental procedures
Body mass and height were assessed by a digital scale and a standard anthropometer, respectively. Percent body fat was assessed using a bioelectric impedance method (In Body 720; USA).
Leg extensors' strength was assessed through maximum voluntary contraction of the knee extensors (MVC), and one-repetition maximum squat (1RM squat) performed on a Smith machine. The MVC lasting 4-5 s was recorded under isometric conditions on a Kin-Com isokinetic dynamometer according to manufacturer recommendations (Chatex Corporation, Chattanooga, TN). Knee angle was set at 60 deg of flexion. 1 RM squat testing was performed from a semi-squat position and conducted according to the standard procedure [c.f., (McBride et al. 1999; Markovic and Jaric 2007a)]. It included a series of warm-up trials with a gradual increase in external loads. Concentric contraction was initiated in the level where the knee angle measured 90°. Rest between both MVC trials and series of 1 RM squat trials was set to 2–5 min.
The main part of the testing procedure was conducted on 3 different types of vertical jumps. Regarding the squat jump (SJ), the subjects were instructed to perform it from the static starting position where the knee joint angle was fixed at 90°, while keeping their hands on their hips. Visual inspection of the force signal was used to detect a possible additional counter movement prior to the SJ. When detected, the trials were repeated. Regarding the countermovement jump without arm swing (CMJ), the subjects were instructed to perform an unconstrained maximum vertical jump from a standing upright position that includes the initial counter movement, while keeping their hands on their hips. Regarding the countermovement jump with arm swing (CMJa), the subjects were allowed to use natural arm swing while performing the CMJ.
The rest period between 2 consecutive jumping trials was 20 s and approximately 2 min among different jump types and/or loading magnitudes. In line with both the participants' reports and our recent studies performed according to a similar procedure (Pazin et al. 2013; Markovic and Jaric 2007b; Leontijevic et al. 2012), fatigue was never an issue. Subjects were also instructed to avoid any strenuous exercise over the course of study.
Data processing and analyses
The force plate (AMTI, Inc., Newton MA, USA; sampling frequency 1,000 Hz) was mounted and calibrated according to the manufacturer's specifications. Custom-designed software (LabVIEW, National Instruments, Version 10.0, Austin, TX) was used to record and process the vertical component of the ground reaction force (F). The data were low-pass filtered (a second-order recursive Butterworth filter at a cut-off frequency of 10 Hz) and the time series of the velocity (V) and position of the center of mass were calculated by consecutive integrations of the acceleration signal assessed from F (see Fig. 1 for illustration). Subjects body mass (recorded by the force plate) and F recorded during quiet standing prior to the jump with external load (if applied) were used for that calculation. Thereafter, the maximum and averaged value of F, as well as the maximum and averaged V were calculated from the jumps' concentric phase. The experimentally recorded maximum power output was also assessed as the maximum value of the instantaneous power computed from the product of F and V at each instant.
F-V relationships were assessed from individual F and V variables (separately for their maximum and averaged values) obtained under 7 loading magnitudes. Specifically, both a linear and second-order polynomial regression were calculated for each set of data, together with the corresponding correlation coefficients (r) and their 95% confidence intervals (95% CI). The linear regressions were extrapolated to determine the F- (F0; F at zero V) and V- (V0; the velocity at zero F) intercepts, as well as the regression slopes (a = F0/V0). Finally, the maximum power output was calculated from the linear regression parameters as Pmax = (F0 V0)/4 (see Introduction for details).
Finally, note that squat lifting inevitably includes lifting of both the added load and subject's body mass without shanks (i.e., about 88% of body mass according to standard Dempster's model). Therefore, the outcome of 1RM squat was calculated as their sum (1RM+88%BM).
Statistical analyses
To assess the reliability of the linear regressions obtained from the last two sessions, we calculated the standard error of measurement (SEM), coefficient of variation (CV%), intraclass correlation coefficients (ICC), and the difference (one-group t-test) for F0, V0, a, and Pmax. Pearson's correlations were employed to assess the concurrent validity of F0 and Pmax with respect to the directly recorded strength (i.e., MVC and 1RM squat) and the experimentally recorded maximum power output, respectively. Two-way repeated measures ANOVA were applied on the same variables to assess the differences among the 3 jump types (i.e., SJ vs. CMJ vs. CMJa) and 2 variable types (i.e., maximum vs. averaged F and V variables). The same ANOVA was also applied to the Z-transformed r. The transformation was expected to provide normally distributed data. Eta squared (η2) was calculated for the ANOVAs where the values of the effect sizes 0.01, 0.06 and above 0.14 were considered small, medium, and large, respectively (Cohen 1988). The level of statistical significance was set at P < 0.05.
Results
Figure 1 shows the profiles of ground reaction force (F) and velocity of the center of mass (V) profiles observed from maximum unloading (0.7 BW), no-load (1.0 BW), and maximum loading (1.3 BW) conditions applied to SJ and CMJa of a representative subject. The CMJ is not shown because it typically reveals force profiles similar to CMJa. As expected, an increase in the applied load is associated with a decrease in the maximum jumping velocity and an increase in both the ground reaction force and jump duration.
Pattern and reliability of F-V relationships
Figure 2 shows averaged across the subjects ground reaction forces and velocities of the center of mass, recorded from the tested jumps performed under 7 loading magnitudes. Both the calculated linear (solid lines) and second-order polynomial regression lines (dashed lines) are shown for 3 jump and 2 variable types. All correlation coefficients were significant at the level P < 0.005. Four polynomial regressions were concave and the remaining 2 were convex. Of more importance could be that none of the correlation coefficients of polynomial regressions was above 95% CI of the corresponding linear regressions suggesting no significant differences between them.
Figure 2.
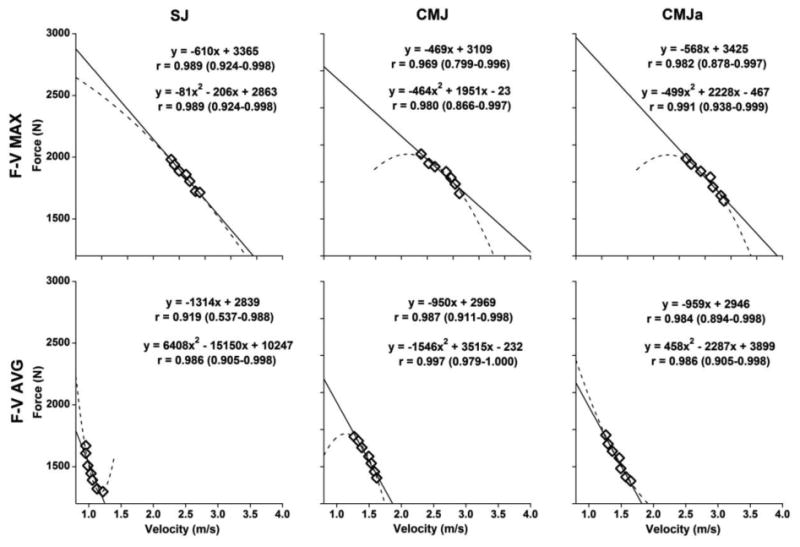
Averaged across the subject ground reaction forces (F) and velocities of the center of body mass (V) that served for the assessment of the F-V relationships. The data were obtained from the concentric phase of the squat jump (SJ; left hand panels), countermovement jump without (CMJ; middle panels) and the with arm swing (CMJa; right hand panels) performed under 7 loading conditions. The upper and lower panels show data obtained from the maximum and averaged F and V values, respectively. The linear (solid line) and second-order polynomial regression models (dashed line) are also shown together with the correlation coefficients and the corresponding 95% CI.
Table 1 shows averaged across the subjects parameters of the linear F-V regressions observed from 2 consecutive sessions. In addition to the differences obtained across the different jump and variable types (see further text for details), of particular importance here are the indices of their reliability. Both the directly assessed parameters of the linear regressions F = F0 - aV (i.e., F0 and a) and the calculated values of V0 (equals F0/a) and Pmax (F0V0/4) revealed high ICC (all above .80) and relatively low CV and SEM. Nevertheless, both F0 and Pmax consistently revealed somewhat higher indices of reliability regarding ICC and CV than the corresponding V0 (p < .05; sign test).
Table 1. Linear regression data obtained from 3 jump types and both maximum and averaged variables, and the corresponding indices of reliability.
| Jump type | Variable type | Variable | Session 3 | Session 4 | CV % | SEM | ICC | t |
|---|---|---|---|---|---|---|---|---|
| SJ | Maximum | F0 | 3293 ± 496 | 3210 ± 450 | 3.6 | 121 | 0.94 (0.83, 0.97) | 1.52 |
| V0 | 5.92 ± 1.52 | 5.90 ± 1.17 | 6.5 | 0.42 | 0.91 (0.75, 0.96) | 0.12 | ||
| a | 582 ± 149 | 562 ± 126 | 9.7 | 53 | 0.86 (0.63, 0.94) | 0.85 | ||
| Pmax | 4847 ± 1322 | 4717 ± 1096 | 4.4 | 254 | 0.96 (0.89, 0.98) | 1.15 | ||
|
| ||||||||
| Average | F0 | 2613 ± 539 | 2519 ± 516 | 5.1 | 127 | 0.95 (0.85, 0.98) | 1.65 | |
| V0 | 2.51 ± 0.51 | 2.60 ± 0.52 | 6.0 | 0.14 | 0.93 (0.8, 0.97) | -1.51 | ||
| a | 1096 ± 371 | 1019 ± 362 | 9.8 | 82 | 0.96 (0.87, 0.98) | 2.12 | ||
| Pmax | 1610 ± 321 | 1610 ± 309 | 5.4 | 86 | 0.93 (0.81, 0.97) | -0.01 | ||
|
| ||||||||
| CMJ | Maximum | F0 | 3116 ± 602 | 3094 ± 617 | 3.5 | 103 | 0.97 (0.93, 0.99) | 0.48 |
| V0 | 7.04 ± 1.48 | 7.05 ± 1.18 | 7.5 | 0.55 | 0.85 (0.59, 0.93) | -0.06 | ||
| a | 475 ± 187 | 464 ± 185 | 11.0 | 43 | 0.95 (0.86, 0.98) | 0.56 | ||
| Pmax | 5340 ± 909 | 5344 ± 881 | 4.4 | 229 | 0.94 (0.83, 0.97) | -0.04 | ||
|
| ||||||||
| Average | F0 | 2962 ± 584 | 2930 ± 621 | 2.7 | 80 | 0.98 (0.95, 0.99) | 0.91 | |
| V0 | 3.27 ± 0.52 | 3.34 ± 0.58 | 3.3 | 0.11 | 0.96 (0.89, 0.98) | -1.31 | ||
| a | 949 ± 339 | 926 ± 344 | 5.7 | 52 | 0.98 (0.94, 0.99) | 1.01 | ||
| Pmax | 2381 ± 435 | 2395 ± 465 | 2.4 | 59 | 0.98 (0.96, 0.99) | -0.53 | ||
|
| ||||||||
| CMJa | Maximum | F0 | 3407 ± 883 | 3412 ± 891 | 3.7 | 149 | 0.97 (0.93, 0.99) | -0.07 |
| V0 | 6.77 ± 1.95 | 6.74 ± 1.76 | 7.5 | 0.59 | 0.91 (0.74, 0.96) | 0.09 | ||
| a | 560 ± 258 | 554 ± 234 | 10.6 | 57 | 0.95 (0.86, 0.98) | 0.24 | ||
| Pmax | 5500 ± 1092 | 5501 ± 1020 | 5.5 | 300 | 0.93 (0.8, 0.97) | -0.01 | ||
|
| ||||||||
| Average | F0 | 2859 ± 563 | 2857 ± 671 | 3.0 | 84 | 0.98 (0.95, 0.99) | 0.04 | |
| V0 | 3.27 ± 0.57 | 3.26 ± 0.40 | 5.6 | 0.2 | 0.85 (0.59, 0.93) | 0.08 | ||
| a | 906 ± 273 | 903 ± 299 | 7.3 | 52 | 0.97 (0.91, 0.99) | 0.09 | ||
| Pmax | 2319 ± 530 | 2296 ± 467 | 5.4 | 132 | 0.94 (0.82, 0.97) | 0.38 | ||
SJ - squat jump; CMJ - countermovement jump without arm swing; CMJa - countermovement jump with arm swing; F0 - force intercept; V0 - velocity intercept; a - slope; Pmax - maximum power; CV% - coefficient of variation; SEM - standard error of measurement; ICC - intraclass correlation coefficient shown with the corresponding 95% CI; t - t-value
Differences across the jumps and variables
Figure 3 shows the median correlation coefficients and their ranges obtained from the linear F-V regressions. Repeated measures 2-way ANOVA applied on their Z-transformed values showed neither the significant effect of the jump type (F(2,8)=1.6, η2 = 0.06, P = 0.27), nor of the variable type (F(1,9)=1.31, η2 = 0.03, P = 0.47). However, their interaction was significant (F(2,8)=10.3, η2 = 0.17, P < 0.01) due to a significant difference between the correlation coefficients obtained from the maximum and averaged variables observed in SJ, but not in CMJ and CMJa.
Figure 3.
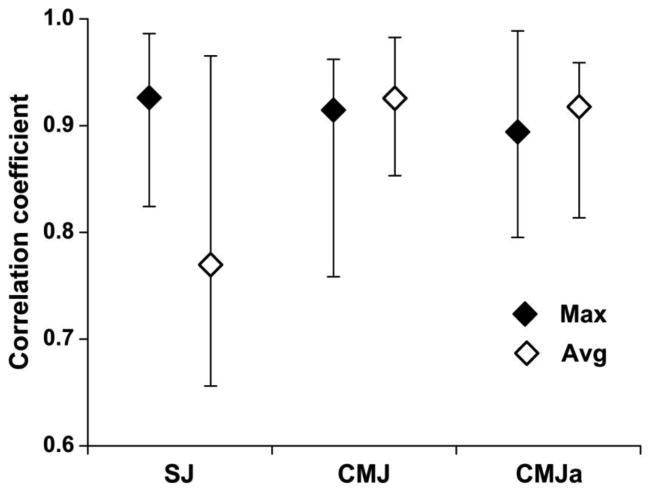
Median correlations (error bars depict their ranges) of the linear F-V regressions observed from 3 jumps and the maximum and averaged F and V variables.
Figure 4 shows averaged across the subjects data calculated from the individual linear regressions. Two-way repeated measures ANOVA were applied to assess the main effects of jump and variable types. The F-intercept (F0; Figure 4a) revealed no main effect of jump type (F(2,8)=0.63; η2 = 0.03, P = 0.53), while the main effect variable type (F(1,9)=64.9; η2 = 0.33, P < 0.01) and their interaction (F(2,8)=6.8; η2 = 0.08, P = 0.019) were significant. In particular, the differences between the variables were significant for the SJ and CMJa, but not for CMJ. The V-intercept (V0; Figure 4b) revealed the main effect of jump type (F(2,8)=4.6, η2 = 0.04, P = 0.046) and variable type (F(1,9)=121.9, η2 = 0.76, P < 0.01), but not their interaction (F(2,8)=0.44; η2 = 0.01, P = 0.66). V0 was higher for CMJ and CMJa than for SJ. Regarding the regression slopes (a; Figure 4c), data revealed a significant main effect of variable type (F(1,9)=109.9, η2 = 0.59, P < 0.01), but not the main effect of jump type (F(2,8)=0.82, η2 = 0.04, P = 0.48) and the interactions (F(2,8)=2.6; η2 = 0.02, P = 0.13) were significant. Finally, the maximum power output (Pmax; Figure 4d) revealed significant main effects of the jump type (F(2,8)=16.9, η2 = 0.04, P < 0.01) and variable type (F(1,9)=202.8, η2 = 0.89, P < 0.01), but not their interaction (F(2,8)=2.16; η2 = 0.01, P = 0.18). Pmax was higher for both CMJ and CMJa than for SJ. Note that all 4 sets of data revealed higher values for the maximum than for averaged variables. Note also that V0 revealed more than a twofold difference between the regressions obtained from maximum and averaged variables, while the same difference in F0 was relatively small, albeit significant. Therefore, the prominent differences in both a and Pmax obtained through linear regressions calculated from the maximum and averaged F and V variables mainly originated from the differences in V0 rather than the differences in F0.
Figure 4.
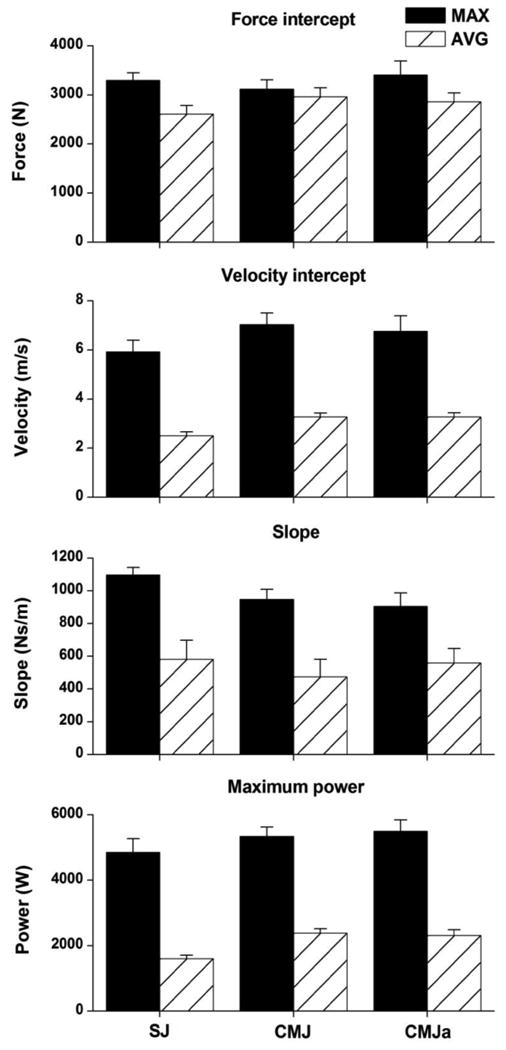
Results obtained from linear F-V regressions calculated for 3 jump and 2 variable types (maximum and averaged; data averaged across the subjects with SE error bars). The individual data sets show force intercepts (F0; panel a), velocity intercepts (V0; panel b), regression slopes (a = F0/V0; panel c), and maximum power output (Pmax = (F0 V0)/4; panel d).
Concurrent validity
Regarding the directly recorded strength and power, MVC reveled 821 ± 110 N, 1RM squat calculated as 1RM+88%BM revealed 192.2 ± 38.6 kg, while the maximum value of the instantaneous power revealed 3922 ± 790 W, 3839 ± 677 W, and 4429 ± 1009 W in SJ, CMJ, and CMJa, respectively. Figure 5 shows the concurrent validity of F0 and Pmax assessed through the linear F-V regressions with respect to the directly recorded strength and power. On average, F0 revealed moderate-to-large correlations with both the MVC and 1RM squat. The relationships for SJ were significant, but the same applies only to one correlation obtained from other jump types. Regarding the differences between the jump and variable types, only the correlation between F0 (observed from averaged variables) and 1RM obtained from SJ was above the 95% CI of the same value obtained from CMJ. However, all relationships between Pmax and the experimentally recorded maximum P output appeared to be exceptionally high and significant. Their comparison revealed the value obtained from the averaged F and V variables of CMJ to be above 95% CI for all 5 remaining correlation coefficients.
Figure 5.
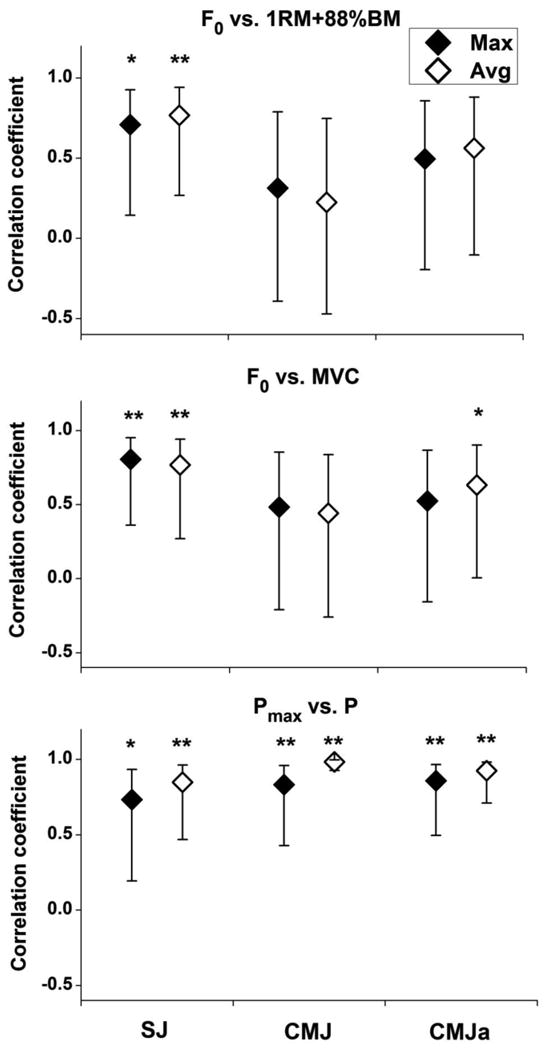
Concurrent validity of F0 and P0 obtained from linear F-V regressions assessed through their Pearson's correlations with the directly tested strength (1RM+88%BM and MVC) and power. Correlation coefficients (medians with the corresponding 95% CI) are shown for 3 jump and 2 variable types (* p<0.05; ** p<0.01; N=10).
Discussion
Within the present study we applied a range of positive and negative external loads to obtain the F-V relationships (i.e., the relationship between the ground reaction force and the velocity of the center of mass) of leg muscles from various maximum vertical jumps. Regarding the first aim of the study, we found the F-V relationships to be both remarkably strong and fairly linear, while the indices of reliability were exceptionally high. Regarding the second aim, the strength of the linear F-V relationship appeared to be somewhat weaker for SJ than for CMJ and CMJa, while the same jump also suggested a lower Pmax mainly due to a lower V0, rather than lower F0. The studied F-V and the related P-V relationships also revealed a markedly lower a and higher Pmax, respectfully, when calculated from the maximum F and V variables. Again, these differences mainly originated from a higher V0 rather than from a higher F0. Regarding the third aim, data revealed a high concurrent validity of Pmax, while the same validity of F0 on average appeared to be considerably lower, albeit partly significant.
Pattern and reliability of F-V relationships
The results revealed both exceptionally strong and fairly linear F-V relationships across both the jump and variable types. None of the correlation coefficients obtained from the polynomial regressions were significantly above the corresponding values obtained from the linear regressions. These results are in line with the findings observed from various tasks based on leg extensions without preceding counter movement when only positive loads were applied (Yamauchi et al. 2009; Samozino et al. 2012). Moreover, the same studies revealed values of the obtained strength, velocity, and power (i.e., F0, V0 and Pmax), similar to the values observed from SJ tested in the present study. Therefore, it appears that the addition of the negative loads may not considerably alter the pattern of F-V relationship observed from the positive loads alone. A particularly novel finding of the present study is a high reliability of the observed F-V regression parameters. Collectively, the discussed findings encourage further research aimed to develop a routine test of leg extensors based on the linear F-V relationship obtained from loaded vertical jumps (Samozino et al. 2008; Samozino et al. 2013).
When different jumps are compared, the data suggest a future use of CMJ and CMJa could provide stronger F-V relationships than SJ, particularly when calculated from the averaged F and V variables. Furthermore, although the reliability of the F-V relationships could be comparable across both different jumps and variable types, assessments of F0 and Pmax could be more reliable that the assessment V0. Not surprisingly, Pmax was higher in CMJ and CMJa than in SJ (Suzovic et al. 2013; Pazin et al. 2013). Regarding the comparison of F-V relationships obtained from maximum and averaged F and V variables, note that the instants of maximum F and V apparently do not coincide (see Fig. 1 for illustration), as well as that their values are highly sensitive to jumping technique (Markovic et al. 2013; Markovic et al. 2014; Samozino et al. 2008; Samozino et al. 2012). Nevertheless, both the strength of the F-V relationships and the indices of reliability of their parameters appear to be comparable to those obtained from the averaged F and V values. Note also that when compared with the averaged ones, the maximum values of F and V provide only a moderately higher F0, but approximately twice as high values of V0 and, consequently, of a and Pmax. Overall, the discussed findings suggest that future research of F-V properties of leg extensors should use the natural vertical jumps that are simpler to perform (i.e., CMJ and CMJa), rather than squat jumps. In addition, both the maximum and averaged F and V data could be used to obtain the F-V relationships, while their parameters should be used for the assessment of the muscle strength, power, and velocity properties of the tested muscles. Finally, note that despite the previously observed effects of arm swing (Walsh et al. 2007; Suzovic et al. 2013), we were not able to detect significant differences in the F-V relationship parameters observed from CMJ and CMJa.
Concurrent validity
Regarding the concurrent validity of the regression parameters, Pmax revealed exceptionally high correlations with the experimentally recorded maximum P output, while the concurrent validity of F0 with respect to the experimentally tested strength was on average moderate-to-high. However, note that F0 is not only an outcome of a distant extrapolation of the experimentally recorded F and V data, but also compared with 1RM squat that was obtained from concentric (albeit slow) dynamic conditions. Moreover, it corresponds to muscle isometric strength that typically reveals either moderate or low correlations with maximum movement performance (Nuzzo et al. 2008; Jaric et al. 1989; Jaric 2002). Moreover, MVC reflects the mechanical output of the quadriceps muscle only, while 1RM was obtained from a concentric (albeit slow), but not isometric contraction. Therefore, one should not expect high concurrent validity of F0 and V0 although most of literature considers both MVC and 1RM as standard muscle strength tests. Conversely, Pmax was calculated from the F-V regression in a close proximity of the experimentally recorded F and V values, which could explain the high concurrent validity of Pmax. The high validity of Pmax could be additionally stressed by the findings suggesting that the maximum muscle power output normalized for body size observed from unloaded jumps could closely correspond to the maximum jumping performance (Markovic et al. 2014; Markovic and Jaric 2007a).
Limitations and future directions
Several limitations of the present study should be both acknowledged and taken into consideration when planning for future research. First, although we applied both the positive and negative loading to increase the total loading range, the range still remained rather limited with respect to the values of F- and V-intercepts (i.e., F0 and V0) obtained from the applied linear regression. From this perspective, the custom designed dynamometers (Yamauchi et al. 2009; Samozino et al. 2012) and bench press throws (Leontijevic et al. 2013) could have an apparent advantage, despite lacking the ecological validity of vertical jumps. Second, to shorten the testing procedure and avoid possible fatigue our subjects performed only 2 trials per condition and always the second one was taken for further analysis. Therefore, it remains possible that a more typical protocol that includes a higher number of trials and select the best one for analysis would provide even higher reliability and concurrent validity than we observed. Third, note that we only applied a constant loading force that mimics added weight, but not inertia, which could have markedly different effects on the force and power output in both vertical jumps and bench press throws (Leontijevic et al. 2012; Leontijevic et al. 2013). Fourth, we could not control for the possible effect the depth of countermovement that has been shown to affect both F and P of loaded vertical jumps (Samozino et al. 2012; Markovic et al. 2013). Here we can only speculate that the differences in countermovement depth could have affected the observed differences in F0 and Pmax among different jump types.
Regarding the practical application of the present findings, future studies could focus on the development of methods that could be applied in routine testing of force, power and velocity production of leg muscles. Such a test could be based on a brief series on loaded maximum CMJ, where only a force platform and a simple loading system (e.g., weight bar, loaded west, Smith machine) would be needed. For example, a part of the methods already developed for SJ (Samozino et al. 2008; Samozino et al. 2013) could be adapted to CMJ. Nevertheless, a number of methodological details should also be dealt with, such as the possible confounding effect of the patterns of vertical jumps and other multi-joint tasks on the observed F-V relation, ranges of loads applied etc. Finally, future studies also need to explore the sensitivity of the assessments of F, V, and P, generating capacity based on the linear F-V relationship in detecting both the effectiveness of training and rehabilitation interventions, as well as the differences among various populations.
Conclusions
To conclude, the findings observed from the given range of the recorded F and V suggest that the obtained F-V relationships of leg extensors could be exceptionally strong, fairly linear, highly reliable, and of a moderate-to-high validity. Those findings appeared to be generally consistent across different types of loaded vertical jumps, as well as for both the maximum and averaged F and V variables. Nevertheless, the data also suggests that the assessment of F0 and Pmax could be somewhat more reliable and valid than the assessment of V0, while the more natural and easier to perform CMJ should be the jump type of choice for the assessment of F-V relationship rather than SJ. Taken together, the data suggests that the loaded vertical jumps could be developed into a routine method for testing the force, velocity and power generating capacity of leg extensors.
Acknowledgments
The study was supported in part by NIH grant (R21AR06065) and a grant from the Serbian Research Council (#175037).
List of abbreviations
- 1RM squat
one repetition maximum squat
- a
slope of F-V regression
- BW
body weight
- CMJ
countermovement jump without arm swing
- CMJa
countermovement jump with arm swing
- CV
coefficient of variation
- F
ground reaction force
- F0
maximum ground reaction force (i.e., F-intercept of F-V regression)
- ICC
intraclass correlation coefficient
- MVC
tested isometric maximum voluntary force of quad muscle
- P
power output
- Pmax
maximum power output calculated from F-V regression
- SEM
standard error of measurement
- SJ
squat jump
- V
velocity of center of mass
- V0
maximum velocity of center of mass (i.e., V-intercept of F-V regression)
References
- Bobbert MF. Why is the force-velocity relationship in leg press tasks quasi-linear rather than hyperbolic? J Appl Physiol. 2012;112(12):1975–1983. doi: 10.1152/japplphysiol.00787.2011. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd. Lawrence Erlbaum Associates; Hillsdale, NJ: 1988. [Google Scholar]
- Cormie P, McGuigan MR, Newton RU. Adaptations in athletic performance after ballistic power versus strength training. Med Sci Sports Exerc. 2010;42(8):1582–1598. doi: 10.1249/MSS.0b013e3181d2013a. [DOI] [PubMed] [Google Scholar]
- Cormie P, McGuigan MR, Newton RU. Developing maximal neuromuscular power: part 2 - training considerations for improving maximal power production. Sports Med. 2011;41(2):125–146. doi: 10.2165/11538500-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Driss T, Vandewalle H. The measurement of maximal (anaerobic) power output on a cycle ergometer: a critical review. Biomed Res Int. 2013;2013:589361. doi: 10.1155/2013/589361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driss T, Vandewalle H, Le Chevalier JM, Monod H. Force-velocity relationship on a cycle ergometer and knee-extensor strength indices. Can J Appl Physiol. 2002;27(3):250–262. doi: 10.1139/h02-015. [DOI] [PubMed] [Google Scholar]
- Fenn WO, Marsh BS. Muscular force at different speeds of shortening. J Physiol. 1935;85:277–297. doi: 10.1113/jphysiol.1935.sp003318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frost DM, Cronin J, Newton RU. A biomechanical evaluation of resistance: fundamental concepts for training and sports performance. Sports Med. 2010;40(4):303–326. doi: 10.2165/11319420-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Hill AV. The Heat of Shortening and the Dynamic Constants of Muscle. Proc R Soc Med (Lond) 1938;126(843):136–195. [Google Scholar]
- Hintzy F, Tordi N, Predine E, Rouillon JD, Belli A. Force-velocity characteristics of upper limb extension during maximal wheelchair sprinting performed by healthy able-bodied females. J Sports Sci. 2003;21(11):921–926. doi: 10.1080/0264041031000140392. [DOI] [PubMed] [Google Scholar]
- Jaric S. Muscle strength testing: use of normalisation for body size. Sports Med. 2002;32(10):615–631. doi: 10.2165/00007256-200232100-00002. [DOI] [PubMed] [Google Scholar]
- Jaric S, Ristanovic D, Corcos DM. The relationship between muscle kinetic parameters and kinematic variables in a complex movement. Eur J Appl Physiol Occup Physiol. 1989;59(5):370–376. doi: 10.1007/BF02389813. [DOI] [PubMed] [Google Scholar]
- Jaskolska A, Goossens P, Veenstra B, Jaskolski A, Skinner JS. Comparison of treadmill and cycle ergometer measurements of force-velocity relationships and power output. Int J Sports Med. 1999;20(3):192–197. [PubMed] [Google Scholar]
- Leontijevic B, Pazin N, Bozic PR, Kukolj M, Ugarkovic D, Jaric S. Effects of loading on maximum vertical jumps: Selective effects of weight and inertia. J Electromyogr Kines. 2012;22(2):286–293. doi: 10.1016/j.jelekin.2011.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontijevic B, Pazin N, Kukolj M, Ugarkovic D, Jaric S. Selective effects of weight and inertia on maximum lifting. Int J Sports Med. 2013;34(3):232–238. doi: 10.1055/s-0032-1312606. [DOI] [PubMed] [Google Scholar]
- Limonta E, Sacchi M. Morphological analysis of force/velocity relationship in dynamic exercise at varying loads. J Strength Cond Res. 2010;24(8):2065–2072. doi: 10.1519/JSC.0b013e3181db23ac. [DOI] [PubMed] [Google Scholar]
- Markovic G, Jaric S. Is vertical jump height a body size-independent measure of muscle power? J Sports Sci. 2007a;25(12):1355–1363. doi: 10.1080/02640410601021713. [DOI] [PubMed] [Google Scholar]
- Markovic G, Jaric S. Positive and negative loading and mechanical output in maximum vertical jumping. Med Sci Sports Exerc. 2007b;39(10):1757–1764. doi: 10.1249/mss.0b013e31811ece35. [DOI] [PubMed] [Google Scholar]
- Markovic S, Mirkov DM, Knezevic OM, Jaric S. Jump training with different loads: effects on jumping performance and power output. Eur J Appl Physiol. 2013;113(10):2511–2521. doi: 10.1007/s00421-013-2688-6. [DOI] [PubMed] [Google Scholar]
- Markovic S, Mirkov DM, Nedeljkovic A, Jaric S. Body size and countermovement depth confound relationship between muscle power output and jumping performance. Mum Mov Sci. 2014 doi: 10.1016/j.humov.2013.11.004. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McBride JM, Triplett-McBride T, Davie A, Newton RU. A comparison of strength and power characteristics between power lifter, olympic lifters, and sprinters. J Strength Cond Res. 1999;13(1):58–66. [Google Scholar]
- Morin JB, Samozino P, Bonnefoy R, Edouard P, Belli A. Direct measurement of power during one single sprint on treadmill. J Biomech. 2010;43(10):1970–1975. doi: 10.1016/j.jbiomech.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Nikolaidis PT. Age- and sex-related differences in force-velocity characteristics of upper and lower limbs of competitive adolescent swimmers. J Hum Kinet. 2012;32:87–95. doi: 10.2478/v10078-012-0026-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzzo JL, McBride JM, Cormie P, McCaulley GO. Relationship between countermovement jump performance and multijoint isometric and dynamic tests of strength. J Strength Cond Res. 2008;22(3):699–707. doi: 10.1519/JSC.0b013e31816d5eda. [DOI] [PubMed] [Google Scholar]
- Pazin N, Berjan B, Nedeljkovic A, Markovic G, Jaric S. Power output in vertical jumps: does optimum loading depend on activity profiles? Eur J Appl Physiol. 2013;113(3):577–589. doi: 10.1007/s00421-012-2464-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pazin N, Bozic P, Bobana B, Nedeljkovic A, Jaric S. Optimum loading for maximizing muscle power output: the effect of training history. Eur J Appl Physiol. 2011;111(9):2123–2130. doi: 10.1007/s00421-011-1840-4. [DOI] [PubMed] [Google Scholar]
- Rahmani A, Viale F, Dalleau G, Lacour JR. Force/velocity and power/velocity relationships in squat exercise. Eur J Appl Physiol. 2001;84(3):227–232. doi: 10.1007/PL00007956. [DOI] [PubMed] [Google Scholar]
- Samozino P, Edouard P, Sangnier S, Brughelli M, Gimenez P, Morin JB. Force-Velocity Profile: Imbalance Determination and Effect on Lower Limb Ballistic Performance. International journal of sports medicine. 2013 doi: 10.1055/s-0033-1354382. [DOI] [PubMed] [Google Scholar]
- Samozino P, Morin JB, Hintzy F, Belli A. A simple method for measuring force, velocity and power output during squat jump. J Biomech. 2008;41(14):2940–2945. doi: 10.1016/j.jbiomech.2008.07.028. [DOI] [PubMed] [Google Scholar]
- Samozino P, Rejc E, Di Prampero PE, Belli A, Morin JB. Optimal force-velocity profile in ballistic movements--altius: citius or fortius? Med Sci Sports Exerc. 2012;44(2):313–322. doi: 10.1249/MSS.0b013e31822d757a. [DOI] [PubMed] [Google Scholar]
- Samozino P, Rejc E, di Prampero PE, Belli A, Morin JB. Force-Velocity Properties' Contribution to Bilateral Deficit during Ballistic Push-off. Med Sci Sports Exerc. 2014;46(1):107–114. doi: 10.1249/MSS.0b013e3182a124fb. [DOI] [PubMed] [Google Scholar]
- Sheppard JM, Cormack S, Taylor KL, McGuigan MR, Newton RU. Assessing the force-velocity characteristics of the leg extensors in well-trained athletes: the incremental load power profile. J Strength Cond Res. 2008;22(4):1320–1326. doi: 10.1519/JSC.0b013e31816d671b. [DOI] [PubMed] [Google Scholar]
- Suzovic D, Markovic G, Pasic M, Jaric S. Optimum load in various vertical jumps support the maximum dynamic output hypothesis. Int J Sports Med. 2013;34(11):1007–1014. doi: 10.1055/s-0033-1337942. [DOI] [PubMed] [Google Scholar]
- Taylor-Piliae RE, Norton LC, Haskell WL, Mahbouda MH, Fair JM, Iribarren C, Hlatky MA, Go AS, Fortmann SP. Validation of a new brief physical activity survey among men and women aged 60-69 years. Am J Epidemiol. 2006;164(6):598–606. doi: 10.1093/aje/kwj248. [DOI] [PubMed] [Google Scholar]
- Vandewalle H, Peres G, Heller J, Panel J, Monod H. Force-velocity relationship and maximal power on a cycle ergometer. Correlation with the height of a vertical jump. Eur J Appl Physiol Occup Physiol. 1987;56(6):650–656. doi: 10.1007/BF00424805. [DOI] [PubMed] [Google Scholar]
- Walsh MS, Bohm H, Butterfield MM, Santhosam J. Gender bias in the effects of arms and countermovement on jumping performance. J Strength Cond Res. 2007;21(2):362–366. doi: 10.1519/R-19825.1. [DOI] [PubMed] [Google Scholar]
- Yamauchi J, Ishii N. Relations between force-velocity characteristics of the knee-hip extension movement and vertical jump performance. J Strength Cond Res. 2007;21(3):703–709. doi: 10.1519/R-20516.1. [DOI] [PubMed] [Google Scholar]
- Yamauchi J, Mishima C, Nakayama S, Ishii N. Force-velocity, force-power relationships of bilateral and unilateral leg multi-joint movements in young and elderly women. J Biomech. 2009;42(13):2151–2157. doi: 10.1016/j.jbiomech.2009.05.032. [DOI] [PubMed] [Google Scholar]
- Yamauchi J, Mishima C, Nakayama S, Ishii N. Aging-related differences in maximum force, unloaded velocity and power of human leg multi-joint movement. Gerontology. 2010;56(2):167–174. doi: 10.1159/000235814. [DOI] [PubMed] [Google Scholar]


