Insights into affinity and specificity in the complexes of α-lytic protease and its inhibitor proteins: binding free energy from molecular dynamics simulation

Abstract

We report the binding free energy calculation and its decomposition for the complexes of α-lytic protease and its protein inhibitors using molecular dynamics simulation. Standard mechanism serine protease inhibitors eglin C and OMTKY3 are known to have strong binding affinity for many serine proteases. Their binding loops have significant similarities, including a common P1 Leu as the main anchor in the binding interface. However, recent experiments demonstrate that the two inhibitors have vastly different affinity towards α-lytic protease (ALP), a bacterial serine protease. OMTKY3 inhibits the enzyme much more weakly (by ~10⁶ times) than eglin C. Moreover, a variant of OMTKY3 with five mutations, OMTKY3M, has been shown to inhibit 10⁴ times more strongly than the wild-type inhibitor. The underlying mechanisms for the unusually large difference in binding affinities and the effect of mutation are not well understood. Here we use molecular dynamics simulation with molecular mechanics–Poisson Boltzmann/surface area method (MM-PB/SA) to investigate quantitatively the binding specificity. The calculated absolute binding free energies correctly differentiate the thermodynamic stabilities of these protein complexes, but the magnitudes of the binding affinities are systematically overestimated. Analysis of the binding free energy components provides insights into the molecular mechanism of binding specificity. The large ΔΔG_bind between eglin C and wild type OMTKY3 towards ALP is mainly attributable to the stronger nonpolar interactions in the ALP-eglin C complex, arising from a higher degree of structural complementarity. Here the electrostatic interaction contributes to a lesser extent. The enhanced inhibition in the penta-mutant OMTKY3M over its wild type is entirely due to an overall improvement in the solvent-mediated electrostatic interactions in the ALP-OMTKY3M complex. The results suggest that for these protein-complexes and similar enzyme-inhibitor systems (1) the binding is driven by nonpolar interactions, opposed by overall electrostatic and solute entropy contributions; (2) binding specificity can be tuned by improving the complementarity in electrostatics between two associating proteins. Binding free energy decomposition into contributions from individual protein residues provides additional detailed information on the structural determinants and subtle conformational changes responsible for the binding specificity.

1. Introduction

The reversible, specific binding of proteins is an essential element in many biological processes. Understanding how proteins interact with each other to form stable complexes is therefore a necessary step in understanding many cellular processes such as signal transduction, antigen-antibody recognition, and the regulation of gene expression.^1,2 A molecular insight into the specificity in protein–protein binding is also useful for the design of potent and specific small molecule protease inhibitors with therapeutic value.³ In this work, we study the molecular mechanism of the binding of α-lytic protease to serine protease inhibitors.

Eglin C and Turkey Ovomucoid Third Domain (OMTKY3) are standard mechanism serine protease inhibitors.⁴ When the two inhibitors are bound to serine protease bovine chymotrypsin, their binding loops are embedded in the enzyme’s active site cleft with almost identical backbone conformations. The binding loop regions in the two inhibitors have several identical or similar residues in their primary contact regions, including a common P1 Leu residue which acts as the main anchor in the binding interface and docks into the primary specificity S1 pocket in the active site. Eglin C and OMTKY3 are potent inhibitors towards many serine proteases, with binding equilibrium constants K_a > 10⁸ M⁻¹.

Despite their similarities, a recent study⁵ by Qasim et al. reported that eglin C and OMTKY3 show vastly different inhibition towards bacterial serine protease α-lytic protease (ALP), with K_a values of 1.2 × 10⁹ M⁻¹ and 1.8 × 10³ M⁻¹, respectively. α-Lytic protease is an extracellular serine protease from soil bacterium Lysobacter enzymogenes. It adopts the same 3-D fold as the chymotrypsin family serine proteases.⁶ Although eglin C is a stronger inhibitor than OMTKY3 for several serine proteases, the 10⁶ -fold difference between the K_a values towards α-lytic protease is the largest among all serine proteases that are known to bind the two inhibitors.⁵ To understand the exceptionally large difference, Qasim et al. performed mutations on OMTKY3. Based on mutation data, they designed a penta-mutant of OMTKY3 variant (K13A-P14E-L18A-R21T-N36D, denoted as OMTKY3M) which has a K_a of 1.1 × 10⁷ M⁻¹, an increase of nearly 10⁴ fold in affinity, relative to the wild type. Qasim et al. also performed computational protein docking using the ZDOCK/RDOCK program ^7,8 to obtain structural models for the complexes and compared the desolvation energies calculated by the ZDOCK/RDOCK scoring function for the docked complexes.

Despite the binding and structural information gained from these studies, the molecular mechanism for the unusually large difference in binding affinity and the underlying causes for the greatly enhanced affinity in OMTKY3M are not well understood. Key elements in binding such as the role of electrostatics, van der Waals interactions and relative importance of specific residues remain unknown. From theoretical point of view, understanding the molecular detail of binding requires quantitative information on both free energy components and structural determinants in molecular association.² While the protein docking program ZDOCK/RDOCK program is highly successful in predicting the structures of protein complexes, its energy function is relatively simple and thus not suitable for calculating binding free energy, which requires a more detailed energy function and extensive conformational sampling. Binding free energy calculation is the focus of the current study.

The calculation of free energy of binding is based on the statistical mechanics of macromolecules in solution.⁹ In principle, absolute binding free energy can be computed using the double-decoupling method (DDM) or the potential of mean force (PMF) method. In DDM, interaction between a ligand and its environment is reversibly turned off in the complex and in solution using two series of simulations. In PMF, the physical process of reversible binding/unbinding is simulated using umbrella potentials.¹⁰ Since all the intermediate states along transformation paths need to be adequately sampled, both DDM and PMF are computationally expensive, and their applications are currently limited to the binding of proteins with small molecules. For protein–protein complexes, the molecular mechanics Poisson–Boltzmann surface area method (MM-PB/SA) offers a computationally practical approach to binding free energy.^11,12 This method only considers two end points in a binding reaction, i.e. the bound and unbound states, and the binging free energy is obtained as the difference of the free energies of the two. Thus the method has significantly lower computational cost compared to free energy simulation methods DDM and PMF. However, one disadvantage of MM-PB/SA is that the small binding free energy is obtained as the difference of two large numbers. In MM-PB/SA, free energy consists of gas-phase molecular mechanics energy, solvation free energy and solute entropy, averaged over snapshots from molecular dynamics trajectory for a solute molecule in explicit solvent. The solvation free energy contains electrostatic and nonpolar components. The electrostatic contribution to the solvation free energy is calculated by solving Poisson–Boltzmann equation (PB), and the nonpolar contribution is described by solvent accessible surface area. Calculation can be speed up by using Generalized Born (GB) models¹³ instead of solving the Poisson–Boltzmann equation in estimating the electrostatic solvation free energy. The formulation of MM-PB(GB)/SA allows the binding free energy to be readily decomposed into group contributions from individual protein residues.^14,15 This can provide insights into the role of specific residues in binding and is useful for a molecular interpretation of the mutation effects.

The approximate free energy formula of MM-PB/SA (i.e. a combination of gas-phase energy and continuum solvent model) are sometimes applied to energy minimized crystal structures instead of configurations extracted from MD trajectory to calculate binding free energy. Noskov et al. developed such a method to obtain accurate estimates of binding free energies for antibody-antigen and protease-inhibitor complexes.¹⁶ Replacing long MD simulations with energy minimization reduces the computational time enormously, as the sampling is usually the slowest phase in MM-PB/SA. However, due to the sensitivity of energy components to small conformational variation, especially the PB(GB) component, it is advantageous to average the energy components over many configurations to obtain statistically significant results.

In principle, the ensemble averages of free energy components should be calculated using snapshots extracted from separate trajectories of protein complex and unbound proteins in solution. In practice however, the single trajectory approach, in which the configurations of protein complex and unbound proteins are both taken from the same trajectory of the protein complex, is often found to yield better results.^15,17 Despite having the disadvantage of neglecting the protein reorganization upon binding, the single trajectory method has an important advantage of error cancellation which is lacking in the separate trajectory approach: In MM-PB/SA, the property of interest is the free energy difference between bound and unbound states; the noise associated with conformational fluctuations from atoms far away from the binding site cancel out in the single trajectory approach when the difference in energy is taken; such noise cancellation will not be complete in the separate trajectory approach due to the limited sampling of the conformational space in nanoseconds MD simulations.

The MM-PB(GB)/SA method has been widely used in studies of biomolecular association in aqueous solutions.^{10–12,14–20} In the area of protein–protein interaction, this method was first developed by Kollman and coworkers et al. to estimate the relative free energies of HIV-1 protease dimers.¹⁸ Their study showed that MM/PBSA can differentiate stabilities of different HIV-1 protease dimers, even though the magnitude of the calculated binding free energies are overestimated. The authors have also developed a method of computational alanine scanning to probe the effect of mutation on stability.¹⁸ More recently, Gohlke et al. reported a detailed methodological study of different MM-PB(GB)/SA protocols and applied the MM-GB/SA to examine the Ras–Raf and Ras–RalGDS complexes.^14,19 They also estimated the contribution of individual protein residues to the binding free energy in a non-perturbing way, and showed that the results of such calculations correlate well with the results from experimental alanine scanning mutagenesis.¹⁴ Although the calculated absolute free energies in their study are in the correct range, the experimental ranking order is not reproduced. It is possibly related to the structural noise associated with the separate trajectory approach used in the study. In a recent MM-GB/SA study on the insulin dimerization, Zoete et al. compared single trajectory and separate trajectories approaches, and found that the single trajectory approach yields more accurate estimates of binding free energy.¹⁵ The authors also performed per-residue binding free energy decomposition and accurately identified residues that are most important to binding. Zoete et al. also applied the MM-GB/SA and binding free energy decomposition to study the binding of the T-cell receptor with peptide-MHC Complex.²⁰

It should be mentioned that continuum electrostatics treatment based on the PB/GB models is not the only practical method for calculating solvent mediated electrostatic interactions in molecular association. In an early study of protein–protein binding, Warshel and coworkers applied the Protein Dipoles Langevin Dipoles (PDLD) method to investigate the electrostatics contributions to the interaction between Rap1A (Rap) and the Ras binding domain of c-Raf (Raf-RBD).²¹ Using appropriate thermodynamic cycles, their study addressed both absolute binding energy and the effects of mutations. The accuracy of this method appears to be sensitive to the choices of dielectric constant of the protein interior ε_in, and very large value of ε_in (e.g. 25) is found to be necessary in reproducing relative binding energy due to mutations.

In the current study, we use MM-PB/SA method to quantitatively address the unusually large difference in the inhibition between eglin C and OMTKY3 towards ALP, and the mutation effect in OMTKY3M. We compare the calculated binding free energies with experiments, and analyze the different free energy contributions in determining affinity and specificity. To probe roles of individual amino acid residues in determining binding specificity, we calculated the per-residue contributions of binding free energy and analyzed the results in the context of structural information of the protein complexes gained from MD simulations. A molecular picture for the binding of ALP with the three serine protease inhibitors emerges from this computational study.

2. Results and discussion

Structures of enzyme-inhibitor complexes

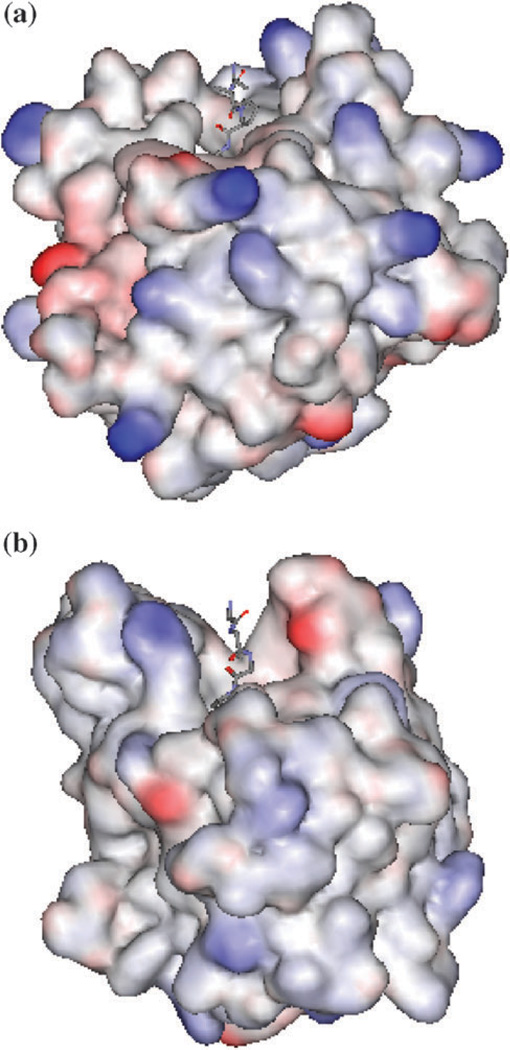
The schematic covalent structures of eglin C and OMTKY3 are shown in Fig. 1. In the absence of experimental structures of the protein complexes, the structural models generated by the computational protein docking program ZDOCK/RDOCK are used as the starting conformations for MD simulations.⁵ The computationally predicted structures of the ALP-eglin C and ALP-OMTKY3 complexes are shown in Fig. 2 and Fig. 3, in ribbon and solvent accessible surface representation, respectively. As expected, the binding loop of the inhibitor protein is inserted into reactive site cavity. The structure of ALP-OMTKY3M is not shown, as in these representations it is almost identical to the structure containing the wild type OMTKY3.

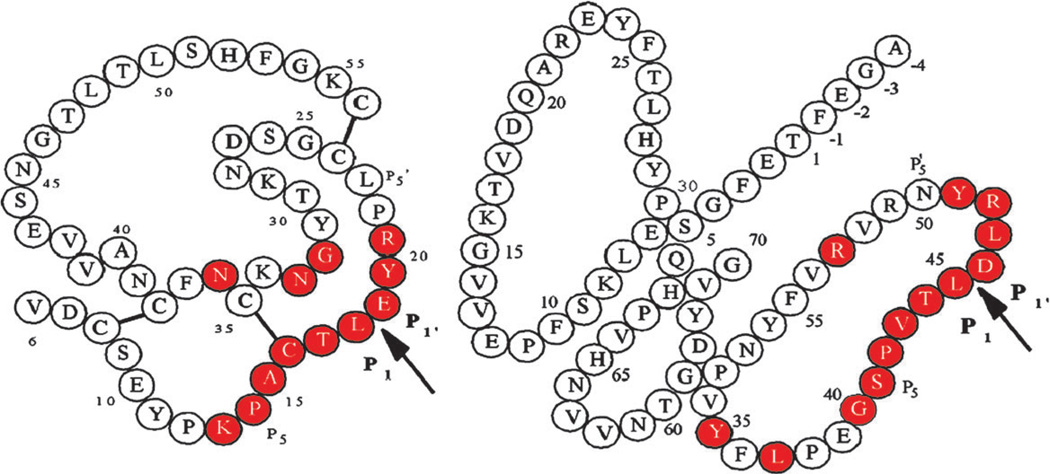
Fig. 1.

Schematic covalent structures of OMTKY3 (left) and eglin C (right). The arrows indicate the reactive site peptide bonds. In each inhibitor, the consensus sets of residues that come in contact with the cognate enzyme are colored red. The disulfide linkages are represented as thick lines between cysteines. There are no disulfide bridges in eglin C. Reprinted with permission from Fig. 1 in ref. 5. © 2006, American Chemical Society.

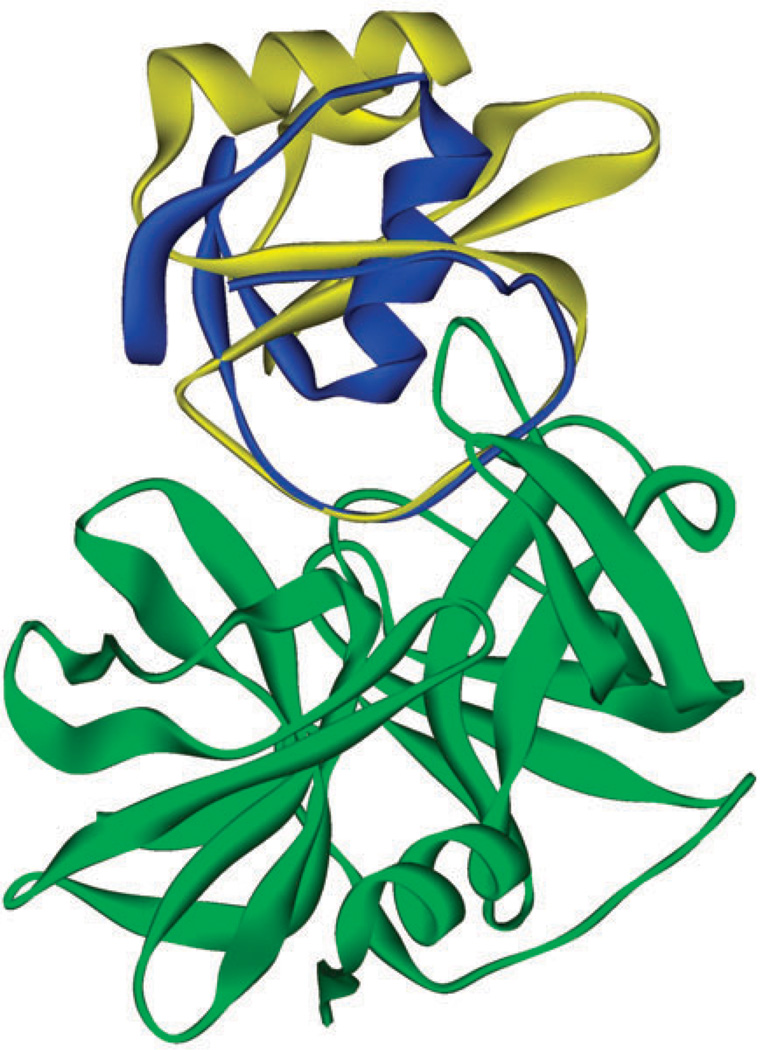
Fig. 2.

Eglin C (yellow) and OMTKY3 (blue) in the binding site of ALP (green). The structure of the protein complex is predicted by ZDOCK/RDOCK.

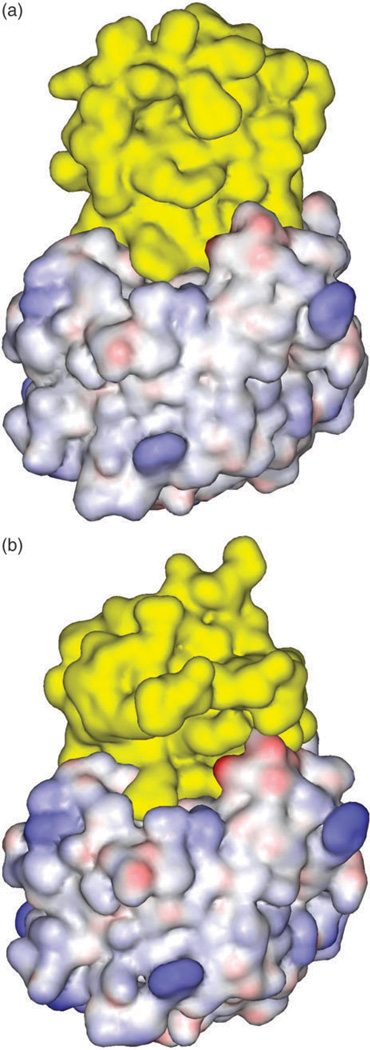
Fig. 3.

Surface complementarity in protein complex: (a) ALP-eglin C; (b) ALP-OMTKY3. The inhibitor proteins are colored in yellow.

How accurate are these computationally predicted structures? Several lines of evidence suggest that they are close to the actual complex. First, when the enzyme in the ZDOCK/RDOCK predicted complex is superimposed with the crystal structure of ALP bound to peptide boronic acid inhibitor,²² the backbone atoms of the contact loop in the protein inhibitors overlap with those in the peptide boronic acid inhibitor from residues P1 to P4 to a high degree, with RMSD < 1.1 Å: see Fig. S1 of the ESI.† Second, ZDOCK/RDOCK is known to be highly successful in predicting enzyme-inhibitor complexes similar to the ones examined here. According to Weng and coworkers,⁸ the algorithm has a success rate (defined as the percentage of interface C_α RMSD < 2.5 Å from the crystal complex) of ≥ 90% for a total of 23 enzyme-inhibitor complexes tested. For the two serine protease–inhibitor complexes chymotrypsin–eglin C and chymotrypsin–OMTKY3, the RMSD between the predicted best docked poses and X-ray structures are 1.86 A and 1.28 Å, respectively.⁸ Lastly, in the subsequent three 10 ns MD simulations starting from the ZDOCK/RDOCK predicted structures, the complexes undergo limited structural fluctuations with average Cα RMSD ≤ 2.5Å. Taken these observations together, we believe that the ZDOCK/RDOCK generated complex conformations provide reasonably accurate starting models for a detailed theoretical investigation at atomic levels.

Structural stabilities from MD simulation and convergence of calculated free energies

To reliably calculate thermodynamic properties from MD trajectories, it is essential that the system is adequately equilibrated before the data collection phase. For each of the three enzyme-inhibitor complexes, 10 ns MD simulations are performed in explicit solvent and counter ions with PME method for calculating electrostatics interactions. The first 5 ns of the simulation are considered as thermal equilibration, and the last 5 ns of the trajectory are used for calculating thermodynamic properties. Here the relatively long equilibrations are employed to allow extensive relaxation of the computationally predicted initial structures. The structural stability from nanoseconds MD gives an indication for sufficient thermal equilibration. This can be seen from Fig. 4, which shows the Cα atoms RMSD relative to the ZDOCK/RDOCK predicted conformations for the three enzyme–inhibitor complexes during 5 ns production phase. No systematic drift is observed in these systems and the RMSDs are below 2 Å throughout 5 ns trajectories.

Fig. 4.

Time series of Cα atom RMSD during the last 5 ns MD. The RMSD is relative to the starting conformations. (a) ALP-eglin C; (b) ALP-OMTKY3.; (c) ALP-OMTKY3M.

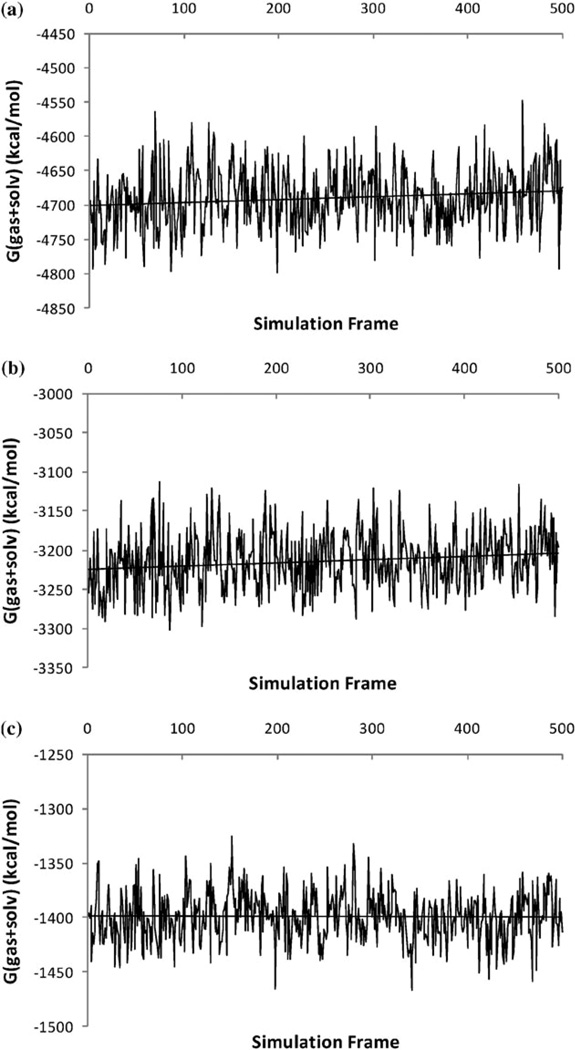
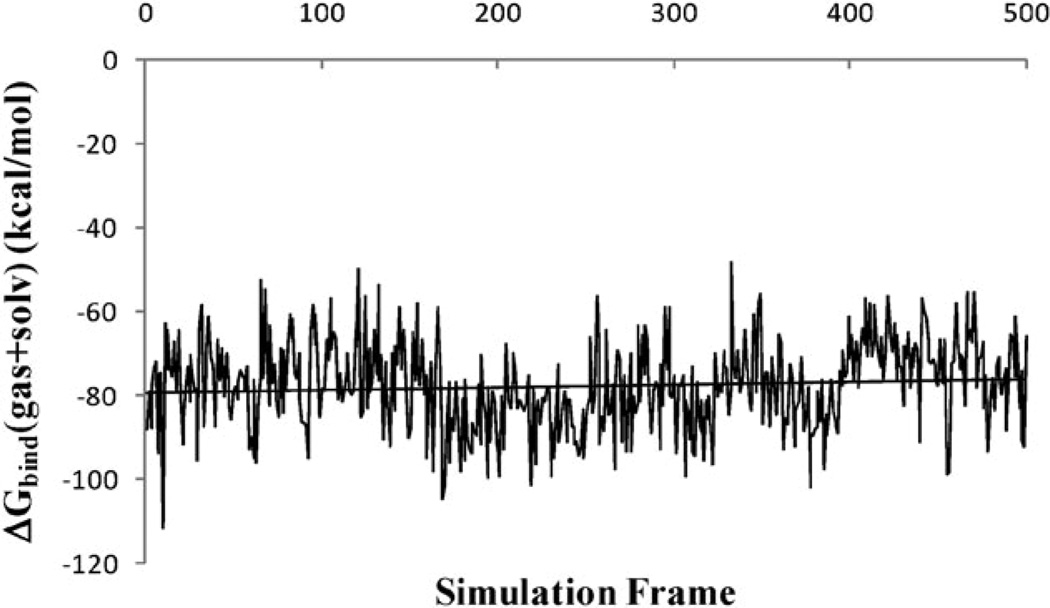
In order to obtain meaningful estimates of energetics from a MM-PB(GB)/SA calculation, the calculated free energies need to show good convergence. In the formulation of MM-PB/SA, the free energy is the sum of effective energy G(gas + solv) and solute entropy. The effective energy consists of gas-phase energy and the solvation free energy. In the present work, G(gas + solv) is calculated for 500 frames of the last 5 ns of MD trajectory, while solute entropy is calculated for 50 frames due to its high computational cost. We therefore examine the convergence in the effective energy G(gas + solv) only. The time series of the calculated effective energies for the ALP–eglin C complex are presented in Fig. 5. The results for the other two complexes are similar. Despite the significant fluctuations in the instantaneous values of the effective energies, the overall time series appear to be stable. The drifts in the effective energies are relatively small: the slopes of the linear regression in both ALP–eglin C complex and the unbound ALP are 4 × 10⁻³ kcal mol⁻¹ × ps (unbound eglin C shows zero drift in free energy). The magnitude of the slope is similar to those reported in other MM-PB(GB)/SA studies for the Ras-Raf,¹⁹ Ras-RalGDS¹⁴ and TCR-p-MHC²⁰ complexes. The effect on the calculated binding free energy is also small: as shown in Fig. 6, the slope of the linear regression of the effective binding energy for the ALP-eglin C complex is 1 × 10⁻³ kcal mol⁻¹ × ps.

Fig. 5.

Time series of calculated effective energies G(gas + solv) during the last 5 ns MD. (a) ALP-eglin C complex; (b) unbound ALP; (c) unbound eglin C.

Fig. 6.

Convergence of the effective binding free energy ΔG_bind(gas + solv) during the last 5 ns of simulation in the ALP-eglin C complex.

The small drifts in effective energy have been attributed to the fact that the length of the MD simulation is still short compared with the characteristic relaxation time (i.e. the full cycle) of the macromolecules in solution.^14,19 However, the positive slope of the effective energy drift with time is counterintuitive. For equilibration, the slope of long time trend is expected to be negative, since overall effective energy curve is downhill as the system evolves towards free energy minimum in a funnel-like energy landscape. This apparent contradiction regarding the slope of effective energy drift can be explained by recognizing that effective energy is only one part of the total free energy. The other part, i.e. solute entropy component, is likely to change in a different direction than the effective energy, due to the enthalpy–entropy compensation. But the trend of entropy change may not be easily demonstrated with time series plot, since it is related to the volume in configuration space and thus it is not an instantaneous property.

Analysis of calculated binding free energies and their components

The calculated binding free energies and their components are presented in Table 1. The gas phase energies and the solvation free energies are calculated every 10 ps for a total of 500 snapshots during the last 5 ns of the trajectory. The vibrational entropy is computed for only 50 snapshots, due to its high computational cost. To mimic the experimental condition, an ionic concentration of 0.05 M is used to compute the electrostatic solvation free energy using PB. The statistical uncertainty of the calculation is estimated from the standard error of the mean, obtained with the assumption that the individual sampling points are uncorrelated. This property is a more meaningful measure for the statistical uncertainty than standard deviation, since free energy is an ensemble averaged property, rather than an instantaneous property.

Table 1.

Binding free energies and their components.^a Units: kcal mol⁻¹

Complex	ALP-OMTKY3	ALP-OMTKY3M	ALP-eglin C
ΔE(vdw)	−78.7 (0.2)	−77.4 (0.2)	−106.3 (0.2)
ΔE(elec)	−43.9 (1.1)	−523.1 (1.1)	−99.7 (0.8)
ΔG(solv_elec)b	93.5 (1.2)	544.8 (1.0)	140.5 (0.9)
ΔG(total_elec)c	49.6 (0.5)	21.7 (0.5)	40.8 (0.5)
ΔG(solv_np)d	−9.8 (<0.1)	−10.4 (<0.1)	−12.3 (<0.1)
ΔG(gas + solv)e	−38.9 (0.5)	−66.1 (0.5)	−77.8 (0.5)
-TΔS(vib)	2.1 (0.8)	3.8 (0.7)	10.6 (0.8)
-TΔS(trans/rot)	27.4 (<0.1)	27.5 (<0.1)	27.9 (<0.1)
ΔGbind(calc)f	−9.4 (0.5)	−34.8 (0.5)	−39.4 (0.5)
ΔGbind(expt)	−4.4	−9.9	−12.3

^aNumbers in parentheses are the standard errors of the mean.

^bΔG(solv_elec): the electrostatic solvation free energy component of ΔG_bind, computed by solving the Poisson-Boltzmann equation at 0.05 M salt concentration.

^cΔG(total_elec) = ΔE(elec) + ΔG(solv_elec), the total electrostatics interaction contribution.

^dAG(solv_np): the nonpolar solvation free energy component of ΔG_bind, approximated by the linear solvent accessible surface area (SASA) relation.

^eΔG(gas + solv) = ΔE(vdw) + ΔE(elec) + ΔG(solv_elec) + ΔG(solv_np), the sum of the gas phase energy and the solvation free energy contributions to ΔG_bind. Also known as the effective energy contribution.

^fΔG_bind(calc) = ΔG(gas + solv) − TΔS(trans/rot) − TΔS(vib).

As shown in Table 1, the mean values of the calculated binding free energies are −9.4 kcal mol⁻¹ (ALP-OMTKY3), −34.8 kcal mol⁻¹ (ALP-OMTKY3M) and −39.4 kcal mol⁻¹ (ALP-eglin C), which are compared with the experimentally determined binding free energies of −4.4 kcal mol⁻¹ (ALP-OMTKY3), −9.9 kcal mol⁻¹ (ALP-OMTKY3M), and −12.3 kcal mol⁻¹ (ALP-eglin C). Thus, the calculated binding free energies are consistent with the trend of the experimental data. This shows that as a physical model the MM-PB/SA is able to explain the specificity in the binding of ALP and its three inhibitor proteins.

A number of factors contribute to the overestimation of the absolute binding free energy. First, as will be shown below, several charged residues participate in the protein binding. The ionic interactions involving these residues may be overly attractive in the continuum electrostatics treatments using the PB (or GB) model. Second, using the single trajectory method means that the energy related to protein reorganization upon binding is neglected. Third, in the normal mode calculation of entropy, only the vibrational entropy is included, while conformational entropy contribution to the solute configurational entropy is neglected. All these factors can make the calculated binding free energy less negative. Overestimation of the absolute binding free energy by the MM-PB(GB)/SA calculations have been reported in other protein complexes such as the HIV-1 protease dimer¹⁸ and the TCR-p-MHC complex.²⁰ It is likely that all these overestimation in the calculated ΔG_bind share the same causes. In the current study, however, the systematic overestimation in the absolute binding free energies does not present a major problem, since the focus here is on the relative binding free energies ΔΔG_bind which determine the binding specificity. As we have seen from Table 1, the predicted relative stabilities are in good agreement with the experiments. This probably results from the fact that the protein complexes studied here are significantly similar and the errors caused by the approximations in the physical model largely cancel out when the relative binding free energies are considered.

We now analyze the binding free energy components, to gain insights into the molecular driving forces for binding affinity and specificity. As can be seen from Table 1, binding is driven by the effective energy contribution ΔG(gas + solv) of −38.9 kcal mol⁻¹ (ALP-OMTKY3), −66.1 kcal mol⁻¹ (ALP-OMTKY3M), and −77.8 kcal mol⁻¹ (ALP-eglin C). These favorable contributions are partially offset by the unfavorable solute entropy contributions − TΔS(solute) of 29.5 kcal mol⁻¹ (ALP-OMTKY3), 31.3 kcal mol⁻¹ (ALP-OMTKY3M), and 38.5 kcal mol⁻¹ (ALP-eglin C). Note that the effective energy change ΔG(gas + solv) anti-correlates with the vibrational entropy contribution − TΔS(vib) of 2.1 kcal mol⁻¹ (ALP-OMTKY3), 3.8 kcal mol⁻¹ (ALP-OMTKY3M), and 10.6 kcal mol⁻¹ (ALP-eglin C). This trend is of course an example of enthalpy-entropy compensation, a universal phenomenon in most chemical transformations.²³

Among the components of the effective energy, the van der Waals interaction ΔE(vdw) and the nonpolar solvation free energy ΔG(solv_np) are strongly favorable to binding: see Table 1. The latter implicitly accounts for the hydrophobic effect and the solute–water dispersion interaction. The protein-protein Coulombic interaction ΔE(elec) is highly attractive, especially in the case of ALP-OMTKY3M (discussed below). As expected for molecular association in polar medium, Coulombic interaction is anti-correlated with electrostatic desolvation free energy ΔG(solv_elec). The net electrostatic contribution ΔG(total_elec) are found to disfavor binding for all three complexes studied here (Table 1).

These results are consistent with many continuum electrostatics calculations in which the overall effects of electrostatics are found to be destabilizing.^{14–16,18–20} Favorable electrostatic contributions to protein association in aqueous solution are rarely observed. One notable case is the Rap1A–RBD domain of cRaf kinase.²⁴ The electrostatic potential of the two partner proteins of the protein complex are highly complementary. Using a protein dielectric constant of two, Sheinerman et al. estimated a favorable total electrostatic contribution of −12 kcal mol⁻¹.²⁴

This nearly universal trend of electrostatic destabilization in binding is striking. What it means is that in terms of electrostatics, protein molecules interact more strongly with water than they do with each other. However, there are no physically fundamental reasons that would prevent one from designing binding interfaces for which the overall electrostatics is highly complementary and hence favorable to binding. One explanation for the generally observed trend of electrostatic destabilization is that, an unfavorable electrostatics contribution is required to balance the strongly attractive nonpolar interactions, such that the overall binding affinity is not too strong and the association remains thermodynamically reversible. Otherwise, the only thermodynamic force that opposes binding would come from the solute entropy changes, and protein association would be effectively irreversible in relevant biological timescales.

As seen from Table 1, the Coulombic interaction ΔE(elec) in ALP-OMTKY3M (−523.1 kcal mol⁻¹ ) is much stronger than those in ALP-OMTKY3 (−43.9 kcal mol⁻¹ ) and ALP-eglin C (−99.7 kcal). These large differences are the result of the net charges carried by the proteins: +8e in ALP, zero in OMTKY3 and eglin C, and −4e in OMTKY3M. Because ΔE(elec) is calculated using the dielectric constant of the vacuum, the attraction between the oppositely charged ALP and OMTKY3M is significantly greater than those between ALP and the charge neutral eglin C and OMTKY3.

This strong Coulombic attraction in ALP-OMTKY3M is largely compensated by the electrostatic solvation free energy ΔG(solv_elec) of 544.8 kcal mol⁻¹, and the net result is a small overall electrostatic interaction ΔG(total_elec) of 21.7 kcal mol⁻¹, which disfavors binding. However this unfavorable contribution is smaller in magnitude than in ALP-OMTKY3, and the difference in ΔG(total_elec) between the two complexes appears to be responsible for the 10⁴-fold increase in the affinity in mutant OMTKY3M over the wild type OMTKY3. As Table 1 reveals, the relative binding free energy components ΔΔE(vdw), ΔΔG(total_elec) and ΔΔG(solv_np) between complexes ALP-OMTKY3M and ALP-OMTKY3 are 1.3 kcal mol⁻¹, −27.9 kcal mol⁻¹ and −0.6 kcal mol⁻¹, respectively. Therefore the enhancement in binding affinity in ALP-OMTKY3M is entirely an electrostatic effect.

Next we examine the specificity for the binding of ALP to Eglin C and OMTKY3. Experimentally eglin C is found to be a much stronger inhibitor than OMTKY3 towards ALP (by 10⁶ times). As seen from Table 1, the relative binding free energy components ΔΔE(vdw), ΔΔG(total_elec) and ΔΔG(solv_np) between the two complexes are −27.6 kcal mol⁻¹, −8.8 kcal mol⁻¹ and −2.5 kcal mol⁻¹, respectively. Thus, the vast difference in the inhibition between eglin C and OMTKY3 is mainly due to the stronger van der Waals interaction, with the total electrostatics contributing to a smaller extent. The stronger nonpolar interaction reflects better structural complementarity in the ALP–eglin C complex. The details of the structural determinants for this binding specificity are revealed by the calculation of per-residue contribution to binding, see discussions below.

A related question that needs to be addressed is: why do the two inhibitors show a much smaller difference in the binding constants towards other serine proteases? For example, eglin C inhibits chymotrypsin (CHYM) more strongly than does OMTKY3 by only 3.5 times,⁴ which compares with the million times difference in binding constants between complexes ALP–eglin C and ALP-OMTKY3. The answer to this question appears to be related to the shapes of the active site cavities of chymotrypsin and ALP, which are shown in Fig. 7. The cavity of ALP is narrower and deeper than that of CHYM. The relatively wide and shallow binding pocket in CHYM immediately suggests that it should be much less discriminative towards OMTKY3. To confirm it, we performed MM-PB/SA calculations on the CHYM–Eglin C and CHYM–OMTKY3 complexes from two 1.2 ns MD trajectories. The calculated ΔΔG(gas + solv) between the two complexes is −0.9 kcal mol⁻¹, in excellent agreement with the experimentally determined result of −0.8 kcal mol⁻¹. The ΔΔE(vdw) is calculated to be 10.3 kcal mol⁻¹, which compares with the ΔΔE(vdw) of −27.6 kcal mol⁻¹. between ALP–Eglin C and ALP–OMTKY3. The positive sign of ΔΔE(vdw) indicates that, in sharp contrast to ALP, CHYM interacts more strongly with OMTKY3 than it does with eglin C. This result is consistent with the above observation regarding the nature of the binding pockets in CHYM and ALP and its influence on the binding specificity towards eglin C and OMTKY3.

Fig. 7.

Comparisons of shape of the binding site cavity in (a) bovine chymotrypsin (CHYM) and (b) ALP in solvent accessible surface representation. The location of the binding site cleft is indicated by the inhibitor residues displayed as lines. The coordinates of CHYM and ALP are taken from PDB structures 1ACB and 1GBK, respectively. In order to show the sizes of the two cavities with the same ratio, the two structures are first superimposed based on the coordinates of their respective catalytic groups: His57, ASP102 and Ser195. The solvent accessible surfaces are then generated on the two structures.

Decomposition of binding free energy into per-residue contributions

In order to elucidate the roles of individual amino acid residues in determining protein association, the effective binding energy ΔG_bind(gas + solv) is decomposed into contributions from the residues of the two partner proteins.^14,15 The decomposition starts with partitioning the total effective energy of a macromolecule in solution among its constituent atoms:

$$G(\text{gas}+\text{solv})=\sum _i{G}_i(\text{gas}+\text{solv})=\sum _i[E_i(\text{vdw})+E_i(\text{elec})+G_i(\text{solv}\_\text{elec})+G_i(\text{solv}\_\text{np})]$$ (1)

The partitions of van der Waals energy E_i(vdw) and Coulombic energy E_i(elec) are straightforward, with each atom receiving one-half of its interaction energy with others:

$$E_i(\text{vdw})=\frac{1}{2}\sum _j{E}_{ij}(\text{vdw})$$ (2)

$$E_i(\text{elec})=\frac{1}{2}\sum _j\frac{q_i{q}_j}{4\pi {\epsilon }_0{r}_{ij}}$$ (3)

The non-polar solvation free energy contribution from atom i is estimated from the solvent accessible surface area of the atom:

$$G_i(\text{solv}\_\text{np})=\gamma {\text{SASA}}_i+\beta$$ (4)

The per-atom electrostatic solvation free energy follows naturally from the expression of the total electrostatics free energy for a macromolecule in solution

$$G(\text{total\_elec})=\frac{1}{2}\sum _i{q}_i\phi (r_i)$$ (5)

Here φ(r_i) is the total electrostatic potential, which is the linear superposition of the Coulombic potential due to solute charges and the reaction field potential φ_rf(r_i) due to polarized solvent, i.e.

$$\phi (r_i)=\sum _j\frac{q_j}{4\pi {\epsilon }_0{r}_{ij}}+{\phi }_{\text{rf}}(r_i)$$ (6)

The total electrostatic free energy G(total_elec) is therefore the sum of total Coulombic interaction E(elec) and the electrostatic solvation free energy G(solv_elec):

$$G(\text{total\_elec})=\frac{1}{2}\sum _{i,j}\frac{q_i{q}_j}{4\pi {\epsilon }_0{r}_{ij}}+\frac{1}{2}\sum _i{q}_i{\phi }_{\text{rf}}(r_i)$$ (7)

The electrostatic solvation free energy contribution from atom i is thus obtained as the product of half the atomic charge and the electrostatic potential of solvent reaction field at the atom i:

$$G(\text{solv}\_\text{elec})=\frac{1}{2}{q}_i{\phi }_{\text{rf}}(r_i)$$ (8)

The solvent reaction field φ_rf(r_i) is calculated by solving the PB equation for the macromolecule in the solution phase and in vacuum, and taking the difference of the two resultant potentials at position r_i.

In the paper by Hendsch and Tidor²⁵ in which the per-atom decomposition of electrostatic solvation free energy is first introduced, the contribution from atom i was obtained by summing one-half the charge at all atom positions times the potential at that atom due to atom i:

$$G_i(\text{solv}\_\text{elec})=\frac{1}{2}\sum _j{q}_i{\phi }_{\text{rf}}^i(r_j)$$ (9)

Here φ_rfⁱ(r_i) is the electrostatic potential of the solvent reaction field at r_i due to atom j. Using Green’s reciprocity relation,²⁶ it can be seen that eqn (9) is equivalent to eqn (8). In the application of eqn (9), for each residue of interest, a separate PB calculation has to be performed to obtain the potential at all atom positions due to the charges of the group of interest (other charges need to be turned off during the PB calculation). In contrast, using eqn (8), it requires only two PB calculations to determine φ_rf(r_i), which contains contributions to solvent reaction field from all solute charges.

Finally, the effective binding energy contribution from atom i is obtained by calculating the difference of G_i(gas + solv) in the complex and that in the unbound state, i.e.

$$\mathrm{\Delta }{G}_i(\text{gas}+\text{solv})=G_i^{\text{complex}}(\text{gas}+\text{solv})-G_i^{\text{unbound}}(\text{gas}+\text{solv})$$ (10)

Summing the contributions from all the atoms in a residue yields the effective binding energy contribution from that residue.

The per-residue free energy decomposition was first used by Hendsch and Tidor to investigate atomic group contributions to the electrostatics binding free energy in GCN4 Leucine zipper.²⁵ The approach has been applied to study the effect of mutations or changes in ligand on the binding of aspartyl-tRNA synthetase with Asp and Asn.²⁷ More recently, the per-residue binding free energies have been calculated using the GB model, which is computationally inexpensive compared with PB, to investigate the details of binding at the atomic level in the insulin dimer,¹⁵ TCR-p-MHC,²⁰ Ras-Raf and Ras-RalGDS¹⁴ complexes. The results in these studies demonstrated good correlations between the calculated per-residue binding free energy and the experimental binding free energy differences for the alanine mutants.

While the free energy decomposition has been shown to be useful for understanding the nature of the binding interfaces, the information it provides is largely qualitative and needs to be taken with caution. First, although the decomposition scheme discussed above follows naturally from free energy expression, it may not be unique and the degree of its applicability may vary with the molecular system. Second, the per-residue free energy decomposition used here and in previous studies^14,15,20 is based on the MM-PB/SA model, thus it shares the same intrinsic limitations of MM-PB/SA as we discussed earlier, including having a substantial statistical error in the results. Other caveats include the neglect of the solute entropy in the calculation of ΔG_i(gas + solv). As shown below, with these cautions in mind, the results of the calculated per-residue decomposition combined with the structural information provide a physical basis for explaining the experimentally observed binding and mutation effect.

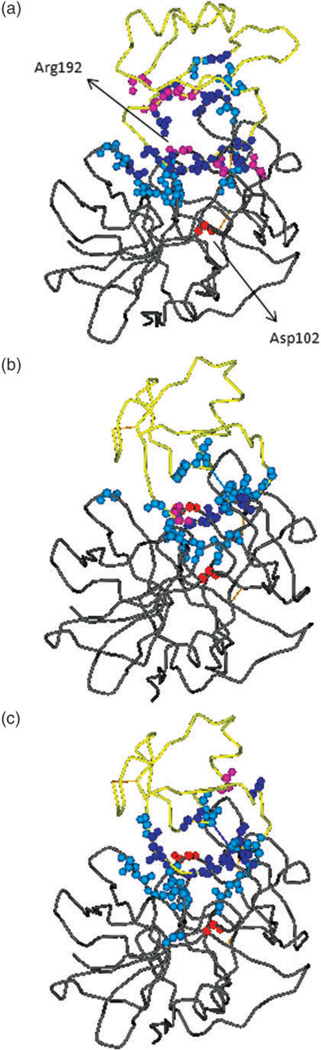
The per-residue effective binding energy has been calculated according to eqn (10), for the same 500 coordinate frames for which the total binding free energies are calculated (see discussions above). On the basis of calculated ΔG_i(gas + solv), we have identified the residues with the largest impact on the protein-protein binding: see Table 2–Table 4. The spatial distributions of these hot spots (defined as having |ΔG_i(gas + solv)| > 0.5 kcal mol⁻¹) are shown in Fig. 8–Fig. 10. As can be seen, most of the hot spots are located near the binding interface, within 8 Å from the nearest residue of the partner protein, with most of them making direct contact with the partner protein. The protein-protein interaction is dominated by these high energy residues, which represent ≥75% of the total effective binding energy: see Table 5. The rest of the binding energy comes from numerous low energy residues, which have a broad spatial distribution throughout protein complexes. Because of their large number, these non-hotspots contribute a substantial amount of effective binding energy of −10 kcal mol⁻¹ (Table 5). But this portion of the binding energy should be considered as a background interaction, as their magnitudes are almost uniform across the three protein-protein complexes and are uncorrelated with the relative binding free energies ΔΔG_bind (Table 5). Thus, the non-interface residues do not seem to be involved in determining the binding specificity. Related to these findings, we noted that in the binding free energy decomposition study of Raf-Ras and Ras-RalGDS complex,¹⁴ residues 25 Å away from the binding interface are found to contribute to protein–protein interaction. The calculated binding free energies from non-interface residues are −1 kcal mol⁻¹ (Ras-RalGDS) and −5 kcal mol⁻¹ (Ras-Raf),¹⁴ which compare with the corresponding values of −10 kcal mol⁻¹ for the three protein complexes studied here.

Table 2.

(a) Per-residue effective binding energy ΔGi (gas + solv) for ALP residues in the complex of ALP-eglin C. Residues whose |ΔGi (gas + solv)| ≤ 0.5 kcal mol−1 are omitted. Unit: kcal mol−1
Residue	ΔEi (vdw)	ΔGi (total_elec)b	ΔGi (solv_np)	ΔGi (gas + solv)a
SER219A	−3.0	0.5	−0.6	−3.2
TYR171	−3.6	0.8	−0.2	−3.0
LEU41	−2.4	−0.2	−0.3	−2.9
ASN219B	−3.1	1.4	−0.3	−2.0
SER195	−1.4	0.1	−0.1	−1.5
GLY215	−1.5	0.2	−0.1	−1.4
GLY216	−1.7	0.5	−0.2	−1.4
HIS57	−2.0	1.1	−0.3	−1.2
ALA39	−1.3	0.6	−0.3	−1.0
GLN219	−3.0	2.2	−0.3	−1.0
SER40	−2.0	1.2	−0.2	−1.0
ASP194	−0.8	−0.1	0.0	−0.9
CYS58	−0.8	0.0	−0.1	−0.9
GLY193	−0.5	−0.3	−0.1	−0.9
CYS42	−0.9	0.1	0.0	−0.8
ASN170	−0.8	1.6	−0.1	0.7
GLU174	−0.7	1.8	−0.3	0.8
ARG192	−6.7	8.9	−0.8	1.3
ASP102	−0.2	4.1	0.0	3.9

(b) Same as Table 2a, except for eglin C residues in the complex of ALP-eglin C
GLY70c	0.1	−12.6	−0.1	−12.6
LEU45	−7.3	−1.7	−1.0	−10.0
THR44	−4.8	−0.6	−0.5	−5.9
HIS65	−2.5	−1.5	−0.4	−4.4
HIS68	−2.1	−2.0	−0.2	−4.3
LEU47	−4.7	1.1	−0.6	−4.2
PRO42	−4.2	1.4	−0.6	−3.4
VAL43	−3.3	0.4	−0.3	−3.2
ASP46	−4.6	2.4	−0.4	−2.7
PHE55	−2.7	1.1	−0.3	−1.9
TYR35	−0.6	−0.2	−0.2	−1.0
LEU37	−0.7	−0.1	−0.1	−0.9
VAL66	−1.3	0.6	0.0	−0.7
VAL52	−0.3	1.0	0.0	0.6
LYS8	−0.1	0.8	0.0	0.7
ARG51	−0.9	2.0	0.0	1.1
ARG53	−2.0	3.6	−0.1	1.5

^aΔG_i(gas + solv) = ΔE_i(vdw) + ΔG_i(total_elec) + ΔG_i(solv_np).

^bΔG_i(total_elec) = ΔE_i(elec) + ΔG_i(solv_elec).

^cGly70 is the charged C-terminal residue of eglin C.

Table 4.

(a) Same as Table 2a, except for ALP residues in the complex of ALP-OMTKY3M
Residue	ΔEi (vdw)	ΔGi (total_elec)	ΔGi (solv_np)	ΔGi (gas + solv)
GLU174	0.1	−3.6	−0.4	−3.9
TYR171	−3.7	0.9	−0.2	−3.1
VAL218	−3.1	0.6	−0.5	−3.0
HIS57	−2.2	0.5	−0.3	−2.0
GLY216	−0.9	−0.8	−0.2	−1.9
LEU41	−1.8	0.3	−0.2	−1.7
SER40	−1.0	−0.4	−0.2	−1.7
SER214	−0.9	−0.5	0.0	−1.3
GLY215	−1.2	0.1	−0.1	−1.3
ASN217	−1.1	0.0	−0.1	−1.1
ASP194	−0.8	−0.4	0.0	−1.1
CYS58	−1.0	0.0	−0.1	−1.1
ALA173	−2.6	2.2	−0.6	−1.0
SER195	−1.2	0.4	−0.1	−0.9
GLY193	−0.6	0.0	−0.1	−0.8
ARG90	−0.1	−0.7	0.0	−0.8
ASP102	−0.2	2.7	0.0	2.6
ARG192	−5.8	9.8	−0.8	3.2

(b) Same as Table 2a, except for OMTKY3M residues in the complex of ALP-OMTKY3M
ALA18	−3.9	−2.4	−0.6	−6.9
THR17	−4.7	0.2	−0.5	−5.0
TYR20	4.6	1.0	0.6	4.2
CYS16	−3.3	−0.3	−0.3	−3.9
LYS34	0.4	−3.4	−0.2	−3.2
THR21	−1.3	−1.6	−0.2	−3.1
TYR11	−1.0	−1.2	−0.2	−2.4
ALA15	−3.4	1.5	−0.4	−2.3
ASP36	−0.8	−0.9	−0.2	−2.0
CYS35	−1.2	0.1	−0.1	−1.2
GLU19	−4.8	4.2	−0.4	−1.0
PRO22	−0.9	0.4	−0.1	−0.6
ASN39	−0.8	2.1	−0.2	1.1

Fig. 8.

Per-residue effective binding energy ΔG_i(gas + solv) in (a) ALP-eglin C, (b) ALP-OMTKY3, and (c) ALP-OMTKY3M. The enzyme and the inhibitor are represented by grey and yellow tube, respectively. Backbone atoms of residues with |ΔG_i(gas + solv)| > 0.5 kcal mol⁻¹ are shown in a sphere. The color code indicates the sign and magnitude of ΔG_i(gas + solv) to binding: Blue, highly favorable: ΔG_i(gas + solv) < −2 kcal mol⁻¹ ; Light blue, favorable: −2 kcal mol⁻¹ ≤ ΔG_i(gas + solv) < −0.5 kcal mol⁻¹ ; Pink, unfavorable: 2 kcal mol⁻¹ ≥ ΔG_i(gas + solv) > 0.5 kcal mol⁻¹; Red, highly unfavorable: ΔG_i(gas + solv) > 2 kcal mol⁻¹.

Fig. 10.

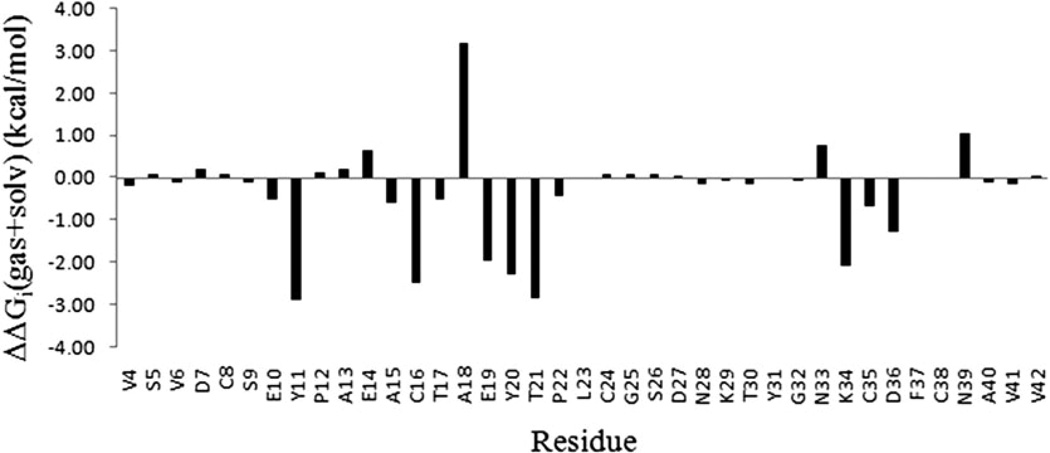
Difference in per-residue binding free energy ΔΔG_i(gas + solv) between residues in OMTKY3M and OMTKY3, which are, respectively, in complex with ALP.

Table 5.

Effective binding free energy contributions ΔG(gas + solv) from high impact and low impact residues. Residues whose ΔG_i (gas + solv)| is greater than 0.5 kcal mol⁻¹ are considered high impact ones. Unit: kcal mol⁻¹

Complex	High-impact residue	Low-impact residue	Total
ALP-eglin C	−67.5	−10.2	−77.7
ALP-OMTKY3M	−55.3	−10.5	−65.8
ALP-OMTKY3	−28.6	−9.7	−38.3

As can be seen from Tables 2–4, residues that contribute favorable binding energy have varied composition of amino acid types and do not show a clear preference for hydrophobic or hydrophilic side chain. While majority of the residues show positive per-residue total electrostatic energy ΔG_i(total_elec), a small number of the residues, many of them in the ALP-OMTKY3M complex, make favorable contributions of per-residue total electrostatic energy of binding. This reflects the subtle balance between the protein–protein Coulombic interaction and the cost of electrostatic desolvation upon binding. The repulsive binding interactions arise almost exclusively from charged residues, many of them, but not all, are due to the burial of charge groups upon binding. This point is highlighted by Asp102 and Arg192 of ALP in complex with eglin C (Fig. 8a). Both residues consistently oppose binding, showing large, positive ΔG_i(gas + solv), but their mechanisms for the repulsive interaction are not identical. Arg192 is fully exposed on the surface in the unbound protein. Upon binding to eglin C, it experiences a burial of solvent accessible surface area (SASA) of 146 Ų, with an associated unfavorable electrostatic desolvation free energy of 22.5 kcal mol⁻¹, which is larger than the favorable Coulombic and van der Waals interaction with eglin C. In contrast to Arg192, Asp102 is located 7 Å beneath the protein surface and is thus fully buried in the unbound state (Fig. 8a). What is interesting is that, although it experiences no change in SASA upon binding, Asp102 still shows a sizable increase in electrostatic desolvation free energy of 11 kcal mol⁻¹, which prevails over the favorable Coulombic interaction of −6.9 kcal mol⁻¹ with the binding partner eglin C. This example demonstrates an important point: electrostatics desolvation is not limited to surface residues that are buried upon the formation of interface; non-surface residues which bear significant charges could also experience a substantial increase in solvation free energy upon binding. The physical reason lies in the long-range nature of electrostatic solvation free energy, which is essentially the Coulombic interaction between a solute charge and solvent polarization charges located at the solute-solvent dielectric boundary. Binding changes the spatial distribution of solvent polarization charges, as surfaces in the unbound state is replaced by protein–protein interface. This alters the long range interactions between the solvent polarization charges and the solute charges, for residues located on the surface and those underneath the surface prior to binding. The effect on surface residues tend to be more pronounced, as they are rich in charged and polar groups, thus the electrostatic desolvation is generally large. As we have seen, a non-surface residue could also be strongly affected when it bears a significant charge and is located not too far away from the binding interface.

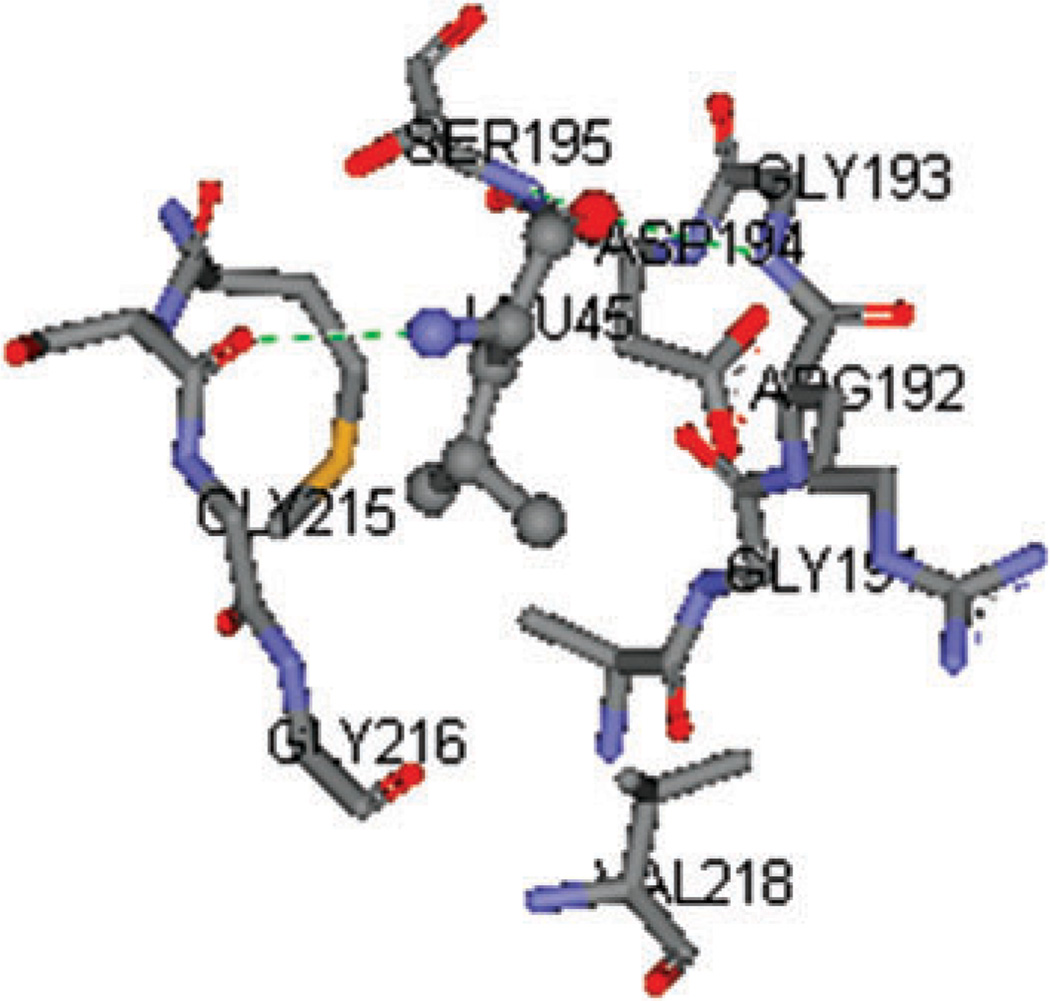
The calculation of per-residue binding free energy confirmed the critical role of the primary specificity residue P1.⁴ The contributions to binding free energy from P1 residues are − 10.0 kcal mol⁻¹ from P1 Leu45 of eglin C, −10.1 kcal mol⁻¹ from P1 Leu18 of OMTKY3, and −6.9 kcal mol⁻¹ from P1 Ala18 of OMTKY3M. As in other serine protease-inhibitor complexes, the P1 residue is docked into the S1 pocket of the enzyme, generating strong van der Waals interactions. Its backbone atoms O and N form hydrogen bonds with neighboring ALP residues, yielding favorable net electrostatic contribution ΔG_i(tot_elec) (Tables 2–4). These interactions are demonstrated in Fig. 9 which shows P1 Leu45 of eglin C embedded in the S1 pocket of ALP.

Fig. 9.

P1 residue Leu45 of eglin C embedded in the S1 pocket of ALP. The hydrogen bonds between Leu45 and ALP residues are shown in green dotted lines.

In order to understand the enhanced affinity in ALP-OMT-KY3M due to the mutations K13A-P14E–L18A-R21T–N36D, we analyze the difference in the per-residue binding energy between the corresponding residues of OMTKY3M and OMTKY3, since the change in ΔG_i(gas + solv) contains information on the effect of mutation at the amino acid residue level and serve as a powerful probe for elucidating the complex network of atomic interactions: see Table 6 and Fig. 10. On the basis of the binding free energy difference, we further examine the molecular environment surrounding those residues with the largest ΔΔG_i(gas + solv). Several major structural factors responsible for the affinity enhancement in the mutant are identified from the following analysis:

1. The Asn36 → Asp mutation introduces a salt bridge between Asp36 and Arg192 of ALP in the mutant. The interactions of Asn36 and Asp36 with its neighbors are illustrated in Fig. S2(a) and S2(b) of the ESI.† The improved electrostatics complementarity is reflected in the favorable ΔΔG_i(gas + solv) for both Asp36 (−1.3 kcal mol⁻¹ ) and Arg192 (−1.2 kcal mol⁻¹ ) of ALP.

2. The Arg21 → Thr mutation has two effects on binding affinity enhancement. First, it lowers the electrostatic desolvation free energy upon complex formation, giving rise to an overall favorable ΔΔG_i(gas + solv) of −2.9 kcal mol⁻¹ (Table 6). The structural basis of the energetics consequence of this mutation can be seen from Fig. S3.† The charged residue Arg21 of OMTKY3 is not adjacent to any oppositely charged residues of ALP, thus the electrostatic free energy of desolvation is not well compensated by the formation of any intermolecular ionic interaction in the bound state. Since the electrostatic desolvation free energy for a neutral group is lower than that for a charged group, the replacement of Arg21 with Threonine is favorable to binding.

   The second effect of Arg21 → Thr mutation is indirect, and is reflected on the ΔΔG_i(gas + solv) of −2.0 kcal mol⁻¹ for Glu19 (Table 6). In the wild type complex ALP-OMTKY3, the side chain of Arg21 forms intramolecular ionic pair with that of Glu19 (Fig. S4a†). This interaction does not contribute to protein–protein binding, because of its intramolecular nature. Due to the Arg21 → Thr mutation, this ionic side chain interaction is absent in the mutant complex ALP-OMTKY3M, which enables Glu19 to interact more closely with His57 of ALP (Fig. S4a). This intermolecular interaction contributes substantially to binding free energy. The structural evidence for the enhancement of intermolecular interaction involving Glu19 due to the Arg21 → Thr mutation can be seen from Fig. S4 of the ESI.†

3. Comparing the structures of the binding interface in mutant and wild type complex, we find a small backbone conformation change in inhibitor which can be crudely described as a small anti-clockwise rotation of around 8 degrees: see Fig. S5 of the ESI.† This rotation causes the backbone atoms of Tyr20 of the binding loop to form intermolecular hydrogen bond with residues of ALP (Fig. S6),† which contributes a favorable ΔΔG_i(gas + solv) of −2.3 kcal mol⁻¹. The conformational change is likely to be induced by the Leu18 → Ala mutation, as the shortening of the side chain of the anchor residue Leu18 allows adjacent residues of the binding loop to move more closely towards the binding pocket.

Table 6.

Per-residue binding energy difference ΔΔG_i (gas + solv), between residues of OMTKY3M and OMTKY3, when the two inhibitors are in complex with ALP. Residues whose |ΔΔG_i (gas + solv)| is smaller than 1.0 kcal mol⁻¹ are omitted. Unit: kcal mol⁻¹

Residuea	ΔΔEi (vdw)	ΔΔGi (total_elec)	ΔΔGi (solv_np)	ΔΔGi (gas + solv)
Tyr11	−0.1	−2.7	−0.1	−2.9
Arg21 → Thr	1.3	−4.2	0.1	−2.9
Cys16	−0.6	−1.9	−0.1	−2.5
Tyr20	0.0	−2.3	0.0	−2.3
Lys34	0.1	−2.2	0.0	−2.1
Glu19	−1.2	−0.7	−0.1	−2.0
Asn36 → Asp	0.6	−1.9	0.0	−1.3
Asn39	−0.6	1.8	−0.2	1.1
Leu18 → Ala	3.9	−1.2	0.5	3.2

^aMutated residues indicated by arrows.

In ALP-OMTKY3M complex, Tyr11 and Lys34 of OMTKY3M and Glu174 of ALP form an ionic pair and hydrogen bonds, which causes favorable binding free energy changes ranging from −2 to −2.9 kcal mol⁻¹ for these residues (Table 6 and Fig. S7†). Here, the Pro14 → Glu mutation is likely to play a role in the conformational change responsible for the formation of the Tyr11-Glu174 hydrogen bond: the replacement of Pro with Glu makes the backbone less rigid, which allows the Tyr11 to move towards Glu174 (Fig. S8, ESI).†

3. Conclusions

We calculated the binding free energy for the association of α-lytic protease with serine protease inhibitors eglin C, OMTKY3 and OMTKY3M using the MM-PB/SA method. The calculated binding free energies reproduce the trend of the experimental binding affinities, indicating that MM-PB/SA is suitable for probing the molecular recognition in these protein-protein systems. The absolute binding free energies are systematically overestimated, and the error has been attributed to the approximate nature of the MM-PB/SA method, which suggests that error cancellation for structurally similar systems is still an important element in the applicability of the MM-PB/SA method in the study of binding. While absolute binding free energies from MM-PB/SA need to be interpreted with caution due to the approximations made in the method, the estimates of the trend of binding free energies are reliable, provided that the protein complexes studied do not differ significantly.

Binding free energy decomposition into different energy components shows that the complexes of enzymes and inhibitor proteins studied here are stabilized by van der Waals interaction and nonpolar solvation free energy, and they are destabilized by overall electrostatic interactions and the solute entropy contribution. The analysis of different free energy contributions indicates that binding specificities in the enzyme-inhibitor complexes studied here have different physical origins. The difference in nonpolar interactions is the main reason for the large difference in the inhibitions between eglin C and wild type OMTKY3 towards ALP. Here electrostatics contributes to a smaller degree. In the case of the mutation effect of OMTKY3M, the improvement in the solvent-mediated electrostatic interactions is the only cause for the enhanced binding affinity in the mutant.

Detailed information on the structural determinants of binding are inferred from the decomposition of free energy at an amino acid residue level. The calculation of per-residue binding free energy shows that binding hot spots reside within a belt around the binding interface. The numerous low energy residues that have a broad spatial distribution contribute about −10 kcal mol⁻¹ of binding free energy, but this background interaction is uncorrelated with the binding specificity. The prominent role of the anchor residue P1 was confirmed by the calculated residue binding free energy. Residues with large favorable binding energy have varied composition of amino acid types. Although the overall electrostatics interactions are destabilizing, several charged residues have favorable per-residue binding free energy. Not surprisingly, unfavorable binding free energy contributions come from charged residues, as the formation of interface is accompanied by the burial of polar or charged groups at protein surfaces, which gives rise to large increase in electrostatic desolvation free energy. Based on the analysis of binding free energy for Asp102 of ALP, we demonstrate that a non-surface charged residue which experiences no change in the solvent accessible surface area could also have a significant electrostatics desolvation free energy. This observation underscores the long-range nature of the interaction between solute charge and the solvent polarization charge.

The calculated per-residue binding free energy was used in combination with structural analysis to probe the mechanism for the effect of the mutations K13A-P14E-L18A-R21T-N36D in OMTKY3M. The Asn36 → Asp mutation improves electrostatics complementarity by introducing a salt bridge between Asp36 and Arg192 of ALP in the mutant. The Arg21 → Thr mutation lowers the electrostatic desolvation free energy and removes an intramolecular ionic pair between Arg21 and Glu19. There is evidence that the Leu18 → Ala mutation, with the shortening of side chain, induces a conformational change that allows the adjacent residue Tyr20 to form intermolecular hydrogen bond with the enzyme. Finally, the Pro14 → Glu mutation increases the backbone flexibility of the binding loop, which allows Tyr11 to form hydrogen bond with Glu174 of the enzyme.

In conclusion, the present computational study addresses the main questions regarding specificity in the binding of ALP to serine protease inhibitors eglin C, OMTKY3 and its mutant OMTKY3M. The results demonstrate the usefulness and limitations of the MM-PB/SA method and the binding free energy decomposition in probing protein–protein interaction.

4. Materials and methods

Computational protein docking

The initial conformations of the protein complexes used in the MD simulations were generated by the computational protein docking program ZDOCK/RDOCK,^7,8 since the experimental structures have not been determined. The procedures of the computational docking ZDOCK/RDOCK calculations on these protein complexes have been described in detail elsewhere.⁵ ZDOCK is an initial-stage rigid-body docking algorithm based on the fast Fourier transform (FFT) technique that efficiently searches the six-degree of freedom translational and rotational space of protein–protein complexation. RDOCK refinement uses energy minimization to re-rank the ZDOCK predicted poses with an empirical scoring function. The protein–protein docking was performed to generate structures of ALP-eglin C and ALP-OMTKY3. In both cases, the structures of the unbound ALP, eglin C and OMTKY3 are taken from PDB entry 1GBK, 1ACB and 1CHO, respectively. The structure of ALP-OMTKY3M complex was obtained by carrying out the mutations K13A-P14E-L18A-R21T-N36D manually using the structure of ALP-OMTKY3, and performing energy minimization of the mutated structure.

Binding free energy calculation

The binding free energy for two associating molecules in solution is the difference between the free energies (chemical potentials) of the complex and those of the two free molecules:⁹

$$\mathrm{\Delta }{G}_{\text{bind}}=-k_{\mathrm{B}}T\text{ln}{K}_{\text{eq}}=G_{\text{complex}}-G_{\text{prot}1}-G_{\text{prot}2}$$ (11)

The free energy of a solute × in solution can be expressed as a function of solute atom configurations only, with the influence of solvent treated in a mean-field fashion. The free energy G_X consists of three terms: the energy of the solute in gas phase, the solvation free energy of the solute, and the solute entropy contribution:

$$G_X=E_X(\text{gas})+G_X(\text{solv})-T{S}_X(\text{solute})$$ (12)

This expression follows directly from the statistical mechanical formula of the Helmholtz free energy for a solute molecule in solution, given by Lazaridis and Karplus:²⁸

$$A=A^0+k_{\mathrm{B}}T\left(\frac{{\Lambda }^{3M}}{V8{\pi }^2}\right)+\int p(q)(H_{\text{gas}}+\mathrm{\Delta }{G}^{\text{slv}})\mathrm{d}q+k_{\mathrm{B}}T\int p(q)\text{ln}p(q)\mathrm{d}q$$ (13)

In eqn (13), the second and fourth terms are the solute translational/rotational entropy and the solute configurational entropy contributions, respectively. The third term is identified as the sum of ensemble-averaged gas phase energy and the solvation free energy, also known as the effective energy.

The gas phase energy in eqn (12) is the sum of intramolecular interaction energy (bonds, angle, and torsion) and nonbonded interaction energy (van der Waals and Coulombic terms):

$$E_X(\text{gas})=E_X(\text{intra})+E_X(\text{elec})+E_X(\text{vdw})$$ (14)

The solvation free energy consists of electrostatic and non-polar contributions:

$$G_X(\text{solv})=G_X(\text{solv}\_\text{elec})+G_X(\text{solv}\_\text{np})$$ (15)

Combining eqn (11), (12), (14) and (15) yields

$$\mathrm{\Delta }{G}_{\text{bind}}=\mathrm{\Delta }E(\text{intra})+\mathrm{\Delta }E(\text{elec})+\mathrm{\Delta }E(\text{vdw})+\mathrm{\Delta }G(\text{solv}\_\text{elec})+\mathrm{\Delta }G(\text{solv}\_\text{np})-T\mathrm{\Delta }S(\text{solute})$$ (16)

In the single trajectory approach used in the present study, the contribution from intramolecular interaction energy ΔE(intra) vanishes, as the configurations of protein complex and unbound proteins are taken from the same trajectory snapshots of the protein complex. Intermolecular Coulombic interaction ΔE(elec) and van der Waals interaction ΔE(vdw) are given by the corresponding terms in the force field. In the MM-PB/SA approach, the electrostatics solvation free energy G_X is computed by using continuum electrostatics formula

$$G(\text{solv}\_\text{elec})=\frac{1}{2}\sum _i{q}_i{\phi }_{\text{rf}}(r_i)$$ (17)

The solvent reaction field φ_rf(r_i) is obtained by solving the Poisson–Boltzmann equation for the electrostatic potentials for the solute X in the dielectric medium of water and in that of vacuum, and taking the difference of the resultant electrostatic potentials at position r_i. The Poisson–Boltzmann equation was solved using the PBEQ module in the CHARMM program version 33b1, with a grid spacing of 0.4 Å. The re-entrant molecular surface is used to define the dielectric boundary between solute and solvent.

The non-polar solvation free energy is estimated by assuming that this contribution is linearly proportional to the solvent accessible surface area (SASA) of the solute molecule:

$$G(\text{solv}\_\text{np})=\gamma \text{SASA}+\mathrm{\beta }$$ (18)

In the present study, a surface tension coefficient γ of 5.42 cal mol⁻¹ Ų and a constant β of 0.92 kcal mol⁻¹ are used in estimating ΔG(solv_np).^13,18

The solute entropy is approximated as the sum of translational, rotational and vibrational contributions. The translational and rotational contributions are calculated using the standard statistical mechanics expressions for entropies of rigid-body translation and rotation in ideal gas.³⁰ The vibrational entropy is calculated by solving the normal mode frequency of the solute and use the standard statistical mechanics formula for harmonic oscillators.³⁰ Prior to the normal mode calculation, the solute system without water and counterions was energy minimized using a distance dependent dielectric constant with ε = 4r, until the root-mean-square energy gradient was less than 10⁻⁵ kcal mol⁻¹ Å. The VIBRAN utility in the CHARMM program was used to diagonalize the second derivative matrix and generate normal mode frequencies.

Finally, each free energy component in eqn (16) is computed using snapshots extracted from the MD trajectory for solute X in explicit solvent, and the ensemble averaged values are used to obtain an estimate of binding free energy.

MD simulation

In the present work, the MD simulations were performed using the CHARMM²⁹ program version 33b1. The all-atom CHARMM22 parameter set³¹ with CMAP³² correction for the backbone torsion angles was used to model proteins in aqueous solutions. Sodium chloride counterions were added to make the solution charge neutral. A truncated octahedral box containing TIP3P water molecules³³ previously equilibrated at 300 K and 1 atm pressure was used to solvate the protein molecules. The solute atoms are separated from nearest walls of the water box by at least 11 Å. Waters within 2.8 Å of solute atoms or counterions were removed. Electrostatic interactions were computed using the particle-mesh Ewald (PME)³⁴ method with a real space cutoff of 10 Å and a grid spacing of 1.05 Å. A switching function between 8 Å and 10 Å was used for van der Waals interactions. SHAKE³⁵ was used to constrain bond lengths involving hydrogen atoms. The Verlet leapfrog integrator was used to solve the equation of motion with an integration step of 2 fs. MD simulations were performed in the NpT ensemble, under atmospheric pressure, using constant pressure/temperature (CPT) dynamics. The following protocol has been used to minimize and equilibrate the solvated system: the solvent alone was first minimized for 500 steps using steepest descent method followed by 500 steps of adopted basis Newton–Raphson (ABNR) method, with the solute molecules fixed in space. The whole system was then minimized for 500 steepest descent steps and 500 ABNR steps with a harmonic restraint on the solute atoms. Following the minimization steps, the system was heated to 295 K from 50 K within 100 ps, with the solute atoms harmonically restrained. The harmonic restraint on solute atoms was gradually removed during the next 300 ps equilibration, which was followed by the production MD run without any restraints. The MD trajectories were saved every I ps for analysis.

Table 3.

(a) Same as Table 2a, except for ALP residues in the complex of ALP-OMTKY3
Residue	ΔEi (vdw)	ΔGi (total_elec)	ΔGi (solv_np)	ΔGi (gas + solv)
TYR171	−4.0	0.9	−0.3	−3.5
HIS57	−2.3	1.0	−0.3	−1.6
GLU174	−0.2	−1.0	−0.3	−1.5
SER214	−1.3	0.0	−0.1	−1.4
ALA173	−2.6	1.9	−0.6	−1.2
GLY193	−0.5	−0.5	−0.1	−1.1
ALA39	−1.1	0.5	−0.3	−0.9
ASP194	−0.8	0.0	0.0	−0.8
VAL218	−0.9	0.3	−0.1	−0.7
PHE94	−0.5	0.0	−0.1	−0.6
GLY215	−1.4	0.9	−0.1	−0.6
ASP102	−0.2	3.6	0.0	3.3
ARG192	−6.5	12.5	−0.8	5.2

(b) Same as Table 2a, except for OMTKY3 residues in the complex of ALP-OMTKY3
LEU18	−7.8	−1.2	−1.1	−10.1
THR17	−4.9	1.1	−0.6	−4.4
TYR20	−4.6	3.3	−0.6	−1.9
ALA15	−2.5	1.2	−0.4	−1.7
CYS16	−2.8	1.6	−0.2	−1.4
PRO14	−1.2	0.2	−0.2	−1.2
LYS34	0.3	−1.2	−0.2	−1.1
ASN33	−1.3	0.5	−0.1	−0.9
ASN36	−1.4	0.9	−0.2	−0.7
GLU19	−3.6	4.8	−0.3	0.9