Geodesic shape regression in the framework of currents

Abstract

Shape regression is emerging as an important tool for the statistical analysis of time dependent shapes. In this paper, we develop a new generative model which describes shape change over time, by extending simple linear regression to the space of shapes represented as currents in the large deformation diffeomorphic metric mapping (LDDMM) framework. By analogy with linear regression, we estimate a baseline shape (intercept) and initial momenta (slope) which fully parameterize the geodesic shape evolution. This is in contrast to previous shape regression methods which assume the baseline shape is fixed. We further leverage a control point formulation, which provides a discrete and low dimensional parameterization of large diffeomorphic transformations. This flexible system decouples the parameterization of deformations from the specific shape representation, allowing the user to define the dimensionality of the deformation parameters. We present an optimization scheme that estimates the baseline shape, location of the control points, and initial momenta simultaneously via a single gradient descent algorithm. Finally, we demonstrate our proposed method on synthetic data as well as real anatomical shape complexes.

1 Introduction

Shape regression is of crucial importance for statistical shape analysis. It is useful to find correlations between shape configuration and a continuous scalar parameter such as age, disease progression, drug delivery, or cognitive scores. When only few follow-up observations are available, regression is also a necessary tool to interpolate between data points and provide a scenario of continuous shape evolution over the parameter range [5,13]. Longitudinal studies also require to compare such regressions across different subjects [5,8,10,11].

Extending traditional scalar regression for shape is not straightforward as shape intrinsically live on a Riemannian manifold. Therefore, methods differ according to the choice of metric on the shape space and the corresponding regression function. In [5], a piecewise geodesic method has been proposed, which extends piecewise linear regression for shape time-series. In [7,16] second-order models have been proposed which are controlled by the acceleration of shape changes or the deviation from geodesic paths. Non-parametric regression has been proposed in [3], extending kernel regression to Riemannian manifolds. In [9] geodesic regression is proposed as a straightforward extension of linear regression on Riemannian manifolds. Geodesic regression is fully characterized by the baseline shape (the intercept) and the tangent vector defining the geodesic at the baseline shape (the slope). Therefore, it seems well adapted for longitudinal studies, since different regressions could be compared by transporting baseline and tangent vectors from subject to subject, using parallel transport for instance [12].

Methods in [5,7,14] are based on the large deformation diffeomorphic metric mapping (LDDMM) paradigm, which is well suited for regression purposes since it is built on a continuous flow of diffeomorphisms that model continuous shape changes over a time period. In [14], geodesic regression is proposed in the LDDMM framework for image data. Extending it for geometric data such as curves and surfaces is challenging for at least two reasons.

First, images seen as measures on ℝ³ inherit from a linear structure which eases the estimation of the baseline image (images could be averaged by averaging grey levels for instance). Curves or surfaces could be also embedded into a vector space if we assume point correspondences between shapes [2]. Alternatively, we can avoid explicit correspondence by embedding shapes into the space of currents, which defines a generic metric which can handle both surfaces and curves or any mix of them. However, the average of surfaces in the space of currents is usually not a surface anymore [5]. To overcome this limitation, we will use here the new formulation initiated in [6], which allows to optimize a given template in the space of currents, while preserving its topology.

Second, the parameterization of the deformations in the LDDMM setting is given by a scalar momenta map (which plays the role of the tangent vector defining the geodesic path), which has the same dimension as the images. For point data, the parameterization is given by one momentum vector at every point of the baseline shape. The dimension of this parameterization explodes when shape complexes are analyzed. To overcome this limitation, we will use the control point formulation in the LDDMM setting that has been introduced in [4]. Consequently, our geodesic model characterizes complex evolution with a small number of parameters (defined by the user), compared to [5,7] which require vectors at every shape point and every time point in the discretization.

2 Methods

2.1 Shape regression

In shape regression, the goal is to estimate a continuous shape evolution from a discrete set of observed shapes O_ti at time t_i within the time interval [t₀, T]. Here we consider shape to be generic geometric objects that can be represented as curves, landmark points, or surfaces in 2D or 3D. Shape evolution is modeled as the geodesic flow of diffeomorphisms acting on a baseline shape X₀, defined as X(t) = ϕ_t(X₀) with t varying continuously within the time interval determined by the observed data. The baseline shape X₀ is continuously deformed over time to match the observation data (X(t_i) ~ O_ti) with the rigidity of the evolution controlled by a regularity term. This setting is naturally expressed as a variational problem, described by the regression criterion

$$\begin{array}{l}E({\mathbf{X}}_0,{\varphi }_t)=\sum _{i=1}^{N_{\mathit{obs}}}{\Vert ({\varphi }_{t_i}({\mathbf{X}}_0)-{\mathbf{O}}_{t_i})\Vert }_{W^{\ast }}^2+\text{Reg}({\varphi }_t)\\ =\sum _{i=1}^{N_{\mathit{obs}}}D(\mathbf{X}(t_i),{\mathbf{O}}_{t_i})+L({\varphi }_t)\end{array}$$ (1)

where D represents the squared distance on currents ( ${\Vert ·\Vert }_{W^{\ast }}^2$) and L is a measure of the regularity of the time-varying deformation ϕ_t.

2.2 Control point parameterization of deformations

We adopt a discrete parameterization of deformations, where dense diffeomorphisms of the underlying space are built by interpolating momenta located at control points [4]. Let c₀ = {c₁, …, c_Nc} be a finite set of control points which carry initial momenta vectors α₀ = {α₁, …α_Nc}, together referred to as the initial state of the system S₀ = {c₀, α₀}.

The set of control point positions c₀ and initial momenta α₀ serve as initial conditions for the geodesic equations, which define the time evolution of the system of control points and momenta, given by

$$\{\begin{array}{l}{\stackrel{.}{c}}_i(t)=\sum _{p=1}^{N_c}K(c_i(t),c_p(t)){\alpha }_p(t)\hfill \\ {\stackrel{.}{\alpha }}_i(t)=-\sum _{p=1}^{N_c}{\alpha }_i{(t)}^t{\alpha }_p(t){\nabla }_{1}K(c_i(t),c_p(t))\hfill \end{array}$$ (2)

where K is the interpolating kernel assumed (without loss of generality) to be Gaussian: K(x, y) = exp(−|x−y|²)/σ²). These equations describe the evolution of the state of the system S(t) = {c_i(t), α_i(t)} and can be written in short as Ṡ(t) = FS(t)

Thanks to the geodesic equations, the trajectories of control points c_i(t) and α_i(t) now parameterize the time-varying velocity field v(x, t) defined at any point in space x and time t as

$$\stackrel{.}{x}(t)=v(x,t)=\sum _{p=1}^{N_c}K(x,c_p(t)){\alpha }_p(t).$$ (3)

which can be written in short as ẋ(t) = G(x(t), S(t)).

The time-varying velocity field v(x, t) can then be used to build the flow of deformations ϕ_t(x) in the spirit of the LDDMM framework by integrating the ODE: ϕ̇_t(x) = v(ϕ_t(x), t). Using the coordinates of the baseline shape X₀ as initial conditions, integrating this ODE computes the deformation of the baseline shape from time t₀ to T. Therefore the flow of diffeomorphisms is fully determined by the initial state of the system S₀: the set of initial control points c₀ and initial momenta vectors α₀.

2.3 Minimization of regression criterion

The geodesic flow of diffeomorphisms ϕ_t in the criterion (1) is parameterized by N_c control points and momenta vectors S₀ = {c₀, α₀}, which act as initial conditions for the flow equations (2). The baseline shape X₀ can then be deformed according to this flow by applying equation (3). Therefore we seek to estimate the position of the control points, initial momenta, and position of the points on the baseline shape such that the resulting geodesic flow of the baseline shape best matches the observed data. An overview of our control point formulation of geodesic shape regression is shown in Fig. 1. With all elements of our framework defined, geodesic shape regression can now be described by the specific regression criterion

Fig. 1.

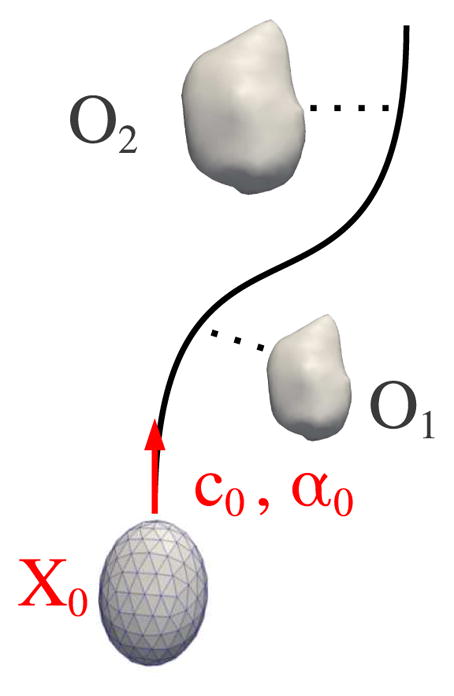
Overview of geodesic regression with estimated parameters in red.

$$E({\mathbf{X}}_0,{\mathbf{S}}_0)=\sum _{i=1}^{N_{\mathit{obs}}}\frac{1}{2{\lambda }^2}D(\mathbf{X}(t_i),{\mathbf{O}}_{t_i})+L({\mathbf{S}}_0)$$ (4)

subject to

$$\{\begin{array}{ll}\stackrel{.}{\mathbf{S}}(t)=F(\mathbf{S}(t))\hfill & \text{with}\mathbf{S}(0)=\{{\mathbf{c}}_0,{\mathit{\alpha }}_0\}\hfill \\ \stackrel{.}{\mathbf{X}}(t)=G(\mathbf{X}(t),\mathbf{S}(t))\hfill & \text{with}\mathbf{X}(0)={\mathbf{X}}_0\hfill \end{array}$$ (5)

where λ² is used to balance the importance of the data term and regularity, $L({\mathbf{S}}_0)={\sum }_{p,q}{\alpha }_{0,p}^{t}K(c_{0,p},c_{0,q}){\alpha }_{0,q}$ is the regularity term defined by the kinetic energy of the control points. The first part of (5) describes the trajectory of the control points and momenta as in (2). The second equation of (5) represents flowing the baseline shape along the deformation defined by S(t) as in (3).

As shown in the appendix, the gradients of the criterion (4) are

$${\nabla }_{{\mathbf{S}}_0}E=\xi (0)+{\nabla }_{{\mathbf{S}}_0}L{\nabla }_{{\mathbf{X}}_0}E=\theta (0)$$ (6)

where the auxiliary variables θ(t) and ξ(t) = {ξ^c, ξ^α} satisfy the ODEs:

$$\begin{array}{ll}\stackrel{.}{\theta }(t)=-{\partial }_{1}G{(t)}^t\theta (t)+\sum _{i=1}^{N_{\mathit{Obs}}}{\nabla }_{\mathbf{X}(t_i)}D(t_i)\delta (t-t_i)\hfill & \theta (T)=0\hfill \\ \stackrel{.}{\xi }(t)=-({\partial }_{2}G{(t)}^t\theta (t)+d_{\mathbf{S}(t)}F{(t)}^t\xi (t))\hfill & \xi (T)=0\hfill \end{array}$$ (7)

The gradient is computed by first integrating equations (2) forward in time to construct the flow of diffeomorphisms. The deformations are then applied to the baseline shape by integrating forward in time equation (3). With the full trajectory of the deformed baseline shape, one can compute the gradient of the data term ∇_X(ti)D(t_i), corresponding to each observation. The ODEs (7) are then integrated backwards in time, with the gradients of the data term acting as jump conditions at observation time points, which pull the geodesic towards target data. The final values of the auxiliary variables θ(0) and ξ(0) are then used to update the location of the control points, the initial momenta, and the location of the points on the baseline shape.

The method, summarized in Algorithm 1, is implemented via a gradient descent scheme. The parameters of the algorithm are the tradeoff between data matching and regularity λ, the standard deviation of the deformation kernel σ_V, and the standard deviation of the metric on currents σ_W. The value of σ_V controls the scale at which points in space move in a correlated manner, while the value of σ_W controls the scale at which shape differences are considered noise. The algorithm also requires an initial baseline shape. For surfaces, initialization consists of an ellipsoid for each connected component of the shapes, which defines the number of shape points as well as the connectivity, which is preserved during optimization.

Algorithm 1.

Geodesic shape regression

3 Results

Synthetic Transformations

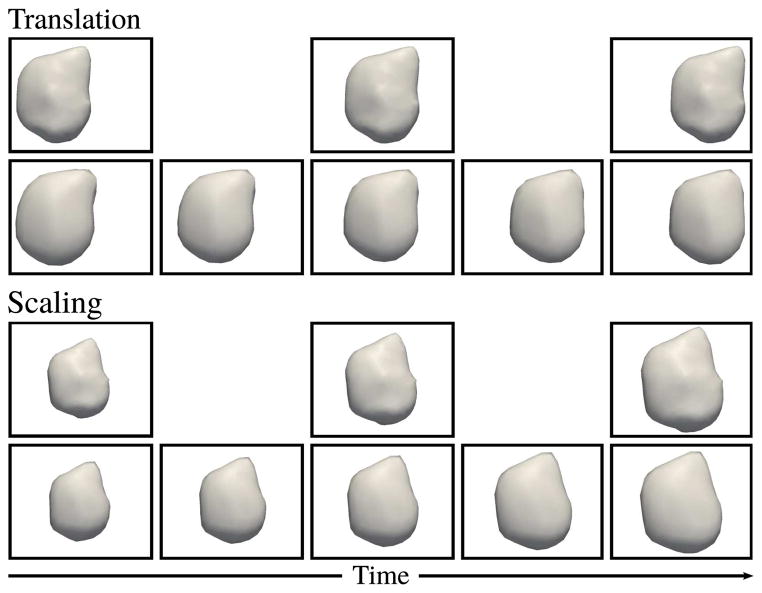
We explore the ability of the geodesic regression model to capture simple synthetic transformations applied to a real anatomical surface. We consider the amygdala surface extracted from a 4 year old child and investigate translation and scaling. For both experiments, we initialize the baseline shape to be an ellipse, as shown in Fig. 2, which defines the topology of the baseline shape, which will remain unchanged during optimization. We define 12 control points on a regular grid and parameters σ_V = 12 mm, σ_W = 5 mm, and λ = 0.1. Both experiments contain three shape observations spaced one time unit apart.

Fig. 2.

Initial baseline shape and observed amygdala.

For both experiments, the baseline shape estimated by our method closely matches the amygdala surface at the earliest time point and the dynamics of shape evolution are well captured by the geodesic model (Fig. 3). However, very accurate matching of the target shapes is not the goal with a geodesic model (and is generally not possible). The power of the model lies in the low dimensional parameterization of shape evolution, which facilitates statistical analysis. These experiments demonstrate the compactness of the geodesic model – continuous shape evolution is described by the baseline shape and 12 momentum vectors.

Fig. 3.

For both translation and scaling panels, the top row shows discrete shape observations of the amygdala surface, while the bottom row shows shapes estimated during geodesic regression at observation times as well as intermediate stages. Our method estimates a baseline shape and momenta vectors that capture shape evolution.

Synthetic Tumor Evolution

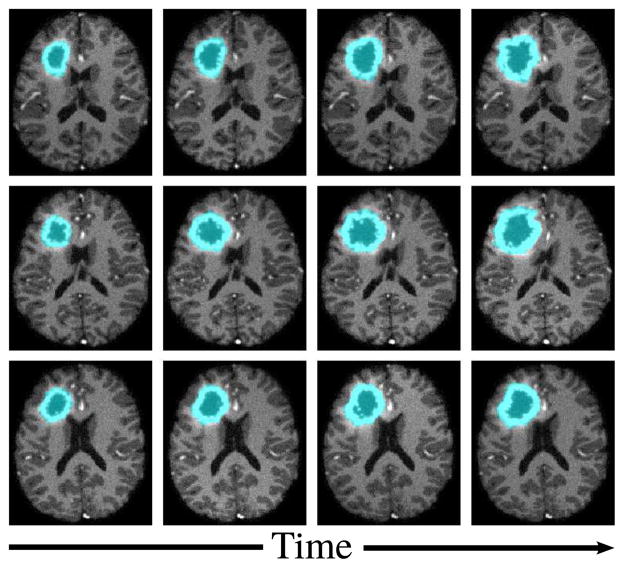
Next, we apply our geodesic model to study tumor evolution over time. Using TumorSim [15], we simulate three differing tumor scenarios : a slowly deforming tumor, a rapidly deforming tumor, and a tumor which infiltrates rather than deforming surrounding tissue. We obtain four observations in the time span of one year, obtained at the same baseline time 0, 5 ± 1, 8 ± 1, and 12 months. This mimics the acquisition of real medical images, which are not necessarily acquired at the same time for every patient. The simulated images and tumor segmentations are shown in Fig. 4.

Fig. 4.

Four observations of synthetic tumor evolution. Top) Slowly deforming tumor. Middle) Rapidly deforming tumor. Bottom) Tumor which infiltrates surrounding tissue. The first two cases show different degrees of deformation in surrounding tissue and ventricles, while the third has little deformation.

In order to compare the differing tumor evolutions, we leverage the control point formulation. We establish a common reference space which is shared among each geodesic model by placing 125 control points on a regular grid with 12 mm spacing and freeze these locations during optimization. We estimate a geodesic model for each tumor scenario, using parameters σ_V = 12 mm, σ_W = 5 mm, λ = 1.0, and initialize the baseline shape with an ellipse.

The estimated baseline tumor and initial momenta are displayed in Fig. 5 for each of the three tumor scenarios. The magnitude of the momenta describing the rapidly deforming tumor are the largest among the three tumor scenarios, which is also evident in the speed of growth overlaid on the baseline tumor. The orientation of the momenta vectors encode the direction of tumor growth, which highlight the differences in the way each tumor evolves. We note that the initial momenta vectors do not differentiate well between deforming and infiltrating tumors, as the infiltration process cannot be described by tumor shape alone. However, the estimated baseline shape and dynamics of shape change are well captured by the geodesic model for all three tumor scenarios.

Fig. 5.

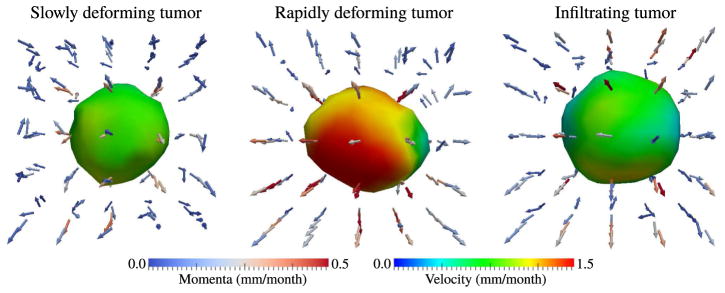
Baseline shape and initial momenta for geodesic models of tumor evolution. Our regression framework captures the different tumor growth characteristics, with momenta vectors constrained to be in the same coordinates for comparison purposes.

Pediatric Subcortical Development

We next investigate the application of geodesic shape regression to model pediatric subcortical development. Three subcortical shapes are considered as a multi-object shape complex: putamen, amygdala, and hippocampus. The structures were obtained from MRI of a healthy child scanned at approximately 9, 13, and 24 months of age. Geodesic regression was conducted using 126 control points and parameters σ_V = 8 mm, σ_W = 6 mm, and λ = 1.0. To improve speed of convergence, we initialize the baseline shapes for each subcortical structure with an ellipse that has been coarsely registered to its corresponding subcortical shape. Regression was conducted on all shapes simultaneously, resulting in one deformation of the ambient space.

Several snapshots of the evolution of subcortical structures is shown in Fig. 6, with estimated baseline shape shown at 6 months. From 6 to 26 months, all subcortical structures increase in size, with the putamen demonstrating the most dramatic growth. The evolution of the putamen is characterized by accelerated growth at the superior anterior and inferior posterior regions, while the hippocampus grows mostly at the extreme posterior region, expanding and bending at the tip. The geodesic model is able to capture interesting non-linear growth patterns with few parameters; the full time evolution is modeled by three baseline shapes and 126 momenta vectors.

Fig. 6.

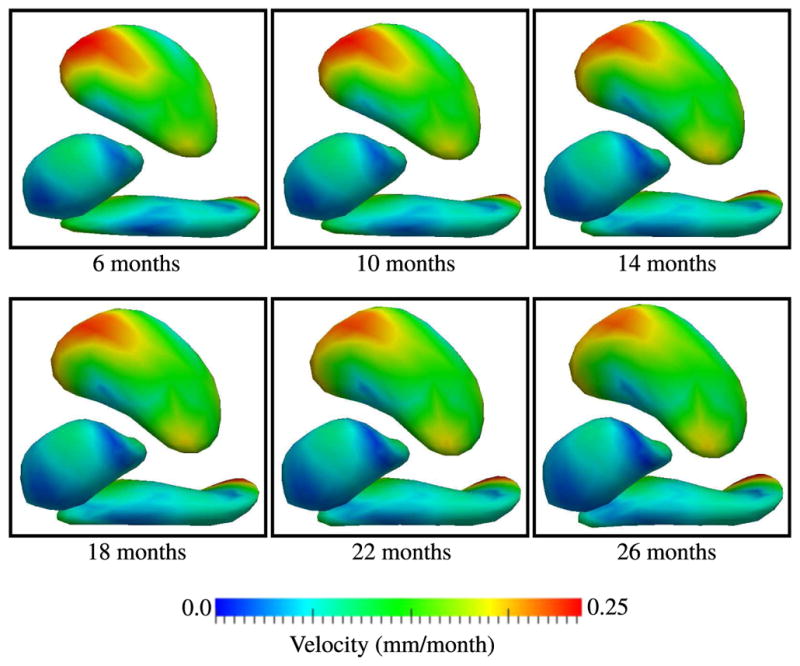
Snapshots of subcortical shape evolution after geodesic regression on a multi-object complex: putamen, amygdala, and hippocampus.

This experiment demonstrates the applicability of the geodesic model in characterizing pediatric subcortical development. Our regression framework simultaneously handles multiple shapes, including those with complex geometry. Multi-object regression allows for a more complete analysis, compared to an independent treatment of each subcortical structure, which ignores potentially important spatial relationships between structures. This single subject experiment can also be extended to a population analysis thanks to the control point formulation of deformations. As with the previous tumor experiment, one can fix the control point locations for all subjects. The differences between and within populations can be quantified by exploring the variability between estimated baseline shapes, and between initial momenta at identical locations for all subjects.

White Matter Fibers in Early Brain Development

Finally, we study early brain development by considering the evolution of white matter connections from birth to 2 years of age. For this experiment, we have diffusion tensor imaging (DTI) data from 17 subjects with scans obtained at clustered time points of 2 ± 2, 12 ± 2 months, and 24 ± 2 months. We extract the genu fiber tract from each DTI using the framework of [1]. In our experiment, we use 26 genu fiber tracts which are represented as a collection of 3D curves. By considering fiber geometry obtained from multiple subjects, the estimated geodesic model can be considered as the development of the genu tract for an average child. We initialize the baseline shape with the genu fiber bundle from the atlas space, define 75 control points on a regular grid, and set parameter values as σ_V = 5 mm, σ_W = 8 mm, and λ = 0.1.

The average development of the genu tract estimated by our geodesic model is summarized in Fig. 7, which shows several snapshots on the genu fibers over time. The elongation of the fibers reflects the myelination process that occur during early development, where myelin sheaths grows to cover white matter regions outward to the cortex. Our geodesic regression framework handles the multiple fiber structure that form the genu fiber bundle, using the currents framework to match the curvilinear fiber structures.

Fig. 7.

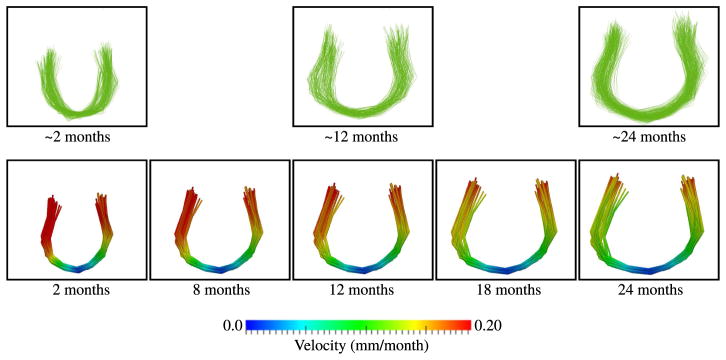
Average development of genu fiber tract from 2 to 24 months. Top row shows observed data for all subjects, which is clustered around 2, 12, and 24 months. Bottom row shows genu fiber tracts estimated from geodesic regression at several time points with velocity of fiber development displayed on the surface of the estimated fibers.

4 Conclusions

We have presented a geodesic regression model for shapes represented as currents in the large deformation diffeomorphic metric mapping (LDDMM) framework where dense diffeomorphisms are built using a control point formulation. This provides a discrete and low dimensional parameterization of large diffeomorphic transformations, decoupling the parameterization of deformations from the specific shape representation. By representing shapes as currents, our regression model can seamlessly handle both surfaces and curves, or any combination of them represented as multi-object complexes. This is a powerful representation that incorporates potentially important spatial relationships between anatomical shapes into the regression framework.

By analogy with linear regression, our generative geodesic model is fully characterized by a baseline shape (intercept) and initial momenta vectors (slope). We have introduced an optimization scheme which estimates the baseline shape, location of the control points, and initial momenta simultaneously via a single gradient descent algorithm. Finally, we presented results from experiments carried out on a diverse collection of shape data, demonstrating the widespread applicability of our geodesic shape regression framework. Future work will focus on incorporating the geodesic model into a framework for the statistical analysis of longitudinal data. We will explore approaches which simultaneously estimate a population baseline as well as momenta for individual subjects in homologous locations. We will also explore methods for transporting baseline shapes and momenta vectors between subjects and between population groups to enable hypothesis testing on 4D growth models.

A Differentiation of the Regression Criterion

Consider a perturbation δS₀ to the initial state of the system (c₀, α₀), which leads to a perturbation of the motion of the control points δS(t), a perturbation of the template shape trajectory δX(t), and a perturbation of the criterion δE

$$\delta E=\sum _{i=1}^{N_{\mathit{obs}}}({({\nabla }_{\mathbf{X}(t_i)}D(t_i))}^t\delta \mathbf{X}(t_i))+{({\nabla }_{{\mathbf{S}}_0}L)}^t\delta {\mathbf{S}}_0.$$ (8)

The perturbations δS(t) and δX(t) satisfy the ODEs:

$$\begin{array}{ll}\delta \stackrel{.}{\mathbf{S}}(t)=d_{\mathbf{S}(t)}F(t)\delta \mathbf{S}(t)\hfill & \delta \mathbf{S}(0)=\delta {\mathbf{S}}_0\hfill \\ \delta \stackrel{.}{\mathbf{X}}(t)={\partial }_{1}G(t)\delta \mathbf{X}(t)+{\partial }_{2}G(t)\delta \mathbf{S}(t)\hfill & \delta \mathbf{X}(0)=\delta {\mathbf{X}}_0\hfill \end{array}$$ (9)

Let $R_{st}=exp\left({\int }_s^t{d}_{\mathbf{S}(u)}F(u)du\right)$ and $V_{st}=exp\left({\int }_s^t{\partial }_{1}G(u)du\right)$. The first ODE is a linear homogeneous ODE with well known solution

$$\delta \mathbf{S}(t)=R_{0t}\delta {\mathbf{S}}_0$$ (10)

The second ODE is a linear inhomogeneous ODE with solution

$$\delta \mathbf{X}(t_i)=\left({\int }_0^{t_i}{V}_{{ut}_i}{\partial }_{2}G(u)R_{0u}du\right)\delta {\mathbf{S}}_0+V_{0t_i}\delta {\mathbf{X}}_0$$ (11)

which can now be plugged into (8). After arranging terms we have

$$\delta E=\sum _{i=1}^{N_{\mathit{obs}}}{\left[{\int }_0^{t_i}{R_{0u}}^t{\partial }_{2}G{(u)}^t{V_{{ut}_i}}^t{\nabla }_{\mathbf{X}(t_i)}D(t_i)du\right]}^t\delta {\mathbf{S}}_0+{[{\nabla }_{{\mathbf{S}}_0}L]}^t\delta {\mathbf{S}}_0+\sum _{i=1}^{N_{\mathit{obs}}}{[{V_{0t_i}}^t{\nabla }_{\mathbf{X}(t_i)}D(t_i)]}^t\delta {\mathbf{X}}_0$$ (12)

Letting $\theta (t)={\sum }_{i=1}^{N_{\mathit{obs}}}{V_{{tt}_i}}^t{\nabla }_{\mathbf{X}(t_i)}D(t_i){\mathbf{1}}_{\{t\le t_i\}}$, g(t) = ∂₂G(t)θ(t), and $\xi (t)={\int }_t^{t_i}{R_{tu}}^{t}g(u)du$ leads to the gradient of the criterion written as

$$\{\begin{array}{l}{\nabla }_{{\mathbf{S}}_0}E={\int }_0^{t_i}{R_{0u}}^{t}g(u)du+{\nabla }_{{\mathbf{S}}_0}L=\xi (0)+{\nabla }_{{\mathbf{S}}_0}L\hfill \\ {\nabla }_{{\mathbf{X}}_0}E=\theta (0)\hfill \end{array}$$ (13)

where auxiliary variables θ(t) and ξ(t) satisfy the ODEs

$$\begin{array}{ll}\stackrel{.}{\theta }(t)=-{\partial }_{1}G{(t)}^t\theta (t)+\sum _{i=1}^{N_{\mathit{Obs}}}{\nabla }_{\mathbf{X}(t_i)}D(t_i)\delta (t-t_i)\hfill & \theta (T)=0\hfill \\ \stackrel{.}{\xi }(t)=-({\partial }_{2}G{(t)}^t\theta (t)+d_{\mathbf{S}(t)}F{(t)}^t\xi (t))\hfill & \xi (T)=0.\hfill \end{array}$$ (14)