On individual genome-wide association studies and their meta-analysis

Abstract

Individual genome-wide association (GWA) studies and their meta-analyses represent two approaches for identifying genetic loci associated with complex diseases/traits. Inconsistent findings and non-replicability between individual GWA studies and meta-analyses are commonly observed, hence posing the critical question as to how to interpret their respective results properly. In this study, we performed a series of simulation studies to investigate and compare the statistical properties of the two approaches. Our results show that: 1) As expected, meta-analysis of larger sample size is more powerful than individual GWA studies under the ideal setting of population homogeneity among individual studies; 2) Under the realistic setting of heterogeneity among individual studies, detection of heterogeneity is usually difficult and meta-analysis (even with the random-effects model) may introduce elevated false positive and/or negative rates; 3) Despite of relatively small sample size, well-designed individual GWA study has the capacity to identify novel loci for complex traits; 4) Replicability between meta-analysis and independent individual studies or between independent meta-analyses is limited, thus inconsistent findings are not unexpected.

Introduction

Genome-wide association (GWA) studies are commonly used to discover genetic loci responsible for complex diseases. To date, nearly 8,000 SNPs have been identified to be associated with a variety of complex diseases through over 1,400 GWA studies (Hindorff et al. 2009). This number is anticipated to increase dramatically with the maturation of next-generation sequencing technologies which permit direct mapping of causal SNPs. Nevertheless, for most traits/diseases studied, only a small portion of phenotypic variation or disease risk is accounted for by the genetic variants that have been identified thus far. The unidentified “missing” heritability may be due, in part, to genetic variants with minor phenotypic effects that escaped detection by individual GWA studies with insufficient statistical power (Altshuler and Daly 2007; Wang et al. 2005). In order to increase statistical power, meta-analysis of multiple GWA studies attempts to combine summary statistics from multiple individual studies. This enlarges the study sample size dramatically, and may therefore provide a substantial increase in statistical power. A variety of GWA meta-analyses conducted to date have indeed proven their superiority over individual GWA studies in detecting many additional genetic loci underlying complex diseases/traits (Bradfield et al. 2012; Elks et al. 2010; Franke et al. 2010; Kato et al. 2011).

As the number of meta-analyses of GWA studies increases, however, it has been observed that there are frequent inconsistencies between meta-analyses and individual studies or between different meta-analyses. This situation raises a critical question as to how to interpret association results derived from different studies. Large-scale meta-analyses have been generally used to analyze the value, and judge the robustness, of findings of individual GWA studies, because of the presumed increased power associated with meta-analyses (Richards et al. 2012). However, without a systematic investigation on the relative statistical properties of different studies such as individual GWA studies versus their meta-analyses, it may be premature to routinely accept the superiority of meta-analyses.

In this study, we assessed and compared the relative statistical properties of individual GWA studies and their meta-analyses. We explored possible mechanisms for discordant results between individual GWA studies and meta-analysis, and those between different meta-analyses. The results we present have significant implications for the design and, in particular, the interpretation of results for individual GWA studies and their meta-analyses.

Methods

We focused on a quantitative trait and performed simulation studies with a variety of contexts. Under each context, multiple individual studies of homogeneous or heterogeneous setting were simulated. Association analyses were performed on each individual study. Summary statistics from individual studies, e.g., regression coefficient, were then combined for a meta-analysis with fixed-effects (FE) or random-effects (RE) model.

Assessing the effect of different LD patterns and allele frequencies on heterogeneity

Between-study heterogeneity is a common issue in meta-analyses (Ioannidis et al. 2001), and it could be caused by a variety of factors, such as study-specific analytical approaches, unmatched study designs; different linkage disequilibrium (LD) patterns, different allele frequencies and/or effect sizes, and different patterns of interaction between genetic variants and environmental exposures (Evangelou and Ioannidis 2013; Glasziou and Sanders 2002; McCarthy et al. 2008). Here, we selected different LD patterns and allele frequencies that were of most interest, and investigated their effects on between-study heterogeneity.

We simulated 10 individual studies. For ease of illustration, all studies had an equal number of 2,000 subjects. Three scenarios were considered. In the first scenario, a causal SNP was simulated and tested with a homogeneous setting across the 10 studies in terms of effect size and allele frequency. In the second scenario, a causal SNP was simulated with a heterogeneous setting in terms of allele frequency. Specifically, individual studies were drawn from three distinct populations with proportions 60%:30%:10%. Allele frequency for each population was generated using the Balding-Nichols model (Balding and Nichols 1995). Briefly, it was drawn from a Beta distribution with parameters p(1−F_st)/F_st and (1−p)(1−F_st)/F_st, where p was the ancestral allele frequency and F_st was a measure of genetic distance between populations (Wright 1950). We set a moderate level of F_st at 0.05 and set p to vary from 0.05 to 0.95, respectively. In the third scenario, a causal SNP was simulated but tested by another proxy SNP that was in LD with it. The minor allele frequencies (MAFs) of both causal and proxy SNPs were set at 0.1. A heterogeneous setting in terms of LD was assumed. Specifically, the LD measure r² between the causal and proxy SNPs varied among 0.3-0.5-0.8, 0.7-0.8-0.9, and 0.8-0.8-0.8, respectively, in the three populations. Under each scenario, we simulated 5,000 replicates and measured heterogeneity by I² index (see below for details) (Higgins and Thompson 2002; Higgins et al. 2003).

In what follows, we disregarded the detailed sources of heterogeneity effects, and introduced a single parameter ${\sigma }_{bp}^2$ to measure between-population heterogeneity, and ${\sigma }_{wp}^2$ to describe the within-population heterogeneity (see below for detail).

Model for heterogeneous effects

Assuming there are s populations and there are n_i (i = 1, 2,…, s and ∑n_i = k) individual studies in the i_th population. Let θ_ij be the effect size for the j_th study from the i_th population,

$${\theta }_{ij}={\theta }_{\mathrm{o}}+u_i+w_{ij},$$ (1)

where θ_o is the mean effect size; $u_i~N(0,{\sigma }_{bp}^2)$ is the population specific random effect and $w_{ij}~N(0,{\sigma }_{wp}^2)$ is the study-specific random effect. The variance ${\tau }^2={\sigma }_{wp}^2+{\sigma }_{bp}^2$ measures between-study heterogeneity effect.

Various heterogeneous effects could be simulated by setting different values for ${\sigma }_{wp}^2$ and ${\sigma }_{bp}^2$: 1) ${\sigma }_{wp}^2={\sigma }_{bp}^2=0$, the component individual studies were all homogeneous; 2) ${\sigma }_{bp}^2=0$ and ${\sigma }_{wp}^2>0$, the component individual studies were sampled from the same population and within-population variation existed due to different phenotype measures, study designs and analytical approaches etc.; 3) ${\sigma }_{bp}^2>0$ and ${\sigma }_{wp}^2=0$, the component individual studies were sampled from different populations and all studies were homogenous with respect to study design, analytical approach and other study-level properties; between-study heterogeneity was entirely attributable to variance in LD levels, allele frequencies and other population-level properties; 4) ${\sigma }_{bp}^2>0$ and ${\sigma }_{wp}^2>0$, the component individual studies were sampled from different populations and between-study heterogeneity existed due to different study designs, phenotype measures, LD levels, allele frequencies, etc. In reality, the 4^th scenario would most closely reflect GWA studies and meta-analyses in the field, as individual GWA studies included in meta-analyses generally come from populations that differ to varying extents (${\sigma }_{bp}^2>0$) and often also have different phenotyping approaches, study designs and analytical approaches (${\sigma }_{wp}^2>0$).

The phenotypic value y_ijk of the k_th individual in the j_th study and the i_th population is modeled as,

$$y_{ijk}={\theta }_{ij}{x}_{ijk}+{\epsilon }_{ijk},$$ (2)

where x_ijk is genotype score encoded in an additive mode of inheritance; ${\epsilon }_{ijk}~N(0,{\sigma }_{\epsilon }^2)$ is random error. Assuming independence between u_i and w_ij, phenotypic variance ${\sigma }_y^2=\text{var}({\theta }_0{x}_{ijk})+\text{var}(u_i{x}_{ijk})+\text{var}(w_{ij}{x}_{ijk})+{\sigma }_{\epsilon }^2$. The heritability h² of the SNP is defined as,

$$h^2=\text{var}({\theta }_0{x}_{ijk})/{\sigma }_y^2=2{\theta }_0^{2}q(1-q)/{\sigma }_y^2,$$ (3)

where q is the MAF of the causal SNP. The proportion of phenotypic variation explained by the between-population heterogeneity effect is

$$\text{var}(u_i{x}_{ijk})/{\sigma }_y^2=({\sigma }_{bp}^2/{\sigma }_y^2)(2q-q^2),$$ (4)

and that explained by the within-population heterogeneity effect is

$$\text{var}(w_{ij}{x}_{ijk})/{\sigma }_y^2=({\sigma }_{wp}^2/{\sigma }_y^2)(2q-q^2).$$ (5)

The total proportion of phenotypic variation explained by between-study heterogeneity is thus

$$\text{var}(w_{ij}{x}_{ijk}+u_i{x}_{ijk})/{\sigma }_y^2=(({\sigma }_{bp}^2+{\sigma }_{wp}^2)/{\sigma }_y^2)(2q-q^2),$$ (6)

which depends on MAF q, ${\sigma }_{bp}^2,{\sigma }_{wp}^2$, and ${\sigma }_y^2$.

Meta-analysis

Two distinct models can be used to perform meta-analyses: FE model and RE model. Briefly, the FE model assumes that all individual studies have a common effect size and that differences between observed effect sizes are attributable merely to sampling error. The RE model, on the other hand, assumes that effect sizes are drawn from a distribution. Within the RE model, two sources of variance contribute to differences between the observed effect size estimates: sampling error and between-study heterogeneity. Assuming β_ij and ν_ij are the observed effect size and its variance. We adopted the inverse variance weighted method to construct the test statistic for both FE and RE meta-analyses (de Bakker et al. 2008). The test statistic

$$z_{\mathit{\text{meta}}}=\frac{\mathrm{\beta ̂}}{SÊ},$$ (7)

where $\mathrm{\beta ̂}=\frac{{\sum }_i{\sum }_j{\beta }_{ij}{w}_{ij}}{{\sum }_i{\sum }_j{w}_{ij}}$ is the combined effect size across studies and $SÊ=\sqrt{\frac{1}{{\sum }_i{\sum }_j{w}_{ij}}}$ is the corresponding standard error; the weight $w_{ij}=\frac{1}{{\nu }_{ij}}$ in the FE model and $w_{ij}=\frac{1}{{\nu }_{ij}+{\mathrm{\tau ̂}}^2}$ in the RE model, where τ̂² is the estimate of between-study heterogeneity τ². It is a function of Cochran's Q (Cochran 1954),

$${\mathrm{\tau ̂}}^2=\{\begin{array}{cc}\frac{Q-(k-1)}{{\sum }_i{\sum }_j{w}_{ij}-({\sum }_i{\sum }_j{w}_{ij}^2)/({\sum }_i{\sum }_j{w}_{ij})}\hfill & \mathit{\text{for}}Q>(k-1)\hfill \\ 0\hfill & \mathit{\text{for}}Q\le (k-1)\hfill \end{array},$$ (8)

where Q = ∑_i∑_j (β_ij − β̂)² and $w_{ij}=\frac{1}{{\nu }_{ij}}$.

z_meta approximately follows a standard normal distribution under the null hypothesis, which is the basis for assessing its statistical significance.

Heterogeneity test

Cochran’s Q test is widely used to determine whether the between-study heterogeneity τ² =0. Under the null hypothesis that the effect sizes are equal in all studies, the Q statistic follows a chi-square distribution with k−1 degrees of freedom. A significance level of p<0.1 suggests the existence of significant heterogeneity (Cochran 1954).

I² index is another widely used measure for quantifying degree of heterogeneity (Higgins and Thompson 2002; Higgins et al. 2003),

$$I^2=\{\begin{array}{cc}\frac{Q-(k-1)}{Q}\times 100\%\hfill & \mathit{\text{for}}Q>(k-1)\hfill \\ 0\hfill & \mathit{\text{for}}Q\le (k-1)\hfill \end{array}.$$ (9)

An I² index larger than 50% indicates substantial heterogeneity (Kavvoura and Ioannidis 2008). We evaluated the performance of the heterogeneity test by summarizing the proportion of simulations with an I² index larger than 50% or a p-value for the Q test less than 0.1.

In the following, we investigated the relative statistical properties of individual studies and meta-analysis under two simulation settings: single SNP test and genome wide scan.

Invfestigating the statistical properties of meta-analysis when testing a single SNP

Type-I error rate estimation

We simulated a total of k (k=5, 10, 20, and 50) individual studies, each with 2,000 unrelated subjects. These individual studies were either from the same population (${\sigma }_{bp}^2=0$) or from three different populations with proportions 60%:30%:10% (60%:20%:20% for k=5). The latter setting attempted to model the current situation in human genetics in which GWA studies are performed in different populations. θ₀ and ${\sigma }_y^2$ were set at 0 and 100, respectively. Diverse levels of heterogeneity were simulated by setting different values for ${\sigma }_{wp}^2$ and ${\sigma }_{bp}^2$. The allelic effect in each individual study may deviate from 0 because of study-specific and population-specific components. We tested the average effect size across all studied samples. The null hypothesis was thus defined as θ₀ =0. The statistically significant level was set at 0.05 and type-I error rates were estimated from 10,000 replicates.

Power estimation

Power was estimated by setting a non-null average effect size θ_o according to a pre-specified value of h². The simulation setting was the same as that used for estimating type-I error rates. Four combinations of ${\sigma }_{wp}^2$ (0, 0.6) and ${\sigma }_{bp}^2$ (0, 0.1) were considered to represent different levels of heterogeneity effects. Causal SNPs were population specific so their effect may only be present in some populations. The purpose of this scenario was to evaluate the performance of meta-analysis when combining samples with a true effect and samples without any effect, a situation that may occur, for example, with ethnic specific loci (Lei et al. 2009). The significance threshold was set at the genome-wide significance level (GWS, 5 × 10⁻⁸) and powers were estimated on 10,000 simulated replicates.

Rare variants vs. common variants

To compare the performance of meta-analysis for common and rare variants, we investigated type-I error rates and power for SNPs with different MAFs. We simulated 10 studies under a heterogeneous setting (${\sigma }_{wp}^2=0.6$ and ${\sigma }_{bp}^2$ varied from 0 to 1). Privacy issue is common in real applications, especially for sequencing based rare variants (de Bakker et al. 2008; Singh et al. 2013). As the focus of the present study was heterogeneity effects and statistical power of meta-analysis, we did not extensively study privacy issues and assumed that no private alleles were present. The MAF of the causal SNP was set at 0.005, 0.01, 0.1, 0.3 and 0.5. Type-I error rates and power were estimated at different h² values.

Effect of population stratification on meta-analysis

Our above simulations sampled subjects from a homogeneous population within each individual study. To simulate a more complicated situation, we introduced population structure within individual studies. Specifically, in each of the individual studies, subjects were sampled from an admixture of two ancestral populations (A and B). A total of 10,000 SNPs were simulated to constitute each subject's genotype profile. For each SNP, allele frequencies were generated using the Balding-Nichols model (Balding & Nichols, 1995). Briefly, an ancestral allele frequency p was drawn from the uniform distribution U(0.1,0.9). Allele frequencies in populations A and B were then drawn from a beta distribution with parameters p(1−F_st)/F_st and (1−p)(1−F_st)/F_st. We set F_st at 0.05 to simulate moderate population stratification. Each individual’s genotype were then drawn from population A with probability f~U(0.3, 0.7) and from population B with probability 1−f. The heritability h² varied from 0.0 to 1.0% and the difference in population phenotypic mean was set at 10. Principal component analysis (Price et al. 2006) was performed on these 10,000 SNPs to evaluate the ancestral backgrounds, and the top 10 principal components were used to adjust phenotypes in association analyses.

Meta-analysis vs. mega-analysis

Meta-analysis refers to the analysis of the combination of association summary statistics, e.g., regression coefficients, from individual studies. With the availability of participant-level data, an alternative approach to meta-analysis is the analysis of the combined samples of individual participant-level samples, e.g., mega-analysis (Lin and Zeng 2010a, 2010b). To investigate the relative performance of these two analyses, they were compared on a set of 10 individual studies from 3 populations with proportions 60%:30%:10%. Both type-I error rates and power estimates were evaluated.

Investigating the performance of individual study and meta-analysis in genome-wide scan

Under this simulation setting, we simulated 1,000 independent causal SNPs to mimic a genome-wide distribution. The average h² of these causal SNPs was set at 0.05% so that the total heritability was approximately 50%. Values of h² were drawn from an inverse gamma distribution IG(15, 75), and then divided by 10,000. The empirical distribution of the generated values is plotted in Supplementary Fig. 1. For simplicity, all individual studies were drawn from a single population so that ${\sigma }_{bp}^2=0$, while ${\sigma }_{wp}^2=0.6$.

Comparison of individual GWA studies and meta-analysis for identifying novel loci

In the presence of large-scale meta-analyses, the question of ‘what was the value of analyzing individual studies’ was of interest. Here we attempted to explore this question by evaluating the relative value of a smaller individual study compared to a larger meta-analysis. The individual GWA study was simulated with 10,000 unrelated individuals; this number was reasonable considering both discovery and replication phases (Styrkarsdottir et al. 2008; Xiong et al. 2009). Meta-analysis was simulated with 10 individual studies, each with 2,000 unrelated subjects. The GWS level (5×10⁻⁸) was used to declare positive results.

Comparisons were also made between meta-analysis and individual studies under equal sample size. Specifically, meta-analysis of 5 individual studies with 2,000 subjects each was compared with an individual GWA study with 10,000 subjects.

Power of identifying multiple loci and at extremely stringent levels

We noticed that many research consortia have reported extremely small p-values (such as 10⁻³⁰–10⁻⁵⁰) at multiple loci (Estrada et al. 2012; Speliotes et al. 2010). Given effect size and sample size, the question of how likely it was to generate extreme p-values was of interest. To answer this question, we evaluated the power of meta-analysis to simultaneously identify multiple loci and to identify loci at two extremely stringent levels (10⁻²⁰ and 10⁻²⁵). The two thresholds were set arbitrarily in accordance with published studies using extremely small p-values.

Assessing power of meta-analysis to replicate individual GWA studies’ findings

We simulated a collection of k+1 (k=5, 10, 20, and 50) individual studies, each with 2,000 unrelated individuals. The first GWA study was treated as the discovery study. Meta-analysis combining the remaining k studies was performed to replicate discovery findings. We performed 5,000 replicates to estimate power, which was defined as the proportion of replicates in which at least m SNPs identified by the discovery individual study were successfully replicated by the meta-analysis at the GWS level.

One phenomenon observed in the current genetic mapping era is that individual studies are often part of bigger meta-analysis consortia. Under these conditions, samples used for individual studies and meta-analyses are not independent. Nonetheless, there has been a trend toward regarding the results of meta-analysis as the standard for judging findings of individual studies, even when samples overlapped (Richards et al. 2012). To evaluate the replicability between GWA studies and meta-analysis when samples overlapped, we designed a simulation scenario in which individual study was part of meta-analysis samples.

Assessing replicability between meta-analyses

We simulated a collection of 2k (k=5, 10, 20, and 50) individual studies, each with 2,000 unrelated individuals. Meta-analysis combining the 1^st to k^th GWA studies was considered as the discovery study. Meta-analysis combining the remaining k GWA studies was considered as the replication study. We repeated the simulation 5,000 times to estimate power, which was defined analogously.

We also evaluated the power of replicability between two meta-analyses with overlapped samples. Specifically, 3 individual studies were included into both meta-analyses samples.

Results

We first evaluated the potential effects of population-specific properties, including different allele frequencies and LD levels, on heterogeneity. Our results showed that differences in either allele frequency or LD levels could lead to significant heterogeneity (Supplementary Fig. 2). Larger variations in LD levels and lower ancestral MAF corresponded to higher levels of heterogeneity (see Supplementary notes for interpretation).

Performance of meta-analysis when testing a single SNP

Average I² estimates under different parameter settings

Changes in the heterogeneity measure I² with MAF are presented in Table 1. Generally, I² increased with increasing MAFs (see supplementary notes for detailed interpretation). For example, when only within-population heterogeneity was present (${\sigma }_{wp}^2=0.6$ and ${\sigma }_{bp}^2=0$), the average I² increased from 15.5% to 81.8% as MAF increased from 0.005 to 0.5. Throughout the following simulations, MAF was set at 0.1 for common variants, and at 0.005 for rare variants, unless otherwise stated. For ease of reference, major parameter settings are presented in Table 2.

Table 1.

The effects of MAF on the level of heterogeneity (average I² (%)).

MAF	${\sigma }_{bp}^2$
	0	0.2	0.4	0.6	0.8	1
0.005	15.5	15.9	16.9	17.4	18.4	19.1
0.01	19.2	20.8	22.5	23.9	25.7	26.8
0.1	60.7	64.8	67.9	69.7	71.8	73.8
0.3	78.9	81.5	83.6	85.1	85.9	86.8
0.5	81.8	84.2	85.7	87.1	88	88.8

Note: ${\sigma }_{bp}^2$ denotes between-population variance; within-population variance ${\sigma }_{wp}^2$ was set at 0.6.

Table 2.

Major simulation parameters.

Simulation settings		No. of studies	Sample sizes	MAF	${\sigma }_{bp}^2$	${\sigma }_{wp}^2$	h2
Single SNP test
Type-I error		5, 10, 20, 50	2,000	0.1	0~1	0~1	0
Power (${\sigma }_{bp}^2=0$)		5, 10, 20, 50	2,000	0.1	0	0,0.6	0.1~2%
Power (${\sigma }_{bp}^2>0$)		10	2,000	0.1	0.1	0,0.6	0.1~2%
Genome-wide scan
Power		5, 10, 20, 50	2,000	0.1	0	0.6	0.02~0.12%
Replicability		5, 10, 20, 50	2,000	0.1	0	0.6	0.02~0.12%
Specific setting
Rare vs. common variants		10	2,000	0.005, 0.01, 0.1, 0.3, 0.5	0~1	0.6	0.1~1%
Effects of population stratification		10	2,000	Fst=0.05, p=0.1	-	-	0.3
Meta vs. Mega		10	2,000	0.1	0.1	0.6	0.1~1%
Sample structure from real data		17	220~7,394	Fst=0.11, p=0.1	-	-	0.1~1%

Note: F_st is a measure of genetic distance between populations; p denotes ancestral allele frequency; ${\sigma }_{bp}^2$ and ${\sigma }_{wp}^2$ denote between- and within-population variances, respectively; h² represents heritability (phenotypic variation explained by the SNP).

When the average effect size θ_o was the same in all populations, the level of between-study heterogeneity increased with increasing values of ${\sigma }_{wp}^2$ and ${\sigma }_{bp}^2$ (Supplementary Figs. 3A, 3B, and 3C). For example, when meta-analyzing 5 individual studies from a homogeneous population (${\sigma }_{bp}^2=0$), ${\sigma }_{wp}^2$ values of 0.0 and 0.6 corresponded to average I² values of 14% and 53%, respectively. When meta-analyzing 5 studies from different populations (e.g. ${\sigma }_{bp}^2=0.1$), ${\sigma }_{wp}^2$ values of 0.0 and 0.6 corresponded to average I² values of 20% and 55%, respectively. Note that average I² always deviated from zero, even in an ideally homogeneous situation.

Variation of θ_o among different populations introduced additional heterogeneity, as illustrated by Supplementary Figs. 3D and 3E. For example, when only between-population variation existed (${\sigma }_{bp}^2=0.1$ and ${\sigma }_{wp}^2=0$) and the tested SNP presented an effect in only the first population, the average I² could be as high as 91% when the h² for the first population was 2% (Supplementary Figs. 3D and 3E).

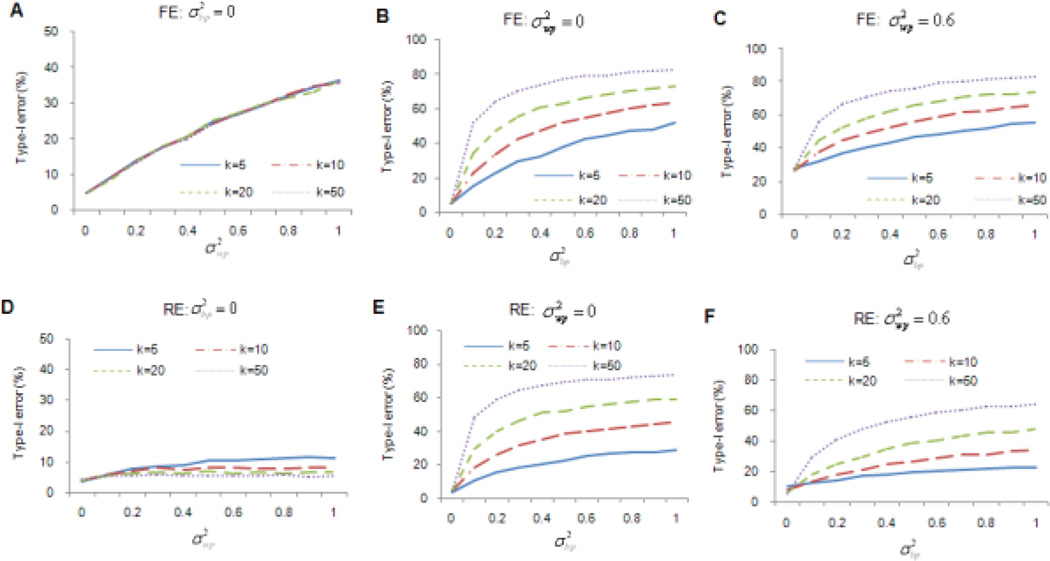
Type-I error rate

When individual studies were ideally homogeneous (${\sigma }_{wp}^2=0$ and ${\sigma }_{bp}^2=0$), both the FE and RE models had error rates close to the target level of 5% (Figs. 1A and 1D). When different studies were from a homogeneous population (${\sigma }_{bp}^2=0$), but individual studies had within population heterogeneity (${\sigma }_{wp}^2>0$), the FE model had an inflated type-I error rate, regardless of the number of studies being meta-analyzed. The error rate could be as high as 36% (Fig. 1A). This may be because the FE model tended to underestimate the variance of effect size when there was between-study heterogeneity. In this setting, the RE model was robust when k was large (e.g. k>10). However, for small k’s (e.g. k=5) the type-I error rate for RE was not well controlled, and became increasingly inflated as ${\sigma }_{wp}^2$ increased (Fig. 1D).

Figure 1. Type-I error rates of meta-analyses.

k is the number of studies included in the meta-analysis. Figures 1A, 1B, and 1C present the type-I error rates of the fixed-effects (FE) model, and Figures 1D, 1E, and 1F present the type-I error rates of the random-effects (RE) model. ${\sigma }_{wp}^2$ and ${\sigma }_{bp}^2$ represent within- and between-population variances, respectively. For figures 1A and 1D, only within-population variation was present. For figures 1B and 1E, only between-population variation was present. For figures 1C and 1F, both within- and between-population variations were present. The statistically significant level was set at 0.05.

When individual studies were sampled from different populations, neither the FE nor the RE model could control type-I error rates (Figs. 1B, 1C, 1E and 1F), regardless of whether within-population variation existed or not, though the RE model was less liberal than the FE model. For example, when ${\sigma }_{bp}^2=0.1,{\sigma }_{wp}^2=0$, and k = 10 (corresponding to an average I² value of 18%), the type-I error rates for the FE and RE models were 23% and 18%, respectively. Type-I error rates increased with larger k’s and increases in ${\sigma }_{bp}^2$ and/or ${\sigma }_{wp}^2$. At an extreme setting in which ${\sigma }_{bp}^2=1,{\sigma }_{wp}^2=0.6$ and k=50 (average I²=77%), type-I error rates were as high as 83% and 64% for the FE and RE models, respectively (Figs. 1C and 1F).

The simulations for Type-I error rates discussed above analyzed common variants. Results for rare variants showed inflated type-I error rates as well. Notably, these error rates were less severe than those for common variants under the same parameter settings (Supplementary Fig. 4).

Power estimation

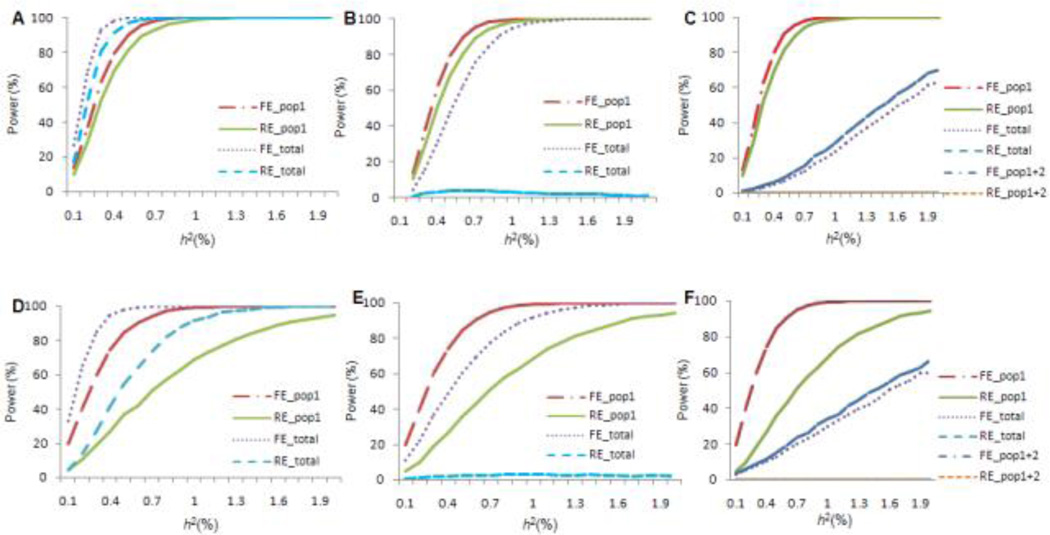
Under ideally homogeneous settings (${\sigma }_{wp}^2=0$ and ${\sigma }_{bp}^2=0$), the FE model was more powerful than the RE model. As expected, both models were more powerful than individual studies due to enlarged sample sizes (Supplementary Figs. 5A and 5C). For example, the power for identifying a SNP with an h² of 0.3% was 95%, 63% and 0.1% for the FE, RE models (k=10) and analysis by an individual study.

Compared to the ideally homogeneous setting analyzed in the previous paragraph, a loss of power was observed for both the FE and RE models when only within-population heterogeneity effects existed (${\sigma }_{bp}^2=0,{\sigma }_{wp}^2>0$) (Supplementary Figs. 5B and 5D). For example, when ${\sigma }_{wp}^2=0.6$, the power to detect a SNP with an h² of 0.3% decreased from 95% to 91% and from 63% to 34% for the FE and RE models, respectively. The severity of the power loss was greater for the RE model than for the FE model.

When only between-population variation existed (${\sigma }_{bp}^2=0.1$), the pattern of power change depended on the variation of θ_o. For these simulations, we used various combinations of 10 individual studies of equal size from three populations, with proportions of 60%:30%:10%. If the average effects of the SNP were equal in all populations (corresponding to an average I² value of 18%, i.e., a level that was generally regarded to reflect no heterogeneity or non-detectable heterogeneity in meta-analyses), meta-analyzing samples from different populations had the potential to increase power. For example, when meta-analyzing the six studies from the first population, the power of the FE and RE models for identifying a SNP with an h² of 0.3% was 63% and 52%; the power increased to 93% and 81% for the two models when meta-analyzing all 10 studies (Fig. 2A). Compared with meta-analysis of multiple samples from a single population, all of which showed a causal effect, power decreased with the addition of samples from other populations without causal effect. For example, when the SNP was causal in only the first population (h² =0.3%), power of meta-analysis of 6 studies from this population was 63% and 52% for the FE and RE models, respectively. When adding 4 samples from the two other populations in which the SNP was neutral, power decreased to 32% and 3%, respectively (Fig. 2B). Power loss was even more severe when combining samples with effects in opposite directions. For example, if the causal SNP produced effects of the same magnitude, but in opposite directions, in studies from the first and second populations, while that from the third population had no effect, including samples of the second population into the analysis decreased power to 4% and <1% for the FE and RE models, respectively. Finally, meta-analysis of all 10 studies (corresponding to average I² value of 82%) had powers of 3% and <1% for the FE and RE models (Fig. 2C). Therefore, including heterogeneous studies from different populations with opposite directional effects, or without effect, may actually lead to a serious loss of power for both the RE and FE models.

Figure 2. Power estimates of meta-analyses including studies from different populations.

“FE” and “RE” denote fixed- and random-effects meta-analyses, respectively. ${\sigma }_{wp}^2$ and ${\sigma }_{bp}^2$ represent within- and between-population variances, respectively. 10 individual studies were simulated from three populations with proportions 60%:30%:10%. The suffixes “pop1”, “pop1+2”, and “total” denote meta-analyses including studies from the first population, the first two populations, and all three populations, respectively (see Methods for details). h² on the x-axis represents heritability (phenotypic variation explained by the SNP). The statistically significant level was set at 5×10⁻⁸. For figures 2A, 2B, and 2C, only between-population variation was present. For figures 2D, 2E, and 2F, both within- and between-population variations were present. For figures 2A and 2D, the SNP had the same effect in all populations in terms of both magnitudes and direction. For figure 2B and 2E, the SNP had an effect in only the first population. For figures 2C and 2F, the SNP produced effects with the same magnitude but in opposite directions in samples from the first and second populations, while the SNP had no effect on the third population.

When both within- and between-population variations existed (${\sigma }_{bp}^2=0.1$ and ${\sigma }_{wp}^2=0.6$), the results were similar to that obtained when only between-population variation was present, although power loss was more severe due to the additional heterogeneity introduced by within-population variation (Figs. 2D, 2E and 2F).

The simulations for power estimates discussed above analyzed common variants. For rare variants, there was also a serious power loss for both the FE and RE models when adding samples with no causal effects (Supplementary Fig. 4).

To facilitate comprehension, we listed major results of type-I error rates and power estimates in Table 3.

Table 3.

Type-I error rates and power estimates under the major parameter settings.

Model	${\sigma }_{wp}^2$	${\sigma }_{bp}^2$	Type-I error (%)	Power (%)
				h2=0.2%	h2=0.4%	h2=0.6%	h2=0.8%	h2=1%
FE	0	0	5.0	75.2	99.1	99.9	100.0	100.0
	0	0.1	23.1	70.2	98.3	99.9	100.0	100.0
	0.6	0	27.3	69.0	97.1	99.9	100.0	100.0
	0.6	0.1	38.0	22.0	48.9	69.4	83.8	91.7
RE	0	0	3.8	41.5	75.6	89.4	95.7	98.6
	0	0.1	17.9	52.9	91.1	98.8	99.7	99.9
	0.6	0	8.1	13.4	43.9	71.9	86.5	94.4
	0.6	0.1	13.6	1.0	2.0	2.1	2.7	2.9

Note: “FE” and “RE” denote fixed-effects and random-effects models, respectively; ${\sigma }_{bp}^2$ and ${\sigma }_{wp}^2$ denote between- and within-population variances, respectively; h² represents heritability (phenotypic variation explained by the SNP). 10 individual GWA studies, each with 2,000 individuals, were included in the meta-analysis.

Heterogeneity test

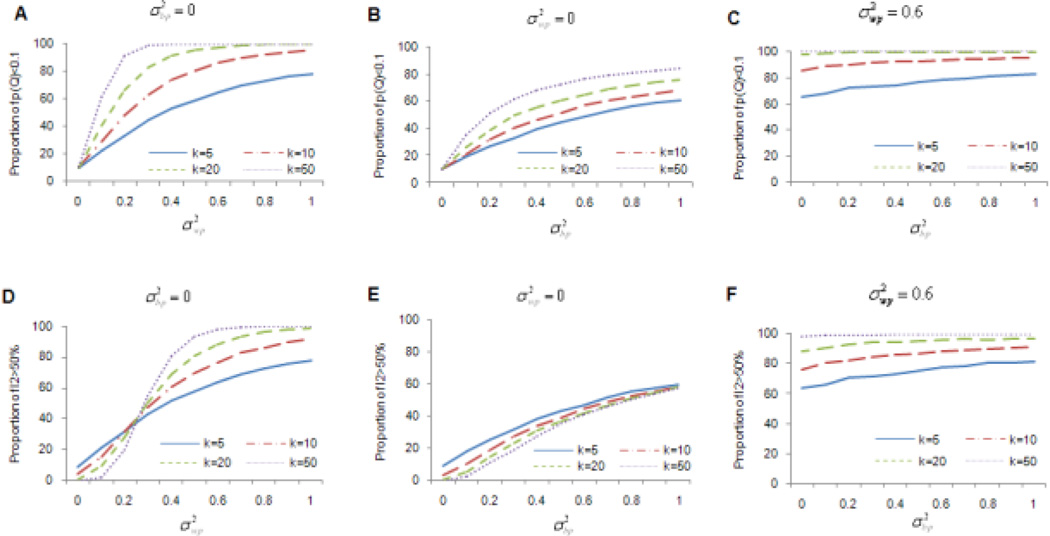
As expected, the power for detecting heterogeneity increased with increasing levels of heterogeneity and with larger k’s (Fig. 3). Importantly, both Q test and I² measures were under-powered for detecting heterogeneity with small k’s. For example, for k=5 and ${\sigma }_{bp}^2=0$, the power of detecting heterogeneity induced by ${\sigma }_{wp}^2$ did not reach the recommended 80% threshold (Cohen 1988). Even when k=10, the 80% threshold for both Q and I² was reached only when ${\sigma }_{wp}^2$ exceeded 0.6. Considering that heterogeneity tests were found to be underpowered (Pereira et al. 2010), even when the number of studies increased to 20, it is important to recognize failure to detect heterogeneity does not guarantee the absence of heterogeneity.

Figure 3. Power estimates for heterogeneity tests.

${\sigma }_{wp}^2$ and ${\sigma }_{bp}^2$ represent within- and between-population variances, respectively. k is the number of studies included in the meta-analyses. Figures 3A, 3B, and 3C present power estimates for the Q test, while figures 3D, 3E, and 3F present power estimates for I² index method. For figures 3A and 3D, only within-population variation was present. For figures 3B and 3E, only between-population variation was present. For figures 3C and 3F, both within- and between-population variations were present.

Effect of population stratification on meta-analysis

Correcting for population stratification within each individual study had a significant effect on the performance of subsequent meta-analyses in that heterogeneity, type-I error rates, and power were all decreased. For example, when this correction was applied, the proportion of replicates with I²>50% decreased from 20.1% to 4.1%, and the proportion of replicates with p(Q)<0.1 decreased from 30.1% to 11.2% (data not shown); power decreased from 97.7% to 71.0% for the FE model, and from 89.8% to 67.8% for the RE model; Type-I error rate decreased from 88.4% to 5.2% for the FE model, and from 87.4% to 4.1% for the RE model (data not shown).

Meta-analysis vs. mega-analysis

When jointly analyzing data from multiple studies, one can either merge participant level data for analysis of a single mega-sample or combine summary statistics for a meta-analysis. In the current study, we compared the performance of meta-analysis and mega-analysis. Our results showed that the FE meta-analysis had an approximately equal performance to the mega-analysis. It is notable that this equivalence held even under heterogeneous setting. For example, when meta-analyzing 10 heterogeneous studies (${\sigma }_{wp}^2=0.6$ and ${\sigma }_{bp}^2=0.1$) for a SNP with h²=0.3%, the power of the FE meta-analysis and mega-analysis was 85.0% and 84.9%, respectively, while the type-I error rates were both 37.0% (data not shown).

Performance of meta-analysis and individual study in a genome-wide scan

Power to identify novel loci

We first compared the power of a smaller individual study with that of a larger meta-analysis. The power of individual GWA studies to identify any particular (pre-selected) locus was very limited (Fig. 4A). For example, the power of individual GWA studies to detect a particular SNP with an h² of 0.05% was as low as <1%. However, the power to identify any one of the 1,000 SNPs was much better, and could increase to 74%. This phenomenon may explain the reason that individual studies, despite limited sample sizes, have had reasonable success at identifying a number of true novel loci. Therefore, given the large number of yet unidentified loci, individual studies are still valuable in identifying at least some of the underlying causal loci.

Figure 4. Power estimates for identifying a particular SNP and at least one SNP on a genome-wide scan.

h² on the x-axis represents phenotypic variation explained by the SNP. “FE” and “RE” denote fixed- and random-effects meta-analyses, respectively. For GWA studies (Fig. 4A), a total of 10,000 unrelated individuals were simulated. For meta-analyses, 10 (Fig. 4B) and 5 (Fig. 4C) individual studies, each with 2,000 unrelated individuals were simulated. For “at least one” case, the x-axis corresponds to the h² threshold. The statistically significant level was set at 5 × 10⁻⁸.

Meta-analyses, under the conditions defined for Figure 4B, had higher power than individual studies in identifying these SNPs, however, the power to identify any particular locus was still rather limited. To detect a SNP with an h² of 0.05%, the power was <10% for the FE model and <1% for the RE model. On the other hand, the power to identify any one of the 1,000 SNPs achieved 100% for both the FE and RE models (Fig. 4B). Importantly, the sample size for this comparison was twice as large for the meta-analysis as it was for the individual studies. Next, we compared the power of meta-analysis vs. individual studies under the condition of equal sample size (Figs 4C vs. 4A). Results showed that meta-analysis had increased power over analysis of individual studies. However, the type-I error rate was also inflated for meta-analysis (data not shown). Therefore the increased power of meta-analysis compared to individual studies may actually be attributable to elevated type-I error rates. To address this, we compared measures of positive predictive value (PPV) (Altman and Bland 1994) which corrects for type-I error rates when estimating power. The results showed that meta-analysis actually had a lower PPV than individual GWA analysis. For example, the PPV for identifying a particular SNP with h²=0.03% was 100%, 89%, and 80%, respectively, for individual study, the FE and RE meta-analyses (data not shown). The results were not unexpected given a heterogeneous setting for meta-analysis versus a homogeneous setting for individual studies.

Power to simultaneously identify multiple loci and to identify loci at stringent levels

Our simulation showed that the FE model was quite powerful for identifying multiple loci at the GWS level (Supplementary Fig. 6), while the RE model was more limited. For example, with 80% power, the number of loci detected by the FE meta-analysis (k=10) was as large as 106, while that for the RE model was only 8. At a more stringent level of significance, the power of both models was limited (Supplementary Fig. 7). At a level of 1×10⁻²⁰, for example, the power to detect at least one SNP was only 36% for the FE model and 2% for the RE model. At a level of 1×10⁻²⁵, the power of these models decreased to 3% and 0%, respectively. Even if k increased to 20, the power to detect at least one SNP at the level 1×10⁻²⁵ was only 63% and <1% for the FE and RE models, respectively. Therefore, at an extremely stringent level of significance (e.g. <1×10⁻²⁵), the power to detect a SNP was rather small even with a large scale meta-analysis; detecting multiple SNPs at this level of significance was even smaller or essentially unattainable, under the current simulation settings.

Power of meta-analysis to replicate findings from individual GWA studies

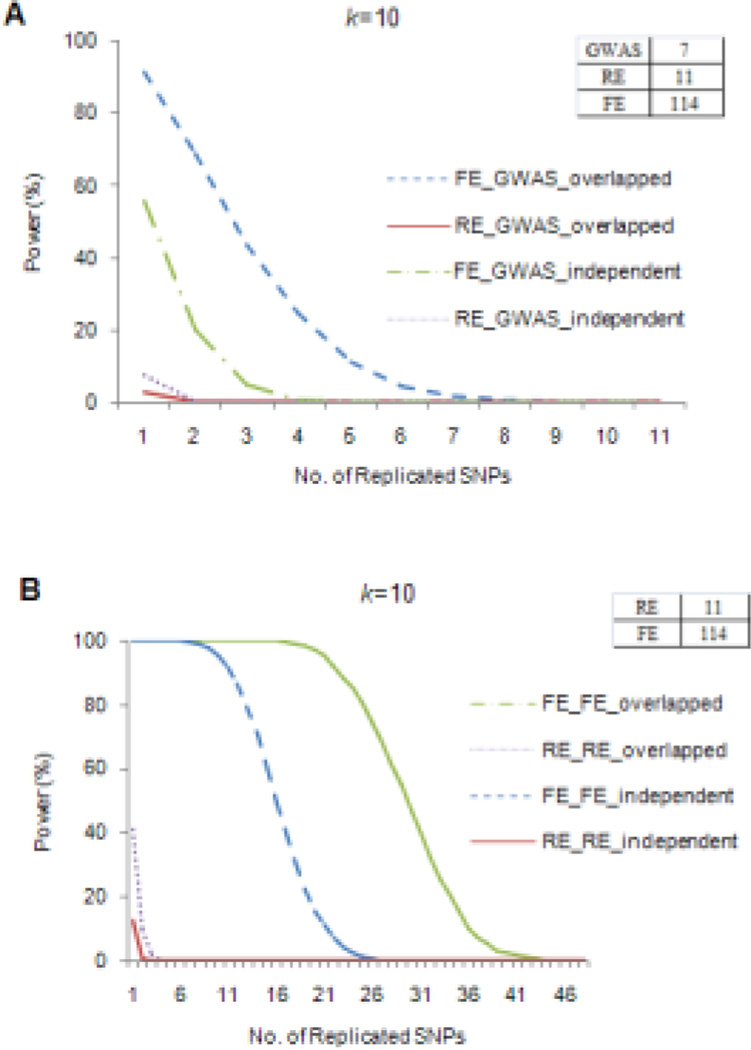
Our simulation demonstrated that the replicability between meta-analysis and an independent individual GWA study was quite limited. On average, individual GWA studies could identify 7 of the 1,000 causal SNPs at the GWS level. The power of meta-analysis to replicate at least 2 of these 7 SNPs was 20% and <1% for the FE and RE models, respectively (Fig. 5A). Therefore, even powerful meta-analyses had limited power to replicate findings from individual GWA studies. As expected, including more studies into meta-analysis increased its power of replicability (Supplementary Fig. 8), but even then, the power was rather small under the RE model.

Figure 5. Power for replication between individual GWA studies (GWAS) and meta-analysis.

Tables on the top right of the figures give the average number of significant SNPs identified by each method. “FE” and “RE” denote the fixed- and random-effects meta-analyses, respectively. k is the number of studies included in meta-analyses. Figure 5A shows the power of meta-analysis to replicate findings from individual GWA studies at the genome-wide significance level (p< 5 × 10⁻⁸). “Overlapped” denotes that samples from GWA studies were included in the meta-analysis, whereas, “independent” denotes that samples from GWA studies and meta-analysis were independent. Figure 5B shows the replicability between different meta-analyses at the genome-wide significance level. For “overlapped” simulations, 3 studies were overlapped between two meta-analyses.

When the individual study was included in the samples used for meta-analysis, the power of replicability for the FE model improved, while that for the RE model was still limited. For example, the power of the FE model (k=10) to replicate at least 2 SNPs identified by a discovery GWA study increased to 69%, while the power of the RE model was still <1% (Fig. 5A). It is worth emphasizing the point that in such situations consistency of findings between individual GWA studies and meta-analysis did not confer independent replication because of the overlapped samples.

Replicability between meta-analyses

The replicability of results between two distinct meta-analyses was surprisingly low under the simulation conditions described for Figure 5 in which FE meta-analysis (k=10) identified an average of 114 SNPs at the GWS level. The power of a second independent FE meta-analysis to replicate at least 20 of these 114 SNPs was 15%, and the power for replicating at least 30 SNPs decreased dramatically to <1% (Fig. 5B). The RE model (k=10) identified 11 SNPs under these conditions, and the power to replicate at least 2 of them in a second independent RE model was <1%. As expected, the power increased with larger k (Supplementary Fig. 9).

As seen in Fig. 5B, power of replication increased dramatically with overlapping samples. For example, the power to replicate 20 and 30 SNPs increased to 97% and 47%, respectively, for the FE model. However, the successfully replicated SNPs still represented only a small proportion of the SNPs identified by the discovery meta-analysis. The results of our simulations help to explain the failure of published meta-analyses to replicate the findings of one another.

Discussion

In the present study, we performed comprehensive and comparative investigations to study the relative statistical properties of individual GWA studies and their meta-analyses. Using simulations under a variety of heterogeneity settings, we concluded that detection of heterogeneity was usually difficult and that either FE or RE models could introduce elevated false positive and/or negative rates. Regarding individual GWA studies and meta-analyses, well-designed individual GWA studies had the capacity to identify novel loci that were missed by meta-analyses for complex traits. Non-replicability between meta-analysis and individual GWA studies was not uncommon. Our study may be helpful for the design and interpretation of results from individual GWA studies and their meta-analyses.

Among previous works, Lin et al. compare the performance of meta-analysis and mega-analysis and their results show, theoretically and numerically, that the FE model of meta-analysis is statistically as efficient as analysis of mega-samples, with or without the condition of equal effect size across individual studies (Lin and Zeng 2010a, 2010b). The results of our simulations support their conclusions. Given the approximate equivalence of FE meta-analysis and mega-analysis, the replicability of mega-analysis should be equal to the FE models investigated in the present simulations.

A critical issue in any meta-analysis is the potential effects of heterogeneity among samples (Munafo and Flint 2004). In our simulation studies we modeled heterogeneity effects with two components: within-population and between-population variations. Between-population variation was of particular interest because of its likely existence in real applications, especially for studies involving more than one ethnic group (Torgerson et al. 2011). In the present study, we assumed that between-population heterogeneity only explained a small portion of the phenotypic variation (e.g. <0.19%) under most scenarios. Our simulation results clearly indicated that between-population heterogeneity, even at these relatively miniscule levels, would significantly impact the results of a meta-analysis (e.g. this heterogeneity would introduce significantly inflated false positive/negative results). Heterogeneity in real data may greatly exceed that simulated in our study, especially when considering interactions between genetic variants and environmental exposures. Consequently, researchers should exercise caution when combining samples from different populations, or should recognize that meta-analyses may introduce false positive/negative results even for samples from the same population.

FE meta-analysis has been extensively investigated (Evangelou and Ioannidis 2013; Ioannidis et al. 2009), and these excellent reviews emphasize the caution necessary when using FE models. Pereira et al. (2009) investigated the properties of discovery GWA meta-analyses under heterogeneous settings. They concluded that FE models could maximize findings of discovery studies at the expense of elevated false discovery rates. The simulations used in our current study represent another attempt to quantitatively measure the impact of heterogeneity on power estimations and type-I error rates. Our results supported the conclusion that the FE model had a rather tenuous assumption (Evangelou and Ioannidis 2013; Ioannidis et al. 2009; Pereira et al. 2009), however, it (Gogele et al. 2012), is more commonly used than the RE model, partly because of its improved statistical power.

Under a variety of realistic conditions, even the RE model could not control type-I error rates in the presence of heterogeneity, as demonstrated by our simulations. Consequently, further exploration of potential sources of heterogeneity becomes important (Ioannidis et al. 2007). The inferred source of heterogeneity can be used to correct for its effects through the mixed-effects (van Houwelingen et al. 2002) meta-analysis, Bayesian models (Morris 2011), or sub-group analysis (Bhattacharjee et al. 2012). Among other works (Ioannidis et al. 2007; Patsopoulos and Ioannidis 2010; Zeggini and Ioannidis 2009), Ioannidis et al.(2007) and Patsopoulos et al (2010) provide excellent demonstrations for exploiting the source of heterogeneity to help draw causal inferences in the study of type 2 diabetes and rheumatoid arthritis association signals.

The majority of parameter settings in our simulations fell into the ranges of empirical applications conducted to date (Gogele et al. 2012) (Supplementary Table 1). One noticeable exception was the assumption of equal individual study sample sizes (2,000) in our simulation versus varied sample sizes in practice. Our assumption of equal sample sizes was made for ease of presentation, and we did not expect it to have a significant impact on analyses or conclusions. To verify this, we performed additional simulation studies with varying individual sample sizes. Specifically, we simulated individual studies with sample sizes exactly equal to those in a recently published meta-analysis (Estrada et al. 2012), which included 17 GWA studies with sample sizes varying from 220–7,394 (Supplementary notes). The results of these simulations were similar to those attained with equal sample size (Supplementary Fig. 10).

Significant heterogeneity may also be caused by population stratification. In the present study, by using a simple illustration, we found that correction for population stratification within each individual study could reduce heterogeneity at the cost of decreased power. One potential explanation for these findings could be that correction for phenotypes by ancestral backgrounds eliminated systematic differences in effect size between ancestral populations within each individual study, which in turn reduced heterogeneity effects in subsequent meta-analysis.

Though individual GWA studies are virtually always have a smaller sample size than meta-analysis, they are also more likely to be homogeneous in subject background, study design and analytical method. Consequently, individual GWA studies are still likely to provide some novel findings. Our simulations clearly demonstrated that well-designed individual GWA studies in homogeneous samples can identify additional novel loci for complex diseases which might escape detection in meta-analysis with larger samples. Consequently, it is critical to recognize that meta-analysis of GWA studies is not necessarily superior to an adequately powered GWA study (Munafo and Flint 2004).

Failure to replicate findings from other studies is common in the genetics field (Ioannidis 2007). Our previous study showed that replication between individual GWA studies is quite difficult in principle (Liu et al. 2008). The present simulation study extends this point to meta-analyses, emphasizing that meta-analyses introduce additional levels of complexity. Therefore, although meta-analysis can be a powerful approach for uncovering novel genetic components underlying complex diseases, it should not be used as a gold standard to evaluate and judge findings from individual studies or from other meta-analyses.