Determination of Accuracy and Precision of Lesion Uptake Measurements in Human Subjects with Time-of-Flight PET

Abstract

Inclusion of time-of-flight (TOF) information in positron emission tomography (PET) reconstructions has been demonstrated to improve image quality through better signal-to-noise, faster convergence, better lesion detectability, and better image uniformity. The goal of this work was to assess the impact of TOF information on the accuracy and precision of quantitative measurements of activity uptake in small lesions in clinical studies.

Methods

Data from small (10–mm diameter) spheres were merged with list-mode data from six normal volunteers following injection of [¹⁸F]-fluorodeoxyglucose. Six spheres were embedded in both the liver and lung of the patient data with known activity uptake with respect to the average whole-body uptake. Images were reconstructed with and without TOF information. The measured uptake was compared with the known activity; the variability was measured over 60 bootstrapped replicates of the merged data, over the six spheres within a given organ, and across all spheres in all subjects.

Results

The average uptake over all spheres and subjects was ~50% higher in the lung and 20% higher in the liver with TOF compared with non-TOF reconstruction at comparable noise levels. The variabilities across replicates, over spheres within an organ, and across all spheres and subjects were 20–30% lower with TOF in the lung; in the liver, the variability metrics were 10–20% lower with TOF compared to non-TOF reconstruction.

Conclusion

TOF reconstruction leads to more accurate and precise measurements, both within a subject and across patients, of the activity in small lesions under clinical conditions.

INTRODUCTION

The benefit of including time-of-flight (TOF) information in the reconstruction of positron emission tomograph (PET) data was demonstrated in the 1980s (1–3) when TOF-PET scanners were first developed and followed the predictions of reduced variance (4–6). The TOF gain was characterized by an improved signal-to-noise ratio (SNR) with higher gains predicted for larger objects and better timing resolution. Since the resurgence of interest in TOF in the last decade and the subsequent development of commercial TOF-PET systems (7–9), the advantages of reconstruction with TOF information over non-TOF reconstruction have been studied more thoroughly through simulation and measurement using iterative reconstruction methods (10–22). Iterative TOF-PET reconstructions of simulated phantoms (10) demonstrated faster and more uniform convergence of contrast recovery with TOF that improved further with better timing resolution; this faster convergence with TOF resulted in a higher contrast recovery than that achieved without TOF at similar noise levels. Measurements of the TOF benefit in physical phantoms showed higher contrast recovery of small lesions with TOF for a large uniform phantom at matched noise (11). In clinical studies the contrast recovery of lesions with unknown uptake was higher with TOF than that with non-TOF reconstruction for all subjects, and the TOF gain in contrast recovery increased with patient mass (11). In a visual assessment of the TOF benefit in patient studies, Lois, et al. (14) showed that images reconstructed with TOF have better definition of small structures, better uniformity, lower noise, and higher lesion contrast. In a prototype scanner with better timing resolution (23), we showed higher contrast recovery with reduced variability across the object and with reduced sensitivity to potential errors in the corrections (e.g., the scatter estimate) (15). Other groups have also remarked on this decreased sensitivity to inconsistencies in the data or corrections with TOF reconstruction (24, 25).

The impact of TOF on lesion detection has also been investigated with numerical and human observers. TOF information was shown to improve lesion detectability using numerical observers for spherical lesions in simple uniform cylindrical phantoms (12, 18). Kadrmas, et al. (13, 20) found improved lesion detectability with TOF reconstruction in physical anthropomorphic phantoms of two sizes containing spherical lesions using localization receiver operating characteristic (LROC) analysis with both numerical and human observers with a greater TOF impact for the larger phantom. More recently, the benefit of TOF on lesion detectability has been demonstrated, especially for low-contrast lesions or large subjects, using both numerical and human observers in clinical whole-body patient data with embedded artificial lesions (16, 17, 22).

The goal of this work was to adapt the sphere insertion technique used in our lesion detectability studies to assess the impact of TOF information on both the accuracy and the precision of the measurement of uptake in lesions in clinical TOF-PET data. The power of this technique is that it combines the advantages of a phantom study where truth is known with the non-uniform activity and attenuation distributions seen in patient studies.

MATERIALS AND METHODS

TOF Scanner

Data were acquired on the University of Pennsylvania prototype TOF-PET scanner based on LaBr₃ scintillators (15, 23). This fully 3D scanner comprises 24 modules of 1620 4 mm×4 mm×30 mm crystals in a 93-cm diameter ring. The transverse field of view (FOV) is 57.6 cm; the axial FOV is 19.2 cm. The intrinsic timing resolution of the scanner measured with a point source in air is 375 ps. The energy resolution of 6.5% after energy calibration allows the lower energy threshold to be raised to 470 keV. Data are acquired in list-mode with 25-ps timing bins to preserve the timing and spatial resolutions of the data. The spatial resolution of the scanner is 5.8 mm (full-width at half-maximum, FWHM) at a 1-cm radius.

Data Reconstruction and Corrections

The image reconstruction algorithm was the 3D list-mode iterative ordered subsets expectation-maximization algorithm (OSEM) (26, 27) with a TOF kernel applied in both the forward- and back-projection operations (28). The TOF response function was modeled as a one-dimensional Gaussian function along the line of response (LOR). All physical effects were incorporated into the system model of the reconstruction. Resolution modeling to compensate for detector blurring was not explicitly included in the reconstruction; instead of voxels, however, modified Kaiser-Bessel (“blob”) basis functions (29, 30) were used to constrain the image to be a continuous function during reconstruction. Blob basis functions control image noise without the need for post-filtering while maintaining spatial resolution (30), albeit in a spatially invariant manner. The blobs used for this study had a 7.5-mm radius placed on a 6-mm body center cubic grid (shape parameter = 8.63). The final image was interpolated to 2 mm×2 mm×2 mm voxels. All TOF-OSEM reconstructions used 25 chronologically ordered subsets. While clinical TOF reconstructions are typically stopped after 4–5 iterations, the data were reconstructed for up to 20 iterations to determine the convergence behavior with clinical data.

A rotating line source was used to correct the measured timing differences between crystals (23). Attenuation correction was performed using transmission imaging with a rotating ¹³⁷Cs point source (31). The model-based single scatter simulation (SSS) was extended to estimate the 4D scatter distribution in the radial and TOF domains (32, 33). The scatter estimate used in non-TOF reconstructions was derived from the 4D SSS-TOF scatter sinogram by compressing the sinogram along the time domain. Random coincidences were estimated by the delayed coincidence window technique with Casey smoothing (34).

Normal Volunteer Studies

The institutional review board (IRB) of the University of Pennsylvania approved this study, and all subjects signed a written informed consent before the study. Six normal volunteers (5 males and 1 female, BMI=25–38) were injected with 555 MBq (15 mCi) of [¹⁸F]-fluorodeoxyglucose (FDG) and scanned following an average 105-min uptake period. Four frames were acquired to cover the region from the neck to the pelvis. The patient bed was moved between frames to allow for close to a 50% overlap between bed positions in order to ensure uniform axial noise behavior. The scan duration for each subject was chosen to give counts comparable, on average, to the events measured in a two-min/frame clinical FDG study on a Philips Gemini TF TOF-PET scanner for our standard 60-min post-injection protocol. A total of 115–270 Mcts (prompts) and 45–100 Mcts (true events) were acquired in the four-frame studies, where the ranges in counts are the ranges seen over the six subjects.

Sphere Insertion Methodology

In order to assess the impact of TOF information on the accuracy and precision of sphere uptake measurements in clinically realistic conditions, spheres of known uptake were inserted into the measured normal volunteer data. El Fakhri and Surti (16, 17) developed a technique for merging list-mode data from spherical lesions measured in air with data from patients for their studies on lesion detectability. In those studies spheres were embedded with an activity ratio calculated with respect to the local activity in the organ. Their technique was modified for this work to insert spheres of known activity with respect to the whole-body average uptake, similar to a fixed standardized uptake value (SUV).

Spheres (10–mm diameter, 1-mm wall thickness) were scanned in air at 77 locations throughout the scanner FOV (r = 0–12 cm, z = 0–±4 cm from the center of the scanner), and the data were stored in list-mode format. Spheres were selected to insert in the liver and lung regions of the normal volunteer data such that no two spheres were closer than 3.5 cm center-to-center. A total of six spheres were chosen for each organ.

The desired ratio (a_o) of sphere uptake to the average whole-body activity concentration was 10:1. The average whole-body uptake per volume, B_WB, was determined by averaging all voxels inside the body in the image after 20 iterations of list-mode TOF-OSEM. The transmission image was used to define the interior of the body for this calculation. Voxels in slices within 28 mm of the ends of the whole-body image were excluded from the calculation because those slices are very noisy due to low slice sensitivity near the ends of the axial FOV.

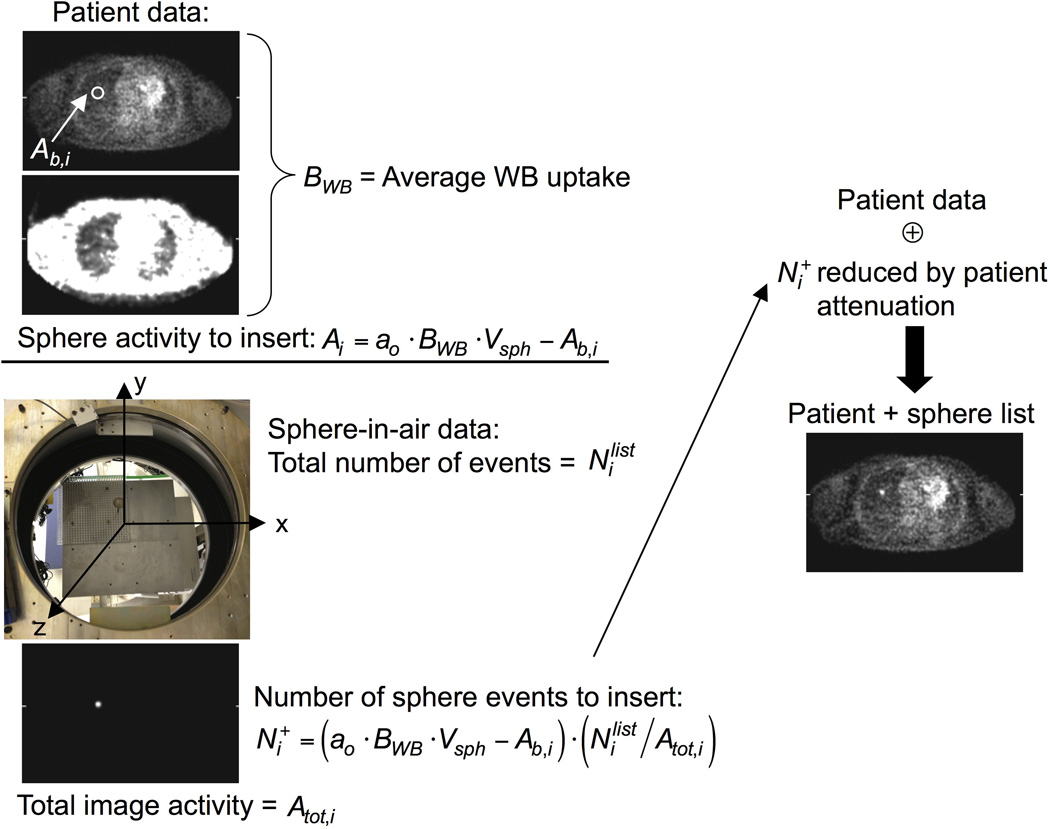
The procedure for calculating the number of sphere events to insert is illustrated in Figure 1 and described below. The desired total sphere activity at the location of each sphere is

$$A=a_o·B_{WB}·V_{sph}$$ (1)

where V_sph is the volume of the sphere, and a_o was 10 for this study. However, the whole-body image before sphere insertion has some background activity in the region of the sphere (A_b,i), so the total activity to be inserted for sphere i into the normal volunteer data is given by

$$A_i=a_o·B_{WB}·V_{sph}-A_{b,i}$$ (2)

The number of list-mode events for sphere i to be inserted ($N_i^{+}$) was calculated by scaling A_i by the ratio of the number of events in the sphere dataset ($N_i^{list}$) by the total activity (A_tot,i) in the sphere-in-air image:

$$N_i^{+}=(a_o·B_{WB}·V_{sph}-A_{b,i})·(N_i^{list}/A_{tot,i})$$ (3)

This scaling undoes any geometric efficiency corrections performed during reconstruction (e.g., solid angle correction).

FIGURE 1.

Schematic of the sphere insertion process for list-mode data. The sphere activity to insert (A_i) depends on the desired activity ratio (a_o) with respect to the average whole-body uptake per unit volume (B_WB) reduced by the activity already present in the patient image at the location of the sphere (A_b,i). Sphere-in-air data were acquired at known locations on a grid (photograph). The sphere data were reconstructed, and the ratio of sphere-in-air list events to total sphere image activity ($N_i^{list}/A_{tot,i}$) was used to scale A_i to determine the number of list-mode events ($N_i^{+}$) that would generate that activity. These list-mode events were reduced by sampling the probability of attenuation by the patient for a given event’s LOR and then merged with the subject’s list-mode data, represented by the addition symbol. This procedure was adapted from that used in our earlier lesion detectability studies (16, 17).

To compensate for attenuation effects seen in the whole-body study but not present in the sphere-in-air data, the selected sphere events were reduced by rejecting events using random sampling of the probability of attenuation by the body for the line of response (LOR) of each sphere event. The “attenuated” sphere events were then merged with the normal volunteer’s data by randomly inserting them into the subject’s list-mode data stream. The net result was an increase in the total number of events by <1%. This technique implicitly includes partial volume blurring of the sphere but does not include wall effects. Unlike physical spheres in phantom measurements, the sphere wall does not displace activity around the spheres, since counts are present in the subject’s data in the region of the sphere wall; this results in effectively wall-less lesions inserted into the clinical data. The merged list-mode data were then reconstructed with and without TOF information, as described earlier.

The sphere insertion process was validated by scanning a 35-cm cylinder that had five physical spheres (10–mm diameter, 6:1 activity ratio) located at radial positions from 0 to 11 cm. Fifteen additional 10-mm diameter spheres were inserted into the phantom data following the procedure described above with a_o = 6. The data were reconstructed with list-mode TOF-OSEM for 20 iterations. Volumes of interest (VOIs, 10-mm diameter) were drawn on the spheres, and the background activity was determined by averaging all voxels inside the phantom image without inserted spheres, analogous to B_WB. The average uptake in the physical spheres, divided by the background activity, was 2.37 ± 0.13 (range: 2.19 – 2.48); the average uptake in the inserted spheres was 2.51 ± 0.14 (range: 2.29 – 2.69). The slightly higher (<10%) uptake measured in the inserted spheres compared with that in the physical spheres can be explained by and is consistent with the findings for wall-less spheres compared with spheres with glass walls (35).

Bootstrapped Replicates

In order to determine the statistical variability of the measured sphere uptake for TOF and non-TOF reconstructions, 60 replicates of the list-mode data with and without inserted spheres were generated using bootstrapping as proposed by Haynor and Woods (36) and demonstrated and validated by Dahlbom (37) and Buvat (38). Bootstrapping permits an assessment of the statistical variability in TOF and non-TOF images with clinically realistic noise levels.

Analysis

The sphere uptake was calculated for VOIs with a 10-mm diameter. The VOI centers were determined from the sphere-in-air reconstructions, and the same VOIs were used on the images reconstructed from the merged sphere + subject data. The sphere VOIs were normalized by the average whole-body uptake (B_WB) after 20 iterations to define a normalized uptake ratio (NUV):

$$NUV=VO{I}_{sph}/B_{WB}$$ (4)

B_WB was calculated separately for TOF and non-TOF images in order to compensate for differences in calibrations for TOF and non-TOF reconstructions. Without partial volume effects the NUV in each sphere should be 10 (i.e., equal to a_o). Because no resolution modeling was included in the reconstruction, the measured NUV was lower than 10.

From the 60 replicates of the six patient studies with six inserted spheres in the lung and liver, we calculated the following measures:

• average NUV_j for one replicate over all subjects and spheres in each organ j,

  $$\overline{NU{V}_j}=\frac{1}{6·6}\sum _{p=1}^6\sum _{s=1}^{6}NU{V}_j(1,s,p)$$ (5)

  where NUV_j (1,s, p) is the uptake of sphere s in subject p in organ j for one replicate. This quantity was not averaged over all replicates, since each bootstrapped replicate is derived from the same dataset (37).
• statistical variability of the sphere uptake over the 60 bootstrapped replicates, expressed as a percent coefficient of variation (COV) and averaged over all subjects and spheres for each organ j

  $${\overline{COV}}_{repl,j}=\frac{1}{6·6}\sum _{p=1}^6\sum _{s=1}^6\frac{\sqrt{\frac{1}{59}\sum _{r=1}^{60}{\left[NU{V}_j(r,s,p)-NU{V}_j(1,s,p)\right]}^2}}{NU{V}_j(1,s,p)}\times 100$$ (6)

  where NUV_j(r,s,p) is the uptake in organ j of sphere s in subject p for replicate r.
• variability of the sphere uptake over sphere location for the six spheres in each organ j of a subject, averaged over all subjects

  $${\overline{COV}}_{loc,j}=\frac{1}{6}\sum _{p=1}^6\frac{\sqrt{\frac{1}{5}\sum _{s=1}^6{\left[NU{V}_j(1,s,p)-\overline{NU{V}_j}(p)\right]}^2}}{\overline{NU{V}_j}(p)}\times 100$$ (7)

  where $\overline{NU{V}_j}(p)$ is the average uptake in all spheres in organ j for subject p for one replicate.
• variability of the sphere uptake across subjects and spheres in organ j

  $$CO{V}_{subj,j}=\frac{\sqrt{\frac{1}{(6·6-1)}\sum _{p=1}^6\sum _{s=1}^6{\left[NU{V}_j(1,s,p)-\overline{NU{V}_j}\right]}^2}}{\overline{NU{V}_j}}\times 100$$ (8)

  where $\overline{NU{V}_j}$ is defined in eqn. (5). Since the same six spheres could not be inserted in all subjects because the relative locations of the subjects within the scanner with respect to the sphere positions varied, the variability across subjects includes the variability across location within a subject.

Image noise was calculated as the average statistical noise (over the 60 replicates) for a group of voxels in a large ROI drawn in the liver. A cylindrical ROI with a diameter of 50–80 mm and an axial length = 7 slices (14 mm) was drawn in the liver for this average.

RESULTS

Average Uptake

Figure 2 shows a typical plot for one subject of NUV_j(1,s,p) as a function of image noise for the six spheres in the lung and liver with TOF and non-TOF reconstructions. This plot demonstrates the typical variation seen among the six spheres in a given subject. As has been previously noted [e.g., (10, 11, 23, 39)], the rate of convergence is higher with TOF compared with non-TOF reconstruction; after five iterations, the sphere uptake has largely converged for TOF reconstructions while more iterations are required to reach convergence for some spheres with non-TOF reconstruction. It is also not apparent that the NUV without TOF would ever reach the value achieved with TOF. The NUV in the liver is higher than that in the lung for both TOF and non-TOF reconstructions although the spheres were inserted with the same activity ratio with respect to the average whole-body uptake. This difference is a consequence of the partial volume effect because the spill-in from the lower activity in the lung does not contribute as much to the VOI as spill-in from the higher uptake in the liver.

FIGURE 2.

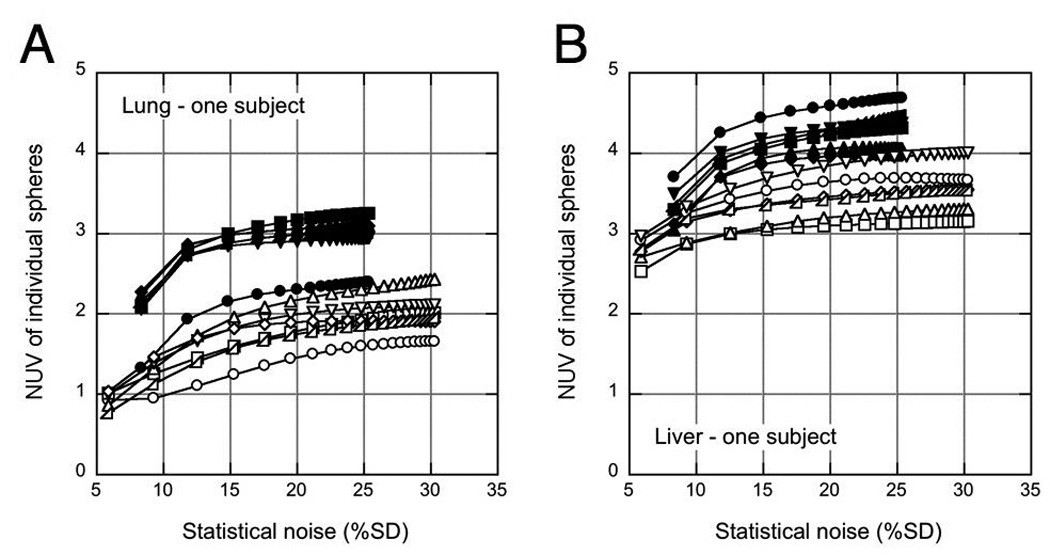
Normalized sphere uptake values (NUV_j (1,s, p)) for one replicate in one subject as a function of image noise are shown for each of the six inserted spheres in the lung (A) and liver (B), demonstrating the typical variation seen across locations and organs. Solid symbols: TOF reconstruction; open symbols: non-TOF reconstruction. Each curve represents one sphere; the data points correspond to each of the 20 iterations used.

Figure 3 shows $\overline{NU{V}_j}(p)$ for all six subjects as a function of image noise. Qualitatively, the difference in NUV between the liver and lung appears somewhat smaller with TOF than without TOF, and this is examined in more detail later. As was observed in the results from a single subject (Fig. 2), the sphere uptake is higher with TOF than non-TOF reconstruction, and the TOF and non-TOF reconstructions appear to converge to different values.

FIGURE 3.

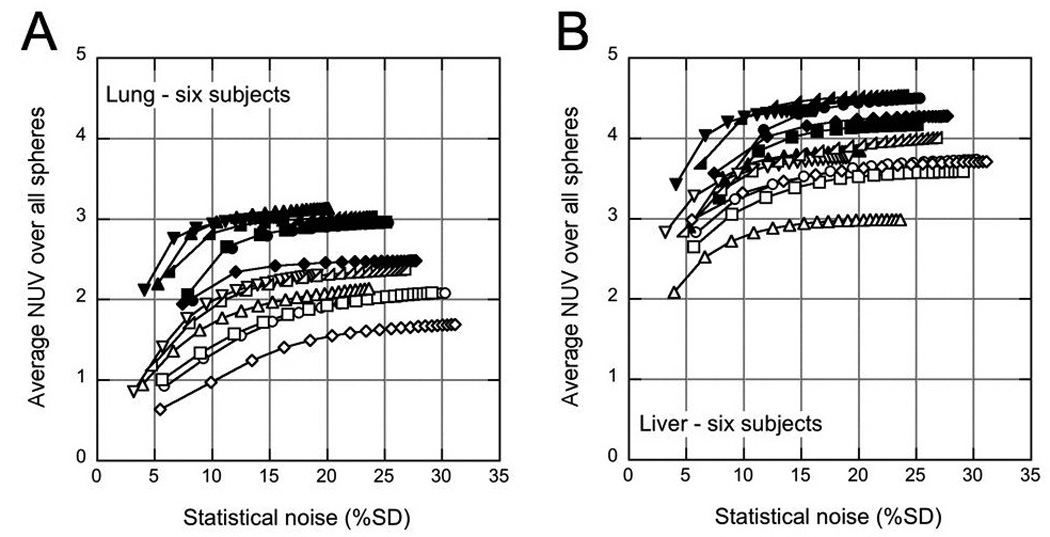
Average NUV over all six spheres ($\overline{NU{V}_j}(p)$) in a given organ for each of the six subjects as a function of image noise in the lung (A) and liver (B). Solid symbols: TOF reconstruction; open symbols: non-TOF reconstruction. Each curve represents one subject; the data points correspond to each of the 20 iterations used.

Variability of Uptake

Figure 4 shows the variabilities of the NUV measurements over replicates (${\overline{COV}}_{repl,j}$ ), locations within an organ (${\overline{COV}}_{loc,j}$ ), and subjects (COV_{subj, j}) as a function of iteration for TOF and non-TOF reconstructions. In both the lung and liver, all variability metrics are smaller with TOF than without TOF. The differences in variability between TOF and non-TOF reconstructions are also generally larger in the lung than in the liver. By 5 iterations ${\overline{COV}}_{loc,j}$ and COV_{subj, j} have converged to within 98% and 92% of their values at 20 iterations in the lung and liver, respectively, for TOF reconstructions (95% and 92% for non-TOF reconstructions); however, ${\overline{COV}}_{repl,j}$ is slower to converge and continues to increase with more iterations, especially for non-TOF reconstructions.

FIGURE 4.

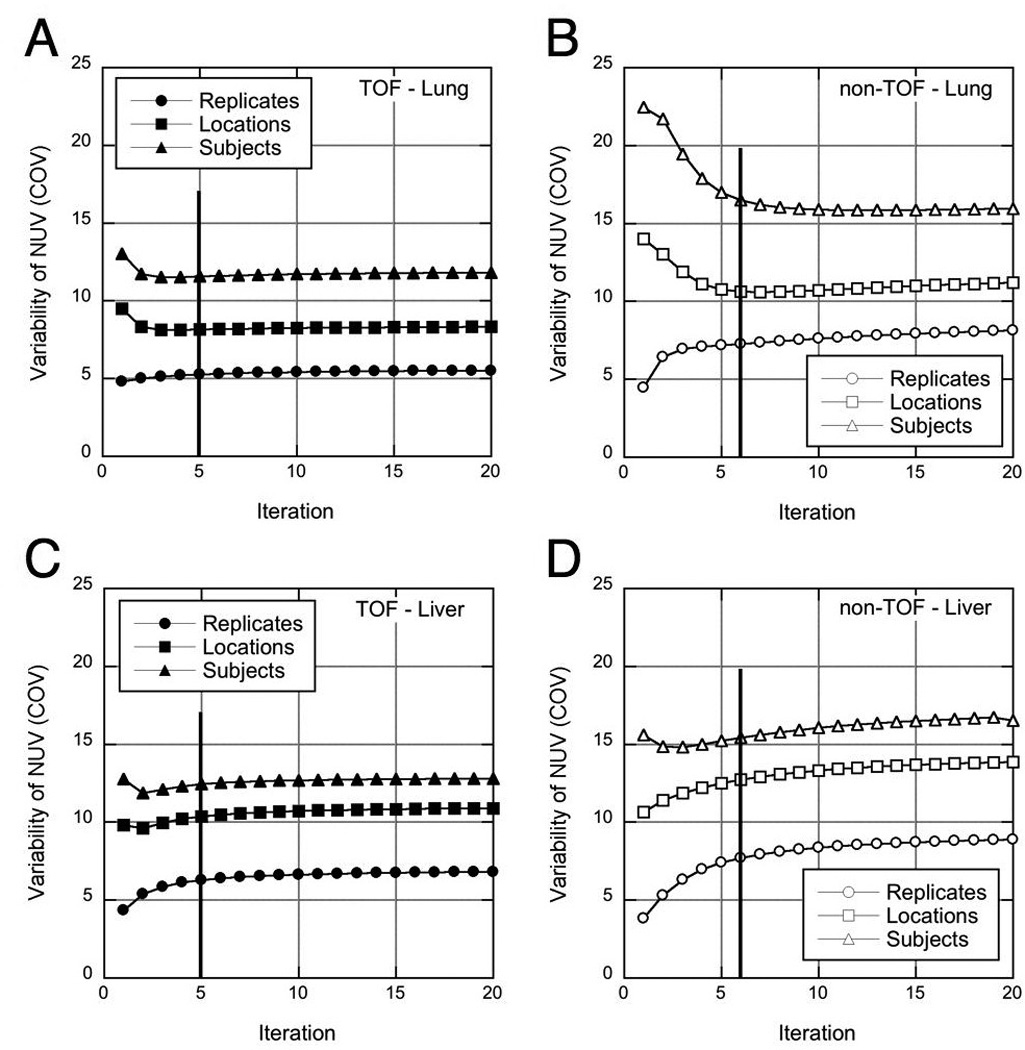
Variability measures for TOF (left) and non-TOF (right) reconstructions of spheres in the lung (A-B) and liver (C-D). The variability over replicates (${\overline{COV}}_{repl,j}$ - circles), across sphere locations within an organ (${\overline{COV}}_{loc,j}$ - squares), and across spheres and subjects (COV_{subj, j} - triangles) are shown as a function of iteration. The vertical lines at 5 TOF iterations (6 non-TOF iterations) show the points with similar image noise where reconstructions were stopped for subsequent analysis.

Uptake Average and Variability for Clinical Reconstructions

Clinical image reconstructions are typically not run to convergence but are stopped after a fixed, smaller number of iterations where the image noise is sufficiently low for good visual image quality and lesion detection. We stopped the TOF reconstructions after five iterations. At this stopping point ${\overline{NUV}}_j$ was within 98% of convergence with TOF. For non-TOF reconstructions, we stopped the reconstruction at a comparable image noise (six iterations) although it is evident from Fig. 3 that ${\overline{NUV}}_j$ will be farther from convergence (on average, 92% and 97% of the values at 20 iterations in the lung and liver, respectively). Figure 5(A) shows ${\overline{NUV}}_j$ achieved in the lung and liver at this stopping point. The average sphere uptake is higher for TOF than non-TOF reconstructions at matched image noise and is higher in the liver than in the lung. Figure 5(B) summarizes the variability metrics when the reconstructions are stopped early. All variability metrics are consistently lower for TOF reconstructions, especially in the lungs.

FIGURE 5.

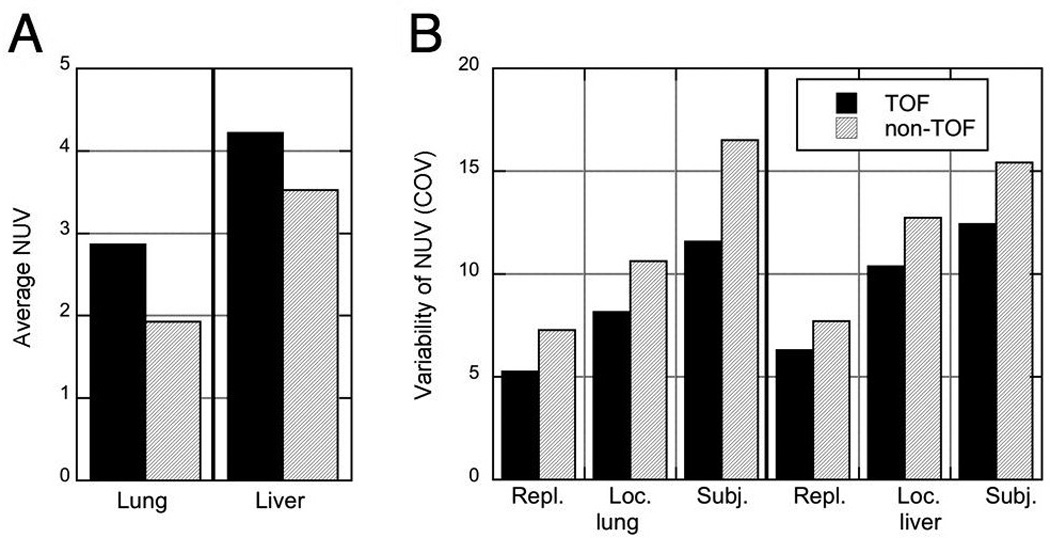
Average uptake and variability at a fixed number of iterations with corresponding image noise (5 iterations with TOF, 6 iterations with non-TOF reconstruction). (A) Sphere uptake (${\overline{NUV}}_j$) in the lung and liver, averaged over all spheres in all subjects. (B) Variabilities of NUV measurement over replicates (${\overline{COV}}_{repl,j}$), sphere locations (${\overline{COV}}_{loc,j}$), and subjects (COV_{subj, j}) for spheres inserted in the lung and liver.

DISCUSSION

This study shows the impact of TOF reconstruction on lesion quantification under clinically realistic but controlled conditions (i.e., known uptake). In contrast to previous studies of the impact of TOF on lesion uptake measurements (11, 14), the uptake in the spheres was known, so quantitative accuracy could be assessed. Further, unlike a phantom study, the non-uniform activity and attenuation distributions seen in patient studies were included to create a situation virtually identical to that seen in the clinic. Under these conditions TOF reconstruction leads to improved recovery of the sphere uptake (higher NUV) with lower variability (higher precision) across replicates, across locations within an organ, and across subjects. This study focused on 10-mm spheres at locations dictated by the positions of the liver and lung inside the scanner, but we believe the conclusions would be similar for the different lesion sizes or locations seen clinically.

The increase in NUV observed with TOF (a factor of 1.5 ± 0.1 in the lung and 1.20 ± 0.05 in the liver at 5 TOF iterations) is consistent with the higher contrast recovery observed in clinical studies with lesions of unknown uptake and with the higher contrast recovery seen for spheres in a large, 35-cm phantom (11). It is interesting, however, that the increase in NUV with TOF had no obvious correlation with BMI, although Karp, et al. (11) had previously shown a TOF gain in contrast recovery that increased with patient size. In the current work the lesions were limited to 10-mm diameter spheres, and the locations of the lesions were restricted to the lung and liver, whereas the previous study used data from patients with disease who had lesions with unknown uptake of varying sizes and locations throughout the body. In addition, the current study had a smaller range of BMI (25–38) than the previous work (19–46). However, the small numbers of subjects in both studies make it difficult to make a definitive statement about the impact of patient size on the accuracy and precision of lesion uptake measurements with TOF.

Because the size of the VOIs was equal to the physical inner diameter of the spheres, the measured NUV values included partial volume effects. To minimize these effects, the maximum uptake in each sphere (NUV_max) was also determined, analogous to the SUV_max commonly used in clinical studies, and the analysis was repeated for two subjects. While NUV_max was higher than the NUV measured in a VOI by an average of 60%, the results were more variable, as would be expected for a single-voxel measurement: ${\overline{COV}}_{repl,j}$ increased by 35–100% while ${\overline{COV}}_{loc,j}$ increased by 10–80%. However, the relative increase in measured uptake and decrease in variability with TOF compared to non-TOF reconstruction for NUV_max were consistent with the results presented for VOIs. Further improvement in the accuracy of the uptake measurement could also be achieved with resolution modeling during reconstruction (20–22). However, because convergence is also slowed with resolution modeling, variability across locations and subjects may also increase.

It was observed that the difference between liver and lung spheres is smaller with TOF than without TOF. The ratio of the average liver NUV to the average lung NUV is 1.48 ± 0.06 with TOF and 1.85 ± 0.08 without TOF. Some difference between liver and lung sphere VOI values is expected for images without resolution modeling or partial volume correction due to different amounts of spill-in from activity outside the sphere into the VOI. This effect is reduced with a smaller VOI. However, differences in the rate of convergence of the OSEM algorithm, which depends on the local activity distribution and is less uniform for non-TOF reconstruction, and differences in the sensitivity of TOF and non-TOF reconstruction algorithms to errors in data corrections (24, 25) may also play a role.

The increase in NUV with TOF reconstruction is accompanied by a decrease in variability (improved precision) of the NUV measurement for all three variability metrics studied. At five TOF iterations the variability metrics in the lung were 20–30% lower with TOF reconstruction; in the liver the variability metrics were 10–20% lower. This improvement in precision with TOF will lead to increased confidence in the uptake measurements of lesions with unknown activity in clinical studies.

While it is tempting to compare the TOF gain in NUV to the theoretical metrics of TOF gain in signal-to-noise ratio (SNR) (4–6), we believe it is not the right comparison for these data. The classical TOF gain metrics were derived from an assessment of image noise, where the signal was assumed to be unchanged, at the center of a uniform object for an analytical reconstruction. With a non-linear algorithm such as TOF-OSEM and the non-uniform emission and attenuation distributions in this study, the TOF gain in SNR is more difficult to quantify. In addition, the focus of this work was the impact of TOF on measurement of the uptake of lesions in a warm background, not image noise reduction.

This study was performed on a prototype TOF-PET scanner with a TOF resolution of under 400 ps. While clinical TOF-PET scanners currently have TOF resolutions closer to 600 ps, the impact of timing resolution on the accuracy and precision of lesion uptake measurements is an ongoing investigation. Theoretical and simulation studies suggest an improvement in SNR gain (40) and higher contrast recovery with better lesion detectability (10) for better TOF resolution. The normal volunteers used in this study were also scanned on a TOF-PET system with 600-ps TOF resolution, so a similar analysis can be performed in the future.

CONCLUSIONS

This study demonstrates in clinical data that the accuracy and precision of lesion uptake measurements are improved with TOF reconstruction. The results have implications for individual lesion measurements, where the uncertainty is reduced with TOF to yield a more reliable result for improved confidence of diagnostic interpretation. By reducing the underlying inter-subject variability of lesion uptake measurements, TOF reconstruction also has the potential to reduce the number of subjects needed for clinical trials compared with non-TOF reconstruction.