Individual Differences in Memory Search and Their Relation to Intelligence

Abstract

Attempts to understand why memory predicts intelligence have not fully leveraged state-of-the-art measures of recall dynamics. Using data from a multi–session free recall study we examine individual differences in measures of recall initiation and post–initiation transitions. We identify four sources of variation: a recency factor reflecting variation in the tendency to initiate recall from an item near the end of the list, a primacy factor reflecting a tendency to initiate from the beginning of the list, a temporal factor corresponding to transitions mediated by temporal associations, and a semantic factor corresponding to semantically–mediated transitions. Together these four factors account for 83% of the variability in overall recall accuracy, suggesting they provide a nearly complete picture of recall dynamics. We also show that these sources of variability account for over 80% of the variance shared between memory and intelligence. The temporal association factor was the most influential in predicting both recall accuracy and intelligence. We outline a theory of how controlled drift of temporal context may be critical across a range of cognitive activities.

Complex behavior such as having a conversation, reading a paper, or making a decision relies on the coordinated operation of many cognitive processes. For over 100 years psychologists have attempted to understand how such coordination is achieved. One of the earliest findings was that performance on simple memory span tasks predicts success on more complex tasks (Jacobs, 1887). Dozens of studies have since confirmed that span performance correlates with a wide range of cognitive abilities (for meta-analyses see Ackerman, Beier, & Boyle, 2005; Daneman & Merikle, 1996). In trying to understand the connection between memory and complex cognition, the literature has come to focus on general intelligence, as it constitutes a theory-neutral statistical factor that contributes to almost all cognitive tasks (i.e., the “positive manifold”; Carroll, 1993). The question of which memory processes are critical in predicting intelligence has animated the individual differences literature for over 30 years (Daneman & Carpenter, 1980; Mogle, Lovett, Stawski, & Sliwinski, 2008; Turner & Engle, 1989; Unsworth, Brewer, & Spillers, 2009).

Most of this work has focused on limitations in working memory and attention (e.g., Hasher, Lustig, & Zacks, 2007; Kane, Conway, Hambrick, & Engle, 2007; Oberauer, 2002; Towse, Hitch, & Hutton, 1998). The focus on working memory likely has roots in the fact that span tasks were developed to measure the ability to hold information active in primary memory rather than to measure the ability to retrieve information from secondary memory (Jacobs, 1887). As the idea of a passive primary memory matured into the notion of a working memory system that both stores and manipulates information (Baddeley, 2003; Miyake & Shah, 1999), new “complex” span tasks were designed that required simultaneously storing and processing of information (Daneman & Carpenter, 1980; Turner & Engle, 1989). These complex span tasks have proven to be even better predictors of intelligence than simple span tasks, further solidifying the central role of working memory in the search for the link between memory and intelligence. Despite extensive investigation, a consensus on which processes are critical has failed to emerge (for a variety of competing perspectives see Conway, Jarrold, Kane, Miyake, & Towse, 2007).

Recent evidence suggests that part of the difficulty is that in addition to working memory, episodic memory also contributes to the correlation between span and intelligence. Healey and Miyake (2009) found that span tasks require considerable attentional resources during retrieval, which is inconsistent with the view that items are held in working memory and easily accessible. Mogle et al. (2008) and Unsworth et al. (2009) have shown that after accounting for variation in episodic tasks such as free recall, paired associate learning, and prose recall, the correlation between span and intelligence is either eliminated or considerably reduced. Discovering which episodic memory processes are related to intelligence is now a priority for individual differences research (Ratcliff, Thapar, & McKoon, 2011; Unsworth, Brewer, & Spillers, 2013).

Prior to the current focus on working memory, some early individual difference work examined episodic memory tasks (e.g., Carlson, 1937; Christal, 1958; Games, 1962; Kelley, 1964; Underwood, Boruch, & Malmi, 1978). This work attempted to understand the relationships among both span and classic episodic memory tasks (e.g., free recall, paired associates, recognition) by deriving an overall summary measure for each task, such as overall recall accuracy, and examining the correlations among the summary measures. The main conclusion was that although there were identifiable sub-groups of memory tasks (e.g., span tasks versus associative tasks), the tasks also loaded onto a common factor (for reviews see Beier & Ackerman, 2004; Kane & Miyake, 2008). Although this older literature clearly established that episodic memory tasks share common variance, perhaps due to the focus on summary measures, it has not shed much light on which memory processes underlie the correlation with intelligence.

Proceeding largely in parallel to the individual difference literature (Carroll, 1993; Cronbach, 1957; Kane & Miyake, 2008; Underwood, 1975), the experimental study of episodic memory has focused not on the correlations of summary measures across tasks but on developing a detailed understanding of the cognitive processes at work within particular tasks. This work has provided a set of sophisticated measures of recall dynamics, which have only recently begun to inform the individual difference literature (e.g., Healey & Kahana, in press; Sederberg, Miller, Howard, & Kahana, 2010; Unsworth, 2009). Here we examine individual differences in recall dynamics in an effort to illuminate the correlation between memory and intelligence. We begin by reviewing the dynamics of memory search.

The Dynamics of Memory Search

The dynamics of memory search can be decomposed into recall initiation and post–initiation transitions. Probability of first recall (PFR) curves (Figure 1A) measure initiation by showing the probability of initiating from each serial position (Hogan, 1975; Howard & Kahana, 1999; Laming, 1999). In immediate free recall of supra-span lists (Grenfell-Essam & Ward, 2012), participants tend to initiate from the last serial position (Deese & Kaufman, 1957).

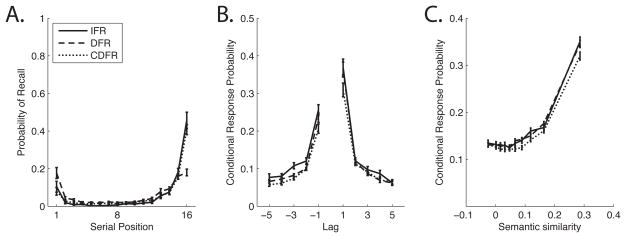
Figure 1.

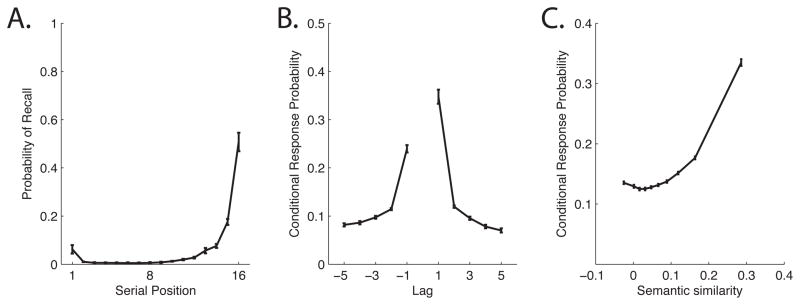
The Recall Dynamics Functions. Data are from the 141 participants who completed Experiment 1 of the Penn Electrophysiology of Encoding and Retrieval Study. Participants studied multiple 16–item lists for immediate free recall (see the Methods section for details). A. Probability First Recall curve. B. Lag-Conditional Response Probability curve. C. Semantic-Conditional Response Probability curve. See the text for details on how these curves are computed. Error bars are 95% within-subject confidence intervals (Loftus & Masson, 1994).

Post-initiation dynamics are revealed by the order in which items are recalled. Both long–standing semantic associations and newly formed episodic (temporal) associations exert a powerful influence on recall order. The influence of temporal associations can be described by how the probability that recall of item i is followed by recall of item j changes as a function of the distance, or lag, between i and j in the original list. For example, if i = 5 and j = 6 we would have a lag, j − i, of +1. Plotting these probabilities for a range of lags gives a lag-CRP (Conditional Response Probability) function. Lag-CRPs are computed by dividing the number of times a transition of a given lag was actually made by the number of times it could have been made (Kahana, 1996). Lag-CRPs (Figure 1B) show a strong temporal contiguity effect.

We can examine the influence of long–standing semantic associations on transition probabilities (Bousfield, 1953; Romney, Brewer, & Batchelder, 1993) using Latent Semantic Analysis (LSA; Landauer & Dumais, 1997), which measures the proximity of words in a multidimensional model of semantic space. Using LSA values to create a semantic-CRP curve (Figure 1C) reveals a strong semantic contiguity effect (Howard & Kahana, 2002). Together the three curves (Figure 1), which we call the Recall Dynamics Functions, provide a summary of the dynamics of memory search.

We have recently shown that these three Recall Dynamics Functions exhibit a remarkable level of qualitative consistency across individuals (Healey & Kahana, in press). The functions do, however, show individual differences. Examining the PFR curves of individual participants revealed that whereas most participants tend to initiate recall with the very last item of the list, there are two additional sub–groups that show different initiation patterns. In contrast to the beginning–first pattern, one sub–group of participants tended to initiate from the beginning of the list. The final sub–group of participants tended to initiate from a few items back from the end. We argued that this recall pattern results from participants encoding trains of several successive items into a chunk (Farrell, 2012). Post–initiation dynamics also show variation, but it is quantitative variation in level of the functions, not their shape. Here we provide a more detailed examination of these individual differences and their relation to intelligence.

Individual Differences in Memory Search

The fundamental goals of studying individual differences in memory and intelligence are to identify which processes show variation across individuals, and which of those processes are correlated with IQ. A common approach in the individual differences literature has been to identify a cognitive process that may be critical in both memory and intelligence tasks. Researchers then administer several tasks designed to measure memory ability, intelligence, and the putative mediating process and derive a summary measure from each task. These summary measures are then used to extract latent variables, which are taken as indices of the underlying constructs. An assumption here is that although the putative mediating process contributes to all three types of tasks, the latent variable extracted from the third set of tasks provides a purer measure of that process. Researchers can then test if statistically controlling for variation on that new, purer measure eliminates (i.e., mediates) the correlation between memory performance and IQ. This logic has been applied to testing the idea that episodic memory processes explain the correlation between memory tasks and IQ. For example, Mogle et al. (2008) showed that the correlation between span tasks and fluid intelligence was no longer significant when variation in episodic memory tasks, including free recall, was controlled for. Unfortunately, this approach has failed to provide consistent results. For example, Unsworth et al. (2009) have shown evidence for partial but not complete mediation.

One reason for this difficulty may be that the mediation approach attempts to infer the internal factor structure of memory from the pattern of correlations among summary measures derived from a variety of different memory and non–memory tasks. As such, the approach is highly theory driven in that the researcher must have some prior hypothesis about which processes are critical and use this to decide which tasks to administer. The need for prior theories is, in part, due to the reliance on summary measures. Summary measures reflect the final outcome of all the contributing cognitive processes. In other words, they take the output of multiple processes and compress them into a single number. This compression makes it difficult to directly determine how many processes contributed to the summary measure, forcing the researcher deduce the underlying processes from correlations among different tasks.

The Recall Dynamics Functions, however, allow us to take a more data–driven approach to studying individual differences. Instead of inferring the internal factor structure of memory from correlations across different tasks, we can examine detailed measures of performance derived from a single task. Essentially, the recall dynamics functions uncompress the summary measure of overall recall, providing a window on the cognitive processes that produce overall performance.

Some important facts about individual differences in recall dynamics have already been discovered: temporal and semantic contiguity seem to be universal principles across individuals (Healey & Kahana, in press), temporal contiguity is positively correlated with overall recall (Sederberg et al., 2010; Spillers & Unsworth, 2011), and individuals who exhibit both strong primacy and strong recency effects tend to have higher fluid intelligence scores than individuals who exhibit either weak primacy or recency (Unsworth, Brewer, & Spillers, 2011). Although important first steps, these studies have not fully embraced the idea of moving beyond summary measures to examine the full richness of the Recall Dynamics Functions and have instead used summary measures such as temporal contiguity scores and latency to first recall (e.g. Sederberg et al., 2010; Unsworth, 2009).

An advantage of summary measures is that they provide a single variable on which to compare individuals. By contrast, the Recall Dynamics Functions of Figure 1 include 36 separate variables (16 points in the PFR, and 10 points each in the lag-CRP and semantic-CRP). Directly examining individual differences on these 36 dimensions would be intractable. Instead, we use factor analysis as a tool to reduce the Recall Dynamics Functions to a manageable number of dimensions while retaining the richness of the data. This approach allows us to address three questions.

First, how many sources of variance underlie individual differences in the Recall Dynamics Functions, and what do these sources mean in terms of cognitive processes? Answering this question will place constraints on models of memory search (Underwood, 1975). Intuitively, one may predict that separate sources of variance contribute to each of the Recall Dynamics Functions (i.e., an initiation factor, a temporal contiguity factor, and a semantic contiguity factor). Under most models of memory, however, each of the Functions results from multiple interacting mechanisms, making it unclear how many factors a model predicts. For example, under retrieved context models (e.g., Polyn, Norman, & Kahana, 2009), one parameter governs the influence of new temporal associations, another governs existing semantic associations, and both are scaled by a third parameter. In principle, individuals could differ on any or all of these parameters; thus, the model could predict that as few as one and as many as three sources of variance underlie the temporal and semantic Recall Dynamics Functions. The predictions of other models are similarly ambiguous (see the Discussion for more on this issue).

Second, do the Recall Dynamics Functions provide a complete description of the processes governing memory search? If so, they should contain all of the information needed to reconstruct an individual’s overall probability of recall, which represents the outcome of all memory search processes. Answering this question will help identify gaps in our understanding of recall dynamics; if a substantial proportion of the variance in overall recall is unexplained, it suggests that the Recall Dynamics Functions miss important memory processes.

Finally, which memory processes are related to intelligence? Knowing which aspects of the Recall Dynamics Functions correlate with intelligence will allow modelers to test whether the corresponding parameter in a model is also correlated with intelligence. For the individual differences literature, knowing how the internal factor structure of recall dynamics relates to intelligence will advance the goal of understanding why memory predicts intelligence.

Methods

Participants

The data reported here are from the Penn Electrophysiology of Encoding and Retrieval Study (PEERS). PEERS aims to assemble a large database on the electrophysiological correlates of memory encoding and retrieval. The present analyses are based on the 141 college students (age 17–30) who had completed Experiment 1 of PEERS as of September 2013. Participants were recruited through a two–stage process. First, we recruited right-handed native English speakers for a single session to introduce participants to EEG recordings and the free recall task (EEG data are not reported here). Participants who completed this introductory session were invited to enroll in the full study, on the condition that they did not make an excess of eye movements during item presentation epochs of the experiment and their probability of recall was less than 0.8. Approximately half of the subjects recruited for the preliminary session qualified for, and agreed to participate in, the multi-session study. Participants were consented according the University of Pennsylvania’s IRB protocol and were compensated for their participation.

PEERS Experiment 1

For completeness, we provide a full description of PEERS Experiment 1, but note that our primary analysis was conducted on the immediate free recall data. Participants performed a free recall experiment consisting of 1 practice session and 6 subsequent experimental sessions (the practice session is not included in the analyses reported below, though we note that including it produces almost identical results and does not change any conclusions). Each session consisted of 16 lists of 16 words presented one at a time on a computer screen. Each study list was followed by an immediate free recall test and each session ended with a recognition test. The practice session and half of the experimental sessions were randomly chosen to include a final free recall test before recognition, in which participants recalled words from any of the lists from the session.

Words were either presented concurrently with a task cue, indicating the judgment that the participant should make for that word, or with no encoding task. The two encoding tasks were a size judgment (“Will this item fit into a shoebox?”) and an animacy judgment (“Does this word refer to something living or not living?”), and the current task was indicated by the color and typeface of the presented item. Using the results of a prior norming study, only words that were clear in meaning and that could be reliably judged in the size and animacy encoding tasks were included in the pool. There were three conditions: no-task lists (participants did not have to perform judgments with the presented items), single-task lists (all items were presented with the same task), and task-shift lists (items were presented with either task). The first two lists were task-shift lists, and each list started with a different task. The next fourteen lists contained four no-task lists, six single-task lists (three of each of the task), and four task-shift lists. List and task order were counterbalanced across sessions and participants.

Each word was drawn from a pool of 1638 words. Lists were constructed such that varying degrees of semantic relatedness occurred at both adjacent and distant serial positions. Semantic relatedness was determined using the Word Association Space (WAS) model described by Steyvers, Shiffrin, and Nelson (2004). WAS similarity values were used to group words into four similarity bins (high similarity: cosθ between words > 0.7; medium–high similarity, 0.4 < cosθ < 0.7; medium-low similarity, 0.14 < cosθ < 0.4; low similarity, cosθ < 0.14). Two pairs of items from each of the four groups were arranged such that one pair occurred at adjacent serial positions and the other pair was separated by at least two other items.

For each list, there was a 1500 ms delay before the first word appeared on the screen. Each item was on the screen for 3000 ms, followed by jittered (i.e., variable) inter-stimulus interval of 800–1200 ms (uniform distribution). If the word was associated with a task, participants indicated their response via a keypress. After the last item in the list, there was a jittered delay of 1200–1400 ms, after which a tone sounded, a row of asterisks appeared, and the participant was given 75 seconds to attempt to recall aloud any of the just-presented items.

If a session was selected for final free recall, following the immediate free recall test from the last list, participants were shown an instruction screen for final free recall, telling them to recall all the items from the preceding lists. After a 5 s delay, a tone sounded and a row of asterisks appeared. Participants had 5 minutes to recall any item from the preceding lists.

After either final free recall or the last list’s immediate recall test was a recognition test, which is not considered here (for full details see Lohnas & Kahana, 2013).

PEERS Experiment 2

PEERS Experiment 2 was used to test the generalizability of our factor analysis. Of the 141 participants included in our main analyses, 127 also completed Experiment 2, which differed from Experiment 1 as described below. There was one practice session (not analyzed) followed by 6 experimental sessions each consisting of 12 study lists of 16 words. Experiment 2 included a mix of immediate recall lists, delayed recall lists (in which the final word was followed by a distractor task), and continual distractor lists (in which each word was followed by a distractor task). Distractor tasks consisted of answering math problems A + B + C =?, where A, B, and C were positive, single-digit integers, though the answer could have been one or two digits. When a math problem was presented on the screen, the participant typed the sum as quickly as possible. The task was self-paced, such that a participant may have been presented with, but not responded to, a problem at the end of the distraction interval. Participants were given a monetary bonus based on the speed and accuracy of their responses. In the first two trials, participants performed free recall with one trial having a distractor period following the last word presentation for 8 s. For the other of the first two trials, participants performed the distractor task for 8 s prior to and following each word presentation. In the remaining 10 trials, participants performed free recall with 5 possible time durations for the between-item and end-of-list distractor tasks. As listed here, the first number indicates the between-list distractor duration and the second number indicates the end-of-list distractor duration, both in seconds: 0-0 for immediate recall, 0–8 or 0–16 for delayed recall, and 8–8 or 16-16 for continual distractor recall. A 0 s distractor refers to the typical, non-filled duration intervals as described for Experiment 1. Within each session, 50% of the lists were randomly chosen to be task-switch lists, and the other half were single-task lists.

Intelligence Testing

The Wechsler Adult Intelligence Scale (WAIS) IV (Wechsler, 2008) was administered to 101 of the participants who completed Experiment 1. WAIS testing was conducted by a trained clinical psychologist in one–on–one sessions after completing all free recall sessions. We omitted the working memory index of the WAIS as we were concerned that participants’ extensive practice with free recall would artificially inflate their scores.

Results

Identifying Sources of Variance in Recall Dynamics

The Recall Dynamics Functions are composed of 36 variables (16 points in the PFR, and 10 points each in the Lag-CRP and Semantic-CRP). We want to know how many cognitive processes contribute to individual differences on these 36 variables. If we call the true number of underlying process m, then we should be able to represent most of the variability in the Dynamics Functions by using a factor analysis to extract m statistical factors from the data. Extracting fewer than m factors will fail to capture all of the variability in the dataset, whereas extracting more than m factors will overestimate the number of contributing processes. The question then becomes, what is the value of m.

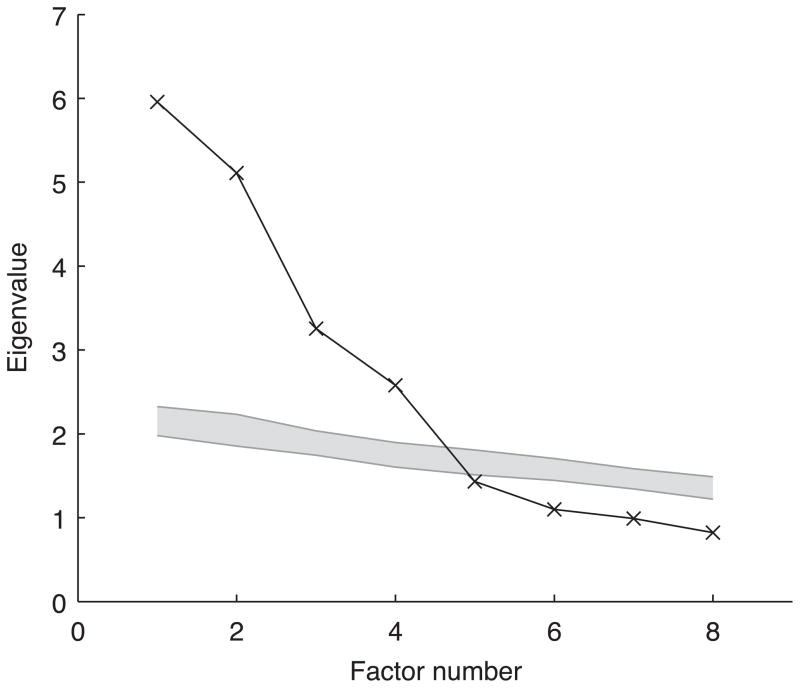
To find the appropriate value of m, we use a Monte Carlo method (Glorfeld, 1995; Horn, 1965) that starts with the intuition that a dataset with m underlying sources of variance (i.e., factors) will look different than a dataset with uncorrelated variables. Given a particular dataset, we can start by extracting a single factor and seeing how much of the variance in the data is accounted for by that factor. As we increase the number of factors extracted, the total amount of variance accounted for will tend to increase. If the data contain no true factors, then each factor should account for only a small proportion of the variance (i.e., each factor should have a small eigenvalue). By contrast, if the data actually have m factors, then the first m factors should account for a considerable proportion of the variance (i.e., should have large eigenvalues), and factors > m should account for less variance. In other words, the first m eigenvalues of a dataset with m factors should be higher than the corresponding eigenvalues for uncorrelated datasets. Thus, to find the value of m we need to determine what the eigenvalues would be if there were no true factors, and then compare these with the eigenvalues obtained from the participants’ data.

We determined the expected eigenvalues for uncorrelated data by running a factor analysis on a simulated dataset that has the same means and variance as the actual data, but in which the variables are uncorrelated. Taking the PFR as an example, the value of a person’s PFR at serial position 1 will likely be correlated with the value of their PFR at serial position 2. To create a simulated PFR that has the same shape as the original, but lacks its correlation structure, we started with serial position 1 and drew values (one for each actual participant) from a random distribution with a mean and variance equal to the mean and variance of the actual PFR at serial position 1. We did the same for serial position 2, and so on. Because each serial position is drawn from an independent random distribution, there will be no correlation between serial positions. We created simulated lag-CRPs and simulated semantic-CRPs in the same way, providing us with a full set of simulated Recall Dynamics Functions.

We then ran a factor analysis on the simulated dataset and saved the eigenvalues. We repeated this procedure for 1000 simulated datasets to build a distribution of expected eigenvalues for uncorrelated data. We then compared eigenvalues computed from the actual data with this distribution: If the data have m factors, the eigenvalues for the first m factors should lie above the 97.5^th percentile of the simulated distribution but those for factors greater than m should not. Figure 2 indicates that 4 factors underlie the Recall Dynamics Functions.¹

Figure 2.

Results of Monte Carlo factor identification procedure (Glorfeld, 1995; Horn, 1965). The shaded region represents the middle 95% of the distribution of eigenvalues from 1000 simulated datasets that contained no factor structure. The line represents eigenvalues for the actual data. Only Factors 1–4 in the actual data fall above the shaded region indicating they explain more variability than expected by chance, and that the data contain 4 significant sources of variance.

Linking Factors to Memory Processes

Once we have identified the correct number of factors, extracting those factors from the data provides two key sets of numbers that can help to link the factors to cognitive processes. The first is a set of factor loadings that describe how much each factor contributes to variation on each of the 36 original variables (e.g., a process that controls recall initiation would likely have strong loadings for the PFR, but weaker loadings for the Lag-CRP and the Semantic-CRP). The second is a set of factor scores, one for each factor, that shows where in the distribution of variation on that factor each individual lies and can be used to compare sub–groups of participants (e.g., those that show different patterns of recall initiation).

The initial set of loadings returned by the factor analysis algorithm requires the factors to be orthogonal. However this initial solution can be “rotated” to make it more theoretically meaningful (Kline, 2005). Because there is no strong theoretical reason to believe that memory processes should be uncorrelated, we applied an oblique rotation (the Promax rotation), which allows factors to correlate. To ensure that the factor loadings are not biased by outliers and to provide confidence intervals on the loadings, we ran a jackknife procedure in which we ran the factor analysis multiple times, each time leaving one participant out of the sample (Clarkson, 1979). We used the distribution of loadings across samples to create 99% confidence intervals around the mean loadings. These mean loadings were then used to calculate factor scores using the Bartlett (1937) method. Next, we examined the factor loadings and scores to link the factors to memory processes.

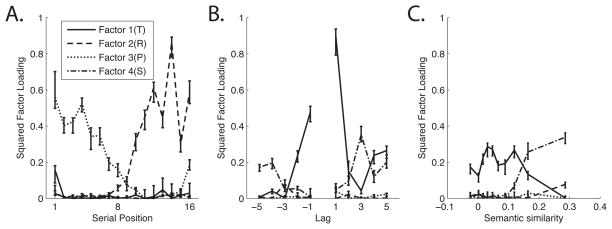
Each point in the Recall Dynamics Functions has one loading for each of the factors, and the square of these loadings tells us how much of the variance in that variable is explained by the factor (analogous to the R² in a regression). Figure 3 shows squared loadings mapped onto the original variables and Table 1 shows the non–squared loadings.

Figure 3.

Squared loadings mapped onto the Recall Dynamics Functions: A. Probability First Recall curve. B. Lag-Conditional Response Probability curve. C.

Semantic-Conditional Response Probability curve. The values at each point indicate the percentage of variance across participants that is accounted for by each factor. Error bars represent 99% confidence intervals (see text for details on how confidence intervals were computed). N = 141.

Table 1.

Promax rotated factor loadings.

	Factor 1(T)	Factor 2(R)	Factor 3(P)	Factor 4(S)
Serial position	PFR
1	0.40	−0.16	0.75	−0.18
2	0.07	−0.09	0.63	0.08
3	−0.01	0.02	0.65	0.11
4	0.05	−0.15	0.73	0.10
5	0.03	0.04	0.59	0.13
6	−0.03	0.11	0.59	0.08
7	−0.12	0.14	0.45	−0.06
8	−0.05	0.24	0.41	−0.06
9	−0.05	0.32	0.27	0.07
10	−0.14	0.57	0.22	0.00
11	−0.01	0.67	0.03	−0.01
12	−0.10	0.78	−0.00	0.02
13	0.22	0.67	−0.12	−0.14
14	−0.01	0.93	−0.15	−0.12
15	−0.13	0.55	−0.19	0.15
16	−0.17	−0.77	−0.43	0.08
Lag	Lag-CRP
−5	−0.08	−0.09	−0.02	0.41
−4	−0.20	0.03	0.02	0.44
−3	−0.05	0.28	−0.10	0.22
−2	0.49	0.06	−0.09	0.24
−1	0.69	−0.09	−0.07	−0.09
1	0.95	−0.01	0.20	−0.22
2	0.39	0.15	−0.05	0.31
3	−0.20	0.04	−0.00	0.59
4	−0.49	−0.01	−0.11	0.35
5	−0.51	−0.04	0.15	0.45
Similarity Bin	Sem-CRP
1	0.42	0.11	0.10	−0.05
2	0.35	0.17	0.04	−0.15
3	0.47	0.07	0.03	−0.13
4	0.54	0.08	−0.11	−0.02
5	0.52	0.09	−0.06	0.14
6	0.43	−0.02	−0.04	0.02
7	0.44	0.04	0.15	−0.04
8	0.52	−0.09	0.03	0.26
9	0.37	−0.06	0.17	0.51
10	0.05	−0.28	0.04	0.58

T = Temporal; R = Recency; P = Primacy; S = Semantic

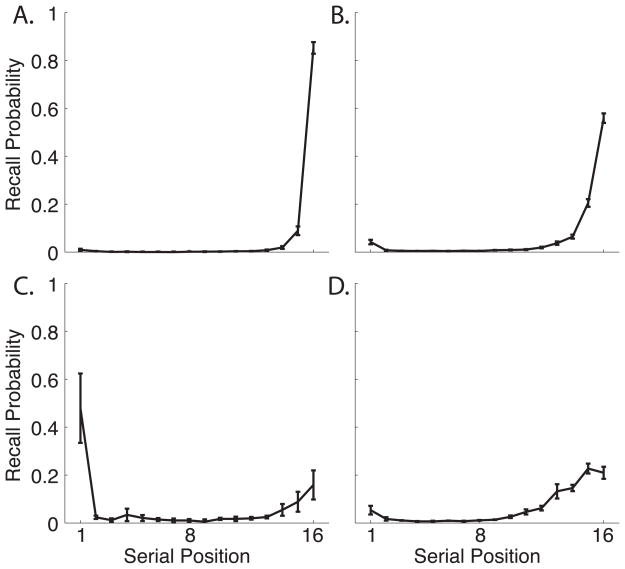
The PFR loads primarily on factors 2 and 3, suggesting two major sources of individual differences in recall initiation. As discussed above, we have recently identified sub–groups of participants that exhibit distinct patterns of recall initiation (Healey & Kahana, in press). To provide a clearer interpretation of the two recall initiation factors, we divided participants into these sub–groups using the same k-means clustering procedure we employed in that earlier work. Figure 4 shows the average PFR curves for each subgroup: the strong recency sub–group shows a strong tendency to initiate recall from the final item, the moderate recency sub–group shows a more moderate tendency to initiate from the final item, the primacy sub–group shows a strong tendency to initiate from the very first item, the final sub–group shows a tendency to initiate 3–4 items back from the end of the list. We argue that this sub-group encodes the last few items as a chunk (Farrell, 2012), and thus label it the chunking sub–group.

Figure 4.

Mean Probability First Recall curves for each of the four clusters of participants identified by Healey and Kahana (in press). K-means with k = 4 was used to assign each participant to a cluster. A. The strong recency cluster. B. The moderate recency cluster. C. The primacy cluster. D. The chunking cluster. Error bars are 95% within-subject confidence intervals (Loftus & Masson, 1994).

We focus first on interpreting factor 2. Table 2 shows the average factor scores for reach of the recall initiation sub–groups. Looking at the factor 2 row of the table, we see that the chunking sub–group has the highest factor scores, the recency sub–groups have the lowest scores and the primacy sub–group has scores near zero. This pattern suggests that factor 2 captures a tradeoff between the recency and chunking patterns (participants with high scores on this factor tend to initiate recall several items back from the end of the list, whereas those with low scores tend to initiate from the very last item). This interpretation is bolstered by examining how the loadings for factor 2 vary across serial positions (Figure 3A). The loadings are lowest for early serial positions and largest for late serial positions (those greater than 9), suggesting that the factor describes a tendency to initiate from the recency portion of the list. Note, however, that it is serial position 14 and not the very last serial position (position 16) that loads most strongly on Factor 2. Moreover, the non–squared loadings in Table 1 indicate that whereas serial positions 9–15 have strong positive loadings on Factor 2, serial position 16 actually has a strong negative loading. In other words, a large positive score on factor 2 predicts a high probability of initiating from somewhere near, but not at, the end of the list, whereas a large negative score on factor 2 predicts initiating from the very end of the list. Together, the differences in factor scores across initiation sub–groups and the differences in factor loadings across serial positions indicate that factor 2 captures two patterns of initiating from recency items. We therefore label this factor the recency factor.

Table 2.

Mean (± 95% CIs) factor scores, overall recall, and IQ by PFR cluster.

	Cluster
	Strong Recency	Moderate Recency	Primacy	Chunking
n total (n with IQ)	35 (24)	57 (44)	8 (5)	41 (28)
Factor 1(T)	−0.30±0.33	−0.05±0.21	1.03±1.04	0.12±0.37
Factor 2(R)	−1.19±0.10	−0.17±0.11	−0.10±0.27	1.28±0.20
Factor 3(P)	−0.73±0.09	−0.13±0.16	2.47±0.97	0.32±0.34
Factor 4(S)	−0.28±0.35	0.21±0.33	−0.88±0.83	0.13±0.28
Overall Recall	0.59±0.04	0.61±0.03	0.70±0.10	0.63±0.04
IQ Score	128.88±3.96	127.50±3.22	129.40±14.97	126.79±3.91

T = Temporal; R = Recency; P = Primacy; S = Semantic

Focusing on factor 3, we see that factor scores are highest for the primacy sub–group and lowest for the strong recency sub–group (Table 2) and intermediate for the moderate recency and chunking groups (participants in these groups very occasionally initiate from the beginning of the list; see Figure 4). This pattern of scores across sub–groups suggests that factor 3 captures the tendency to initiate recall from primacy items. Supporting this interpretation, early serial positions (positions less than 9) loaded most strongly onto Factor 3 (Figure 3A and Table 1). We therefore label factor 3 the primacy factor.

The finding that there are distinct primacy and recency factors is consistent with models that assume primacy and recency derive from separate mechanisms. For example, retrieved context models (e.g., Lohnas, Polyn, & Kahana, submitted; Polyn et al., 2009) assume primacy is due to increased attention to early list items whereas recency is due to mental context states at retrieval providing strong cues for recently presented items. We return to this point in the discussion.

Post–initiation dynamics, as described by lag-CRP and semantic-CRP, load primarily on factors 1 and 4 (Figure 4B and C). Factor 1 is strongly related to near temporal transitions and far semantic transitions. By contrast, factor 4 loads most strongly on near semantic transitions and distant temporal transitions. Therefore we label factor 1 and factor 4 as the temporal and the semantic Process Factors respectively. The fact that the temporal factor has high loadings not just for near temporal transitions but also for far semantic transitions (and that the semantic factor has high loading not just for near semantic transitions but also for distant temporal transitions), likely reflects a natural tradeoff between temporal and semantic clustering. Take the extreme example of a participant who shows perfect temporal clustering (i.e., recalls in perfect serial order) and makes no use of semantic associations. Because our lists are arranged so that most words with strong semantic associations are not temporally contiguous, such a participant would tend to make few transitions between close semantic associates, which necessarily means they will show stronger contiguity for items with low semantic similarity than for items with strong semantic similarity².

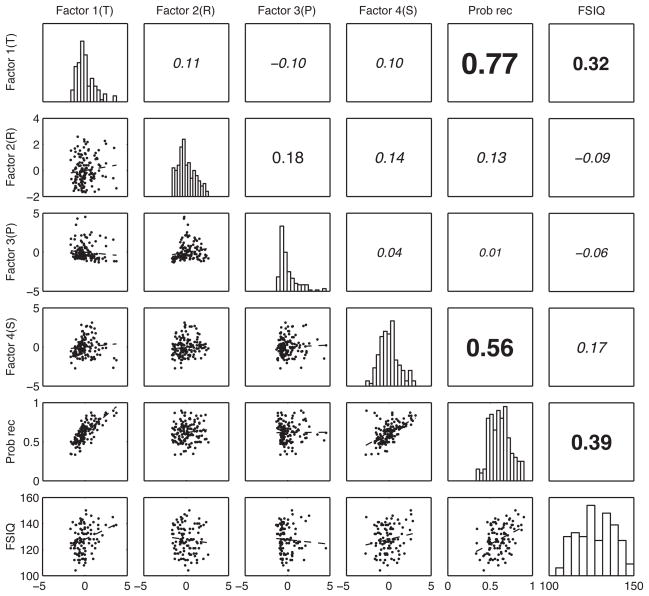
For each participant, we can use their factor scores as measures of their primacy, recency, temporal, and semantic processes. Before we use the scores as individual differences measures, however, we must ensure they are reliable. To assess reliability we used the split–half technique. Specifically we used the factor loadings from the full dataset to compute a set of factor scores for half of the 6 sessions and another set of factor scores for the other half of the six sessions and correlated the two sets of scores. We repeated this procedure for 100 split–half samples to compute average split-half reliability. These reliabilities for the Primacy, Recency, Temporal, and Semantic factors (± a 95% confidence interval computed across the samples) were .86 ± .005, .88 ± .005, .82 ± .007, and .68 ± .006, respectively. The reliability of overall recall, computed using the same procedure, was .90 ± .005. These values are well above the common threshold of .6 for acceptable reliability. To determine how the 4 factors relate to each other, we correlated participants’ scores across the factors (Figure 5). Despite our use of an oblique factor rotation, the factor scores remain largely uncorrelated. The lack of a correlation between temporal and semantic factors (see also Sederberg et al., 2010) suggests that temporal and semantic clustering arise from two distinct cognitive processes.

Figure 5.

Correllelogram for the Process Factors (Factor T = Temporal Factor, Factor R = Recency Factor, Factor P = Primacy Factor, Factor S = Semantic Factor), overall recall, and WAIS-IV IQ. All correlations involving IQ have N = 101; all other correlations have N = 141. Plots on the diagonal show histograms of each variable; plots in the bottom triangle are scatter plots; the upper triangle shows the correlation coefficients. For correlation coefficients, the size of the typeface is proportional to the absolute size of the coefficient. Correlation values in italics are non–significant.

Using recall dynamics to predict overall accuracy

Overall accuracy reflects the outcome of all the processes that contribute to memory search. If the Recall Dynamics Functions provide a complete description of recall dynamics, we should be able to use the factors derived above to predict overall recall. Because none of these Recall Dynamics Functions reflect recall success directly, there is no a priori reason for the factors to correlate with recall success (Sederberg et al., 2010).

As shown in Figure 5, the temporal and semantic factors are both predictive of overall recall success, but the initiation factors are not. In a meta-analysis, Sederberg et al. (2010) found that for random word lists a temporal clustering summary score was moderately correlated with recall success, but that a semantic summary score was not, whereas in lists that include pairs of semantically related words, as did our lists, semantic clustering was predictive of recall success. This pattern of results suggests that the relationship between clustering and recall success depends on the content of the lists. As we elaborate in the discussion, participants may dynamically tune their memory systems to up–weight associations that facilitate performance and down–weight those that do not.

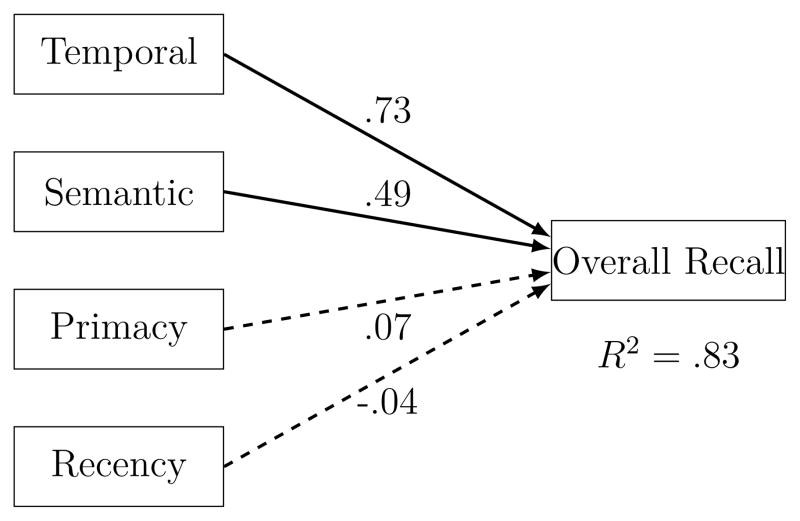
To determine how well the factors account for overall recall accuracy, we can use all four factors to simultaneously predict recall. Figure 6 shows the results. The figure is essentially a simultaneous regression but we present it as a path analysis model to maintain consistency with more complex analyses we present later. Each box in the figure represents a variable, and the arrows connecting the boxes represent the influence of variables on each other, with the direction of the arrow giving the presumed direction of the effect (e.g., we assume that the process factors cause variance in overall recall). The numbers next to the paths are analogous to standardized beta weights in a regression. Note that in this and all subsequent path analyses the factors were allowed to correlate, but because these correlations are very similar to those in Figure 5 they are omitted from the path diagrams to improve clarity. The figure shows that together the four factors account for 83% of the variability in overall recall, suggesting that the Recall Dynamics Functions provide a near–complete description of recall dynamics. No doubt other factors (e.g., idiosyncrasies in semantic relationships not captured by LSA) account for some proportion of overall recall, but apparently not more than 17%. Examining the individual paths, we see that the temporal and semantic factors were significant predictors of overall recall (solid lines represent significant paths), but that the primacy and recency factors were not. Participants who initiate recall from the beginning of the list will tend to experience output interference that lowers recall of items from later serial positions, whereas participants who initiate from near the end of the list will experience interference that lowers recall of early items (Cowan, Saults, Elliott, & Moreno, 2002). To ensure that these opposing interference effects were not obscuring any true correlation between overall recall and either the primacy or recency factors, we recalculated the correlations excluding the 8 participants in the primacy sub–group (see table 2), leaving only participants who initiate recall from near the end of the list. Excluding these participants did not change the direction or significance of the correlations among the factors, overall recall, and IQ. That is, variation in how participants initiate recall (which item they start with) does not predict overall recall success. Instead it is how participants transition among items after initiating that is critical.

Figure 6.

A path analysis model predicting overall recall from the four process factors. Each box represents a variable. The single-headed arrows connecting the variables represent hypothesized direct effects of one variable on another; the numbers next to single-headed arrows are standardized path coefficients and can be interpreted as standardized regression coefficients. In fitting the model, the process factors were allow to correlate but the paths are omitted from the diagram for clarity. The R² value is the proportion of variance in overall recall accounted for by the process factors. N = 141.

Validating the factor structure

A strong test of the validity of the factor structure would be to use the factors computed above to predict performance on a second dataset. Of the 141 participants who completed Experiment 1 of PEERS, 127 also completed Experiment 2. We can use the data from this second experiment to validate the factor structure we discovered in the Experiment 1 data. One approach would be to independently rerun the entire factor analysis on the Experiment 2 data. A more stringent test, however, would be to use the factors derived in Experiment 1 to predict Experiment 2 performance.

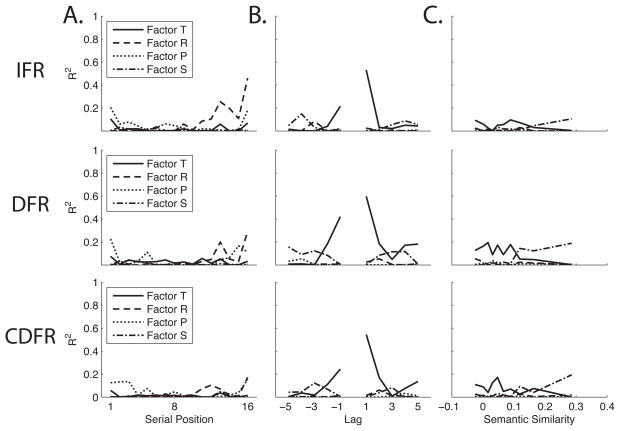
Figure 7 shows the Recall Dynamics Functions for Experiment 2. Figure 8 shows the squared correlations between each Experiment 1 factor and the Experiment 2 Recall Dynamics Functions, which can be interpreted in the same way as the squared factor loadings in Figure 3. Examining Figure 8 reveals that the loading patterns are quite similar across the three versions of free recall in Experiment 2, and also quite consistent with the loading pattern observed in Experiment 1. The most notable deviation is that the primacy and recency factors explain less of the variability in the PFRs from Experiment 2 than they did for Experiment 1. Why would the recall initiation factors show less generalization across experiments than the post–initiation transition factors? We have recently shown that whereas all participants show qualitatively similar lag– and semantic–CRP functions, there is more variability in the shape of PFR functions, with most participants showing a recency heavy function but a minority showing either a non–monotonic “clustering” pattern or a primacy pattern (Healey & Kahana, in press). We suggested that the variability in PFR functions may reflect, in part, differences in strategy. It is possible that because Experiment 2 intermixes immediate recall trials, which tend to show a recency initiation pattern, with delayed trials which tend to show a shift toward a primacy initiation pattern (compare the PFR curves in Figure 7). Participants may vary in the extent to which they show this shift, reducing the predictive power of the initiation factors derived from Experiment 1. In contrast, the fact that the temporal and semantic factors tend to correlate with the same Recall Dynamics Function points across all three recall tasks suggests that the same processes govern post–initiation dynamics regardless of distractor condition.

Figure 7.

The Recall Dynamics Functions from the 127 participants who completed Experiment 2 of the Penn Electrophysiology of Encoding and Retrieval Study. A. Probability First Recall curve. B. Lag-Conditional Response Probability curve. C. Semantic-Conditional Response Probability curve. Within each panel the three lines correspond to Immediate Free Recall (IFR), Delayed Free Recall (DFR), and Continual Distractor Free Recall (CDFR). See the text for details on how these curves are created. Error bars are 95% within-subject confidence intervals (Loftus & Masson, 1994).

Figure 8.

Squared loadings mapped onto the Recall Dynamics Functions of Experiment 2 of the Penn Electrophysiology of Encoding and Retrieval Study: A. Probability First Recall curve. B. Lag-Conditional Response Probability curve. C. Semantic-Conditional Response Probability curve. The first row shows Immediate Free Recall (IFR), the second row shows Delayed Free Recall (DFR), and the third row shows Continual Distractor Free Recall (CDFR). The values at each point indicate the percentage of variance across participants that is accounted for by each factor. N = 127

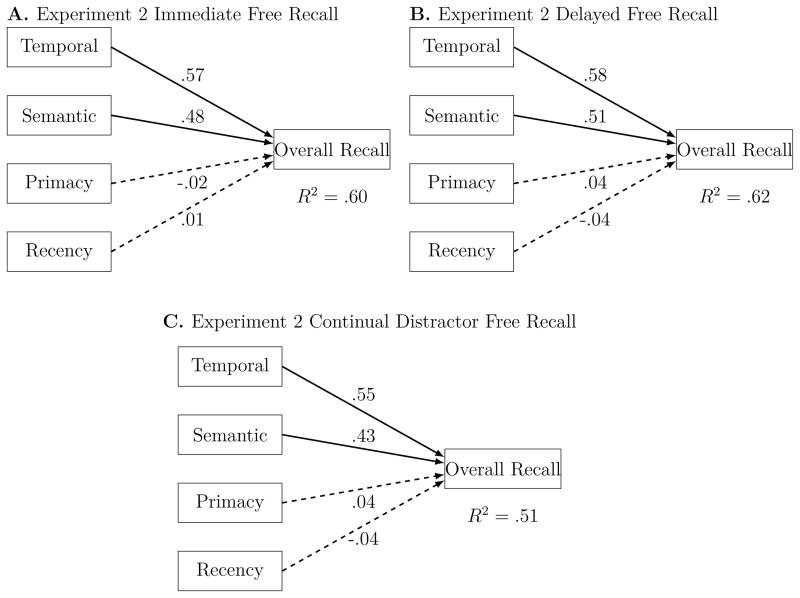
This interpretation of the relative consistencies of the factors across task type is supported by examining the ability of the Process Factors derived from Experiment 1 to predict overall recall on the three Experiment 2 tasks. Figure 9 shows path diagrams of these predictions. For immediate free recall (Figure 9A), the pattern is very similar to that seen in Experiment 1 (Figure 6), with the temporal and semantic factor both being significant predictors but the primacy and recency factors being non-significant. This strengthens our claim that variation in post recall dynamics is more diagnostic of episodic memory ability than variation in recall initiation patterns. An even stronger test is to use the factors from immediate free recall to predict delayed and continual distractor tasks. If the three tasks rely on the same mechanisms, as predicted by retrieved context models (e.g., Polyn et al., 2009), we would expect the quality of prediction to be quite high. If, however, the tasks rely on different processes (e.g., short– versus long–term memory; Davelaar, Goshen-Gottstein, Ashkenazi, Haarmann, & Usher, 2005) the quality of prediction should suffer. Panels B and C of Figure 9 show that the quality of prediction is, in fact, excellent: The immediate free recall factors predict 62% of the variability on delayed free recall, and 51% of the variability on continual distractor free recall. Once again, the temporal and semantic factors were significant predictors, but the primacy and recency factors were not.

Figure 9.

Path analysis models predicting overall recall from the four process factors for each condition of Experiment 2: A. Immediate Free Recall, B. Delayed Free Recall, and C. Continual Distractor Free Recall. Each box represents a variable. The single-headed arrows connecting the variables represent hypothesized direct effects of one variable on another; the numbers next to single-headed arrows are standardized path coefficients and can be interpreted as standardized regression coefficients. In fitting the models, the process factors were allow to correlate but the paths are omitted from the diagram for clarity. The R² values are the proportion of variance in overall recall accounted for by the process factors. N = 127.

The ability of the factor structure derived from IFR in Experiment 1 to predict delayed recall in Experiment 2 is particularly striking in that it suggests that any sources of variance uniquely related to a short–term buffer, which should be emptied by the distractor, account for a relatively small proportion of the variance in both overall recall and the dynamics functions. We note that the R² for continual distractor free recall is somewhat lower than for the other two conditions. This suggests the possibility that continual distractor recall may capture a source of individual differences that is not (as fully) captured by immediate free recall. One possibility is that participants may vary in the extent to which mental context drifts during distractor intervals.

Using recall dynamics to illuminate the memory/intelligence correlation

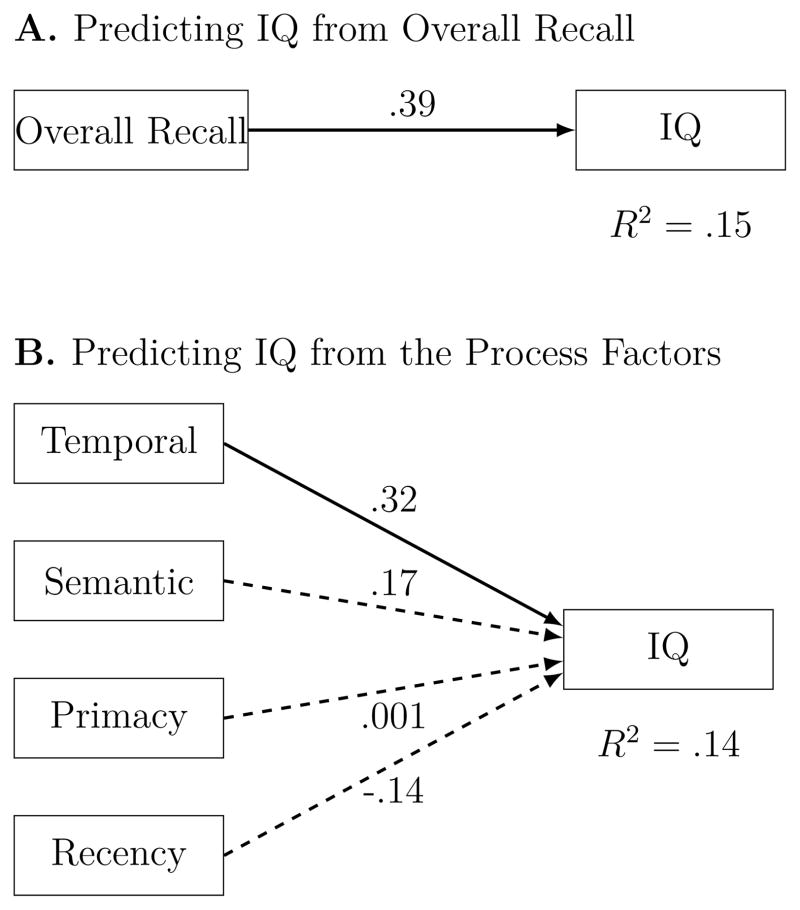
The distribution of IQ scores in our sample (Figure 5), while roughly normal, is above the population average. Despite this abbreviated range, which will tend to produce underestimates of the true correlations between memory and IQ, we found a correlation between overall recall and IQ of .39 (see Figure 5), within the range reported in meta–analyses (Ackerman et al., 2005). Translating this correlation into proportion of variance, overall recall accounted for 15% of the variability in IQ (Figure 10A). One of the main goals in the study of individual differences in memory is to determine which memory processes are responsible for the variance shared between overall recall and IQ. That is, why does overall recall success predict IQ? Do the Process Factors we have identified here help answer this question?

Figure 10.

Path analysis model predicting IQ from Overall Recall (A) and the four process factors (B). Each box represents a variable. The single-headed arrows connecting the variables represent hypothesized direct effects of one variable on another; the numbers next to single-headed arrows are standardized path coefficients and can be interpreted as standardized regression coefficients. In fitting the models, the process factors were allow to correlate but the paths are omitted from the diagram for clarity. The R² values are the proportion of variance in overall recall accounted for by the process factors. N = 101.

The first step is to examine the correlations between the factors and IQ. Figure 5 shows that both the temporal and the semantic factor are significantly correlated with IQ but that neither the primacy nor the recency factors are. Next we ran a simultaneous regression using the four factors to predict IQ. Together, the factors accounted for 14% of the variability in IQ scores (Figure 10B), with the temporal factor being the strongest predictor. Note that overall recall and the process factors account for almost identical proportions of variance in IQ (i.e., 15% and 14% respectively). If the processes factors are measuring individual differences in the memory processes that drive the correlation between overall recall and IQ, we should find that the factors and overall recall account for overlapping portions of the variability in IQ.

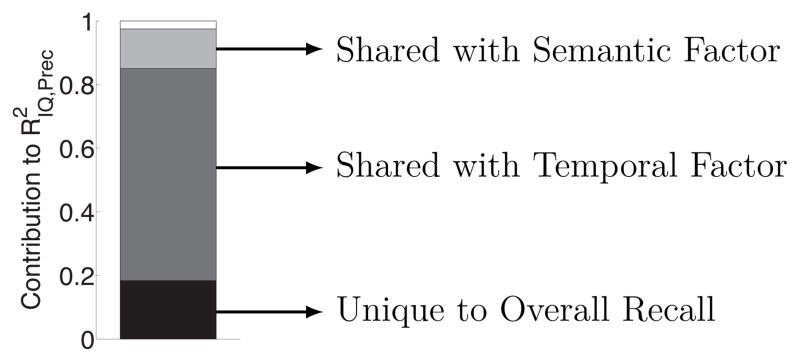
To test if our factors fully account for the relationship between memory and IQ we conducted a commonality analysis (Nimon, Lewis, Kane, & Haynes, 2008). A commonality analysis takes the total variance in one variable explained by a set of predictor variables and attempts to break it down into variance that is uniquely accounted for by one predictor (but not others), and variance that is explained by several predictors (i.e., shared variance). Commonality analysis has previously been used to partition the variance in IQ explained by working memory versus episodic memory tasks (Unsworth & Spillers, 2010). If you imagine all of the variation in IQ as a pie, the variability accounted for by overall recall would be a slice (15%) of the pie. The bar in Figure 11 represents that slice of the pie. We can further divide the slice into parts that represent variability uniquely explained by recall (but not the factors) and variance that is common to overall recall and the factors. Our prediction is that the portion unique to overall recall will be small. Consistent with our prediction, less than 20% (i.e., less than 3% of the entire IQ pie) of the variance was unique to overall recall. That is, overall recall and the factors account for almost completely overlapping variance in IQ suggesting that recall dynamics capture the processes that allow memory to predict IQ.

Figure 11.

Commonality analysis of correlation between overall recall and IQ. The bar represents all of the variability in IQ that is accounted for by overall recall (i.e., 15%). The shaded regions represent the portion of that variability that is uniquely accounted for by overall recall, and the portion that is shared with the process factors. There is a small unique contribution of overall recall, but most is shared with the temporal and semantic factors. A small portion (the white region at the top of the bar) is shared with the primacy or recency factors or with multiple factors. N = 101.

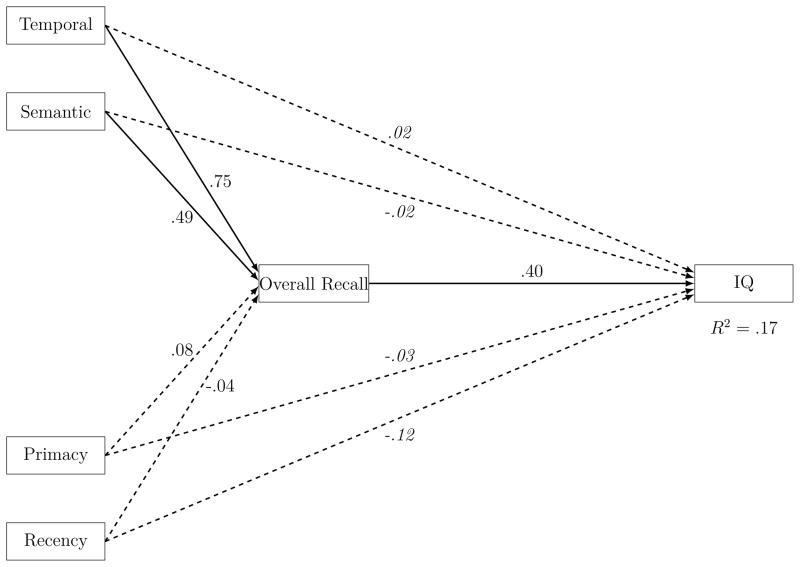
This view of the relationship among the factors, overall recall and IQ is made explicit in the path analysis model in Figure 12. As we discussed in the introduction, the standard approach to determining whether a particular cognitive process accounts for the relationship between memory and IQ is to statistically control for variation in a third task that measures the process in question. This mediation logic assumes that the third task provides a purer, or more sensitive, measure of the process in question than does either memory or IQ. By contrast we have extracted measures of memory processes directly from detailed measures of task performance rather than using a non–memory proxy task. That is, overall recall contains the same information as our process factors but compresses the information into a single measures; our factors uncompress the data.

Figure 12.

Path analysis model of the effects of the process factors and overall recall on IQ. Each box represents a variable. The single-headed arrows connecting the variables represent hypothesized direct effects of one variable on another; the numbers next to single-headed arrows are standardized path coefficients and can be interpreted as standardized regression coefficients. The direct paths from the factors to IQ were constrained to zero in the final model, the estimates from the non–constrained model are provided in italics for completeness. In fitting the model, the process factors were allow to correlate but the paths are omitted from the diagram for clarity. The R² values are the proportion of variance in Overall Recall accounted for by the process factors. N = 101.

Consistent with the logic that the factors represent the processes contributing to overall performance, the path model in Figure 12 includes direct paths (i.e., single-headed directly connecting boxes) from each factor to overall recall, which in turn has a direct path to IQ. Each factor also has an indirect path to IQ via their influence on overall recall. In the language of path analysis, our prediction is that these indirect effects of the process factors on IQ via overall recall should account for the bulk of the direct effect of overall recall on IQ. As expected, the direct effects of the factors on IQ are all non-significant. Indeed, constraining the direct paths from each of the factors to IQ to be equal to zero, provided a very good fit to the data (χ²(4) = 2.3, p = 0.68). That is, none of the factors directly contribute to variation in IQ. Instead their effects are mediated by their influence on overall recall.

Discussion

Performance on memory tasks predicts many other cognitive abilities (Daneman & Carpenter, 1980; Jacobs, 1887; Mogle et al., 2008). To better understand which memory processes underlie these correlations we examined individual differences in measures of recall dynamics. We found that four distinct factors contribute to individual differences in memory search: a tendency to initiate recall from near the end of the list (recency), a tendency to initiate from near the beginning of the list (primacy), a temporal factor corresponding to transitions mediated by temporal associations, and a semantic factor corresponding to transitions mediated by long–standing semantic associations. We show that the four factors account for 83% of the variability in overall recall, suggesting that they provide a near–complete description of the processes that contribute to individual differences in recall success. To validate this factor structure, we used the factors computed from immediate free recall in PEERS Experiment 1 to predict recall performance in PEERS Experiment 2: the Experiment 1 factors accounted for 60%, 62%, and 51% of the variance in Experiment 2 immediate, delayed, and continual distractor recall, respectively. Moreover, the factors accounted for over 80% of the relationship between memory and IQ, with the temporal factor being the most important single factor.

Implications for Models and Theories

The factor structure reported here places a new class of constraints on memory models. The dominant approach to model validation has been to fit models to data averaged across participants. An accurate model of memory search, however, should also account for differences among individuals: That is, the covariance of the data. To our knowledge, no attempt has been made to fit the covariance structure of recall dynamics. Some preliminary observations are possible, however. For example, under dual–store models, temporal contiguity effects emerge from items spending time together in short-term memory; short-term memory also powerfully influences the tendency to initiate recall from the end of list, which may suggest temporal contiguity and initiation would share variance. Under retrieved context models, which assume memory is mediated by associations between items and a drifting internal context representation, there is also reason to predict contiguity and initiation should be correlated, as both mechanisms are influenced by a common context drift rate parameter. Contrary to these intuitive predictions, we found that recall initiation and temporal contiguity are largely independent. Future modeling work should explore whether existing models can simulate the factor structure discovered here.

For the individual difference literature, our results provide a fresh perspective on which memory processes correlate with IQ. Most of the correlation between memory and IQ is accounted for by individual differences in temporal contiguity: Individuals who show stronger temporal clustering tend to recall more items and have higher IQs. This finding is not an obvious prediction of theories that assume that individuals with higher IQs can recall more items because they can hold more items in working memory (Kane et al., 2007; Oberauer, 2002). Indeed, it is difficult to predict how variation in working memory storage capacity would impact temporal clustering. Under most dual–store memory models (e.g. Kimball, Smith, & Kahana, 2007; Raaijmakers & Shiffrin, 1981; Sirotin, Kimball, & Kahana, 2005), temporal associations are formed between items that spend time together in working memory (see Cowan, Donnell, & Saults, 2013, for empirical evidence of this assumption). Therefore one possible prediction is that individuals who hold more items in working memory at a time will form longer–range temporal associations. Longer–range temporal associations would lead to more transitions at longer lags (i.e., a shallower lag-CRP curve) and fewer transitions at the short lags that load strongly on the temporal factor. Therefore, one would expect individuals with large working memory capacities to have lower temporal factor scores. An alternative prediction is that having more items in working memory at once will allow the formation of longer chains of associated items. For example, a small working memory capacity individual may form associations between two items (A and B), whereas a large working memory capacity individual may form associations among four (A, B, C, and D). If participants tend recall items in serial order within such chains (e.g., because each item serves as a cue for the next item in the chain; Lohnas & Kahana, 2014), then the higher capacity individual would make more short–lag transitions (A to B, B to C, C to D) than would the lower capacity individual (A to B), leading to a steeper lag-CRP curve.³ In our view, rigorous modeling will be required to clarify these predictions and determine if dual–store models are consistent with the factor structure we have described here.

The ability of the factors derived from immediate free recall in Experiment 1 to account for roughly equal amounts of variance in both immediate and delayed recall in Experiment 2 (i.e., 60% and 62% respectively) is also challenging for theories that emphasize working memory. From a dual–store perspective, one may have predicted that variance related to the short–term buffer would be more important in predicting performance in immediate than delayed recall because the distraction filled delay would empty the buffer, forcing participants to rely on other memory processes.

The data are more easily interpreted within frameworks that assume that, although working memory capacity is an important correlate of IQ, the ability to efficiently search long–term memory is also key (e.g., Unsworth & Engle, 2007). Spillers and Unsworth (2011) found that individuals with large working memory span scores showed more temporal clustering than individuals with lower span scores. Drawing from retrieved context models that assume memory is mediated by associations between items and a drifting mental context representation, they argued that this difference resulted from low–span individuals being less able to use contextual information associated with a just–recalled item to guide retrieval of the next item. Promising theories such as this highlight the value of bringing the individual differences and episodic memory modeling literatures into closer contact. Below we sketch how episodic memory models might further illuminate the connections between temporal contiguity, memory ability, and IQ.

Temporal Contiguity and Intelligence

The temporal factor, corresponding to a tendency to make near temporal transitions, was most predictive of memory accuracy and IQ. What does the importance of temporal contiguity tell us about memory and IQ?

One possibility is that the degree of temporal contiguity a participant shows in free recall is a measure of their ability to adapt to the demands of the task. Such adaptation may be achieved by dynamically tuning the relative influence of different types of associations as required by the demands of different tasks (Healey & Kahana, in press). For example, when recalling lists that contain pairs of words with moderate semantic associations, such as those used here, it is likely beneficial to allow both existing semantic associations and new temporal associations to guide recall. Consistent with this suggestion, we found that although the temporal factor was the most important in predicting recall success and IQ, the semantic factor was also correlated with recall (r = .56) and was the second most important factor in predicting IQ. Free recall of completely random lists is likely to benefit from increasing the influence of temporal associations and down–tuning the influence of semantics, consistent with the finding of Sederberg et al. (2010) that temporal but not semantic clustering correlated with recall for random lists. Dynamically tuning the memory system to adapt to the demands of a task likely occurs outside of conscious awareness in response to experience with the task. For example, Golomb, Peelle, Addis, Kahana, and Wingfield (2008) used the serial recall task, in which relying on existing semantic associations is likely to impair recall and it would be optimal to have temporal associations dominate recall. They found that across multiple learning trials, young adults progressively came to rely on temporal associations, showing stronger temporal clustering but weaker semantic clustering across trials. Intelligence tasks likely require a similar ability to quickly tune cognitive systems to optimally meet the task demands.

Although the ability to dynamically adapt to task demands is likely part of why strong temporal clustering predicts recall success and IQ, retrieved context models of the contiguity effect (e.g., Polyn et al., 2009) suggest a deeper connection between clustering and intellectual ability. To illustrate, we must first describe how temporal contiguity arises in such models: When an item is presented it becomes associated with an internal context representation. The context representation drifts through a high–dimensional space as items are presented, but in an autocorrelated fashion so that items presented in temporal proximity become associated with similar contextual states. During retrieval, context is used as a cue. When item i is recalled, its associated context is retrieved and integrated into the context representation that cues the next item. This retrieved context is a strong cue for items presented near i as those items were associated with similar contexts, giving rise to the temporal contiguity effect.

Recall success may depend on a participant’s ability to regulate the drift of their context representation such that each recalled item retrieves a context that serves as an effective cue for another list item. We can picture the current state of context as a point in multi–dimensional space. When context drifts, it moves to another part of the space. Some parts of the space (i.e., different possible states of context) were active during the study phase and became associated with list items. Other parts of the space were not active during study and are not strongly associated with list items. Therefore, allowing mental context to drift to some parts of this space will result in a highly effective cue for list items, whereas allowing it to drift to other parts of the space will provide a very poor cue. Participants may vary in the ability to guide context toward favorable parts of the space, perhaps by using the current state of context to weight the retrieved state of context, preventing it from drifting too far from the context associated with list items. The converse of guiding context to favorable states is preventing it from drifting to states that make non-list items, such as those that were presented on earlier lists or those that are semantically related to true list items, more accessible. Such “context gating” could be used to demarcate list boundaries, making task-irrelevant memories inaccessible, and may reflect the computational basis of the ability to resolve interference (Healey, Campbell, Hasher, & Ossher, 2010).

How do context regulation and gating relate to intelligence? A simple answer is that any complex task requires selective memory access. A deeper answer, however, is suggested by Duncan’s (2010) idea of a multiple demand system. Under this view, frontal neurons instantiate distinct connection patterns reflecting current task demands, with orthogonal connection patterns across different phases of an experiment forming boundaries between different tasks. This notion of rapidly changing frontal networks is closely related to the notion of an internal context representation that dynamically modulates the accessibilities of various memories. It may be that the ability to use internal contextual representations to dynamically gate access to relevant memories and response tendencies is a basic computational principle across tasks and a key component of intelligence.