Suppression of tunneling two-level systems in ultrastable glasses of indomethacin

Significance

Glasses are disordered solids usually obtained by supercooling a liquid bypassing crystallization. A remarkable feature of glasses is that, independently of their nature and composition, they exhibit universal properties in the low-temperature range. Of interest here, the specific heat is characterized by a linear term below 1 K, ascribed to quantum tunneling between two states of similar energy. We have investigated if this ubiquitous behavior also applies to so-called “ultrastable glasses,” directly synthesized from the vapor phase into low-energy positions of the potential-energy landscape. Interestingly, we find a full suppression of the linear term in the specific heat, which questions the current view of the popular tunneling model and sheds light on the microscopic origin of two-level systems in glasses.

Abstract

Glasses and other noncrystalline solids exhibit thermal and acoustic properties at low temperatures anomalously different from those found in crystalline solids, and with a remarkable degree of universality. Below a few kelvin, these universal properties have been successfully interpreted using the tunneling model, which has enjoyed (almost) unanimous recognition for decades. Here we present low-temperature specific-heat measurements of ultrastable glasses of indomethacin that clearly show the disappearance of the ubiquitous linear contribution traditionally ascribed to the existence of tunneling two-level systems (TLS). When the ultrastable thin-film sample is thermally converted into a conventional glass, the material recovers a typical amount of TLS. This remarkable suppression of the TLS found in ultrastable glasses of indomethacin is argued to be due to their particular anisotropic and layered character, which strongly influences the dynamical network and may hinder isotropic interactions among low-energy defects, rather than to the thermodynamic stabilization itself. This explanation may lend support to the criticisms by Leggett and others [Yu CC, Leggett AJ (1988) Comments Condens Matter Phys 14(4):231–251; Leggett AJ, Vural DC (2013) J Phys Chem B 117(42):12966–12971] to the standard tunneling model, although more experiments in different kinds of ultrastable glasses are needed to ascertain this hypothesis.

Glasses or amorphous solids are well known (1, 2) to exhibit thermal and acoustic properties very different from those of their crystalline counterparts. Even more strikingly, many of these properties are very similar for any glass, irrespective of the type of material, chemical bonding, etc. Hence the low-temperature properties of noncrystalline solids are said to exhibit a universal “glassy behavior.” In particular, below 1−2 K the specific heat of glasses depends approximately linearly on temperature, C_p∝T, and the thermal conductivity almost quadratically, κ ∝ T², in clear contrast with the cubic dependences successfully predicted by Debye theory for crystals. In addition, a broad maximum in C_p/T³ [originated from the so-called “boson peak” in the reduced vibrational density of states g(ω)/ω²] is also typically observed in glasses around 3−10 K, as well as a universal plateau in the thermal conductivity κ(T) in the same temperature range (1, 2).

Very soon after the seminal paper by Zeller and Pohl (1) in 1971, Phillips (3) and Anderson et al. (4) independently introduced the well-known standard tunneling model (TM). The fundamental idea of the TM is the ubiquitous existence of atoms or small groups of atoms in amorphous solids due to the intrinsic atomic disorder, which can perform quantum tunneling between two configurations of very similar energy, usually named two-level systems (TLS). This simple model was able to account for the abovementioned thermal and acoustic anomalies of glasses below 1−2 K, and soon acquired unanimous recognition. Only very few authors (5) posed then criticisms against the standard TM, pointing out how improbable it was that a random ensemble of independent tunneling states would produce essentially the same universal constant for the thermal conductivity or the acoustic attenuation in any substance. Indeed, significant discrepancies with the TM below ∼100 mK have also been reported (6–9), in particular a strong, unexpected strain dependence in the acoustic properties exhibited by both dielectric and metallic glasses (8, 9). More recently, single-molecule spectroscopy experiments above 2 K have shown that the spectral dynamics in low-molecular-weight glasses and short-chain polymers on a microscopic scale cannot be described within the standard TM, unlike the single-molecule spectral dynamics in long-chain polymers (10).

Conventional glasses are obtained by cooling the liquid quickly enough. Slowing down the cooling rate drives the system to lower energy positions in the potential energy landscape, with the minimum cooling rate ruled by the occurrence of crystallization. This limitation has been recently defeated by growing glasses directly from the vapor phase (11, 12). Those glasses, dubbed “ultrastable glasses,” can be synthesized by physical vapor deposition in short time scales and show unprecedented thermodynamic and kinetic stability (13–17). Changing the growth parameters has a strong effect on the properties of the glass. An appropriate deposition rate in combination with an optimal substrate temperature (typically around 0.85 T_g, where T_g stands for the glass-transition temperature) has proved to drastically favor 2D mobility and, as a consequence, access to local minima of very low energy in the potential-energy landscape (18, 19). An ordinary glass obtained by supercooling the liquid should theoretically be aged for 10³−10⁹ y to achieve the same stability and density of these vapor-deposited glasses (20).

To the best of our knowledge, no study has been performed to date to investigate the possible effects that the dramatic increase in thermodynamic and kinetic stability of vapor-deposited ultrastable glasses could have on the universal low-temperature anomalies of glasses. In what follows we present low-temperature specific-heat data for ultrastable glasses prepared by physical vapor deposition. In particular, we measured ultrastable, ordinary (cooled at 10 K/min from the liquid), and crystalline samples of indomethacin in the range 0.18 K ≤ T ≤ 32 K. We also describe the effect of the loss of stability and water absorption on the low-T properties of an ultrastable glass, providing complementary enlightening information about the nature of the TLS suppression.

Results

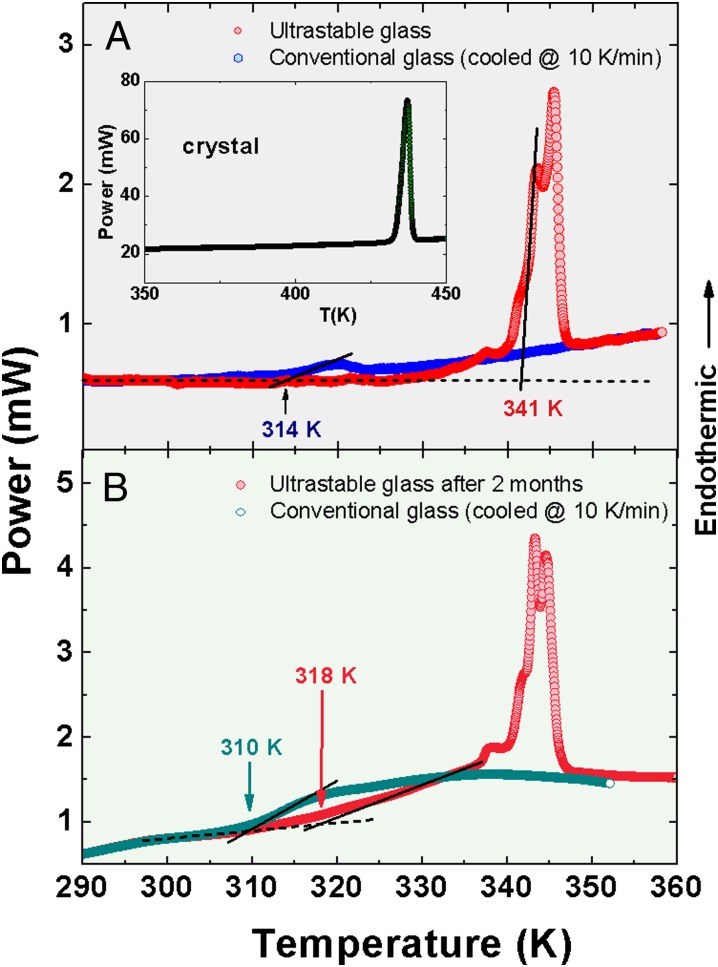
We prepared indomethacin (IMC) samples by vapor deposition at 0.85 T_g with a growth rate of 0.15 ± 0.05 nm/s on Si(100) substrates for low-temperature specific-heat and X-ray diffraction (XRD) measurements, as well as on Al pans for differential scanning calorimetry (DSC) analysis. In this way, we produced samples with thicknesses ranging from 50 to 80 μm with the aim to maximize the signal-to-noise ratio required in the specific-heat measurements (Materials and Methods). The extraordinary kinetic and thermodynamic stability of the ultrastable glass (USG) is characterized by the noteworthy difference in the calorimetric onset temperature T_on for the glass transition with respect to the conventional (conv) glass cooled at 10 K/min (ΔT_on = T_on^USG−T_on^conv = 27 K), as shown in Fig. 1A, as well as in the limiting fictive temperature (ΔT_f = T_f^conv−T_f^USG = 33 K) obtained from the corresponding enthalpy extrapolations. These data agree well with previous results found in the literature (11, 16). The melting curve of the crystalline phase is also shown in Fig. 1A (Inset) for comparison. The presence of several peaks in the calorimetric curve of the USG is related to changes of stability, produced by variations in the growth rate during deposition (20).

Fig. 1.

(A) Calorimetric up-scans for conventional glass (cooled at a rate of 10 K/min) and USG of IMC. (Inset) Melting of the crystal at T_m = 430 K. The glass transition temperatures of the conventional glass and USG are approximately determined by the onset in the heat flow curves, T_g ^conv ≡ T_on ^conv = 314 K and T_on^USG = 341 K, depicted by the intersection of the corresponding solid line (taking the main peak for the USG) and the extrapolated dashed line of the glass. (B) Calorimetric curves for a 50-μm-thick USG after being stored in poor vacuum conditions for 2 mo, and for the subsequent conventional glass obtained by cooling the melt sample at 10 K/min. For these degraded (including water absorption) glasses, T_on^conv = 310 K and T_on^USG = 318 K, here signaling the onset of the deviation from the glass background (dashed line).

In Fig. 1B, we show DSC measurements for a USG sample, after being stored in poor vacuum conditions for 2 mo. This causes a loss of stability and water absorption (21) which shifts 4 K downward the calorimetric glass transition of the conventional glass. The calorimetric data show that the sample has notably decreased its thermodynamic and kinetic stability, because a significant fraction of the glass exhibits a ΔT_on of only 8 K, relative to the conventional glass.

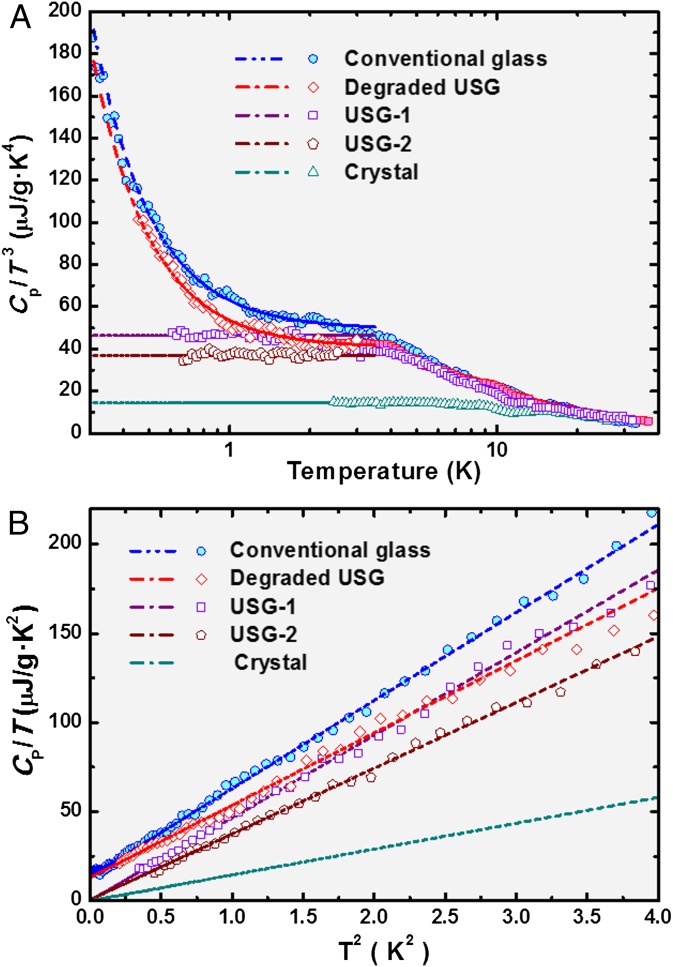
The specific heat of several IMC samples in different states was measured in the temperature range 0.18 K ≤ T ≤ 32 K. Fig. 2A shows the whole specific-heat data in the Debye-reduced C_P/T³ representation. Fig. 2B amplifies the very-low-temperature region in the usual C_P/T vs. T² plot where a least-squares linear fit provides the TLS linear term (the intercept with the y axis) and the Debye coefficient (the slope). The crystal of IMC exhibits the expected C_P ∝ T³ below 8 K. The same shoulder-like behavior [a very shallow boson peak, as typically occur in other fragile glass formers (22)] is observed in both USG and ordinary glasses below ∼5 K in Fig. 2A. This is consistent with earlier Raman-scattering experiments in IMC (23), where a hardly visible boson peak was found both in the normal glass state and in a high-pressure amorphous state. As can also be seen in Fig. 2, a modest difference between the Debye levels of the two ultrastable samples (USG-1 and USG-2, prepared with slightly different conditions) is observed, both of them below that of the conventional glass. It is noteworthy that the Debye coefficient of the crystal is very much smaller (its elastic constants are much harder) than those of the glasses. The so-obtained calorimetric Debye coefficients agree very well with the elastic Debye coefficients obtained from room-temperature sound velocity and mass density data from the literature (24), as can be observed in Table 1. This agreement further supports our analysis of the low-temperature specific-heat curves.

Fig. 2.

Specific-heat data for USGs of IMC 50 μm- (USG-1) and 80 μm (USG-2) thin films, compared with the crystalline phase (Debye extrapolated at lower temperatures) and the conventional glass. A degraded USG (Materials and Methods) has also been measured and is presented. Dashed lines show the corresponding linear fits C_P = c_TLS·T + c_D·T³ for experimental data below 2 K. (A) Debye-reduced C_P/T³ versus T representation; (B) C_P/T versus T² plot at very low temperatures to determine the TLS and the Debye coefficients, which are given in Table 1.

Table 1.

Specific heat coefficients

Sample state	cTLS (μJ/g·K2)	cD (μJ/g·K4)	cDelas (μJ/g·K4)
Crystal	––	15.0 ± 0.3	––
Conventional glass	13.7 ± 0.3	49.4 ± 0.2	51
USG-1	0.2 ± 0.9	46.4 ± 0.6	41
USG-2	0.02 ± 0.8	36.9 ± 0.4	41
Degraded USG	13.0 ± 0.7	40.6 ± 0.5	––

Coefficients and statistical errors from the least-squares linear fits at low temperatures to the function C_P = c_TLS·T + c_D·T ³ (Fig. 2B). The last column indicates the expected Debye coefficient c_D^elas for conventional and USGs of IMC, obtained from published elastic data at room temperature (24).

Nevertheless, the most surprising behavior found in both USGs is the full suppression of the linear term of the specific heat ascribed to the tunneling TLS. This is demonstrated in Fig. 2B, where the intercept with the ordinate axis goes to zero within experimental error (Table 1), in clear contrast with the case of conventional glass, or even for a degraded USG after being stored in poor vacuum for 2 mo. We note that the lack of experimental points below 0.6 K for the USGs (USG-1 and USG-2 in Fig. 2) is an experimental manifestation of the dramatic reduction in the specific heat at very low temperatures compared with the conventional glasses. In the former case, the total measured heat capacity becomes so low that it rapidly approaches the contribution of the addenda and hence the net specific heat of the sample cannot be assessed with accuracy.

Some glasses obtained by physical vapor deposition show evidence of molecular anisotropy which is partly due to the growth method of thin films from the vapor phase. In particular, ultrastable IMC glasses exhibit an extra, low-q, peak in wide-angle X-ray scattering (WAXS) spectra (25) and birefringence in ellipsometric measurements (26). Also, computer simulations of “stable” glasses of trehalose revealed a distinct layered structure along the direction normal to the substrate that was absent in the “ordinary” glass (27). However, recent experiments conducted in vapor-deposited glasses of the four isomers of Tris-naphthylbenzene have shown that anisotropy is unrelated to glass stability, rather being a secondary feature that will appear more or less prominently depending upon molecular structure (28).

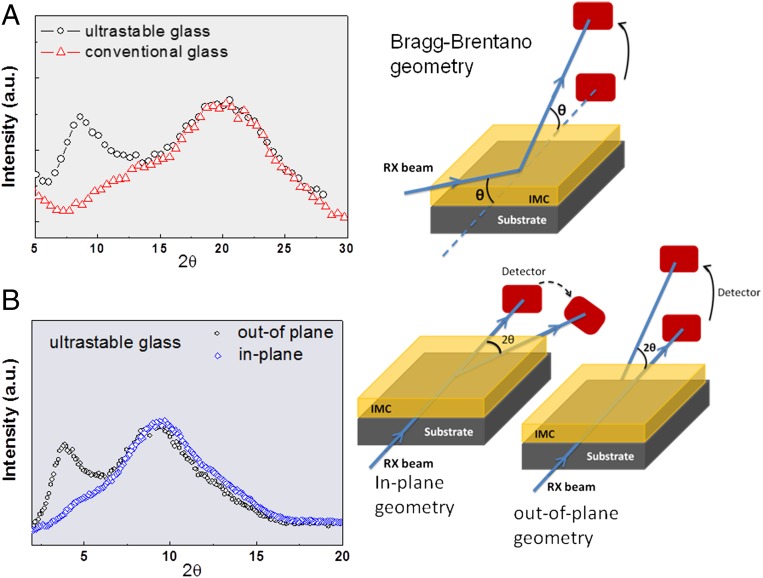
In Fig. 3 we show that the low-q peak appears indeed in the WAXS pattern of our vapor-deposited USG, whereas it is absent in the conventionally prepared glass. The presence of this peak for the USG should be related to some sort of molecular order along the growth direction, perpendicular to the substrate, as clearly revealed in the in-plane–out-of-plane diffraction experiments of Fig. 3B. This orientation may be enabled by the high mobility of the IMC molecules when they impinge the substrate surface from the vapor (25). Molecular orientation in vapor-deposited glassy films of organic semiconductors has been widely recognized as a potential source to increase carrier mobility through an enhancement of π-conjugation. The longer the molecular length is, the larger the anisotropy of the molecular orientation becomes (29).

Fig. 3.

(A) WAXS spectra comparing USGs and conventional (conv) glasses of IMC. USG (conv) data are the result of box-averaging over 20 (10) points, respectively. The appearance of a peak at low-q angles in the USG is related to molecular ordering in the direction perpendicular to the substrate, an indication of molecular anisotropy. (B) In-plane and out-of-plane scattering experiments using synchrotron X-rays on layered USG of IMC. The disappearance of the low-angle peak for the USG film in the in-plane experiment indicates that extra ordering occurs mainly in the z direction (perpendicular to the substrate) and is absent in the xy plane. The sketches show the configuration of the X-ray scattering experiments.

Let us discuss more specifically our case of IMC. In melt-quenched or grinded amorphous IMC the most favorable nearest-neighbor packing direction occurs normal to the plane containing the indole ring, as occurs in the γ-crystalline polymorph. The dominant XRD peak at 2θ ∼ 20° (Cu K_α, Fig. 3A) corresponds to an average distance between nearest neighbors of 0.45 nm, which matches the IMC molecular thickness when including the van der Waals radii. Interaction between molecules thus occurs from hydrogen-bonding cyclic dimers through the carboxylic groups. Nonetheless, vapor-deposited IMC glasses exhibit another strong XRD peak at 2θ ∼ 8.5° (Fig. 3A), indicative of an additional order within the structure, with a molecular packing distance of 1.1 nm. This value approximately corresponds to the distance between IMC molecules along the long axis. As we have verified from in-plane and out-of-plane synchrotron XRD experiments (Fig. 3B), molecular anisotropy occurs mainly in the growth direction. This is again a strong indication of a layered growth (27).

Discussion

Our experimental work is not the first one reporting lack of TLS in an amorphous solid. Nonetheless, previous reports (30–33) claiming the absence of TLS in amorphous solids are scarce and somewhat controversial. Angell et al. (34) proposed the designation of “superstrong liquids” for some “tetrahedral liquids” which could be potential “perfect glasses,” with a residual entropy near zero, and where the defect-related boson peak and TLS excitations were weak or absent. Specifically, they identified two instances where TLS had been reported to be absent: (i) amorphous silicon (a-Si) and (ii) low-density amorphous (LDA) water.

Let us stress, however, that Pohl and coworkers (30) did find TLS in pure a-Si (the ideal superstrong liquid). It was only in 1 atomic % hydrogenated silicon where they observed a dramatic reduction of the internal friction plateau, which is proportional to the amount of TLS weighted by the TLS–phonon coupling energy. The suppression of TLS in hydrogenated a-Si was attributed by the authors (30) to a more compact fourfold coordination due to the passivation of the dangling bonds by the hydrogen, hence producing an overconstrained vibrational network. On the other hand, Hellman and coworkers (31, 32) have reported thermal measurements suggesting a zero density of TLS in some a-Si thin films. Their conclusion was based on the variation of the specific heat above 2 K in a series of a-Si thin-film samples with different densities and preparation methods. In general, measurements in these and other tetrahedrally bonded amorphous semiconductors have given conflicting results (32).

The case of amorphous water seems clearer in this respect. At low temperatures, there are (at least) two different amorphous states of water, high-density amorphous (HDA) and low-density amorphous (LDA), associated with a high-density liquid (HDL) and a low-density liquid (LDL), respectively. The LDL of water has been found to be the strongest of all liquids known (35). Agladze and Sievers (33) reported no far-infrared resonant absorption by TLS in LDA ice at low temperature, whereas HDA ice exhibited the typical TLS response of other glasses.

At first glance, one might thus ascribe the found suppression of the tunneling TLS in USGs of IMC to the extraordinary stability (either thermodynamic or structural) of these particular glasses, and its corresponding large reduction in enthalpy or entropy. This conclusion seems however to be at odds with our opposite recent finding in a related system: hyperaged glasses of geological amber. In pristine amber, a bulk isotropic glass which has been aging for millions of years, the amount of TLS has been found to remain constant after rejuvenation (36, 37). Then, it seems reasonable to seek other plausible explanations for this unusual disappearance of the TLS in ultrastable IMC.

As outlined in the Introduction, several authors (5, 6, 38) have pointed out that, besides the unexplained universality of the TM fitting parameters, the model in its original form neglects the fact that as a result of interaction with the strain (phonon) field, the tunneling TLS must acquire a mutual interaction. It can be shown (5, 6) that the effective interaction between two TLS separated by a distance r is dipolar elastic and the interaction strength goes as ∼ g/r³, with g = γ²/ρv², where γ is the TLS–phonon coupling constant, ρ is the mass density, and v is the sound velocity of a given substance. An ensemble of independent, noninteracting TLS would not be possible nor could it justify the observed quantitative universality. Instead, the observed astonishing universality could emerge as the general result of some renormalization process of (almost) any ensemble of defects or many-body energy levels and stress matrix elements, interacting through the usual bath of thermal phonons, implying the existence of some cross-over length scale r₀ (roughly estimated to be about 1.3 nm) (5).

Therefore, we speculate that the picture of a spherical volume of size r₀³ comprising an isotropic random distribution of structural defects (TLS) embedded in a 3D vibrational lattice, allowing the interaction between resonant defects via the acoustic-phonon bath, may fail in the case of these layered and anisotropic USGs of IMC. We suggest that a possible interpretation of the found suppression of TLS in ultrastable IMC thin-film glasses grown at 0.85 T_g could then be related to the modification of the molecular interaction in vapor-deposited USG films, through a decrease of free hydrogen bonds and an enhancement of π–π interactions between chlorophenyl rings. As studied by Dawson et al. (21), water uptake in IMC increases with the decrease in stability, so that loss of stability and increase of water absorption are concomitant processes. Water absorption seems to take place by occupying free sites of the IMC glass where water can hydrogen bond (21). Thus, without modifying the intrinsic structure of the layer, absorbed water molecules are able to bridge IMC molecules through hydrogen bonds, feeding the interconnection of the dynamical network (water is known to be a good plasticizer), and hence recovering the interacting TLS excitations. Therefore, the found suppression of the TLSs would not be related to the extraordinary stability of the glass, but rather to the particular molecular arrangement ruled by the deposition conditions in this USG.

In our view, highly stable “ideal glasses” can be associated with a negligible excess in configurational entropy, whereas noncrystalline solids devoid of low-energy excitations (TLS, boson peak, etc.) could be somehow associated with a small vibrational entropy. Both features may be related sometimes, but they are not automatically interlinked. Hyperaged amber (36, 37) seems to be a good counterexample. It is also true, nonetheless, that the case of this canonical glassy polymer, without any crystalline reference, is far from the other cases considered. All of the latter have shown––or they have been predicted to show––polyamorphism and liquid–liquid transitions, which could facilitate the creation of superstrong ideal glasses devoid of low-energy glassy excitations, whereas the former may still have enough residual entropy and TLS despite its extraordinary thermodynamic stabilization. The fact that the density of TLS remains exactly the same in amber after rejuvenation casts doubts on this interpretation.

Following the line of reasoning used above, however, it may well be that in some (few) cases an isotropic perfect glass (related to a superstrong liquid) is lacking the necessary low-energy structural defects (34), whereas in some other cases an anisotropic and layered ultrastabilized glassy structure hinders a normal interaction between those low-energy molecular excitations mediated by lattice vibrations. In both cases, the result could be the same: a lack of an effective amount of (renormalized) TLS.

Conclusion

In conclusion, the main result of our work is the found suppression within experimental error of tunneling TLS in USGs of IMC, in clear contrast with the usual behavior observed in conventionally prepared glasses, and even in the same samples of previously USGs after losing stability and absorbing water. This important finding has revealed another remarkable exception to the universal behavior of glasses at low temperatures, and hence should shed light on the unclear microscopic nature of the so-called tunneling TLS. Although other explanations have been considered, we believe that our finding in very anisotropic and layered USGs of IMC may support the arguments by Leggett and others (5, 6, 38), which have claimed against the standard TM and have emphasized the critical role played by the coupling of the (isotropic) structural defects of the amorphous solid to the acoustic phonons, and the consequent impossibility of regarding these entities as independent, noninteracting excitations.

Although our interpretation of these remarkable results is not definitive at all, we expect that our work can pave the way to trigger new investigations on these issues, including similar experiments in nonlayered USGs.

Finally, we want to stress that our results should not be considered relevant only for organic USGs. On the contrary, the fact that we have identified another significant exception to the universality of TLS in glasses is important, for it provides an invaluable hint to unveil the abovementioned mystery of the TLS.

Materials and Methods

Sample Growth.

IMC [C₁₉H₁₆ClNO₄; T_g = 315 K and T_m (γ form)= 428 K] crystalline powders with 99% purity were purchased from Sigma-Aldrich. USG films of IMC were grown by vapor deposition, both on Si(100) substrates and DSC Al pans, at 0.85 T_g, i.e., T_dep = 300 K. An effusion cell filled with IMC powder was heated to achieve the desired deposition rate, as measured by a quartz crystal microbalance. When this rate was attained, the shutter was removed to start deposition. The thickness of the films ranged from 50 to 80 μm, due to the importance to enhance the signal-to-noise ratio in the low-T specific-heat measurements. The growth rate was 0.15 ± 0.05 nm/s. Note that variations of the growth rate during the time required to grow a 50−80-μm-thick layer, i.e., 1 wk, account for the observation of several peaks in the calorimetric traces of Fig. 1. All samples were stored in vacuum-sealed bags with desiccant in a freezer to minimize aging before the low-T specific-heat measurements. Low-temperature data of the USGs in high vacuum were acquired a few days after preparation, with the exception of a sample stored in those conditions for 2 mo, named “degraded” USG.

DSC.

A Perkin-Elmer 7 DSC was used to monitor the power absorbed–released during heating scans at a rate of 10 K/min on IMC thin films with masses of the order of 8−11 mg. The first scan typically corresponds to a USG, whereas the second one is characteristic of a conventional glass obtained by cooling the liquid at 10 K/min. The variation in onset temperatures and enthalpy overshoots are a clear indication of the much higher kinetic and thermodynamic stabilities of a USG compared with a conventional one.

XRD.

To confirm the glassy nature of the as-grown samples, we carried out XRD measurements using an X-Pert diffractometer from Phillips in the Bragg–Brentano configuration with Cu K_α radiation. The samples were scanned in Bragg–Brentano geometry from 2θ = 2° to 30° with an angular step of 0.025° (0.05°) and time per point of 18 (12) s for the USG and conventional IMC glasses, respectively. The raw data are box-averaged every 20 (10) points to improve signal-to-noise ratio (Fig. 3A). We also conducted experiments at the beamline ID28 of the European Synchrotron Radiation Facility (ESRF). The energy of the X-rays was set to 23.725 eV. Photons were detected with a photodiode with the sample aligned parallel (in-plane) or perpendicular (out-of-plane) to the detector axis, as schematically shown in Fig. 3B.

Thermal-Relaxation Calorimetry at Low Temperatures.

The IMC samples used for the low-temperature specific-heat measurements were all grown on silicon substrates of dimension 12 × 12 mm², and with typical masses m ∼ 0.1g, which enabled the handling of the samples, as well as optimal attachment and thermal contact to the calorimetric cell. Due to the versatility of the low-temperature calorimeter used, the same experimental setup (36) was used in both a ⁴He cryostat and a ³He–⁴He dilution refrigerator, to cover a temperature range 0.18 K ≤ T ≤ 32 K. The calorimeter was calibrated using a clean silicon substrate, to accurately determine the empty-cell contribution to the total heat capacity curves and hence obtain the IMC specific heat. The heat capacity at low temperatures was measured using the relaxation method (see SI Text for more details).