Lunar-forming impacts: processes and alternatives

Abstract

The formation of a protolunar disc by a giant impact with the early Earth is discussed, focusing on two classes of impacts: (i) canonical impacts, in which a Mars-sized impactor produces a planet–disc system whose angular momentum is comparable to that in the current Earth and Moon, and (ii) high-angular-momentum impacts, which produce a system whose angular momentum is approximately a factor of 2 larger than that in the current Earth and Moon. In (i), the disc originates primarily from impactor-derived material and thus is expected to have an initial composition distinct from that of the Earth's mantle. In (ii), a hotter, more compact initial disc is produced with a silicate composition that can be nearly identical to that of the silicate Earth. Both scenarios require subsequent processes for consistency with the current Earth and Moon: disc–planet compositional equilibration in the case of (i), or large-scale angular momentum loss during capture of the newly formed Moon into the evection resonance with the Sun in the case of (ii).

1. Introduction

The giant impact theory proposes that an impact with the early Earth ejected material into an Earth-orbiting disc that subsequently accumulated into the Moon [1,2]. The impact theory has been favoured for several decades, because giant impacts are believed to be common during the final stages of assembly of Earth-sized terrestrial planets [3], and a large, oblique collision provides a natural way to account for the Earth's rapid initial spin rate and the extreme deficit of iron in the Moon compared with that of the bulk Earth [4]. Despite its successes, the impact theory has struggled to account for other key properties of the Earth–Moon system, most notably the essentially identical isotopic composition of the Moon compared with the Earth's mantle in multiple elements.

(a). Constraints

The Earth–Moon system angular momentum is L_EM=3.5×10⁴¹ g cm² s⁻¹. An Earth-like planet rotating at the critical rate for rotational stability, ω_crit=(4πGρ/3)^1/2 (where G is the gravitational constant and ρ is the Earth's mean density), would have a spin angular momentum L_crit≈10⁴² g cm² s⁻¹. Thus, the Earth and Moon currently contain about one-third the angular momentum of an Earth rotating at the fission rate.

The angular momentum delivered by an impactor of mass M_i=γM_T, where M_T=M_t+M_i is the total mass and M_t is the target mass, is [5]

1.1

where 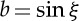is the scaled impact parameter, ξ is the impact angle (defined so that a grazing impact has ξ=90° and b=1), ρ is an assumed common density for the target and impactor, v_i is the impact velocity, v_esc is the mutual escape velocity, 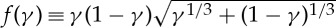and M_⊕ is the Earth's mass.

For a single impact to provide the Earth–Moon system angular momentum, L_i must be comparable to or greater than L_EM. How large L_i could reasonably be depends on several factors. Angular momentum will be lost if material escapes during the impact or as the Moon later accretes. The magnitude of the former is primarily a function of v_i, whereas the latter leads to a reduction of only of order a few ×10⁻²L_EM [6,7]. The Earth–Moon angular momentum would have also been decreased by a few per cent by tides raised on the Earth by the Sun that slow the Earth's rotation [8]. Recent work [9] proposes that a very large angular momentum loss could have occurred if the early Moon was captured into the evection resonance with the Sun, as discussed below. In this case, L_i could be as large as approximately 2–3L_EM (and thus comparable to L_crit).

A successful impact must produce a disc that can later accrete into a lunar mass (M_L=7.35×10²⁵ g) moon outside the Roche limit for lunar density material, which is located at a_R≈3R_⊕. Simulations of the disc's evolution show the formation of a single moon somewhat exterior to the Roche limit, and find that disc material not accreted by the moon is largely accreted by the Earth, with less than 5% of the disc's mass escaping [10]. A mass and angular momentum conservation argument can then be used to estimate the mass of the moon (M_M) that forms from a disc as a function of the initial disc mass (M_D), the initial disc angular momentum (L_D), the initial position of the moon (a=λa_R) and the angular momentum of material that escapes or collides with the Earth. The predicted moon mass is

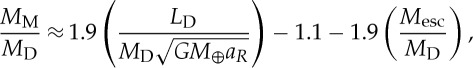1.2

where M_esc is the escaping mass. Here, λ=1.3 and the mean specific angular momenta of material that escapes or collides with the Earth seen in N-body simulations [6,10] have been assumed. Equation (1.2) provides a simple, approximate way to determine whether a disc produced by a given impact could later yield a lunar mass Moon. It is physically invalid for cases that would give M_M/M_D>1; these correspond to initial discs with specific angular momenta too high to be consistent with the assumption that the final moon forms at 1.3a_R. It is also likely to be overly optimistic, as recent lunar accretion models find larger λ values and therefore smaller accretion efficiencies than implied by equation (1.2) [7].

The Moon's composition relative to that of the Earth must ultimately be reconciled with any lunar origin model. The Moon differs from the Earth in that it contains less than approximately 10% of its mass in elemental iron, and it is more depleted in volatile elements [11]. Impact models assume that an appropriate disc must contain less than 10% iron by mass. The origin of the depletion of volatile elements in the Moon compared with the Earth is not well understood, but is likely to be a result of processes occurring in the disc after the impact and so has not to date been used as a direct constraint on impact models.

There is a remarkable suite of compositional similarities between the Moon and the Earth's mantle. The Earth and Moon have identical oxygen isotope compositions to within measurement precision, which are quite distinct from those of most meteorites and Mars [12]. Yet, in the giant impact model, the Moon forms from a mixture of material derived from two separately formed objects: the impactor and the target protoearth. It had been suggested that an impactor formed in an orbit close to that of the Earth could have had the same oxygen composition as the Earth, because observed oxygen compositions vary with heliocentric position [12,13]. This seemed to agree well with the canonical impact (see below) that requires a low impact velocity and therefore an impactor orbit similar to that of the Earth. However, more recent work by Pahlevan & Stevenson [14] argues that it is very improbable that the impactor and Earth would have identical oxygen compositions even if they were in close orbits. Using the impacts from one of Chambers' terrestrial accretion simulations [15], together with the assumption that the oxygen composition of planetary embryos varied linearly with initial heliocentric distance, Pahlevan and Stevenson estimate that the typical difference between the oxygen composition of an impactor and its final target planet is comparable to the offset between the Earth and Mars fractionation lines, which is more than 60 times greater than the allowable difference in Earth–Moon oxygen compositions. Expressed in epsilon units, in which ϵ is the compositional deviation in parts per 10 000 from the terrestrial value, the Moon's oxygen composition has |ϵ_M|<0.05 (see [14] and references therein), whereas Mars has |ϵ_Mars|=3.2±0.13.

Consider an impactor and target whose oxygen compositions vary from that of the Earth by ϵ_i and ϵ_t, respectively. The resulting compositions of the post-impact planet and moon are

1.3

where F_P,t is the fraction of the planet's silicate mass that is derived from the target, F_D,t is the fraction of the silicate disc that is derived from the target, and the second equation assumes that the resulting moon's composition will be equal to that of the initial disc. Setting the final planet's value equal to that of the Earth (ϵ_P=ϵ_⊕=0 by definition) and solving for the moon's compositional deviation gives

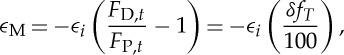1.4

where δf_T≡(F_D,t/F_P,t−1)×100 is the percentage deviation between the planet and disc [16,17]. For a Mars-like impactor (|ϵ_i|=3.2), |δf_T|<1.6% is needed to yield |ϵ_M|<0.05. An impactor that is substantially more Earth-like than Mars but still within the distribution of impactor compositions found in Pahlevan and Stevenson's analysis [14] implies |δf_T|<15% for consistency with the Earth–Moon oxygen similarity.

In addition to oxygen, the isotopic compositions of multiple other elements also now appear essentially identical in the silicate Earth and Moon, including chromium [18], titanium [19], tungsten [20] and silicon [21]. This suite of similarities seems to require that the Earth and Moon formed from a nearly identical mix of impactor and target material. Silicon and tungsten are notable because they can be isotopically fractionated during core formation processes. Thus, even two planets formed from the same mix of material would be expected to have different Si and W compositions if they had substantially different masses (in the case of Si) or had experienced different core formation histories (in the case of W). Together, these data provide critical constraints for impact models.

(b). Simulating giant impacts

Most models of lunar-forming impacts use smooth particle hydrodynamics (SPH), a Lagrangian method that describes the colliding objects by a multitude of particles that are evolved owing to self-gravity and pressure forces [22]. Each particle is assigned a composition, i.e. silicate or iron representing the mantle or core, and represents a spherically symmetric, three-dimensional distribution of material within a region whose characteristic radius is defined by a smoothing length. Modern SPH simulations use approximately 10⁵–10⁶ particles and variable smoothing lengths. Alternatively, impacts can be modelled with a grid-based, Eulerian hydrocode [23]. Recent work [24] found that simulations with SPH and the grid-code CTH yield broadly similar results, with the predicted protolunar disc mass and its angular momentum converging to within of order 10% for simulations of very similar impact conditions.

A key element in any hydrodynamic simulation is the equation of state. Modern simulations typically use the semi-analytical M-ANEOS package [25], whose output includes pressure, temperature and phase information (e.g. melt, vapour, two-phase melt and vapour) for representative mantle (dunite/forsterite) and core (iron) materials.

2. Moon-forming impacts

Several decades of impact simulations show that a very broad range of large impacts produce circumplanetary discs, with consistent trends in impact outcome as a function of b, v_i/v_esc and γ [5,26–31]. For a given impactor size and total colliding mass, the most massive discs are produced by low-velocity, oblique impacts. For v_i/v_esc<1.2, the disc mass generally increases with b, because a progressively larger portion of the impactor grazes past the target where it can most effectively be gravitationally torqued into bound Earth orbit [31]. For a fixed M_T, b and v_i/v_esc, increasing the impactor mass fraction γ increases the final disc mass for the same reason. In oblique (b≥0.7), high-velocity impacts (v_i/v_esc≥1.2), most of the impactor and the collisional angular momentum escapes, and little or no mass is placed into an orbiting disc [30]. Less oblique, high-velocity impacts produce a variety of outcomes, including cases that can produce both a bound disc and substantial escape of mass and angular momentum [16]. Pre-impact rotation in the target and/or impactor can affect impact outcomes if its angular momentum is comparable to the total angular momentum of the collision [31,9].

(a). Canonical impacts

Most models assume that the Moon-forming impact must produce a planet–disc system whose angular momentum, L, is close to L_EM, with cases having L≤1.2L_EM considered viable. For L_i≈L_EM, those impacts that produce an iron-poor disc having M_M (from equation (1.2)) of at least a lunar mass typically have b∼0.7 (approx. a 45° impact angle), a low-impact velocity v_i/v_esc<1.1, and an impactor mass ratio 0.1<γ<0.15 (a roughly Mars-sized impactor) for M_T∼M_⊕ [32,5]. An impact involving a low-velocity, Mars-sized impactor with L_i≈L_EM has generally been considered the ‘canonical’ impact for forming the Moon, because it accounts for the main dynamical properties of the Earth and Moon and the Moon's lack of iron while relying on conditions believed to be probable during the late stages of terrestrial planet accretion, i.e. large, randomly orientated impacts, with 45° being the most probable impact angle [3].

In canonical impacts, gravitational torques—both across the trailing arc of impactor material that exists immediately after the initial oblique impact and between this material and the distorted figure of the post-impact planet—are the primary mechanism that acts to raise the perigee of some of the material above the Earth's surface, allowing it to achieve bound orbit and produce a disc. Most of the disc (typically >80%) originates from a region of the impactor's mantle, whereas the impactor's iron core collides more directly with the planet and is nearly entirely accreted by the planet. Disc material is initially on eccentric orbits, but, after a typical simulation time of a day, most debris with perigees below the Earth's surface have collided with the Earth, allowing the predicted properties of the disc to reach a quasi-steady state. Typically, somewhat less than half of the disc mass is placed into orbits exterior to a_R, and disc temperatures are approximately 3000–4000 K, corresponding to a silicate vapour–melt state containing of order tens of per cent vapour by mass [5,33]. In all cases that leave a system with L≈L_EM, the resulting disc mass is ≤2M_L, indicating the need for rather efficient subsequent accretion to produce a lunar mass Moon.

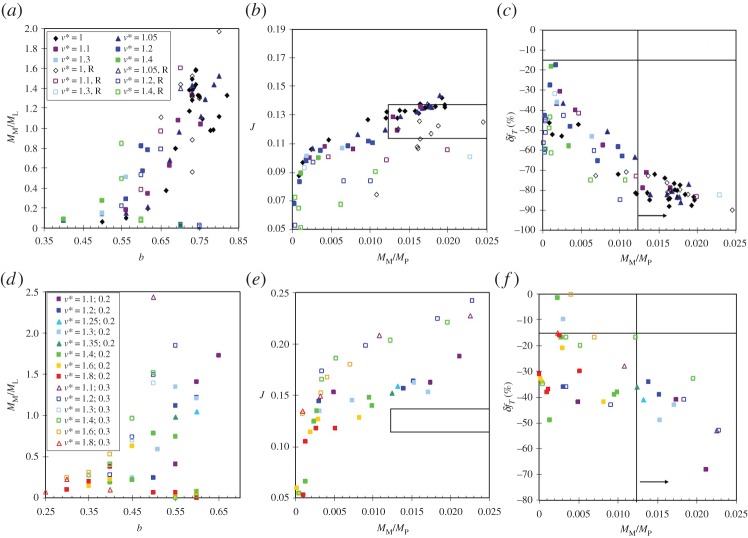
The key difficulty with canonical impacts is the impactor origin of the disc material. Figure 1a–c shows results of canonical impacts having γ=0.13 both with and without pre-impact rotation [5,31]. Discs consistent with a lunar mass moon and a final system angular momentum ∼L_EM have −90%≤δf_T≤−70%, which is a vastly larger difference than implied by the Earth–Moon oxygen compositions, assuming a roughly Mars-like impactor composition.

Figure 1.

Results of SPH impact simulations from [5,17,31]. The top row shows results for canonical impacts with γ=0.13, whereas the bottom row shows results for impacts with γ=0.2 (solid symbols) and γ=0.3 (open symbols). Colour scales with impact velocity as indicated in the figure legends. Cases with pre-impact retrograde rotation in the target are indicated by an ‘R’; these consider pre-impact target days between 4 and 50 h. Frames (a,d) show the predicted mass of the moon (M_M) per equation (1.2) in lunar masses versus the scaled impact parameter, b. Frames (b,e) show the scaled post-impact angular momentum of the planet–disc system (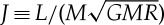, where M is the total bound mass and R is the radius of an object containing mass M with an Earth-like mean density) versus the mass of the resulting Moon, scaled to the mass of the final planet (M_P). Systems consistent with the Moon's mass and the current Earth–Moon system angular momentum (allowing for up to 20% angular momentum removal after the Moon-forming impact) fall within the solid lines. Frames (c,f) show the compositional deviation between the planet and the disc versus the satellite-to-planet mass ratio. Cases that could produce a lunar mass Moon fall to the right of the vertical solid line, whereas those that produce a disc composition similar enough to the planet to be consistent with the Earth–Moon oxygen similarities lie above the horizontal solid line.

(i). Planet–disc equilibration

As a solution to the compositional mismatch between the initial disc and the planet produced by a canonical impact, Pahlevan & Stevenson [14] proposed that the vapour components of the disc and the Earth's silicate atmosphere diffusively mixed after the impact, allowing the disc to compositionally equilibrate with the Earth's mantle (and for 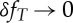) before the Moon accretes from the disc. For this to occur, one must assume that the mixing mechanism does not also transport angular momentum at the same efficiency, because, if it did, then much of the disc's mass would spread into the Earth on a similar time scale. It is plausible that convection could provide such a mechanism [34].

Equilibration of the disc–planet compositions requires approximately 10² years or more for reasonable diffusivities [14]. The Moon's accumulation would need to be delayed by this time after the impact, and the bulk of the Moon's mass would need to be processed through a vapour phase in the inner disc in close proximity to the Earth. Recent lunar accretion models [7] suggest that the completion of the Moon's accretion occurs some approximately 10² years after the impact. However, the same models find that only approximately 10–50% of the Moon's mass is processed through the inner disc, with the rest originating from material placed into orbits exterior to the Roche limit by the impact itself which can, if primarily molten, accrete rapidly in situ. This outer disc material would tend to retain its impactor-rich composition (although perhaps with some loss of volatiles). The last portions delivered to the Moon are processed through the inner disc where compositional equilibration with the Earth is most likely [7]. It is not clear that such a picture is necessarily inconsistent with the Moon: direct evidence of the Moon's composition extends only to depths of approximately 500 km (i.e. mare basalt source regions), and if interior mixing has been limited it is possible that the Moon's interior is heterogeneous, with a deeper interior that is compositionally less Earth-like. An additional question is whether equilibration between the disc and planet vapour phases could account for the Earth–Moon similarities in refractory elements (including notably titanium), although if the disc lasts for 10² years or more, there may be sufficient time for even refractory elements in the magma layer to equilibrate with the disc's vapour atmosphere [19].

Thus, the compelling dynamical aspects of the canonical impact—its ability to account for the masses and angular momenta of the Earth–Moon system with what is believed to be a quite common type of collision—are accompanied by the need for a much less well understood process to account for the Earth–Moon compositional similarities—post-impact diffusive equilibration between the disc and the planet.

(b). Variation in disc properties with impact conditions

The inability of canonical impacts to directly produce a disc with an Earth-like composition has motivated additional studies to determine whether other impact conditions could lead to a disc with a much more planet-like composition.

(i). Pre-impact rotation

The terrestrial planets would have had substantial rotation rates throughout the final stages of their accretion owing to the cumulative effects of large impacts. Canup [31] studied the effect of pre-impact rotation for impacts that leave a planet–disc system with an angular momentum, L, comparable to L_EM. Cases involving a target protoearth with a pre-impact ‘retrograde’ rotation (i.e. defined as a pre-impact spin in the opposite rotational sense to the impact itself) allowed for somewhat larger impactors and produced discs containing up to 40% target material, with a resulting compositional deviation between the disc and planet of δf_T≤−50%, a modest improvement compared with canonical impacts. They also allowed for improved agreement between the post-impact angular momentum and L_EM for cases that produce a lunar mass Moon.

Canup [31] examined the effect of a misalignment between the pre-impact spin axis (L_s) and the angular momentum vector of a Moon-forming impact (L_i), because, for randomly orientated impacts, the two are unlikely to be closely aligned. Cases in which L_s was perpendicular to L_i produced only modest changes in disc properties (mass and angular momentum) compared with cases that assumed non-rotating targets, even when |L_s| was as large as 0.5L_EM. Cases in which L_s was perfectly aligned or anti-aligned with L_i produced comparable outcomes to cases that assumed non-rotating targets until the target's pre-impact surface velocity was a substantial fraction of the impact velocity, which for v_i≈v_esc occurs once |L_s|≥0.3L_EM. Thus many—and perhaps most—pre-impact rotational states in the colliding objects have a relatively minimal effect on the resulting disc's dynamical properties, and are reasonably well approximated by simulations that consider non-rotating objects. The key exception is when there is a large component of pre-impact spin angular momentum aligned or anti-aligned with the impact angular momentum, and/or when |L_s|≥|L_i| (the case considered by [9] discussed below).

(ii). Varying γ and v_i

From figure 1, it can be seen that the fraction of the disc derived from the impactor (and, with it, the absolute magnitude of δf_T) generally increases as the collision becomes more oblique. Thus, more head-on impacts produce discs with lower, more desirable |δf_T| values. Reufer et al. [16] considered higher velocity, more head-on impacts in which a substantial fraction of the impact angular momentum escapes, so that L_i may be greater than L_EM and still leave a planet–disc system with L∼L_EM. They found that collisions with 1.2≤v_i/v_esc≤1.3, 0.15≤γ≤0.2, and ξ=30–40° produced appropriately massive discs that contained up to approximately 60% target material. The most successful Reufer et al. [16] cases have −40%≤δf_T≤−30%, which is substantially improved compared with canonical impacts, but larger in absolute value than needed to account for oxygen assuming a Mars-like composition impactor (|δf_T|≤15%). In addition, the angular momenta of such cases are generally higher than can be explained through solar tides and escaping material alone (figure 1e).

(c). High-angular-momentum impacts

An important recent development is the work of Ćuk & Stewart [9], who argue that the Earth–Moon system angular momentum could have been decreased by a factor of 2 or more if the newly formed Moon was captured into the evection resonance with the Sun. This result implies that impacts that leave an extremely rapidly rotating Earth could be viable Moon-forming candidates, which allows for different types of impacts than considered previously.

(i). Angular momentum removal via the evection resonance

The evection resonance occurs when the precession period of the Moon's perigee is commensurate with the Earth's orbital period about the Sun. For an initial Earth–Moon system with an angular momentum ∼L_EM (corresponding to an initial Earth day of about 5 h), the resonance occurs when the Moon's semi-major axis is a≈4.6 Earth radii; this case was previously investigated by [35]. Ćuk and Stewart considered a more rapidly spinning Earth with an initial approximately 2.5 h day, corresponding to a system angular momentum approximately 2L_EM. The Earth's increased oblateness causes the location of the resonance to shift outwards to about a≈7 Earth radii. At this larger distance, the rate of the Moon's orbital expansion owing to tidal interaction with the Earth is slower, which increases the likelihood of capture into evection. Once the Moon is captured into evection, the resonance causes its orbital eccentricity to increase until the expansion of the Moon's orbit stalls owing to a balance between Earth tides (for which 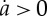) and satellite tides (for which 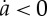for high-eccentricity orbits). The Moon's orbit then contracts, whereas its orbital eccentricity decreases modestly. During this period, Ćuk and Stewart find that the resonance slows the spin rate of the Earth and drains a large amount of angular momentum from the Earth–Moon system. Once the Moon escapes evection, tides in the satellite rapidly damp its eccentricity and the Moon resumes its outward orbital evolution owing to tides raised on the Earth.

Ćuk and Stewart used a tidal model motivated by the constant ‘Q’ model [36], together with a frequency-dependent factor that smoothed the tidal torque in the region surrounding the Earth's co-rotation radius (the distance at which the orbital period equals the Earth's spin period). Their successful cases that leave a system with an angular momentum comparable to L_EM occur across a quite narrow range of values for the relative rate of tidal dissipation in the Earth and Moon: if lunar tides are too strong compared with Earth tides, then the system leaves the resonance before enough angular momentum is lost, whereas if lunar tides are too weak compared with Earth tides, they find that the lunar eccentricity reaches overly high values that destabilize the resonance [9]. If one assumes that the post-impact Earth and Moon were largely molten with tidal Love numbers similar to that of a fluid body, then the successful cases require that the Moon's initial Q be about an order of magnitude larger than that of the Earth, corresponding to relatively weak dissipation in the Moon.

That the Earth–Moon system angular momentum could have been altered by a factor of 2 is an important claim that merits detailed study, including whether and under what conditions the required prolonged residence in the resonance will occur for other tidal models. Ward & Canup [37] considered the Mignard tidal model [38–40] with a non-synchronously rotating Moon and find both cases with substantial angular momentum removal and those with minimal removal. Wisdom [41] considers the Darwin–Kaula tidal model [42] and finds that the evection removes only a small fraction of the system angular momentum when the Moon's thermal evolution is included. Further work is needed to clarify why different tidal models appear to produce such varied outcomes and the overall likelihood of substantial angular momentum removal.

(ii). Fast-spinning Earth impact

Ćuk & Stewart [9] showed that a high-velocity, relatively head-on impact by a sub-Mars-sized impactor into a protoearth that was rapidly spinning before the Moon-forming impact can produce a massive, iron-poor disc derived overwhelmingly from the target's mantle. In this scenario, the Moon-forming impact itself adds little or no angular momentum to the Earth, but causes the planet, which is already rotating at near its rotational stability limit, to eject a portion of its mantle into a disc. The successful fast-spinning Earth cases produce discs containing 1.8–2.6M_L that closely resemble the planet compositionally, with |δf_T| values ranging from 6% to 15%. The final planet–disc angular momenta (L) in these cases are between 1.9 and 2.8L_EM, so that the evection resonance is then needed to reduce L to ≈L_EM.

The key strength of the fast-spinning Earth model is that it forms the Moon predominantly from Earth mantle material, providing a straightforward explanation for the Earth–Moon isotopic similarities. The model requires a protoearth that is rotating within about 30% of the fission rate at the time of the Moon-forming impact. Ćuk & Stewart [9] point out that such rapid planet spin rates are seen in N-body simulations of terrestrial planet accretion [3,43]. However, N-body simulations assume that planets grow through perfect mergers. Even in the limit that there is no escaping mass during a collision, this remains a poor assumption, because some portion of the colliding mass and angular momentum is usually placed into an orbiting disc rather than into the central planet. Neglecting this disc—and any satellite that forms from it—leads to a relatively small error in estimating the planet's mass, because the satellite is usually much less massive than the planet. But the same is not true for angular momentum. Even when the satellite first accretes just outside the Roche limit, the angular momentum contained in its orbit can be significant compared with that in the planet's spin. In the time between when the satellite forms and when the next giant impact is expected (approx. 10⁷ years [3,44]), the satellite's orbit typically expands owing to tidal interaction with the planet, and this further slows the planet's rotation relative to that which is computed by an N-body accretion code. Because of such approximations, current N-body models do not accurately reflect planetary spin rates to better than within about a factor of 2.

Planet spin rates can instead be directly estimated from SPH impact simulations. While the parameter space of all possible collisions is vast, there is a relatively limited set of impacts that leave a planet rotating with a near-fission rate. High-velocity oblique collisions lead to the escape of most of the impactor [30], and, in these cases, most of the impact angular momentum is lost, and little is retained by the planet [43]. Low-velocity collisions that are either nearly head-on or that involve small impactors (i.e. γ<0.1) do not deliver sufficient total angular momentum to bring the target to near the fission rate, per equation (1.1). It is the large, oblique and low-velocity collisions that generate the fastest spin rates in the target, and these have been relatively well studied in the context of satellite formation.

Consider the simplest case in which the protoearth's rotation in the fast-spinning Earth model was due to a single impact that immediately preceded the Moon-forming one.¹ The critical angular momentum for rotational stability for a mass M_P planet with an Earth-like bulk density is approximately L_crit=3.0L_EM(M_p/M_⊕)^5/3, where the second term reflects the expected dependence on M_p for a planetary moment of inertia that varies with 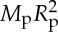. Figure 2 shows results of about 200 SPH simulations of collisions between non-rotating objects with varied impactor-to-total mass ratios (γ=0.13,0.2,0.3,0.4 and 0.45) that consider a wide range of impact angles and speeds for the accretionary regime of giant impacts having M_T≈M_⊕. The majority are detailed in [5,,17,31]; those shown here include additional simulations with γ=0.4 and 0.45, b=0.7 and 0.8, and v_i/v_esc=1 and 1.1.

Figure 2.

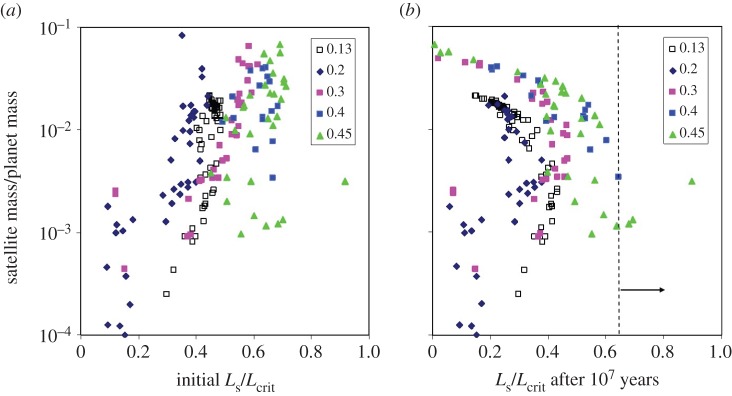
Results of SPH impact simulations from [5,17] for a variety of values of the ratio of the impactor to total mass (γ, values indicated in legend). (a) The predicted mass of the satellite produced by each impact, from equation (1.2), versus the post-collision planet's spin angular momentum scaled to the angular momentum for rotational stability, L_crit. (b) Predicted planet spin angular momentum after the satellites in these systems have tidally evolved for 10⁷ years, assuming k₂/Q=10⁻² for the planet. This approximates the state of the system at the expected time of the next giant impact. As the satellite's orbit expands, the planet's rotation rate slows and L_s/L_crit is reduced. Successful cases in Ćuk & Stewart [9] involve impacts into planets having L_s/L_crit≥0.64, or to the right of the vertical dashed line, consistent with the collision of a roughly half-Earth mass impactor prior to the Moon-forming event.

Figure 2a shows the estimated satellite mass produced by each impact versus the ratio of L_s to L_crit for the post-impact planet, where L_s is the angular momentum contained in the planet's post-impact spin. To estimate the satellite's mass, either the M_M value from equation (1.2) or the total disc mass having orbits exterior to the Roche limit is used, whichever is larger. To calculate L_s, I assume that any disc mass and angular momentum not accreted into a moon at an assumed initial distance of 1.3a_R (for consistency with (1.2)) is accreted by the planet. Figure 2b shows the estimated L_s/L_crit values for the planet 10⁷ years after the impact, i.e. at the likely time of the next giant impact [3,44]. Here, I use a constant Q model to estimate the tidal expansion of the satellite orbits (all are located outside the planet's post-impact co-rotation radius) assuming a ratio of the Love number to the tidal dissipation parameter for the planet of k₂/Q=0.01. Results are broadly similar if the time interval is shortened to 10⁶ years, appropriate if the Moon-forming impact occurred unusually soon after the preceding large impact.

The results in figure 2 suggest that impacts into planets rotating at near-fission rates will not be common. Most impacts do not produce rotation rates this rapid, and the majority of those that do also produce substantial moons whose tidal evolution slows the spin of the planet by the time of the next large impact. The successful cases in Ćuk and Stewart involve 2.7≤(L_s/L_EM)≤3.1 and 0.99≤(M_p/M_⊕)≤1.05, corresponding to (L_s/L_crit)≥0.65 and the region to the right of the dashed vertical line in figure 2. Across the relatively large set of impacts considered here, only a few satisfy this condition, and they involve a subset of impacts between nearly like-sized objects with γ≥0.4.

The requirement of a near-fission rotation rate in the target in the fast-spinning Earth model thus constrains the nature of the impact that occurs just prior to the Moon-forming one, implying in the simplest scenario that the prior impact involved the collision of two approximately half-Earth mass planets. In this model, the Moon-forming impact itself then involves a relatively small impactor (M_i=0.03 to 0.1M_⊕) with a high impact speed. Successful cases in [9] have 1.5≤v_i/v_esc≤2.5, which for an Earth-mass target requires an impactor velocity at infinity .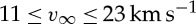

(iii). Half-Earth impact

If the mass of the Moon-forming impactor is small compared with that of the target Earth, then forming a disc that has the same composition as the planet requires that the disc be composed overwhelmingly of target-derived material, as in [9]. However, if the impactor's mass is large compared with that of the target, then a disc and planet with equal compositions can occur even if the disc contains substantial material from the impactor, because, in this case, the impactor substantially affects the composition of both the disc and the final planet. The extreme case of a completely symmetric collision (γ=0.5 and no pre-impact rotation) will produce δf_T=0 by symmetry, as the final disc and planet will each comprise 50% target, 50% impactor material, and thus have equal relative compositions. While perfect symmetry is extremely improbable, Canup [17] found that somewhat asymmetric collisions with 0.4≤γ≤0.45 could produce discs with nearly equal compositions to the final planet's mantle, with successful cases having |δf_T| values between 0.3% and 15% and disc masses between 1.7 and 5.5 lunar masses. Such impacts leave the Earth–Moon system with an angular momentum between 1.8 and 2.7L_EM, so that, like the fast-spinning Earth cases, they too require the subsequent, large-scale removal of angular momentum by the evection resonance.

The successful half-Earth impacts in [17] occur across a relatively broad range of impact speeds (1≤v_i/v_esc≤1.6) and impact parameters (0.35≤b≤0.7), and do not require a particular rotational state for the protoearth before the Moon-forming event. The most restrictive element in this scenario is the required closeness in size of the impactor to the target, with successful cases requiring 0.4≤γ≤0.5. Late-stage impacts with γ≥0.4 do occur, but they are less common than those with γ∼0.1 (appropriate for canonical impacts). Early, low-resolution N-body terrestrial accretion models [3] found that 20% of the Earth-like planets (defined as those with a final mass ≥0.5M_⊕) experienced a final impact with γ≥0.4. Because these early models started with few and thus fairly large protoplanets, they may overestimate the likelihood of collisions between similar-sized planets. Analyses of terrestrial impact histories in higher-resolution simulations are unfortunately limited. Raymond et al. [44] detail the growth histories of six terrestrial planets in their fig. 5, and, of these, one experiences a final impact with γ=0.46. Thus, a final collision as large as that needed in the half-Earth model appears to occur with approximately 10% probability, although this merits further analysis across a larger number of simulations.

A half-Earth impactor is massive enough to potentially perturb the Earth's orbit. Assuming an inelastic collision, the centre-of-mass velocity of the post-impact Earth is 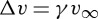, and the eccentricity impulsively delivered to the Earth's orbit by the impact is e∼Δv/v_orb, where v_orb=30 km s⁻¹ is the Earth's heliocentric velocity. The successful half-Earth impacts have 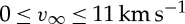, and so would produce 0≤Δv<5 km s⁻¹. Consistency with the current relatively circular planetary orbits (as reflected by the so-called angular momentum deficit in the inner Solar System; [15]) requires approximately Δv≤2 km s⁻¹, which is satisfied by about 70% of the successful cases in [17]. If an eccentricity damping mechanism was active at the time of the Moon-forming event, such as dynamical friction with small planetesimals [44], this could allow the higher Δv cases to be also consistent with the current system.

(iv). Discussion

High-angular-momentum impacts identified in [9,17] can, for the first time, produce discs that are compositionally similar enough to the planet to account for the Earth–Moon oxygen composition without requiring post-impact equilibration, assuming a roughly Mars-like composition for the impactor. In addition to oxygen, such impacts would also be consistent with the Earth–Moon similarities in titanium and chromium.

An additional issue is whether the new impacts can account for Earth–Moon similarities involving elements that partition into metals and therefore can be affected by core formation, including tungsten and silicon. Whether the disc is formed from the target's mantle (as in [9]) or from an approximately equal mix of target and impactor mantles (as in [17]), the impactor's iron core is absorbed by the planet, whereas the disc contains little iron. Substantial mixing and equilibration of the impactor's core with the target's mantle would tend to alter the planet's tungsten and silicon compositions relative to that of the disc (and the resulting Moon). However, it appears likely that the impactor cores merged rapidly with the Earth's core in a largely intact state in both models, and thus would not substantially equilibrate with the Earth's mantle. Dahl & Stevenson [45] estimate that only 0.7 wt% of a 1000 km radius core would mix with the mantle as it descended through a maximal magma ocean, with the mixing efficiency decreasing as core size increases. The impactor cores in [9,17] are larger still, with radii of about 1400 and 2900 km, respectively. Such small amounts of metal–silicate interaction might not lead to measurable fractionation in W or Si. In addition, if the Moon-forming impact occurred late when ¹⁸²Hf is essentially extinct, metal–silicate interactions would have limited ability to alter the ¹⁸²W/¹⁸⁴W ratio of the Earth compared with that of the disc (and the Moon).

The fast-spinning Earth and half-Earth impact events each have several times the kinetic energy of the canonical impact.² The discs produced by the high-angular-momentum impacts are predominantly vapour, in contrast to the discs produced by canonical impacts that are initially approximately 80–90% melt [33]. Heating of the Earth is also more extreme in the new scenarios, which raises the question of whether such energetic events would thoroughly melt and mix the Earth, thereby erasing any distinct chemical reservoirs within the Earth. At face, this would seem inconsistent with recent inferences that the Earth's mantle was not thoroughly mixed [46,47]. Ćuk & Stewart [9] argue that incomplete mixing may result from the non-uniform heating experienced by the Earth during the collision. The post-impact protoearth has a positive radial entropy gradient, implying stability against convective mixing [9,33], although it may still be subject to mixing owing to Kelvin–Helmholtz instabilities because there is a radial gradient in the angular spin velocity in the post-impact planet [33]. This issue merits further investigation.

Both the high-angular-momentum impacts are less probable than the canonical impact. Impactors as large as those required for the half-Earth scenario will occur less frequently than Mars-mass impactors, but perhaps not prohibitively so based on current terrestrial accretion models. The fast-spinning Earth scenario requires a sequence of at least two giant impacts: for example, a first by an object containing about half the Earth's mass to produce a protoearth rotating with a near-fission rate, and the second by a sub-Mars-sized object with a high velocity at infinity. The multiplicative likelihood of such a series of impacts would appear to be less than that of either the canonical or half-Earth impact.

3. Conclusion

Several impact models for forming the Moon are now being considered. The canonical impact of a Mars-sized body can produce a lunar-mass, iron-depleted Moon together with an angular momentum consistent with that in the current Earth and Moon [32,5]. But because such impacts produce a disc derived primarily from material originating in the impactor's mantle, post-impact mixing between the disc and planet is then required to account for the observed compositional similarities between the Earth and Moon [14]. Recently proposed high-angular-momentum impacts can produce discs whose silicate composition matches that of the Earth [9,17], but they require that subsequent capture of the Moon into the evection resonance reduced the spin rate of the Earth by a factor of 2 or more. Intermediate cases that require both equilibration and much more modest angular momentum removal also exist [16]. All of the impacts produce a disc that is heated substantially above the solidus. Whether this can be reconciled with evidence for a cool, initially subsolidus lunar interior [48] will depend on the subsequent thermal evolution of the material as it accumulates into the Moon.

It is notable that current models all require a process after the impact to effectively ‘erase’ a primary outcome of the event—either by changing the disc's composition through mixing or by changing the Earth's spin rate by the evection resonance. To date, no single scenario is able to explain all of the data without such a secondary step. Because of this, current models are more complex and therefore seem less probable than the original giant impact theory.

It is possible that future work may find that equilibration and/or substantial removal of angular momentum by the evection resonance would have been highly probable events. Alternatively, an underlying assumption in the model interpretations may be incorrect (such as the degree of compositional difference expected between the impactor and the planet), or there may yet be an unidentified class of impacts that are less constraining. Another possibility is that the impact models are neglecting a physical effect that is important in determining the relative proportion of impactor versus target material placed into the disc. Karato [49] argues that, prior to their collision, a smaller impactor would have a solid mantle while the target protoearth would have a molten mantle, and that the corresponding difference in equations of state between the two would lead to greater vaporization of the protoearth material compared with that of the impactor. However, this would seem unlikely to substantially affect the provenance of the disc material, because the primary process that lifts material into bound orbits is gravitational torques, not pressure gradients owing to vaporization. This is why substantial improvements in the equation of state used in the SPH codes [25] have not fundamentally changed the conclusion that canonical impacts produce discs derived predominantly from the impactor's mantle ([5] and references therein).

The same types of accretionary collisions that are effective at growing Earth-sized planets are also efficient producers of impact-generated satellites (figures 1 and 2). Thus, it is quite possible (and perhaps even probable) that the Earth would have already had a moon owing to a prior impact at the time of the Moon-forming collision, an issue that to date has been neglected by giant impact models. The extremely close compositional similarity of the Earth and Moon places constraints on the size and fate of such a prior moon. The addition of several per cent or more of the Moon's mass in either Mars-like or chondritic material would lead to a measurable difference between the oxygen compositions of the Earth and Moon which is not seen [12], and so either the prior moon was unusually small or it avoided being accreted by the Moon. The latter could occur if the Earth's rotation was quite slow before the Moon-forming event so that the prior moon's orbit tidally decayed into the Earth, or if the prior moon was removed from Earth orbit owing to a close encounter with a passing object (K. Pahlevan 2013, personal communication) or the Moon-forming impact itself.

Funding statement

Support from NASA is gratefully acknowledged.