Kinetic model facilitates analysis of fibrin generation and its modulation by clotting factors: implications for hemostasis-enhancing therapies

Abstract

Current mechanistic knowledge of protein interactions driving blood coagulation has come largely from experiments with simple synthetic systems, which only partially represent the molecular composition of human blood plasma. Here, we investigate the ability of the suggested molecular mechanisms to account for fibrin generation and degradation kinetics in diverse, physiologically relevant in vitro systems. We represented the protein interaction network responsible for thrombin generation, fibrin formation, and fibrinolysis as a computational kinetic model and benchmarked it against published and newly generated data representing diverse experimental conditions. We then applied the model to investigate the ability of fibrinogen and a recently proposed prothrombin complex concentrate composition, PCC-AT (a combination of the clotting factors II, IX, X, and antithrombin), to restore normal thrombin and fibrin generation in diluted plasma. The kinetic model captured essential features of empirically detected effects of prothrombin, fibrinogen, and thrombin-activatable fibrinolysis inhibitor titrations on fibrin formation and degradation kinetics. Moreover, the model qualitatively predicted the impact of tissue factor and tPA/tenecteplase level variations on the fibrin output. In the majority of considered cases, PCC-AT combined with fibrinogen accurately approximated both normal thrombin and fibrin generation in diluted plasma, which could not be accomplished by fibrinogen or PCC-AT acting alone. We conclude that a common network of protein interactions can account for key kinetic features characterizing fibrin accumulation and degradation in human blood plasma under diverse experimental conditions. Combined PCC-AT/fibrinogen supplementation is a promising strategy to reverse the deleterious effects of dilution-induced coagulopathy associated with traumatic bleeding.

Introduction

The conversion of fibrinogen to fibrin, catalyzed by the enzyme thrombin, is the central biochemical process in blood clotting.^1–3 Fibrin generation and polymerization are parts of a vast enzymatic network responsible for thrombin generation and subsequent inhibition,⁴ fibrin formation,¹ and controlled fibrin degradation (i.e., fibrinolysis⁵). Fibrin is the main structural element forming the body of the clot. Fibrin fibers stabilize the platelet plug, thereby providing the growing clot with the mechanical strength necessary for hemostasis (i.e., the cessation of bleeding from the disrupted blood vessel). Therefore, fibrin can be regarded as the main output of the biochemical blood coagulation network. This unique functional role makes fibrin a natural target for therapeutic intervention in blood clotting disorders. Furthermore, fibrinogen has been the subject of numerous studies investigating its potential as a hemostatic agent in trauma and surgery.^{6, 7} These applications necessitate detailed understanding of fibrin formation and degradation mechanisms at the molecular level.

Fibrin is a fibrous polymer that is formed from monomers obtained as a result of fibrinogen cleavage by thrombin. Biochemical studies have provided a wealth of information about individual molecular interactions that lead to thrombin and fibrin formation (see, e.g., the reactions shown in Fig. 1), as well as about the typical time course of thrombin and fibrin generation. However, the use of these findings to understand the blood clotting process is complicated by three main challenges. First, molecular details of the biochemical thrombin/fibrin generation network have largely been elucidated in experiments with simple cell-free in vitro systems that may only partially reflect the complexity of natural blood clotting mechanisms.^{8, 9} Second, the kinetics of fibrin generation and degradation in vitro are typically studied via turbidimetric measurements,^10–12 and it is often difficult to discern between different mechanistic factors that contribute to the observed dynamic changes in light absorbance. Third, experimental systems (which can be cell-free or cell-based with different types of cells) and protocols used to measure blood clotting dynamics are characterized by high diversity and a lack of universally accepted standards. The resulting variability in kinetic data, widely recognized for thrombin generation experiments,^{13, 14} may easily skew the patterns characterizing fibrin accumulation and degradation kinetics. Consequently, the relationship between the detailed biochemical mechanisms established or postulated for idealized systems and the fibrin/thrombin kinetics in many biologically relevant in vitro settings is unclear and requires further investigation.

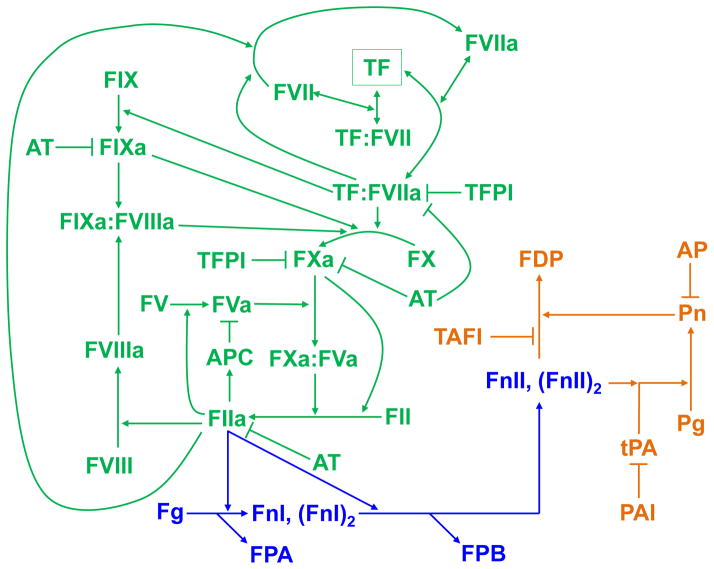
Fig. 1.

Protein interaction network responsible for tissue-factor-activated thrombin generation, fibrin formation, and fibrinolysis. The schematic shows protein interactions reflected in the kinetic model. Arrows represent molecular conversion, enzymatic catalysis, or binding/unbinding; T-shaped lines designate inhibition. Thrombin (FIIa) generation is initiated when, in the course of hemorrhage, blood comes in contact with the extravascular protein tissue factor (TF).^{4, 73} The formation or activity of thrombin is inhibited by the three natural anticoagulant systems: TF pathway inhibitor (TFPI), antithrombin (AT), and protein C. While active, thrombin converts fibrinogen (Fg) monomers into fibrin I (FnI) monomers. FnI is cleaved further and converted to fibrin II (FnII).^{2, 3} Fibrin degradation is catalyzed by the enzyme plasmin (Pn), whose precursor, plasminogen (Pg), is activated by tissue-type plasminogen activator (tPA).⁵ This degradation is inhibited at different levels by α₂-antiplasmin (AP), plasminogen activator inhibitor 1 (PAI), and thrombin-activatable fibrinolysis inhibitor (TAFI, which, like the protein C pathway, requires thrombomodulin for full activity³⁸). For the sake of a convenient visual presentation, some intermediate complexes and reactions were omitted in the schematic. For a full list of the protein interactions in the model, see Table S1 (ESI^†). Green: thrombin generation; blue: fibrin formation; orange: fibrin degradation. Further abbreviations: APC, activated protein C; FDP, fibrin degradation products; FPA, fibrinopeptide A; FPB, fibrinopeptide B; FII, prothrombin. The letter “F” followed by a Roman numeral designates a clotting factor, and if the Roman numeral is followed by the letter “a,” then the clotting factor is in its active form.

Here, we attempted to address these challenges by using a combined computational/experimental analysis strategy. We hypothesized that some of the essential kinetic features of thrombin and fibrin generation curves in diverse cell-free or cell-based experimental systems with human (or synthetic) blood plasma can be captured by one unified set of rigorously defined biochemical mechanisms. It is well recognized that, due to kinetic output variations between in vitro systems used by different laboratories, the development of quantitatively accurate kinetic models of thrombin generation in diverse experimental settings is difficult.^{13, 15, 16} Because fibrin production is catalyzed by thrombin, such inter-system variations are expected to play a significant role in kinetic studies of fibrin generation. Therefore, we further hypothesized that one unified set of kinetic mechanisms could account primarily for qualitative and semiquantitative features of fibrin generation and degradation kinetics. We tested that hypothesis by comparing the predictions of a kinetic model implementing the postulated biochemical mechanisms with published and newly generated data sets in which thrombin generation was supported by platelets, human saphenous vein endothelial cells (HSVECs), human umbilical vein endothelial cells (HUVECs), or phospholipids. Our kinetic model represents both thrombin/fibrin generation and fibrinolysis mechanisms, because we were particularly interested in understanding the interplay between these processes when they occur on the same time scale. Indeed, fibrin generation and fibrinolysis can occur simultaneously,^{3, 17, 18} which may contribute to blood clotting abnormalities in severe trauma situations.^{19, 20}

We applied the kinetic model to analyze therapeutic strategies to restore normal blood clotting in trauma patients. Globally, trauma is a leading cause of death, with a death toll exceeding the combined mortality of cardiovascular disease and HIV.²¹ Because uncontrollable bleeding is the major cause of lethal outcomes after trauma,²² the development of efficacious and safe therapeutic strategies to control hemorrhage is a top priority for modern healthcare. We specifically focused on the problem of blood dilution occurring in trauma patients. To prevent hemorrhagic shock, bleeding trauma patients are often subjected to intravenous infusion of resuscitation fluids, such as normal saline or colloids, which do not contain the biochemical and cellular components of the blood clotting system. This results in the dilution of blood plasma, which inhibits clotting.^21–23 An emerging concept in the treatment of traumatic and surgical hemorrhage is the use of prothrombin complex concentrates (PCCs, which are combinations of clotting factors, i.e., the protein components of the coagulation system)^{24, 25} and/or fibrinogen.²⁶ The question of optimal choice of PCC composition has not yet been resolved. Here, we analyzed the recently proposed PCC composition designated PCC-AT and consisting of the coagulation factors II, IX, X, and antithrombin.²⁷ The addition of the natural anticoagulant antithrombin to the standard procoagulant components of PCCs was suggested as a means to balance the procoagulant effects of those standard components and thereby effect a therapeutic intervention that does not excessively distort thrombin generation kinetics.²⁷ The results of this work indicate that PCC-AT, used in combination with fibrinogen, may be particularly efficacious in simultaneously restoring both thrombin and fibrin generation in diluted plasma.

Materials and Methods

Molecular interaction network and the kinetic model

The biochemical reaction network represented in our kinetic model reflects the protein interactions considered essential for thrombin generation, fibrin formation, and fibrinolysis in human plasma (Fig. 1). The reaction mechanisms and their parameters defining the protein interactions were derived from the works of a number of experimental groups with necessary adjustments (ESI^†). In particular, the thrombin generation part of our model was based on the Hockin–Mann model^{28, 29} validated by different research groups.^{13, 29–32} This model gives a detailed representation of the tissue factor (TF)-activated pathway of thrombin generation, which is the main pathway responsible for this process in vivo.⁴

The model development followed the standard approach of biochemical kinetics, where a reaction system is represented by a system of ordinary differential equations (ODEs) linking reactant concentrations with their rates of change (the full list of reactions is given in Table S1, ESI^†). Our model comprises 80 ODEs and one algebraic equation [representing the effects of thrombin-activatable fibrinolysis inhibitor (TAFI)]. The ODEs were solved numerically to obtain concentration curves reflecting the kinetics of each reactant. The parameters (80 rate constants and 4 equilibrium constants) and default initial conditions for the equations are given in Tables S1 and S2 (ESI^†), respectively. The initial conditions were the mean normal human plasma concentrations of the system’s protein components, unless stated otherwise. The main input of the system was the initial concentration of TF, the protein activator of the blood clotting process.⁴ The default TF concentration was 5 pM, which is a typical value for in vitro assays.^{33, 34} The main model output was the concentration, C_FnII, of fibrin II (FnII) protomers (henceforth referred to as “fibrin”): C_FnII = [FnII] + 2[(FnII)₂], where brackets designate concentration and FnII and (FnII)₂ stand for monomeric and dimeric fibrin forms, respectively. The current version of our model does not account for fibrin polymerization, but we assume that the level of polymerized fibrin (as reflected by turbidimetric data) is roughly proportional to the FnII concentration predicted by the model. Another essential output was the concentration of active thrombin (i.e., experimentally observable thrombin²⁹) or simply “thrombin,” defined as the weighted sum of the concentrations of free thrombin and meizothrombin (with weights 1.0 and 1.2, respectively).

Our model reflects the activity of protein C and thrombomodulin, whose expression on endothelial cells in the vicinity of the wound can inhibit thrombin generation.³⁵ While very little is known about the amounts of thrombomodulin expressed on the vascular endothelium,³⁵ our model represents it as a spatially distributed protein characterized by a volume concentration (with a default initial value of 1 nM),³⁶ in a similar way to TF, which is also expressed on cell surfaces.^{28, 29} Further details about the kinetic model and computational procedures are given in the ESI^†.

Modeling the effects of TAFI

To display its activity as a fibrinolysis inhibitor, TAFI needs to be activated to TAFIa by thrombin, and this process is greatly accelerated by thrombomodulin.^{37, 38} The biochemical mechanisms of TAFIa action on fibrinolysis are known to be complex,⁹ and specific expressions for the rates of the corresponding biochemical reactions, as well as quantitative estimates of the rate constants (necessary for rigorous mechanistic modeling), are not available. Due to this, TAFI (TAFIa) activity has not been previously reflected in kinetic models. Here we attempted an empirical representation of TAFI-mediated effects that relied on available experimental data.

To represent the dependency of clot lysis time (LT, the time it takes the turbidity level to reach 50% of its pre-lysis value) on the concentration of added TAFI, we approximated published experimental data using a two-parameter hyperbolic function. [In those experiments, lysis was initiated by adding tissue-type plasminogen activator (tPA),³⁹ which is the fibrinolysis trigger in our model and its essential activator in vivo.⁵] We then combined that representation with the finding that LT is approximately inversely proportional to the tPA concentration (see Equation 11 in Ref. 40). This allowed us to phenomenologically represent the effect of TAFI on fibrinolysis kinetics as an equivalent change in the tPA concentration (see ESI^†). Because we do not explicitly model the mechanism of TAFI activation, our approach relies on the assumption that the thrombin and thrombomodulin present in the system cause sufficiently rapid TAFI activation. We therefore set the TAFI concentration to 0 when modeling situations where thrombomodulin was absent in the system or where fibrinolysis was known to be inhibited under given experimental conditions.

Tenecteplase titration experiment

To test our modeling predictions regarding the effects of fibrinolysis on the fibrin curve, we performed a titration experiment with tenecteplase, a recombinant tPA analog.⁴¹ TF and phospholipids (phosphatidylserine, phosphatidylcholine, and phosphatidylethanolamine at a ratio of 20:60:20, respectively) were from Diagnostica Stago (Parsippany, NJ). Contact-inhibited, platelet-free normal plasma (NPP) was obtained with informed consent and prepared as previously described¹⁰ from whole blood from 40 healthy subjects (50% female:50% male,68% non-Caucasian) in a protocol approved by the Institutional Review Board of the University of North Carolina.¹⁰ Plasma from individual donors was pooled. The fibrinogen concentration in NPP (3 mg/ml = 8.82 μM) was determined by ELISA. Tenecteplase was a generous gift from Genentech (San Francisco, CA) to one of the authors (A.S.W.). No external thrombomodulin was added to plasma. Clotting was initiated with TF and phospholipid (final concentrations: 1 pM and 4 μM, respectively) addition to recalcified (final concentration: 16 mM) human NPP diluted 1:2 in the presence of 0, 0.125, 0.25, 0.5, 1, 2, 4, 8, or 16 μg/ml TNKase. Clot formation and lysis were followed by measuring turbidity at 405 nm on a SpectraMax Plus 340 plate reading spectrophotometer (Molecular Devices, Sunnyvale, CA).

Modeling plasma dilution and supplementation with prothrombin complex concentrates (PCCs)

In our computational studies of diluted plasma and coagulation factor supplementation, we followed our previously established modeling protocol.^{27, 42} Here, we focused on 5-fold dilution; to represent it in the model, the initial concentrations of all but two biochemical components were reduced by 5 fold. The exceptions were thrombomodulin and TF, which in vivo are localized on the blood vessel endothelium and tissue TF-expressing cells, respectively, rather than dissolved in blood plasma. To represent supplementation of diluted plasma with PCC-AT components (i.e., coagulation factors II, IX, X, and antithrombin), we set the initial concentrations of those four factors to their normal (i.e., pre-dilution) values while leaving all other factors at their post-dilution levels. A similar modeling strategy was applied for supplementation with fibrinogen alone, fibrinogen with PCC-AT, and the three procoagulant PCC-AT components (i.e., factors II, IX, and X) with or without fibrinogen.

Results

Prothrombin and fibrinogen titrations have distinct impact on fibrin generation

Prothrombin and fibrinogen, being the two most abundant proteins naturally promoting blood coagulation, are among the main plasma components used as therapies to stop excessive bleeding and reverse coagulopathy in trauma and surgery.^{6, 7, 24, 25} We therefore wished to verify our kinetic model’s ability to capture the effects of prothrombin and fibrinogen titrations on fibrin kinetics. For 1% initial prothrombin (with respect to its average normal value), the model captured the fibrin generation delay and reduced fibrin level measured in a synthetic system containing human platelets¹² (Fig. 2A). In that experiment, the initial fibrinogen concentration was 5.88 μM, which is somewhat below the average value (i.e., 9.0 μM) but still is in the normal range.³ That experimental system lacked the fibrinolytic system components and protein C (as well as thrombomodulin),¹² which was reflected in our simulation. The model-predicted fibrin plateau was insensitive to prothrombin variations for prothrombin levels above 10%, which reflects the relative insensitivity of the plateau to such variations demonstrated in the experiment (Fig. 2A). The experimental data and model simulations for 150% prothrombin (not shown) were similar to the results for 100% prothrombin. To summarize, prothrombin variations in the 50%–150% range caused relatively small variations in the fibrin output (Fig. 2A), which also agreed with our modeling results for 9.0 μM initial fibrinogen (Fig. S1, ESI^†).

Fig. 2.

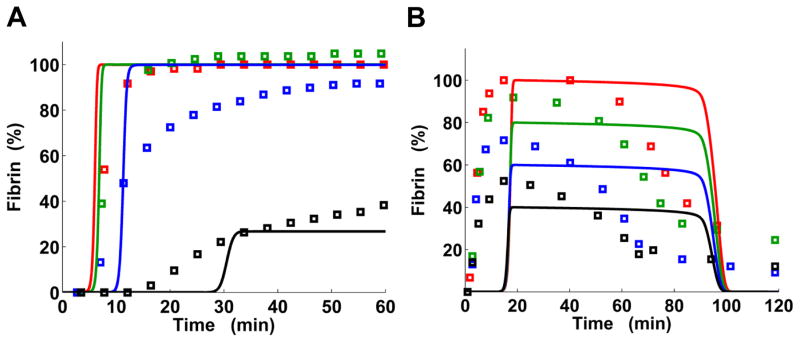
Kinetic model captures fibrin formation modulation by prothrombin and fibrinogen. Solid lines, model output; square markers, turbidimetric measurements. A: Prothrombin titration. The colors represent different levels of initial prothrombin: black, 1% of the normal average value (i.e., 1.40 μM); blue, 10%; green, 50%; and red, 100%. Experimental data were extracted from Fig. 2 of Ref. 12. To facilitate comparisons with model predictions, the absorbance baseline was set to 0 and the data were normalized to the maximum absorbance level achieved for 100% prothrombin. Model output was normalized to the maximum concentration achieved in the simulation for 100% prothrombin. While in the experiment the TF concentration was not determined, we used the default TF concentration in the simulation. B: Fibrinogen titration. The colors represent different levels of initial fibrinogen: black, 8.82 μM; blue, 13.24 μM; green, 17.65 μM; and red, 22.06 μM. Experimental data were extracted from Fig. 5D in Ref. 11. The absorbance baseline was set to 0 and the experimental data were normalized to the maximum absorbance level. The model output was normalized to the maximum fibrin concentration achieved for 22.06 μM fibrinogen. In the model, thrombin generation was initiated with 1 pM TF and fibrinolysis was activated by adding external tPA (at time 0) at a concentration of 3.50 nM; these values were chosen to match the experimental conditions.

Model simulations for the fibrinogen titration captured the main effect of increasing fibrinogen level, which led to a progressive increase in the fibrin peak but did not affect the fibrin generation timing in an experimental system containing HSVECs, with fibrinolysis induced by tPA¹¹ (Fig. 2B). While the HSVECs could possibly act as a source of thrombomodulin, the presence of sufficient amounts of functional thrombomodulin contradicted the observed fibrinolysis timing. Indeed, the thrombomodulin activity would have led to the activation of TAFI, which would cause a considerable delay in fibrinolysis timing (see Fig. 3 and the next subsection). To reflect the observed fibrinolysis timing, the initial concentration of thrombomodulin in the simulation was set to 0. Our model reproduced the synchronous timing of the fibrin peaks, whose left-hand slopes practically coincided. Yet, the simulated onset of fibrin generation was substantially delayed in comparison with the experimental data (Fig. 2B). This difference in timing appears to reflect the properties of the thrombin-generation part of our model, which has been originally designed to reflect thrombin generation in cell-free, synthetic plasma.²⁹ That model gives a clotting time (which approximately corresponds to the onset time for fibrin curves) of ~4 min upon activation with 5 pM TF.³⁴ That is similar to in vitro clotting time measurements (~4.7 min) in whole blood for the same TF concentration.⁴³ In contrast, in the HSVEC-based system, even with a lower trigger concentration (i.e., 1 pM TF), fibrin generation onset occurs much faster (Fig. 2B).

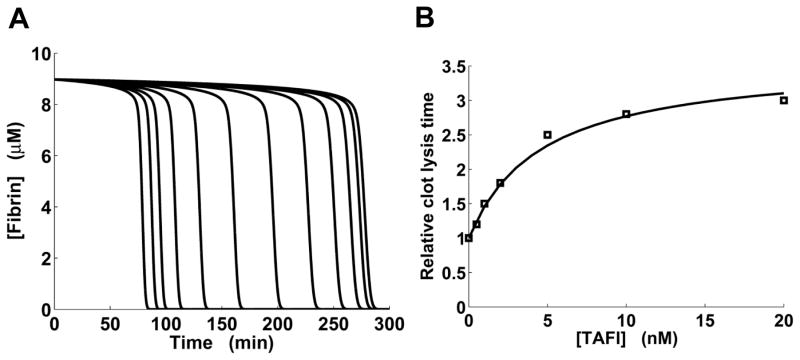
Fig. 3.

Effects of thrombin-activatable fibrinolysis inhibitor (TAFI) on fibrinolysis kinetics. A: Model-generated fibrinolysis kinetic curves for preformed clots for different concentrations of added TAFI. In the simulations, clots were initially formed for 30 min in the absence of TAFI. Fibrinolysis was initiated by 3.5 nM external tPA added at time 0. Left to right, TAFI was added at time 0 at a concentration of 0, 0.20, 0.39, 0.78, 1.56, 3.12, 6.25, 12.5, 25, 50, 100, and 200 nM. B: Experimentally determined dependency of relative lysis time for preformed clots on the concentration of added TAFI (square markers) is approximated by a model-generated curve (solid line). Experimental data for clots formed in TAFI-deficient normal human plasma were extracted from Fig. 6 in Ref. 39. In the simulations, the lysis times were computed directly from simulated fibrinolysis kinetic curves, which looked similar to the curves shown in panel A.

In our simulations for both prothrombin and fibrinogen titrations, the simulated fibrin output reflected the rising and falling of the turbidity levels from in vitro experiments (Fig. 2). Yet, there were visible discrepancies between the model-generated and experimentally measured fibrin curve shapes. For example, the left- and right-hand slopes of the fibrin curves predicted by our model were steeper than observed in experiments (Fig. 2). This tendency for steeper simulated slopes, which has also been reported (in the context of thrombin generation) for a related “platelet–plasma” computational model,³⁰ could be attributed to the model design which, by necessity, only partially reflects the complexity of thrombin/fibrin generation. This increased steepness also appears to be responsible for the “quasi-plateau” segments of the model-generated trajectories, which correspond to gradually decaying peaks in the experimental data (Fig. 2B). The deviations from direct proportionality between model-predicted fibrin levels and experimentally measured turbidity levels are likely to contribute to the discrepancies between the model and experiments.

TAFI delays fibrinolysis in a saturable manner

Our computational model gives a representation of TAFI-modulated fibrinolysis kinetics (Fig. 3A), with model outputs reproducing the typical shape of kinetic curves observed experimentally for tPA-induced fibrinolysis in the presence of TAFIa.^{8, 37} For different levels of added TAFI, we used such kinetic curves to calculate the LT values, which show the extent of TAFI-mediated inhibition of fibrinolysis. (LT can be regarded as a special case of the 50%-deactivation time, a quantity frequently used to gauge the timing of biological processes.⁴⁴) The addition of increasing amounts of TAFI (or TAFIa) in vitro typically produces an increasing LT curve that approaches a plateau when LT in the presence of TAFI (or TAFIa) is ~3-fold larger than the LT value in its absence.^{37, 39, 45} Our model captured this saturation effect, and the model-generated LT curve was in good agreement with experimental data (Fig. 3B).

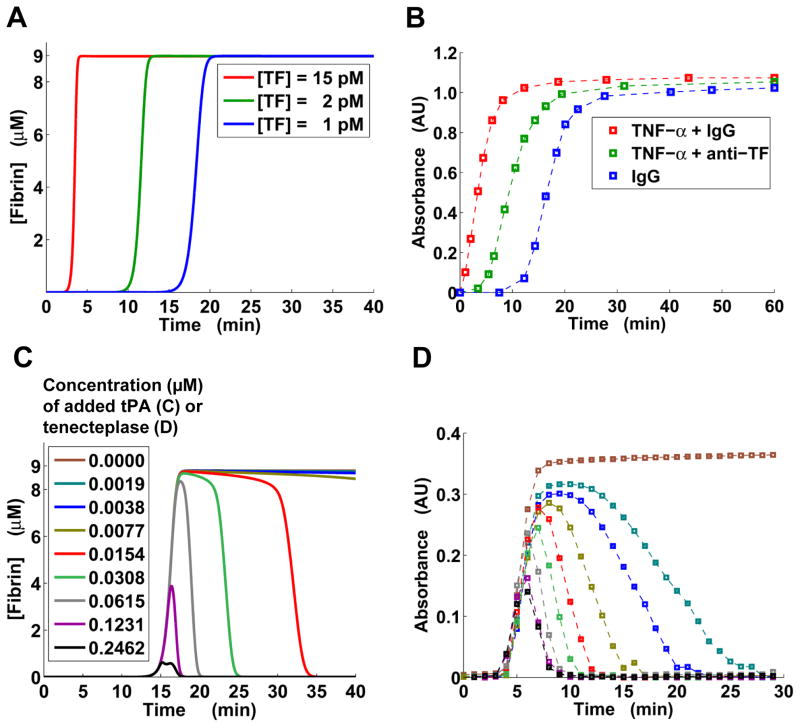
Tissue factor level determines the timing of fibrin generation

Our computations showed that, for TF concentrations in the picomolar range (typical for in vitro assays³³), higher TF levels resulted in a faster onset of fibrin generation, but the fibrin curve plateau did not depend on TF concentration (Fig. 4A). [In this simulation, the initial thrombomodulin concentration was equal to its default value (Table S2, ESI^†).] This was consistent with experimental results showing that the slope of the fibrin curve is shifted to the right for higher TF dilution degrees in human blood plasma deficient in factor XII and/or factor XI.⁴⁶ Moreover, recent experiments with human platelet-free plasma added to monolayers of HUVECs (which produce thrombomodulin in vitro)¹⁰ showed that adding tumor necrosis factor-α (TNF-α, which stimulates TF expression) to the cells accelerated the onset of fibrin generation, whereas adding TNF-α and an anti-TF antibody gave an intermediate onset timing between full stimulation with TNF-α and control IgG (Fig. 4B). In view of our computational predictions (Fig. 4A), the observed differences in the fibrin generation curves (Fig. 4B) can be attributed directly to progressively increasing TF levels for the control, TNF-α + anti-TF antibody, and TNF-α-only cases. Furthermore, our model predicted that an increase in TF concentration leads to both an increase in thrombin peak height and a decrease in thrombin peak time (Fig. S2, ESI^†). This is in agreement with thrombin measurements for the HUVEC-based system (Fig. 7A–B in Ref. 10). The time of the simulated onset of fibrin generation (Fig. 4A) was in good agreement with clotting time predicted from the simulated thrombin curves (Fig. S2, ESI^†; black circles), indicating that the model is internally consistent.

Fig. 4.

Triggers of thrombin generation and fibrinolysis impact fibrin kinetics. A: Model-predicted fibrin generation at different TF levels. B: Baseline-subtracted turbidimetric data (squares) extracted from Fig. 7B in Ref. 10. To enhance the visual perception of the experimentally detected patterns, the data points are connected by thin dashed lines. The colors represent three types of reagents added to the cells supporting thrombin generation (i.e., human umbilical vein endothelial cells). “anti-TF” denotes anti-TF antibody. AU, arbitrary units. C: Model-predicted fibrin levels for a tissue-type plasminogen activator (tPA) titration. Thrombin generation was initiated with 1 pM TF. The initial fibrinogen concentration was 8.82 μM. D: Baseline-subtracted turbidimetric data (squares) for a tenecteplase titration performed as described (see Materials and Methods). AU, arbitrary units.

tPA and tenecteplase modulate fibrinolysis timing and fibrin curve peak height in a similar, dose-dependent fashion

Our model predicted that increasing tPA concentration by a few orders of magnitude can profoundly impact fibrin abundance by affecting both fibrinolysis timing and maximum fibrin level (Fig. 4C). (Note that, because blood plasma itself is expected to contain only trace amounts of functional thrombomodulin, the initial thrombomodulin concentration in this simulation was set to 0.) Qualitatively, the impact of tPA can be characterized by discerning tPA-dependent “phases” of fibrinolysis activation. When the concentration of added tPA was <0.01 μM, there was almost no fibrinolysis (on a 40-min time interval). An increase in tPA concentration beyond 0.01 μM resulted in progressively increasing fibrinolysis rates. The fibrin peak (~9 μM high, corresponding to full fibrinogen conversion into fibrin), however, was not affected until tPA concentration exceeded 0.06 μM. Further increase in the tPA concentration resulted in a diminished fibrin peak, suggesting that fibrinolysis was faster than fibrin formation and that active fibrin degradation began before fibrinogen conversion into fibrin was completed.

We tested these computational predictions by comparing them with fibrin data obtained for human NPP supplemented with phospholipids; fibrinolysis was activated with tenecteplase (Fig. 4D). While quantitative differences could be detected between the modeling predictions and the experiment, the model captured the main qualitative features of fibrinolysis activation. For example, the turbidimetric data followed the tPA-dependent fibrinolysis phases predicted by the model (Fig. 4C–D). Similarly to our results for the fibrinogen titration (Fig. 2B), the onset of thrombin generation predicted by the model was slower than that observed in the experiment, which could be accounted for by a similar rationale (see the first subsection in the Results Section). Interestingly, while our model predicted zero fibrin levels upon completion of fibrinolysis (Figs. 2B, 4C), the fibrinogen titration experiment with the HSVEC-based system showed some residual, non-zero turbidity at 120 min after clotting initiation (Fig. 2B). Yet, in the tenecteplase titration experiment with phospholipid-containing plasma, the turbidity curves converged to zero after reaching the peak value, as predicted by the model (Fig. 4D). These variations support the notion that certain kinetic features of thrombin formation and fibrin generation/lysis are inherently system-specific and cannot be captured by a general kinetic model or by experiments following distinct protocols.

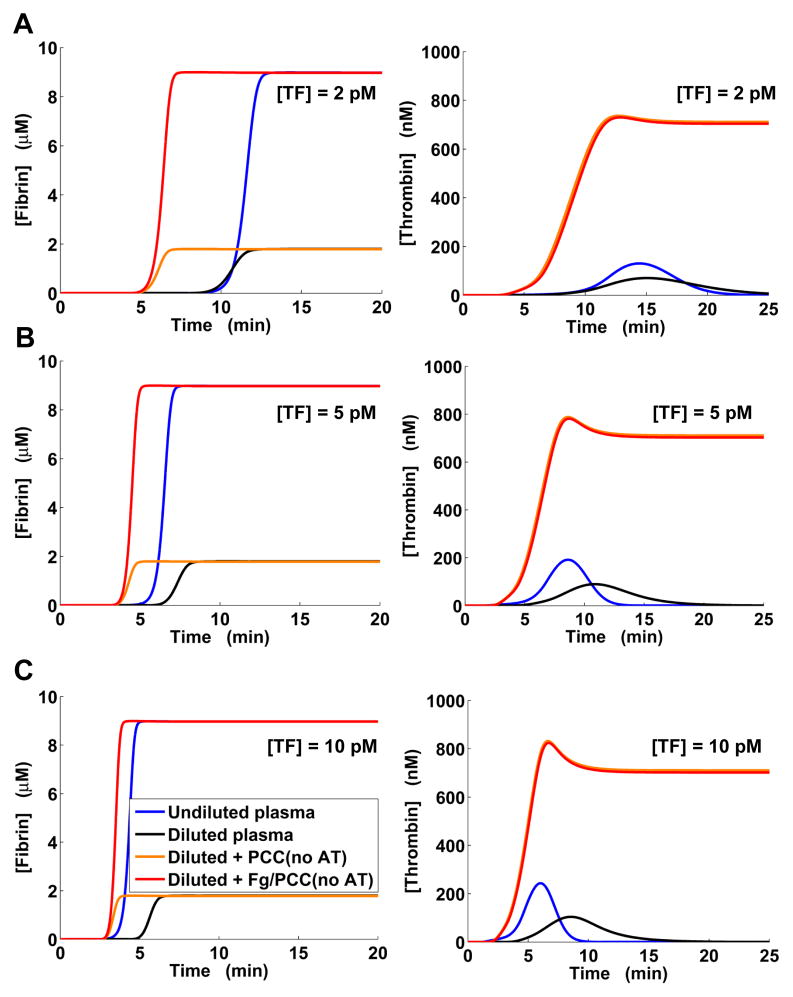
PCC-AT combined with fibrinogen restores normal clotting kinetics in a model of dilution-induced coagulopathy

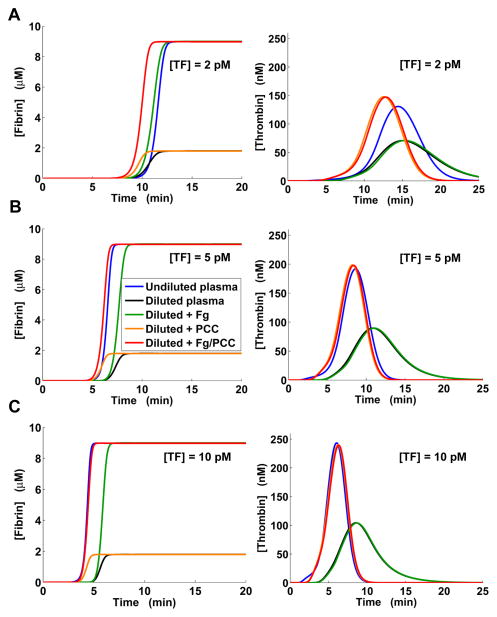
We performed computational plasma dilution and supplementation simulations for TF levels of 2, 5, 10, 15, 20, and 25 pM (Fig. 5 and Fig. S3, ESI^†) as described in Materials and Methods. In those simulations, no external tPA was added to the system and fibrinolysis was suppressed by the natural inhibitors at all considered TF levels, which is in accord with our laboratory experience. The thrombomodulin concentration was set at its default level (see Table S2, ESI^†), to reflect the in vivo-relevant effects of thrombomodulin (which in fact corresponds to externally added thrombomodulin in the in vitro situation). Simulated plasma dilution reduced thrombin peaks (Fig. 5 and Fig. S3, ESI^†), in agreement with the findings from several studies of thrombin generation in diluted plasma.^47–49 Dilution reduced the fibrin plateau level by 5 fold, which can be explained by the 5-fold dilution of initial fibrinogen and subsequent full conversion of fibrinogen to fibrin. By design, our model’s dilution behavior is consistent with that of the Hockin–Mann model of thrombin generation,⁴² which was used as a component in our model (see ESI^†).

Fig. 5.

Model-predicted restoration of normal thrombin and fibrin generation in diluted plasma by clotting factor supplementation. “Fg” stands for supplementation with fibrinogen, “PCC” denotes supplementation with PCC-AT (a combination of the factors II, IX, X, and antithrombin), and “Fg/PCC” denotes simultaneous supplementation with fibrinogen and PCC-AT. A: Clotting was initiated with 2 pM TF. B: Clotting was initiated with 5 pM TF. C: Clotting was initiated with 10 pM TF. Here, the blue and red lines for fibrin generation practically coincide, as do the orange and red lines for thrombin generation.

By causing a delay in thrombin generation, dilution noticeably delayed the onset of fibrin formation. In all simulations, PCC-AT supplementation alone could not produce a fibrin curve approximating the normal fibrin curve (i.e., the fibrin curve in undiluted plasma), whereas adding fibrinogen (with or without PCC-AT) restored normal fibrin plateau level. These results are in agreement with experimental studies showing that adding fibrinogen to diluted human plasma improves viscoelastic properties of the clot (measured by thromboelastography), but not thrombin generation, whereas adding commercially available PCC has the converse effect.^{49, 50} At 2 pM TF, supplementation with fibrinogen alone approximated the normal fibrin curve more accurately than combined supplementation with fibrinogen and PCC-AT (Fig. 5A). For all other TF levels, it produced a fibrin curve shifted by ~1.13–1.60 min (estimated from the curve half-maximum times) with respect to the normal fibrin curve. Yet, the addition of fibrinogen did not alter the ability of PCC-AT to modulate thrombin generation. PCC-AT supplementation accurately approximated thrombin generation for [TF] > 2 pM (Fig. 5 and Fig. S3, ESI^†). Moreover, for [TF] > 2 pM, the fibrin curve in diluted plasma after combined supplementation with fibrinogen and PCC-AT nearly coincided with the normal fibrin curve (Fig. 5B–C and Fig. S3, ESI^†).

To assess the role of antithrombin in our PCC-AT supplementation strategy, we performed computational experiments in which diluted plasma was supplemented only with the procoagulant components of PCC-AT (i.e., factors II, IX, and X), which are essential components of commercially available PCCs. In our simulations, adding the procoagulant components without fibrinogen noticeably accelerated fibrin generation but, as expected, did not improve the final fibrin level (Fig. 6 and Fig. S4, ESI^†). Fibrin level normalization was achieved when the added factors II, IX, and X were supplemented with fibrinogen. Starting at 10 pM TF, normalization of the fibrin curve by adding the procoagulant factors and fibrinogen was becoming increasingly accurate (Fig. 6C); at 25 pM TF, the normal and post-supplementation fibrin curves almost coincided (Fig. S4, ESI^†). However, for all considered TF levels, adding the three procoagulant factors led to an above-normal rate of thrombin generation and the resulting significant overproduction of thrombin.

Fig. 6.

Model-predicted effects of supplementing diluted plasma with the three procoagulant PCC components (i.e., factors II, IX, and X) with and without fibrinogen; no antithrombin was added. The PCC component supplementation is denoted “PCC(No AT)” without fibrinogen and “Fg/PCC(No AT)” with fibrinogen. A: Clotting was initiated with 2 pM TF. B: Clotting was initiated with 5 pM TF. C: Clotting was initiated with 10 pM TF.

Comparison with existing mechanistic models

Recent years have seen a rapid growth in applications of approaches that combine computational and experimental techniques to study blood coagulation.^{31, 34, 51} The mechanistic model developed and validated in this work represents a unique attempt to devise a predictive strategy whose main output (i.e., fibrin concentration) can be directly mapped to turbidimetric data characterizing fibrin formation and degradation in vitro. While the literature contains numerous examples of predictive modeling applications in coagulation research,^{13, 16, 27, 29, 30, 34, 42, 52–56} most of the reported work focuses only on some part of the full process, such as thrombin generation or fibrin formation (e.g., see Refs. 29, 54, 57). An exception is the work of Anand et al., which modeled thrombin generation, fibrin formation, and fibrinolysis as a reaction–diffusion process; however, neither parts of the model nor the model’s final output were experimentally validated.⁵² A recently developed combined model of thrombin and fibrin generation was fine-tuned to accurately reproduce the kinetics of thrombin generation initiation for a given experimental system; however, its ability to capture later stages of thrombin generation, or the process of fibrin accumulation, was not tested directly.³⁰ It should also be noted that none of the previously developed models reflect the effects of TAFI. To sum up, the goals of this investigation required the development of a new predictive model by integrating previously described and rigorously validated “parts” (see Materials and Methods), which represent some of the protein interactions expected to occur in the course of blood clotting.

Discussion

The ability of rigorously defined protein interaction mechanisms to account for kinetic features of thrombin generation, fibrin formation, and fibrinolysis in biologically realistic in vitro systems has remained largely unexplored. Here, we attempted to fill this knowledge gap by developing a unified kinetic model of thrombin-generation-driven fibrin formation and degradation. The model’s output was compared with turbidimetric data from diverse in vitro systems, where thrombin generation was supported by platelets (Fig. 2A), HSVECs (Fig. 2B), HUVECs (Fig. 4B), or externally added phospholipids (Fig. 4D). The model could reproduce essential qualitative or semi-quantitative patterns detected for each of those systems. At the same time, because the model was defined by one set of biochemical mechanisms and parameters, it could not achieve a high quantitative accuracy for all of the considered experimental systems simultaneously. This is evidently due to the discrepancies between the biochemical mechanisms postulated in the model and the specifics of each particular experimental system (e.g., the distinct dynamics of clotting factors interacting with HUVECs vs. HSVECs vs. platelets). Yet, here we focused on one set of mechanisms because quantitatively accurate, molecular-level, specific descriptions of the thrombin/fibrin generation biochemistry for every experimental setup are not (and, likely, will not be) available. Taken together, our results suggest that the postulated protein interaction mechanisms, which give a simplified representation of the physiological blood clotting system, can account for the essential kinetic features of fibrin and thrombin accumulation, as well as fibrinolysis.

The literature contains numerous examples of mathematical modeling applications in blood coagulation research;^{13, 15, 29, 30, 32, 54–59} yet, the vast majority of the reported works focus only on certain components of the full process, such as thrombin generation or fibrin formation. Our modeling efforts were aimed at developing a hypothesis-generation tool (or, a “thinking tool,” as the role of mathematical models in hematology was recently defined⁵¹) that could capture some of the main features of fibrin kinetics for a broad range of experimental setups. It has been argued that even very simple kinetic models, which do not reflect the known details of thrombin generation biochemistry, can realistically reproduce the shape of thrombin curves; as a result, detailed kinetic models may not be mechanistically revealing.⁶⁰ Our goal, however, was to test the utility of the existing mechanistic knowledge for the prediction of general system behavior under various perturbations, rather than to test the ability of a specific hypothesized mechanism to yield quantitatively accurate predictions for a specific system under fixed conditions (e.g., for normal average coagulant concentrations). Our approach appears adequate in view of the high degree of diversity of in vitro setups and protocols used to study thrombin and fibrin generation and lysis.^{13, 14} Furthermore, a mechanistic approach to modeling allowed us to represent the system components (such as factors IX and IXa, which are absent in the “minimal” thrombin generation model⁶⁰) that could be regarded as intervention points to modulate the kinetics of the system.^{16, 56} Without representing the components and associated mechanisms, a large variety of “what if” modeling studies, including investigations of promising therapeutic strategies, would be impossible.⁶¹

Thrombin-activatable fibrinolysis inhibitor (TAFI) in its activated form (TAFIa) is known to suppress tPA-activated fibrinolysis by a number of distinct mechanisms.⁹ First, TAFIa removes the exposed arginine and lysine residues from nicked (i.e., partially degraded) fibrin, thereby preventing the latter from enhancing tPA-catalyzed conversion of plasminogen to plasmin. Second, TAFIa inhibits the conversion of Glu-plasminogen to Lys-plasminogen (which is a much better substrate for tPA), thus leading to slower overall plasminogen activation. Third, TAFIa can directly inhibit plasmin. Additionally, TAFIa can make plasmin more susceptible to inhibition by antiplasmin.⁶² While the rates for TAFIa-induced lysine residue removal from fibrin degradation products have been determined,⁶³ complete rate expressions for other pertinent reactions and estimates for the corresponding rate constants, necessary for mechanistic modeling, are currently unavailable. Mechanistic, quantitative analysis of fibrinolysis is further complicated by the fact that some of such rates can substantially depend on the dynamically changing concentration of fibrin degradation products,^{39, 63} which is difficult to measure or model for clot lysis in plasma. Taken together, these considerations motivated us to include a descriptive (rather than mechanistic) representation of TAFI effects in our model. This description relies on two empirical parameters, a and b (Representation of TAFI effects, ESI^†), whose values cumulatively reflect the complex interplay of all TAFI activation and action mechanisms. By adjusting their values, we fine-tuned the model to quantitatively reproduce experimental data (Fig. 3B).

Because we focused on the interconversions of molecular species rather than the development of spatial structures, our kinetic model does not take into account the processes that determine polymer organization of fibrin, such as protofibril growth, lateral protofibril aggregation, and fiber cross-linking. Yet, comparisons of our predictive results with experimental data indicate that the principal features of fibrin kinetics can be attributed primarily to changes in fibrin abundance. Moreover, because the structure and parameters of our mechanistic model give a simplified representation of reality, the modeling results suggest that essential kinetic features of fibrin accumulation are comparatively insensitive to the details of the underlying molecular processes, and can be attributed largely to the interactions between the system’s main protein components.

Massive anticoagulation and markedly enhanced fibrinolysis have been implicated as major factors of acute traumatic coagulopathy.^{19, 20, 64, 65} It is therefore conceivable that the development of this pathologic condition is shaped by the interplay between fibrin formation and degradation, which can occur simultaneously.^{3, 17, 18} Because fibrinolysis activation is strongly associated with the release from endothelial cells, or de-inhibition, of tPA,^{64, 65} we wanted to investigate how fibrin accumulation is affected by increasing amounts of tPA and its recombinant analog, tenecteplase. Our computational model predicted that an initial increase of tPA concentration accelerated the lysis of fibrin without considerably affecting maximum fibrin level; yet, further increase in tPA level led to a significantly diminished fibrin peak (Fig. 4C). These predictions were consistent with the results of our tenecteplase titration experiment (Fig. 4D). Taken together, these findings indicate that sufficiently high tPA levels may not only accelerate the lysis of already formed thrombi, but may in fact prevent the accumulation of fibrin necessary for thrombus formation. This can perhaps account for the intensity of acute traumatic coagulopathy and warrants further investigations of the interaction between blood clotting and clot lysis mechanisms.

Existing evidence demonstrates that fibrinogen supplementation may be an efficacious and safe strategy to control trauma-related hemorrhage.^{6, 7} This evidence, together with our findings (Fig. 5 and Fig. S3, ESI^†), suggests that a combined fibrinogen and PCC-AT supplementation might provide an even higher level of efficacy and safety as a therapeutic strategy. Overall, our results are in accord with experimental studies reporting that simultaneous supplementation with fibrinogen and factor VIIa (which stimulates thrombin generation) resulted in improved hemostatic outcomes.^{66, 67} Yet, because factor VIIa may distort thrombin generation curves,^{13, 27} the use of PCC-AT combined with fibrinogen may be preferable. The model-predicted ability of PCC-AT alone to improve (or even restore) the timing, but not the final level, of fibrin generation (Fig. 5 and Fig. S3, ESI^†) is in accord with a rotational thromboelastometry study reporting that concentrated fibrinogen exceeded fresh frozen plasma (containing potentially diluted/deactivated clotting factors and fibrinogen) in improving mechanical clot properties after plasma dilution.⁶⁸ Conversely, the inability of fibrinogen alone to fully restore normal fibrin generation (Fig. 5B–C and Fig. S3, ESI^†) is in full agreement with a recent clinical study of dilutional coagulopathy.⁶⁹ Experimental studies are now needed to test our computational predictions and directly assess the potential of PCC-AT to improve hemostasis. Interestingly, our computations for supplementation with only the procoagulant PCC-AT components suggest that, for higher TF levels, these components (with fibrinogen) may be sufficient for the restoration of the normal fibrin curve (Fig. S4, ESI^†). Yet, our modeling predicted that such a scenario would also result in a gross overproduction of thrombin, which is consistent with our earlier results for a PCC containing FVII instead of antithrombin.²⁷ Given thrombin’s many functional roles,⁷⁰ such overproduction is likely to be detrimental for human physiology.

The limitations of our approach are determined by the scope and main focus of our work as well as by the nature of the analyzed experimental data. First, the current version of the model should in many cases be expected to provide only a qualitative (or semi-quantitative) level of predictive accuracy, and does not capture certain quantitative kinetic aspects. Retuning the model to increase its accuracy for a given in vitro system or protocol may lead to a decrease in the model’s generality, and this is a tradeoff whose resolution should be dictated by specific modeling applications. Second, our comparisons between our modeling results and experimental data could be improved if information about the actual concentrations of coagulation proteins in all the considered experimental systems was available. Third, including a mechanistic representation of cell activation and cell surface effects in the model could allow us to represent the contributions of protein–membrane interactions to fibrin generation kinetics. Furthermore, explicit mechanistic representation of fibrin polymerization and TAFI action in our model could lead to further insights into the role of fibrin structure in blood clotting. Because it is known that fibrin structure affects fibrinolysis,³ such an extension of the model may allow us to obtain more accurate predictions of fibrin degradation kinetics under different experimental conditions. Finally, developing computational and empirical models to account for the role of blood flow could bring our modeling studies closer to the in vivo setting.

Modeling-based approaches have successfully been applied to investigate the effects of blood coagulation therapies acting at the level of thrombin generation.^{13, 15, 27, 32, 56, 58} The computational model proposed in this work allows one to extend such approaches to include new and promising pharmacological agents that act at the level of fibrin formation and lysis. Mechanistic modeling of the complete blood coagulation system may facilitate rapid testing of single drugs, as well as drug combinations, and thereby accelerate the pace of therapeutic development for blood clotting disorders.

Conclusion

Existing approaches to biological model building and parameter estimation are diverse, and the choice of approach depends on the biological situations that the model is intended to address. On one side of the spectrum is the classic approach of biochemical modeling, where the equations describing a kinetic mechanism are fitted to, or benchmarked against, a particular data set or a number of closely related data sets. This approach was used to build each of the components of our integrated kinetic model, and each of the model components for thrombin generation,²⁹ fibrin formation,⁵⁷ plasminogen activation,⁷¹ and fibrinolysis⁴⁰ (see ESI^†) was developed independently. On the other side of the spectrum is the recently developed ensemble modeling, where a model is in fact an ensemble (or group) of kinetic mechanisms and parameter sets intended to describe essentially the same biological phenomenon studied under different experimental protocols.⁷² In view of the widely recognized inter-laboratory variability, ensemble modeling was recently applied to thrombin generation kinetics.¹⁵

Here, we used one set of reaction equations and one parameter set to account for the main kinetic features of fibrin generation in experimental systems that were substantially different from one another. Such singular model structure offers the advantages of comparatively simple modeling protocols and direct interpretation of modeling results. However, it is clearly impossible to guarantee a high quantitative accuracy of such modeling without fine-tuning the model to a specific experimental system. (While increasing the descriptive accuracy of modeling with respect to a given in vitro system or protocol, extensive parameter fitting might lead to a decrease in the model’s generality and predictive power.) Yet, the nature of fibrin turbidimetric kinetic data, which are reported in arbitrary units, and the above-mentioned experimental variability imply that qualitative and semiquantitative predictions can provide sufficient information for a meaningful analysis.