Automatic Iceball Segmentation With Adapted Shape Priors for MRI-Guided Cryoablation

Abstract

Purpose

To develop and evaluate an automatic segmentation method that extracts the 3D configuration of the ablation zone, the iceball, from images acquired during the freezing phase of MRI-guided cryoablation.

Materials and Methods

Intraprocedural images at 63 timepoints from 13 kidney tumor cryoablation procedures were examined retrospectively. The images were obtained using a 3 Tesla wide-bore MRI scanner and axial HASTE sequence. Initialized with semiautomatically localized cryoprobes, the iceball was segmented automatically at each timepoint using the graph cut (GC) technique with adapted shape priors.

Results

The average Dice Similarity Coefficients (DSC), compared with manual segmentations, were 0.88, 0.92, 0.92, 0.93, and 0.93 at 3, 6, 9, 12, and 15 min time-points, respectively, and the average DSC of the total 63 segmentations was 0.92 ± 0.03. The proposed method improved the accuracy significantly compared with the approach without shape prior adaptation (P = 0.026). The number of probes involved in the procedure had no apparent influence on the segmentation results using our technique. The average computation time was 20 s, which was compatible with an intraprocedural setting.

Conclusion

Our automatic iceball segmentation method demonstrated high accuracy and robustness for practical use in monitoring the progress of MRI-guided cryoablation.

The Incidence of renal cell carcinoma in the United States has increased by 126% over the past 50 years (1), together with an increase in its associated mortality rates (2). Image-guided percutaneous cryoablation is one of the most promising and prevailing minimally invasive techniques for treating kidney cancer (3–5). Compared with computed tomography (CT), MRI is considered a superior intraprocedural imaging tool to visualize the ablation zone, referred to as the “iceball”, the tumor, and, nearby anatomical structures (6).

The current cryoablation procedure relies on the interventionalist’s constant qualitative assessment of repeatedly acquired intraprocedural MR images during the 15-min freezing cycle. The interventionalist has to evaluate the coverage of tumor and surrounding normal parenchyma by the slowly growing iceball, while at the same time tending to other procedural needs, such as keeping the skin entry site warm and monitoring patient’s medical status. At times, this may lead to inaccurate or incomplete interpretation of the progress of the ablation. Also, it could cause deficient tumor coverage that would later lead to recurrence, and injury to the surrounding critical structures with subsequent complications (7). Hence, there is a need for a computerized monitoring tool to aid the interventionalist by providing quantitative tumor ablation metrics and three-dimensional (3D) visualization of the iceball.

One key component of such a tool is fast and accurate segmentation of the 3D iceball configuration, which is displayed as an approximately ball-shaped signal void region in MR images. The accuracy of many semi-automatic segmentation tools, such as the ITK-SNAP (www.itksnap.org) (8) and the GrowCut module (9) in 3D Slicer (www.slicer.org) (10), is proportional to the manual operations involved, e.g., the inputting of fiducials and the extent of the segmented region growth, and interactive editing until segmentation is complete. The time required to perform these manual operations makes semiautomatic approaches impractical for intraprocedural segmentation during cryoablation.

Automatic iceball segmentation is challenging, as the abdominal anatomy surrounding the iceball, the probe artifacts, and the iceball itself have similar intensity values. This causes the failure of segmentation methods relying solely on intensity information. The approach of Liu et al (11) using graph cut (12–16) with shape priors (17–19) generated from probe locations (named GC-prior) showed promise. However, directly using the modeled iceball shape based on probe locations in the baseline scan is vulnerable to errors, such as those caused by inaccurate probe localization, imperfection of iceball shape modeling, or misregistration between the baseline scan and images obtained during the freeze cycles due to patient’s movement.

The purpose of this study is to develop an automatic iceball segmentation method that is robust to the predetected probes, so that the overall accuracy of the segmentation can be improved. Different from previous work (11), our segmentation method is initialized with semiautomatically detected 3D cryoablation probes rather than manually labeled 2D probes. The former probe localization method is considered more suitable for a clinical setting. We incorporated a pre-segmentation step using the Fuzzy C-means (FCM) classification paradigm (20), and a shape prior adaptation step using a Fast Marching propagation process (21,22). These steps provide an adapted iceball shape for modeling the priors, as well as initial intensity centroids, both to be input into the graph cut segmentation. In addition, we introduce intensity normalization and noise reduction steps for better segmentation results. Finally, this study reports results based on a wider selection of cases (13 subjects) compared with the two cases reported in (11).

MATERIALS AND METHODS

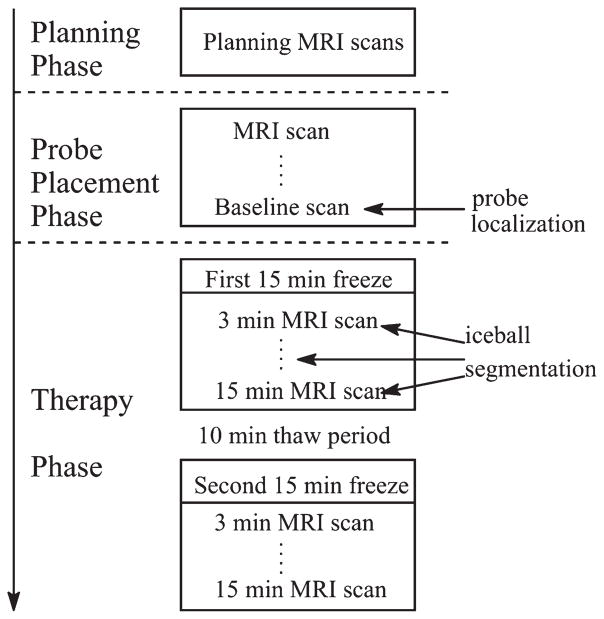
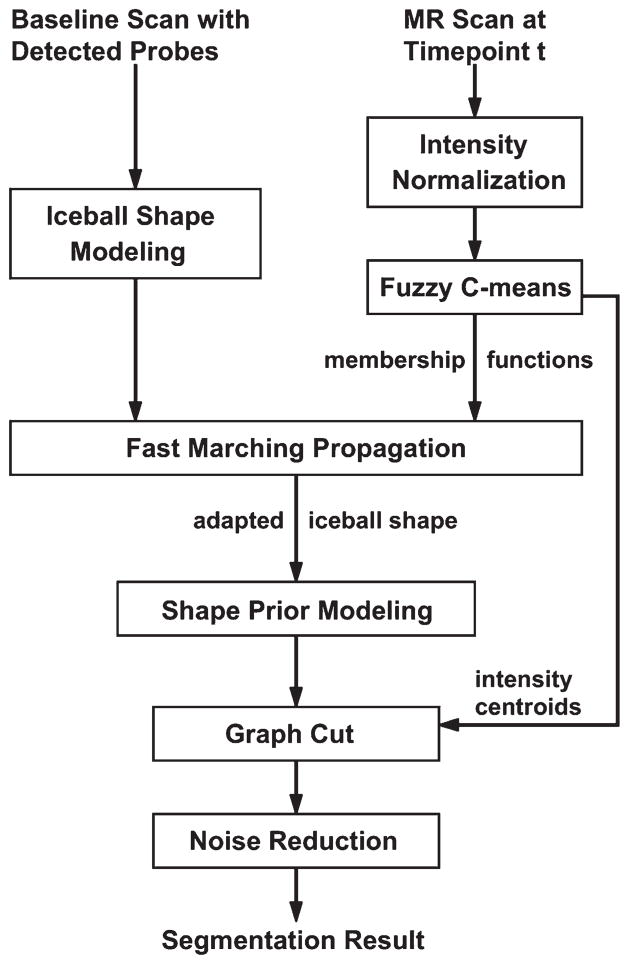
Figure 1 illustrates the standard MRI-guided cryoablation procedure, which includes a Planning Phase, a Probe Placement Phase, and a Therapy Phase. During the Probe Placement Phase, two to five cryoprobes (average three) are sequentially inserted into the patient, interspersed with repeated imaging to confirm proper placement. The last set of scans acquired in this phase is referred to as the “baseline scan”. The Therapy Phase typically consists of two 15-min freeze cycles, separated by a 10-min thaw period. In the first freeze cycle, the iceball starts to grow near the tips of the probes until it fully encompasses the tumor. The Therapy Phase is monitored closely with repeated T2-weighted MRI (3–5 min interval) to assess coverage of tumor by the iceball and to prevent overlap of the ablated volume with adjacent critical structures. Guided by the detected probes in the baseline scan, the iceball segmentation is performed at each time-point during the first freeze cycle (Fig. 1). The general workflow of our segmentation method, named GC-adapted-prior, is shown in Figure 2. Some of the steps in our new method are similar to the method described in (11). These steps are: the initial iceball shape modeling, the shape prior modeling, and the set up of graph cut segmentation framework.

Figure 1.

Flowchart of MRI-guided cryoablation.

Figure 2.

Workflow of our automatic iceball segmentation algorithm.

MRI Protocol and Patients Data

The study was performed under an Institutional Review Board’s approved protocol. Consent was waived because the study used existing patient data retrospectively. Thirteen MRI-guided kidney tumor cryoablation procedures (10M/3F; age 60 ±6) with tumor diameter 3.5 ± 1.2 cm (single tumor for all cases) were investigated. All procedures were performed using a 3 Tesla (T) wide-bore MRI scanner (Siemens Verio; Erlangen, Germany). Spine coils (receive) embedded in the scanner table-top were used in all cases. In addition, a body matrix coil (receive; six channel) was used in 11 cases, and an 11-cm loop coil (receive) was used in 2 cases. The axial T2-weighted breath-hold half-Fourier acquisition single shot turbo spin echo (HASTE) sequence (echo time [TE] 200 ms, 320 × 272 voxels/slice, slice thickness of 3–4 mm, in-plane resolution of 1.0625 mm, no gap between slices, interleaved slice order, 16–20 slices, acquisition time of 16–20 s, 28–34 cm field of view) was used for 12 cases, and 1 case was scanned using the axial T2-weighted turbo spin echo (TSE) sequence (echo train length of 27, TE 106 ms, repetition time [TR] 4100 ms, slice thickness of 4 mm, no gap, 15 slices, acquisition time of 50 s, 28 cm field of view).

Two types of MRI-compatible alloy cryoprobes, the IceSeed and the IceRod from Galil Medical Inc. (Arden Hills, MN) were used, both 17 gauge in diameter and 17.5 cm in total length. An IceRod probe normally creates an ellipsoid-shaped iceball with greater volume than an IceSeed probe. Of the 13 cases, the numbers of cases using 2, 3, 4, 5 probes were 1, 9, 2, 1, respectively; the numbers of cases using IceSeed and IceRod probes were 4 and 9, respectively. During the first 15 min freeze cycle, all cases were scanned every 3 minutes, i.e., at 3-, 6-, 9-, 12-, 15-min timepoints, except for one case which was scanned at 5, 10, 15 min. This yielded a total of 63 timepoints for analysis.

Probe Localization

The cryoprobes inserted into the patient during the Probe Placement Phase are localized in the baseline scan using a semiautomatic approach. Specifically, the 3D probes are first detected automatically using the method described in Liu et al (23). An interventional radiologist then visually assesses the automatic results and manually corrects the failed detections by deleting the failed probe label, substituting two seeds at the tip and the skin entry points of that probe. A 3D line segment representing the corrected probe is then automatically created based on the two seeds. This semiautomatic approach is efficient in effort and time involved, compared with manual segmentation of probes, and is, therefore, designated to be used during the actual procedures, following our early testing. The detected 3D probes in the baseline scan are used to model the iceball shape (Fig. 2).

Iceball Shape Modeling

As illustrated in Figure 3, the shape of an unperturbed iceball generated from a single probe is modeled by a prolate ellipsoid. A voxel p in the image belongs to the ellipsoid if it satisfies:

$$\frac{d_1^2(p)}{{(l/2)}^2}+\frac{d_2^2(p)-d_1^2(p)}{{(L/2)}^2}\le 1$$ [1]

where L and l are the lengths of the major and minor axes of the prolate ellipsoid, respectively. d₁ is the Euclidean distance from p to the major axis of the ellipsoid, and d₂ is the Euclidean distance from p to the centroid of the ellipsoid. The centroid is determined as the point on the probe axis with its distance to the tip of the probe being (L/2-h), where h denotes the distance from the probe tip to one of the farthest points on the ellipsoid’s surface to the centroid (Fig. 3).

Figure 3.

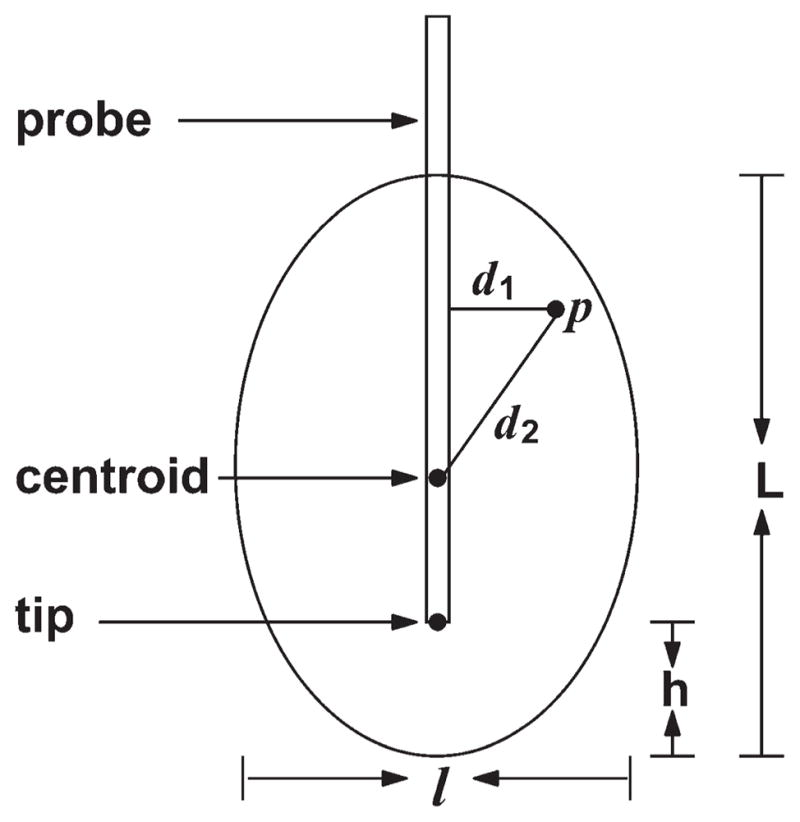
Single iceball shape modeling as a prolate ellipsoid.

We measured and recorded L, l, and h of an evolving iceball at 3, 6, 10, 15 min of freezing from a set of x-ray CT images taken when an individual probe of each type (IceRod and IceSeed) was inserted into an abdominal gel phantom (CIRS Inc., Norfolk, VA). The parameter values at these four timepoints were then fitted with a second order polynomial curve to estimate parameter values for all other timepoints. Finally, the iceball shape generated by all the probes was obtained by combining all individual iceball shapes modeled using Eq. [1], and an example is given in Figure 4b.

Figure 4.

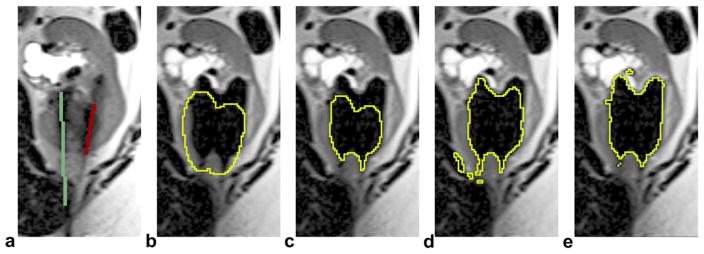
An example of iceball shape adaptation at 6 min of the first freeze (only one slice of the 3D volume is displayed). a: detected probes in the baseline scan (the case has three probes but only two are shown in this slice). b: Initially modeled iceball shape. c: Iceball shape after thinning. d: Iceball shape after growing, the binary image used to generate shape prior. e: Final segmentation using our method. Note that b–d were internal steps of the shape adaptation process but not the segmentation results. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Fuzzy C-means Presegmentation

The HASTE images acquired during freezing are preprocessed with intensity normalization (Fig. 2) to compensate for intensity inhomogeneity between slices. Specifically, intensity values of each slice are normalized to fit the [0, 1] interval. We presegment the normalized HASTE image using the Fuzzy C-means (FCM) technique to estimate a membership function for each voxel that reflects the probability of the voxel belonging to one the two classes, i.e., the iceball and the background. The membership functions drive the adaptation of iceball shape in the next Fast Marching Propagation step. The FCM step also provides intensity centroids—mean intensity values of the two classes, which are used to initiate the final graph cut segmentation.

For images with k desired classes, the FCM classification iterates the following two steps until convergence. First, compute the membership functions given the centroids c_k:

$$u_k(p)=\frac{{(I_n(p)-c_k)}^{2/(1-q)}}{{\mathrm{\sum }}_k{(I_n(p)-c_k)}^{2/(1-q)}}$$ [2]

where q is the fuzziness coefficient. Second, compute the centroids given the membership functions:

$$c_k=\frac{{\sum }_p{u}_k^q(p)·I_n(p)}{{\sum }_p{u}_k^q(p)}$$ [3]

In our case, we used c₁ = 0.33 and c₂ = 0.67 as the initial intensity centroids for the iceball and the background, respectively, to initiate the FCM calculation.

FAST MARCHING PROPAGATION

We perform boundary propagation based on the Fast Marching method (21) to adapt the modeled iceball shape to the actual iceball location in the HASTE image. As shown in Figure 4, the boundary of the modeled iceball shape is propagated through a thinning and a growing processes. The detailed steps are summarized as follows: (A) Extract all the voxels on the (inside) boundary of the modeled iceball shape. (B) Reduce the iceball shape through the thinning process (Fig. 4c): (i) calculate values of the speed function f_th (Eq. [4]) for all voxels inside the iceball; (ii) remove the voxel on the boundary with the lowest value of f_th from the iceball; (iii) add its neighbors belonging to the iceball to the boundary. (C) Expand the iceball shape through the growing process (Fig. 4d): (i) calculate values of the speed function f_gr (Eq. [4]) for all voxels outside the iceball; (ii) add the voxel on the (outside) boundary with the highest value of f_gr to the iceball; (iii) add its neighbors belonging to the background to the boundary.

In both the thinning and growing phases, the process iterates between steps (ii) and (iii) until the stop criterion is met. The stop criterion for the thinning is the instance when 30% of the voxels belonging to the iceball are removed. The stop criterion for the growing step is the point when the number of voxels recovers to equal that of the initial stage. The speed functions, f_th and f_gr, are determined by the membership function of the iceball class, i.e., u₁, resulting from the FCM segmentation. In addition, we add spatial regularization terms to enforce smooth propagation. The regularization terms make the propagation focus on voxels that are closer to the initial boundary in either the thinning or the growing process. The speed functions we use are:

$$\begin{array}{l}{f}_{th}(p)=(1-\mathrm{\alpha })·u_1(p)+\mathrm{\alpha }·exp(-1/T_0(p))\\ f_{gr}(p)=(1-\mathrm{\alpha })·u_1(p)+\mathrm{\alpha }·exp(-T_1(p)/10)\end{array}$$ [4]

where 0 ≤ α ≤ 1 is a parameter to control the relative importance of the regularization terms. T₀ and T₁ are the Euclidean distance transforms to the background and the iceball, respectively. The adapted iceball shape is used to generate the shape priors incorporated into the final graph cut segmentation.

Shape Prior Modeling

The shape prior Pr(O_p) is defined as the probability of a voxel being contained in the iceball based on its location in the adapted iceball shape binary image (Fig. 4d). Pr(O_p) is expressed as:

$$Pr(O_p)\{\begin{array}{l}min\left(\frac{0.5}{max{(T_0)}^2}·T_0^2(p)+0.5,1\right),\text{if}f(p)=1\hfill \\ max\left(-\frac{0.5}{N^2}·T_1^2(p)+0.5,0.001\right),\text{if}f(p)=0\hfill \end{array}$$ [5]

where f(p) is the label function (1 denotes the iceball and 0 denotes the background), T₀ and T₁ are the Euclidean distance transforms to the background and the iceball labels, respectively, and N is a threshhold parameter. The function in Eq. [5] varies between 0.001 and 1, and equals 0.5 for voxels on the boundary of the iceball. Pr(O_p) has the shape of a hyperbolic sine function: it decreases rapidly when the voxel is far from the boundary (both inside and outside the iceball) and changes slowly near the boundary of the iceball. The aim is to let the segmentation be mainly driven by the intensity information in the region around the boundary. When the voxel is a great distance outside the iceball, e.g., T₁(p) ≥ N, its shape prior assumes a minimum value (i.e., 0.001).

Graph Cut Segmentation

The graph cut technique optimally partitions an n-dimensional image with two voxel labels, as either the “object” (O) or a part of the “background” (B), by means of the minimization of a Markov Random Fields type of energy:

$$E(f)=\mathrm{\lambda }·{\sum }_p{R}_p(f(p))+{\sum }_{p,q}{B}_{p,q}(f(p),f(q))$$ [6]

Here f(p) is the voxel label O or B. R_p(·) is the regional term, interpreted as the penalty of assigning a voxel to a label. B_p,q(·,·) is the boundary term, representing the penalty for discontinuity between neighboring voxels (p, q). λ is a weight parameter (i.e., λ > 0).

The regional term is often defined as the negative log-likelihood of a voxel’s fit into predetermined intensity histograms:

$$\begin{array}{l}{R}_p(O)=-lnPr(I(p)\mid O)\\ R_p(B)=-lnPr(I(p)\mid B)\end{array}$$ [7]

where I(p) is the intensity value at p. A common expression for the boundary term is:

$$B_{p,q}(f_p,f_q)=\{\begin{array}{cc}exp\left(-\frac{{(I(p)-I(q))}^2}{2{\mathrm{\sigma }}^2}\right)·\frac{1}{\text{dist}(p,q)}& \text{if}f(p)\ne f(q)\\ 0& \text{if}f(p)=f(q)\end{array}$$ [8]

where dist(p,q) is the Euclidean distance between p and q, and σ is a scale parameter to control the segmentation results. The minimum of energy E in Eq. [6] corresponds to the optimum segmentation, and can be achieved by means of applying the min-cut/max-flow algorithms (13).

Several previous studies have incorporated shape priors into the standard graph cut formulation, e.g., by adding an additional function representing shape information to the regional term (18):

$$\begin{array}{l}{R}_p(0)=-(1-\mathrm{\mu })·\text{In}Pr(I(p)\mid O)-\mathrm{\mu }·\text{In}Pr(O_p)\\ R_p(B)=-(1-\mathrm{\mu })·\text{In}Pr(I(p)\mid B)-\mathrm{\mu }·\text{In}Pr(B_p)\end{array}$$ [9]

where 0 ≤ μ≤ 1 is a parameter to adjust the relative shape influence. In our algorithm, the shape prior Pr(O_p) is given by Eq. [5] and Pr(B_p) = 1 − Pr(O_p). In accordance with the boundary term (Eq. [8]), the likelihood in the regional term (Eq. [9]) is defined to be:

$$Pr(I(p)\mid k)=exp\left(-\frac{{(I(p)-c_k)}^2}{2{\mathrm{\sigma }}^2}\right)$$ [10]

where c_k is the intensity centroid for class k = 1,2 (O,B) obtained in the FCM segmentation step.

Finally, to reduce noise and fill holes resulting from graph cut segmentation, we applied SUSAN noise reduction (24) to the binary image of the segmented ice-ball. The SUSAN algorithm uses nonlinear filtering to reduce noise while preserving the edges and corners.

Implementation and Evaluation

The graph cut segmentation with shape priors was implemented using C++ with a Matlab (MathWorks; Natick, MA) interface, modified from a freely-available graph cut library (http://cbia.fi.muni.cz/projects/graph-cut-library.html), which implements the standard graph cut segmentation method provided by (12,13). The other parts of our algorithm were implemented using Matlab, including generation of the adapted shape priors. Segmentations were performed on a commercially available workstation (Dell T7500n; Intel Xeon CPU X5660, 6 × 2.8 GHz, 12 GB RAM, and Red Hat Enterprise Linux 6.0) with empirically determined parameter values: N = 20, q = 2, α = 0.3, λ = 2, σ= 0.08, μ = 0.9.

An expert evaluator manually segmented (mean execution time 5 min) the 3D iceball volumes using ITK-SNAP (www.itksnap.org) (8) for all the images. The automatically segmented iceball volumes were compared with the manual results using the Dice Similarity Coefficient (DSC) (25) as the metric to quantify image segmentation quality. The DSC varies between 0 and 1, and a greater value indicates a greater degree of similarity of the two segmentations being compared. For further analysis, we tested our GC-adapted-prior algorithm and the algorithm without the adaptation of shape priors, i.e., generating shape priors directly from the initially modeled iceball shape, as the previous GC-prior method. We also segmented the iceball volumes using a semiautomatic tool, the GrowCut image segmentation module (9) based on region growing method, in 3D Slicer (www.slicer.org) (10), and compared its results with the manual results using the DSC. To initiate Grow-Cut segmentation, an evaluator manually input fiducials, separately labeling the interior and exterior of the iceball (mean execution time 40 s).

RESULTS

Table 1 shows results comparing three different methods for iceball segmentation: our GC-adapted-prior method; the approach without the adaptation of shape priors, i.e., the GC-prior method; and, the semiautomatic GrowCut segmentation tool. The results are grouped based on five timepoints of the first freeze cycle. Because 1 of the 13 cases only had three time points (5, 10, 15 min), we assigned its 5- and 10-min results to the 6- and 9-min timepoints in Table 1. As shown in Table 1, both GC-adapted-prior and GC-prior display more accurate segmentation results than GrowCut results, with the average DSC of the GC-adapted-prior method higher than GC-prior at all 5 timepoints.

Table 1.

Mean, Minimum, and Maximum Dice Similarity Coefficient (DSC) for Each Segmentation Method, Compared With Manual Segmentations, at Five Timepoints During the First Freeze Cycle

	3 Min	6 Min	9 Min	12 Min	15 Min
GC-adapted-prior
Mean	0.88	0.92	0.92	0.93	0.93
[min, max]	[0.77, 0.94]	[0.89, 0.95]	[0.9, 0.95]	[0.88, 0.95]	[0.90, 0.95]
Least accurate*	0.81	0.90	0.91	0.91	0.90
GC-prior
Mean	0.85	0.89	0.90	0.92	0.92
[min, max]	[0.73, 0.92]	[0.79, 0.93]	[0.83, 0.94]	[0.86, 0.94]	[0.87, 0.95]
Least accurate	0.78	0.84	0.85	0.88	0.88
GrowCut
Mean	0.75	0.80	0.83	0.85	0.82
[min, max]	[0.34, 0.92]	[0.56, 0.92]	[0.52, 0.93]	[0.68, 0.93]	[0.70, 0.92]
Least accurate	0.50	0.59	0.65	0.74	0.73

^*The least accurate result represents the mean of the three smallest DSC values in a specific group.

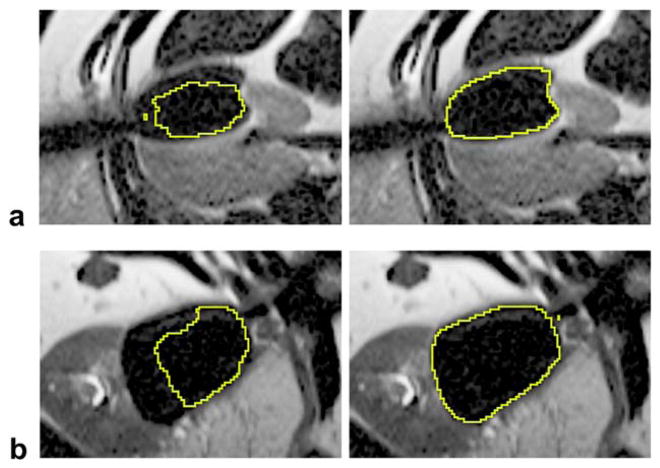
In terms of robustness, GC-adapted-prior produces more accurate segmentation results than GC-prior for those cases that are “hard to segment,” especially for earlier timepoints—3, 6, 9 min. This observation is based on the average DSC of the three least accurate cases for each group, which is given in Table 1. Here, the cases that are “hard to segment” refer to those with inaccurate probe localization, such as the cases shown in Figure 5, which compared segmentation results between GC-adapted-prior and GC-prior. The figure suggests that the GC-adapted-prior method is capable of producing accurate segmentations even though the initially predicted iceball shape deviated significantly from the final computed results. An example showing the tumor location and the propagation of the segmented iceball using the GC-adapted-prior method is given in Figure 6.

Figure 5.

Segmentation results using GC-adapted-prior (right column) and GC-prior (left column). a: A case with three probes at 3 min of the first freeze; DSC = 0.94 for GC-adapted-prior; DSC=0.83 for GC-prior. b: A case with four probes at 6 min of the first freeze; DSC = 0.95 for GC-adapted-prior; DSC = 0.79 for GC-prior.

Figure 6.

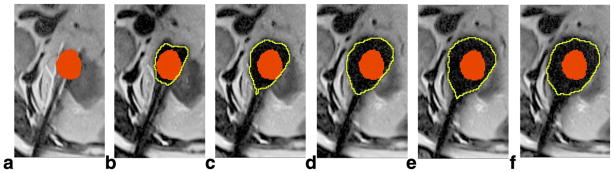
Segmentation results using GC-adapted-prior for a case with four probes. a: Manually labeled tumor (red) by an expert interventionalist in the baseline scan. b–f: Automatically segmented iceball (yellow contour) at 3, 6, 9, 12, and 15 min of the first freeze cycle; the tumor label is transferred and overlaid on each image, as we assume only slight misregistration occurs between these images and the baseline scan.

The mean DSC of the total 63 iceball segmentations using GC-adapted-prior is 0.92 ± 0.03. We performed a t-test between the GC-adapted-prior DSCs and the GC-prior DSCs of the 63 segmentations, and the two-tailed P = 0.026 indicated significant difference between the means of the two groups. Using GC-adapted-prior, the groups of cases with 2, 3, 4, and 5 probes have mean DSCs of 0.92, 0.91, 0.94, and 0.93, respectively, which suggests that the number of probes involved in the procedure has no apparent influence on the accuracy of the segmentation results. Mean execution time of the entire algorithm is approximately 20 s for images of dimension 320 × 272 × 18. The computational speed could be further accelerated if all algorithms are implemented using the compiled language rather than the script language of Matlab.

DISCUSSION

This work presents results supporting the feasibility of using Fast Marching propagation to create adapted shape priors for the guidance of image segmentation. Besides the graph cut segmentation method, this type of approach is applicable to other state-of-the-art segmentation frameworks, such as active contours (26), level sets (27), and the random walker method (28). The thinning and growing steps in the Fast Marching propagation can be used iteratively to segment multiple regions, e.g., in brain segmentation (29). The spatial regularization terms that we added to the speed functions are capable of producing a smoothly propagating frontier in proximity to the initial boundary.

We restrict our experiments to the first freeze cycle of the cryoablation, because this cycle is critical for the effectiveness and safety of the procedure. During this phase, the iceball grows to fully cover the tumor and a margin of normal tissue beyond the tumor. After a 10-min thaw period, the second freeze cycle usually does not reveal significant change in the maximum iceball volume reached, and is therefore less valuable for testing segmentation methods.

The performance of automated segmentation for earlier timepoints during cryoablation is worse than later timepoints. This is likely due to the following reasons. At earlier timepoints, the iceballs generated from individual probes have not fully coalesced, and segmentation results are more vulnerable to errors caused by the initialization, such as detected probe locations, iceball shape modeling, or misregistration. Later in the procedure, the iceball shape during propagation may be altered by perfusion, the presence of nearby vessels, tissue heterogeneity, and other unpredictable sources that distort tissue. These sources would necessarily have a larger effect on the iceball segmentation for earlier timepoints, because the affected volume during that period can represent a greater fraction of the relatively smaller iceball volume.

It is worth mentioning that our segmentation approach is capable of handling cases with multiple tumor masses (either treated individually or simultaneously), although all 13 cases reported in this study had only one tumor. The approach can be extended for treatment of other tumor types such as those in the liver, lung, adrenal gland bone, and soft tissues, or for use under other guidance modalities such as CT or positron emission tomography/CT.

One limitation of our method is that it can only be applied to cases lacking severe misregistration between the baseline scans and the scans acquired at each timepoint during freezing. In our study tests, we excluded two cases with obvious misregistration due to motion artifacts caused by either patient’s breathing during scanning, or by body movements during the therapy. However, image registration techniques (30,31) could be applied to align the baseline scan with the scans acquired during the freeze period, so that the probe locations after registration would be more accurate, allowing analysis of cases with a greater degree of motion.

In conclusion, we have presented an automatic ice-ball segmentation method that is based on the graph cut image segmentation framework, and incorporated with adapted shape priors generated from the predetected probe locations. The method demonstrated high accuracy and robustness for fast automatic segmentation of the iceball in intraprocedural images acquired during the freezing cycles of MRI-guided cryoablation. The proposed algorithms and related software can be immediately applied in practical use. By comparing the 3D segmented iceball volume to the tumor volume segmented initially, ablation metrics can be calculated and displayed in real-time for quantitative monitoring of ablation during the therapy.