Abstract
Background
Both high and low pathogenic subtype A avian influenza remain ongoing threats to the commercial poultry industry globally. The emergence of a novel low pathogenic H7N9 lineage in China presents itself as a new concern to both human and animal health and may necessitate additional surveillance in commercial poultry operations in affected regions.
Methods
Sampling data was simulated using a mechanistic model of H7N9 influenza transmission within commercial poultry barns together with a stochastic observation process. Parameters were estimated using maximum likelihood. We assessed the probability of detecting an outbreak at time of slaughter using both real-time polymerase chain reaction (rt-PCR) and a hemagglutinin inhibition assay (HI assay) before considering more intense sampling prior to slaughter. The day of virus introduction and R0 were estimated jointly from weekly flock sampling data. For scenarios where R0 was known, we estimated the day of virus introduction into a barn under different sampling frequencies.
Results
If birds were tested at time of slaughter, there was a higher probability of detecting evidence of an outbreak using an HI assay compared to rt-PCR, except when the virus was introduced <2 weeks before time of slaughter. Prior to the initial detection of infection Nsample = 50 (1%) of birds were sampled on a weekly basis once, but after infection was detected, Nsample = 2000 birds (40%) were sampled to estimate both parameters. We accurately estimated the day of virus introduction in isolation with weekly and 2-weekly sampling.
Conclusions
A strong sampling effort would be required to infer both the day of virus introduction and R0. Such a sampling effort would not be required to estimate the day of virus introduction alone once R0 was known, and sampling Nsample = 50 of birds in the flock on a weekly or 2 weekly basis would be sufficient.
Electronic supplementary material
The online version of this article (doi:10.1186/1471-2334-14-427) contains supplementary material, which is available to authorized users.
Keywords: H7N9, Influenza, Surveillance, R0, Poultry
Background
Outbreaks of avian influenza (AI) remain an ongoing threat to the commercial poultry industry globally. Such outbreaks can result in substantial economic losses, due to the cost of implementing control measures and the financial loss associated with culling infected flocks [1]. In the Netherlands a highly pathogenic AI (HPAI) outbreak in 2003 led to the culling of 30 million animals resulting in direct costs of 250 million euros [2]. In the United States (US) outbreaks of low pathogenic AI (LPAI), once detected can also cost millions of dollars to control and contain [3–5].
Birds infected with LPAI subtypes (e.g. H9N2, H6N2, H7N9) often present with few or no symptoms, making detection of LPAI particularly challenging. Although LPAI does not present itself as a serious concern to animal health, LPAI subtypes H5 and H7 have been shown to evolve by mutation into highly pathogenic avian influenza (HPAI) [6–8]. Therefore higher numbers of LPAI cases increase the chance that mutations associated with HPAI will arise. Whilst outbreaks of AI in commercial poultry production systems in the developed world are infrequent, an average of two to three cases of H5/H7 are reported in the US annually, in addition to other LPAI subtypes, hence AI outbreaks remain an on-going threat to the commercial poultry production industry.
The emergence of a novel H7N9 LPAI subtype in China [9] presents itself as a serious concern for human health in addition to the risks to the commercial poultry industry. Over 400 human infections have been reported in China, as of June 2014 [10] with a case fatality ratio upon admission to hospital for humans estimated to be 32-36% [11, 12] for the first wave of infections, with estimates from the second wave also within this range [13]. However, infected birds are not reported to have exhibited symptoms [14]. The continuous infection events (spill-over) from birds to humans increase the chance that reassortment with human endemic viruses will occur, or that human adaptation mutations will become fixed. Since the detection of this virus a number of subsequent reassortment events have been reported [15, 16], suggesting that this novel lineage may display a high propensity to reassort. Therefore, identification and control of H7N9 infection within the commercial poultry sector is of paramount importance for human and animal health.
There are currently believed to be at least 17 billion commercial chickens worldwide [17], providing a very large susceptible population for AI subtypes to circulate in. Therefore regular and long term surveillance is strongly encouraged and is the most effective way of controlling and identifying AI in poultry [18]. One important aspect of this control policy is the systematic surveillance and diagnosis of infection [19]. Two tests are commonly used to identify whether birds have been infected: real-time polymerase chain reaction (rt-PCR) [20] and the hemagglutinin inhibition assay (HI). rt-PCR identifies the causative agent of infection and detects current infection by detecting the presence of viral RNA. HI assays test for the presence of antibodies to the hemagglutinin (HA) antigen [21], and hence detect evidence of past infection.
It is unfeasible to test all birds within a barn on a daily basis; therefore optimal sampling strategies need to be considered to detect evidence of a LPAI outbreak and infer parameters of epidemiological interest. Mechanistic models can be used to successfully infer epidemiological events of interest [5], and thus improve surveillance and enable effective response strategies in the event of an outbreak. Models can be used to infer important events such as the day of the virus introduction in an outbreak setting, which is crucial for preventing onwards transmission of infection and identifying the source of infection. For example, Bos et al[22] used mortality data from a HPAI outbreak of H7N7 in the Netherlands to estimate the day of virus introduction into flocks. However given mortality does not occur due to infection during LPAI outbreaks, new methodology is required.
The ability to detect infection within a flock depends on a number of factors including; the type of test used to identify infection, the frequency of sampling, the day of virus introduction (Ts) and the within-flock transmissibility of the strain, R0 (the average number of secondary cases generated by an infectious primary case). There is a complex interaction between these parameters, and we explore how they can alter the chance of detecting infection in a barn. We first evaluated the probability of detecting evidence of an avian influenza H7N9 outbreak at time of slaughter across a range of values of R0 and Ts using two different available tests. Secondly, we tested our ability to estimate R0 and Ts when sampling birds is performed on a weekly basis. Such estimation would be useful in the event of a novel outbreak where little was known about the pathogen. Lastly we investigated how different sampling frequencies affect the ability to correctly estimate the Ts into a barn under a range of different R0 values. Such inference would be useful if an outbreak was or had occurred in a neighbouring area (when it would be reasonable to assume R0 was already known). A deterministic mathematical model of H7N9 transmission with a stochastic observation process was used to investigate these three aims.
Methods
Mathematical model of LPAI transmission in a commercial poultry setting
We developed an extension of the deterministic susceptible, exposed, infectious, recovered model (SEIR), with a time lag after completion of the infectious period before birds could be detected as recovered and sero-positive for infection; we called this the seroconverting class (C). A flow diagram of the system is illustrated in Figure 1. All parameter definitions and values are defined in Table 1.
Figure 1.
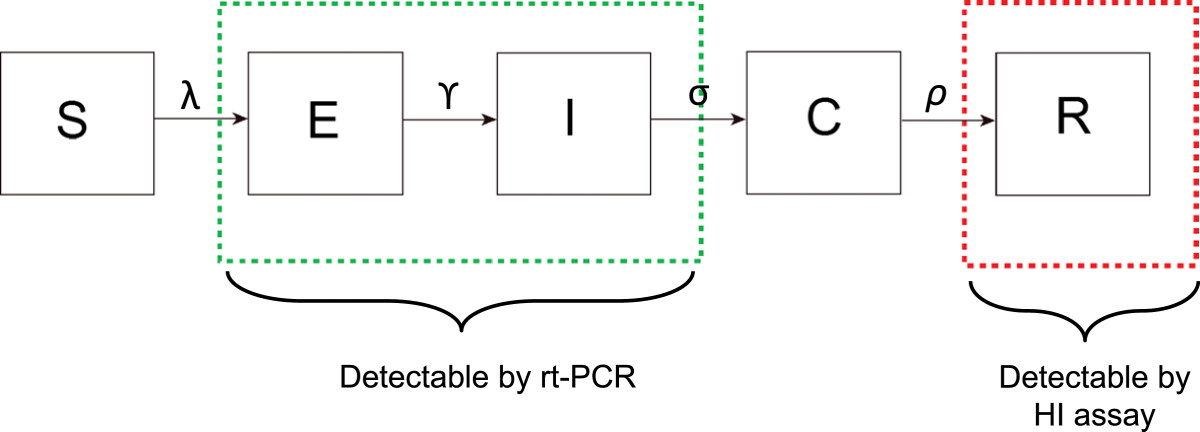
Flow diagram of the SEIR model structure. Boxes around compartments indicate which states will result in a positive test for the rt-PCR test and HI assay.
Table 1.
Table of parameters used in the model
| Parameter | Description | Value |
|---|---|---|
| R 0 | Basic reproductive | 3, 5, 7, 10 |
| number | ||
| γ | Mean latent | 2* [27] (Pantin-Jackwood, |
| period (days) | personal communication) | |
| 1/(γ/no) | Average duration spent | 0.4 |
| in each compartment | ||
| during the latent | ||
| period (days) | ||
| σ | Mean infectious | 6* [27] (Pantin-Jackwood, |
| period (days) | personal communication) | |
| 1/(σ/no) | Average duration | 1.2 |
| spent in each | ||
| compartment during | ||
| the infectious | ||
| period (days) | ||
| ρ | Mean time to | 8 [24] |
| sero-conversion | ||
| post infection (days) | ||
| 1/(ρ/nc) | Average duration | 0.8 |
| spent in each | ||
| compartment during | ||
| the sero-converting | ||
| period (days) | ||
| Sensitivity (ϕ) | Sensitivity of | 95% [20, 28, 29] |
| rt-PCR test | ||
| Specificity | Specificity of | 100 % [20, 28, 29] |
| rt-PCR test | ||
| Sensitivity (η) | Sensitivity of | 86% [30–32] |
| HI assay | ||
| Specificity | Specificity of | 100 % [30–32] |
| HI assay | ||
| N | Population size | 5000* |
| no | Number of | 5 |
| compartments for | ||
| exposed and | ||
| infectious periods | ||
| nc | Number of seroconverting | 10 |
| compartments | ||
| Start time (T s) | Time infection | 0, 7, 20, 40 |
| is introduced (days) |
Values of parameters that have an *next to them indicate uncertainty in these values, these values were varied in the sensitivity analysis.
A flock of N susceptible poultry are moved into the barn once every 8 weeks, this cohort of birds remain within the barn for the full 8 weeks until they are transported. Here we follow one cohort over the 8 week period, i.e. all birds enter and leave together. At the start all birds are assumed to be susceptible and previously unexposed to the virus. Birds experience a force of infection λ(t), which depends on the effective contact rate β, (i.e. the mean number of birds a bird comes into contact with and transmits to per unit time), and I (t), the total number of infectious birds in the barn at each time point. Therefore λ(t), the force of infection experienced by a susceptible bird in the barn per unit time can be written as:
| 1 |
Once a bird has come into contact with virus it is classified as exposed. Exposed birds are not infectious, and have a mean latent period γ. Both exposed and infectious birds are assumed to be asymptomatic. Birds have a mean asymptomatic infectious period σ, following which birds progress into a seroconverting class where they no longer transmit infection. The seroconverting class represents the time lag that occurs as antibodies are developed to infection prior to the birds being detectable as sero-positive and recovered. After this period birds become immune to re-infection with a mean duration ρ and move to the R class. We divide the exposed (E), infectious (I) and sero-converting (C) classes into 5, 5 and 10 compartments respectively to reduce the variance of the time spent in each compartment [23]. This ensures that the majority of birds progress through each class at a rate which ensures that under 10% of birds seroconvert 14 days post infection but that 90% have converted 21 days post infection [24].
The system is governed by the following series of differential equations:
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
We infer the value of R0 from the model by estimating the transmission rate β, using the following relationship.
| 10 |
Testing for infection or antibodies
At a defined time point infection was introduced into the barn. This represents the external introduction of virus, either from contact with other infectious birds nearby or fomites.
We used the transmission model to simulate collected surveillance data. We assumed Nsample = 50 (1%) of birds, were sampled randomly from the barn at a given time point (i) and tested for infection or the presence of antibodies. The number of positive birds sampled at a given time point is a random variable from the following binomial distribution:
| 11 |
E and I birds test positive for infection with an rt-PCR test, therefore the probability of identifying a positive bird in the sample is:
| 12 |
where ϕ is the sensitivity of the rt-PCR test. Only R birds test positive for infection using an HI assay. Therefore the probability of identifying a previously infected bird in the sample is given by:
| 13 |
where η is the sensitivity of the HI assay.
Detecting evidence of infection at time of slaughter
We consider a surveillance system for detecting present or past infection at the time of slaughter. This requires detection of at least 1 bird in our Nsample = 50 sample, the probability can be written as follows:
| 14 |
Simulating sampling data
We chose to only consider testing scenarios using the rt-PCR test, as this test is more suitable for real-time detection of outbreaks than the HI assay.
For the first scenario to estimate Ts and R0 we simulated sampling data on a weekly basis using an rt-PCR test for four different introduction times: i) day 0, ii) day 7, iii) day 20, and iv) day 40. A reactive testing strategy was simulated whereby Nsample = 50 birds were sampled if no infection had previously been detected, with an increase to Nsample = 2000 following detection of infection.
For the second scenario to estimate the Ts with a known R0 we simulated sampling data using the rt-PCR test for four different introduction times: i) day 0, ii) day 7, iii) day 20, and iv) day 40 and for 4 different values of R0: 3, 5, 7 and 10. We assumed all birds would be tested for infection upon entry and exit to the barn (at the end of 8 weeks). We considered several intermediate sampling regimes to supplement this, where birds were additionally sampled once at week 4, three times at week 2, 4 and 6 and an additional 7 times between week 1-7.
Parameter estimation
For each scenario we fitted the deterministic model to 100 different sets of stochastic observations. Model parameter values are given in Table 1.
When estimating R0 and Ts we assumed all other parameters were known. When investigating the effect of different sampling frequencies on the ability to estimate the Ts only we assumed the other parameters were known (including R0). For both scenarios parameters were estimated by maximising the product of the binomial likelihood across the time series of observed data using “optim” in R [25]. The likelihood of observing the sampling data at a given sampling time point i for a given set of model parameters is defined as:
| 15 |
where Nsample is the number of samples taken at that time point, Idata (the number of positive tests) and P, is the probability of a positive test (equation 12). To initialise the optimisation we performed a Markov Chain Monte Carlo (MCMC) search of the parameter space. For each chain we used 500 MCMC iterations to explore the likelihood surface when 1 parameter was estimated and increased to 5000 MCMC iterations for each chain when 2 parameters were estimated. Two Markov Chains with different starting conditions were simulated to ensure the parameter space was fully explored and to avoid the problem of chains becoming stuck in local optima.
We present the mean estimated Ts (and R0 where applicable) across 100 stochastic observations for each scenario and the mean 95% confidence intervals across the 100 observations for each scenario (Table 2 and Table 3). Profile likelihoods were estimated through the MCMC search of the parameter space, and confidence intervals were calculated from the profile likelihood, assuming the likelihood surface was approximately chi-squared distributed [26]. Where greater than one cluster was present (i.e. parameter sets with similar maximised likelihoods) both sets are presented. Confidence intervals were calculated for the clusters for which the maximum likelihood estimated (MLE) value was obtained and both are presented in Table 2.
Table 2.
Mean estimated T s and R 0 , from 100 stochastic realisations using an rt-PCR test
| Day of entry | R 010 | R 07 | R 05 | R 03 |
|---|---|---|---|---|
| 0 | -0.2 (-1.7, 1.2) | -0.6 (- 7.8, 1.8) | -0.8 (-2.8, 1.5) | -0.3 (-1.4, 0.5) |
| 10.5 (9.6, 12.0) | 7.2 (6.9, 7.8) | 5.0 (4.9, 5.8) | 3.0 (2.9, 3.1) | |
| 7 | 7.1 (5.9, 8.5) | 7.1 (5.8, 8.8) | 7.0 (6.1, 7.8) | 6.8 (5.6, 8.1) |
| 10.5 (9.0, 12.0) | 6.9 (6.3, 8.1) | 5.0 (4.8, 5.21) | 2.9 (2.8, 3.1) | |
| 20 | 20.1 (18.3, 22.1) | 20.0 (18.9, 21.0) | 20.0 (18.1, 20.9) | 19.4 (18.5, 21.9) |
| 10.5 (8.4, 13.8) | 6.9 (6.3, 7.5) | 4.8 (4,5, 5.1) | 3.0 (2.9, 3.2) |
Mean lower and upper 95% confidence intervals for each estimate are indicated in brackets. The upper estimate in each row refers to the estimate of T s and the lower is the estimate of R 0.
Table 3.
Mean estimated day of virus introduction into the barn, across 100 simulated testing observations
| Day of entry | R 0 | Weekly sampling | 2 weekly sampling | 4 weekly sampling |
|---|---|---|---|---|
| Day 0 | ||||
| 10 | 0.0 (-0.6, 0.5) | 0.1 (-0.7, 0.7) | 0.0 (-2.3, 1.7) | |
| 7 | 0.0 (-0.7, 0.6) | 0.0 (-1.1, 0.9) | -0.1 (-1.7, 1.5) | |
| 5 | 0.0 (-0.80, 0.9) | -0.3 (-1.8, 1.1) | -1.1 (-3.0, 1.1) | |
| 3 | 0.1 (-1.4, 1.4) | 0.0 (-2.3, 1.8) | -0.2 (-2.8, 2.5) | |
| 3 2nd cluster | NA | NA | 37.6 (26.7 - 40.0) | |
| Day 7 | ||||
| 10 | 7.0 (6.3, 7.5) | 7.3 (6.0, 8.5) | 7.2 (5.8, 8.6) | |
| 7 | 7.0 (6.4, 7.6) | 6.0 (4.9, 7.3) | 2.6 (1.0, 4.5) | |
| 5 | 7.0 (6.1, 7.9) | 7.0 (5.9, 7.9) | 7.2 (5.3, 8.8) | |
| 3 | 6.9 (5.3, 8.3) | 7.0 (5.5, 9.0) | 6.6 (4.0, 9.5) | |
| 3 2nd cluster | NA | NA | 21.6 (17.1, 25.3) | |
| Day 20 | ||||
| 10 | 20.0 (19.4, 20.4) | 20.2 (18.9, 21.5) | 18.3 (16.0, 21.0) | |
| 10 2nd cluster | NA | NA | 46.6 (44.1, 50.0) | |
| 7 | 20.0 (19.4, 20.9) | 19.1 (17.8, 20.3) | 18.0 (15.3, 21.3) | |
| 7 2nd cluster | NA | NA | 43.3 (40.5, 46.0) | |
| 5 | 20.0 (18.9, 20.7) | 20.0 (19.0, 20.9) | 19.5 (18.1, 20.8) | |
| 5 2nd cluster | NA | NA | 34.5 (32.6, 36.6) | |
| 3 | 20.1 (18.1, 22.2) | 20.1 (17.7, 23.2) | 19.7 (15.4, 23.4) | |
| Day 40 | ||||
| 10 | 40.0 (39.4, 40.7) | 40.0 (39.9, 40.8) | 36.0 (34.7, 37.1) | |
| 10 2nd cluster | NA | NA | -9.56 (-10.0, -8.5) | |
| 7 | 39.8 (38.1, 42.0) | 40.0 (38.5, 41.5) | 40.0 (38.5, 41.4) | |
| 5 | 40.0 (36.7, 42.8) | 39.7 (36.5, 42.8) | 40.1 (36.7, 45.2) | |
| 5 2nd cluster | NA | NA | 13.3 (11.6, 15.0) | |
| 3 | 37.6 (30.2, 43.7) | 35.0 (28.2, 42.7) | 33.5 (28.0, 40.8) |
Mean lower and upper 95% confidence intervals for each estimate are indicated in brackets. The second optima that was observed with reduced sampling is referred to as 2nd cluster.
Parameter values
The amount of virus shed, the durations of virus shedding and the infectious dose received upon an infectious challenge will vary and will be host specific, however we generalised values from the experimental data [27]. We assumed the latent period to be 2 days, based on a study which detected the shedding of H7N9 virus using oropharyngeal swabs in 10/11 chickens 2 days post inoculation (DPI) [27] (Pantin-Jackwood, personal communication), (although swabs were not taken between 0 and 2 DPI). We assumed the infectious period to be 6 days, based on the same study, as 7/8 birds were shedding detectable virus 8 DPI, however only 1/8 chickens was shedding virus 11 DPI [27] (Pantin-Jackwood, personal communication). The full experiment is detailed in Pantin-Jackwood et al.[27].
We assumed a fixed sensitivity and specificity of the rt-PCR test. The sensitivity estimate was based on a study where detection probabilities of 95% or greater were achieved for the HA(I) and NA(I) assays at RNA concentrations 7.0 and 7.8 copies per reaction, respectively. Although the confidence internals around the RNA concentrations to achieve this sensitivity were wide [20]. Specificity of the test was assumed to be 100%, as no non-specific cross reactivity of other oligonucleotides was reported. These values are similar to those published in other studies for the detection of H7 viruses [28, 29].
For the HI assay we assumed that the test had a very high specificity of 100% but a much lower sensitivity of 86%. At the time of writing no quantifiable data on the sensitivity and specificity of the H7N9 HI assay in avian hosts was available. We therefore used information on the sensitivity and specificity of HI assays for other avian subtypes [30] along with data available on the sensitivity and specificity of an antibody neutralisation assay [31] and an HI assay when testing human sera for antibodies to H7N9 infection [32].
Sensitivity analysis
We conducted sensitivity analyses on 3 key parameters for which uncertainty surrounded the value used in the baseline model when estimating Ts in isolation, we performed sensitivity analysis on the following 3 parameters barn size, and the latent and infectious periods (results are presented in Additional file 1). It is likely barn size will vary across farms, so it was important to test our ability to estimate the day of virus introduction with variable barn sizes. The latent and infectious periods were based on observations from laboratory experiments, on a relatively small number of birds, and where heterogeneity between birds in the duration of virus shedding was observed [27], it was therefore important to explore variation in these parameters. Equally previous studies have shown that the duration of the latent period and infectious period can affect ones ability to detect virus in a barn [22, 33].
To investigate the model’s ability to estimate Ts with different barn sizes, we took an additional five different barn flock sizes, 500 birds, 2000 birds, 10,000 birds, 20,000 birds and 100,000 birds, while sampling Nsample = 5, Nsample = 20, Nsample = 100, Nsample = 200 and Nsample = 1000 birds from the flock at each sampling point, for each barn size respectively. To investigate how the misspecification of the duration of the latent period affected our ability to estimate the Ts, we varied the value of the latent period used in the baseline model in the range 1-4 days. To investigate whether our estimation of Ts was sensitive to the duration of the infectious period, we tested values in the plausible range 3-12 days. All sensitivity analysis is presented within Additional file 1.
Results
Probability of detecting an outbreak at time of slaughter
We estimated the probability of detecting at least one infected bird at time of slaughter (56 days after birds enter the barn) using two different tests, rt-PCR and an HI assay. A non-linear relationship was observed between the probability of detecting evidence of an outbreak at the time of slaughter, R0 and the day of virus introduction (Figure 2) when using either the rt-PCR test or the HI assay.
Figure 2.
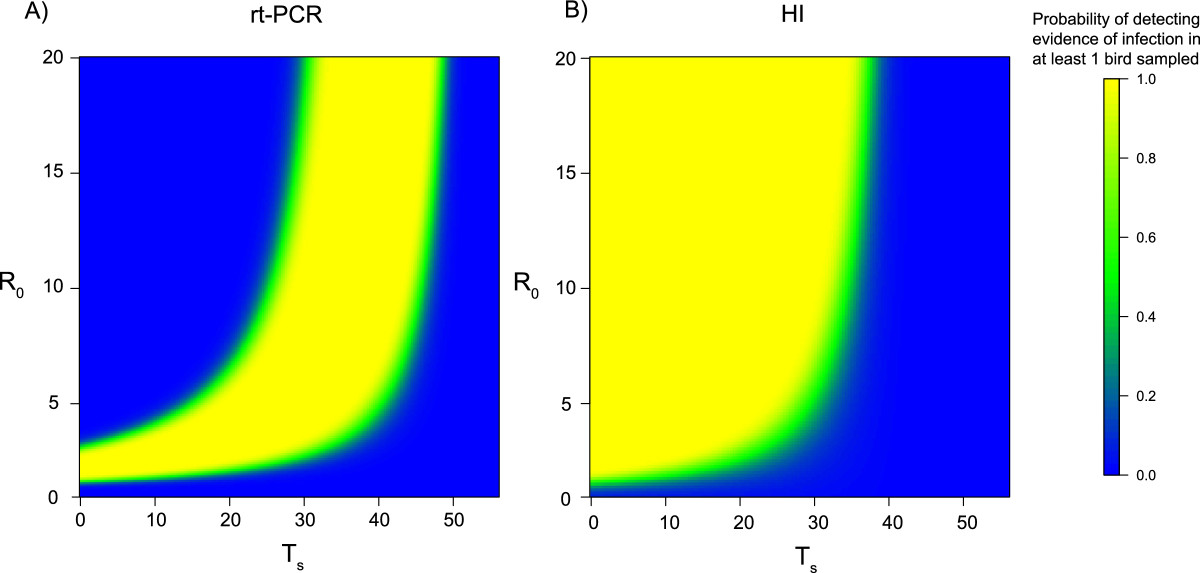
The probability of detecting evidence of infection at time of slaughter with different basic reproduction numbers ( R 0 ) and days of virus introduction T s . A) The probability of detecting at least 1 infected bird at time of slaughter (day 56) using an rt-PCR test, when 1% of the flock is sampled. B) The probability of detecting at least 1 infected bird at time of slaughter (day 56) using an HI assay, when 1% of the flock is sampled. For both panels, as the probability approaches 1 the greater the chance there is of detecting evidence of infection (yellow). As the probability approaches 0 there is no chance of detecting evidence of infection (blue).
The rt-PCR test had a high probability of detecting infected birds at the time of slaughter if Ts was between 20 and 40 days after birds enter the barn, across all values of R0 (Figure 2A). A high probability of detection for earlier Ts values was only apparent when R0 was less than 5, when the virus was likely to still be circulating at the time of slaughter. For the HI assay (Figure 2B) there was a high probability of detecting H7N9 antibodies at the time of slaughter across a range of Ts values (0 - 30 days), especially when R0 was high. However, if the Ts was 30 days or later, the probability of detecting infection was very close to 0, because of the 8 day period after infection required for birds to seroconvert. The probability of detecting at least one infected bird in the system when using either test was remarkably binary, with a very limited range of values giving a 50% probability of detecting evidence of infection. Overall the HI assay was predicted to detect evidence of an outbreak for a larger range of R0 values and introduction times than the rt-PCR test.
Estimating R0and the day of virus introduction
Birds within the barn were sampled and tested for infection using an rt-PCR test on a weekly basis to estimate Ts and R0, whilst assuming all other parameters were known (parameters are described in Table 1). In the absence of reactive sampling (an increase in the number of birds sampled at the next time point following the detection of infection), it was difficult to accurately obtain an estimate for Ts and R0. Here a wide range of different values of Ts gave comparable likelihoods for a fixed value of R0 (Figure 3A). We increased the number of birds sampled after the initial detection of infection in the following manner: Nsample = 50, Nsample = 500, Nsample = 1000 and Nsample = 2000, (Figure 3 A, B, C, D, respectively). The increase in number of birds sampled improved the accuracy of the estimates of R0 and Ts (Figure 3). Of the regimes tested the best accuracy arose from sampling 2,000 birds (40%) after detection of infection (Figure 3D). Anything lower resulted in highly variable estimates of Ts and R0 across different stochastic observations, therefore this was the sampling regime used for all estimates presented. We assumed that in the relatively rare event of such an outbreak resources would be extended to accommodate this sampling regime.
Figure 3.
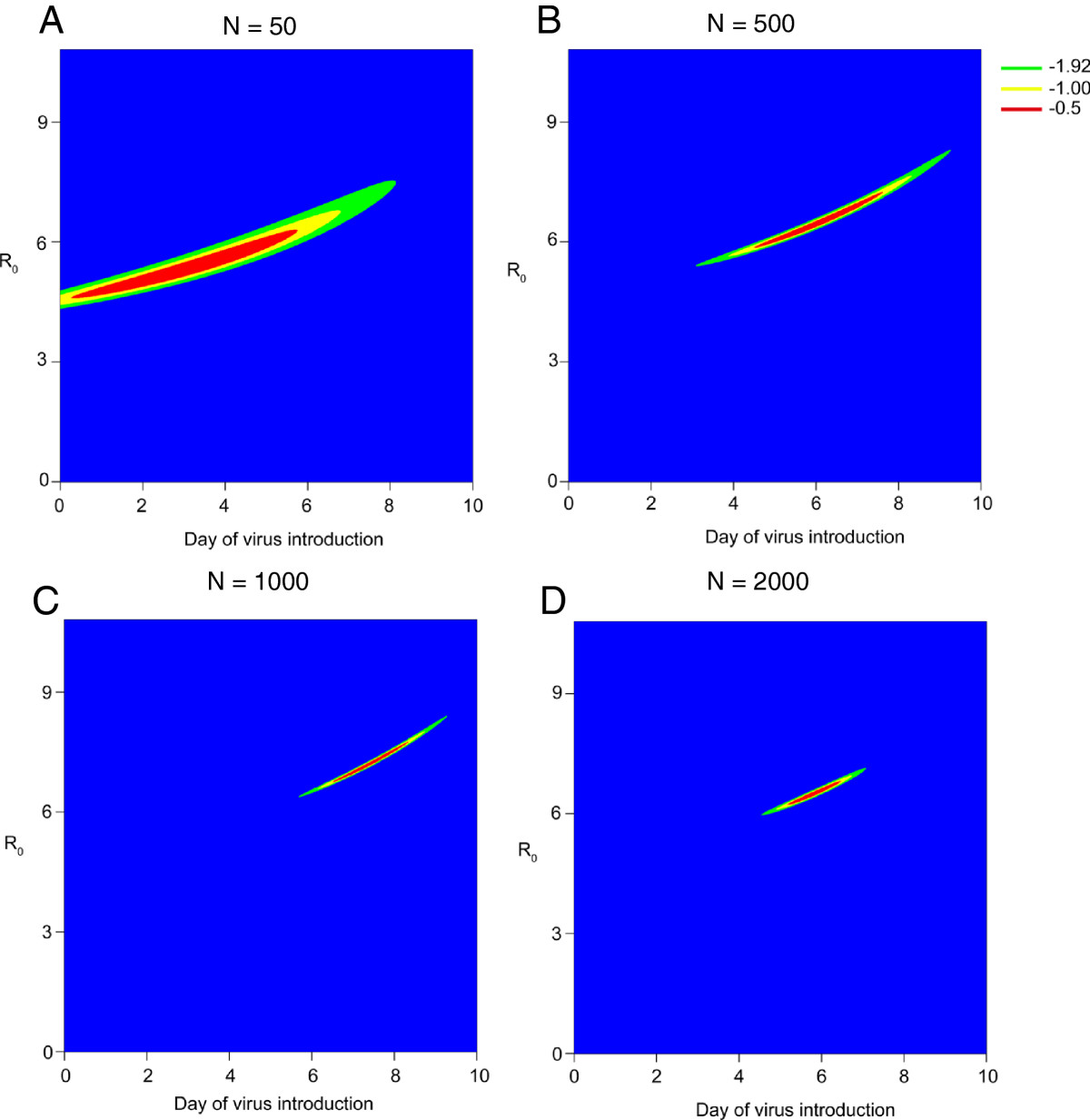
The likelihood of identifying day of virus introduction ( T s ) and basic reproduction number ( R 0 ) simultaneously with and without varying degrees of reactive sampling. A-D the contour of the log likelihood surface around the true values of R 0 and T s. Reactive sampling of N sample = 50, 500, 1000, and 2000 birds for A, B, C and D respectively. For illustration purposes an R 0 = 7 and T s = 7 were used. Different colours represent how close each estimate of the likelihood is to the maximum value. Blue indicates greater than 1.92 from the maximised true estimate, green indicates less than 1.92 likelihood point from the maximised true estimate (corresponding to the 95% confidence intervals), yellow indicates less than 1.0 likelihood point from the maximised true estimate and red indicates less than 0.5 points away from the maximised true estimate.
We present the mean R0 and Ts across 100 simulated observations for each scenario (Table 2). With weekly sampling, across the range of R0 values assessed here, we were able to simultaneously estimate both R0 and Ts (Table 2). In general all values of R0 were estimated accurately across the range assessed here. When considering Ts = 20, and R0 = 10, we estimated an R0 of 10.5 (9.6, 12.0), whilst, for an assumed R0 = 3, we estimated R0 2.9 (2.8, 3.1) (Table 2). It was not possible to accurately estimate R0 and the Ts if the known day of virus introduction was day 40. This is because infection is very unlikely to be detected until day 56, as such we have only 1 informative data point on the presence of infection within the barn for the 8 week time series, thus it is not possible to make inference for the 2 parameters with only 1 data point. As such, a large number of different scenarios gave comparable likelihoods.
Estimating the day of virus introduction under different sampling regimes and R0values
We subsequently estimated Ts on it’s own assuming known different values of R0 and variable sampling regimes. We considered a situation in the absence of reactive sampling, hence Nsample = 50 birds at each time point were sampled even after detection of infection.
We evaluated the quality of our estimate primarily in terms of accuracy, i.e. how close our estimate was to the true known value. In general Ts was accurately estimated across a range of R0 values and sampling regimes (Table 3). As expected, there was a reduction in the overall accuracy of the estimated Ts with each stepwise reduction in sampling frequency, with the most apparent reduction going from 2 weekly to 4 weekly sampling.
We present the mean estimated day of virus introduction across the 100 simulated observations for each scenario (Table 3). However, there was variation between the estimated day of virus introduction across the 100 data sets. We present the variation between the estimated day of virus introduction, for each scenario from each simulated dataset in Additional file 1. As would be expected, the most accurate estimates of Ts were obtained when a high frequency of sampling was used for a wide range of values of R0. At reduced sampling frequencies the precision of the estimate was greatly affected by the value of R0. For example, for R0 = 3, Ts = 40, and sampling conducted every 4 weeks, the estimate was less accurate compared to the true known value 33.5 (28.0, 40.8) (Table 3).
In some instances when intermediate sampling was conducted, only once during the 8 week cohort at week 4, different stochastic observations gave two different estimates of Ts with comparable maximised likelihoods, highlighting the presence of two different optima across the 100 stochastic observations. Results of both values are given in Table 3, where the other best estimated value, not close to the true value is referred to as the 2nd cluster in Table 3. In this sampling regime the estimation of Ts was strongly dependent on whether infection was detected on day 28 (2nd sampling point) or not, it was this observation process that resulted in different maximised likelihoods from different stochastic observations. The two different observed estimates arise because the model was unable to distinguish whether the epidemic was ending or taking off from 1 data point of number of infected’s at day 56. For example, if infection was introduced prior to day 28, but not observed when sampling was conducted on day 28 then Ts was overestimated, but if infection was observed on day 28 Ts was accurately estimated.
Discussion
Outbreaks of LPAI are a threat to animal and human health, but are primarily asymptomatic in poultry. Therefore, if the threat to human health is considered high enough from strains such as novel avian H7N9, efficient surveillance strategies to detect virus and implement control measures may be required. We have simulated surveillance data from commercial poultry farms within the context of H7N9 outbreak surveillance and tried to understand the type of surveillance regime that would be required to help infer parameters and events of epidemiological importance.
In this study we used a mathematical model of transmission and testing to develop an understanding of the within flock dynamics during an outbreak of H7N9 in a single commercial poultry barn. We evaluated a number of different surveillance strategies that could be adopted on farms, and investigated how different surveillance regimes could infer parameters of epidemiological interest in the early stages of an outbreak, such as the day of introduction.
One surveillance strategy for monitoring the presence of LPAI outbreaks is to test birds at time of slaughter, which we assumed to be the end of the rearing period. In general we predicted that the HI assay would detect evidence of an outbreak for a wider range of introduction times and R0 values than the rt-PCR test. However the HI assay can only indicate that birds have experienced infection and cannot distinguish if birds are infected at time of slaughter. For outbreaks that commence 3-4 weeks after birds enter the barn, a higher probability of detecting evidence of an outbreak is expected using the rt-PCR test compared to the HI assay, as detection of live virus is possible very quickly after infection occurs. Importantly, if virus entered the barn during the last week; neither test would detect evidence of infection due to the slow emergence of antibodies for the HI assay and a very low probability of detecting infection using an rt-PCR test as the epidemic would have only just begun in the barn. Our analysis assumes that after rearing, birds would be transported to a slaughterhouse. There may be scenarios where birds are transported to another facility prior to slaughter. If they are tested for infection at this second facility our results suggest that using an HI assay would be a more appropriate than an rt-PCR test, as the overall time period for which it would be possible to detect evidence of infection would be higher. Equally, although most large facilities will have more than a single barn, our results are still applicable in that they are designed to detect the virus in the first affected barn. Once a novel strain is detected in a single barn on a large facility, it is likely that either frequent testing or pre-emptive culling would be started rapidly in other barns as resources would not be constrained in the same way as facilities with no history of infection.
The threat and transmission potential of H7N9 in commercial chickens remains largely unknown, and the within flock R0 remains unquantified. A number of previous studies have used different methodologies to quantify R0 and the transmission rate β from different outbreak settings [33–35]. Within barn estimates have been highly variable across settings and viral subtypes (R0 = 2.26 to 5.50) [33–35], therefore it was important to consider a wide range of values. The R0 value is also likely to vary between countries and farms due to different farming practices. Therefore we examined our ability to estimate the Ts, whilst also estimating R0, which might be a priority during the initial stages of a national outbreak. It was not possible to accurately estimate the two parameters simultaneously when sampling only Nsample = 50 (Figure 3A) (1%) of birds at each time point as the likelihood surface was relatively flat. We found it was necessary to sample at least Nsample = 2000 (40%) birds after the detection of infection to accurately estimate R0 and Ts. We saw the most accurate parameter estimation was performed when Ts was either 7 or 20 days, with the model performing less accurately for day 0. It was not possible to estimate Ts if virus was introduced on day 40.
In situations where R0 is known it would be possible with regular testing to estimate Ts. We investigated this approach using the rt-PCR test, over different frequencies of testing where the R0 value was known. We found that if sampling Nsample = 50 birds at each sampling time point, testing for infection on a weekly basis provided the most precise and accurate estimate of Ts. We observed a slight reduction in the accuracy of our estimate as the value of R0 decreased. This is likely due to epidemics with a lower R0 exhibiting a slower take off which in turn lowers the probability that at a particular point in time infection will be observed as a lower number of overall birds will be infected.
Regular sampling regimes with 4 or more samples in the 8-week period did much better than 3 or fewer samples. We saw that with 4 weekly sampling (3 samples) the model was very sensitive to observations taken on day 28. If infection was not detected then a different global optimum was identified that did not correspond to the true known day of introduction. The presence of two global optima under different stochastic observations of the infection dynamics resulted in uncertainty in the estimated time of introduction. The comparison of entry times between 1 and 2 weekly sampling showed little difference in the point estimates between the two regimes, however 2 weekly sample provided a wider range on the 95% confidence intervals.
Through our sensitivity analysis we have shown that the model estimation is robust to changes in flock size, as well as to the misspecification of the duration of the latent period. However the model was sensitive to changes in the infectious period especially when the infectious period was greatly extended. It has been reported that most birds infected with AI shed virus for around 7 days [36–38], so the upper thresholds explored here may be considered unrealistic.
The differential susceptibility of avian hosts to different influenza strains has been widely described. Turkeys are more susceptible to H7N2 infection than chickens [39], while Muscovy ducks have a higher susceptibility to HPAI H5N1 infection than mallards [40]. Here we focus on chickens because human infections have primarily been associated with chickens from live animal markets [41, 42]. However, it is known that other avian species have been identified as infected within live birds markets in China. Despite possible differences in susceptibility or durations of infectiousness of other avian hosts compared to chickens the same model structure and methodology could still be applied.
Conclusions
We have shown that an unfeasibly large number of birds would need to be sampled to obtain an accurate estimate of R0 and Ts simultaneously. However, a once off significant investment to sample such a high number of birds would be of high utility and justifiable in the early stage of an outbreak, particularly if it was suspected or known that multiple premises were infected. Equally, the high number of birds that would need to be sampled to obtain a precise and accurate estimate of the 2 parameters is likely to reduce as R0 increases, however in a situation where R0 is unknown, caution should be taken. We have also shown that significantly fewer resources would be required to estimate Ts alone, where Nsample = 50 on a weekly or 2 weekly basis during an 8 week cohort, using an rt-PCR test would be enough to provide a good estimate of Ts.
The inference of R0 during the early stages of an outbreak is of high utility in the early stages of an outbreak as it enables control and infection containment strategies to be implemented effectively, and outbreak responses to be co-ordinated. For example, quantifying a value for R0 can help understand the number of birds that would need to be vaccinated, how quickly a virus can spread through a flock, and if culling would be necessary. Equally, estimating Ts with or without R0 can dramatically reduce the resources required to identify the source of infection and may help gain understanding as to whether additional premises have been infected, and can prevent onwards transmission. As such, we feel our method and its findings are of high utility to help guide surveillance to improve the estimation of epidemiological parameters from outbreak data.
Electronic supplementary material
Additional file 1: Variation in the estimated day of virus introduction for the single parameter model and sensitivity analysis for the estimation of T s .(PDF 577 KB)
Below are the links to the authors’ original submitted files for images.
Acknowledgements
We would like to thank Dr Mary Pantin Jackwood for insightful and helpful discussions relating to the transmission of H7N9 in experimentally infected chickens.
Funding
AP would like to acknowledge the Medical Research Council (UK) for PhD studentship funding. MTW would like to acknowledge the Medical Research Council for Research fellowship funding. SR would like to acknowledge: Wellcome Trust University Award 093488/Z/10/Z. R01 TW008246-01 from Fogarty International Centre. The Medical Research Council (UK, Project Grant MR/J008761/1). RAPIDD program from Fogarty International Centre with the Science & Technology Directorate, Department of Homeland Security. National Institute for Health Research (UK, for Health Protection Research Unit funding).
Abbreviations
- AI
Avian influenza
- LPAI
Low pathogenic avian influenza
- HPAI
High pathogenic avian influenza
- rt-PCR
Real-time polymerase chain reaction
- HI assay
Hemagglutinin inhibition assay
- Ts
Day of virus introduction
- R0
Basic reproduction number
- DPI
Days post inoculation.
Footnotes
Competing interests
The authors declare that no competing interest exist.
Authors’ contributions
AP, IMB, MTW and SR conceived and designed the study. AP performed the analysis and interpreted the results. AP wrote the first draft and IMB, MTW and SR contributed to the writing of the manuscript. All authors read and approved the final manuscript.
Contributor Information
Amy Pinsent, Email: amy.pinsent07@imperial.ac.uk.
Isobel M Blake, Email: isobel.blake@imperial.ac.uk.
Michael T White, Email: m.white08@imperial.ac.uk.
Steven Riley, Email: s.riley@imperial.ac.uk.
References
- 1.Lupiani B, Reddy S. The history of avian influenza. Comp Immunol Microbiol Infect Dis. 2009;32:311–323. doi: 10.1016/j.cimid.2008.01.004. [DOI] [PubMed] [Google Scholar]
- 2.Meuwissen MPM, Van Boven M, Hagenaars TJ, Boender GJ, Nodelijk G, De Jong MCM, Huirne RBM. Predicting future costs of high-pathogenicity avian influenza epidemics: large versus small uncertainties. {NJAS} - Wageningen J Life Sci. 2006;54:195–205. doi: 10.1016/S1573-5214(06)80022-9. [DOI] [Google Scholar]
- 3.Davison S, Galligan D, Eckert TE, Ziegler AE, Eckroade RJ. Economic analysis of an outbreak of avian influenza, 1997-1998. J Am Vet Med Asso. 1999;214:1164–1167. [PubMed] [Google Scholar]
- 4.Halvorson DA. Prevention and management of avian influenza outbreaks : experiences from the United States of America influenza (fowl plague) outbreak in the United States of America influenza in the United States of America. Rev Sci Tech. 2009;28:359–369. doi: 10.20506/rst.28.1.1866. [DOI] [PubMed] [Google Scholar]
- 5.Pepin KM, Spackman E, Brown JD, Pabilonia KL, Garber LP, Weaver JT, Kennedy DA, Patyk KA, Huyvaert KP, Miller RS, Franklin AB, Pedersen K, Bogich TL, Rohani P, Shriner SA, Webb CT, Riley S. Using quantitative disease dynamics as a tool for guiding response to avian influenza in poultry in the United States of America. Prev Vet Med. 2014;113:376–397. doi: 10.1016/j.prevetmed.2013.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Suarez DL, Senne DA, Banks J, Brown IH, Essen SC, Lee C, Manvell RJ, Mathieu-benson C, Moreno V, Pedersen JC, Panigrahy B, Rojas H, Spackman E, Alexander DJ. Recombination resulting in virulence shift in avian influenza. Emerg Infect Dis. 2004;10:693–699. doi: 10.3201/eid1004.030396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Berhane Y, Hisanaga T, Kehler H, Neufeld J, Manning L, Argue C, Handel K, Hooper-McGrevy K, Jonas M, Robinson J, Webster RG, Pasick J. Highly pathogenic avian influenza virus A (H7N3) in domestic poultry Saskatchewan Canada 2007. Emerg Infect Dis. 2009;15:1492–1495. doi: 10.3201/eid1509.080231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Senne DA, Suarez DL, Stallnecht DE, Pedersen JC, Panigrahy B. Ecology and epidemiology of avian influenza in north and south america. J Dev Bio. 2006;124:37–44. [PubMed] [Google Scholar]
- 9.Wang D, Hu W, Chen J, Jie Z, Zhu W, Gao Z, Xiang N, Shen Y, Yu H, Li D, Gao GF, Wu G, Wang Y, Yuan Z, Shu Y. Human infection with a novel avian-origin influenza A (H7N9) virus. N Engl J Med. 2013;368:1888–1897. doi: 10.1056/NEJMoa1304459. [DOI] [PubMed] [Google Scholar]
- 10.Centre for Health Protection: CHP Notified additional human case of avian influenza A (H7N9) in Mainland. [http://www.chp.gov.hk/en/content/599/35310.html],
- 11.Cowling BJ, Jin L, Lau EHY, Liao Q, Wu P, Jiang H, Tsang TK, Zheng J, Fang VJ, Chang Z. Comparative epidemiology of human infections with avian influenza A H7N9 and H5N1 viruses in China: a population-based study of laboratory-confirmed cases. The Lancet. 2013;382:129–137. doi: 10.1016/S0140-6736(13)61171-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.European Centre for Disease Prevention and Control . Epidemiological Update A(H7N9) Influenza. 2014. [Google Scholar]
- 13.Li . Summary of the second wave of human infections with Avian Inuenza A(H7N9) virus. 2014. [Google Scholar]
- 14.World Health Organisation . Overview of the emergence and characteristics of the Avian Influenza A(H7N9) virus. 2013. [Google Scholar]
- 15.Zhang L, Zhang Z, Weng Z. Rapid reassortment of internal genes in avian influenza A(H7N9) Virus. Clin Infect Dis. 2013;57:1059–1061. doi: 10.1093/cid/cit414. [DOI] [PubMed] [Google Scholar]
- 16.Wu A, Su C, Wang D, Peng Y, Liu M, Hua S, Li T, Gao G. F, Tang H, Chen J, Liu X, Shu Y, Peng D, Jiang T. Sequential reassortments underlie diverse influenza H7N9 genotypes in China. Cell Host Microbes. 2013;14:446–452. doi: 10.1016/j.chom.2013.09.001. [DOI] [PubMed] [Google Scholar]
- 17.Department for Environment . Poultry in the United Kingdom. 2010. [Google Scholar]
- 18.Fouchier RAM, Osterhaus ADME, Brown IH. Animal influenza virus surveillance. Vaccine. 2003;21:1754–1757. doi: 10.1016/S0264-410X(03)00067-7. [DOI] [PubMed] [Google Scholar]
- 19.United States Department of Agriculture: Foreign animal disease preparedness & response plan: highly pathogenic avian influenza response plan - the Red Book. [http://www.tahc.state.tx.us/emergency/{APHIS}_{AI}_ResponsePlan.pdf],
- 20.Corman V, Eickmann M, Landt O, Bleicker T, Brunink S, Eschbach-Bludau M, Matrosovich M, Becker S, Drosten C. Specific detection by real-time reverse-transcription PCR assays of a novel avian influenza A(H7N9) strain associated with human spillover infections in China. Eurosurveillance. 2013;18:1–10. [PubMed] [Google Scholar]
- 21.Hirst GK. The quantitative determination of influenza virus and antibodies by means of red cell agglutination. J Exp Med. 1942;75:49–64. doi: 10.1084/jem.75.1.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bos ME, Van Boven M, Nielen M. A B, Elbers AR, Nodelijk G, Koch G, Stegeman A, De Jong MC: Estimating the day of highly pathogenic avian influenza (H7N7) virus introduction into a poultry flock based on mortality data. Vet Research. 2007;38:493–504. doi: 10.1051/vetres:2007008. [DOI] [PubMed] [Google Scholar]
- 23.Wearing HJ, Rohani P, Keeling MJ. Appropriate models for the management of infectious diseases. PLoS Med. 2005;2:174. doi: 10.1371/journal.pmed.0020174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Petre M, Fusheng G, Desvaux S, Roger F. Avian influenza vaccines: a practical review in relation to their application in the field with a focus on the asian experience. Epidemiol Infect. 2009;137:1–21. doi: 10.1017/S0950268808001039. [DOI] [PubMed] [Google Scholar]
- 25.R Development Core Team . R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2008. [Google Scholar]
- 26.Wilks SS. The large-sample distribution of the likelihood ratio for testing composite hypotheses. Inst Math Sci. 1938;9:60–62. [Google Scholar]
- 27.Pantin-Jackwood MJ, Miller PJ, Spackman E, Swayne DE, Susta L, Costa-Hurtado M, Suarez DL. Role of poultry in spread of novel H7N9 influenza virus in China. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Slomka MJ, Pavlidis T, Coward VJ, Voermans J, Koch G, Hanna A, Banks J, Brown IH. Validated RealTime reverse transcriptase PCR methods for the diagnosis and pathotyping of Eurasian H7 avian influenza viruses. Influenza Other Respi Viruses. 2009;3:151–164. doi: 10.1111/j.1750-2659.2009.00083.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ma M-J, Yang X-X, Xia X, Anderson BD, Heil GL, Qian Y-H, Lu B, Cao W-C, Gray W-C. Comparison of commercial influenza A virus assays in detecting avian influenza H7N9 among poultry cloacal swabs, China. J Clin Virol. 2014;59:242–245. doi: 10.1016/j.jcv.2014.01.009. [DOI] [PubMed] [Google Scholar]
- 30.Curran JM, Robertson ID, Ellis TM, Selleck PW. Evaluation of avian influenza serologic and virologic diagnostic methods in wild anseriformes and charadriiformes. Avian Dis. 2014;1:53–55. doi: 10.1637/10531-031513-Reg.1. [DOI] [PubMed] [Google Scholar]
- 31.Qiu C, Huang Y, Zhang A, Di T, Wan Y, Xiaoling ZWZX, Zhang Z, Yuan Z, Hu X, Yand Zhang Xu. J: Safe pseudovirus-based assay for neutralization antibodies against Influenza A (H7N9) virus. Emerg Infect Dis. 2013;19:1685–1687. doi: 10.3201/eid1910.130728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dong L, Bo H, Bai T, Gao R, Dong J, Zhang Y, Guo J, Zou S, Zhou J, Zhu Y, Xin L, Li X, Xu C, Wang D, Shu Y. A combination of serological assays to detect human antibodies to the avian influenza A H7N9 virus. PLoS ONE. 2014;9:95612. doi: 10.1371/journal.pone.0095612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Comin A, Klinkenberg D, Marangon S, Toffan A, Stegeman A. Transmission dynamics of low pathogenicity avian influenza infections in turkey flocks. PLoS One. 2011;6:26935. doi: 10.1371/journal.pone.0026935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tiensin T, Nielen M, Vernooij H, Songserm T, Kalpravidh W, Chotiprasatintara S, Chaisingh A, Wongkasemjit S, Chanachai K, Thanapongtham W, Srisuvan T, Stegeman A. Transmission of the highly pathogenic avian influenza virus H5N1 within flocks during the 2004 epidemic in Thailand. J Infect Dis. 2007;196:1679–1684. doi: 10.1086/522007. [DOI] [PubMed] [Google Scholar]
- 35.Bos M, Nielen M, Koch G, Bouma A, De Jong M, Stegeman A. Back-calculation method shows that within-flock transmission of highly pathogenic avian influenza (H7N7) virus in the Netherlands is not influenced by housing risk factors. Preventative Vet Med. 2009;88:278–285. doi: 10.1016/j.prevetmed.2008.12.003. [DOI] [PubMed] [Google Scholar]
- 36.Hilt DA, Williams SM, Pantin-Jackwood MJ, Suarez DL, Spackman E, Stallknecht DE, Jackwood MW, Morales Jr. A C Biologic characterization of H4, H6 and H9 type low pathogenicity avian influenza viruses from wild birds in chickens and turkeys. Avian Dis. 2009;53:552–562. doi: 10.1637/8877-041509-Reg.1. [DOI] [PubMed] [Google Scholar]
- 37.Spackman E, Pantin-Jackwood MJ, Swayne DE, Suarez DL. An evaluation of avian influenza diagnostic methods with domestic duck specimens. Avian Dis. 2009;53:276–280. doi: 10.1637/8520-111708-Reg.1. [DOI] [PubMed] [Google Scholar]
- 38.Spackman E, Gelb JJ, Preskenis LA, Ladman BS, Pope CR, Pantin-Jackwood MJ, Mckinley ET. The pathogenesis of low pathogenicity H7 avian influenza viruses in chickens, ducks and turkeys. Virol J. 2010;7:1–10. doi: 10.1186/1743-422X-7-331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tumpey T, Kapczynski D, Swayne D. Comparative susceptibility of chickens and turkeys to avian influenza A H7N2 virus infection and protective efficacy of a commercial avian influenza H7N2 virus vaccine. Avian Dis. 2004;48:167–176. doi: 10.1637/7103. [DOI] [PubMed] [Google Scholar]
- 40.Phuong D, Dung N, Jorgensen P, Handberg K, Vinh N, Christensen J. Susceptibility of Muscovy (Cairina Moschata) and mallard ducks (Anas Platyrhynchos) to experimental infections by different genotypes of (H5N1) avian influenza viruses. Vet Microbiol. 2011;148:168–174. doi: 10.1016/j.vetmic.2010.09.007. [DOI] [PubMed] [Google Scholar]
- 41.Chen Y, Liang W, Yang S, Wu N, Gao H, Sheng J, Yao H, Wo J, Fang Q, Cui D, Li Y, Yao X, Zhang Y, Wu H, Zheng S, Diao H, Xia S, Zhang Y, Chan K-H, Tsoi H-W, Teng JL-L, Song W, Wang P, Lau S-Y, Zheng M, Chan JF-W, To KK-W, Chen H, Li L, Yuen K-Y. Human infections with the emerging avian influenza A H7N9 virus from wet market poultry: clinical analysis and characterisation of viral genome. The Lancet. 2013;381:1916–1925. doi: 10.1016/S0140-6736(13)60903-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bao C. -J, Cui L-B, Zhou M-H, Hong L, Gao GF, Wang H. Live-animal markets and influenza A (H7N9) virus infection. N Engl J Med. 2013;368:2337–2339. doi: 10.1056/NEJMc1306100. [DOI] [PubMed] [Google Scholar]
Pre-publication history
- The pre-publication history for this paper can be accessed here:http://www.biomedcentral.com/1471-2334/14/427/prepub
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1: Variation in the estimated day of virus introduction for the single parameter model and sensitivity analysis for the estimation of T s .(PDF 577 KB)


