A Preliminary Model of Gastrointestinal Electromechanical Coupling

Abstract

Motility in much of the gastrointestinal (GI) tract is coordinated by an electrical event known as slow waves, and several GI motility disorders are associated with slow wave arrhythmias. The GI smooth muscle cells (SMC) generate contraction, but slow waves are actively regenerated by specialized pacemaker cells called the interstitial cells of Cajal (ICC), which are coupled to the SMC. This unique electrical coupling presents an added layer of complexity to GI electromechanical models, and a major current barrier to further progress is the lack of a framework for ICC-SMC-contraction coupling. In this study, an initial framework for the electromechanical coupling was developed in a 2D model. At each solution step, the slow wave propagation was solved first and the intracellular calcium concentration in the SMC model was related to an adapted tension-extension-calcium relationship to simulate active contraction. With identification of more GI-specific constitutive laws, the ICC-SMC-contraction approach will underpin future GI electromechanical models of health and disease states.

I. Introduction

Motility of much of the gastrointestinal (GI) tract is coordinated by an underlying electrical event known as slow waves. GI slow waves are periodic and omnipresent, occurring at ~3 cycles per minute (cpm) in the human stomach and ~8 cpm in the small intestine [1]. Slow waves are actively regenerated by specialized pacemaker cells known as the interstitial cells of Cajal (ICC), and the subsequent depolarization of the surrounding gastric smooth muscle cells (SMC) via gap junctions is understood to coordinate GI motility, i.e., SMC contractions [2]. Dysfunction in either the ICC and/or SMC are increasingly being linked to a number of functional GI disorders, such as gastroparesis and dyspespia [3].

Existing GI mechanical models have typically modeled the movements of the GI luminal contents by imposing the mechanical deformation of the GI wall from imaging evidence [4]. The next critical step is to link slow wave activity to motility. Electromechanical models represent an active area of research in the cardiac field, offering a prime opportunity to translate the established multi-scale continuum modeling techniques to the GI field [5], [6] - in order to understand the complex interplay of distinct cellular mechanisms and systems across large spatiotemporal scales. However, as outlined above, the unique physiology of the GI tract also necessitates novel adaptations and approaches. This study presents a proof-of-concept framework and perspectives for: (i) cellular electromechanical coupling of ICC-SMC-contraction; (ii) simulation of entrainment of slow waves in a 1D model; (iii) a 2D model of GI electromechanical activity.

II. Cell Electrical and Electromechanical Coupling

A number of biophysically-based ICC and SMC slow wave models have recently been developed [6]–[8]. In further recent studies, the ICC and SMC models were electrically coupled via a gap junction conductance, through which the self-excitatory slow wave activity in the ICC model initiates the slow wave activity in the SMC model (Fig. 1a) [9], [10].

$$I_{couple}=G_{couple}{\eta }_{ICC}(V_{m\left(ICC\right)}-V_{m\left(SMC\right)})$$ (1)

where G_couple is the gap junction conductance between the membrane potentials of ICC (V_m(ICC)) and SMC (V_m(SMC)). The ratio of ICC-to-SMC (η_ICC) at each continuum point also modulates the SMC slow wave activity [10].

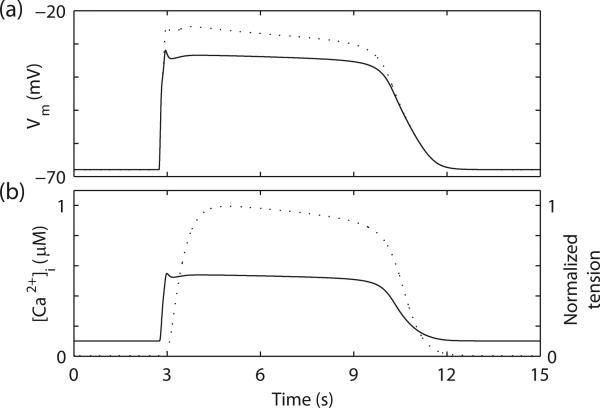
Fig. 1.

Simulated gastric slow waves and mechanical response. (a) Simulated slow waves in gastric smooth muscle cell (SMC) (solid line) and interstitial cell of Cajal (dashed line). (b) Simulated SMC [Ca²⁺]_i (solid line) and the resultant normlized active force (dashed line).

Although many details of the intracellular processes involved in GI motility are still under investigation, the consensus is that contraction of SMC is initiated by myosin light chain (MLC) phosphorylation via the activation of calcium (Ca²⁺)-calmodulin-dependent MLC kinase (MLCK) [2]. The complexity lies in the additional physiological factors that co-regulate the sensitivity of the contractile apparatus to Ca²⁺, such as the spike activity in intestines, noradrenaline, and prostaglandins etc. [2]. A bimodular active force cellular mechanical model has been developed recently [11]. The first module of the mechanical model describes the activation of MLCK by interaction with [Ca²⁺]_i with calmodulin; The second module of the mechanical model describes the cross-bridges ([AM_p]) formation induced by the phosphorylated myosin. The active force generated is proportional to the sum of [AM_p] and latch-bridges ([AM]), for a given total myosin concentration ([M_total]) (2).

$$F=F_{max}\frac{\left[A{M}_p\right]+\left[AM\right]}{\left[M_{total}\right]}$$ (2)

where F_max is the maximum achievable force. The active force was simulated by using the SMC [Ca²⁺]_i as an input to the mechanical model (Fig. 1b).

III. Continuum Models Of Entrainment

Slow wave entrainment at higher spatial scales has been simulated using the bidomain equations in several studies [6], [12]. A system of two equations (3 and 4) constitute the basic bidomain model.

$$\nabla \cdot ({\sigma }_i\nabla V_m)=-\nabla \cdot (({\sigma }_i+{\sigma }_e)\nabla {\varphi }_e)$$ (3)

$$A_m(C_m\frac{\partial V_m}{\partial t}+I_{ion})-\nabla \cdot ({\sigma }_i\nabla {\varphi }_e)=\nabla \cdot ({\sigma }_i\nabla V_m)$$ (4)

where V_m and φ_e are membrane and extracellular potentials, respectively. The ionic current (I_ion) term from the ICC and/or SMC model relates the slow wave activity of the cell model to the bidomain equations. The tissue conductivity tensors (σ), with subscript i denotes the intracellular domain and subscript e denotes the extracellular domain.

ICC exhibit self-excitatory slow waves in a gradient of intrinsic frequencies along the GI tract, and the coupling of ICC slow waves, i.e., entrainment, underlies the major mechanism of slow wave propagation in the intact GI tissues [1]. Two entrainment models have been proposed. First, an IP₃-dependent Ca²⁺-release model (5 and 6) was incorporated into the ICC model [9].

$$\frac{d\left[I{P}_3\right]}{dt}=\beta -\eta \left[I{P}_3\right]-V_{m4}\frac{{\left[I{P}_3\right]}^u}{k_4^u+{\left[I{P}_3\right]}^u}+I{P}_3\left(V_m\right)$$ (5)

where,

$$I{P}_3\left(V_m\right)=P_{MV}(1-\frac{V_m^r}{K_v^r+V_m^r})$$ (6)

where β is a chemical stimulus agent (such as Acetylcholine) that can modulate the sensitivity of IP₃ to the changes in V_m. The temporary surge of IP₃ due to an increase in V_m allows the ICC model to respond to a current source by producing a phase shift relative to its intrinsic slow wave activity. The rate constant of linear IP₃ degradation (η), Hill coefficient (u), maximum rate of nonlinear IP₃ degradation (V_m4), half saturation constant for nonlinear IP₃ degradation (k₄), maximum rate of V_m-dependent IP₃ degradation (P_MV ), half saturation constant for V_m-dependent IP₃ degradation (k_v), hill coefficient (r) were set to 2.7 × 10^–5 mM s^–1, 0.015 s^– 1, 4, 3.3 × 10^–5 mM s^–1, 0.0005 mM, 0.33 × 10^–5 mM s^–1, −58 mV , and 8, respectively [9].

An alternative model of entrainment is a modified V_m-dependent dihydropyridine-resistant conductance (I_{V DDR}) model in ICC [10]. The modified conductance represents a fraction of the whole cell I_{V DDR}, originally denoted as I_{V DDRPU} [10], and here denoted as I_PU for short (7).

$$I_{PU}=G_{PU}{d}_r{d}_{PU}{f}_{PU}(V_m-E_{CaPU})$$ (7)

where G_PU , d_PU , and f_PU are the maximum channel conductance, activation gate, and inactivation gate, respectively [10]. The fraction of the I_PU in I_{V DDR} conductance is denoted by d_r. E_CaPU is the Nernst potential of Ca²⁺ in the pacemaker unit in the ICC model. A Ca²⁺-extrusion mechanism was also added to the ICC cytoplasm to maintain long-term Ca²⁺ homeostasis in the ICC model (8).

$$I_{CaEXT}=\frac{C{a}_{max}}{1+e^{\frac{\left[C{a}^{2+}\right]-C{a}_{50}}{k}}}$$ (8)

where Ca_max was set to be 0.0315 μM ms^–1; Ca₅₀ and k were set to be 100 nM and 15, respectively.

Both mechanisms of entrainment were combined separately with the ICC model [9], [10], and slow waves were simulated in a 1D linear model (8 mm in length). A total of 101 grid-points, i.e., solution points, were distributed at equal spacing along the geometric element of the 1D model. Zero-flux boundary conditions were imposed on the two ends. To simulate propagation of slow waves, a linear gradient of ICC intrinsic frequencies (3-2.68 cpm) was applied to the 1D model. The slow wave activity at each grid point was self-excitatory at the prescribed frequency and occurs independently of each other in a decoupled setting, i.e., no entrainment. No stimulus current term was used to invoke an electrical propagation [6].

IV. 2D Model Of Electromechanical Activity

Propagation of slow waves was simulated using the bido-main equations on an 8×8 mm 2D model, which was defined by 8×8 linear elements, at the same spatial resolution as the 1D model. The physical dimension of each element was 1×1 mm. A linear gradient of ICC slow wave intrinsic frequencies (3-2.68 cpm) was distributed horizontally across the 2D model. Here, as a proof-of-concept step, a steady-state force-extension-Ca²⁺ relationship was used to relate the slow wave propagation to contraction, as previously described in a cardiac study [5].

$$T=C{a}_{max}{T}_0(1+\beta (\lambda -1))\frac{{\left[C{a}^{2+}\right]}_i^h}{{\left[C{a}^{2+}\right]}_i^h+C{a}_{50}^h}$$ (9)

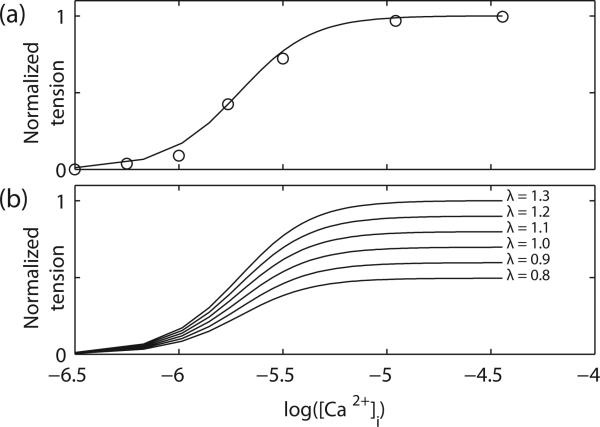
where Ca_max was set to be 0.6 μM and T₀ is the maximum isometric force. The values of the non-dimensional slope parameter (β), Ca₅₀, and Hill coefficient (h) were set to be 1.45, 1.95, and 2.5, respectively; these values were estimated by minimizing the root-mean-square error between a set of isometric force-[Ca²⁺]_i recording from guinea-pig taenia coli [14], and the simulated isometric force using (9 (Fig. 2a). The isometric forces were then simulated over a range of extension-ratios (λ) (Fig. 2b).

Fig. 2.

Steady-state force-extension-Ca²⁺ relationship. (a) Simulated normalized isometric force-[Ca²⁺]_i relationship. circle: experimental data [14]. The [Ca²⁺]_i was presented in a logarithmic scale. (b) Simulated isometric force-[Ca²⁺]_i relationship at different extension-ratios (λ).

The pole-zero law was used as the constitutive law to describe the passive mechanical behavior of the tissue [5]. Parameters for the limiting strains in the fiber and sheet directions were specified as the strains corresponding to maximum stress obtained during uniaxial tensile testing on human small intestine [16]. The 2^nd Piola-Kirchhoff stress tensor was used to relate the force in the reference configuration to areas in the reference configuration. Zero displacements were imposed on the boundaries of the 2D model.

The LSODA and Euler solvers were used to solve for the intracellular and extracellular domains of slow wave activity, respectively, as previously described [9]. The cell models were encoded using the CellML standard [13]. The mechanical deformation was solved using the Newton-Raphson method. At each solution step, the electrical propagation was solved first and then the mechanical deformation was solved to update the mechanical parameters in the geometric elements.

The local deformation was quantified by calculating the area of each column of elements in the 2D model at each solution step. The average stress generated by the 2D model was also calculated at each solution step.

V. Results and Discussion

A. Entrainment Models

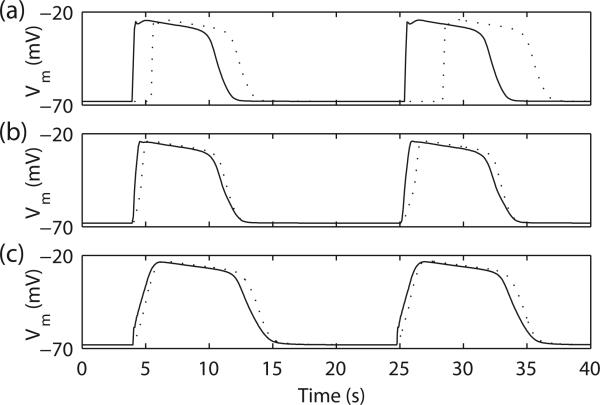
Decoupled slow waves activity is shown in Fig. 3a where entrainment does not occur. Simulations of the entrainment of slow waves demonstrated coupling of ICC with different intrinsic frequencies to a single frequency of 3 cpm. The IP₃-dependent Ca²⁺-release model (Fig. 3b) produced a steeper rate-of-upstroke than the I_PU model (Fig. 3c) (73 vs 23 mV s^–1). In both cases, the entrainment models produced a constant velocity (~12 mm s^–1), in accordance with physiological data [1]. Rather than a V_m-threshold based propagation mechanism, the entrainment models actively propagate slow waves through coupled ICC slow wave activity in the 1D model. While the decoupled slow waves may contribute to ectopic sources of entrainment in disease states.

Fig. 3.

Simulated 1D slow wave entrainment. (a) In the decoupled model (by setting σ_e and σ_i to 0.001 mS mm^–1), the simulated slow waves on the two boundary nodes demonstrated different intrinsic frequencies, 3.00 cpm (solid line) and 2.68 cpm (dashed line). In the entrained model, (b) IP₃-dependent Ca²⁺-release model and (c) I_PU model, the slow wave with the lower intrinsic frequency (dashed line) was entrained to the slow wave with the higher intrinsic frequency (solid line).

B. Electromechanical Model

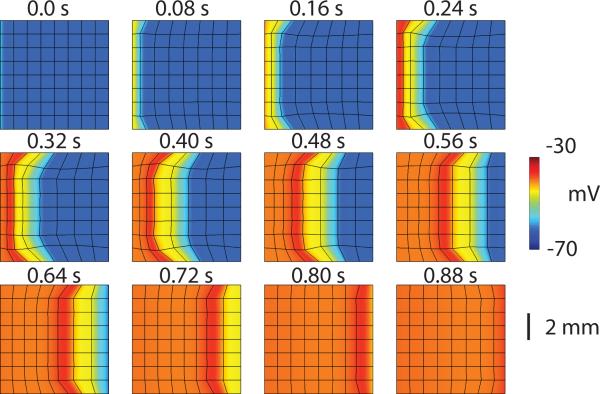
Electromechanical coupling was successfully achieved in a 2D multi-scale model, as shown in Fig. 4. The electromechanical activity resulted in a dynamic regional deformation of the 2D model that followed the slow wave propagation. The geometric elements in column 1 of the 2D model deformed first, followed sequentially by columns 2 to 8.

Fig. 4.

Simulated electromechanical activity. The black lines highlight the boundary of each geometric element (1×1 mm). The deformation of each element followed the direction of the simulated slow wave propagation.

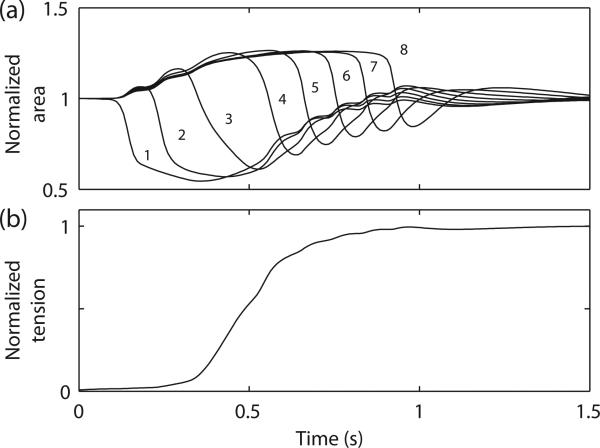
The deformations of the geometric elements in column 1 led to extension in the areas of the remaining elements in the 2D model. The peak deformation occurred in column 1 at 0.54 s (Fig. 5a). The stress developed monotonically in a sigmoidal profile (Fig. 5b). The development of stress in both the cell model (Fig. 1b) and the 2D model was delayed relative to the onset of slow wave activity.

Fig. 5.

Quantification of the mechanical activity. (a) Changes in the normalized area of the geometric elements columns 1-8. (b) Average normalized stress developed in the 2D model.

C. Limitations

There are a number of important limitations in the 2D model which warrant further discussion. The first limitation is the absence of an electromechanical feedback mechanism at the cellular level. For example, a voltage-sensitive sodium channel expressed in the human gut (Nav1.5) has recently been shown to have pronounced mechanosensitivity, providing valuable experimental data to inform future electromechanical models [15]. The incorporation of the cell mechanical model [11], and an electromechanical feedback mechanism will be an important next step.

The second limitation is the application of the pole-zero constitutive law in this study. A key feature described by the constitutive law is the difference in limiting strains in each of the main microstructural axes in the tissue; this has also been observed in human intestinal tissue [16], and incorporated into the 2D model. The remaining material parameters were left with cardiac-specific values. Future GI-specific strain field data from appropriate biaxial tests can be used to properly adapt the constitutive law to describe the passive mechanical properties of GI tissue. Additional parameter values in the constitutive law can be identified through optimization procedures. Similarly, the steady-state force-extension-Ca²⁺ relationship used to model the active force generation in this study could be replaced with the bimodular model [11].

The third limitation is the incomplete knowledge of the intracellular processes that contribute to GI motility. For example, it has been postulated that a V_m-threshold may exist for more vigorous mechanical contractions in the GI tract [1]. Much details of these processes are still under investigations. Future GI electromechanical models will need to incorporate these mechanisms as further details become available.

VI. Conclusions

This study presents a proof-of-concept gastrointestinal (GI) electromechanical model, demonstrating significant potential for relating GI slow waves to motility via a multi-scale framework. With more studies of GI tissue mechanical properties and incorporation of an electromechanical feedback mechanism, the model may be applied to show how mechanical deformation affects the propagation of slow waves; formation of slow wave arrhythmias may in turn exert changes to GI motility. This work provides a foundation for future studies incorporating electromechanical approaches to provide a quantitative understanding of GI motility in health and disease.